0 引言
现代战场中,雷达所代表的有源探测装备是获得目标战场信息的重要途径,也是有效指挥和掌控各类武器攻击系统的基本保证[1]。雷达有源干扰通过产生干扰信号进入雷达接收机,干扰雷达探测和获取目标信息的性能,扰乱其正常工作,从而破坏了作战体系中最为核心的信息来源[2]。近年来,随着雷达干扰技术的快速发展,特别是基于数字射频存储(Digital Radio Frequency Memory,DRFM)的干扰技术的广泛应用,干扰机能在极短的时间内截获雷达信号并进行采样和存储,准确复制雷达信号脉内特征,并在一定的规律下调制并转发存储的雷达信号,从而产生在距离、速度、角度等维度上具有欺骗特性的转发式干扰,达到干扰雷达的目的[3]。由于DRFM技术产生的干扰信号具有很强的相干特性,使得雷达抗干扰方难以有效地识别与抑制,因此基于DRFM的干扰产生技术受到了越来越广泛的应用。
对抗DRFM欺骗干扰的前提是识别出干扰信号,然后再针对干扰信号采用相应的对抗措施。针对DRFM干扰机器件特性,文献[4-5]在数学上分析了DRFM干扰机相位量化所带来的谐波效应和离散延时特性对距离拖引干扰信号频谱的影响,为后续研究奠定了理论基础。文献[6]针对DRFM干扰机相位量化特性,提出一种基于自适应相干估计与广义极大似然比检测的DRFM欺骗干扰信号的识别方法。但该方法只考虑了距离/速度波门内只有目标或干扰的单一情形,而实际情况干扰往往伴随着目标进入雷达接收机。文献[7]利用经验模态分解算法分离出DRFM干扰信号因相位量化产生的谐波分量,针对干扰谐波分量与目标回波在时频域上能量分布差异,利用信息熵进行干扰识别。但在相位量化位数较大的情况下,该方法性能急剧下降甚至失效。文献[8]通过研究DRFM干扰机针对线性调频雷达信号相位量化后的频谱特性,提出基于调频率参数匹配的干扰识别方法,但在高相位量化位数时同样存在方法失效的问题。
上述文献中的干扰识别的算法主要是针对DRFM干扰机中模数/数模转换器(A/D)相位量化所带来的谐波寄生的特性,但现有的DRFM干扰机中的A/D基本不再使用相位量化技术而是采用全幅度量化,且量化位数较大,由A/D量化所带来的谐波功率可以忽略不计。故以往针对A/D相位量化的谐波效应的干扰识别算法已不再适用。文献[9]指出,DRFM干扰机所采用的数控移相器的步进阶跃调相会导致干扰信号产生谐波分量。在此分析基础上,本文提出了一种基于奇异谱分析(Singular Spectrum Analysis,SSA)的数字射频存储速度欺骗干扰识别方法。该方法首先利用SSA算法获取雷达接收信号的奇异值,然后利用目标回波与DRFM速度欺骗干扰信号的奇异值分布差异,提取出奇异值的统计直方图的方差、峰度、偏度、能量和熵作为特征构建特征向量,最后利用支持向量机(Support Vector Machine,SVM)作为分类器实现雷达目标与DRFM速度欺骗干扰信号的识别。
1 数控移相器谐波效应
数控移相器因其体积小、重量轻、灵活性高以及可靠性高等优点,在雷达和电子战系统中得到了广泛的应用。基于DRFM的干扰机主要采用数控移相器对截获存储的雷达信号进行相位调制从而产生虚假多普勒频率,达到干扰目的。数控移相器的基本结构包含D/A转换器、电压缓冲单元以及射频矢量调制器。如图1所示,数字控制输入经D/A转换器转换为模拟电压,后经电压缓冲单元输出两路正交分量,最后通过射频矢量调制器与输入的射频信号进行正交调制,从而实现对射频信号的移相处理。
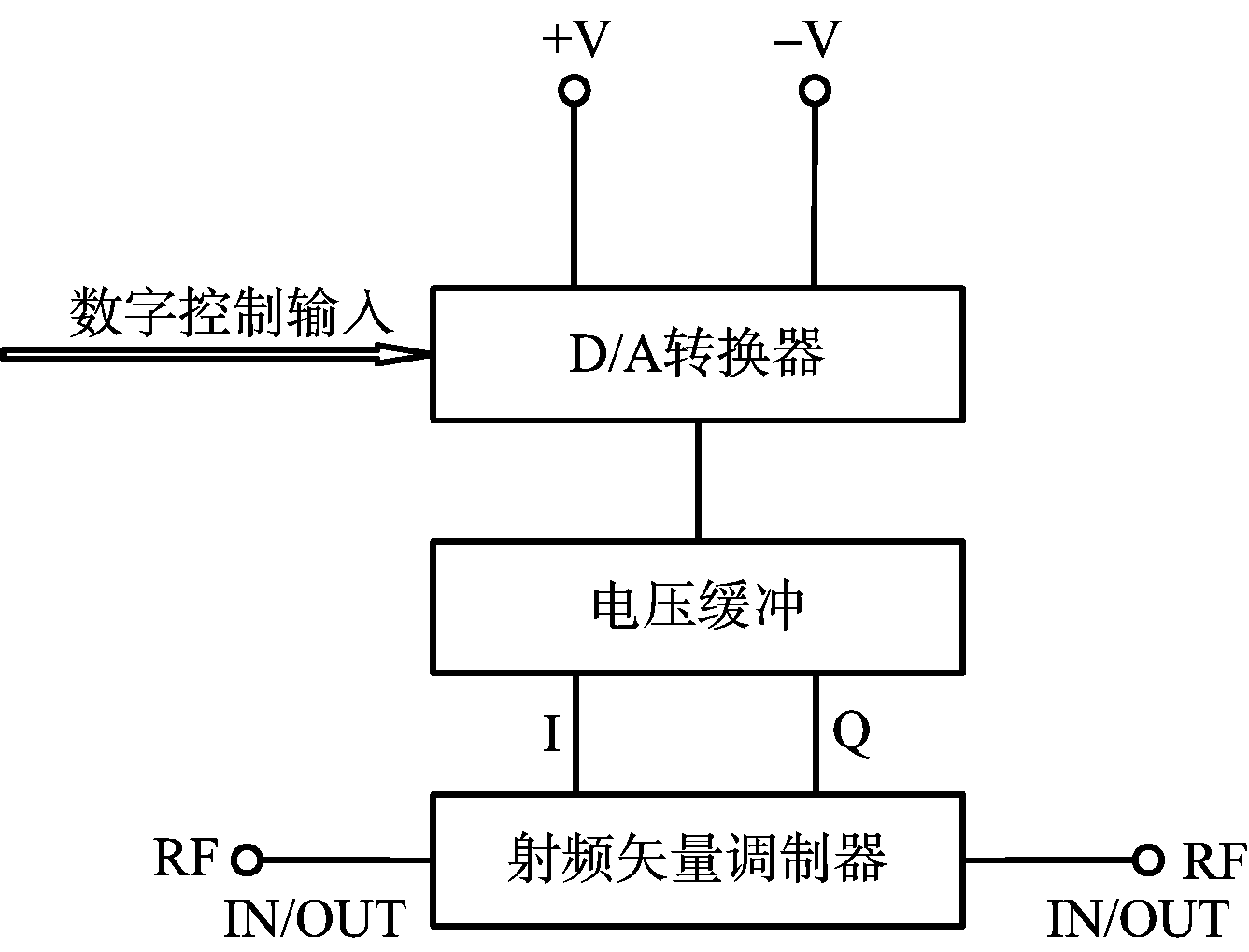
图1 数控移相器组成框图
N位数控移相器可以视为N个移相单元串连而成,每个移相单元有移相和不移相两种状态。当数字控制输入为“全0”时,数控移相器相移量为0;当数字控制输入为“全1”时,实现满度(360°)移相。N位数控移相器的移相精度为360°/2N。
令射频信号uin(t)经过数字控制信号u(t)调制后,输出的移相信号为uout(t)。为了便于分析,设uin(t)=Acos(ω0t),则
uout(t)=KAcos(ω0t+kpu(t))
(1)
式中,kp为调相系数,ω0t+kpu(t)为输出移相信号的瞬时相位。由此可知,输出移相信号的角频率为ωout(t)=ω0+kpu′(t)。
若数字控制信号u(t)为周期性锯齿波,即 u(t)=u(t+nTR)=kt,t∈[0,TR],则
ωout(t)=ω0+kpk
(2)
由式(2)可以看出,输出信号的移频量为常数,其值为fdj=kpk/2π。
对于N位数控移相器,其调相系数相当于相位步进位移量,即kp=2π/2N,而此时输入的锯齿波控制信号的斜率k=±2N/TR,因此可得
![]()
(3)
式(3)表明,若数控移相器的数字控制信号为周期性锯齿波信号,则可实现对输入射频信号的可控移频。移频量的大小由锯齿波信号的周期决定,移频量的正负则由锯齿波信号的斜率的正负决定。因此,可通过调整输入控制信号的周期及其变化规律,来实现对输出信号移频量大小与正负的可控。

图2 数控移相器锯齿波控制信号
图2为数控移相器产生固定移频量时控制信号实际的变化规律。从图中可以看出由于数控移相器的响应时间,实际控制信号会使线性变换的锯齿波相移控制量台阶化,与理想的周期锯齿波控制信号相比,数控移相器的输出会出现虚假谐波分量。
以脉冲多普勒(PD)雷达发射单载频信号为例,仿真测试了干扰信号在PD雷达测速模式下的谐波效应。图3为目标回波和速度欺骗干扰的混合信号在雷达的一个相干处理时间(Coherent Processing Interval, CPI)内的结果图,图4、图5分别为干扰机数控移相器位数N=4,N=5时800 m距离单元(模糊距离)处的多普勒频谱。当N=4时,谐波谱线的最高功率相对于干扰主分量为-22.65 dB,当N=5时,谐波谱线的最高功率相对于干扰主分量为-29.18 dB。从图中可以看出,DRFM干扰机产生的速度欺骗干扰会在多普勒域中产生较明显的谐波效应,移相器位数越大,产生谐波的单个谱线的功率越小。DRFM干扰机因数控移相器步进阶跃调相所产生的谐波效应为干扰识别提供了依据。

图3 雷达干扰混合信号的MTD效果图
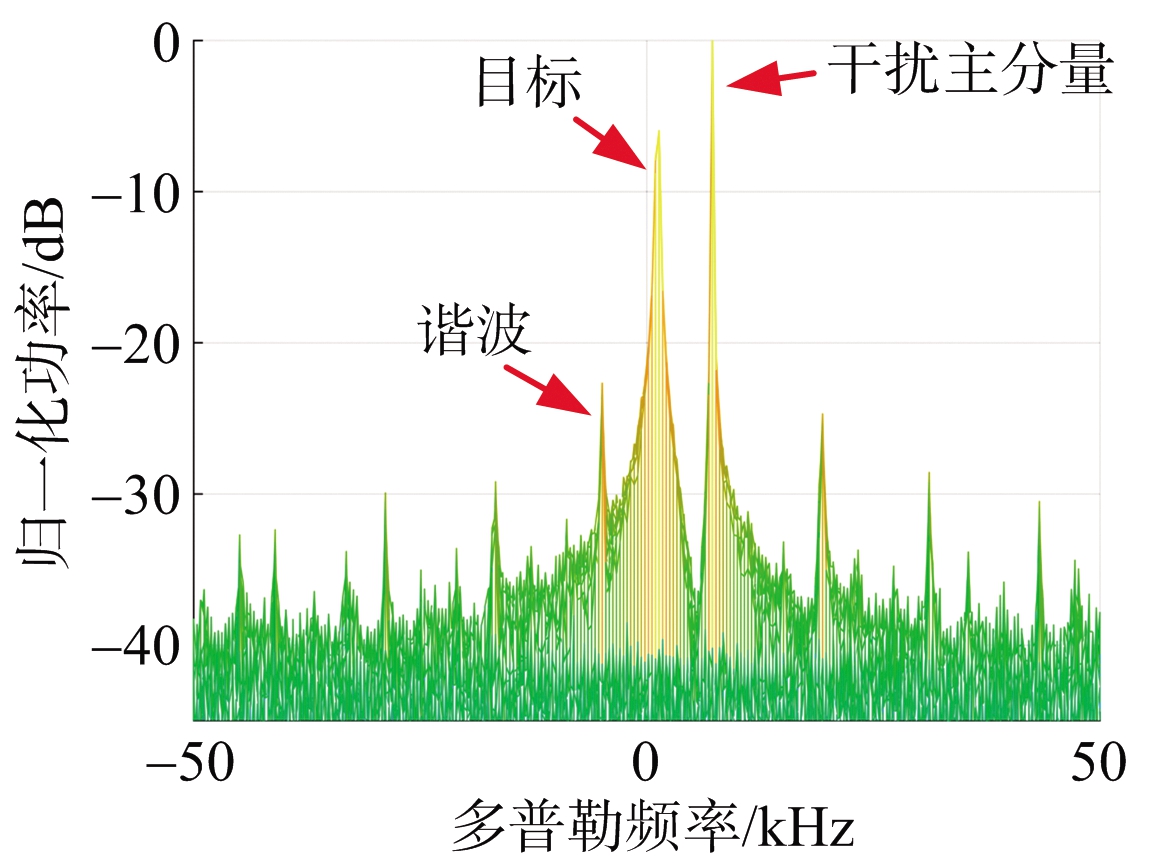
图4 N为4时的多普勒域频谱
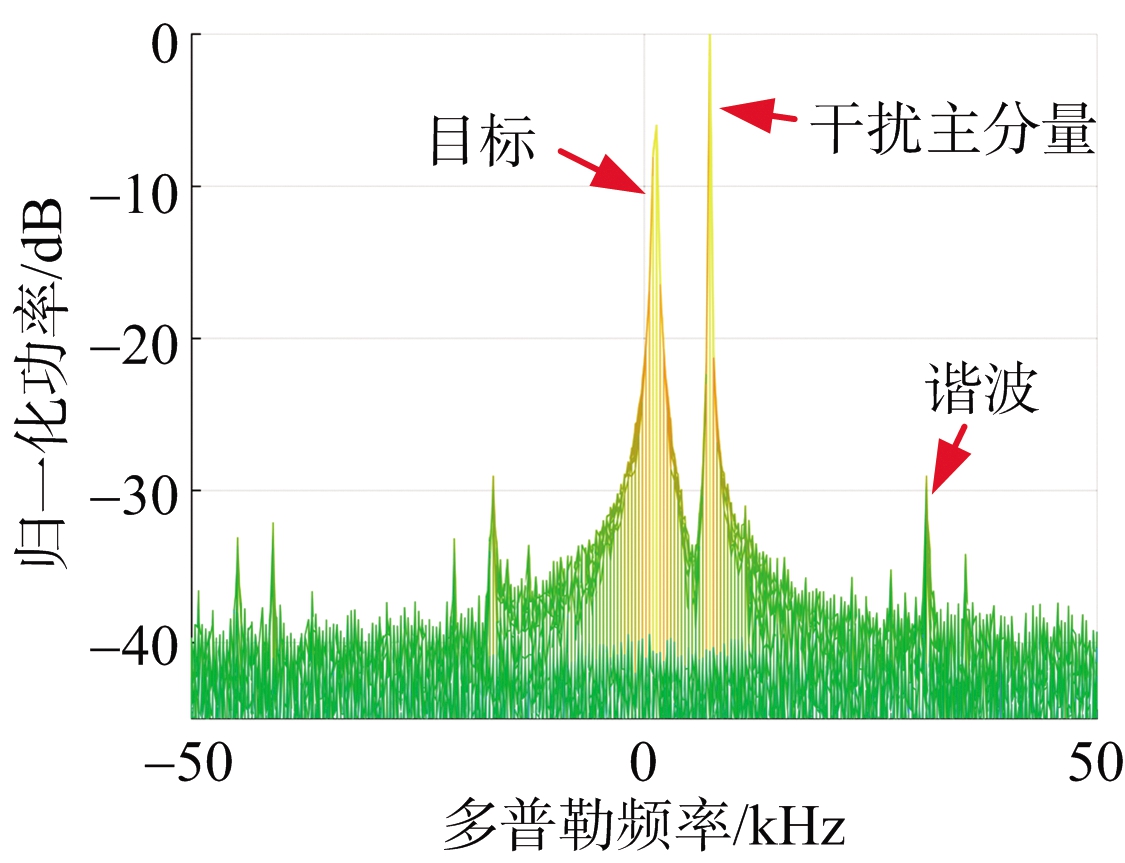
图5 N为5时的多普勒域频谱
2 基于奇异谱分析的速度欺骗干扰识别算法
根据第1节的分析, DRFM干扰机产生的速度欺骗干扰信号因数控移相器的步进阶跃调相会导致其在多普勒域上产生虚假谐波分量。因此,本文提出基于SSA的干扰识别算法,先利用SSA算法分解出接收信号的奇异值,然后利用目标回波和速度欺骗干扰信号的奇异值分布差异提取出5种特征并构建特征向量,最后利用 SVM 实现对雷达目标与 DRFM 速度欺骗干扰信号进行识别。
2.1 SSA分解原理
近年来,奇异谱分析(SSA)广泛应用于时间序列分析中[10-11],主要分为分解和重构两部分。由于本文算法主要目的是识别干扰,重在提取信号SSA分解后的奇异值分布差异,不需要重构信号,故本文的识别算法只利用了SSA算法的分解部分。下面详细介绍SSA算法部分的原理:
针对雷达接收到的信号z=[z1,z2,…,zN],SSA分解算法分为以下两个步骤实现。
步骤1: 定义窗长为L∈[1,N/2],对接收到信号做空间重构,构造出接收信号z的迹矩阵(trajectory matrix)Z:
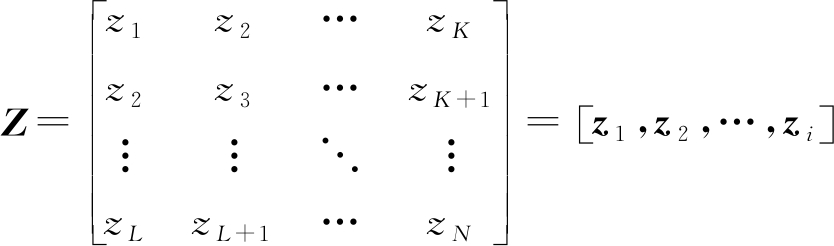
(4)
式中,zi=[zi,zi+1,…,zi+L-1]T∈RL,i=1,2,…,K,K=N-L+1。由式(4)可以看出矩阵Z为Hankel矩阵,即当矩阵元素zi,j的下标i,j之和为常数时矩阵元素的值都相等。
步骤2: 令协方差矩阵Y=ZZT,对Y进行SVD分解,记分解后的特征值和特征向量分别为(λ1≥λ2≥…≥λL)和(U1,U2,…,UL),则迹矩阵Z经SSA分解后可表示为
Z=P1+P2+…+PL
(5)
式中,![]() 为迹矩阵Z的第i个奇异值,Ui,Vi分别为其对应奇异值的左、右奇异向量。
为迹矩阵Z的第i个奇异值,Ui,Vi分别为其对应奇异值的左、右奇异向量。
可以看出SSA算法分解部分的原理主要是先构造出一维信号的迹矩阵,然后对其协方差矩阵作SVD分解,经过SSA分解之后能得到接收信号的各个奇异值。奇异值能表征信号的固有特征,具有良好的稳定性。当目标视为点目标时,其雷达回波为单分量信号,经SSA分解后只包含一个较大的奇异值。而对于DRFM速度欺骗干扰信号而言,由于数控移相器步进阶跃调相产生的谐波效应使得干扰信号包含多个分量,经 SSA分解后除了有一个对应于干扰主分量的较大奇异值,还有部分对应干扰信号谐波分量的非零奇异值。当同时存在目标回波与干扰信号时,经SSA分解后,除了有两个对应干扰信号主分量和目标回波的较大奇异值外,还会有部分对应干扰信号谐波分量的非零奇异值。因而,通过SSA分解可以彰显雷达目标和干扰信号的差异,利用这一差异提取合适的特征可以很好地识别出干扰信号。
2.2 特征提取
当雷达接收机检测到目标后,由于欺骗干扰的存在,无法确定接收到的信号中是否存在干扰机产生的虚假目标,干扰信号往往伴随着真实目标一起进入雷达接收机。因此可以利用双重假设模型来描述该干扰识别问题[12]:
![]()
(6)
式中:H1为只存在目标雷达回波的环境;H2为真实目标与速度欺骗干扰混合的环境;z=[z1,z2,…,zN]为复观测信号;s,j,n分别为目标回波信号向量、速度欺骗干扰信号向量和噪声序列;α,β为信号幅度。
令雷达接收信号经SSA分解后的奇异值为λ=[λ1,λ2,…,λL],且λ1≥λ2≥…≥λL。对于H1环境,在一定信噪比下,由于目标回波功率远大于噪声分量,故信号经SSA分解后目标回波对应的奇异值为λ1,而噪声分量对应的奇异值为{λ2,…,λL}。对于H2环境,由于干扰信号主分量的功率要远大于谐波分量的功率,故经SSA分解后谐波分量对应的奇异值远远小于目标回波和干扰信号主分量对应的奇异值,因此目标回波和干扰信号主分量对应的奇异值为λ1,λ2,而干扰谐波分量对应的奇异值将落入集合φ={λi|i=3,4,…,q},q<L中。对于H1环境,落入集合φ中的奇异值对应于噪声分量,由于随着干扰信号谐波的阶次增加,谐波功率逐渐减小,谐波分量所对应的奇异值也会逐渐减小,而噪声分量分布均匀,对应的奇异值大小也均匀分布。因此,在一定信噪比下H1与H2两种环境中落入集合φ中的奇异值呈现不同的分布规律。利用这一差异,本文提取两种环境下信号经SSA分解后落入集合φ中的奇异值的统计直方图的方差、峰度、偏度、能量和熵作为干扰识别的特征。
信号经SSA分解后落入集合φ中的奇异值的归一化统计直方图为
(7)
式中,K表示直方图区间数,N(l)表示奇异值大小在区间l的个数,M表示奇异值总个数。
令统计直方图的均值为V1=∑lp(l),则提取的5种特征如下:
1) 直方图方差
V2=∑(l-V1)2p(l)
(8)
2) 直方图峰度
![]()
(9)
3) 直方图偏度
![]()
(10)
4) 直方图能量
V5=∑p(l)2
(11)
5) 直方图熵
V6=-∑p(l)lnp(l)
(12)
利用上面得到的5种特征,构建特征向量V=[V1,V2,…,V5]来描述两种环境下的部分奇异值分布差异,进而利用这些特征进行干扰识别。
2.3 分类器设计
考虑到识别对象的特殊性,实际情况中获得真实雷达干扰信号的样本数量有限,且对识别算法的实时性有很高的要求,故本文采用支持向量机(SVM)作为DRFM速度欺骗干扰信号识别算法中的分类器。SVM 是一种基于统计学习理论的机器学习算法,在针对小样本、非线性及高维模式识别中具有很大的优势[13-14]。SVM 通过非线性变换将输入样本空间映射到高维空间,构造出最优分类超平面,将原始线性不可分的问题转化为在高维空间中线性可分的问题。利用SVM进行分类时,无需人为选取判别门限,体现了算法的智能性,同时提高了算法的性能。本文采用台湾大学林智仁教授的SVM工具箱LIBSVM完成分类算法的仿真实验,将仿真样本的66.7%作为训练集训练出合适的支持向量,剩下的作为测试集,测试算法的识别性能。
2.4 干扰识别算法流程
基于奇异谱分析的DRFM速度欺骗干扰识别流程如图6所示,算法分为训练和测试两部分。训练部分先利用已有的雷达真实目标回波和DRFM速度欺骗干扰信号的样本,通过SSA分解得到奇异值,然后提取出奇异值分布差异特征送入SVM中训练,得到支持向量构建SVM分类器。测试部分是在雷达检测到目标的前提下,通过SSA分解后提取奇异值特征,将得到的特征送入SVM分类器中得到干扰识别的结果。
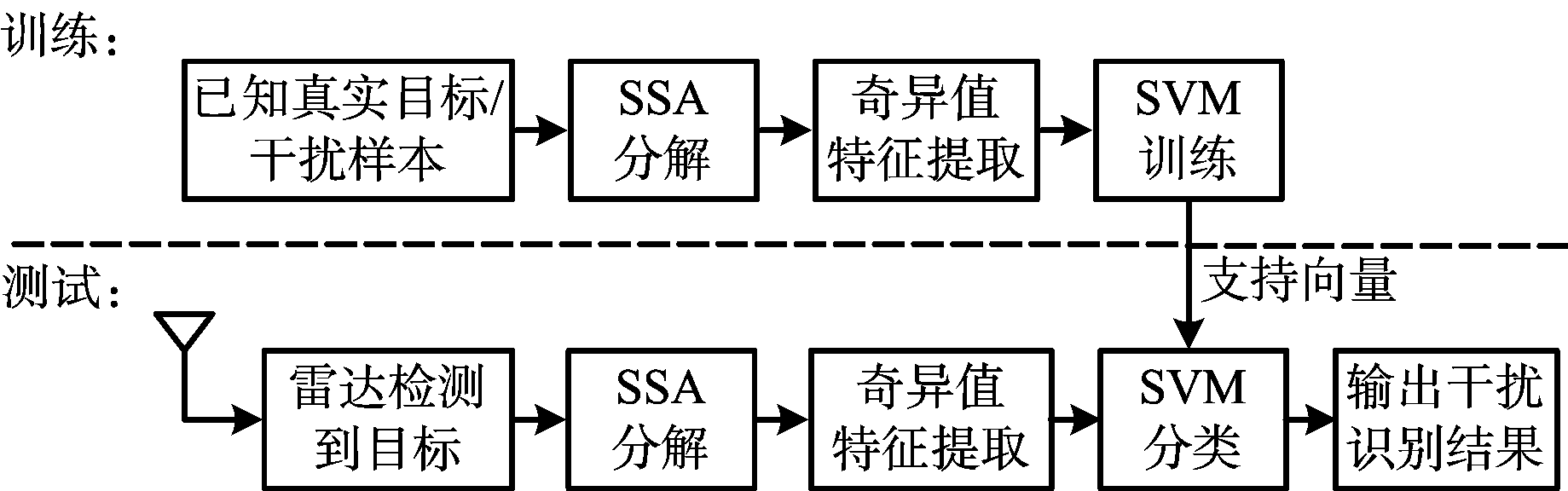
图6 干扰识别算法流程示意图
3 实验结果与分析
实验仿真参数如下:雷达工作于X波段,载频为9.655 GHz。雷达发射信号为单载频脉冲信号,其脉冲宽度为1 μs,脉冲重复周期为10 μs。雷达的一个相干处理时间(CPI)为2.56 ms。视目标为点目标,初始位置位于雷达15.8 km处,该目标上的自卫干扰机对雷达系统施加速度欺骗干扰,目标的多普勒频率和自卫干扰机产生的虚假多普勒频率在3~10 kHz中随机产生。定义信噪比SNR= |s(t)|2/|n(t)|2,干信比JSR=|j(t)|2/|s(t)|2,其中s(t),j(t),n(t)分别为目标回波、干扰信号和噪声分量。
3.1 SSA分解后的奇异值差异仿真分析
图7为当干扰机数控移相器位数N为4,SNR为10 dB,SSA分解窗长L为100时H1环境下的信号经SSA分解后的奇异值分布图(图中间部分为奇异值局部放大图)。从图7可以看出,H1环境下,由于信号主要分量为雷达目标回波,经SSA分解后的奇异值为一个较大的分量(对应于雷达回波)和其他大小均匀的分量(对应于噪声分量)的集合。图8为JSR=3 dB时,相同参数下H2环境的信号经SSA分解后的奇异值分布图(图中间部分为奇异值局部放大图)。由图8可以看出,H2环境下,信号主要分量为雷达目标回波和欺骗干扰信号,经SSA分解后的奇异值除了有两个较大的分量(对应于雷达回波和干扰信号的主分量),还有几个对应于干扰信号谐波分量。图9为H1和H2两种环境下信号经SSA分解后落入集合区间的奇异值对比图(这里的集合区间上限q为22)。由图9可以看出,由于H2环境下落入集合中的信号由干扰信号的谐波与噪声组成,在一定信噪比下,奇异值分布差异较大,而针对H1环境由于落入集合中的信号为噪声分量,故奇异值分布整体比较平稳。由这3幅图可以看出,由于数控移相器步进阶跃调相所带来的谐波效应的确会使产生的速度欺骗干扰信号经SSA分解后的奇异值产生明显的分布差异。
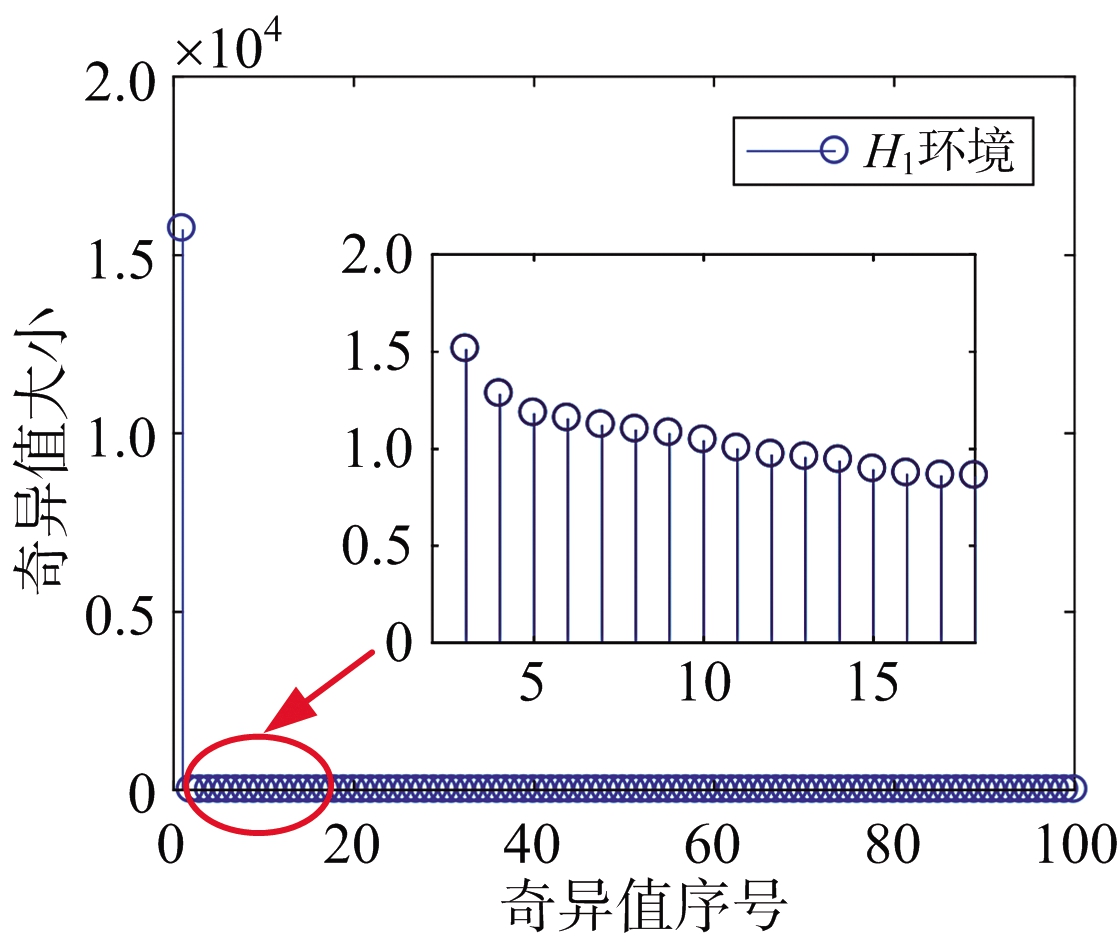
图7 H1环境信号的奇异值分布
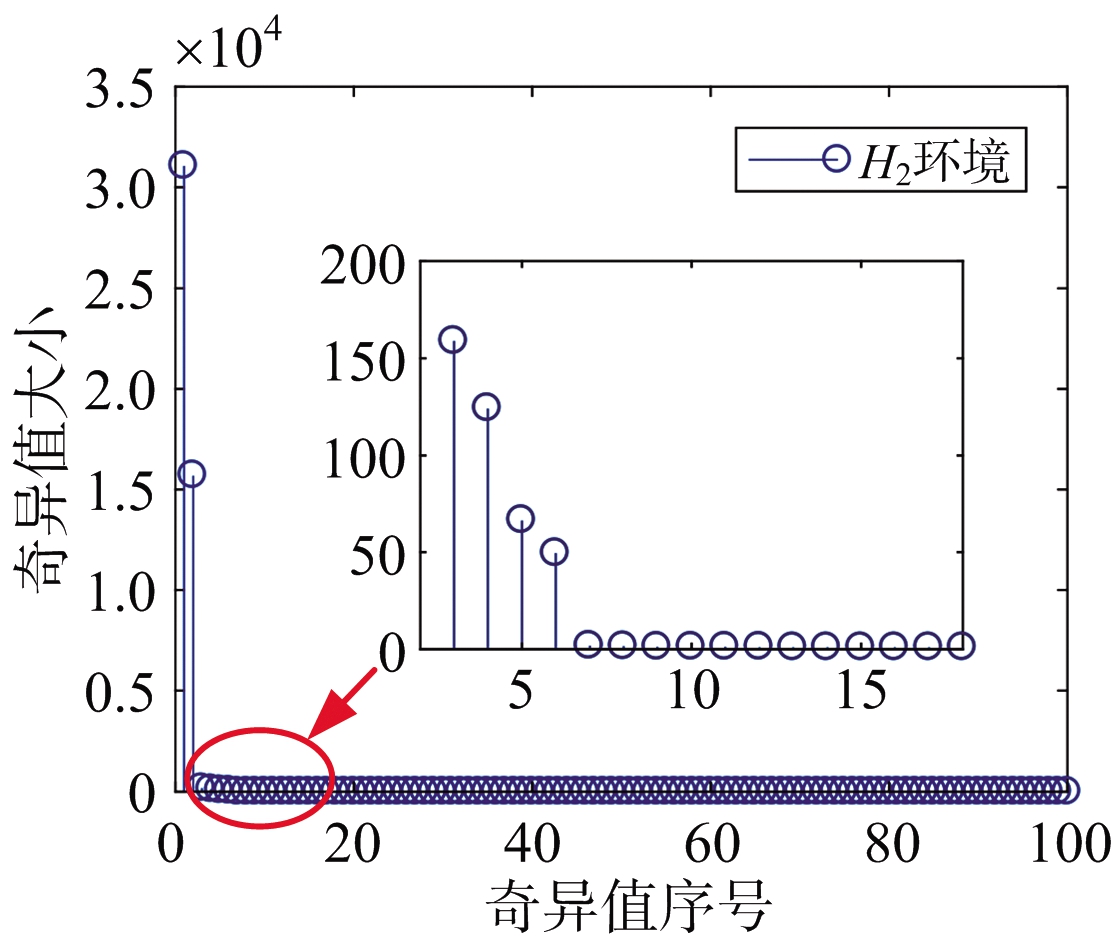
图8 H2环境信号的奇异值分布
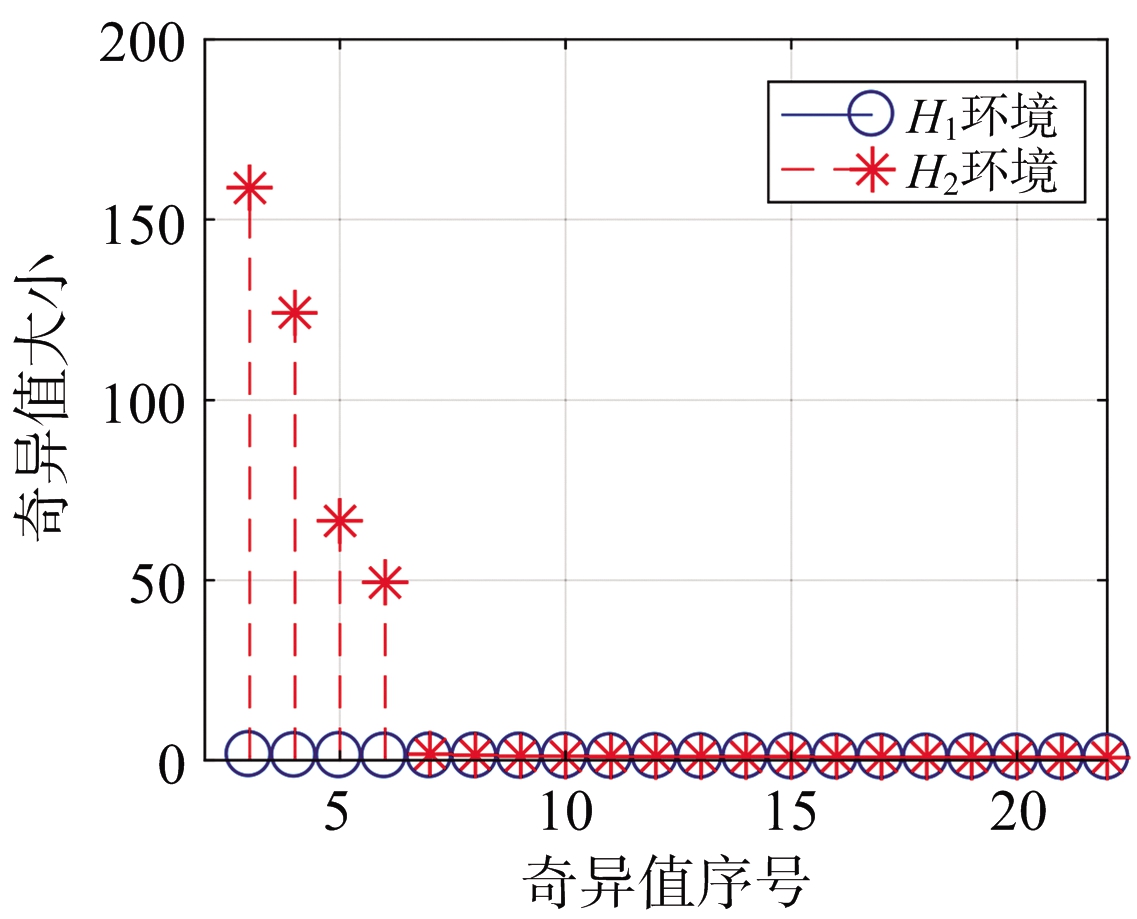
图9 部分奇异值分布对比
3.2 干扰识别概率仿真分析
通过提取奇异值的分布差异可以有效地实现干扰识别。图10给出了当干扰机数控移相器位数N为4,JSR为3 dB,SSA分解窗长L为100时的SVM干扰识别概率曲线。其中每个SNR下均产生了1 000个训练样本和500个测试样本。可以看出随着SNR的不断增大,由于此时干扰谐波对应的奇异值逐渐与噪声分量对应的奇异值产生差异,干扰识别概率不断提升,最终趋于一个较高的值。图11给出了SSA分解窗L为100时不同干扰机数控移相器位数下的干扰识别概率,其中N分别取了3,4,5,JSR为3 dB,每个SNR下均产生了1 000个训练样本和500个测试样本。可以看出,由于移相器位数影响干扰信号谐波分量强度的大小,从而影响干扰识别概率。其中移相器位数越大,干扰信号的谐波分量的强度越低,同一信噪比下的干扰识别概率越低。图12给出了当干扰机数控移相器位数N为5时选取不同SSA分解窗L的干扰识别概率,其中分解窗L分别取了50,80,100,JSR为3 dB,每个SNR下均产生了 1 000个训练样本和500个测试样本。可以看出,由于SSA分解窗的大小对SSA分解后的奇异值差异影响不大,故对最后的干扰识别概率影响不大。
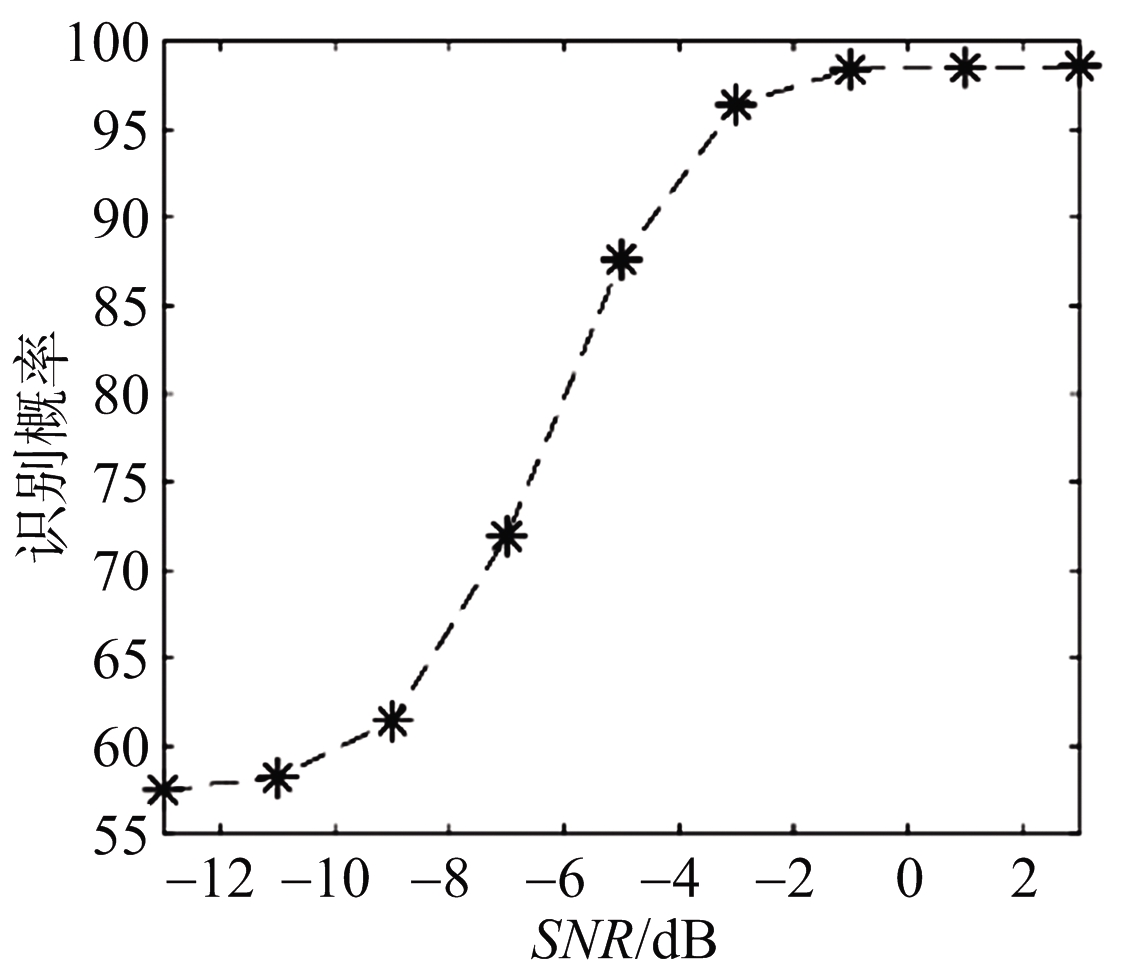
图10 N=4时干扰识别概率
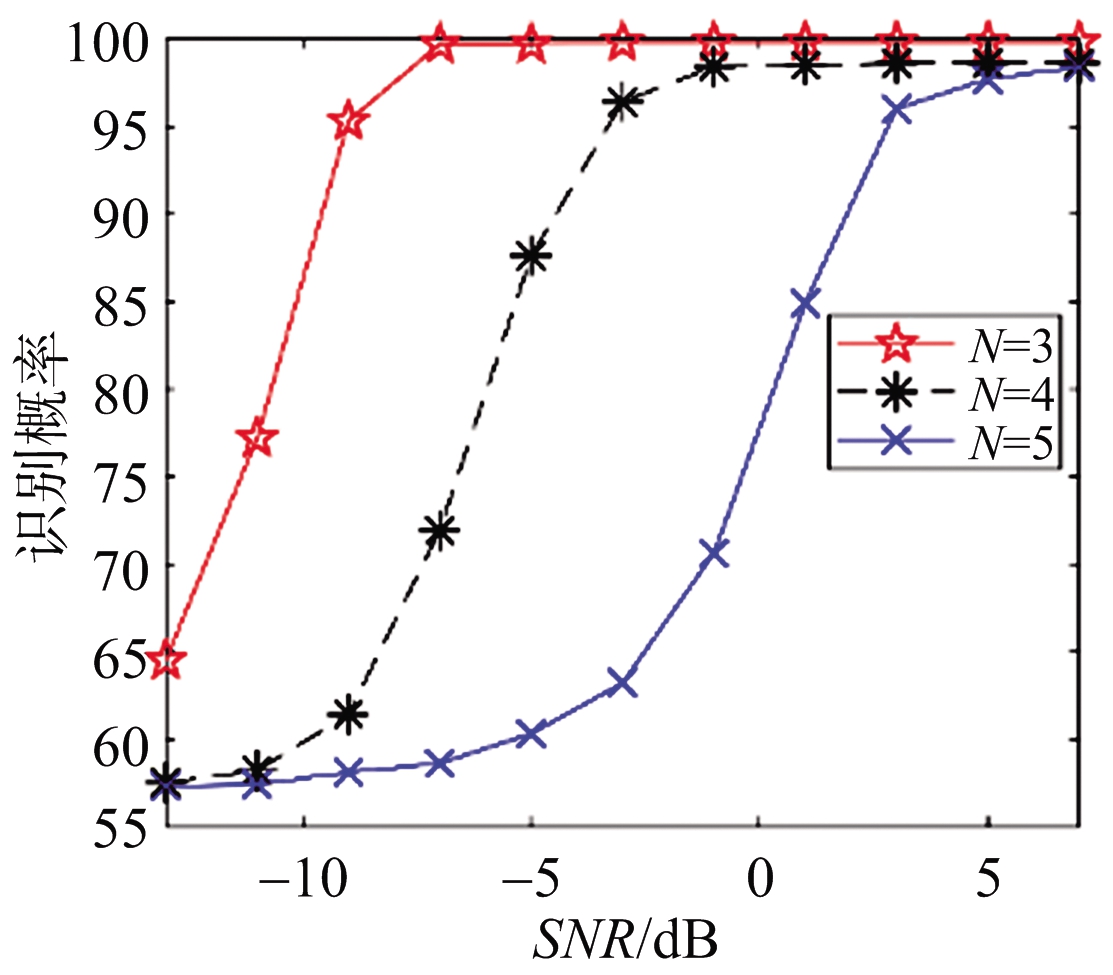
图11 不同N下干扰识别概率
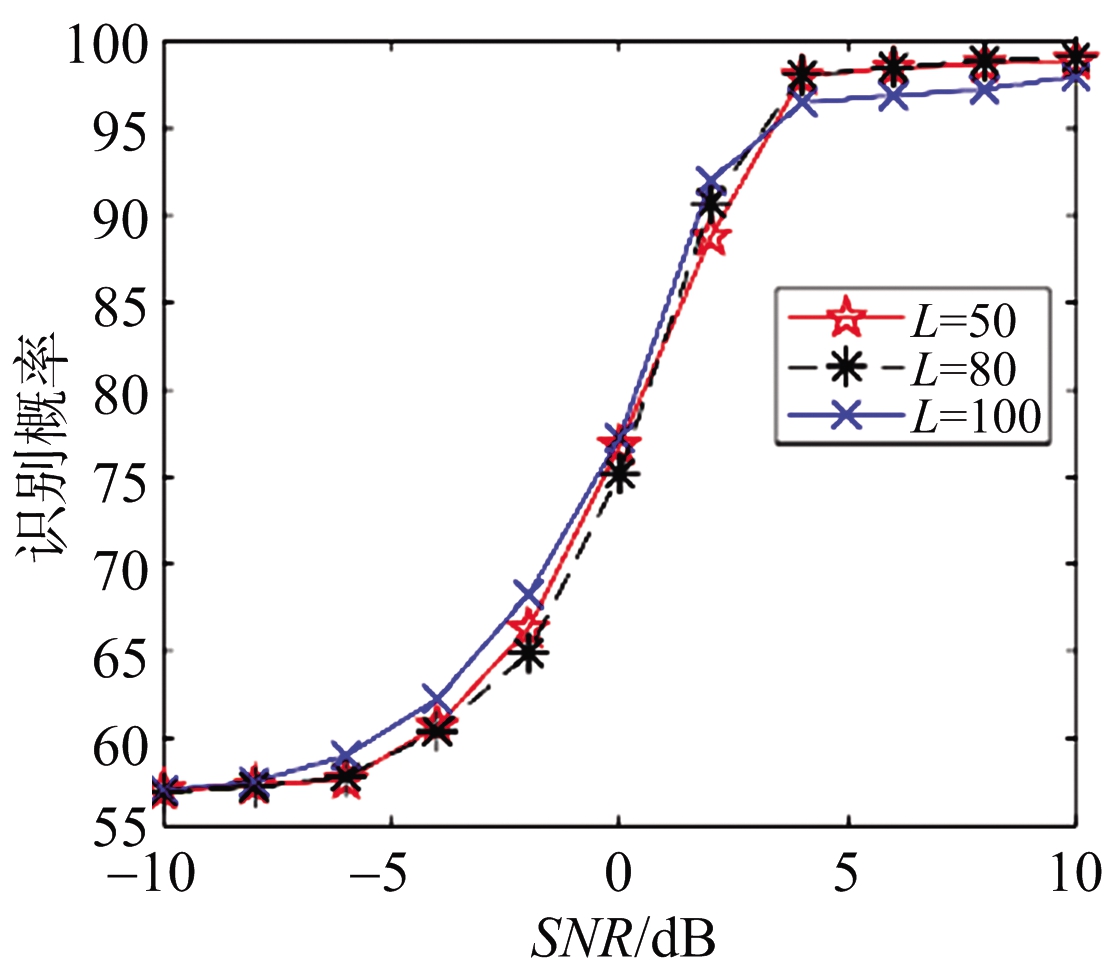
图12 不同L下干扰识别概率
4 结束语
DRFM干扰机产生的有源欺骗干扰信号因与其截获的雷达信号高度相干而难以被雷达识别。本文利用DRFM干扰机数控移相器步进阶跃调相后导致所产生的干扰信号产生谐波分量这一特性,提出了一种基于SSA的DRFM速度欺骗干扰识别算法。该方法利用真实目标回波与干扰信号在SSA分解后的奇异值分布差异,提取出奇异值的统计直方图的方差、峰度、偏度、能量和熵作为特征构建特征向量,并利用SVM作为分类器对干扰进行识别。该方法不再依赖现有的A/D相位量化的谐波模型,且通过计算机仿真验证了本文算法在较低信噪比下能有效识别出干扰信号。
[1] DONG Yangyang, DONG Chunxi, LIU Wei, et al. 2-D DOA Estimation for L-Shaped Array with Array Aperture and Snapshots Extension Techniques[J]. IEEE Signal Processing Letters, 2017, 24(4):495-499.
[2] XU Jin, BAI Bowen, DONG Chunxi, et al. Evaluations of Plasma Stealth Effectiveness Based on the Probability of Radar Detection[J]. IEEE Trans on Plasma Science, 2017, 45(6):938-944.
[3] ZHOU Chao, LIU Quanhua, CHEN Xinliang. Parameter Estimation and Suppression for DRFM-Based Interrupted Sampling Repeater Tammer[J]. IET Radar, Sonar and Navigation, 2018, 12(1):56-63.
[4] GRECO M, GINI F, FARINA A.Effect of Phase and Range Gate Pull-off Delay Quantization on Jammer Signal[J].IEE Proceedings of Radar, Sonar and Navigation, 2006, 153(5):454-459.
[5] GRECO M, GINI F, FARINA A.Radar Detection and Classification of Jamming Signals Belonging to a Cone Class [J]. IEEE Trans on Signal Processing, 2008, 56(5):1984-1993.
[6] BANDIERA F, FARINA A, ORLANDO D, et al. Detection Algorithms to Discriminate Between Radar Targets and ECM Signals[J]. IEEE Trans on Signal Processing, 2010, 58(12):5984-5993.
[7] 卢云龙, 李明, 陈洪猛,等. 基于熵特征的DRFM有源欺骗干扰CFAR检测[J]. 系统工程与电子技术, 2016, 38(4):732-738.
[8] 卢云龙, 李明, 闫琰. 利用调频率匹配的DRFM欺骗干扰检测方法[J]. 西安电子科技大学学报, 2014, 41(5):67-73.
[9] 刘晓东, 徐佳, 郭予并. 基于数字移相器的锯齿调相假多普勒频率干扰分析[J]. 电子对抗, 2015 (2):20-23.
[10] MA Xuejiao, JIN Yu, DONG Qingli. A Generalized Dynamic Fuzzy Neural Network Based on Singular Spectrum Analysis Optimized by Brain Storm Optimization for Short-Term Wind Speed Forecasting[J]. Applied Soft Computing, 2017, 54(5):296-312.
[11] JAIME Z, REN Jinchang, WANG Zheng, et al. Singular Spectrum Analysis for Effective Feature Extraction in Hyperspectral Imaging[J]. IEEE Geoscience and Remote Sensing Letters, 2014, 11(11):1886-1890.
[12] XU Jin, BAI Bowen, DONG Chunxi, et al. Evaluations of Plasma Stealth Effectiveness Based on the Probability of Radar Detection[J]. IEEE Trans on Plasma Science, 2017, 45(6):938-944.
[13] JINDAL A, DUA A, KAUR K, et al. Decision Tree and SVM-Based Data Analytics for Theft Detection in Smart Grid[J]. IEEE Trans on Industrial Informatics, 2016, 12(3):1005-1016.
[14] WU Xiaohe, ZUO Wangmeng, LIN Liang, et al. F-SVM:Combination of Feature Transformation and SVM Learning via Convex Relaxation[J]. IEEE Trans on Neural Networks and Learning Systems, 2018, 29(11):5185-5199.
