0 引言
遥测测距可以有效解决深空测距下行链路同时传输遥测、测距信号会出现的频谱带宽增加、遥测数据传输速率受限等问题[1]，具有巨大的发展潜力。其技术优势在于将有限的飞行器功率完全提供给遥测链路，增加遥测数据的传输速率[2]；由于下行链路不发测距信号，频谱带宽相应压缩，也不存在现有测距技术遥测信号和测距信号相互干扰的问题[3]。
准确估计遥测帧头到达地面站时刻是遥测测距的关键技术之一，这是因为遥测测距求取双向距离是通过对同一遥测帧头到达飞行器和地面站时刻的发射机测距码相位值进行积分实现的。由于该触发帧帧头在飞行器产生，未受噪声干扰，因此相较于飞行器端，地面站对该帧头到达时刻的估计相对来说更难，这是由深空距离极远，干扰极大的特点决定[4]。目前，由于遥测信号的主要功能集中在将飞行器测得的工作参数或科学数据等发回地面，遥测信号的研究重点保证正确、高效判决，鲜见提高遥测帧头到达时刻估计精度的文献。
地面站接收遥测信号后依次进行下变频和载波跟踪处理，载波同步后再进行符号同步、帧同步。符号同步的作用是确定码元的起始和结束时刻，以便最大限度地利用整个符号周期内的能量进行积分，完成遥测符号判决[5]；帧同步目标是在遥测符号流中找到帧头，地面站即可按照预定顺序找到对应参数。两个步骤实质上可分别得到遥测帧头到达地面站的小数时刻和整数时刻。软件无线电技术的发展使地面站用基带处理遥测信号成为现实[6]，地面站完成帧同步后，高性能计算机可以保证帧头到达时刻的整数位精度。目前，广泛采用基于数据转换跟踪环路(Data Transition Tracking Loop，DTTL)的算法完成符号同步[7]，但该算法忽略了离散采样对中相积分器的影响，精度不高，不适合遥测测距。针对上述问题，本文重点研究了文献[8]提出的基于加权系数的DTTL算法，通过对离散点加权消除采样的影响，分析和仿真结果均表明该算法符号同步精度高，适合遥测测距技术。
1 遥测测距原理与帧结构设计
1.1 遥测测距原理分析
图1给出了遥测测距的原理框图。如图所示，地面站持续发送上行再生伪码测距信号，飞行器发送下行遥测信号，飞行器捕获PN码信号并测量当前遥测帧头脉冲前沿到达时刻tS时的测距码相位值ψS(tS)，将该相位值插入遥测帧中下发。地面站接收遥测信号进行同步处理，假设跟踪环路捕获飞行器上该触发帧头到达地面的时刻为tR，地面站测量出tR时刻的发射机相位ψT(tR)。地面站解调出遥测符号流后，提取出星上插入的码相位ψS(tS)，由相位的连续性可知，tS时刻的码相位ψS(tS)等于地面发射机tT(tT<tS)时刻的相位ψT(tT)，即ψS(tS)=ψT(tT)[9]。对发射机相位进行积分，即可确定信号的发送时刻tT，有
(1)
利用信号的收发时刻，可求出飞行器与地面站的单向距离R，有
(2)
式中，c为光在真空中的传播速度，有c=299 792 458 m/s。
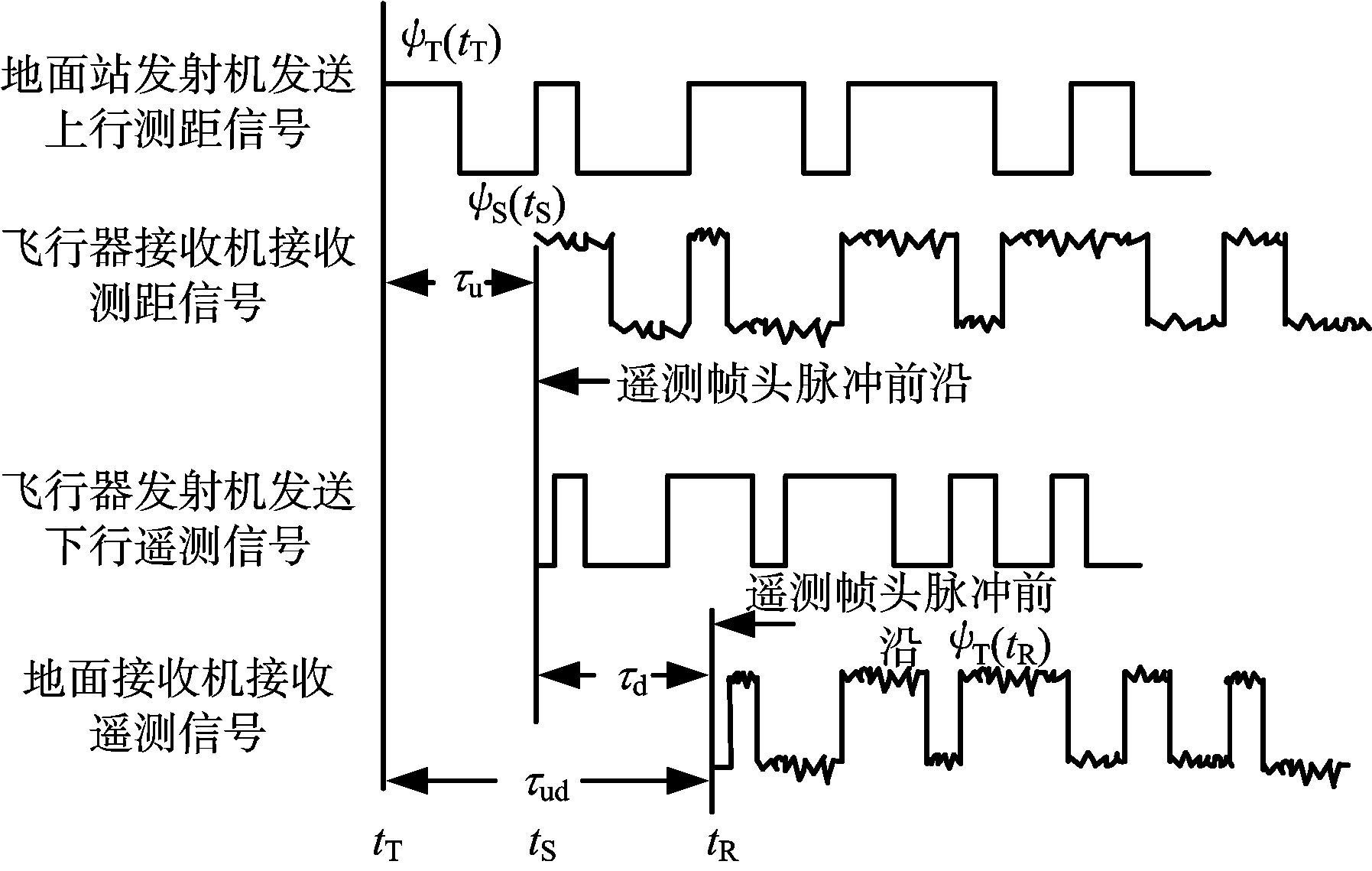
图1 遥测测距原理图
1.2 遥测帧结构设计
遥测帧结构设计参考CCSDS标准，图2给出了遥测帧结构设计图，如图所示，帧结构由帧同步头(ASM)加遥测字的格式构成[10]，遥测帧连续传输形成遥测数据流，中间无间隙或中断。
帧同步头是位于遥测帧最前端的一组已知码组，将相邻遥测帧分开，根据CCSDS的建议无信道编码时可选择32 bit的帧头，用十六进制表示为1ACFFC1D[11]，应注意的是，遥测帧头的选择根据遥测字长度和是否采用信道编码而不同，帧头的作用是辅助地面站进行帧同步，即地面站只有找到帧头才能按预定排列位置找到相应参数，对于遥测测距技术而言，重点是找到相位值ψs(ts)。遥测字由帧数据域和帧尾等结构组成，分别用来存储飞行器测得的数据和帧差错控制字等。本文的遥测字采用CCSDS建议的1 784 bit长度的帧结构，如图2所示，通常默认首位为零位，则码相位值ψs(ts)建议插入遥测字的第128位至第159位[12]。由文献[3]可知，相位ψs(ts)为卷绕值，即ψs(ts)≤ 1 009 470，因此，至少需要20 bit(220=1 048 576)的空间存储ψs(ts)的整数相位值，因此，建议第128位到第147位存储码相位ψs(ts)的整数值；剩余的148位到第159位则存储ψs(ts)相位的小数部分，假设一个PN码片宽度为T s，则ψs(ts)的量化精度可达到2-12T s。帧结构的最后16位存储循环冗余码校验(CRC)，旨在检查数据传输过程中可能引入的差错[13]，遥测字的其他位存储飞行器测得的其他科学数据或飞行器工作参数等相关信息。
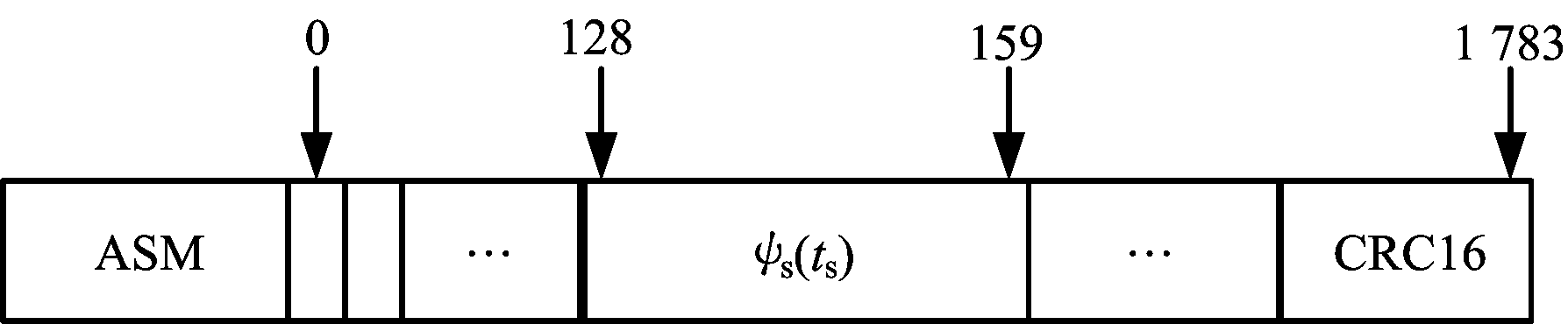
图2 遥测帧结构设计图
2 基于DTTL的符号同步算法
2.1 传统DTTL算法研究
符号同步的目的是跟踪遥测帧头的小数位偏移量，不妨定义该偏移量为ε，可知ε的取值为(0,1]。图3给出了现有基于DTTL的符号同步算法的原理框图。
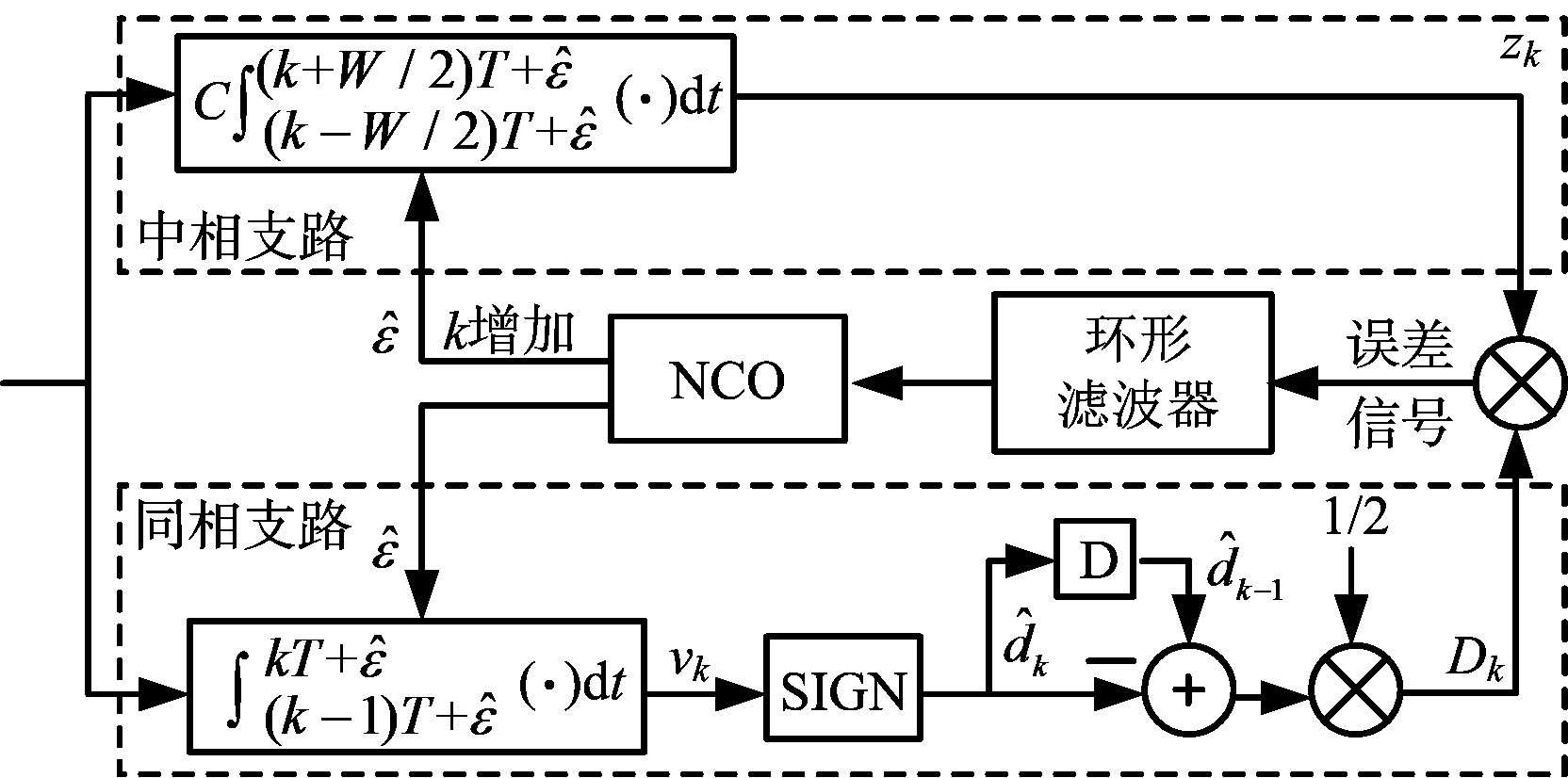
图3 基于DTTL的符号同步算法原理框图
如图所示，DTTL环由同相支路和中相支路构成，环路的输入信号为载波跟踪环的Q路输出[8]，有
(3)
同相支路接收符号定时的估计值后对一个遥测符号周期进行判决，有
(4)
式中，T为一个遥测符号间隔，
为符号定时偏移量的估计值。
式(4)的遥测符号流vk为软符号估计，取符号函数(sign函数)后，得到±1遥测符号流，有
(5)
Dk检测遥测符号是否发生了极性转换，通常定义符号极性由正到负跳变时Dk等于1，由负到正跳变时Dk等于-1，极性不发生变化时Dk等于0，因此有
(6)
中相积分支路在两个相邻符号的WT/2区间内积分，有
(7)
式中：W为积分窗口宽度，有W=2-n，其中，n∈{0,1,2,3,4}；C为归一化因子，有
中相积分支路得到符号定时的估计值。
鉴相器将同相积分支路的输出Dk与中相积分支路的输出zk相乘，利用数据转换信息和当前数据消除遥测符号转换的影响，获得符号同步误差信号，此误差信号经环路滤波器滤波后去控制NCO，用以调整相位，缩小本地时间参考与接收遥测符号流的相对时延，从而实现同步。同步后，NCO输出的定时脉冲即为符号同步时钟输出。
2.2 加权系数的DTTL符号同步算法
传统DTTL算法通过对中相积分器相邻符号间积分提取误差信号，通过对同相积分器遥测符号间隔积分并判断是否发生极性跳变给出误差信号的极性，从而持续跟踪符号定时。但受采样离散化影响，符号跳变时必然存在倾角，且采样率越小，上升沿(或下降沿)的倾角越明显。传统DTTL算法忽略离散化对中相积分器的影响，因此，即使理想情况下该算法的性能效果也不佳。
基于加权系数的DTTL算法利用加权的思想，对每个遥测符号的首位、末位采样点加权处理后再进行积分，DTTL仍采用图3所示的结构，从而最大限度地减小符号跳变时离散采样的影响。文献[8]的思路正确，但公式推导中出现错误，下面对该算法进行重新表述。
算法处理对象为采样后的离散信号，假设一个遥测符号的采样点数为Ns，则符号定时偏移ε对应的采样点数为Nε=⎣ε·Nε」，其中⎣ 」为向下取整运算；中相积分支路的归一化因子
其中NW为积分窗口对应的采样点数，有NW=W·Ns，Pd为遥测信号功率，Pd与总发射功率Pt及遥测信号调制度φd的关系为Pd=Ptsin2(φd)；权重因子αε=ε·Nε-⎣ε·Nε」。该算法的具体步骤如下：
步骤 1： 赋予定时偏移ε一个初始值εk，εk的取值区间为[0,1)，计算得到该值对应的Nε，αε；
步骤 2： 同相积分器和中相积分器利用步骤1得到的Ns，αε，对信号
进行加权积分，分别得到的vk，zk：
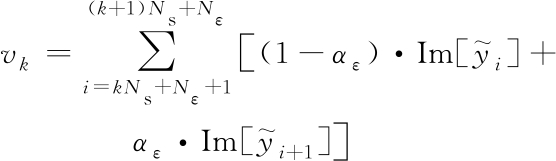
(8)
步骤 3： 同相积分器提取缓存里的vk-1，计算第k个遥测符号与第k-1个符号是否发生了极性跳变：
(10)
步骤 4： 鉴相器将Dk，zk相乘，得到第k个符号间隔的鉴相误差：
Δεk=Dkzk
(11)
步骤 5： 环路滤波器采用二阶结构，利用Δ εk和缓存里的Δεj(1≤j<k)，求出下一遥测符号定时εk+1的估计值：
(12)
式中，K1，K2为环路增益系数。
步骤 6： NCO将εk+1传到中相积分支路和同相积分支路，并重复上述步骤，直到DTTL跟踪上遥测符号定时。
3 理论分析和仿真验证
3.1 误差分析
基于加权系数的DTTL算法对同相积分器和中相积分器进行加权，消除符号跳变的影响。文献[1]给出了DTTL符号同步误差表达式，有
(13)
式中，W为窗口分数，BL为环路带宽，Pd/N0为遥测信号与噪声信号的功率比，SL为平方损失。其中，平方损失为中相积分器和同相积分器两个误差信号相乘时造成的误差，其数学表达式为
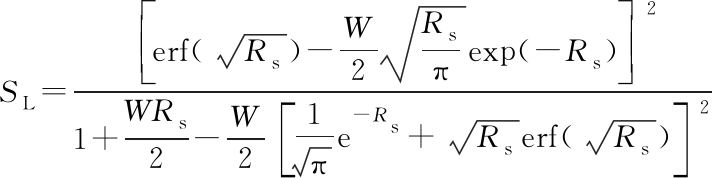
(14)
式中：Rs=PdTs/N0，其中Ts为一个遥测符号的宽度(单位：s)；erf()为误差函数；exp()为指数函数。SL由两个误差信号的乘积得到，其对噪声十分敏感，即信噪比越低，SL越大。低信噪比条件下，Rs≪1，对误差函数和指数函数进行近似替换，有：
将近似函数代入式(14)并化简，有
(15)
式中，f(W)=4/π·[1-W/4]2·[1-W/2π]-1。将式(15)代入式(13)中，可得到低信噪比情况下DTTL的符号同步误差，有
var(Δε)≥
=
(16)
高信噪比条件下可忽略SL的影响，即SL≈1，因此，DTTL的符号同步误差为
(17)
3.2 仿真验证
对上述算法进行仿真实现，遥测帧采用2.2节设计的1 816比特长度的帧结构(含32比特帧头)，不采用信道编码，遥测符号的传输速率Rs为100 ksps(symbol per second)，每个遥测符号取30 个采样点，信号调制度φd为0.4 π，遥测符号定时偏移量设为0.6个符号，中相积分窗口设为1/4，不加噪声，其中，环路滤波器增益系数K1取0.043，K2取9.245×10-4[14]，窗口分数W取0.25，图4给出了无噪声条件下两种DTTL算法的符号同步跟踪性能图。如图所示，传统DTTL算法在理想条件下仍存在较大的定时误差，相比而言，基于加权系数的DTTL算法能平稳跟踪符号定时，蒙特卡罗仿真500次，该算法的均方根误差约为8.375×10-6个符号，符号速率为100 ksps时相当于0.01 ns量级。
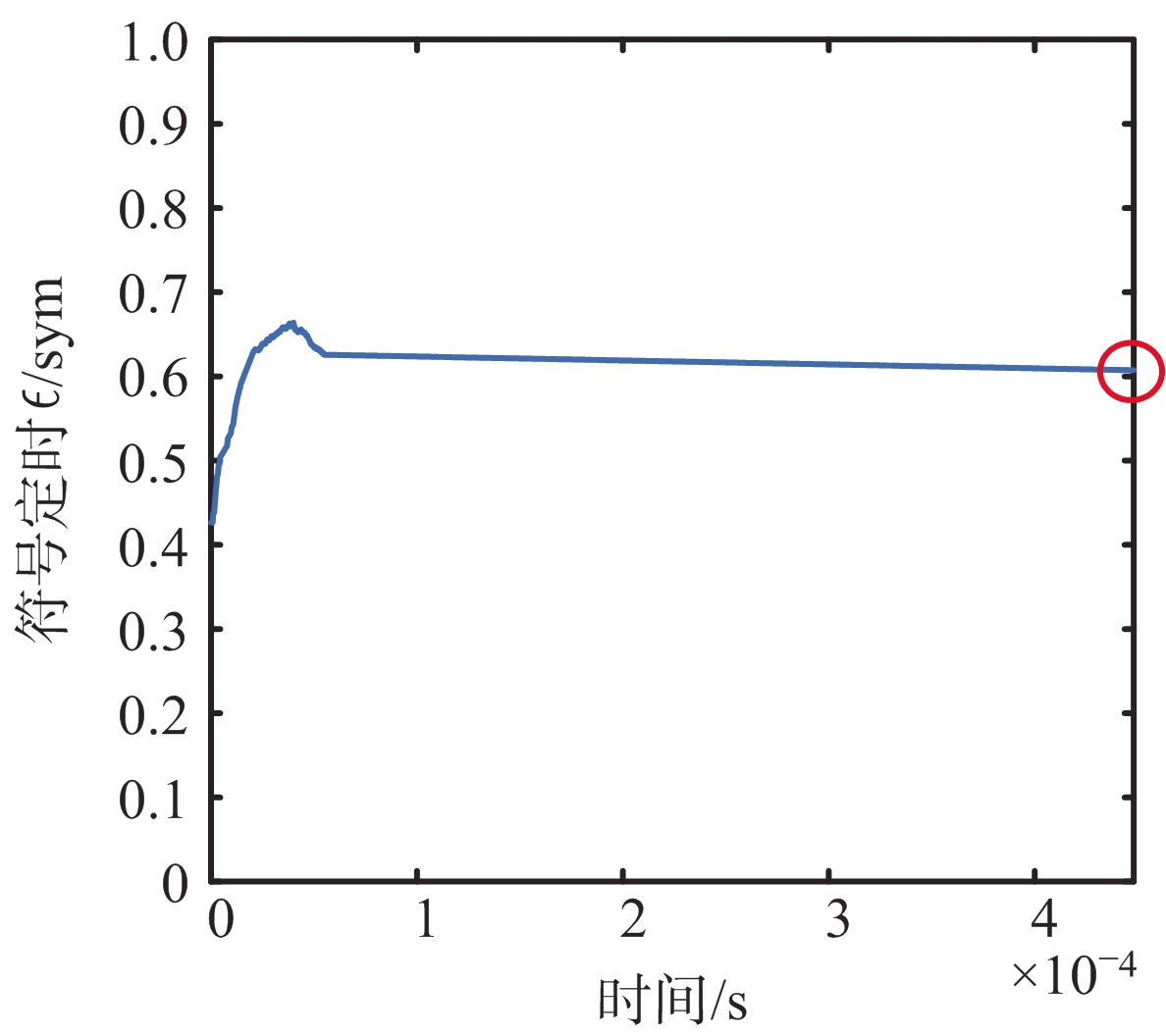
(a) 传统DTTL算法符号同步性能图
(b) 基于加权系数的DTTL算法符号同步性能图
图4 无噪声条件下两种DTTL算法的符号同步跟踪性能图
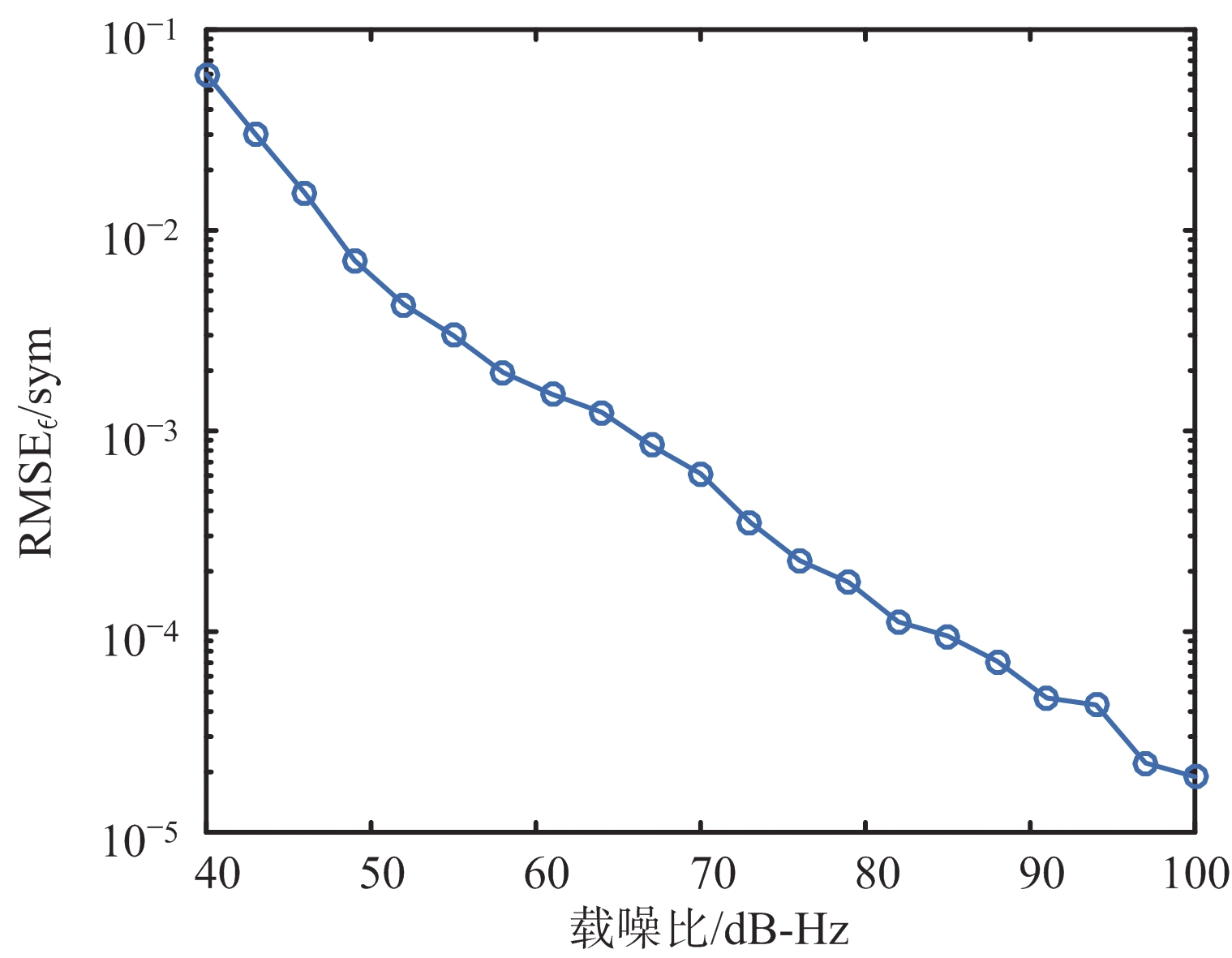
图5 不同信噪比条件下加权DTTL算法的符号定时性能图
进一步对算法不同信噪比条件下的性能进行验证。信噪比区间取-10 dB至50 dB，步长为3 dB，蒙特卡罗各仿真500次，图5给出了不同信噪比时基于加权系数DTTL算法的符号同步性能图。如图所示，该算法在载噪比为40 dB-Hz(即信噪比为-10 dB)时，符号定时均方根误差约为0.06个符号；在载噪比约为45 dB-Hz(对应信噪比为-5 dB)时，符号定时均方根误差与传统DTTL算法理想条件下的性能相当，均方根误差约为0.01个遥测符号；在载噪比约为80 dB-Hz(对应信噪比为30 dB)时，均方根误差优于10-4个遥测符号。地面站通常采用增大天线口径等措施提高接收信号的信噪比，因此，算法的精度能符合遥测测距的需求。
4 结束语
本文研究了一种基于加权系数的DTTL符号同步算法，该算法消除了现有DTTL算法同步性能较差的难题，在信噪比为-5 dB时能达到传统DTTL算法理想条件下的跟踪性能，约为0.01个遥测符号，在信噪比为30 dB时，符号定时均方根误差优于10-4个遥测符号，保证了工作精度，适合遥测测距技术。
但是，本文的环路误差分析建立在输入信号载波跟踪良好的前提下，即载波跟踪不存在误差，对载波跟踪-DTTL级联环路进行误差分析将是下一步进行改进和提高的方向。
[1] ANDREWS K,HAMKINS J，SHAMBAYATI S, et al. Telemetry-Based Ranging[C]∥Proceedings of the 2010 IEEE Aerospace Conference, Big Sky, MT, USA: IEEE, 2010:1-16.
[2] HENNAWY J,ADAMS N,SANCHEZ E, et al. Telemetry Ranging Using Software-Defined Radios[C]∥ Proceedings of the 2015 IEEE Aerospace Conference ,Big Sky, MT,USA: IEEE,2015:1-14.
[3] HAMKINS J，KINMAN P，XIE H, et al. Telemetry Ranging: Concepts [R].Pasadena: Jet Propulsion Laboratory, 2015.
[4] 马宏, 彭保童, 张超.基于simulink的再生伪码测距关键技术实现[J]. 兵器装备工程学报,2019,40(5):151-156.
[5] 李艳华, 李凉海, 谌明, 等. 现代航天遥测技术(下)[M]. 北京: 中国宇航出版社, 2018:983-987.
[6] 罗亨,齐建中,王乐,等.一种新型的可编程遥测收发机设计[J].无线电工程,2018,48(9):727-731.
[7] 王勇. 一种适用于数字卫星接收机的位同步系统的研究与实现[D].北京:中国科学院研究生院(空间科学与应用研究中心), 2010.
[8] HAMKINS J，KINMAN P，XIE H,et al. Telemetry Ranging: Signal Processing[R]. Pasadena: Jet Propulsion Laboratory,2016.
[9] 侯彦兵,焦义文,杨文革.基于遥测信号的测距技术及其发展趋势[J].电讯技术,2019,59(7):863-868.
[10] 张美婷, 邵庆军, 刘洋. 一种基于再生伪码测距的遥测信号测距方法[J]. 电讯技术,2015,55(3):298-302.
[11] CCSDS. TM Synchronization and Channel Coding: CCSDS 131.0-B-3[S].Washington: CCSDS Secretariat,2017.
[12] HAMKINS J, KINMAN P, XIE H, et al. Telemetry Ranging: Laboratory Validation Tests and End-to-End Performance[R]. Pasadena: Jet Propulsion Laboratory, 2016.
[13] 殷璐.带CRC校验终止机制的Turbo码性能仿真分析[J].通信技术,2017,50(7):1371-1374.
[14] STEPHENS S A, THOMAS J B. Controlled-Root Formulation for Digital Phase-Locked Loops[J]. IEEE Trans on Aerospace and Electronic Systems,1995,31(1)：78-95.
