0 引言
多输入多输出(Multiple Input and Multiple Output, MIMO)雷达是基于MIMO通信技术发展起来的一种新体制雷达[1]。相比于传统相控阵雷达，MIMO雷达在目标探测、抗干扰、目标参数估计和目标识别等方面显示出诸多优势[2-3]，因此已成为学术界研究的热点。
波达方向(Direction of Arrival, DOA)估计是MIMO雷达参数估计的一个重要内容。如今关于MIMO雷达DOA估计的算法已经多不胜数，诸如Capon算法[4]、多重信号分类(Multiple Signal Classification, MUSIC)算法[5]、基于旋转不变技术的信号参数估计(Estimation of Signal Parameters via Rotational Invariance Technique, ESPRIT)算法[6]等。通常，目标相对整个观测空间高度稀疏，因此许多学者将压缩感知理论[7]应用到MIMO雷达DOA估计中。然而，l0范数最小化问题属于NP-hard问题，需要组合搜索，当维度增加时难以实现。文献[8]针对传统阵列提出一种基于l1-SVD(l1-norm Singular Value Decomposition)的DOA估计方法，该方法通过对阵列接收数据进行奇异值分解，并建立信号子空间构建l2,1范数联合稀疏模型，然后采用二阶锥规划(Second Order Cone Programming, SOCP)求解该模型。文献[9]提出一种基于加权l1范数算法的单基地MIMO雷达DOA估计方法，该算法利用降维Capon(Reduced-Dimensional Capon, RD-Capon)空间谱的系数构造加权矩阵以促进解的稀疏性，但由于采用SOCP求解方法导致其计算复杂度较高。文献[10]提出一种平滑l0范数(Smoothed l0-norm，SL0)算法，该方法利用梯度投影原理以及最速下降法，采用一个平滑的高斯函数近似l0范数，从而将离散函数的优化问题转化为连续函数的优化问题。该算法的运算效率较高，在保证相同精度的条件下，能够比基追踪算法[11]的重构速度快2～3倍。为了进一步提高目标的重构性能，文献[12]提出一种基于平滑l0范数的MIMO雷达多快拍DOA估计方法，利用接收数据的四阶累积量矩阵构建稀疏表示模型以有效抑制噪声，并将多测量矢量(Multiple Measurement Vector，MMV)问题转化为一个联合平滑函数的求解问题，且该方法相比文献[8]所提方法快约两个数量级。文献[13]基于近端方法[14]提出一种相对SL0算法更为广泛的稀疏重构算法以解决非凸平滑问题，称为迭代稀疏投影(Iterative Sparsification Projection, ISP)算法。针对非凸非平滑问题，文献[15]提出一种迭代近端投影(Iterative Proximal Projection, IPP)算法，该算法通过构造近端函数模型，并利用SCAD(Smoothly Clipped Absolute Deviation Penalty)[16-17]阈值函数获得近端算子来求解该模型以促进解的稀疏度，同时引用外推步骤[18]改善该算法的收敛性能。传统基于压缩感知的MIMO雷达DOA估计算法将非凸非平滑稀疏表示问题近似成凸或平滑函数问题进行求解，稀疏表示模型误差的存在会导致DOA估计性能不理想。目前，迭代近端投影(IPP)算法还未应用到MIMO雷达参数估计的相关领域。
针对MIMO雷达DOA估计的非凸非平滑稀疏表示问题，本文提出一种基于迭代近端投影的MIMO雷达多快拍DOA估计方法。该方法对回波数据进行降维变换以剔除冗余数据，并对降维后的数据进行奇异值分解(SVD)以提取信号子空间，然后建立MIMO雷达多快拍DOA估计的近端函数稀疏信号模型，并采用SCAD函数获得近端算子以求解该模型，从而解决MIMO雷达多快拍DOA估计中的非凸非平滑问题。仿真结果表明，本文方法的相干信源DOA估计性能优于现有方法。
1 MIMO雷达信号模型
假设窄带单基地MIMO雷达系统具有M个发射阵元和N个接收阵元，发射和接收阵列均为均匀线阵，其阵元间隔分别为dt=λ/2和dr=λ/2，λ为接收信号波长。假设存在P个远场窄带相干目标，其入射角度分别为θ1,θ2,…,θP，MIMO雷达接收阵列信号经匹配滤波后可表示为
x(t)=As(t)+n(t)
(1)
式中:A=[at(θ1)⊗ar(θ1),…,at(θP)⊗ar(θP)]∈CMN×P为发射接收联合导向矩阵；at(θp)=[1,ejπsin(θp),ejπ2sin(θp),…,ejπ(M-1)sin(θp)]T∈CM×1为发射阵列的导向向量；ar(θp)=[1,ejπsin(θp),ejπ2sin(θp),…,ejπ(N-1)sin(θp)]T∈CN×1为接收阵列的导向向量；(·)T表示矩阵转置；C表示复数域；⊗表示Kronecker积；s(t)=[s1(t),s2(t),…,sP(t)]T∈CP×1为相干信源信号矢量，其中，sp(t)=αps1(t)，p=1,2,…,P，复常数αp表示sp(t)相对于s1(t)的相干系数；n(t)∈CMN×1为接收阵列的噪声矩阵，服从零均值，方差为σ2的高斯分布，即n(t)～Nc(0,σ2IMN)，IMN表示MN×MN维的单位矩阵。取J个快拍下MIMO雷达虚拟阵列输出数据矩阵，即
X=AS+N
(2)
式中，X=[x(t1),x(t2),…,x(tJ)]∈CMN×J为虚拟阵列输出数据矩阵；S=[s(t1),s(t2),…,s(tJ)]∈CP×J为目标回波信号矩阵；N=[n(t1),n(t2),…,n(tJ)]∈CMN×J为高斯噪声矩阵。
2 基于迭代近端投影的MIMO雷达多快拍DOA估计方法
传统基于压缩感知的MIMO雷达DOA估计算法将非凸非平滑稀疏表示问题近似成凸或平滑函数问题进行求解，为了避免稀疏表示模型误差对DOA估计性能的影响，本文将迭代近端投影思想推广应用于MIMO雷达DOA估计中，提出一种基于迭代近端投影的MIMO雷达多快拍DOA估计方法。对于发射阵列和接收阵列均为阵元间距等于半波长的均匀线阵的单基地MIMO雷达来说，其有效虚拟阵元个数为M+N-1，因此，MN×1维的目标均匀线阵导向矢量可由(M+N-1)×1维的虚拟均匀线阵导向矢量通过线性变换来表示[19]，即
at(θp)⊗ar(θp)=Gb(θp)
(3)
式中，b(θp)=[1,ejπsin(θp),ejπ2sin(θp),…,ejπ(M+N-2)sin(θp)]T表示(M+N-1)×1维的虚拟均匀线阵导向矢量，
CMN×(M+N-1)为转换矩阵，其中，ηm=[0N×M,IN,0N×(M-m-1)]∈CN×(M×N-1)，m=0,1,…,M-1，0N×M为N×M维的零矩阵。根据式(3)，阵列流形矩阵A可进一步表示为
A=GB
(4)
式中，B=[b(θ1),b(θ2),…,b(θP)]为(M+N-1)×P维的虚拟均匀线阵导向矩阵。为了降低算法的计算复杂度，可定义一个大小为(M+N-1)×MN的降维矩阵T对接收数据进行降维预处理。为了使得降维后的噪声是服从N～(0,σ2IM+N-1)的高斯白噪声，降维矩阵T需满足TTH=IM+N-1，因此降维矩阵可选取为T=F-1GH∈C(M+N-1)×MN，其中
(5)
式中，min(·)表示取最小的元素，diag(·)表示对角化操作，(·)H表示共轭转置运算。经过降维变换后，式(2)的接收数据矩阵可表示为
(6)
式中，
C(M+N-1)×J为降维后的接收数据矩阵，
C(M+N-1)×P为降维后的阵列流形矩阵，
C(M+N-1)×J为降维后的高斯白噪声矩阵。
为了进一步降低计算复杂度和对噪声的敏感性，对接收数据矩阵
进行奇异值分解(SVD)：
(7)
式中，USV为由P个大特征值对应的左奇异值矢量组成的信号子空间矩阵，UNV为由其余M+N-1-P个小特征值对应的左奇异特征值矢量组成的噪声子空间矩阵，V为右奇异特征值矢量组成的矩阵，Λ为的特征值构成的对角矩阵。令
进一步推导式(7)得
(8)
式中，
为由P个大特征值组成的对角矩阵，0P×(J-P)为P×(J-P)维的零矩阵。令
则降维后的接收数据模型式(8)可简化为
(9)
对比式(6)和式(9)可知，阵列接收数据矩阵的维数从(M+N-1)×J降到(M+N-1)×P，而实际应用中，目标个数P远小于快拍数J，即P≪J，因此，式(9)的信号矩阵维度得到显著降低，有利于目标DOA估计的快速实现。根据稀疏重构理论，将搜索空域[-90°,90°]按等角度间隔划分为L个单元，且
表示空域内所有可能的入射方向，定义冗余字典
C(M+N-1)×P，其中Bθ=[b(θ1),b(θ2),…,b(θL)]∈C(M+N-1)×L，则式(9)可表示为
(10)
从多个测量矢量
中恢复多个未知的稀疏信号源Sθ，该重建模型式(10)可以称为多测量矢量(MMV)模型。该模型采用多快拍下的阵列接收数据，提高了在低信噪比下DOA估计性能。本文将近端投影思想应用到多快拍DOA估计问题中。为获得式(10)的稀疏解，可将MIMO雷达的多快拍DOA估计问题转化为近端函数[14]优化问题，其稀疏信号表示模型为
(11)
式中，f(zl2)为非凸非平滑函数，z为辅助变量，zl2为由矩阵z每一行向量的l2范数构成的列向量，
为由矩阵Sθ的每一行向量的l2范数构成的列向量。
定义为可行集
的指示函数[20]，即
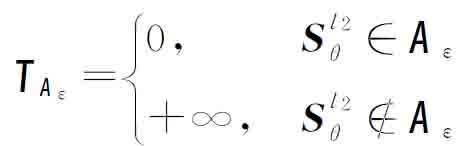
(12)
在式(11)的稀疏信号表示模型中引入惩罚函数方法[21]，即
(13)
式中，λ>0为惩罚因子，
表示l2范数。通过交替最小化方法[22]解决式(13)所表示的优化问题。
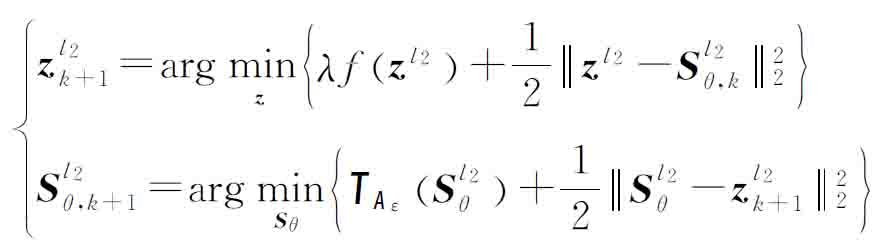
(14)
根据近端投影[14]的定义，式(14)进一步化简为
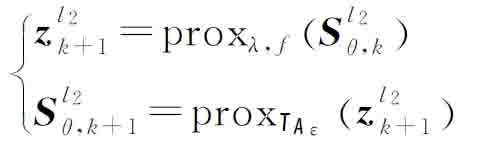
(15)
式中，
为非平滑函数f(zl2)的近端算子。此外，针对求解非凸非平滑问题易存在局部最小值的问题，可以利用外推步骤[18]改善迭代近端投影(IPP)算法的收敛性能，即
(16)
式中，w≥0为权重常数。则式(13)的解可表示为
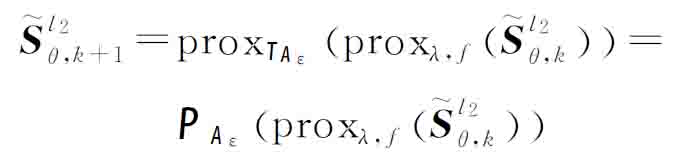
(17)
式中，PAε表示可行集
的投影。由文献[16]和[17]可知，非平滑函数的近端算子
可通过SCAD惩罚函数
产生相应的SCAD阈值函数
获得。该阈值函数不仅克服了硬阈值收缩函数对数据中微小波动的敏感性，而且避免了软阈值收缩函数带来的偏差，因此能够进一步促进解的稀疏度，则求解多快拍稀疏信号模型中非平滑函数的近端算子可被代替为
(18)
式中，SCAD阈值函数可表示为
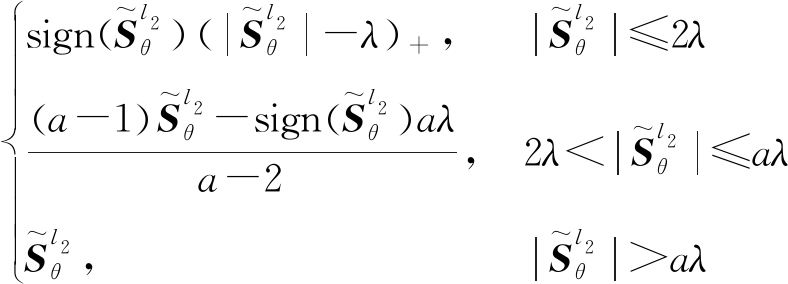
(19)
式中，a>2。通过求解式(17)得到稀疏向量
之后，搜索其谱峰所在位置得到真实目标DOA估计值。
结合以上理论分析，本文算法步骤可总结为：
步骤1 根据式(6)对MIMO雷达的输出信号进行降维变换，得到降维后的接收数据矩阵
步骤2 对MIMO雷达降维后的输出信号进行奇异值分解，得到
选取信号子空间
步骤3 构造多快拍稀疏信号表示模型：
步骤4 采用迭代近端投影算法求解稀疏信号表示模型：
初始化：
a) 设初始值
b) 选取一组合适的序列[λ1,λ2,…,λK]，且λk+1=cλk，0<c<1，λ1=max{|u0|}
算法迭代：
For k=1,2,…,K
a) 令λ=λk
b) 进行Q次迭代求解全局最小值，并将该最小值投影到可行集上
1) 令
2) For q=1,2,…,Q
(a) 计算
(b) 计算
(c) 将
投影到可行集，
3) 令
最终解
步骤5 通过搜索
的谱峰位置确定目标的DOA。
3 仿真结果及分析
为验证本文算法在MIMO雷达DOA估计方面的优势，选取MUSIC算法、前后向空域平滑MUSIC(Forward and Backward Spatial Smoothing_Music, FBSS_MUSIC)算法[23]、SL0(Smoothed l0 -norm, SL0)算法[10]与l1-SVD(l1-norm Singular Value Decomposition, l1-SVD)算法[8]进行对比，其中将本文利用近端函数优化模型求解MIMO雷达多快拍DOA估计的算法称为IPP-SCAD-SVD算法。假设均匀线阵单基地MIMO雷达的发射和接收阵元数均为5，收发阵元间隔为dt=dr=λ/2，在空间角度范围[-90°,90°]以角度间隔0.05°等分。假设存在3个远场窄带相干目标，设置各目标的DOA分别为θ1=-19.8°，θ2=0°，θ3=20.6°。DOA估计的均方根误差定义为
其中，
表示第p个目标在第mt次蒙特卡罗实验中的目标DOA的估计值，MT为蒙特卡罗实验次数。信噪比定义为
在本文算法中，选取a=2 000，w=0.9，外循环次数K=3,衰减因子c=0.8。
仿真实验1 图1为各种算法的DOA估计均方根误差随信噪比变化的曲线图。设置信噪比在-10～15 dB之间变化，快拍数J=100，进行100次蒙特卡罗实验。从图1可以看出，由于信源相干导致协方差矩阵的秩亏缺，信号特征向量发散到噪声子空间，造成MUSIC算法的DOA估计方法失效；FBSS-MUSIC算法利用前后向空间平滑技术实现信号的解相干，能够有效估计DOA，但在高信噪比下该方法的DOA估计性能较差。SL0-SVD算法、L1-SVD算法以及IPP-SCAD-SVD算法均属于基于压缩感知的DOA估计方法，这些方法能够对相干信源的DOA进行有效估计，且DOA估计的均方根误差随信噪比的增加而减小，而本文算法的DOA估计精度明显优于其他算法。
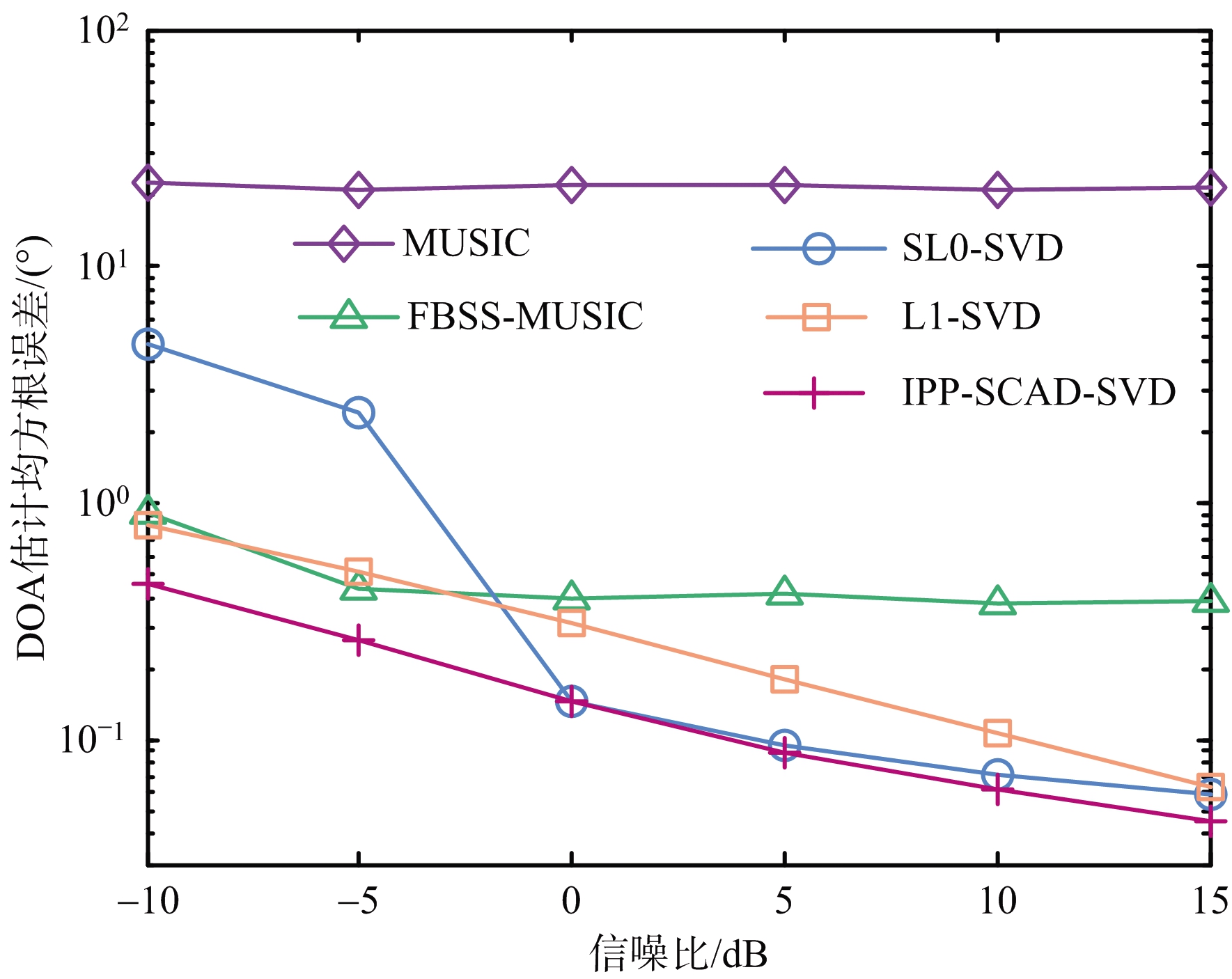
图1 各种算法的DOA估计均方根误差随信噪比变化的曲线图
仿真实验2 图2为各种算法的DOA估计均方根误差随快拍数的变化关系曲线。设置信噪比为-5 dB，进行100次蒙特卡罗实验，快拍数J在50～350之间变化。从图2可以看出，MUSIC算法无法处理相干信源，其他各种算法的角度估计精度均随着快拍数的增加而提高，而本文算法相比其他算法具有更高的DOA估计精度。
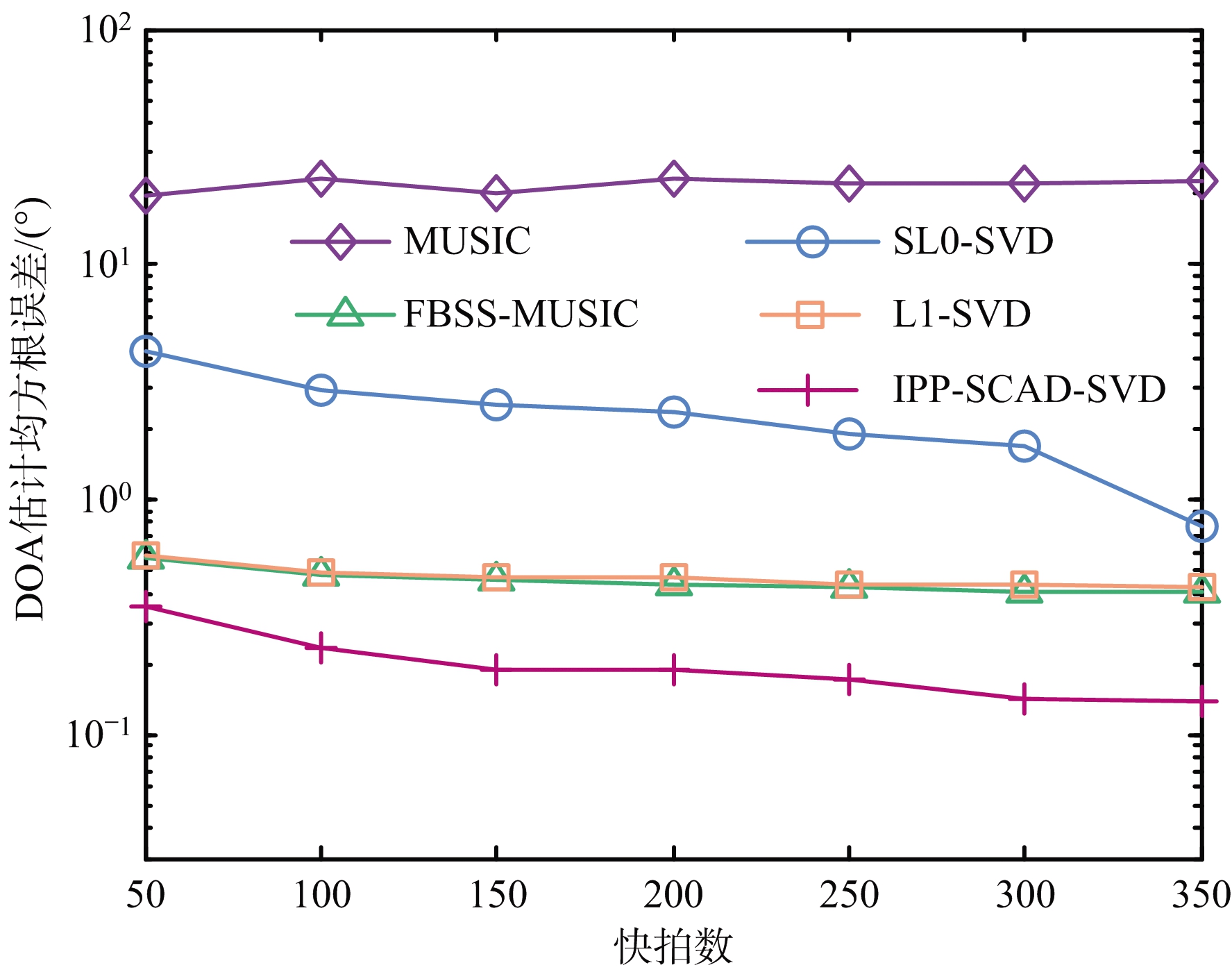
图2 各种算法的DOA估计均方根误差随快拍数的变化关系
仿真实验3 图3为各种算法的DOA估计均方根误差随两个相干目标的入射角度间隔Δθ的变化关系。两个相干目标的入射角度分别为θ1=6°，θ2=6°+Δθ，其中Δθ∈[14°,22°]，信噪比为5 dB，快拍数J=100，进行100次蒙特卡罗实验。从图3可以看出，MUSIC算法无法分辨相干目标，FBSS-MUSIC算法、SL0-SVD算法、L1-SVD算法和本文算法的DOA估计精度均随着目标角度间隔的增大而提高，而本文算法的DOA估计精度始终高于其他算法，表明本文算法相比其他算法能获得更高的空间角度分辨率。
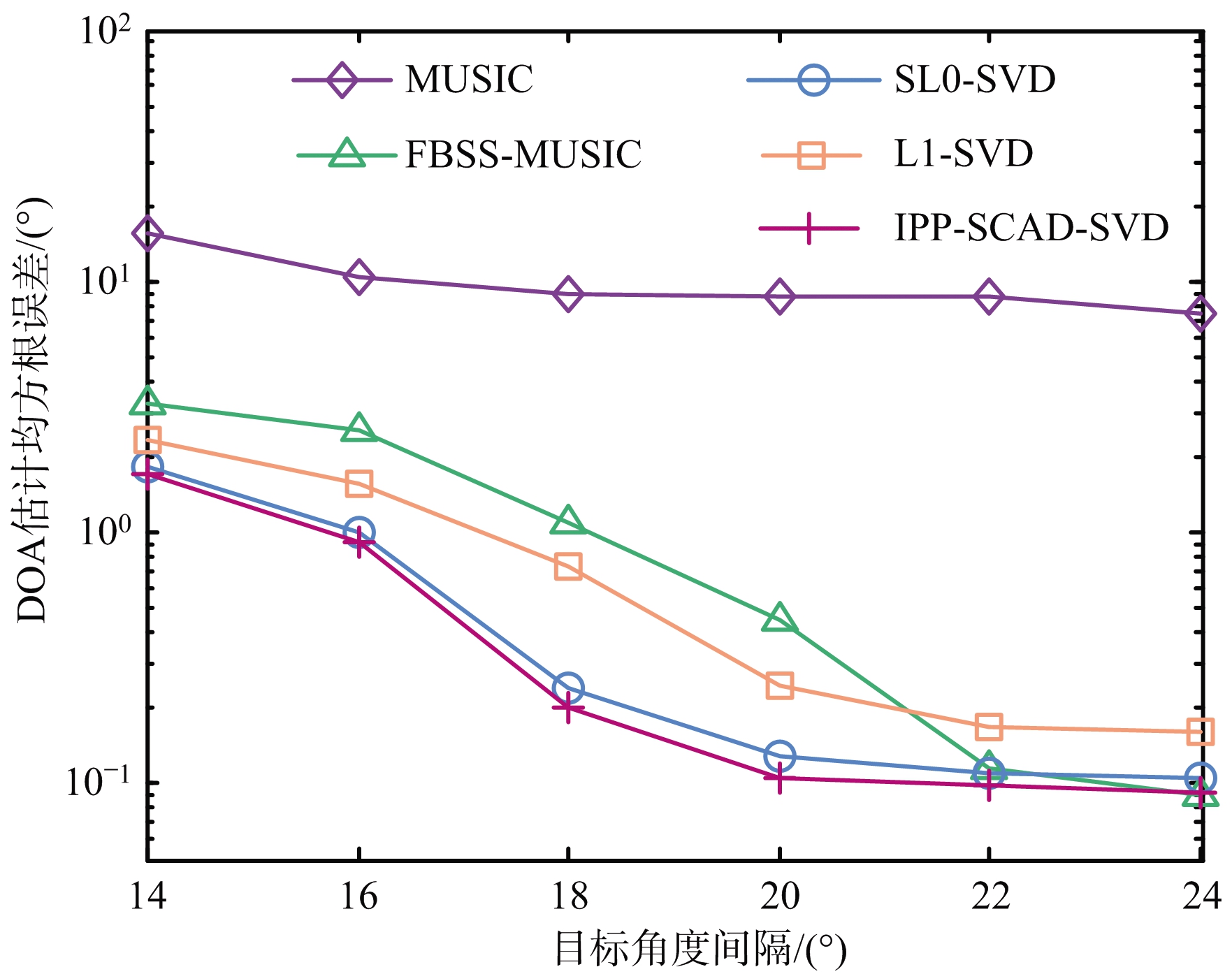
图3 各种算法的DOA估计均方根误差随角度间隔变化关系
4 结束语
在传统基于压缩感知的MIMO雷达DOA估计算法中，由于将非凸非平滑稀疏表示问题近似成凸或平滑函数问题进行求解，因此不可避免地存在稀疏表示模型误差，从而导致DOA估计性能不理想。本文将能解决非凸非平滑稀疏表示问题的迭代近端投影方法应用于MIMO雷达多快拍DOA估计中，首先对回波数据依次进行降维处理和奇异值分解，分别降低空域维度和时域维度，然后将多快拍DOA估计的非凸非平滑稀疏表示问题转化为近端函数优化模型的问题，最后采用SCAD函数获得近端算子以求解该模型。仿真结果表明，本文方法相比现有算法在相干信源的DOA估计方面拥有良好的性能。
[1] CHEN Peng, ZHENG Le, WANG Xiaodong, et al. Moving Target Detection Using Colocated MIMO Radar on Multiple Distributed Moving Platforms[J]. IEEE Trans on Signal Processing, 2017, 65(17):4670-4683.
[2] LIU Jun, HAN Jinwang, ZHANG Zijing, et al. Bayesian Detection for MIMO Radar in Gaussian Clutter[J]. IEEE Trans on Signal Processing, 2018, 66(24):6549-6559.
[3] SALARI S, CHAN F, CHAN Y T,et al. Joint DOA and Clutter Covariance Matrix Estimation in Compressive Sensing MIMO Radar[J]. IEEE Trans on Aerospace and Electronic Systems, 2019, 55(1):318-331.
[4] AUBRY A, CAROTENUTO V, DE MAIO A. A New Optimality Property of the Capon Estimator[J]. IEEE Signal Processing Letters, 2017, 24(11):1706-1708.
[5] TAN Jun, NIE Zaiping, WEN Dingbang. Low Complexity MUSIC-Based Direction-of-Arrival Algorithm for Monostatic MIMO Radar[J]. Electronics Letters, 2017, 53(4):275-277.
[6] ZHENG Guimei, TANG Jun,YANG Xuan. ESPRIT and Unitary ESPRIT Algorithms for Coexistence of Circular and Noncircular Signals in Bistatic MIMO Radar[J]. IEEE Access, 2016, 4:7232-7240.
[7] WANG Xinhai, ZHANG Gong,WEN Fangqing, et al. Angle Estimation for Bistatic MIMO Radar with Unknown Mutual Coupling Based on Three-Way Compressive Sensing[J]. Journal of Systems Engineering & Electronics, 2017, 28(2):257-266.
[8] MALIOUTOV D, CETIN M, WILLSKY A S. A Sparse Signal Reconstruction Perspective for Source Localization with Sensor Arrays[J]. IEEE Trans on Signal Processing, 2005, 53(8):3010-3022.
[9] LIU Qi, WANG Xianpeng. Direction of Arrival Estimation via Reweighted l1Norm Penalty Algorithm for Monostatic MIMO Radar[J]. Multidimensional Systems and Signal Processing, 2018, 29(2) :733-744.
[10] MOHIMANI H, BABAIE-ZADEH M, JUTTEN C. A Fast Approach for Overcomplete Sparse Decomposition Based on Smoothed L0 Norm[J]. IEEE Trans on Signal Processing, 2009, 57(1):289-301.
[11] CHEN S S, SAUNDERS D M A. Atomic Decomposition by Basis Pursuit[J]. SIAM Review, 2001, 43(1):129-159.
[12] LIU J,ZHOU W D, JUWONO F H. Joint Smoothed l0-Norm DOA Estimation Algorithm for Multiple Measurement Vectors in MIMO Radar[J]. Sensors, 2017, 17(5):1068.
[13] SADEGHI M, BABAIE-ZADEH M. Iterative Sparsification-Projection:Fast and Robust Sparse Signal Approximation[J]. IEEE Trans on Signal Processing, 2016, 64(21):5536-5548.
[14] PARIKH N, BOYD S. Proximal Algorithms[J].Foundations and Trends in Optimization, 2014,1(3):127-239.
[15] GHAYEM F, SADEGHI M, BABAIE-ZADEH M, et al. Sparse Signal Recovery Using Iterative Proximal Projection[J]. IEEE Trans on Signal Processing, 2018, 66(4):879-894.
[16] FAN Jianqing, LI Runze. Variable Selection via Nonconcave Penalized Likelihood and Its Oracle Properties[J]. Journal of the American Statistical Association, 2001, 96(456):1348-1360.
[17] FAN Jianqing. Comments on 《Wavelets in Statistics: A Review》 by A. Antoniadis[J]. Journal of the Italian Statistical Society, 1997, 6(2):131-138.
[18] NESTEROV Y. Introductory Lectures on Convex Optimization: A Basic Course[M]. Boston,MA,USA:Kluwer, 2004.
[19] LIU Jing, ZHOU Weidong, JUWONO F H, et al. Reweighted Smoothed l0-Norm Based DOA Estimation for MIMO Radar[J]. Signal Processing, 2017, 137:44-51.
[20] EFTEKHARI A, BABAIE-ZADEH M, JUTTEN C, et al. Robust-SL0 for Stable Sparse Representation in
Noisy Settings[C]∥IEEE International Conference on Acoustics, Speech and Signal Processing，Taipei：IEEE, 2009:3433-3436.
[21] NOCEDAL J, WRIGHT S J. Numerical Optimization[M]. New York: Springer, 1999.
[22] TSENG P. Convergence of a Block Coordinate Descent Method for Nondifferentiable Minimization[J]. Journal of Optimization Theory and Applications, 2001, 109(3):475-494.
[23] QI Chongying, CHEN Zhijie, WANG Yongliang, et al. DOA Estimation for Coherent Sources in Unknown Nonuniform Noise Fields[J]. IEEE Trans on Aerospace & Electronic Systems, 2007, 43(3):1195-1204.
