0 引言
被动导引头利用辐射源发射的信号对目标进行截获跟踪并引导攻击。在密集的信号环境中形成脉冲描述字(PDW),再对PDW流进行分选、参数估计和雷达辐射源识别。重频分选作为其信号处理的重要环节,是复杂电磁环境中稀释脉冲的主要手段,对重频分选过程实施干扰可有效降低反辐射武器攻击能力。在信号预分选成功的前提下,部分学者提出了针对不同重频分选算法的干扰方法[1-2],具有良好的效果。
随着重频分选技术算法的不断改进和发展,对分选过程的干扰难度逐渐加大[3-6]。分选参数的测量作为分选过程的基础,测量结果的准确性决定分选的正确性[7-8],对分选参数测量过程实施干扰同样可以影响重频分选过程。为研究对被动导引头参数分选过程的作用机理,借助导引头对雷达参数的测量模型,从研究影响参数测量精度的起因出发,得到了高重频脉冲的干扰机理,并结合导引头工作过程建立了干扰效能与脉冲参数之间的数学模型。
1 高重频脉冲的信号特征
高重频脉冲是一种重复频率极高的脉冲信号,脉冲宽度通常为几纳秒至几百纳秒,远小于雷达信号的脉冲宽度,具有超宽带的特性。其时域表达式为[9]
(1)
式中,A为脉冲幅度,τ为脉冲宽度,T为脉冲重复周期,N为脉冲数量,rect(·)为矩形函数。对式(1)进行傅里叶变换得到高重频脉冲的频域表达式为
J(f)=A·τ·
(2)
设PRFj为高重频脉冲重复频率,当A=2 mV,τ=1 ns,N=1 000,PRFj=200 kHz时,高重频脉冲时域波形和频谱如图1所示。
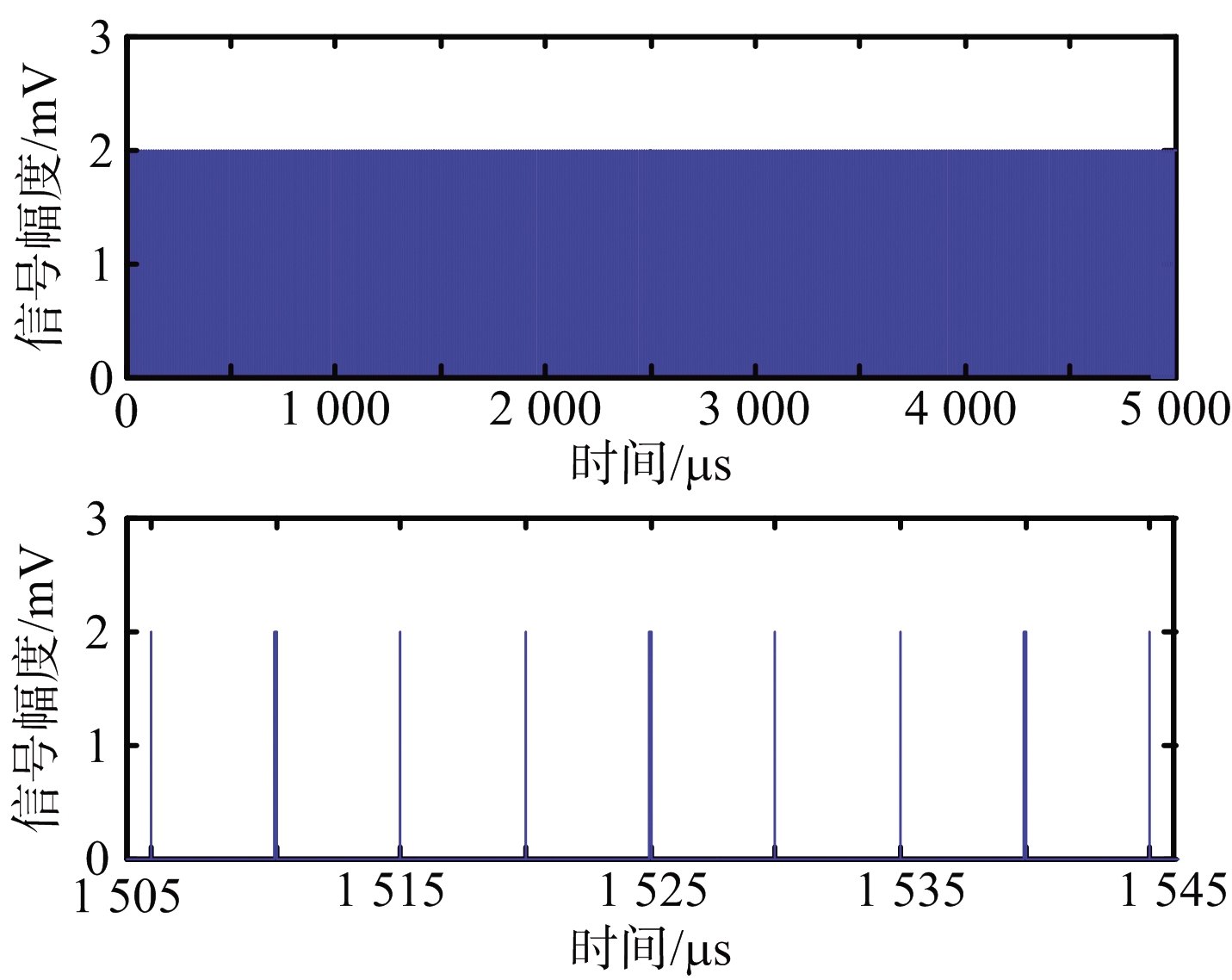
(a) 时域波形
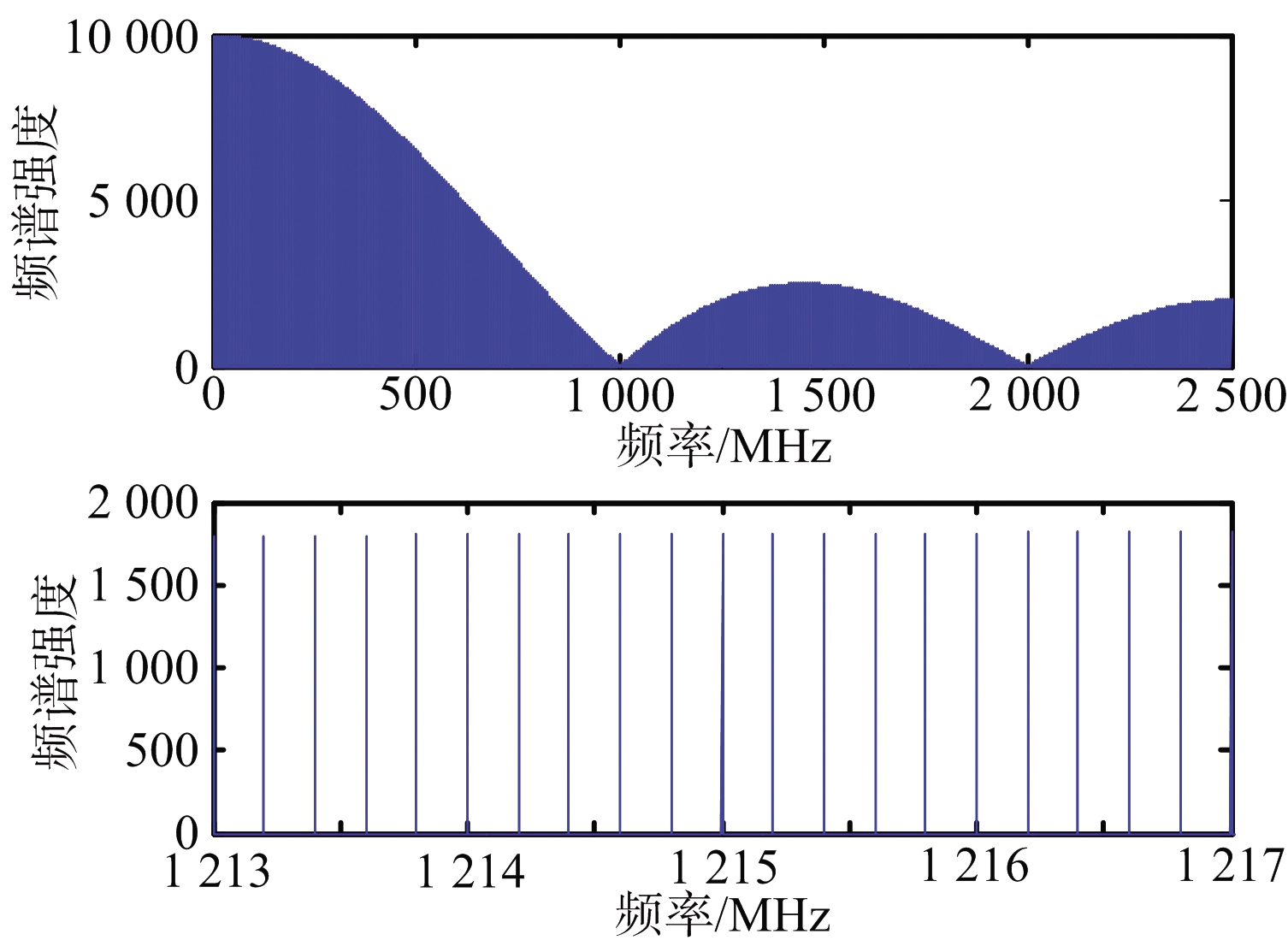
(b) 频谱
图1 高重频脉冲时域波形及频谱图
从图1可以看出,高重频脉冲的频谱由离散谱线组成,相邻谱线间隔为脉冲重复频率,谱线包络同sinc函数,频率覆盖范围极宽。由于模拟器件的非线性特性,高重频干扰进入导引头后在时域上会产生较为严重的瞬态响应[11],其宽频带特性可使得干扰信号频域上覆盖导引头接收频带,影响参数测量。
2 对分选参数测量过程的干扰机理分析
实际应用中,通常根据侦察系统的用途、工作环境及导引头的测量能力选择分选参数。本文以三参数分选为例,分析对载频、到达方向和脉宽测量过程的干扰机理。
2.1 对频域参数的干扰
被动导引头要求测频接收机的测频范围大、精度高,此外,导引头通常空间小、载重有限,要求测频接收机的体积小、重量轻,因此测频接收机通常为超外差接收机。典型搜索式超外差接收机工作原理如图2所示。
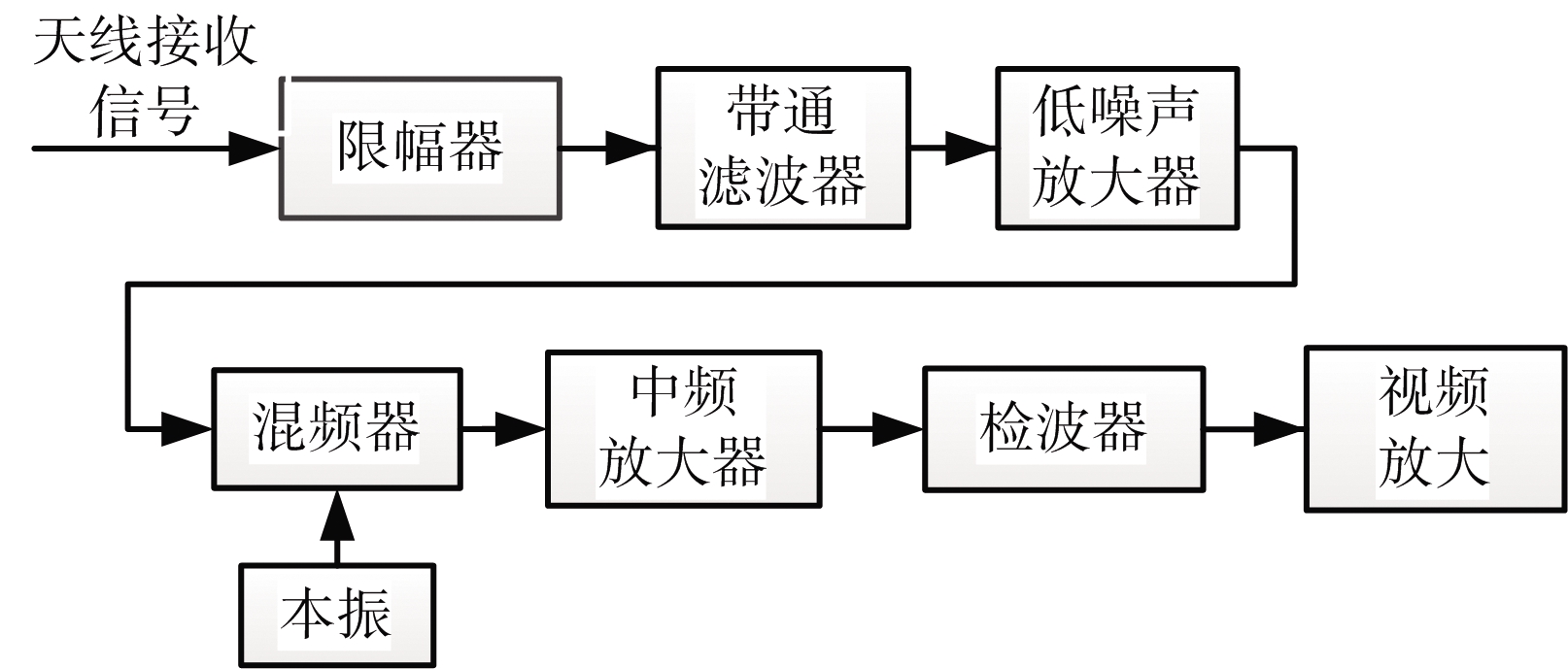
图2 典型搜索式超外差接收机原理
接收机的设计不仅要保证接收灵敏度和动态范围,还要克服噪声的影响以降低虚警概率,为此必须设定一个检测门限[10]。施放高重频脉冲后,由于其超宽频带特性,在中频带宽内将布满干扰谱线,但只有当干扰能量超过信号能量时,才可能对频域参数测量形成干扰。下面分别计算接收机输出的雷达和干扰功率。
设雷达和干扰脉冲的脉宽、重复频率分别为τs、τj、PRFs、PRFj,ds、dj分别为雷达和干扰脉冲占空比,其大小为
ds=τs·PRFs
(3)
dj=τj·PRFj
(4)
导引头前端接收到的雷达信号平均功率Psr和干扰信号平均功率Pjr为
(5)
(6)
式中,Pt、Ptj、Gt、Gtj分别为雷达和干扰源的发射峰值功率及增益,R、Rj为雷达、干扰源与导引头(看作质点)的距离,Gr为导引头天线增益,λ为雷达信号波长,L为信号传播过程中考虑馈线、极化和大气衰减后的总损耗,通常为15~17 dB。
设前端带通滤波器带宽为B,通常情况下B远小于高重频脉冲谱宽,此时认为所有进入滤波器的干扰谱线强度近似相等,均为滤波器中心频率对应谱线的强度。这样,滤波器输出干扰功率为[11]
(7)
式中,PRFj为干扰脉冲重复频率,f0为带通滤波器中心频率,P(f0)为f0对应干扰谱线的功率,大小为
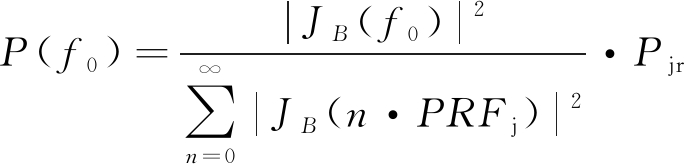
(8)
式中,JB(f0)表示滤波器输出的频率为f0的干扰谱线强度,大小为
JB(f0)=H(f0)J(f0)
(9)
式中,H(f)为带通滤波器传输特性,理想情况下有
(10)
式中,f1、f2为带通滤波器的起始频率和截止频率。
干扰脉冲通过低噪声放大器时,将产生三阶互调分量,其功率大小为
PJ2=3(PJ1·G)-2Q3
(11)
式中,G为放大器增益,Q3为放大器的三阶截交点,通常在放大器的技术指标中给定。
由限幅器、带通滤波器、低噪声放大器组成的导引头前端,假设其能确保不失真地传输雷达信号,那么,中放输出的信号功率可近似为G·Psr。雷达信号经过混频进入检波器后,将其视为大信号,故检波被近似为线性过程,因此输出功率为
(12)
式中,Kd为检波系数。
理论上,脉冲信号具有无限谱宽,当通过有限带宽系统时,包络会因为频率成分的丢失而发生畸变。高重频脉冲进入导引头后,接收频带以外的频率分量会被滤除,干扰脉冲包络会发生形变,且由于重复频率极高,相邻脉冲相互交叠,会形成类噪声信号[12]。将其近似为射频噪声,则检波器输出的干扰脉冲功率变为[13]
(13)
式中,BI为中频放大器带宽,PJ3为直接落入接收机中频通带的频率分量产生的干扰功率,其大小为
(14)
最后,截获信号(含雷达脉冲和干扰脉冲)经过视频放大器时,将其视为线性系统,并考虑接收机热噪声,故接收机输出信干比为
(15)
式中,PN0为接收机内部噪声功率,其大小为
PN0=kT0FBI
(16)
式中,k为玻耳兹曼常数,T0为接收机温度,F为噪声系数。本文假设无干扰情况下,雷达载频可被准确测量,则当SIRout≤0 dB时,干扰脉冲能量将超过检测门限被接收机输出,对测频过程带来影响,此时认为干扰有效。
2.2 对空域参数的干扰
雷达为了实现反干扰、反侦察等目的,它的各项信号参数如载频、重频、脉宽等趋向于快速随机变化。在同一雷达发射的脉冲串中,唯有方位参数是相对稳定的,因此,辐射源方向是被动导引头信号分选和识别的重要参数。被动导引头多采用振幅和差单脉冲比幅测向及角度跟踪技术测量辐射源方位[14],利用两个特性相同的天线同时接收到雷达信号,对两个信号进行幅度比较确定雷达辐射源方位,方向瞄准精度高。
振幅和差单脉冲测向系统的测向误差由系统误差和随机误差构成。随机误差主要是由系统噪声引起的,即两个接收通道的内部噪声不能相互抵消,造成功率比值的变化。噪声带来误差原因示意图如图3所示。
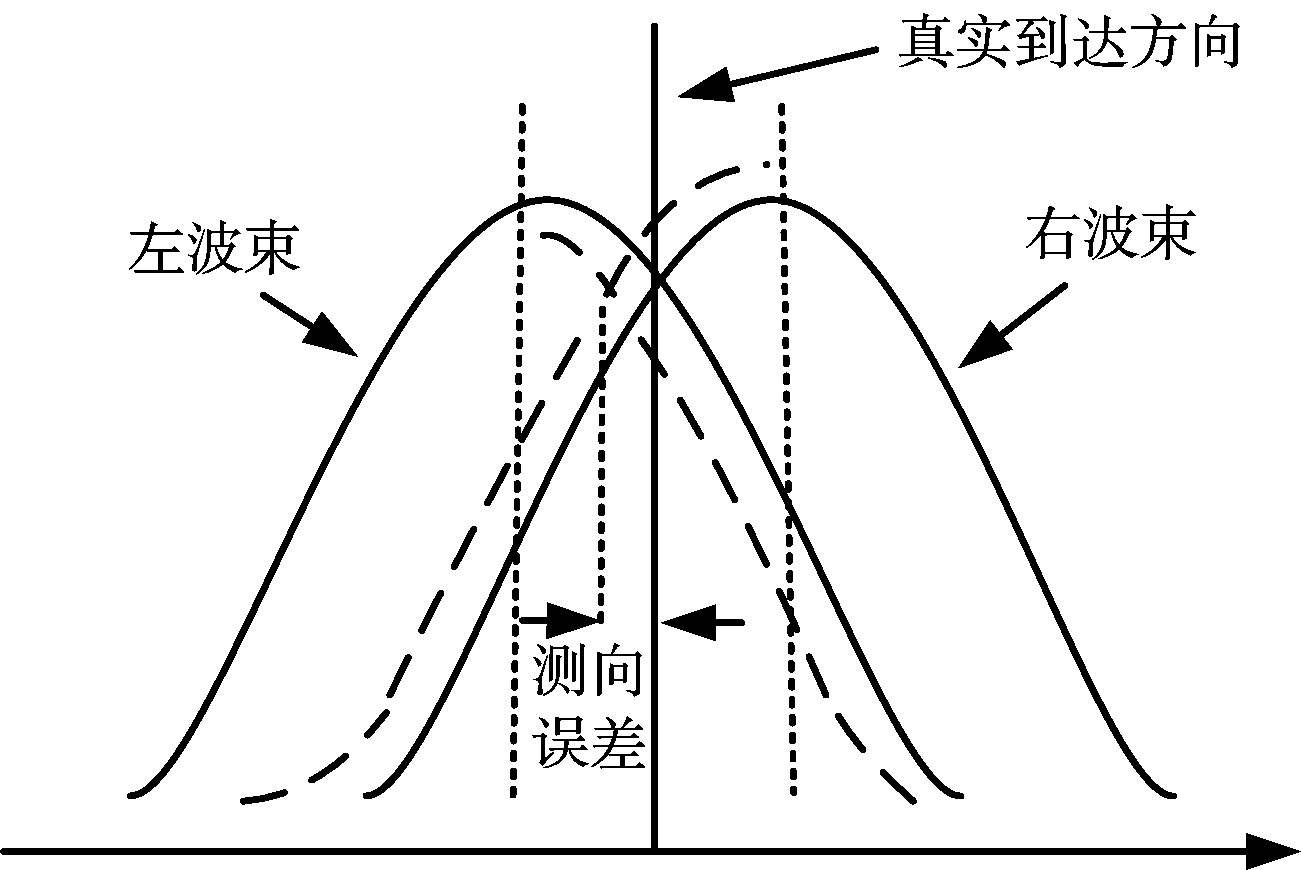
图3 噪声对测角精度的影响示意图
设雷达信号从波束交叉点入射。从图3可以看出,由于噪声的影响使两个支路输出信号的波形发生畸变,从实线变化到虚线位置。显然,两个支路内部噪声越小,则测角误差越小。此外,天线波束宽度越大时,同样大小的噪声会造成更大角度内输出信号的幅度畸变,因此,随机噪声引起的测向误差均方根为[15]
(17)
式中,S/N为接收机输出信噪比,θr为天线半功率波束宽度。在天线波束形变量不大的情况下,由式(17)可以看出,接收机输出信噪比是影响测向精度的重要因素。
干扰脉冲形成的类噪声信号增加了输出噪声功率,降低前端输出信噪比,导致测向精度下降。在式(3)~(16)分析的基础上,考虑接收机热噪声,得到接收机输出信噪比为
(18)
从式(18)可以看出,改变干扰脉冲参数将影响接收机输出信噪比,进而降低测向精度。
2.3 对脉冲宽度的干扰
信号脉冲宽度测量过程中,保宽脉冲包络的完整性和准确性决定了脉宽测量的准确性。与到达方向测量类似,τs的检测和测量也会受到系统噪声的影响[16]。特别是在脉冲前沿较平缓、信噪比较低时,系统噪声不仅影响侦察系统的检测概率和虚警概率,还将引起门限检测时间t的随机抖动δt,其测量误差的均方根为[17]
(19)
式中,trs、tdo分别为脉冲上升沿和下降沿时间。由式(19)可以看出,脉冲宽度测量精度同样受到接收机输出信噪比的影响,S/N的计算方法同式(18),一旦测量误差均方根超过预分选容差,将导致预分选错误。
3 仿真验证
在实际作战过程中,被动导引头分选参数范围的确定是一个复杂的过程。一方面,侦察系统很难精确地掌握此时此地每一部已知雷达的具体工作参数,另一方面,一个作战地域内往往同时存在着敌我双方大量的雷达,同波段、同方向、同脉宽,甚至同型号的雷达同时工作也是司空见惯的。因此,构造的分选单元会有相互交织甚至部分重合的模糊情况,参数范围的确定也是根据实际情况实时变化的。本文假设当测量误差均方根超出真实值10%时,认为预分选错误。并分析最简单的情况,对固定载频雷达进行侦察。
由于前端输出信噪比随被动导引头空间位置的变化而实时变化,为便于分析,仿真中将雷达、干扰源和导引头的位置固定。以雷达为原点,建立空间直角坐标系,设定某一时刻导引头和干扰源坐标为(-3 500 m,-3 700 m,3 000 m)、(-1 050 m,100 m,0)。雷达参数如下:载频f0=1 215 MHz,τs=400 μs,trs=tdo=80 μs,Gt=20 dB,ds=0.2;导引头各器件参数如下:接收天线增益Gr=3 dB,θr=60°;干扰天线增益Gtj=40 dB;带通滤波器参数:f1=1 165 MHz,f2=1 265 MHz,本振频率 fL=565 MHz,k=1.38×10-23 J/K,T0=290 K,F=12 dB,信号传输过程中总损耗L=17 dB,检波器检波系数Kd=0.3。
3.1 对载频测量的干扰效果
设干扰脉冲脉宽1 ns,重复频率200 kHz,则干扰脉冲混频后落入中频通带的频率分量如图4所示。
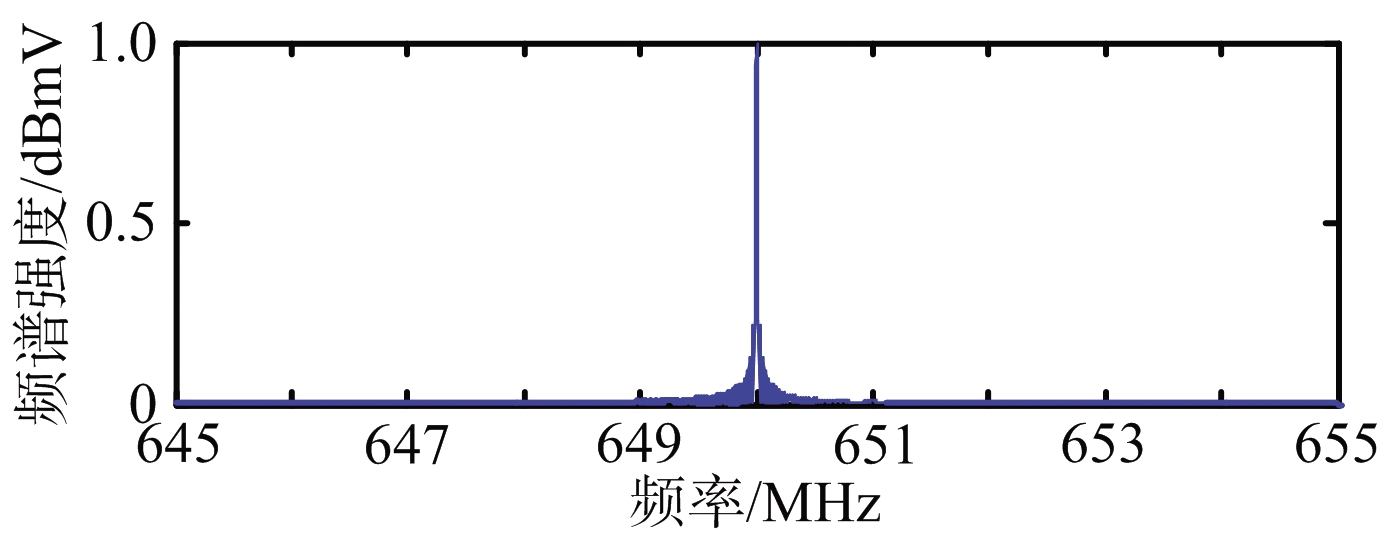
(a) 无干扰时中频频谱
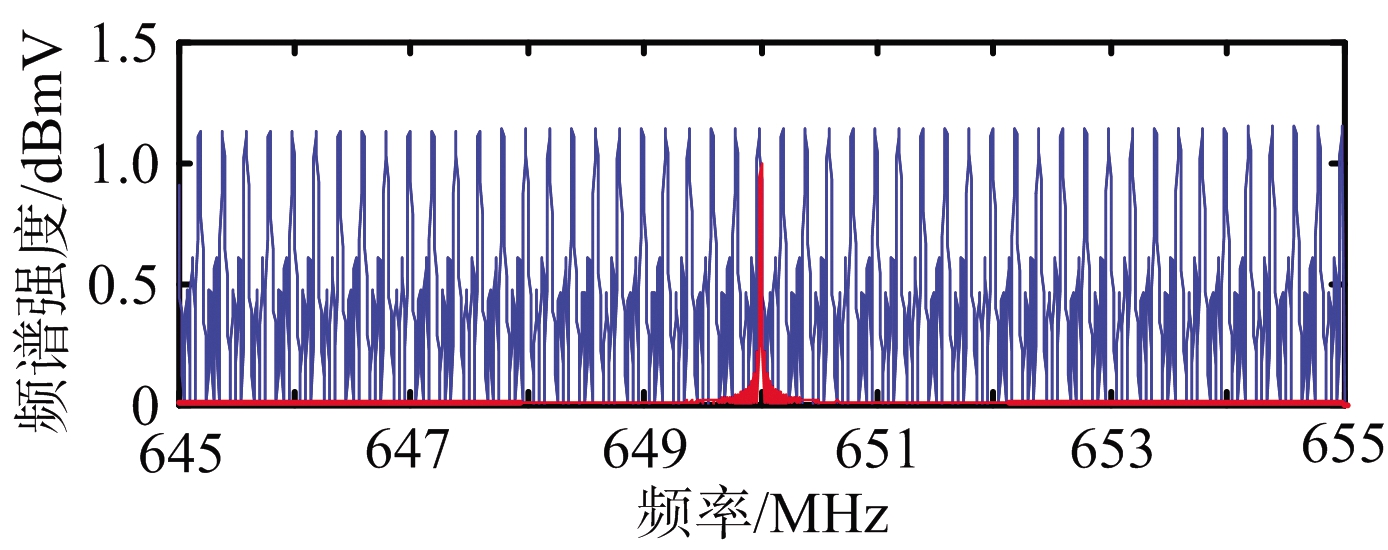
(b) 干扰后中频频谱
图4 干扰前后中频接收频率分量
从图4可以看出,无干扰情况下,接收频带内只有雷达载频。实施干扰后,等间隔分布着密集的干扰谱线,在频域上覆盖了信号载频。改变干扰脉冲参数,分析不同参数对接收机输出信干比的影响。
当PRFj=400 kHz,τj=1 ns时,改变Ptj,得到SIRout随干扰功率变化情况如图5(a)所示;当Ptj=10 kW,τj=1 ns时,改变PRFj,得到SIRout随干扰重频变化情况如图5(b)所示;当Ptj=5 kW,PRFj=2 MHz时,改变dj,得到SIRout随干扰占空比变化情况如图5(c)所示。
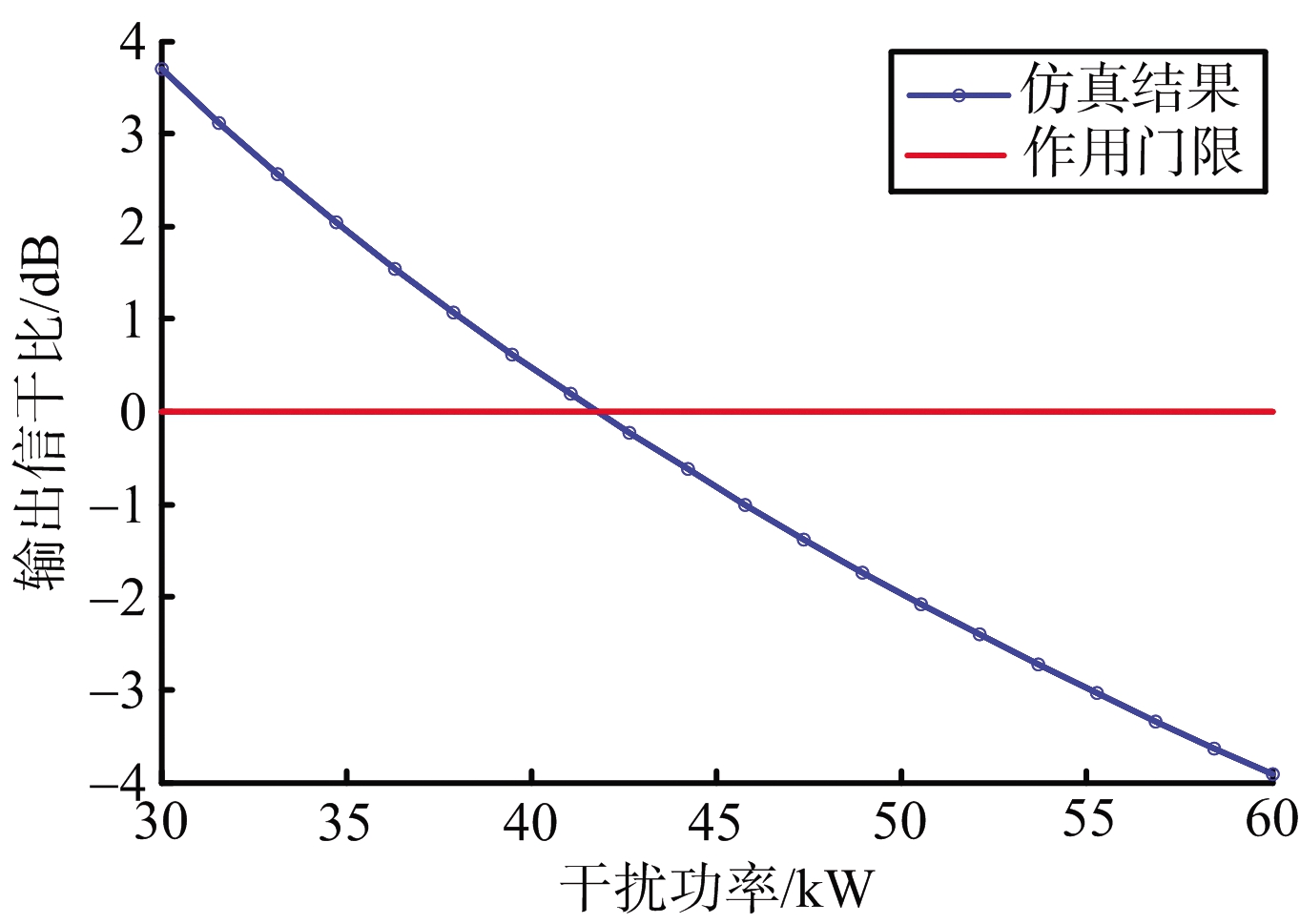
(a) SIRout随干扰功率变化情况
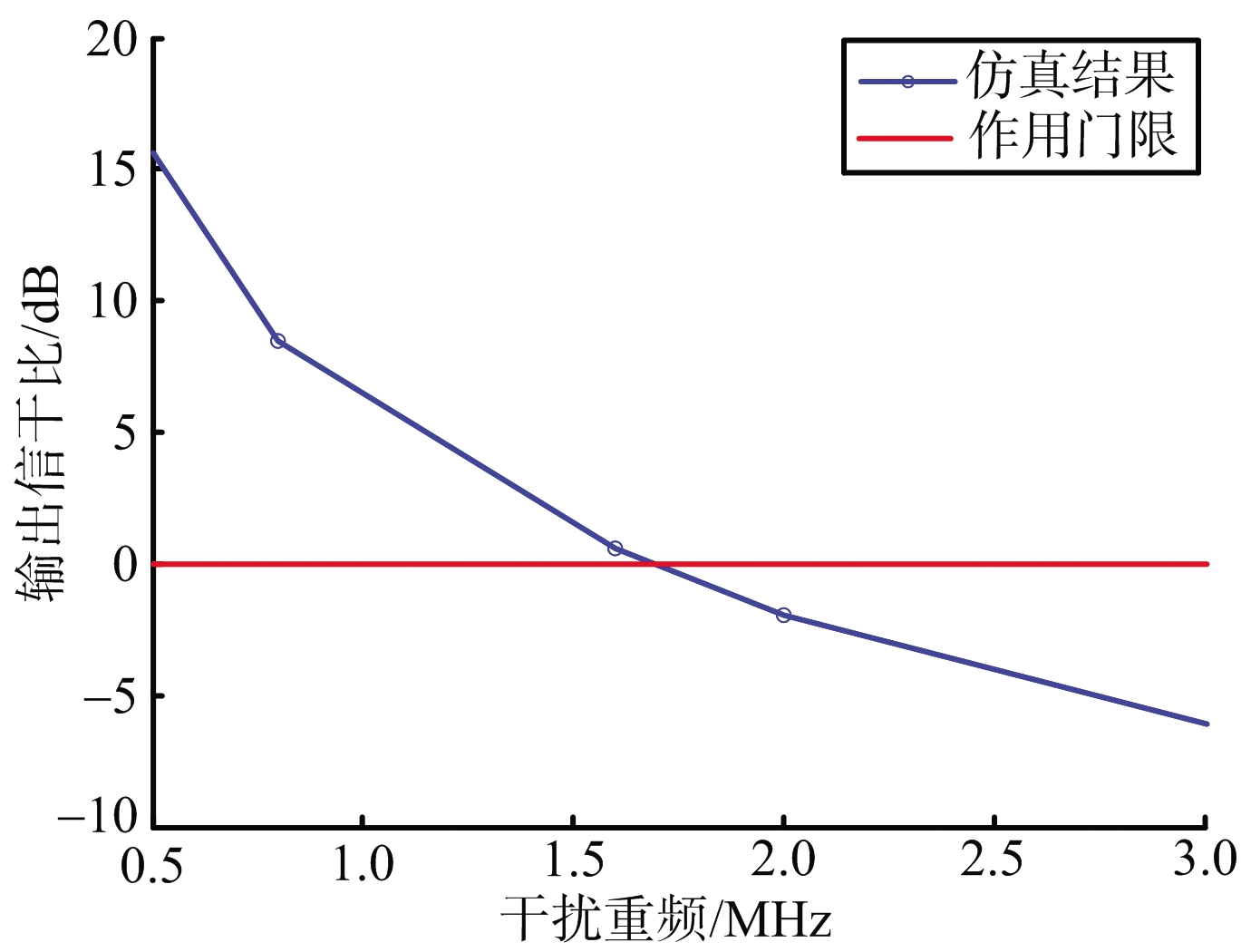
(b) SIRout随干扰重频变化情况
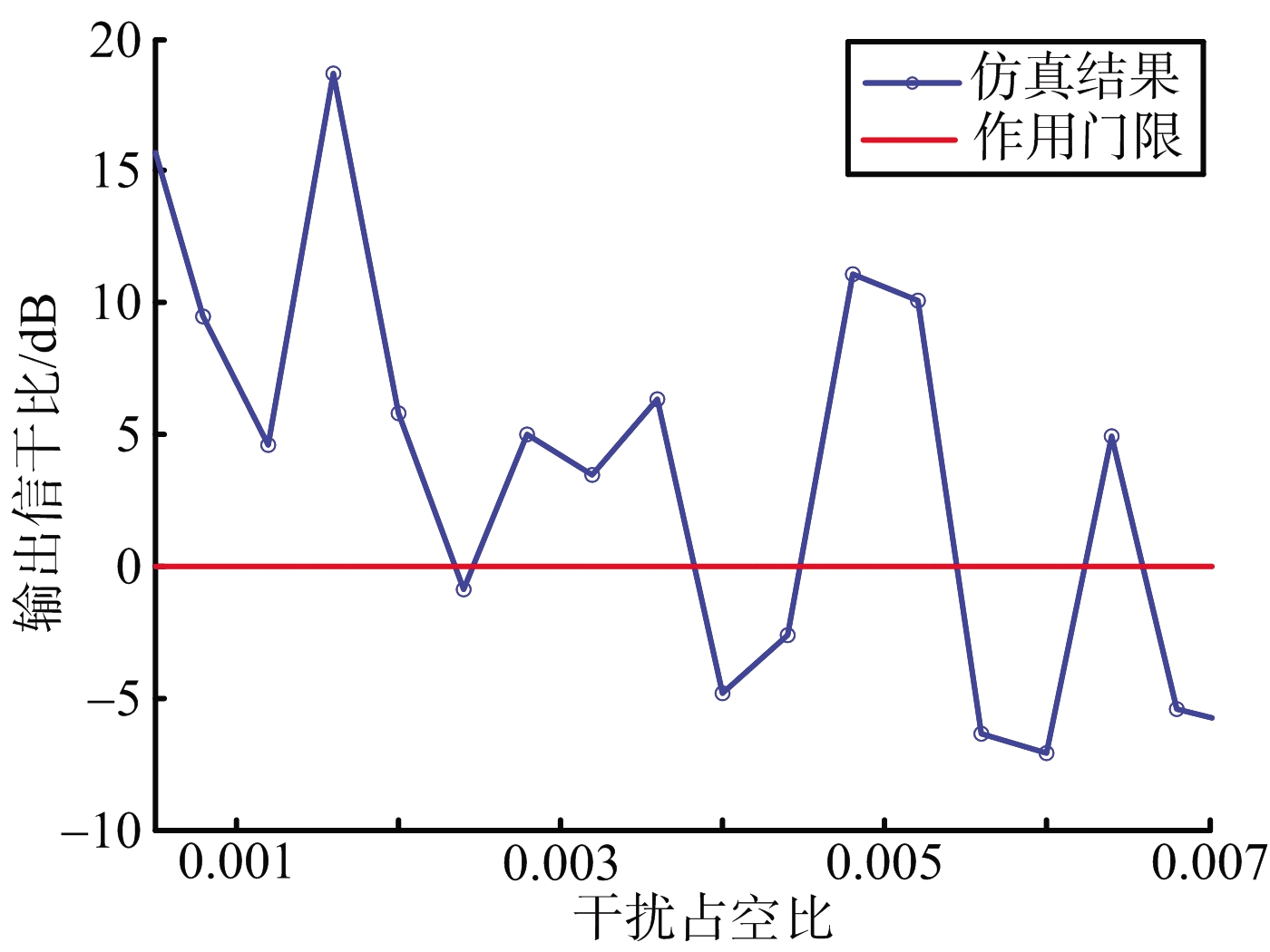
(c) SIRout随干扰占空比变化情况
图5 SIRout随干扰参数变化情况
从图5(a)、(b)可以看出,随着干扰功率、重复频率的增加,接收机输出信干比在逐渐降低。在仿真条件下,当Ptj=42 kW、PRFj=1.75 MHz时,SIRout降至0 dB,此时干扰脉冲将发挥作用。从图5(c)可以看出,整体上SIRout在逐渐降低,但在小范围内出现波动。根据式(2)、式(6)分析其原因,干扰重频固定时,占空比增加会增加脉宽,使落入接收机带宽内的干扰谱线幅值减小,且其包络形状为sinc函数;而脉冲占空比变大,接收到的干扰信号平均功率加大,导致信干比降低,两者共同作用后,会使SIRout出现波动状况,但随着占空比的不断加大,后者作用效果将抵消前者,产生图5(c)所示效果。可见SIRout与占空比不存在单调的线性关系,调节占空比来改变干扰效果不是理想的方法。
3.2 对到达方向测量的干扰效果
当PRFj=400 kHz,τj=1 ns时,改变Ptj,得到σdoa随输出信噪比变化情况如图6(a)所示;当Ptj=200 kW,τj=1 ns时,改变PRFj,得到σdoa随干扰重频变化情况如图6(b)所示;当Ptj=50 kW,PRFj=400 kHz时,改变dj,得到σdoa随干扰占空比变化情况如图6(c)所示。图中横线表示预分选容差,其大小为真实测量角度的10%。
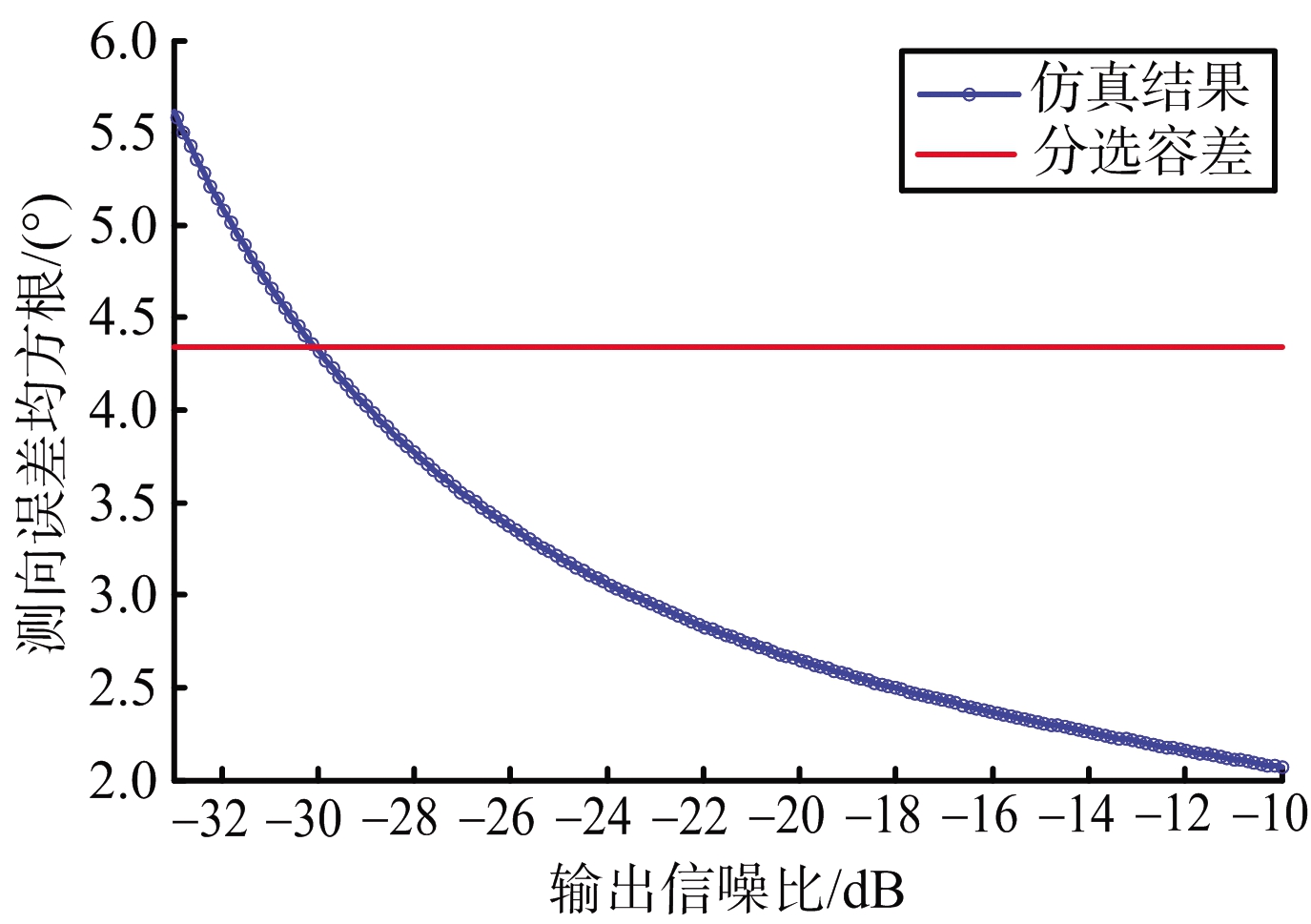
(a) σdoa随信噪比变化情况
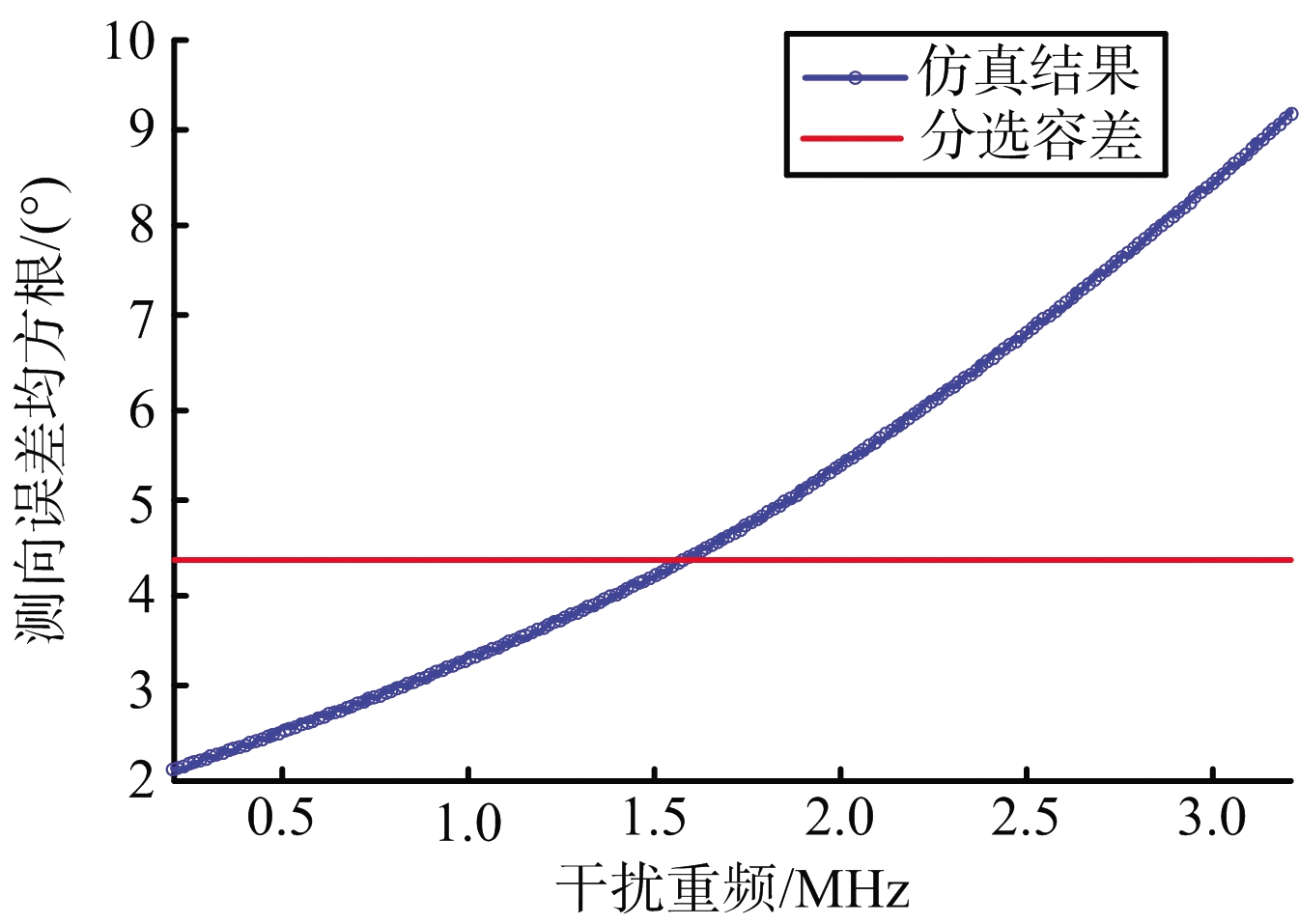
(b) σdoa随重频变化情况
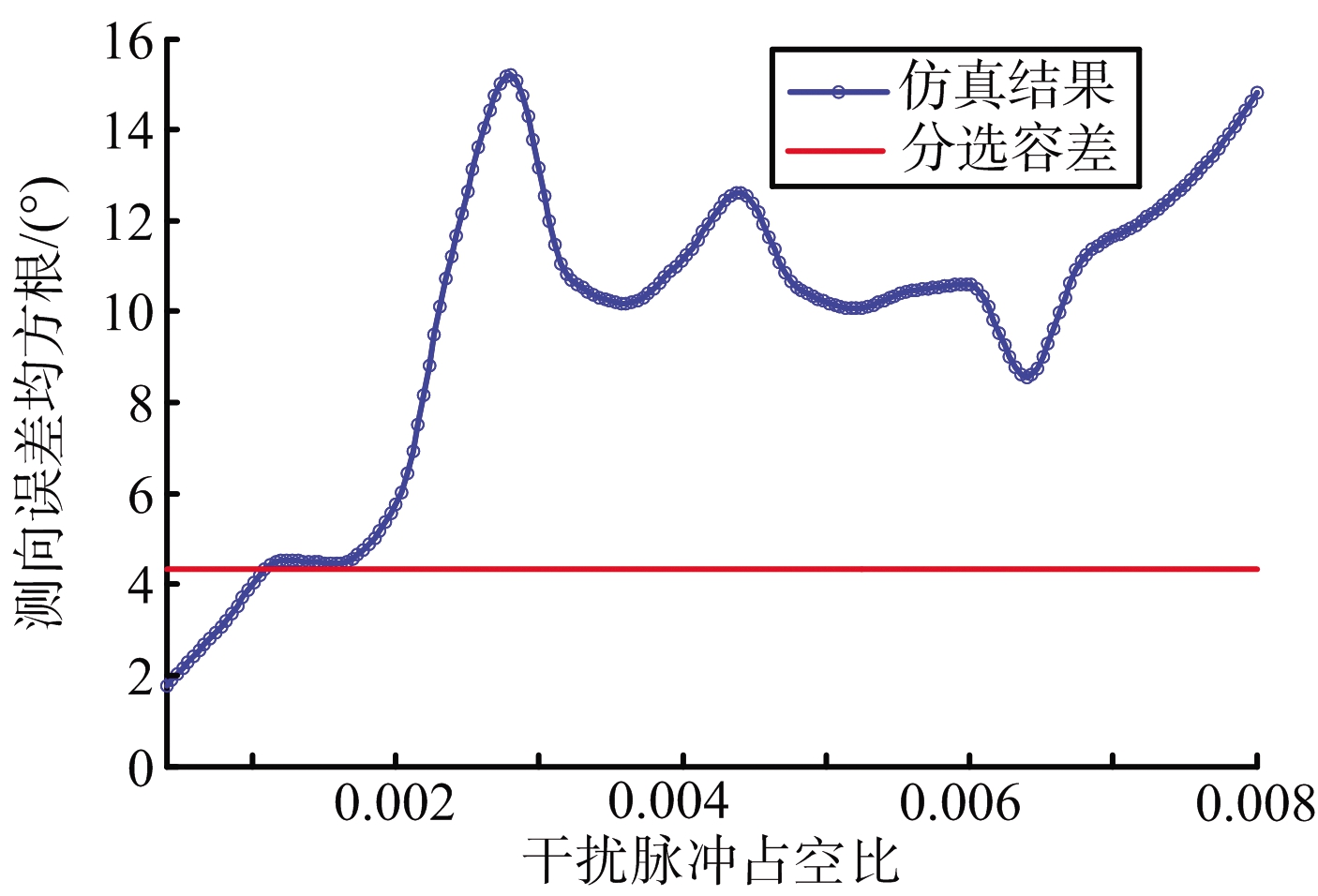
(c) σdoa随占空比变化情况
图6 σdoa随干扰参数变化情况
从图6(a)、(b)可以看出,随着输出信噪比降低、干扰重频增大,测向误差均方根逐渐增大。仿真条件下,当S/N低于-30 dB、PRFj大于1.6 MHz时,将导致分选错误。从图6(c)可以看出,干扰脉冲占空比增加后,整体上σdoa逐渐变大,但曲线仍有起伏情况。如3.1节所述,改变占空比后SIRout出现波动,导致σdoa出现波动。
3.3 对脉宽测量的干扰分析
当PRFj=400 kHz,τj=1 ns时,改变Ptj,得到δτs随输出信噪比变化情况如图7(a)所示;当Ptj=20 kW,τj=1 ns时,改变PRFj,得到δτs随干扰重频变化情况如图7(b)所示;当Ptj=20 kW,PRFj=400 kHz时,改变dj,得到δτs随之变化情况如图7(c)所示。图中横线表示预分选容差,其大小为脉宽测量值的10%。
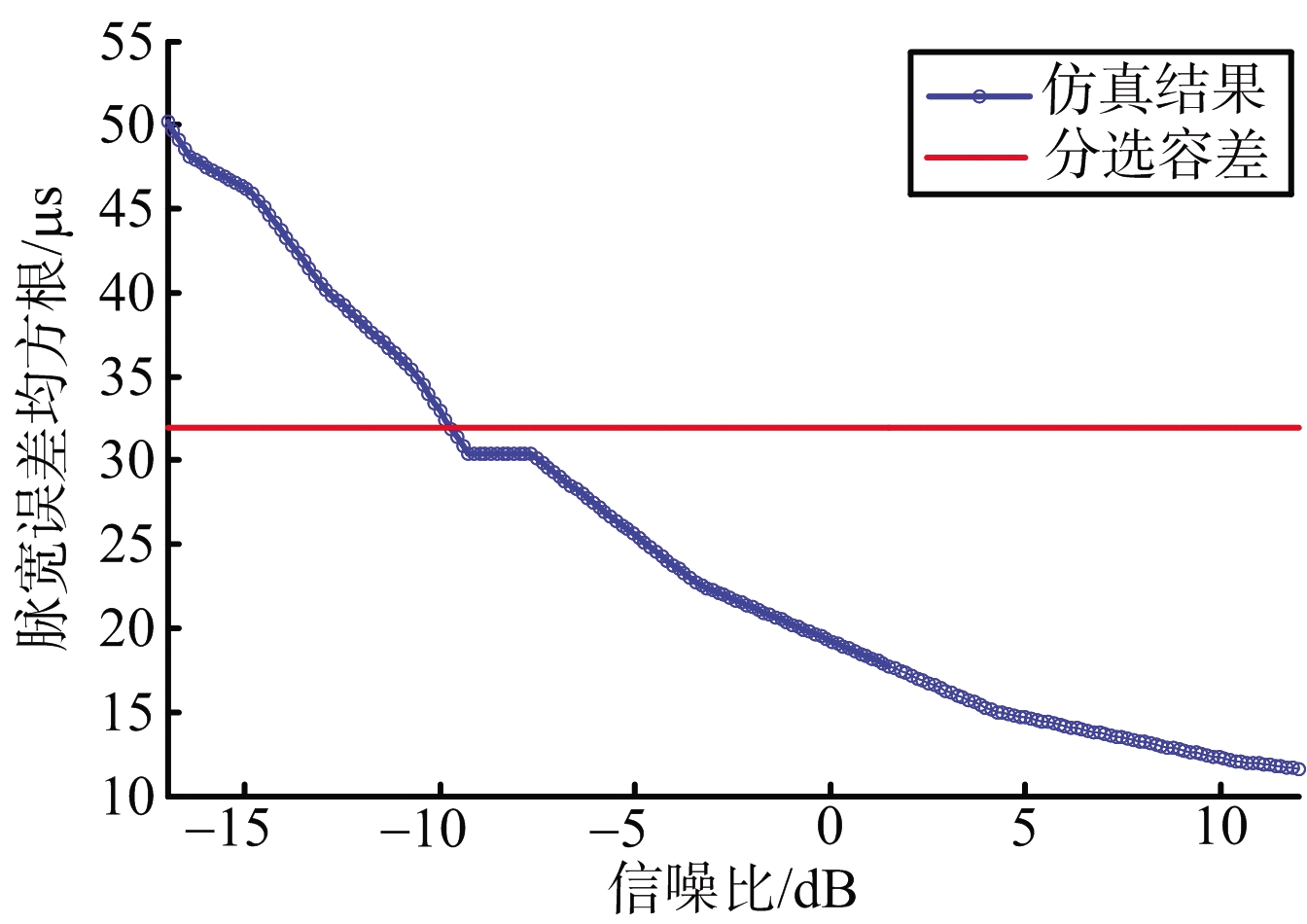
(a) δτs随信噪比变化情况

(b) δτs随干扰重频变化情况
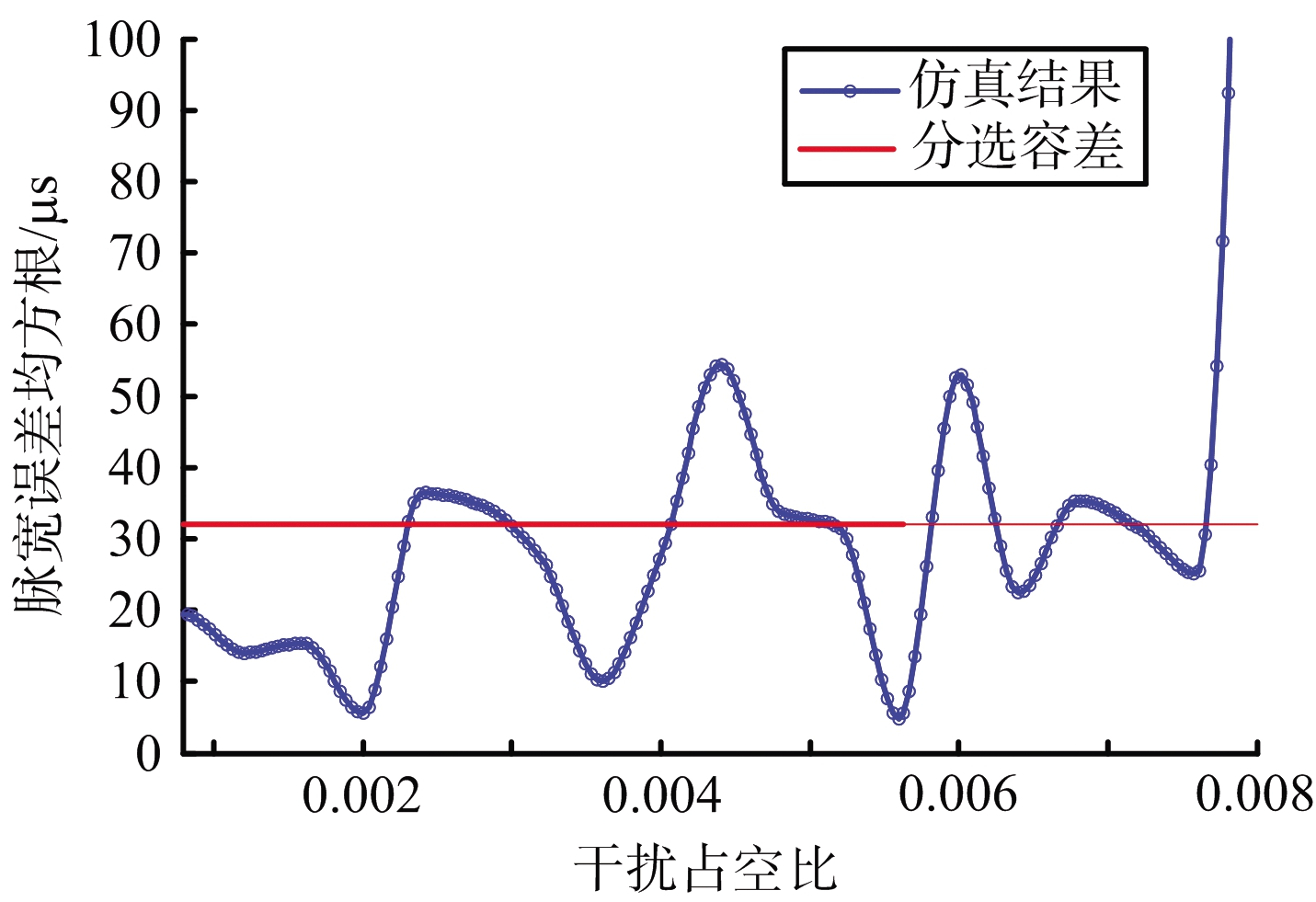
(c) δτs随占空比变化情况
图7 δτs随干扰参数变化情况
从图7(a)、(b)可以看出,随着前端输出信噪比降低、干扰重频增大,脉宽误差均方根逐渐增大。仿真条件下,当S/N低于-9 dB、PRFj大于2.75 MHz时,将导致预分选错误。从图7(c)可以看出,dj增加后整体上δτs逐渐变大,但仍有波动现象,原因同3.2节所述。
4 结束语
采用高重频脉冲对抗被动导引头具有良好的干扰效果。本文首先研究了高重频脉冲对被动导引头分选参数测量过程的干扰机理,之后建立了干扰效果与脉冲参数之间的理论关系并进行了仿真验证。当落入接收频带内的干扰能量超过检测门限时测频过程将被影响;干扰脉冲转化为类噪声信号导致输出信噪比降低,进而增加了到达方向及脉宽的测量误差。仅改变干扰脉冲占空比不是增强干扰效果的理想手段,加大干扰功率、提高重频是强化干扰效果的有效方法。
[1] 徐梁昊,姜秋喜,潘继飞,等.一种抗重频分选的反侦察方法[J].四川兵工学报,2015,36(7):117-120.
[2] 张保群.一种抗SDIF分选的脉冲重复间隔参差设计方法[J].兵器装备工程学报,2016,37(9):87-91.
[3] 徐梁昊,姜秋喜,潘继飞.一种基于PRI变换的雷达信号分选方法研究[J].舰船电子对抗,2014,37(5):1-6.
[4] 魏可友,黄康,梁广,等.基于PRI的雷达信号综合分选方法[J].电子设计工程,2017,25(1):190-193.
[5] 陈涛,王天航,郭立民.基于PRI变换的雷达脉冲序列搜索方法[J].系统工程与电子技术,2017,39(6):1261-1267.
[6] 余强,毕大平,陈璐,等.对ELINT系统基于信号PRI参数分选的干扰技术[J].火力与指挥控制,2016,41(1):143-147.
[7] 张国利,毕大平,沈爱国,等.雷达侦察比幅测向系统干扰技术[J].火力与指挥控制,2013,38(6):48-50.
[8] 戴胜波,雷武虎,程艺喆.基于TOA分选的反电子侦察方法[J].电子信息对抗技术,2014,29(4):45-48.
[9] 赵宇姣.基于高重频超宽带脉冲的雷达干扰技术研究[D].成都:电子科技大学,2015.
[10] 鲁帆,刘治甬.一种超外差接收机的射频前端设计[J].舰船电子对抗,2013,36(4):110-112.
[11] 南昊,彭世蕤,王晓燕,等.高重频脉冲对被动导引头前端的干扰机理研究[J].现代防御技术,2018,46(5):82-87.
[12] 朱斌,金炜东,余志斌.雷达脉冲上升/下降沿测量影响因素分析模型[J].电讯技术,2011,51(10):24-27.
[13] 赵国庆.雷达对抗原理[M].西安:西安电子科技大学出版社,1999:128-131.
[14] 周颖,甘德云,许宝民,等.反辐射武器攻防对抗理论与试验[M].北京:电子工业出版社,2012:37-38.
[15] 林象平.雷达对抗原理[M].西安:西北电讯工程学院出版社,1985:244-245.
[16] 王宏伟,赵国庆,王玉军.基于脉冲包络前沿波形的雷达辐射源个体识别[J].航天电子对抗,2009,25(2):35-38.
[17] 何明浩.雷达对抗信息处理[M].北京:清华大学出版社,2010:29-30.
