0 引言
脉冲雷达是目前广泛使用的雷达体制，而其固有的速度模糊问题一直没有很好的解决方案[1-2]。在雷达信号处理领域，火箭、导弹等高速目标的快速捕获和跟踪一直是研究热点，近年来具有高速高机动特性的临近空间飞行器使脉冲雷达面临更加艰巨的挑战[3-10]。跟踪这类高速目标时的速度模糊现象会产生错误信息并严重影响接下来的目标检测、成像和跟踪等算法的性能[11]。为此，本文对脉冲雷达的速度解模糊问题进行深入研究。
目前已经有多种方法可以实现解多普勒模糊。廉志玲等提出利用发射多重频脉冲信号的方法来解速度模糊，但是这类方法计算量较大且需要改造雷达相应硬件结构，不利于工程实现[12]。孟飞等研究使用距离跟踪数据的微分值来解速度模糊。该方法通常需要2 s以上的观测时间才能得到较为平稳的观测值。另外由于距离跟踪数据存在测量误差，因此该方法的误差较大[13]，滤波器输出结果的速度估计值精度通常在十几米每秒左右。李亚超等对宽带信号采用相邻相关法进行速度估计，可以得到目标的无模糊速度，但是该算法不适用于窄带信号[14]。苏军海等基于Radon变换，通过构造代价函数的方式对速度模糊折叠数进行搜索[15]。该方法由于使用了基于图像的处理方法，因此需要在高信噪比条件下使用大量脉冲数进行估计。综上所述，目前已有的解模糊算法在脉冲雷达上的工程实现受到了诸多限制，且性能还不够理想。
本文分析了脉冲雷达的目标回波信号，在不改变现有脉冲雷达系统的基础上，根据回波信号的似然函数的分布特性提出了一种速度粗估计方法。该方法基于相参脉冲回波信号的距离-速度模糊函数的盲速旁瓣在速度真值处达到最大值，在真值两侧的旁瓣对称逐渐减小的性质，通过合适的算法设计搜索盲速旁瓣的峰值位置，该位置对应的速度即为目标速度估计值。本方法利用通常认为是不利且尽量避免的盲速旁瓣进行速度粗估计，只需要利用少数脉冲即可以得到目标速度的估计值，在脉冲重复频率较低的脉冲雷达里具有较好的应用前景。
1 数学模型
线性调频脉冲是现代雷达常用的一种发射信号形式，其基带信号的复数形式为
(1)
式中，
为信号脉冲宽度，γ为调频斜率。
雷达信号在空间内传播，被目标反射后到达雷达接收端。因此，雷达接收到的目标回波可以写为
(2)
式中，r(t)为在t时刻雷达与目标散射点之间的径向距离，fc为载波中心频率，c为光速，z=A· exp(jθ)为未知的目标复散射系数，u(t)为复加性高斯白噪声。由于本文讨论的是低重频雷达，雷达信号的脉冲宽度远小于脉冲重复间隔(PRI)，因此可以采用走停模型描述回波信号，即认为目标相对于雷达的运动在脉内可以忽略不计，而仅考虑脉间目标相对于雷达运动所产生的时延。因此，可以将回波信号中的瞬时往返时延2r(t)/c近似替换为脉间的往返时延τm。在一个相参处理间隔(CPI)内，假设目标作匀速直线运动，那么第m个脉冲的往返时延可以表示为
(3)
式中，tm=mTr为慢时间，Tr为脉冲重复间隔PRI的时间宽度，r0和v0分别为t=0时刻目标相对于雷达的径向距离和速度。当目标沿着径向远离雷达时v0为正，靠近雷达时v0为负。将式(2)中的2r(t)/c替换为τm，得到走停模型下的基带回波信号：
(4)
对基带回波的时域信号作傅里叶变换，可以推出回波信号的频域表达式：
Srb(f)=
srb(τ)exp(-j2πfτ)dτ=
(5)
式中，
为基带噪声的频谱，S(f)为发射信号的脉冲包络即式(1)的频谱函数。
对基带回波信号进行匹配滤波就可以实现脉冲压缩，并且匹配滤波器的传输函数是发射信号的脉冲包络的共轭。因此，在频域上对基带回波信号进行匹配滤波，实现如下：
YPC(f)=Srb(f)S*(f)
(6)
将式(5)代入式(6)中，得到
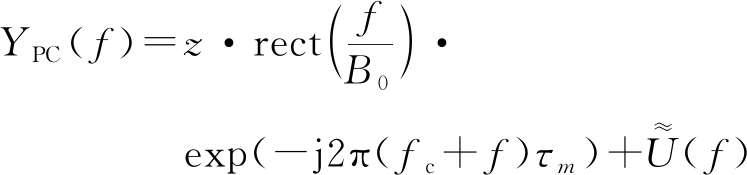
(7)
式中，
为基带噪声经过匹配滤波器后的频谱。在真实的雷达系统中，模拟基带信号会先通过A/D转换器进行正交采样，得到数字基带信号。因此，上述的脉冲压缩过程可以通过数字信号处理实现。对式(7)在频域上进行采样，得到脉压后的频域数字信号为
Yk,m=zexp(-j2π(fc+kΔf)τm)+Uk,m
(8)
式中，k=-K,…0,…K为频域上信号带宽内的采样点，Δf=γΔt为频域采样步长，每个脉冲的带宽B0=(2K+1)Δf，m=-M,…0,…,M为一个CPI内的积累脉冲序号，积累脉冲数Np=2M+1。经过匹配滤波器(线性滤波器)后的噪声项Uk,m仍然可以近似为复加性高斯白噪声，设它的方差为σ2。为了方便下文仿真分析，这里先定义输入信噪比为脉冲压缩后的频域数字信号的信噪比，即
(9)
利用多个相参脉冲回波可以构造目标的距离-速度模糊函数，从中可以得到目标的运动参数信息。接下来首先给出距离-速度二维模糊函数的构造方法，随后分析速度维模糊分析的特性，由此推导出一种快速速度粗估计方法。
2 速度维似然函数分析
由式(8)可知,样本Yk,m服从均值为z· exp(-j2π(fc+kΔf)τm)、方差为σ2的复高斯分布，其概率密度分布为
p(Yk,m;z,r,v)=
(10)
由于不同样本间满足相互独立的条件，因此对所有样本求取似然函数，得到
(11)
进一步求得对数似然函数
lnL(z,r,v)=-(2K+1)(2M+1)ln(πσ2)-
(12)
求解上式的最大值，得到目标运动参数的最大似然估计:
exp(j2π(fc+kΔf)τm(r,v))|
(13)
因此，具体在求取目标运动参数的最大似然估计时，需要在可能的参数空间内对目标的径向距离和速度进行联合搜索。理论上，在满足样本数足够多且搜索步长足够小的条件下，通过最大似然估计就能达到参数估计的克拉美-罗限，即实现理论上的最优估计。
为了分析速度模糊现象并引出本文算法，这里另外定义r，v的似然函数:
(14)
将Yk,m中的信号复散射系数z置为1，噪声项Uk,m置为0后代入上式，得到
H(r,v)=
(15)
注意到r0,v0只是决定了H(r,v)在距离维和速度维上的中心位置。为了分析方便，将r0,v0置为0，将H(r,v)的中心位置设在原点，最终得到了只与r,v有关的似然函数表达式:
(16)
取r≡0代入上式，得到速度维似然函数:
H(0,v)=
(17)
上式中的函数G定义为
(18)
函数G在绝对值符号内是一个周期性的sinc函数，其周期大小为2π且在γ=2nπ(n为任意整数)处周期性地出现峰值。
为了直观地观察展示速度维似然函数分布，这里给出一组典型的雷达参数：载波中心频率fc=3 GHz、带宽B=5 MHz、采样频率fs=10 MHz、脉宽T=25 μs、脉冲重复频率fr=300 Hz以及积累脉冲数Np=33。图1 (a)为速度真值所在的无模糊范围内的速度维似然函数分布，它接近sinc包络。而从大范围进行观察时，速度维似然函数会周期性地出现峰值(除速度真值对应的主峰之外的峰称为盲速旁瓣)，如图1 (b)所示，各峰值之间的间隔即为最大无模糊周期，并且各个峰值形成了巨大的外包络。从整体上看，构成外包络的局部小峰值随着速度与真值的偏移呈现衰减趋势。
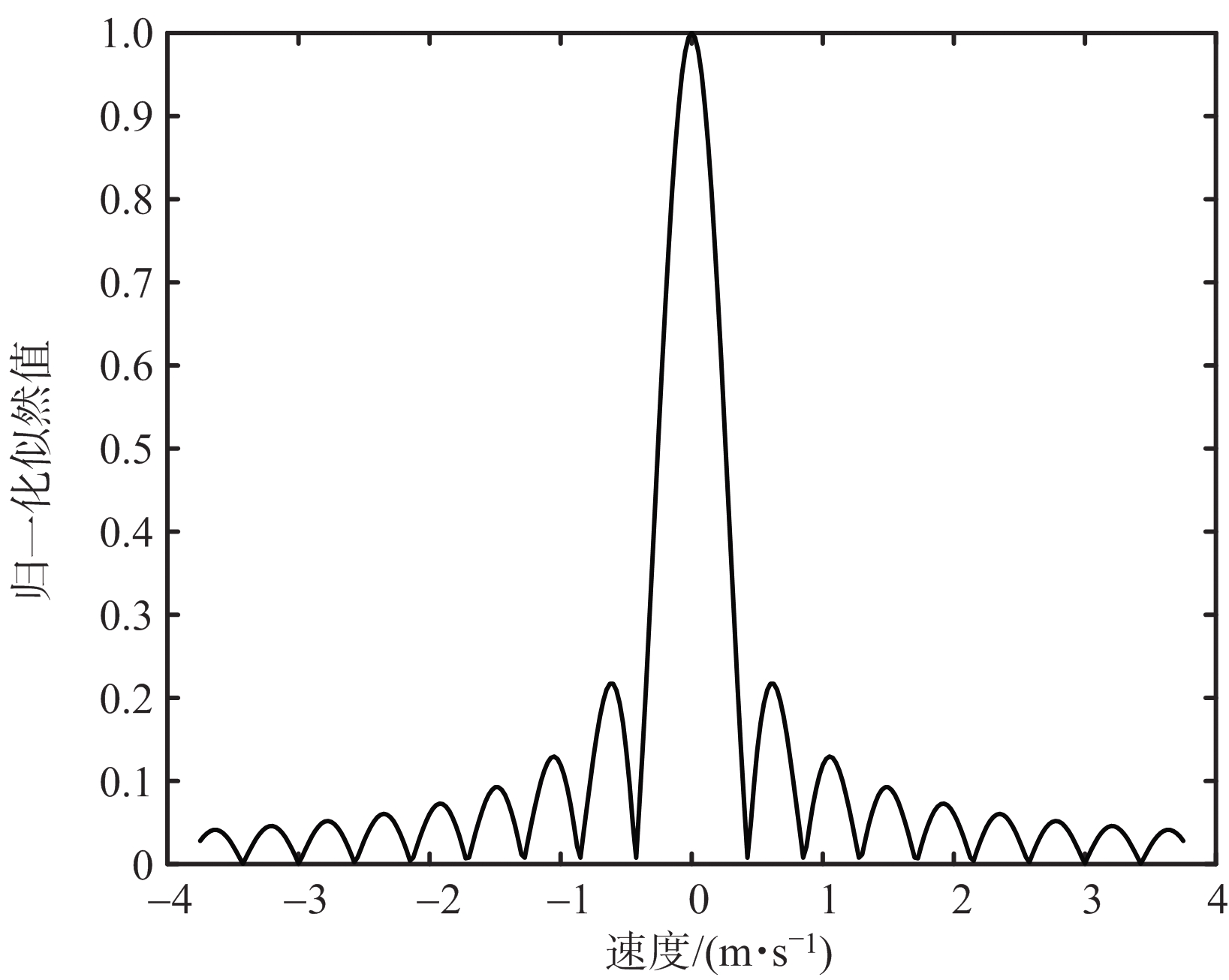
(a) 局部
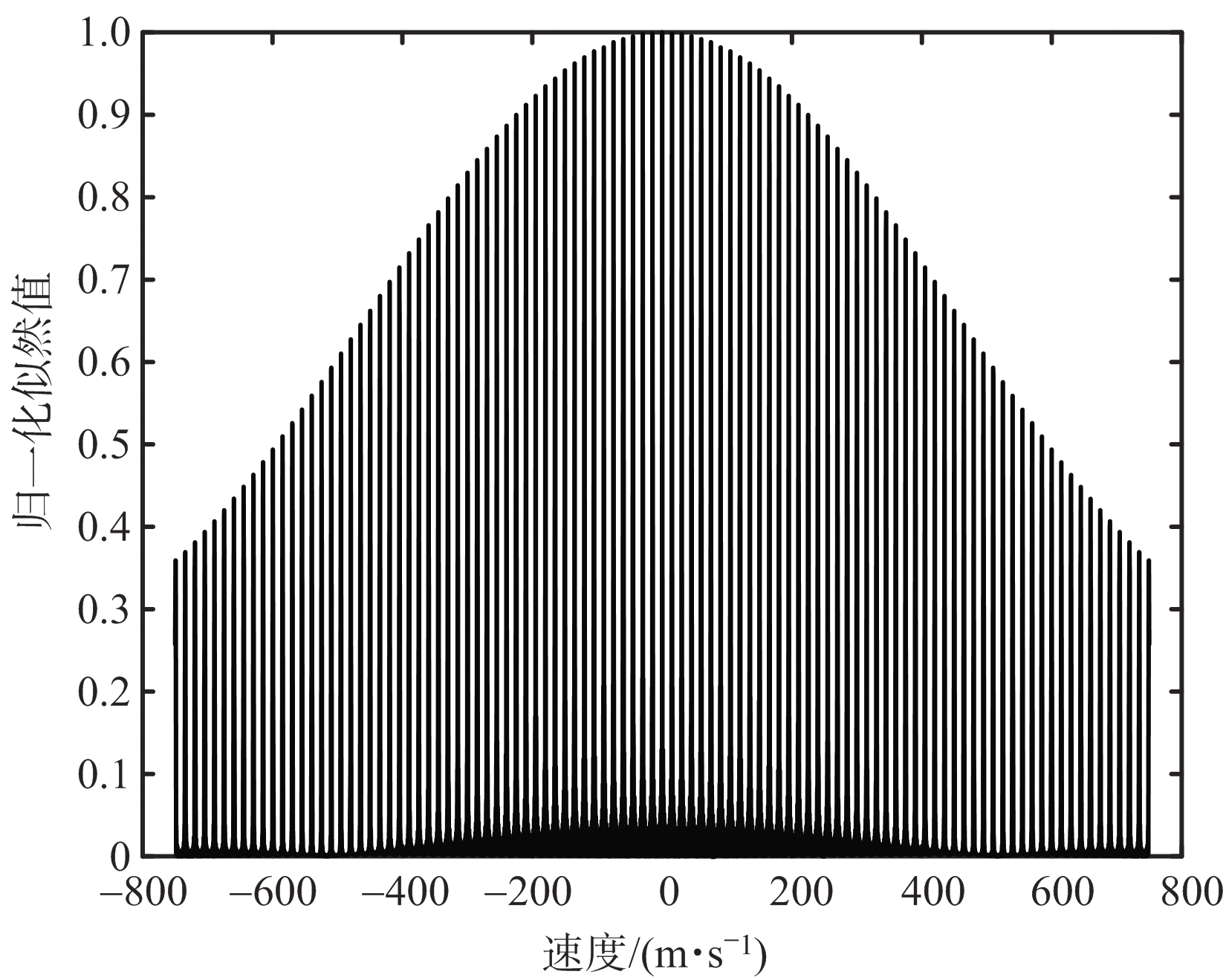
(b) 整体
图1 速度维似然函数分布
由于式(17)的表达式过于复杂，不便于进行定量分析，因此需要继续对式(17)进行化简分析。假设
(19)
(20)
按照前面对函数G的讨论，可以得到函数W(v)的周期为
(21)
可以看到，式(21)的具体值与m有关。而函数 U(v)的周期为
(22)
由于窄带雷达信号满足带宽远小于载频即B0≪fc，而频域采样步长Δf<B0，故对于任意m都有vw≫vs。即在式(17)可以看作一个高频信号对一个低频信号进行调制的结果，因此在速度维上似然函数会周期性地出现局部峰值，这就是速度模糊现象。对于不同的m，函数W(v)的主瓣宽度不相同。参考sinc函数主瓣宽度的定义，得到函数W(v)的主瓣宽度为
当m=M时，可以得到最小主瓣宽度为
在最小主瓣宽度内函数W(v)的值变化不大，因此在最小主瓣宽度内可以近似地认为W(v)的值不变。因此可以认为最大无模糊速度范围就是
的周期，即vu等于最大速度无模糊范围。
假设v为vu的整数倍，即v=Nvu，N为整数，此时有
U(v)=
exp(2π×N)=1
(23)
将式(23)代入式(17)可以得到外包络分布函数：
(24)
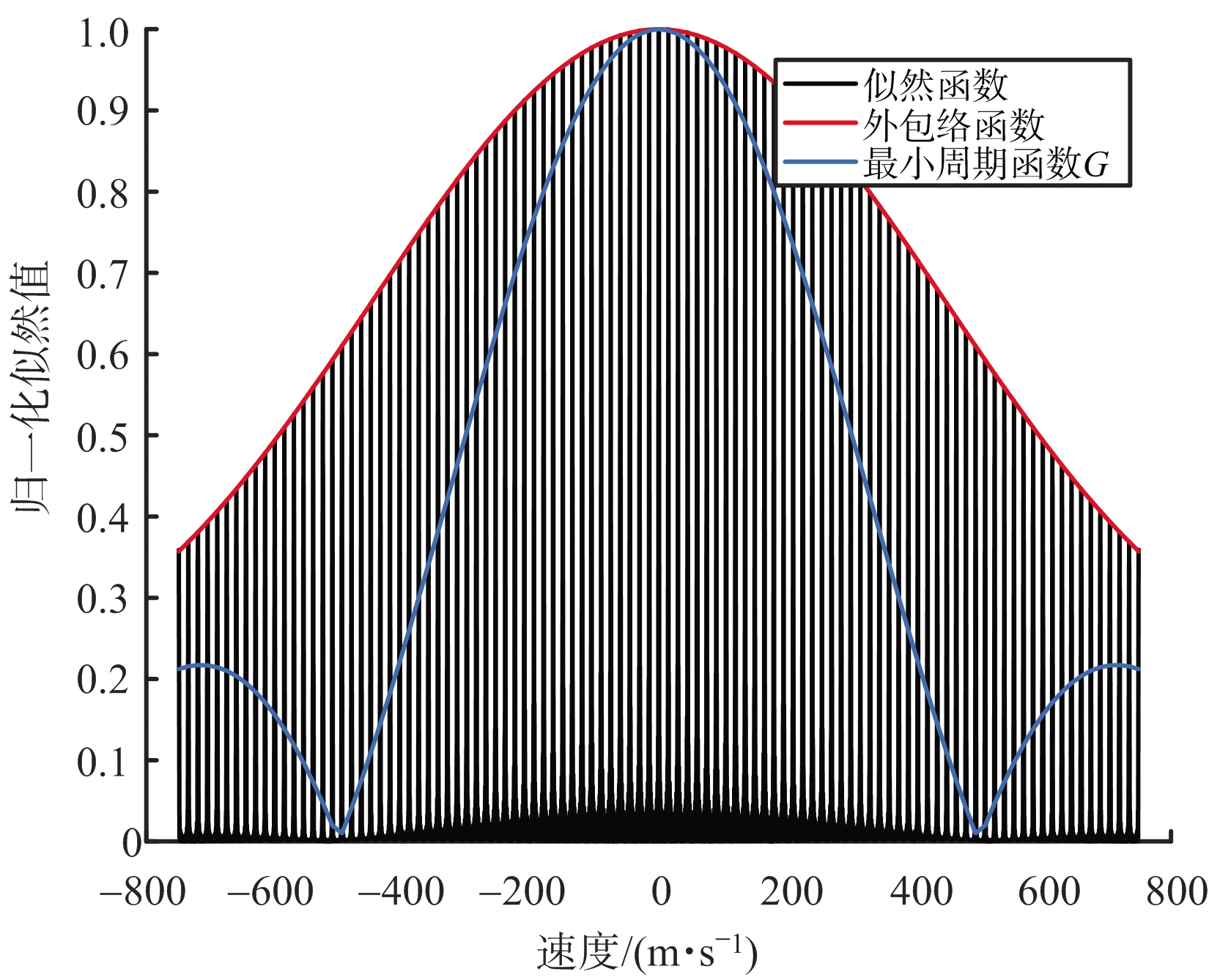
图2 外包络函数、似然函数和最小周期函数G对比
函数J(v)的分布与速度维似然函数的对比如图2所示，两者基本上是重合的。函数J(v)可以看作由一系列不同周期的函数G叠加再求模得到。图2画出了最小周期的函数G，即与函数 J(v)的对比。经过多组参数的对比，我们发现函数J(v)的主瓣宽度接近最小周期的函数G的主瓣1.5倍。故外包络分布的主瓣宽度约为
从速度维模糊函数可以看出，其外包络在速度真值两边随着速度值与真值的差单调减小。由此，可以根据这个特性进行目标速度的估计。
3 准最大似然速度粗估计
按照前面对速度维似然函数分布的分析，一种比较简单、直接的解速度模糊思路是：以获得的目标速度估计值作为初始值，设定vs作为步长，大范围地求取速度维似然函数外包络上的各峰值，最后搜索最高峰所在的位置。但是在图1 (b)的情形下，在真值附近范围的外包络过于平缓，并不存在一个突出的峰值，容易受到噪声影响，因此最终搜索到的不一定是速度真值。
接下来阐述本文提出的解速度模糊算法，这里将得到的存在模糊的速度估计值设为
而速度真值设为v0。定义左偏速度为比
小n个无模糊范围的速度值：
Z+
(25)
右偏速度为比
大n个无模糊范围的速度值：
Z+
(26)
关于间隔数n的选取策略，在下一节仿真实验中再进行详细讨论。根据速度维似然函数的对称性，利用左偏速度
和右偏速度
上的似然函数值可以确定与v0之间的相对位置以及偏移程度。具体地，当
时
时
时
这里需要再次声明，似然函数在作为信号特征的分析工具时，定义中并不包含噪声成分。因此，在存在噪声的真实情况下，速度维似然函数的对称性会在一定程度上受到影响，特别是在
时，
并不会与
满足严格的相等关系。基于上述速度维似然函数的对称特性，这里将提出一种有效的解速度模糊算法，具体步骤如下：
1) 利用目标运动参数的初始估计值(距离跟踪数据的微分值作为速度初始估计值)，在无模糊范围内对似然函数式(14)进行峰值搜索，得到谱峰位置即目标距离和速度的高精度估计值
其中一般存在模糊；
2) 计算左偏速度
上的似然函数值:
(27)
以及右偏速度
上的似然函数值:
(28)
设定二值比较系数，记录最初时与之间的大小关系：
(29)
并计算两者之间的差值
3) 如果F·ΔH>0，则先保留当前的似然函数差值为ΔH′，然后将和分别更新为
和
再根据更新后的和对ΔH进行更新；
4) 重复执行步骤3)，直至F·ΔH<0。如果|ΔH|<|ΔH′|，则得到解模糊后的速度值为
否则
4 仿真及分析
由于前面给出的解速度模糊算法需要对给定雷达参数的速度维似然函数进行具体分析，为了方便讨论，这里使用表1中的B组雷达参数下进行仿真实验与分析。同时，目标运动参数设为r0=100 km，v0=2 000 m/s。假设距离跟踪数据的微分值与目标真实速度相差较大，为vc=2 100 m/s。
无模糊范围间隔数n是本算法的关键参数。但是，目前并没有给出关于间隔数n的合适选值，这里将n设为整数10，20…50，进行5组仿真实验。为了研究噪声和间隔数n对算法精度的影响，在各组仿真中设置输入信噪比-10～5 dB，步长1 dB，每个信噪比下进行1 000次蒙特卡罗仿真。最终得到在给定的具体雷达参数下，本节所提出算法的速度估计值均方根误差与输入信噪比之间的关系如图3所示。如果算法得到的速度估计值落在以速度真值v0为中心的无模糊范围内，即认为正确解模糊；反之，则得到错误的解模糊结果。解模糊的正确率也是评判算法的标准之一。同样地，设置输入信噪比-10～5 dB，步长1 dB，每个信噪比下进行1 000次蒙特卡罗仿真。可以得到算法的解模糊正确率与输入信噪比之间的关系如图4所示。
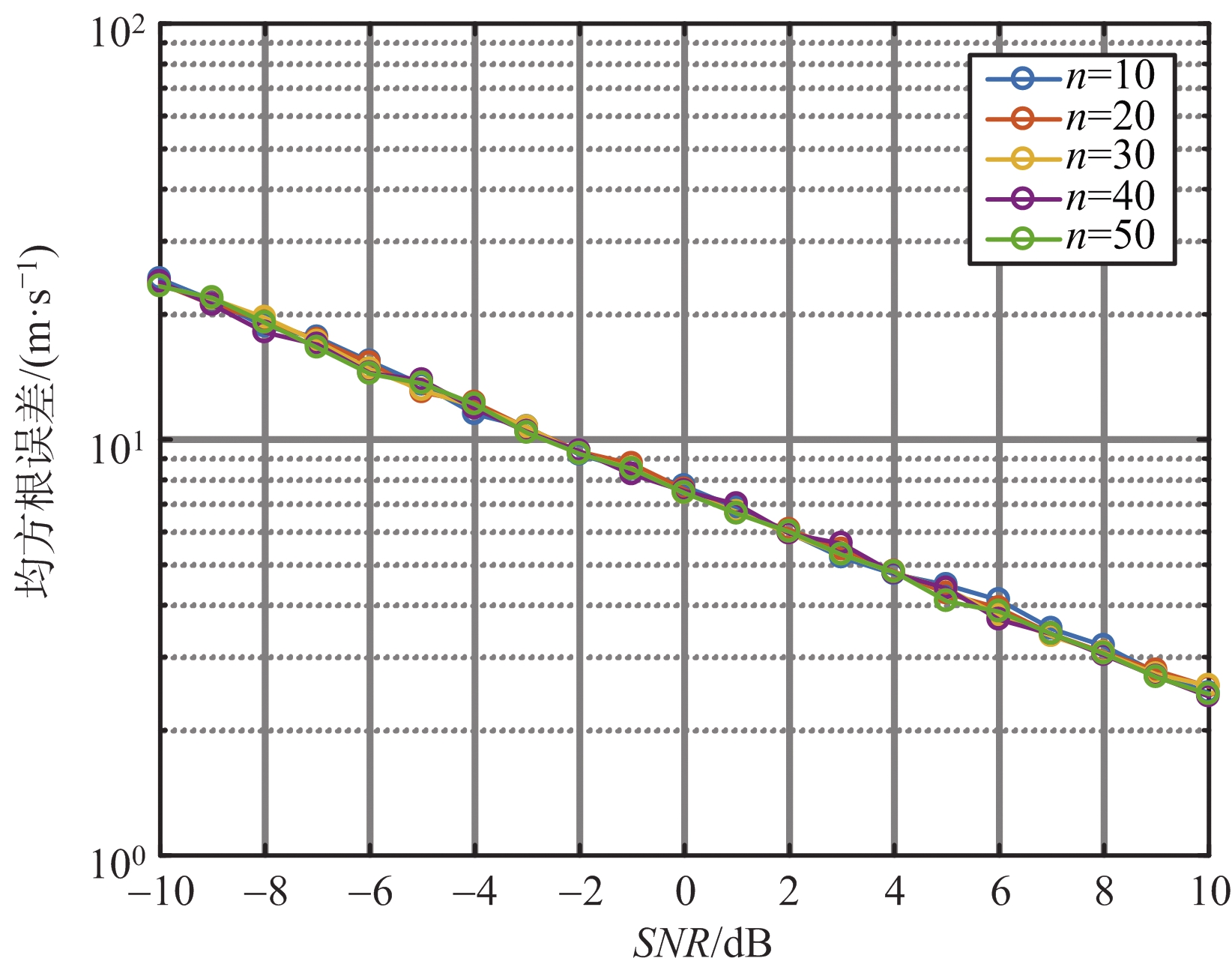
图3 速度估计值均方根误差与间隔数及输入信噪比之间的关系
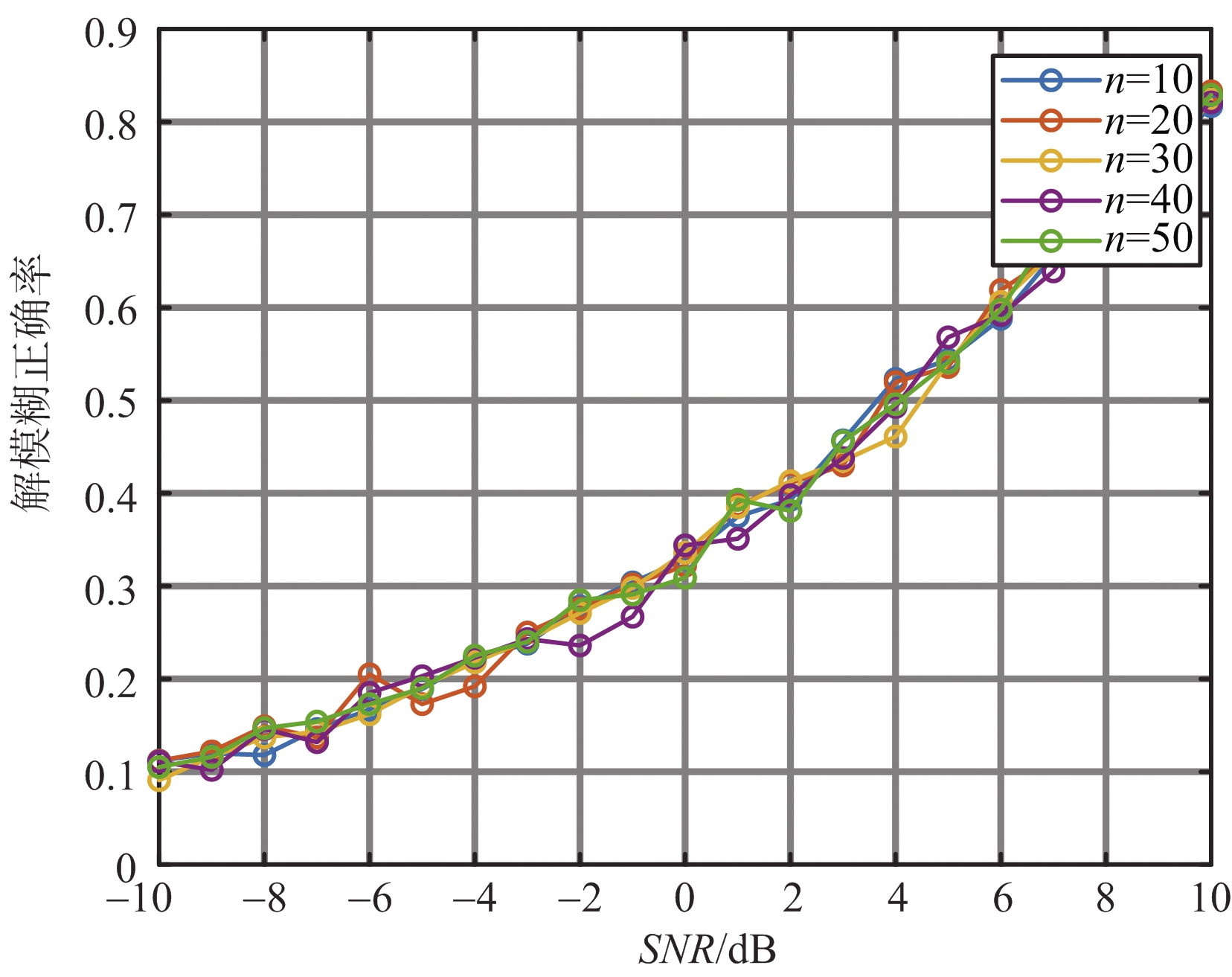
图4 解模糊正确率与间隔数及输入信噪比之间的关系
在理想的无噪声情况下，当时|ΔH1|=0；当
时，根据速度维似然函数的对称性可得
在存在噪声的情况下，速度维似然函数分布的对称性会遭到破坏，因此只能依据|ΔH|的大小作对称性判断。在本算法的实现中，只有满足|ΔH2|>|ΔH1|时，速度估计值将落在速度真值的无模糊范围内，此时才能正确解模糊。因此，这里希望
是一个很大的值，这样才能保证在有噪声的情况下|ΔH2|明显大于|ΔH1|。因此，为了获得最佳的估计性能，间隔数n的大小应取为
n=
n∈Z+
(30)
即n应取在外包络倾斜程度最大的位置上。由于外包络主瓣内的各谱峰位置上的倾斜度基本一致，因此速度估计精度受间隔数n的影响很小。为了在适应不同雷达参数的同时达到满意的估计性能，我们一般选取
(B组参数下，n=34)作为间隔数。另外，由图3和图4可知，随着输入信噪比的提高，算法估计误差随之降低。
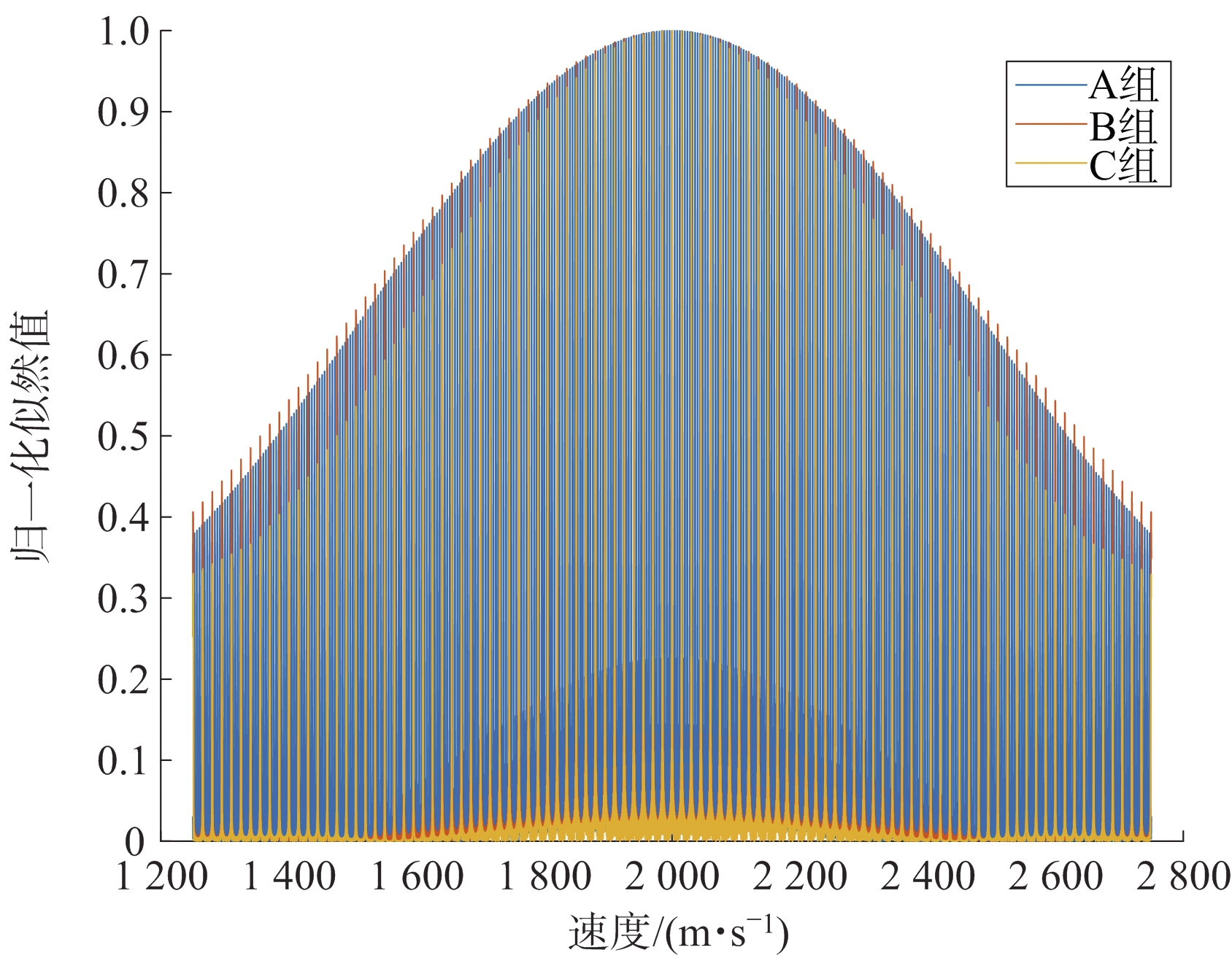
本文提出的算法依赖于速度维似然函数分布的特性，因此本节还将讨论雷达参数对速度维似然函数分布的特性的影响。这里选取表1中3组雷达仿真参数进行仿真分析。如图5所示，A组参数与B组参数的外包络主瓣宽度接近，C组参数外包络主瓣宽度较小。另外，可以看到B组参数与C组参数的无模糊周期一样，而A组参数峰值更为密集。
表1 雷达仿真参数
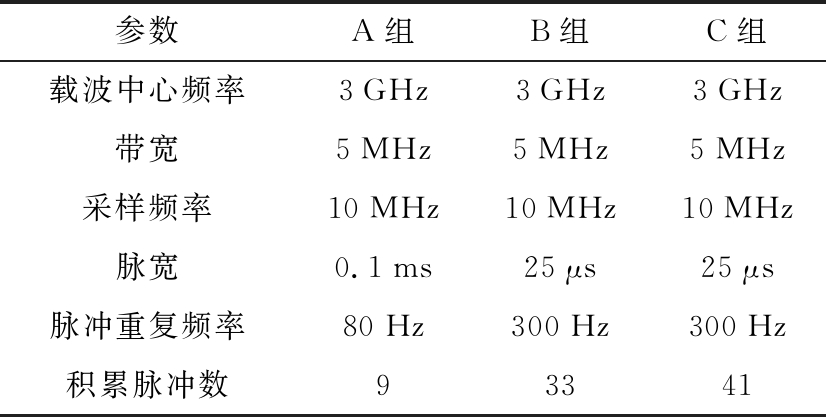
参数A组B组C组载波中心频率3GHz3GHz3GHz带宽5MHz5MHz5MHz采样频率10MHz10MHz10MHz脉宽0.1ms25μs 25μs 脉冲重复频率80Hz300Hz300Hz积累脉冲数93341
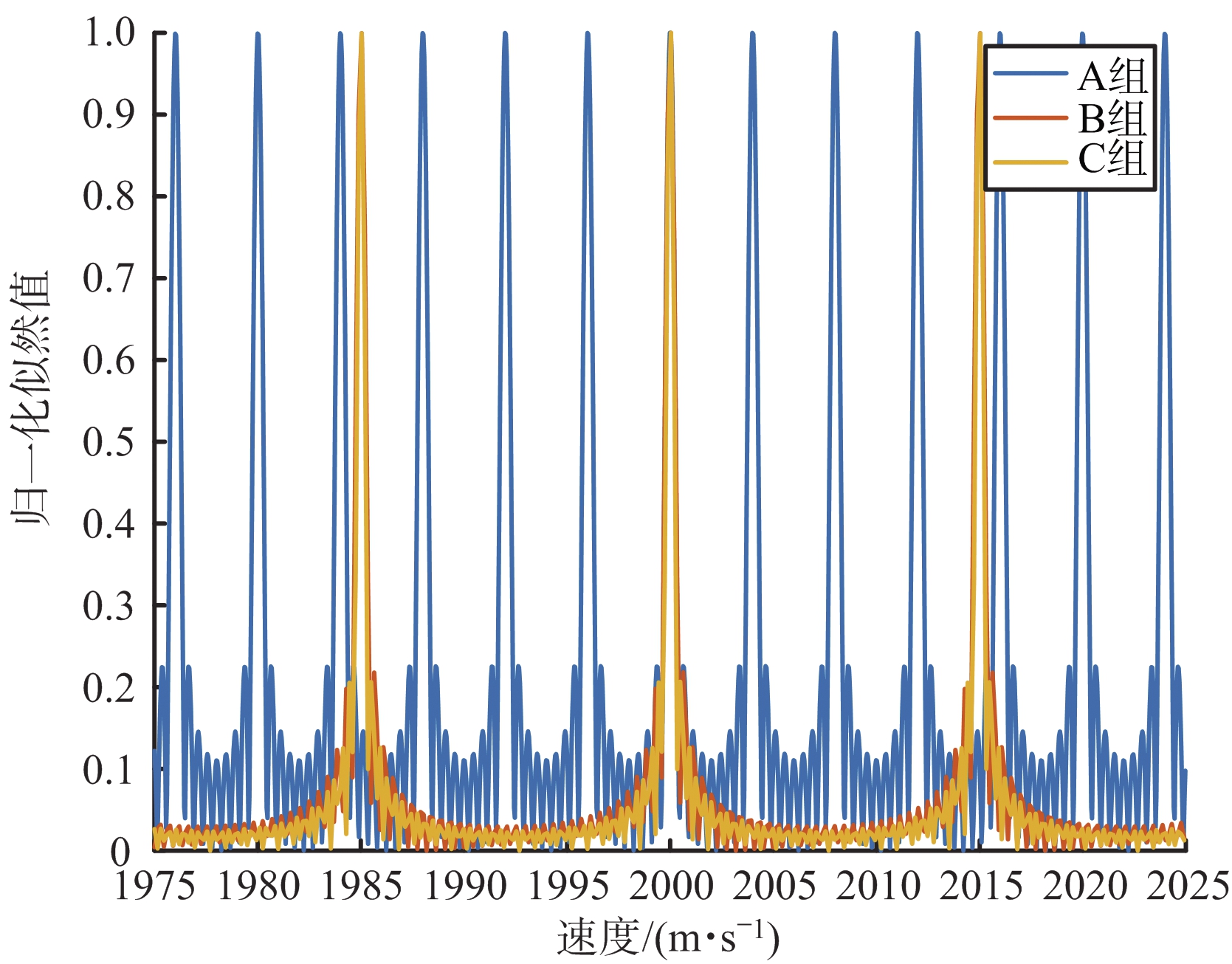
(a) 局部
(b) 整体
图5 A组和B组雷达仿真参数下似然函数对比
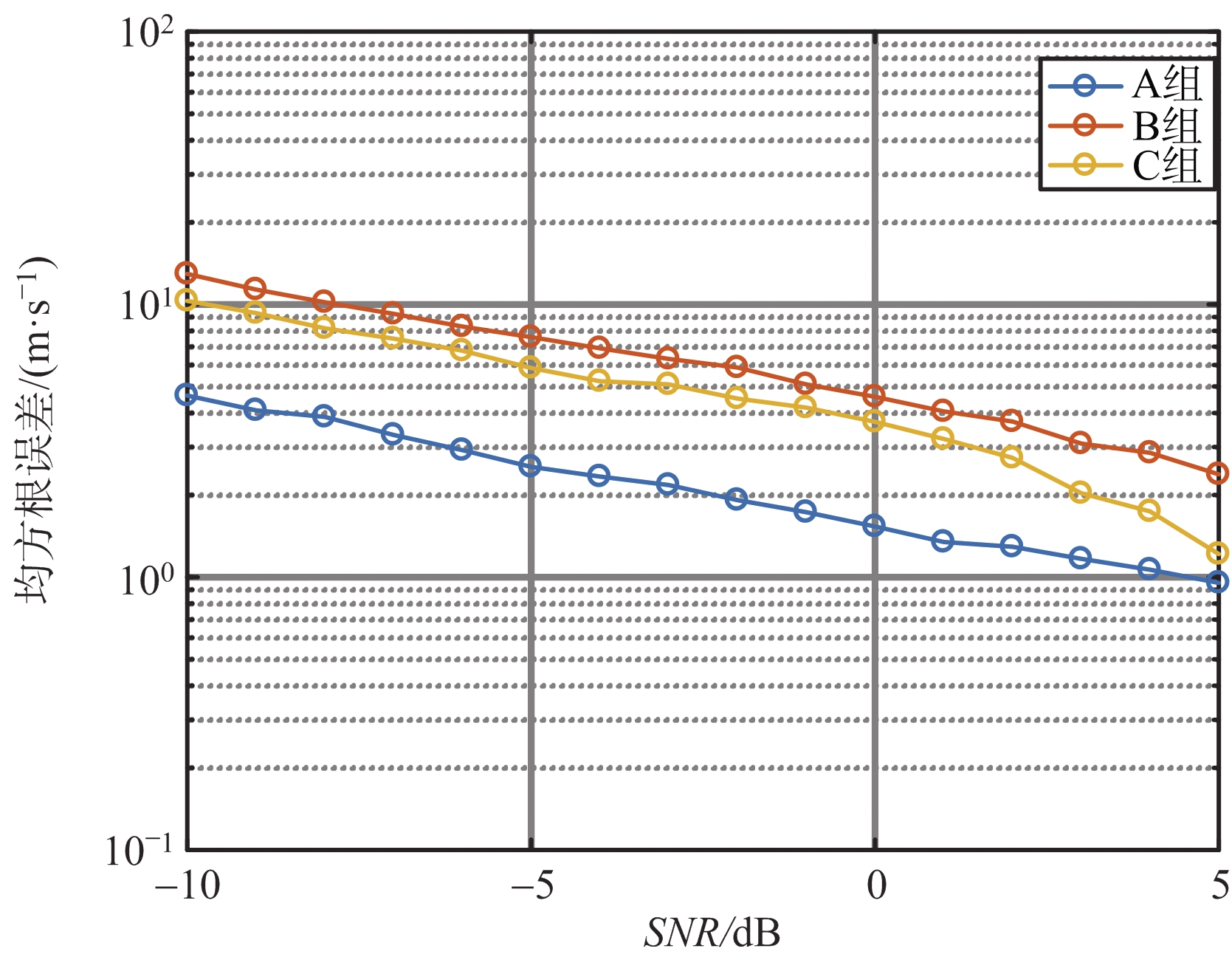
图6 A组、B组和C组雷达仿真参数下均方根误差对比
设置输入信噪比-10～5 dB，步长1 dB，每个信噪比下进行1 000次蒙特卡罗仿真，算法的搜索间隔数按照公式
分别设为248，64和54。在3组参数下，算法的速度估计值均方根误差对比和解模糊正确率对比分别如图6和图7所示。可以从图6看到，虽然A、B两组参数的外包络主瓣宽度很接近，但是由于A组参数的最大无模糊范围更小，故A组参数的估计精度更高。而在外包络主瓣相同的情况下，更小的最大无模糊范围将使得相邻峰值的差值变小，导致噪声的影响变大，解模糊正确率也随之降低。可以从图7看到，A、B两组参数的解模糊正确率有明显的差距，A组参数的解模糊正确率小于B组参数的解模糊正确率。B、C两组参数虽然最大无模糊范围相同，但是C组参数的外包络主瓣更窄，局部峰值的差值更大，因此C组参数的估计精度和解模糊正确率都比B组参数高。从以上讨论可知，外包络主瓣与速度最大无模糊范围影响了算法性能。故为了让算法获得满意的估计精度与解模糊正确率，需要根据外包络主瓣公式与速度最大无模糊范围公式对雷达参数进行合理设计。
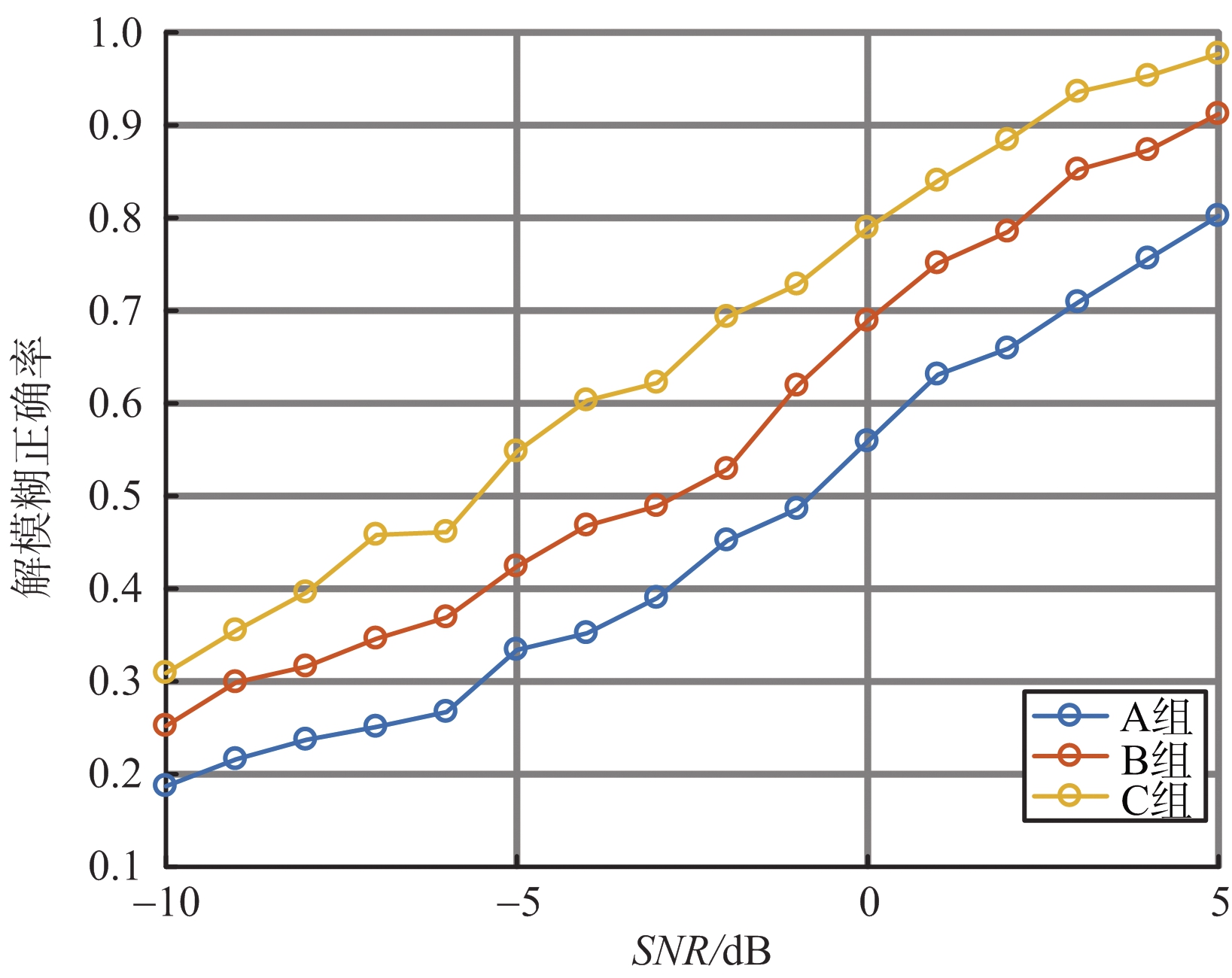
图7 A组、B组和C组雷达仿真参数下解模糊正确率对比
5 结束语
本文针对脉冲雷达中存在的速度模糊现象，以速度维似然函数作为分析工具，提出了一种基于速度维似然函数对称性的解速度模糊算法。仿真结果表明，随着输入信噪比的提高，该算法的估计精度和解模糊正确率也随之提高。同时，通过合理设计雷达参数，可以有效提高本文算法的精度和解模糊正确率。另外，该算法计算量不高。对于与速度真值v0相差kvs的速度初始值本算法最多通过2(k+1)次的似然函数值计算，就能得到满足解模糊精度要求的速度粗估计值，适合工程应用。
[1] 曾涛, 龙腾. 一种脉冲多普勒雷达解模糊新算法[J]. 电子学报, 2000, 28 (12):99-101.
[2] 张代忠, 洪一, 邱炜. 脉冲多普勒雷达中的解模糊算法及实现[J]. 雷达科学与技术, 2004, 2(5):293-297.
ZHANG Daizhong,HONG Yi,QIU Wei. Ambiguity Resolution Algorithms for Pulse Doppler Radar and Their Realizations[J]. Radar Science and Technology,2004, 2(5):293-297.(in Chinese)
[3] DENG Zhenmiao, FU Maozhong, JIN Sheng, et al. Joint Estimation of Motion Parameters Using Newton’s Method[J]. IEEE Trans on Aerospace and Electronic Systems, 2015, 51(4):3386-3398.
[4] ZHU Shengqi, LIAO Guisheng, YANG Dong,et al. A New Method for Radar High-Speed Maneuvering Weak Target Detection and Imaging[J]. Geoscience and Remote Sensing Letters, 2014, 11(7):1-5.
[5] QIAN Lichang, XU Jia, XIA Xianggen, et al. Wideband-Scaled Radon-Fourier Transform for High-Speed Radar Target Detection[J]. Radar, Sonar & Navigation, 2014, 8(5):501-512.
[6] SUO Pangcun, TAO Shan, TAO Ran, et al. Detection of High-Speed and Accelerated Target Based on the Linear Frequency Modulation Radar[J]. IET Radar, Sonar & Navigation, 2014, 8(1):37-47.
[7] CHEN Jinli, LI Jiaqiang, ZHU Yanping.Joint Location and Velocity Estimation for High Speed Target in Multi-Carrier-Frequency MIMO Radar[J]. Advances in Information Sciences and Ser-Vice Sciences, 2013, 5(6)：223-229.
[8] ZHENG Jibin, SU Tao, ZHU Wentao, et al. A Fast Non-Searching Algorithm for the High-Speed Target Detection[M]. Progress in Systems Engineering,2015:777-782.
[9] GAO Zhu. Fast Algorithm of Parameters Estimation of High Speed Moving Target Based on Conjugate Gradients and Its Test[C]∥ International Proceedings of Computer Science and Information Technology,Chengdu:IEEE,2011:6.
[10] ZHENG Jibin, SU Tao, ZHU Wentao, et al. Radar High-Speed Target Detection Based on the Scaled Inverse Fourier Transform[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2015, 8(3):1108-1119.
[11] 侯海燕. 脉冲多普勒雷达中的解模糊算法的工程实现[J]. 大众科技, 2010 (12):59-60.
[12] 廉志玲, 张代忠, 张小菊. 一种基于查表的解速度模糊算法[J]. 雷达科学与技术, 2011, 9(4):358-361.
LIAN Zhiling,ZHANG Daizhong,ZHANG Xiaoju. Velocity Ambiguity Resolution Based on Look-up Table Method[J]. Radar Science and Technology, 2011, 9(4):358-361. (in Chinese)
[13] 孟飞, 谢良贵, 李饶辉. 一种脉冲多普勒雷达解速度模糊新方法[J]. 系统工程与电子技术, 2009, 31(4):791-794.
[14] 李亚超, 邢孟道, 张龙, 等. 一种高机动目标的宽带信号检测、参数估计及成像方法[J]. 中国科学 (F 辑: 信息科学)，2009, 39(8):875-885.
[15] SU Junhai, XING Mengdao, WANG Genyuan, et al. High-Speed Multi-Target Detection with Narrowband Radar[J]. IET Radar, Sonar & Navigation, 2010, 4(4):595-603.
