0 引言
雷达在作战中担负着战场环境感知的作用,分布式无源雷达建设成本低、易安装、有较强的抗干扰能力和高隐蔽性,使其成为现代新体制雷达的研究热点之一[1-2]。分布式无源雷达不依靠自身发射信号,强调的是多空间辐射源(如电视广播、卫星和无线网络等信号)和多接收机在空间中相对于目标的充分展开性[3]。因此,可以通过空间多通道一次采样来增强目标探测能力和成像性能。但分布式无源雷达成像中存在的布站不规则以及辐射源复杂随机等原因导致目标回波数据在其傅里叶变换域分布不均匀,目标反演成像质量不佳的问题还没得到较好的解决[4]。
傅里叶变换是处理雷达回波数据的基本方法,目前普遍使用的快速傅里叶变换(FFT)算法[5]对数据的均匀性和致密性都要求较高。针对非均匀分布的数据,传统方法通过对离散数据进行各种插值获得相对均匀的笛卡尔网格形式,再利用IFFT获得目标图像,这类方法统称为插值傅里叶变换法[6-7]。但插值本身会引入不可避免的误差,同时回波数据的稀疏性会加剧插值误差。为避免插值的误差,文献[8]提出了极坐标成像法,对回波数据在极坐标系下直接求解,文献[9]在文献[8]的基础上,在具有一般意义的球坐标系统下,提出逐点匹配滤波成像方法,对目标所在的反演区域开展匹配搜寻,将获得的不同观测通道的目标反演像进行相干融合,文献[8-9]对分布式无源雷达的构型非规则性有一定的适应性,但却带来了运算量的大幅增加。
Dutt等[10]提出的非均匀快速傅里叶变换法(NUFFT)能直接对非均匀数据进行快速处理,在CT成像和雷达信号处理等领域已得到应用[11-12]。文献[13-14]将NUFFT与CS算法相结合应用于有源SAR成像中,充分体现了NUFFT降低CS重构算法计算复杂度的作用。文献[15]提出基于余弦尺度因子和最小均方差准则的NUFFT方法,在分布式无源雷达图像重建精度和稳定性取得了较好的结果,但重建图像受振铃作用的显著影响,同时文中也指出适用于NUFFT的更好的尺度因子还有待研究。为了进一步提高分布式无源雷达非均匀采样条件下的目标成像质量和性能,本文给出了一种基于快速高斯网格的非均匀傅里叶变换(记作FGG-NUFFT)[16-17]分布式无源雷达成像方法,结合空间谱理论分析了回波采样信号的空间谱非均匀性及与所提算法下的分布式无源雷达成像质量的关系,并进行了算法仿真验证。
1 分布式无源雷达成像模型
考虑实际场景中,分布式无源雷达成像系统在球坐标下的几何构型,如图1所示。成像系统由目标、辐射源和接收机组成,假设目标任意一点P的坐标是(r,θ,φ);M个辐射源的俯仰角和方位角分别表示为θt和φt,N个接收机的俯仰角和方位角分别表示为θr和φr,则第i个辐射源的坐标是(ri,θi,φi),第j个接收机的坐标是(rj,θj,φj)。
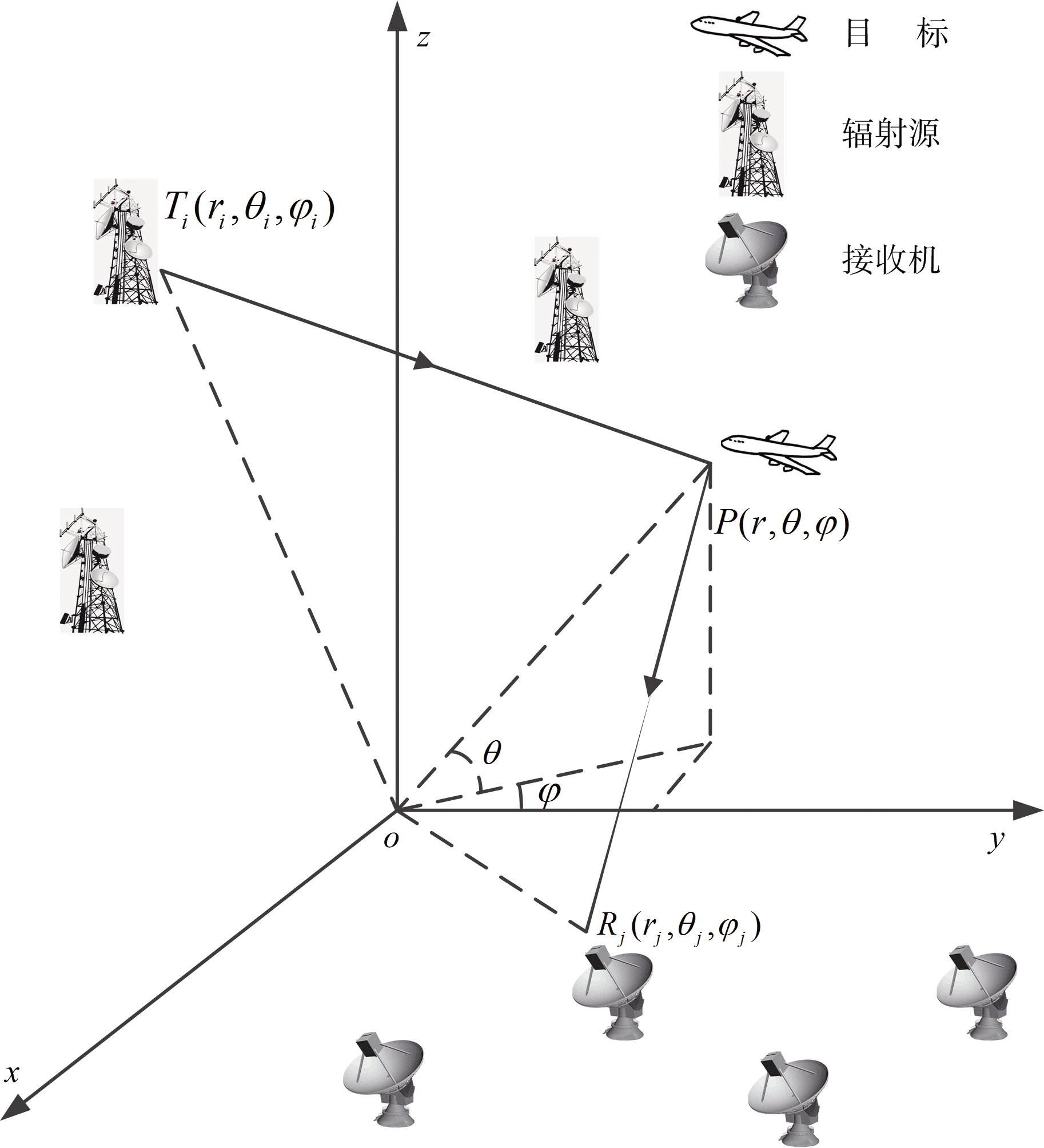
图1 分布式无源雷达成像构型
为分析简单同时保留三维空间构型下的完整构型信息,本文基于分布式无源雷达三维构型下的二维投影成像平面进行讨论,建模如下。
设第i个外辐射源所发出的信号形式为
Si(t)=ui(t)ej(2πfit+φi)
(1)
设空间中目标的散射系数为σ(r,θ,φ),对应二维平面直角坐标是σ(x,y),则投影后得到二维平面上第j个接收机所接收到的第i个外辐射源信号经目标反射回来的回波为
Gij(t)=![]()
ej(2πfi(t-Δtij)+φi)dxdy+nj(t)
(2)
式中,s为辐射源照射的平面成像区,α为回波传播衰减系数,Δtij为传播时延,nj(t)为接收噪声。实际场景下可对信号的传播路径做远场近似,同时对回波进行去载频去噪处理[18],总的散射回波可表示为
G(f,θi,θj,φi,φj)=
![]()
ej2πfi[(cosθicosφi+cosθjcosφj)y]/cdxdy
(3)
利用时间与空间、频谱与波数谱具有对偶关系,将多通道获得的目标回波信息转换到空间谱去处理,令
(4)
式中:i=1,…,M;j=1,…,N;(kx,ky)构成回波的空间谱域,kx,ky组成空间谱域的填充点。可得
(5)
式中,G(kx,ky)为空间谱域观测样本。从式(5)可得目标回波G(kx,ky)与目标散射系数σ(x,y)之间构成了傅里叶映射关系对。每一个辐射源和每一个接收机构成一路采样通道,对应于空间谱域上的一个填充点,分布式的空间分布就形成了多路采样通道,映射为整个空间谱填充,空间谱填充结果由收发布站构型和发射信号决定,若空间谱填充是相对均匀的,则通过式(5)利用傅里叶逆变换就能反演出目标像。而实际构型下空间谱填充有以下关系:
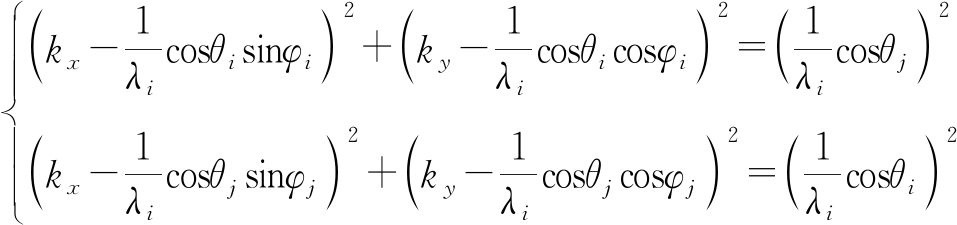
(6)
式中,λi=c/fi。式(6)表明,在投影下的成像模型中回波信号采样在空间谱中的填充点是关于辐射源波长、辐射源和接收机方位角及俯仰角大小的两条非规则弧线的交点,式(6)所示关系表明空间谱填充点的分布必然是非均匀的,如图2所示为任一构型仿真结果示例。
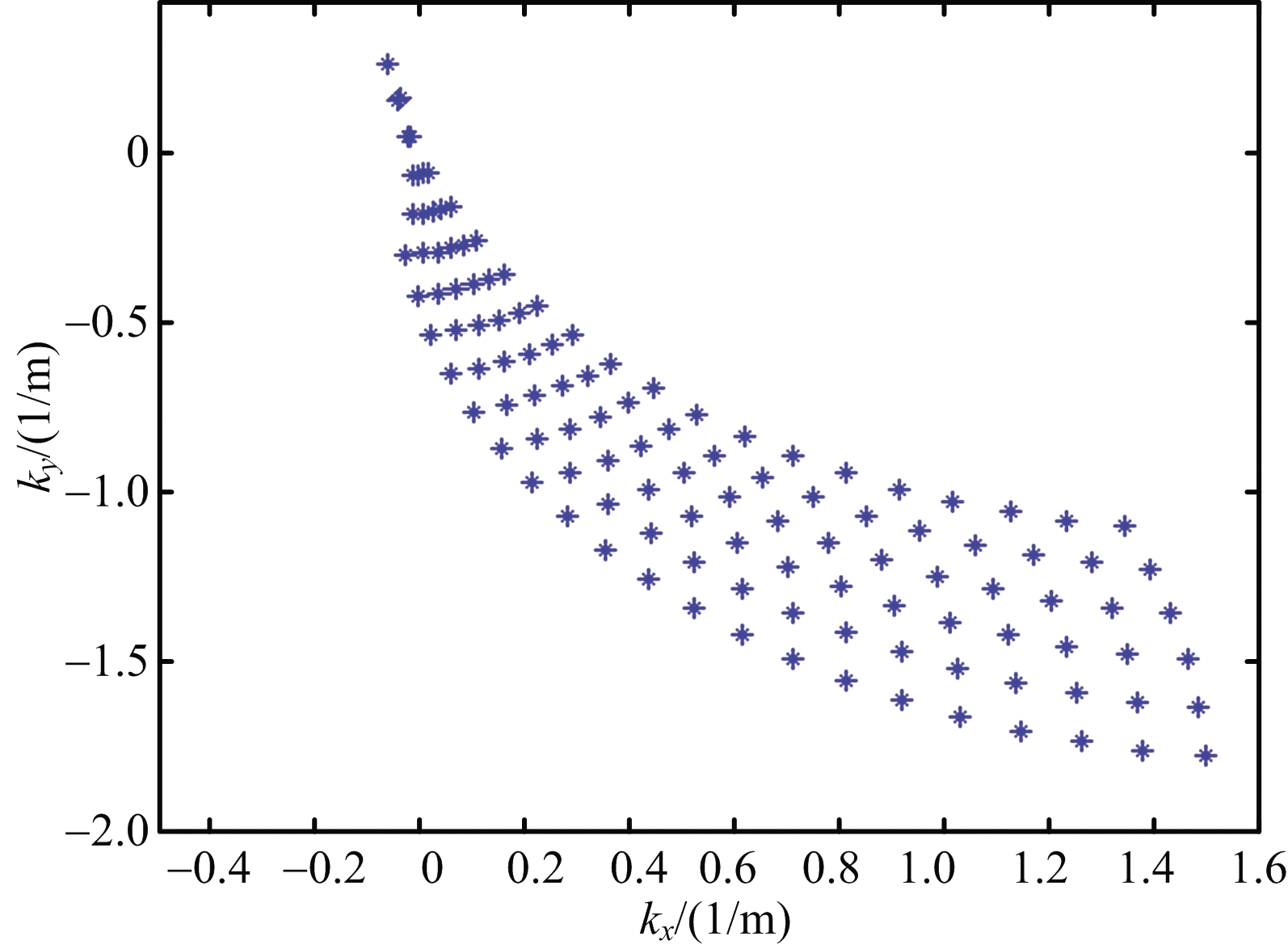
图2 空间谱填充点分布情况示意图
从空间谱的填充结果可以很直观地分析目标回波采样数据的分布情况,因此,考虑通过空间谱域填充的角度分析分布式无源雷达的成像性能和对成像算法进行分析研究是一个很好的方法[3]。
2 基于二维FGG-NUFFT分布式无源雷达成像算法
本文给出基于快速高斯网格(FGG)的NUFFT算法,主要从信号采样角度和卷积尺度方面对非均匀回波进行处理,实现分布式无源雷达目标图像重建的同时且大幅度提高冗余数据的运算速度,具体算法推导如下。
根据式(5)求目标散射函数方程并离散化得
(7)
式中,-Mo/2≤xi,yj≤Mo/2,Mo为散射系数维数,MN表示总的采样通道,kxq,kyq为频域上的采样点且在各自方向上是非均匀排列的。设
G(kX,kY)=![]()
δ(kX-kxq,kY-kyq)
(8)
式中,δ(·)表示狄拉克δ函数。显然可以看出 G(kX,kY)在网格中是非均匀排布的。由文献[19]可知,NUFFT的核心思想是利用窗函数对非均匀的原始数据进行加权平滑,因此窗函数的选择至关重要,文献[16-17]在研究中得出高斯核函数具有钟型结构,是一个用于平滑效果很好的卷积核的结论。因此,为实现对分布式无源雷达目标回波非均匀采样数据进行良好的平滑处理,本文选择周期为[0,2π]×[0,2π]的二维高斯周期核函数作为卷积核,即窗函数,表示如下:
gτ(kX,kY)=![]()
e-(kY-2l2π)2/4τ
(9)
式中,τ为高斯核函数参数,决定核函数的指数衰减率。接着对G(kX,kY)做卷积运算,得
Gτ(kX,kY)=G(kX,kY)*gτ(kX,kY)=
gτ(kX-ξX,kY-ξY)dξXdξY
(10)
则Gτ(kX,kY)经过高斯平滑后可利用标准FFT在过采样网格上进行高精度计算,首先对其进行均匀过采样,得
Gτ(mΔw,nΔw)=
![]()
(11)
式中,m,n为网格采样点,Δw为过采样时采样间隔,Δw=2π/Mr,Mr为过采样点数。接着对 Gτ(mΔw,nΔw)进行FFT可得其离散傅里叶变换谱为
στ(xi,yj)≈![]()
e-j(ximΔw+yjnΔw)
(12)
最后必须消除窗函数gτ(kX,kY)造成的平滑效应,进行去卷积处理得到最终的反演目标函数为
(13)
在求式(11)时,需要遍历所有非均匀分布的数据点(kxq,kxq),可想而知运算量极大,因此可利用高斯核函数的指数衰减特性,对远离(kxq,kxq)的网格点忽略不计,设置网格扩散范围,只考虑(mΔw,nΔw)附近的Msp个点(Msp=6为单精度;Msp=12为双精度[16]),则将大大降低运算量。同时对高斯核函数式(9)指数项考虑使用分裂思想进行分解可得
e-(kX-2l1π)2/4τ·e-(kY-2l2π)2/4τ=
e-(kX2+kY2)/4τ·ekXπl1/τ·ekYπl2/τ·
e-(πl1)2/τ·e-(πl2)2/τ
(14)
式(14)的后两项与kX,kY无关,因此对非均匀数据点平滑处理时只需预计算一次,避免了重复计算,减少了计算所占的内存空间。
综合上述,可将基于FGG-NUFFT的分布式无源雷达成像算法概述如下:
1) 设置过采样比例R=Mr/Mo,网格扩散参数Msp,高斯核函数参数τ=πMsp/[Mo2R(R-0.5)],核参数精度根据需要确定;
2) 预计算和存储高斯核参数与非均匀点无关的固定指数项;
3) 找到非均匀采样数据过采样网格上小于或等于(kX,kY)最近的均匀网格点(ζ1,ζ2)=Δw(m,n);
4) 将高斯核函数与回波采样信号进行卷积平滑处理,计算式(10)、式(11);
5) 用过采样FFT求得目标反演函数 στ(xi,yj),再对其进行去卷积处理得最终成像结果![]()
3 仿真实验与分析
先对分布式无源雷达的空间谱填充非均匀性进行分析,从式(4)可发现空间谱填充结果受外辐射源载频、收发站数量、布站情况等因子影响。本仿真实验选择收发站的空间布站影响因子对空间谱分布进行讨论分析,然后再对FGG-NUFFT算法的成像效果进行验证和评估。所有仿真实验均采用相同设备和编程环境,所有操作均在Windows 10、CPU为2.6 GHz酷睿i5,内存为4G的PC机上运行,编程环境为Matlab R2014a。
本文选取空中目标为研究对象,给出其二维强散射点模型,选取9个坐标点(-4,-2),(-4,2),(0,-4),(0,0),(0,4),(2,-2),(2,2),(4,0),(6,0)构成飞机目标,如图3所示。选择地面电视基站信号作为外辐射源,以20个外辐射源、24个接收站进行空间布站仿真实验。外辐射源的频率采用480~632 MHz范围,且假设以8 MHz为间隔均等分配,方位角φt在-108°~-70°,间隔2°均等分布,俯仰角θt在6°~ 14°间隔0.4°均等分布;保持上述条件不变,通过改变接收站的方位角或俯仰角改变系统的布站情况,设置3种布站构型方式(如表1所示),并针对每一种构型进行分析讨论。
表1 接收站仿真参数

构型方式方位角φrφr分布间隔俯仰角θtθt分布间隔构型1-18°^ 5°1°0°^6°0.25°构型26°^29°1°0°^6°0.25°构型36°^29°1°4°^9°0.25°
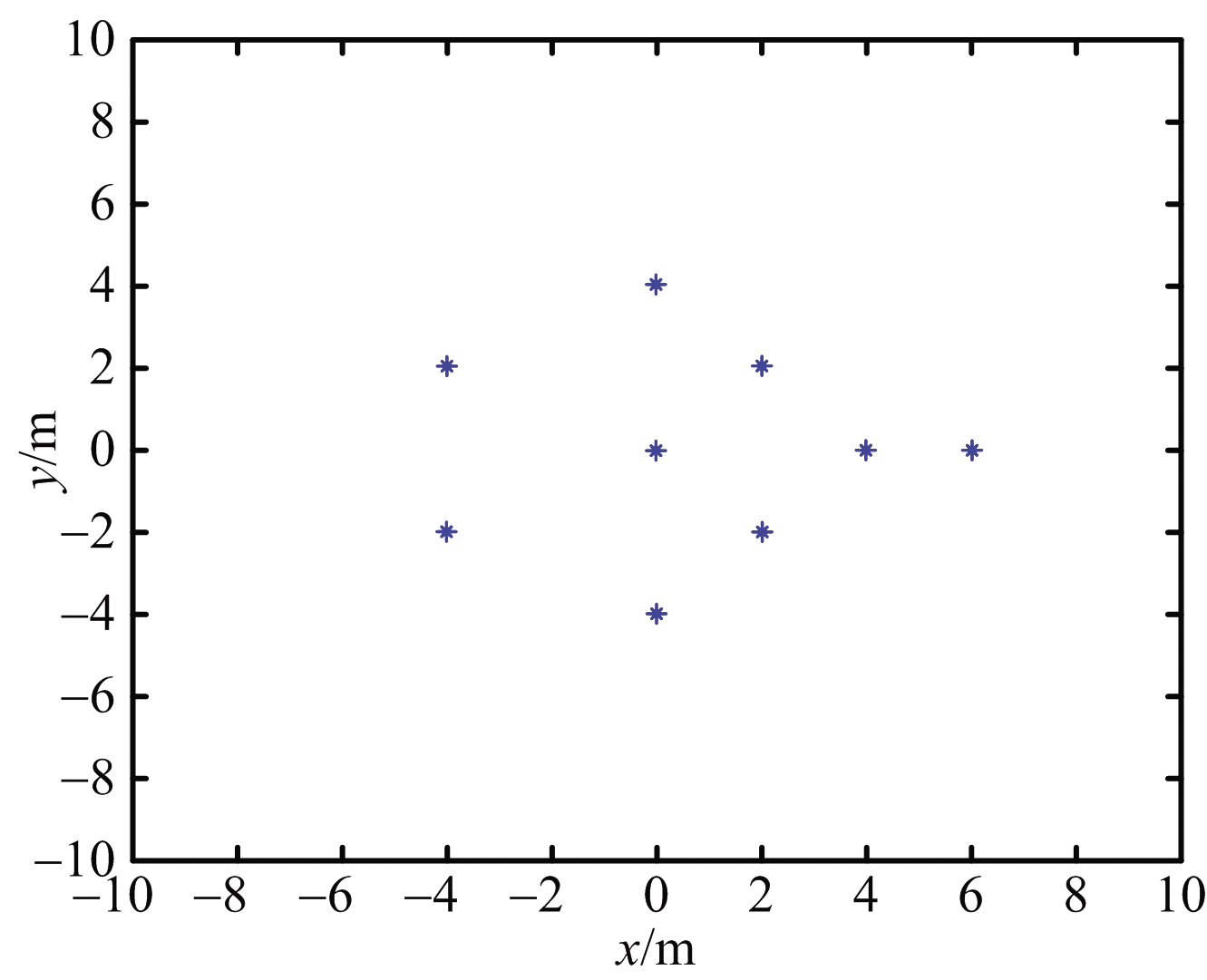
图3 目标强散射点模型
3.1 空间谱非均匀度特性分析
首先分别对3种构型的空间谱分布情况仿真实验,如图4所示。
对空间谱填充点的分布情况进行分析,将图4(a)空间谱局部填充区域利用相同的矩形框进行放大,如图5所示。
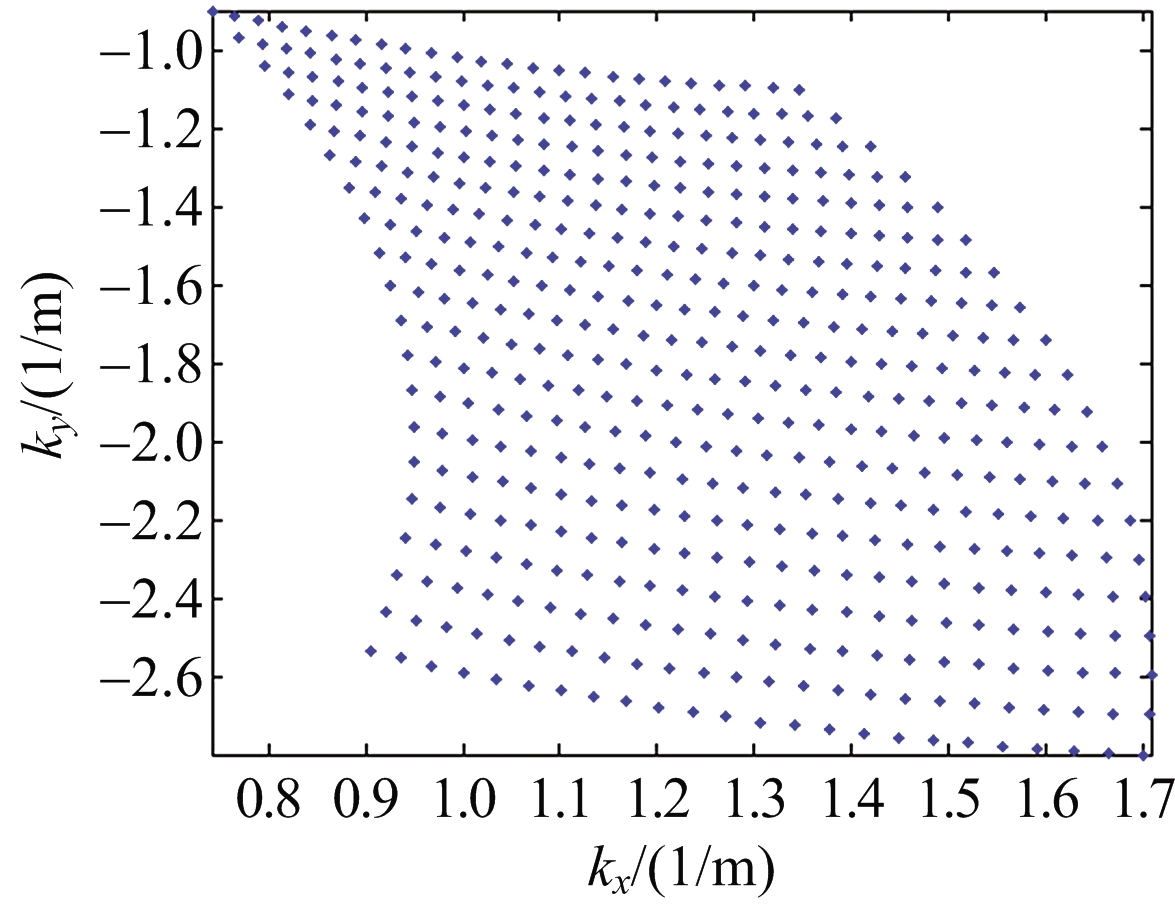
(a) 构型1
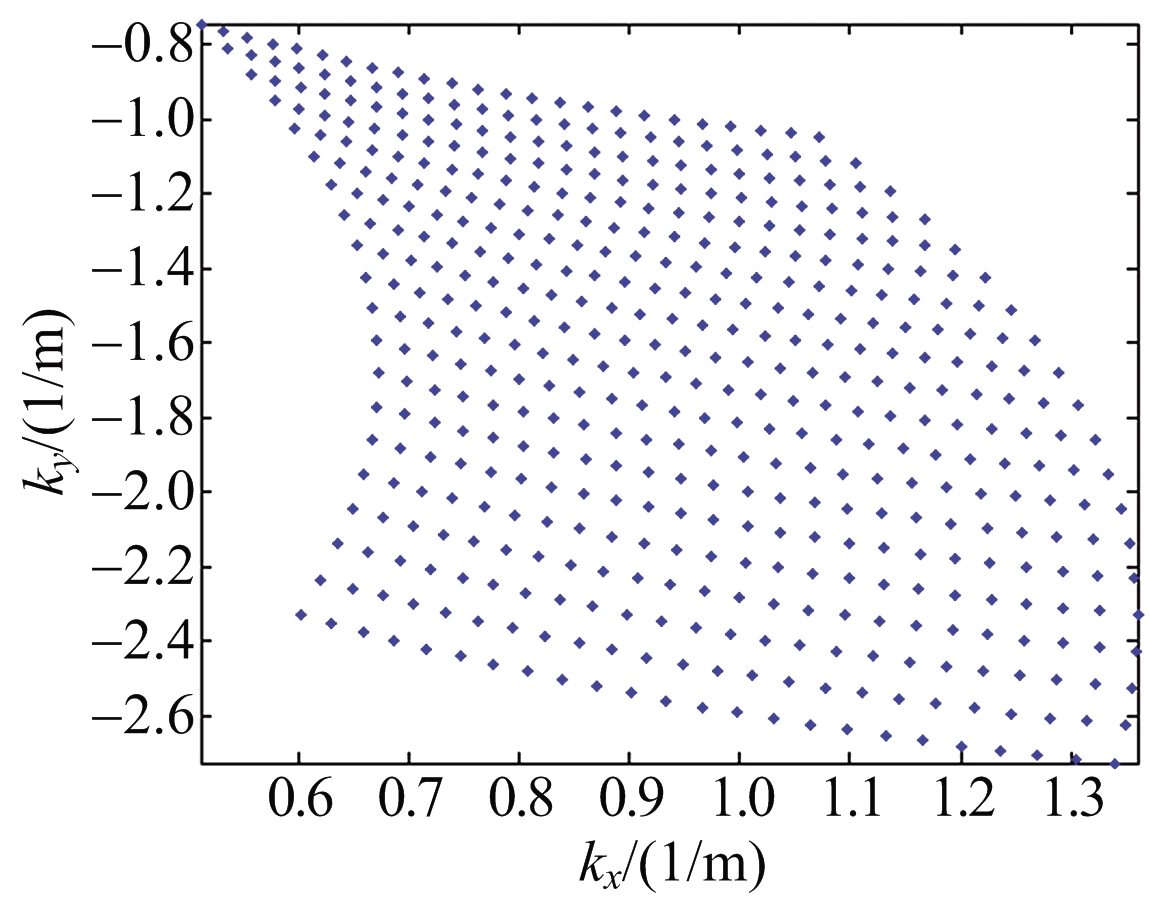
(b) 构型2
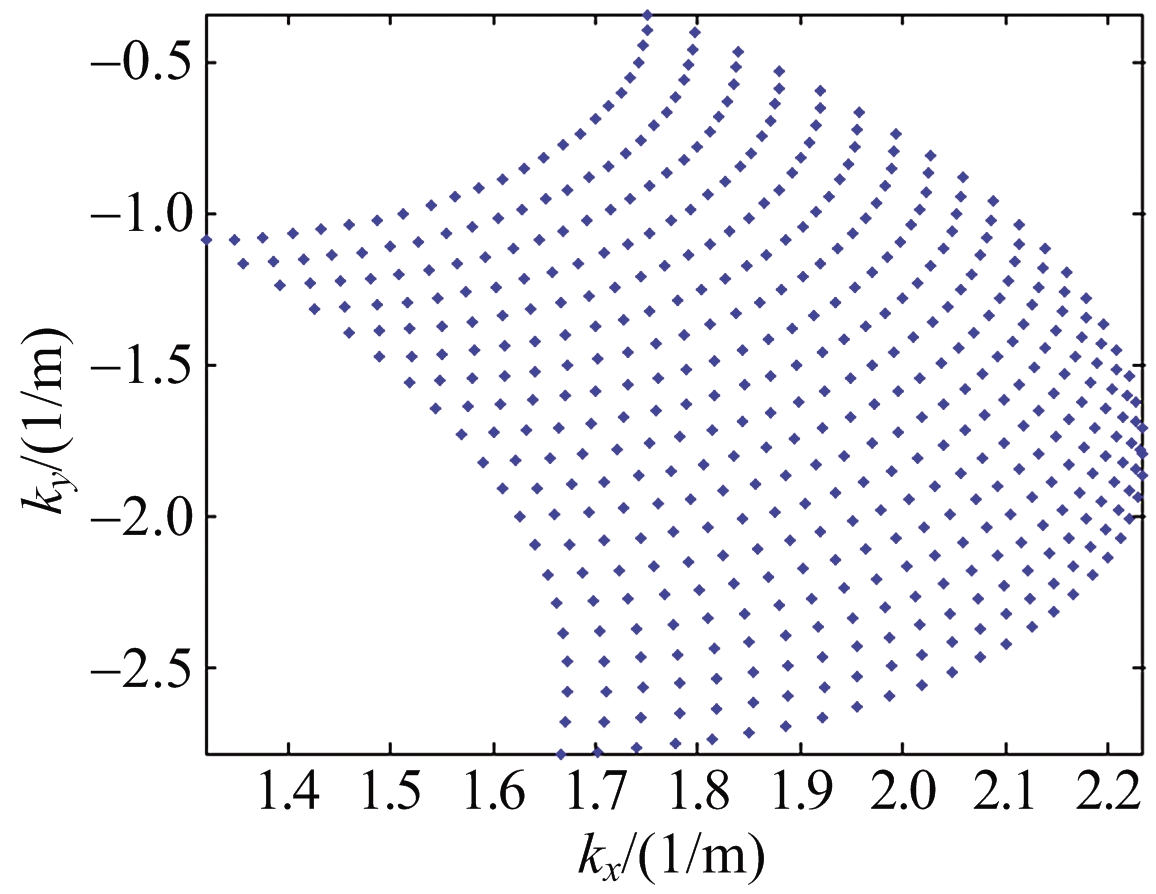
(c) 构型3
图4 空间谱填充图
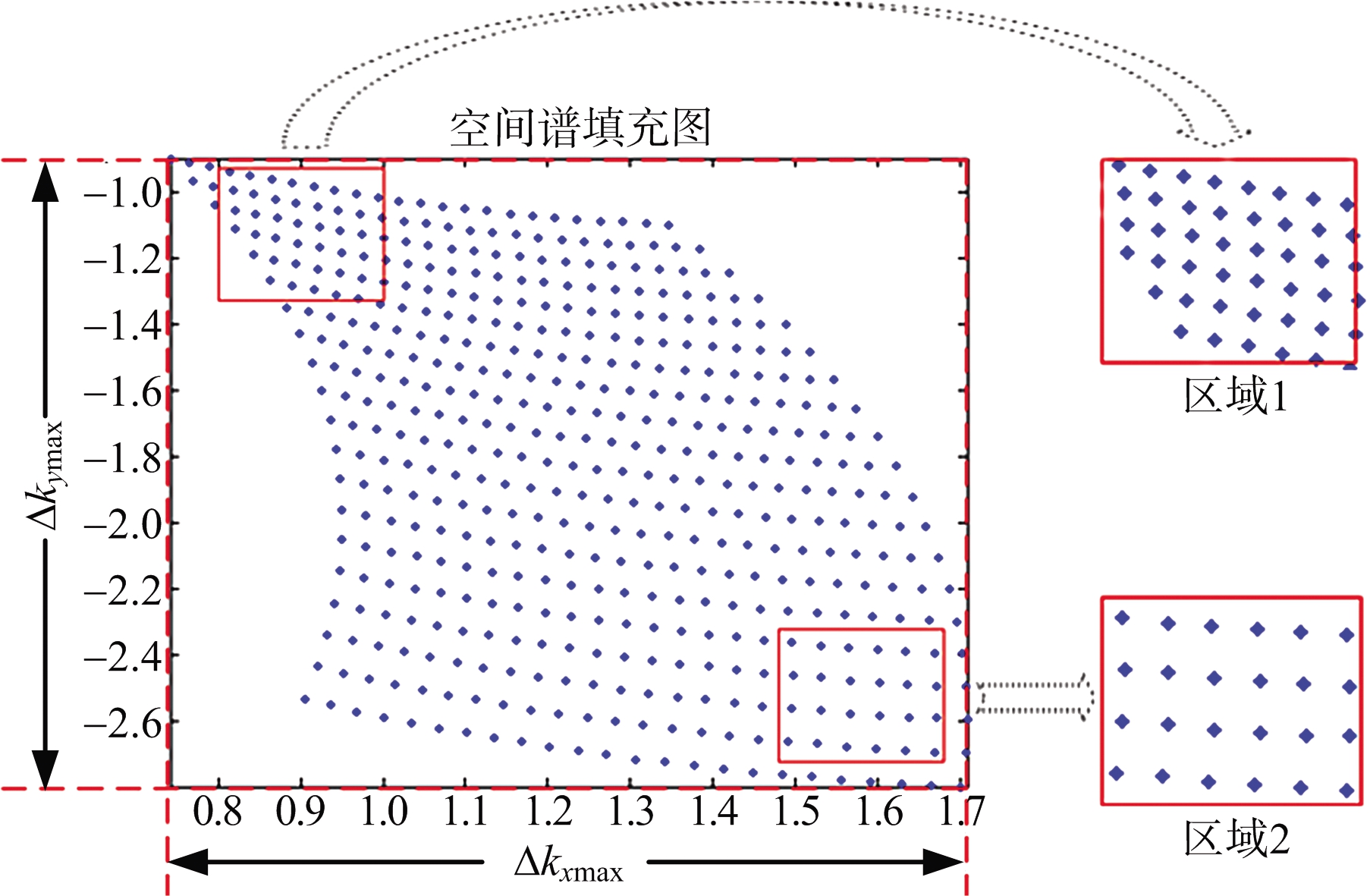
图5 构型1空间谱局部填充区域放大图
从直观角度分析,可发现填充的整体区域不是规则形状,尤其在纵向有明显扭曲现象,若构造规则网格分布,填充点很难都落到网格点上。从客观角度分析,选两块空间谱域的填充点分布间距进行对比,利用空间谱填充点欧氏距离均值![]() 如式(15)所示)对两块弧形区域进行量化,RX表示矩形框内填充点的数量,
如式(15)所示)对两块弧形区域进行量化,RX表示矩形框内填充点的数量,![]() 表示第i个填充点四邻域距离和的均值,经计算区域2填充点之间的欧氏距离均值约是区域1的2倍,进一步证明整个空间谱的填充点之间分布是非均匀的。
表示第i个填充点四邻域距离和的均值,经计算区域2填充点之间的欧氏距离均值约是区域1的2倍,进一步证明整个空间谱的填充点之间分布是非均匀的。
(15)
为了更客观地描述不同条件下的空间谱填充的非均匀程度,本文建立了3项评估指标对其进行量化分析,分别是空间谱支撑域大小、空间谱扭曲度和空间谱RMSE,根据已有知识[9],在支撑域一定时一般空间谱扭曲度越小越均匀,空间谱RMSE越小越均匀,因此需综合利用这三项评估指标实现对空间谱填充质量的评价。
空间谱支撑域是对空间谱填充最大范围的表示,分别用Δkxmax和Δkymax表示kx,ky方向上的最大填充范围,Δkxmax和Δkymax组成的矩形区域即空间谱的支撑域大小,如图5所示;空间谱扭曲程度由空间谱填充弧线的曲率Kq来表示,由式(4)可知,每一个接收机接收到的所有外辐射源的回波对应空间谱填充的一条弧线,曲率公式如式(16)所示;空间谱RMSE表示整个空间谱填充点之间的离散程度,计算公式如式(17)。
(16)
(17)
基于上述三种构型,计算各空间谱填充结果评价指标如表2所示。
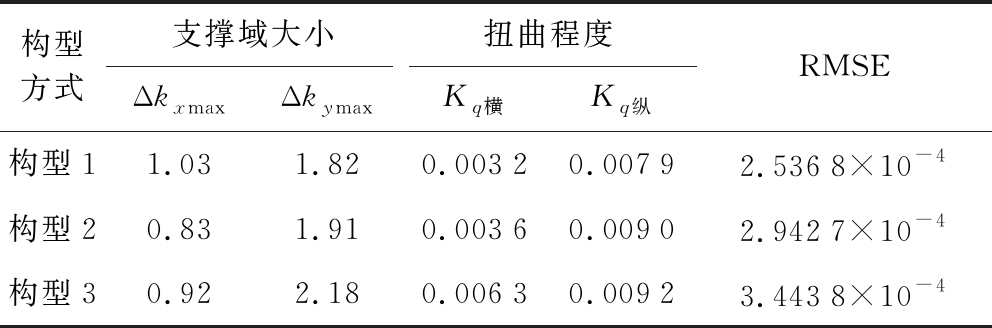
表2 空间谱非均匀度指标分析
构型方式支撑域大小扭曲程度ΔkxmaxΔkymaxKq横Kq纵RMSE构型11.031.820.00320.00792.5368×10-4构型20.831.910.00360.00902.9427×10-4构型30.922.180.00630.00923.4438×10-4
从表2数据对空间谱填充质量进行量化分析,此仿真实验是在控制相同收发机数量的条件下进行的,即空间谱填充点的数量一样。构型1与构型2是基于方位角的角度分析,在保持外辐射方位角不变的情况下,改变收发站的方位角相对位置,构型2的支撑域变小了,空间谱填充变得更紧致,但其扭曲程度较构型1变大,纵向的扭曲程度变化更明显,同时RMSE增大,综合指标分析构型2空间谱非均匀度增加;同理可分析构型3空间谱填充的非均匀度,得出构型3较构型2的空间谱填充非均匀度进一步增加。通过对空间谱量化可基本实现对不同条件下空间谱非均匀度的客观比较,本文建立的3项评估指标可推广到其他不同影响因子影响下的空间谱分析案例中去。
3.2 FGG-NUFFT成像算法仿真及空间谱非均匀度影响成像质量验证
基于上述空间谱的分析结果进行仿真验证,为了证明FGG-NUFFT算法的有效性以及验证本文成像算法对非均匀度空间谱的适应性,与目前已有的一些分布式无源雷达成像方法:常规插值法[3]、文献[15]中基于余弦尺度因子的NUFFT算法和文献[9]逐点匹配滤波法进行对比。成像仿真结果对比如图6所示。
为评估3种算法的成像质量,参考文献[10]中的精度评价指标L2,定义目标反演成像误差为式(18)。
(18)
式中,g′表示重建图像,g表示用于成像质量对比的参考图像,这里以均匀致密空间谱下的良好重建图像作为参考图。文献[15]NUFFT法、文献[9]逐点匹配滤波与本文FGG-NUFFT法误差如图7所示,由于插值法误差过大不列入绘图对比。

图6 目标反演成像结果对比
最后针对每种构型下3种算法进行效率对比,仿真时间如表3所示,单位是s。
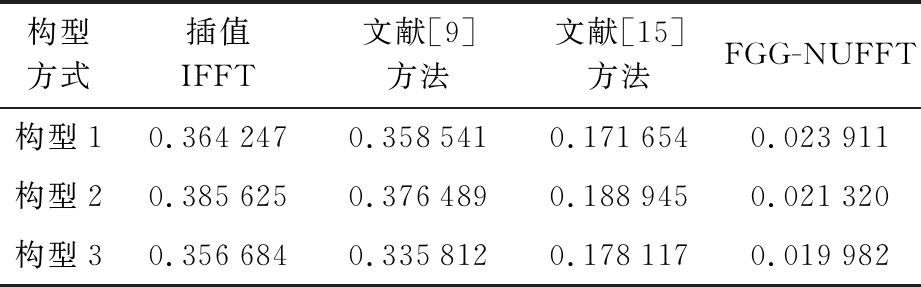
如图6所示,3种构型下插值法都不能较好地进行目标反演,而本文算法和文献[9]、文献[15]方法都能较好地将目标进行反演,但总体上本文的FGG-NUFFT比文献[15]方法效果要好,与文献[9]效果差不多。从图7误差分析上,可以看出3种构型下3种非均匀快速傅里叶变换算法重建目标的误差都控制在5%以下,且本文方法FGG-NUFFT成像精度相较文献[15]的NUFFT高;从表3运算时间效率上,本文FGG-NUFFT明显优于其他3种方法,在实际大批量数据运算时将占绝对优势,总体上本文算法在成像质量和效率上优于其他方法。
表3 目标反演成像运算时间
构型方式插值IFFT文献[9]方法文献[15]方法FGG-NUFFT构型10.3642470.3585410.1716540.023911构型20.3856250.3764890.1889450.021320构型30.3566840.3358120.1781170.019982
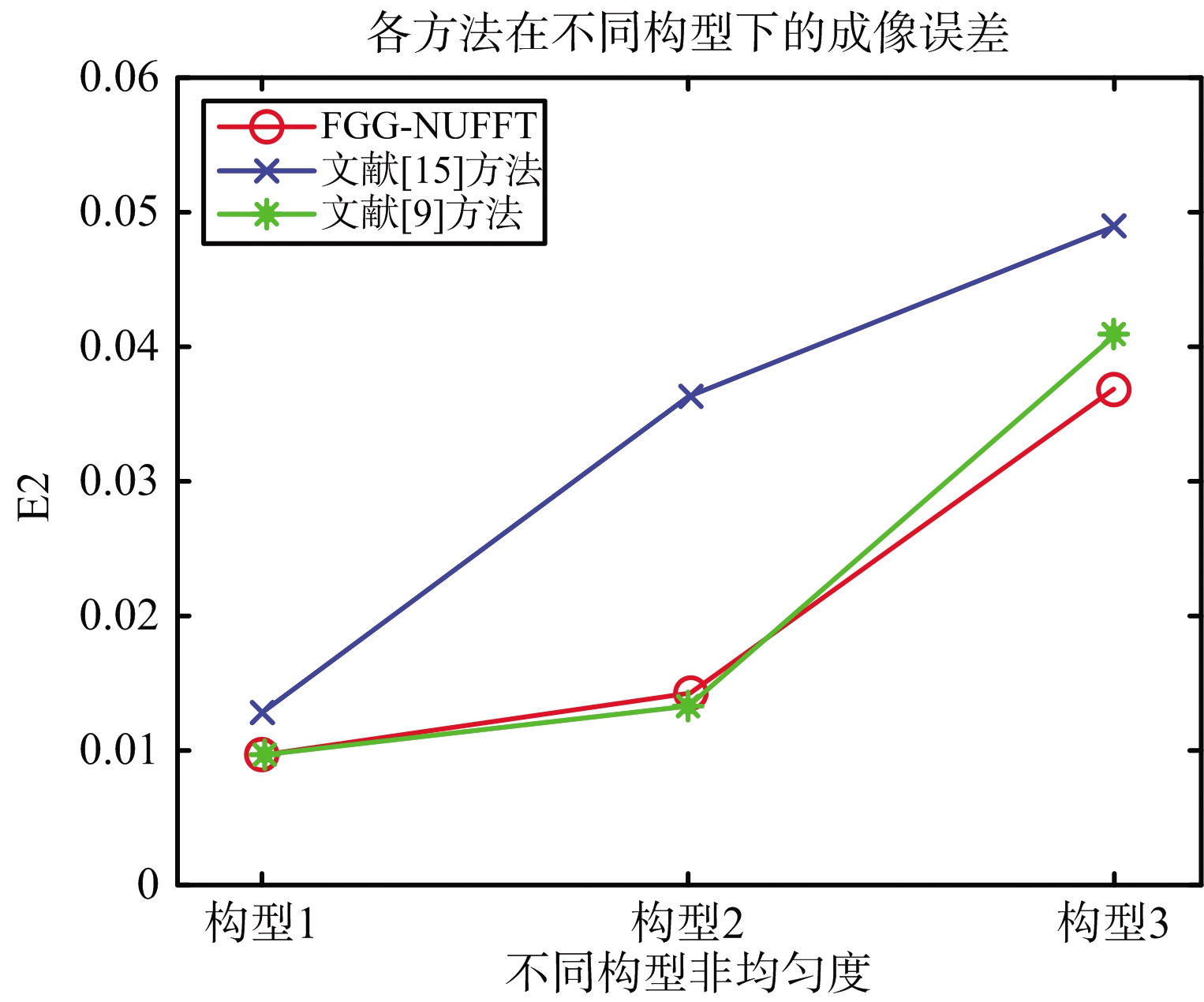
图7 误差分析对比图
图7中横坐标构型1、构型2、构型3分别指各自的空间谱非均匀度,且构型3的空间谱非均匀度>构型2的空间谱非均匀度>构型1的空间谱非均匀度。
4种方法都受空间谱非均匀度的直接影响,随着空间谱非均匀度的增加,成像质量会随之变差,NUFFT算法对空间谱的填充质量有着一定的要求,与空间谱的支撑域、扭曲程度、离散程度密切关联,因此可通过空间谱的3项评价指标优化空间谱分布的各影响因子,获得相对均匀的空间谱填充,获得高质量的目标反演像。
4 结束语
本文基于空间谱分析和FGG-NUFFT成像算法对分布式无源雷达成像进行了研究分析,针对分布式无源雷达非规则构型和外辐射源非合作导致目标回波采样数据在空间谱域的填充往往是非均匀的问题,本文对其进行定量分析评估空间谱的非均匀度,提出3种简单评价指标,空间谱非均匀度评价指标的提出对改善空间谱填充和算法效果的验证具有指导意义;利用一种具有更好平滑效果的快速高斯网格NUFFT算法,进一步改善空间谱非均匀填充下的成像质量,同时大幅提升计算效率,对非均匀填充的空间谱具有一定的适用性。
[1] BRISKEN S, MOSCADELLI M, SEIDEL V, et al. Passive Radar Imaging Using DVB-S2[C]∥IEEE Radar Conference,Seattle, WA, USA:IEEE, 2017: 552-556.
[2] CRISTALLINI D, PISCIOTTANO I, KUSCHEL H. Multi-Band Passive Radar Imaging Using Satellite Illumination[C]∥2018 International Conference on Radar,Brisbane, QLD, Australia:IEEE,2018:1-6.
[3] 唐远航. 分布式雷达高分辨成像方法研究[D].合肥:中国科学技术大学, 2018.
[4] 李银斌. 非均匀快速傅里叶变换及其在SAR成像中的应用[D]. 南京:南京航空航天大学, 2016.
[5] BERGER C R, DEMISSIE B, HECKENBACH J, et al. Signal Processing for Passive Radar Using OFDM Waveforms[J]. IEEE Journal of Selected Topics in Signal Processing, 2010, 4(1):226-238.
[6] YANG C, SHI J, JIANG Z, et al. A Multi-Channel Radar Forward-Looking Imaging Algorithm Based on Super-Resolution Technique[C]∥2018 China International SAR Symposium, Shanghai, China: IEEE, 2018:1-4.
[7] KIM H J, BAE K U, SONG W Y, et al. An ISAR Imaging Method for Search Radar Involving Nonuniform Angle Samples[J]. Progress in Electromagnetics Research, 2018, 65:9-17.
[8] 王俊, 牛溢华. 基于多电视台的两种无源雷达成像算法[J]. 系统工程与电子技术, 2007, 29(8):1263-1267.
[9] LIU Changchang, XU Hao, HE Xuezhi, et al. The Distributed Passive Radar 3-D Imaging and Analysis in Wavenumber Domain[C]∥IEEE 10th International Conference on Signal Processing Proceedings, Beijing, China: IEEE, 2010:2051-2054.
[10] DUTT A, ROKHLIN V. Fast Fourier Transforms for Nonequispaced Data[J]. SIAM Journal on Scientific Computing, 1993, 14(6):1368-1393.
[11] MACIEJEWSKI M W, SCHUYLER A D, HOCH J C. Practical Nonuniform Sampling and Non-Fourier Spectral Reconstruction for Multidimensional NMR[M].New York, NY:Protein NMR, Humana Press,2018:341-352.
[12] KAN Y, ZHU Y, TANG L, et al. FGG-NUFFT-Based Method for Near-Field 3-D Imaging Using Millimeter Waves[J]. Sensors, 2016, 16(9):1525.
[13] SUN Shilong, ZHU Guofu. Accelerating CS Radar Imaging by NUFFT[C]∥2013 IEEE International Conference on Signal Processing, Communication and Computing ,Kunming, China:IEEE, 2013:1-4.
[14] YANG Xiahan, ZHENG Yahong, GHASR M T, et al. Microwave Imaging from Sparse Measurements for Near-Field Synthetic Aperture Radar[J]. IEEE Trans on Instrumentation & Measurement, 2017,66(10):2680-2692.
[15] HE Xuezhi, XU Hao, LIU Changchang, et al. A New Approach to Distributed Passive Radar Imaging by 2-D NUFFT[C]∥IEEE 10th International Conference on Signal Processing Proceedings, Beijing, China:IEEE, 2010:2067-2070.
[16] GREENGARD L, LEE J Y. Accelerating the Nonuniform Fast Fourier Transform[J]. SIAM Review, 2004, 46(3):443-454.
[17] WANG R, DENG Y K. Bistatic SAR System and Signal Processing Technology[M]. Singapore:Springer, 2018:188-198.
[18] 王天云, 刘冰, 凌晓冬, 等. 存在站址误差下的无源雷达稀疏成像[J]. 雷达科学与技术, 2018, 16(3):261-266.
[19] NGUYEN N, LIU Q H. The Regular Fourier Matrices and Nonuniform Fast Fourier Transforms[J]. SIAM Journal on Scientific Computing, 1999, 21(1):283-293.
