0 引言
纵观国内外现役主战装备雷达和在研新型雷达,有源相控阵已成为现代雷达技术的主流体制[1]。有源相控阵雷达的一个重要优势是具有较高的任务可靠性,这是由于在雷达天线阵中设置了若干冗余的射频收发组件(T/R组件),即使有部分组件失效或不能正常工作对雷达系统的性能影响不大。
关于有源相控阵雷达天线的任务可靠性模型,一直是工程领域关注的焦点。目前常用的是表决模型[2],即将构成天线阵面的主要单元进行表决冗余后再串联,该方法没有考虑失效T/R组件在天线阵列中所处的物理位置对于天线性能的影响,为此,丁定浩等[3]提出在表决模型中增加失效单元的最小间距约束,从而对表决模型的冗余量进行压缩;熊年生等[4]则通过对天线方向图的仿真分析,在天线副瓣下降允许范围内确定了失效T/R组件的位置分布要求。但是,对于星载有源相控阵雷达而言,其有源通道数量多且设备间的控制关系复杂,上述表决模型忽略了系统中单元间的故障相关性,若简单地在失效独立的假设下进行系统可靠性分析,常常会产生较大的误差,甚至得出错误的结论[5-8]。
鉴于此,本文结合星载有源相控阵天线的原理和特点,对天线系统的失效判据进行了分析,在以控制T/R组件失效数为系统正常的度量指标框架下,建立了能够全面体现其“冗余性、层次化及故障相关性”等特点的系统可靠性模型。基于该模型,给出了系统可靠度计算的解析法和蒙特卡洛模拟方法。最后,通过具体案例对本文所提模型及算法进行了验证。
1 天线阵系统失效判据
有源相控阵天线系统的可靠性问题较为特殊,其与传统天线通信系统相比,不是通过双机冷/热备份工作模式提高可靠性,而是在系统设计时留有一定的通道余量。因此,为准确评估相控阵系统的可靠性,首先需要确定通道的冗余量,即雷达系统能够完成预定任务,组件允许的合理失效范围。
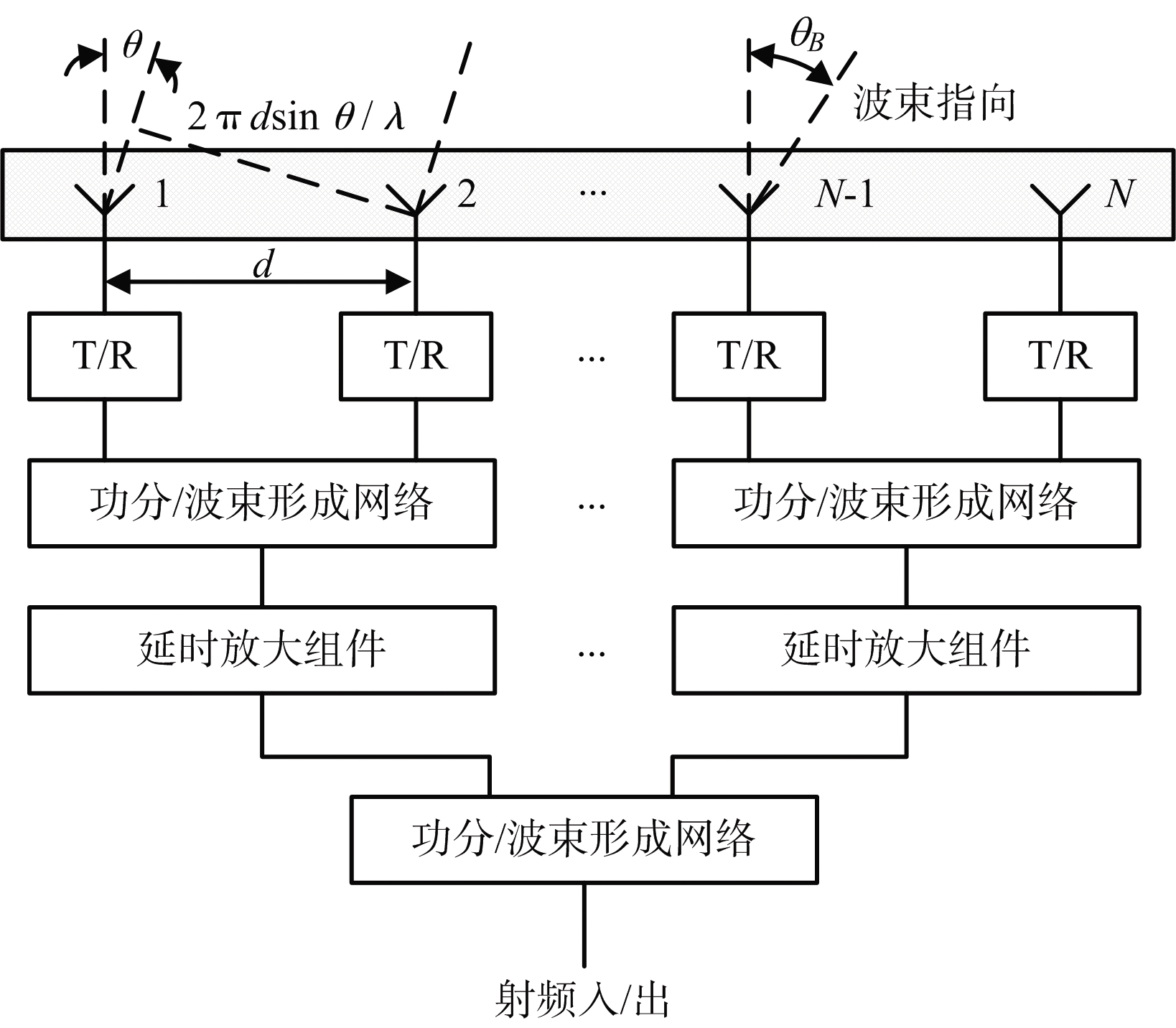
图1 有源相控阵天线系统组成示意图
以线性相控阵天线为例,如图1所示,相控阵有N个天线单元,相邻单元的间距为d,天线波束的最大指向为θB。当天线阵列接收到偏离阵列法线θ角方向来的波长为λ的信号时,信号到达相邻天线单元的路程差为dsinθ,相应地,由该路程差引入的相位差为
(1)
即每个单元的相位都比其右边的单元滞后Δφ,则线性相控阵天线的方向函数可表示为
(2)
式中,ai为幅度加权,![]()
为简化分析,对均匀分布照射函数,取ai=1,由此推导出相控阵幅度方向图的辛格函数为
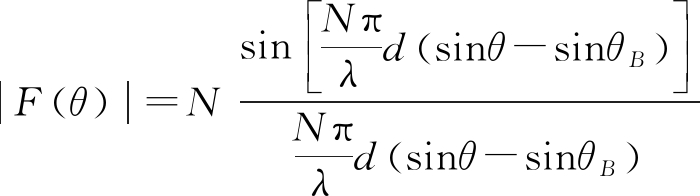
(3)
为形象化描述,利用MATLAB软件对相控阵幅度方向图进行仿真计算,假设信号频率为10 GHz,相邻天线单元间距为30 mm,单元数量分别为12,24,36时,方向图如图2所示,可见有源相控阵天线单元数量对其辐射强度和波束宽度影响很大,同一频率下阵元数量和天线间距越大波束就越窄。对于相控阵雷达而言,辐射功率和波束宽度是重要的功能指标,而辐射功率又与有源相控阵的功率源T/R组件及阵元数量相关。因此,在评估相控阵天线系统可靠性时,可使用T/R组件允许失效数作为系统功能正常与否的判据。一般而言,对于地面相控阵天线,其组件的冗余量设置为10%,而星载相控阵天线该比例通常为5%[3]。

图2 不同单元数量下的天线方向图仿真
2 天线阵系统可靠性建模
目前,对有源相控阵天线系统进行任务可靠性建模通常采用n中取k的表决模型的串联形式,即将图1中的每一类组成单元都作为串联模型中的一项,而每一项中的表决器可根据T/R组件允许的失效数等效获得,该模型的计算公式如下[2]:
![]()
(4)
式中,Rs(t)为天线阵的系统可靠度,Ri(t)为组成系统的单元可靠度,M为组成系统的单元种类,Ni为每一类单元的总数量,Oi为保证天线阵实现规定功能须正常工作的单元数量。
利用上述模型计算系统可靠度是假设各单元失效是互相独立的,这一假设在天线阵系统规模较小时可近似认为是正确的,但当系统规模较大,特别是随着现代有源相控阵天线多通道技术的应用,上述模型的计算误差会显著增大。根据故障相关理论[9-12],系统单元间相互影响的方式一般有三类:Ⅰ类为故障相关;Ⅱ类为故障率相关;Ⅲ类为冲击损伤相关。对于星载有源相控阵天线系统而言,显然属于第Ⅰ类系统,即当一个部件发生故障,会以一定概率引发系统中其他部件发生故障。
为此,这里依据层次建模的思想[13],提出一种表决冗余的故障相关系统“树联”可靠性模型。该模型利用树形结构描述有源相控阵天线系统中各单元的层级关联,同时通过树结构中的父、子节点约束系统中各单元间的控制范围。如图3所示为天线阵的系统可靠性框图,图中M为系统总层数;Ni为第i层单元的总数量(该层单元按顺序编号记为i-1到i-Ni);Ri为第i层单元的可靠度;Ki为第i层单元与其父节点单元数量的比值。
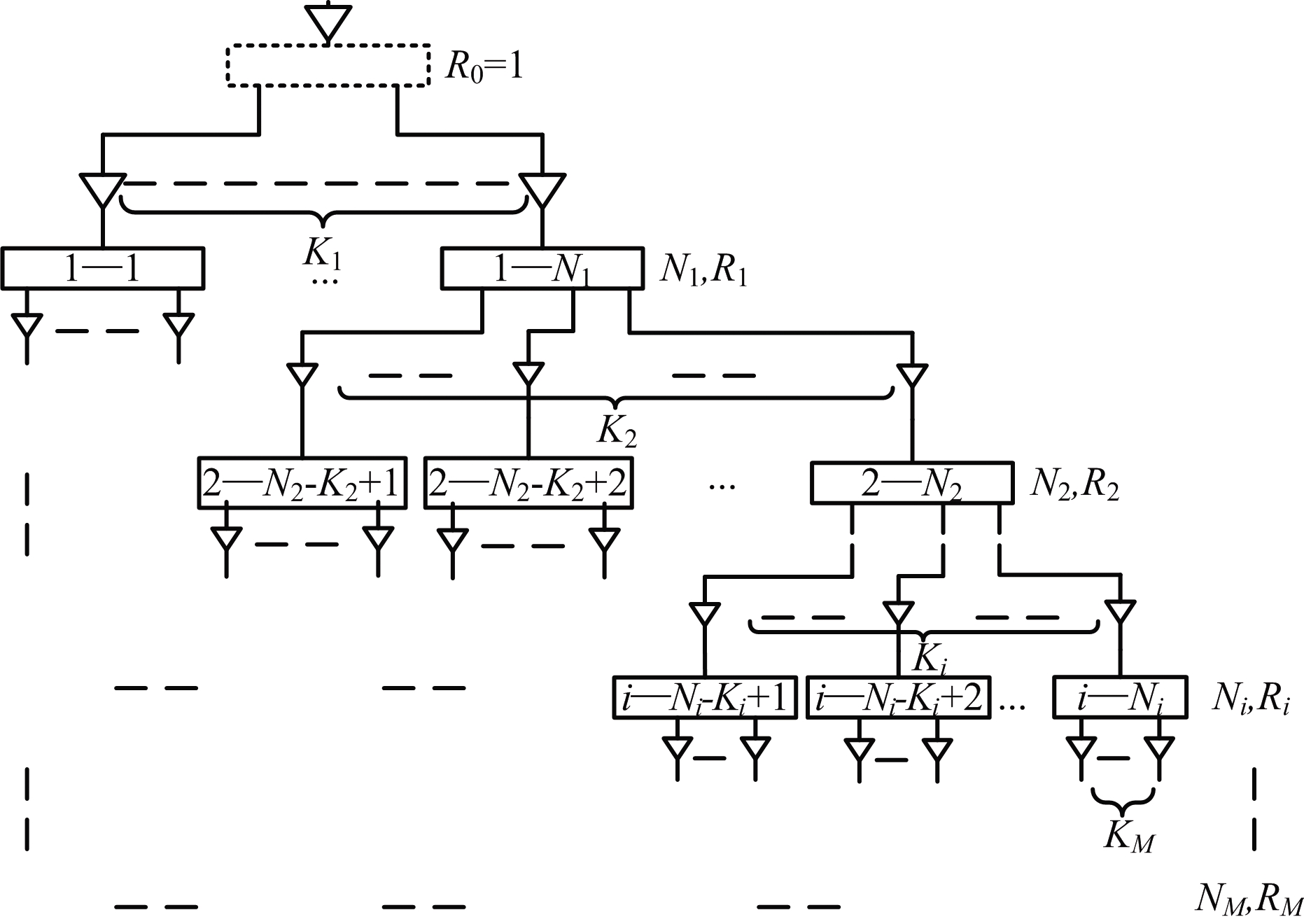
图3 有源相控阵天线“树联”可靠性模型
“树联”可靠性模型构建顺序为自顶向下,模型具备以下特点:
1) 冗余性:系统功能正常的判据为最底层单元正常工作的最小数量应满足特定比例;
2) 层次化:模型拓扑结构为树状、多层、分布式结构;
3) 故障相关性:树中节点间存在关联性,即父节点失效则其控制范围内的子节点全部失效,反之,若子节点正常则其父节点一定正常。
模型的基本假设如下:
1) 不失一般性,假设系统不会发生共因失效,且组成系统的相同层级各单元在独立失效情况下,其寿命具有相同的概率分布;
2) 单元和系统都只考虑两种状态,即正常或故障。
3 天线阵系统可靠性计算及仿真
3.1 解析法
这里采用递归方法计算“树联”模型的可靠度,首先选取图3所示模型的最底层和次底层,若已知最底层T/R组件数量为NM,同时可靠度为RM(t);次底层驱动器数量为NM-1,可靠度为RM-1(t),且每一个驱动器控制KM个T/R组件。
假设在t时刻,将天线阵面能正常工作(等价于有不少于C%的T/R组件能正常工作)记为事件A,其概率为P(A);正好有i个驱动器能正常工作记为事件Bi(i=0,1,…,NM-1),其概率为 P(Bi);在正好有i个驱动器能正常工作的条件下,有不少于C%的T/R组件能正常工作的条件概率记为P(A|Bi)。根据全概率公式有
(5)
式中,P(A),P(Bi),P(A|Bi)都是时间t的函数。P(A)即为天线阵面的可靠度,该模型的求解关键是计算出P(Bi)和P(A|Bi)。
由于每一个驱动器控制KM个T/R组件,因此当t时刻可正常工作的驱动器数量为i时(i∈[0,NM-1]),T/R组件可正常工作的数量为j,j的取值范围为[0,KM·i]。再考虑不少于C%的T/R组件能正常工作的约束条件,i和j的取值范围将进一步缩小。即当所有的驱动器都正常工作,而T/R正常工作的数量小于C%时,判定系统失效;另外,即使所有的T/R组件均无故障,但控制T/R组件的驱动器可正常工作的数量小于C%时,同样判定系统失效,此时的P(A|Bi)=0。因此,要使天线阵面正常工作,i和j的取值范围分别为i∈[OM-1,NM-1],j∈[OM,KM·i],其中OM-1=ceil(NM-1×C%),Om=ceil(NM×C%)(ceil()为向上取整运算)。
由此,在t时刻,NM-1个驱动器中有i个可正常工作的概率为
P(Bi)=![]()
i∈[OM-1,NM-1]
(6)
在有i个驱动器正常工作的条件下,最多有KM·i个T/R组件可正常工作,此时要求天线阵面能正常工作,则构成了KM·i个T/R组件中取OM个的表决模型,其概率为
P(A|Bi)=![]()
i∈[OM-1,NM-1]
(7)
将式(6)、式(7)代入式(5)中,可得到两层“树联”模型的可靠度为
R(t)=![]()
![]()
(8)
在两层“树联”模型的基础上,逐层递归,即可得到如图3所示完整模型的可靠度为
Rs(t)=![]()
(9)
式中:t为任务时间;Rs(t)为天线阵系统在t时刻的可靠度;M为层级数;Ni为第i层的单元数量;Ki为第i层与第i-1层单元数量的比值;Ri为第i层单元在t时刻的可靠度;Oi为满足任务要求第i层正常工作的最少单元数,通常规定最底层T/R组件的正常数量,而其他层级单元的该数值可根据层级比例逐层进行等效。
3.2 蒙特卡洛法
当有源相控阵天线系统层级和单元数量较多或层间控制比例不定时,利用式(9)计算天线阵的任务可靠度计算量较大,这里提供一种基于蒙特卡洛的天线系统可靠性模拟方法。其基本思路是先根据天线阵单元可靠度构建符合该概率分布的单元随机样本,再进行抽样、组装成若干系统样本,最后利用系统失效判据统计正常系统的数量并计算系统可靠度,具体流程如图4所示。
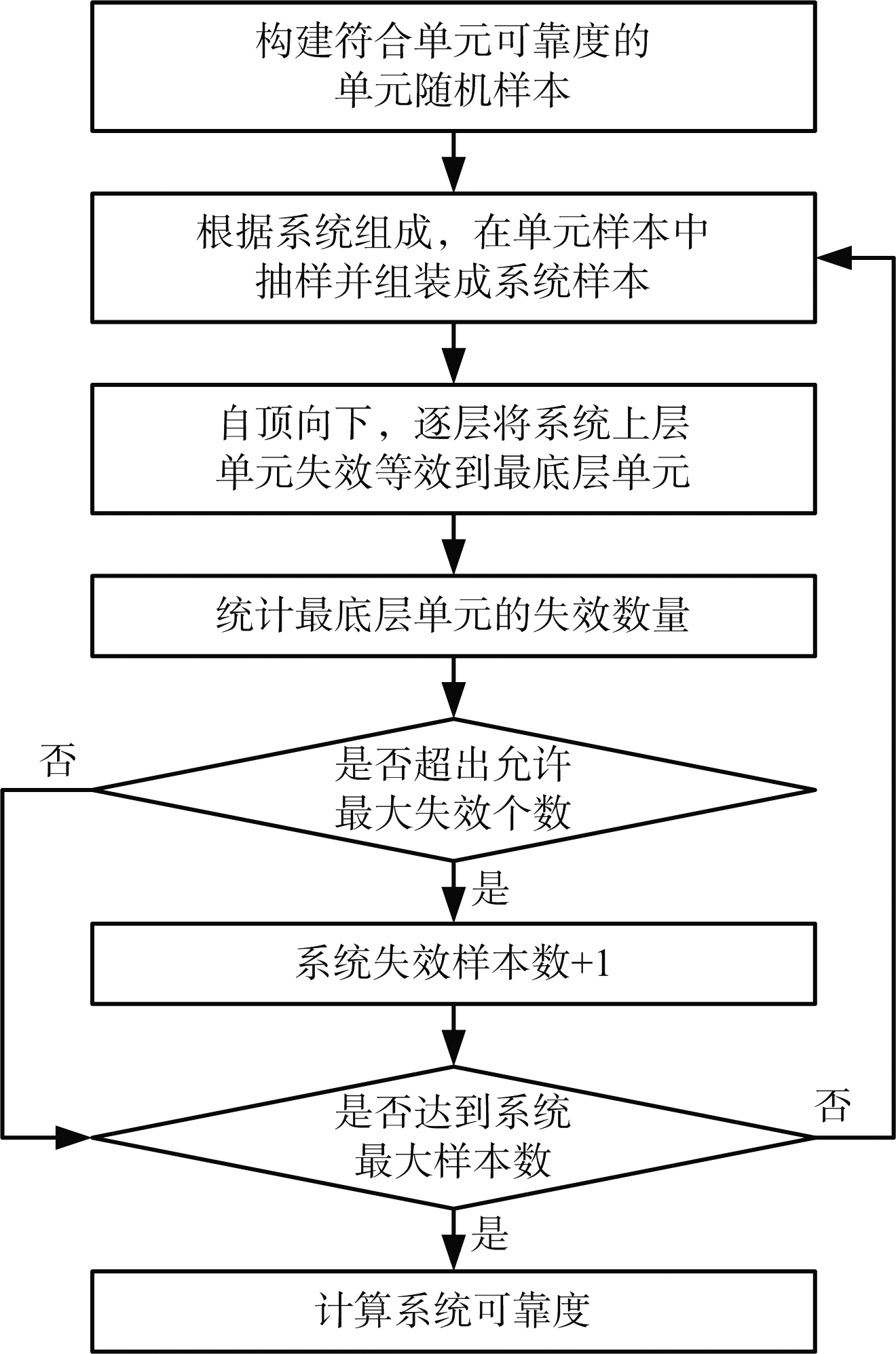
图4 基于蒙特卡洛的星载有源相控阵天线可靠性预计流程
通过蒙特卡洛仿真,得到相控阵天线的系统可靠度为
R′s=NF/NS
(10)
式中,NF为失效的系统样本数,NS为系统样本总数。这里需要说明的是任务时间对系统可靠度的影响体现在单元的随机样本中,即随着任务时间的增加,单元可靠度降低,相应地,单元样本中失效单元的数量增多。另外,随着系统样本数量的增加,仿真结果将趋近于解析值。
4 应用实例
某星载相控阵雷达的天线阵面由二次电源、波控单元、延时放大组件以及T/R组件(单通道)构成,各组成单元的数量、失效率如表1所示。根据卫星总体设计,以卫星在轨2年为例,寿命期内雷达系统总开机时间为1 460 h(每天工作2 h),同时,要满足雷达系统的成像指标则有源通道的失效数不能超过总数的5%,在该条件下,计算天线阵面寿命末期的可靠度。
表1 某天线阵面的单元信息
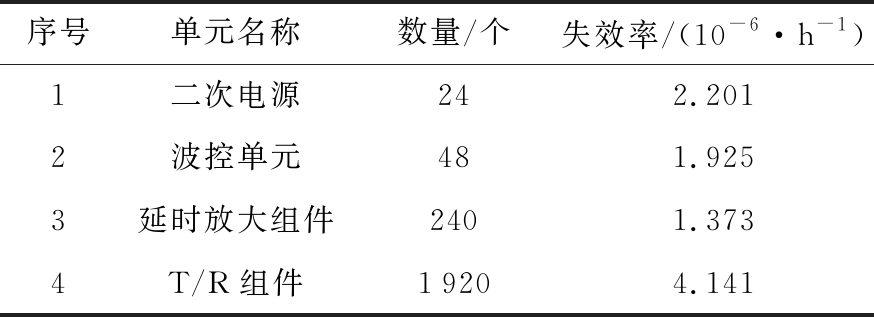
序号单元名称数量/个失效率/(10-6·h-1)1二次电源242.2012波控单元481.9253延时放大组件2401.3734T/R组件19204.141
首先,自顶向下建立“树联”可靠性模型,模型参数分别为:系统层数M=4;每层的单元数为N1=24,N2=48,N3=240,N4=1 920;层间控制比例为K2=2,K3=5,K4=8;维持系统正常工作的最少单元数量为O1=23,O2=46,O3=228,O4= 1 824;各层单元可靠度按指数分布计算为R1= 0.997,R2=0.997,R3=0.998,R4=0.994。将上述参数代入式(9),计算得到系统可靠度的解析值为0.966。
接着,利用蒙特卡洛方法进行系统可靠性仿真,系统样本数设置为2×104个,重复进行104次仿真,结果如图5所示。可见当抽样次数足够多时,系统可靠性符合均值为0.966,标准差为1.3×10-3的正态分布,该结果与采用“树联”模型计算的解析值一致。而采用式(4)传统模型计算的系统可靠度为0.997,相比新模型存在较大偏差。
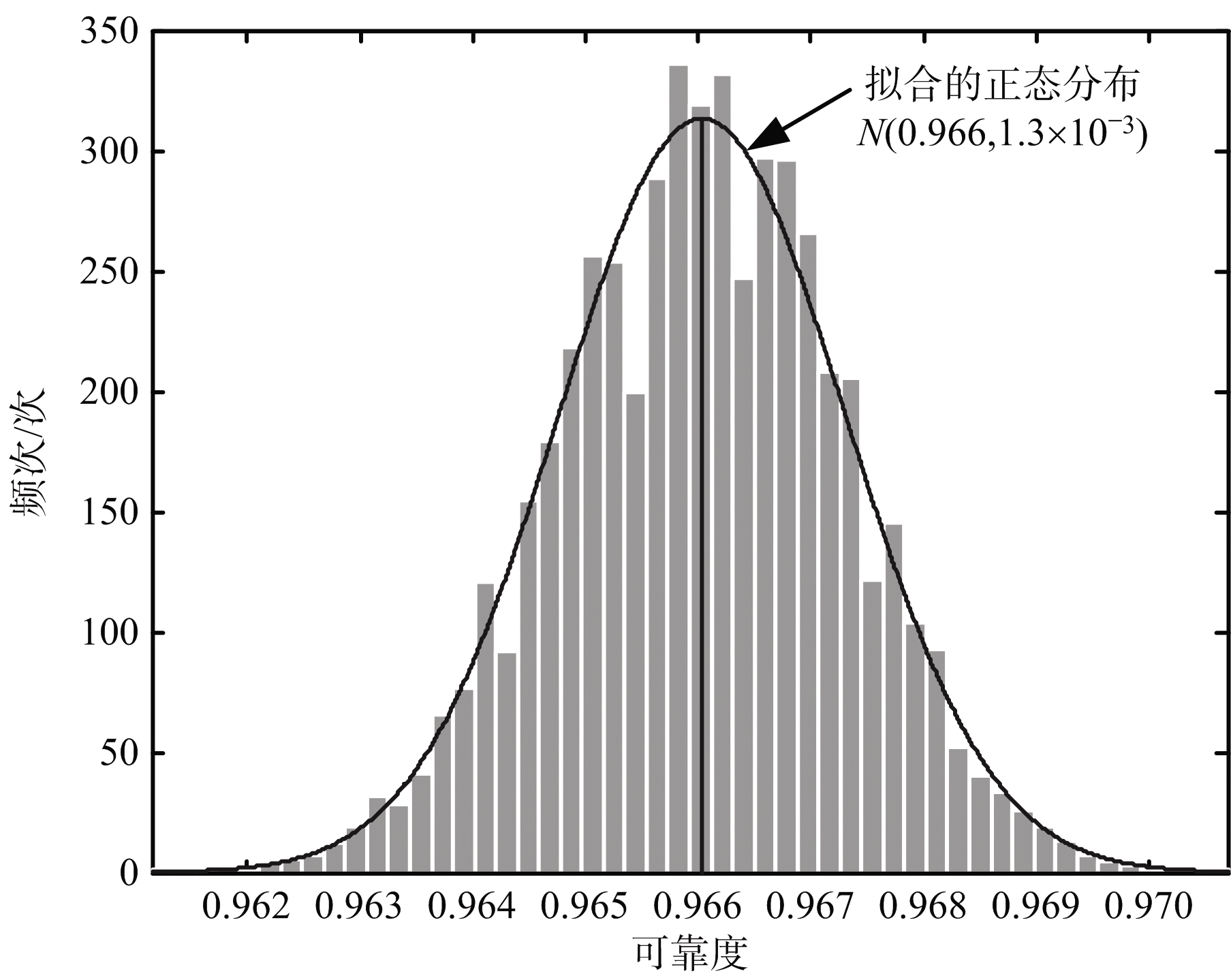
图5 系统可靠度蒙特卡洛仿真结果
最后,进一步对比了3种方式计算的卫星在轨不同时期天线阵面的可靠度,结果如表2所示。可见传统模型因未考虑各组成单元之间的故障相关性,导致对系统可靠性存在明显高估,而采用“树联”模型计算的系统可靠度和采用蒙特卡洛仿真获得的结果具有较好的一致性。
表2 不同方法计算的5年寿命期间天线阵面可靠度
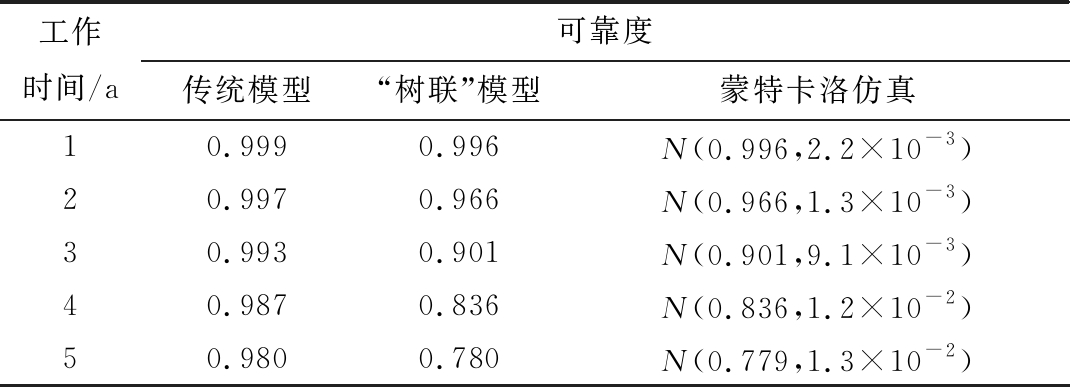
工作时间/a可靠度传统模型“树联”模型蒙特卡洛仿真10.9990.996N(0.996,2.2×10-3)20.9970.966N(0.966,1.3×10-3)30.9930.901N(0.901,9.1×10-3)40.9870.836N(0.836,1.2×10-2)50.9800.780N(0.779,1.3×10-2)
5 结束语
天线阵面是大型相控阵雷达的重要组成部分,它的可靠性对雷达系统至关重要。本文针对星载相控阵天线的特点,构建了可以准确表达天线阵各单元间相互关系的可靠性模型,并基于该模型,给出了两种系统可靠性预计方法:一种为解析法,另一种为蒙特卡洛法。经实例分析,新模型更适合在系统组件数量较多的情况下进行可靠度的计算。本文研究不仅可为天线阵面的方案论证工作提供有力的数据支持,也可为雷达整机制定维修保障方案提供重要的指导。
[1] HERD J S, CONWAY M D. The Evolution to Modern Phased Array Architectures[J]. Proceedings of IEEE, 2016, 104(3):519-529.
[2] 邓林, 邓明, 张成伟, 等. 有源相控阵可靠性分析及设计[J]. 装备环境工程, 2012, 9(2):21-25.
[3] 丁定浩, 李健. 机载相控阵雷达天线阵的可靠性新模型[J]. 雷达科学与技术, 2006, 4(2):81-84.
DING Dinghao, LI Jian. A New Reliability Model of Airborne Phased Array Radar Antenna Array[J]. Radar Science and Technology,2006, 4(2):81-84. (in Chinese)
[4] 熊年生, 黄正英. 机载有源相控阵天线阵的可靠性研究[J]. 雷达科学与技术, 2009, 7(4):250-253.
XIONG Niansheng, HUANG Zhengying. Reliability Analysis of Airborne Phased Array Antenna[J]. Radar Science and Technology, 2009, 7(4):250-253. (in Chinese)
[5] BENOIT L, PHUC D, ERIC L, et al. Opportunistic Maintenance Based on Multi Dependent Components of Manufacturing System[J]. CIRP Annals-Manufacturing Technology, 2016, 65(1):401-404.
[6] MI Jinhua, LI Yanfeng, PENG Weiwen, et al. Reliability Analysis of Complex Multi-State System with Common Cause Failure Based on Evidential Networks[J]. Reliability Engineering & System Safety, 2018, 174(6):71-81.
[7] O’CONNOR A, MOSLEH A. A General Cause Based Methodology for Analysis of Common Cause and Dependent Failures in System Risk and Reliability Assessments[J]. Reliability Engineering & System Safety, 2016, 145(1):341-350.
[8] RAMIRE-MARQUEZ J E, COIT D W. Optimization of System Reliability in the Presence of Common Cause Failures[J].Reliability Engineering & System Safety, 2007, 92(10):1421-1434.
[9] ZHANG Zhouqi, WU Su, LI Binfeng, et al. (n,N) Type Maintenance Policy for Multi-Component Systems with Failure Interactions[J]. International Journal of Systems Science, 2015, 46(6):1051-1064.
[10] SUNG C K, SHEU S H, HSU T S, et al. Extended Optimal Replacement Policy for a Two-Unit System with Failure Rate Interaction and External Shocks[J]. International Journal of Systems Science, 2013, 44(5):877-888.
[11] HUYNH K T, BARROS A, BERENGUER C. Multi-Level Decision Making for the Predictive Maintenance of k-out-of-n: F Deteriorating Systems[J]. IEEE Transactions on Reliability, 2015, 64(1):94-117.
[12] LAI M T. A Discrete Replacement Model for a Two-Unit Parallel System Subject to Failure Rate Interaction[J]. Quality & Quantity,2009, 43(3):471-479.
[13] 胡涛, 俞建. n/k(G)表决冗余多阶段任务系统可靠性优化模型[J]. 系统工程与电子技术, 2012, 34(1):217-220.
