0 引言
挖掘窄带雷达信息能够为雷达目标识别提供了重要途径[1-4]。虽然直接从RCS观测序列中提取目标物理特征比较困难,但可以提取RCS序列的数学特征,再采用各种机器学习方法(支持向量机[5-6]、最近邻分类器、人工神经网络[7]和深度学习[8]等),能够对空间多目标的类属——重点目标类群和非重点目标类群(例如碎片等目标)进行初步的分类识别筛选。在此基础上,可以为后续跟踪识别提供位置信息,雷达体系可集中更多的时间和能量资源重点对关心的目标进行跟踪。
非合作式多目标雷达的数据资源限制了脉冲重复频率的提升,而脉冲重复频率和雷达数据传输协议确定了RCS采样数据率上限。研究者常常采用滑窗法提取RCS序列的数学特征,即积累固定数目的数据点,计算统计特征作为一个多维特征的样本数据,再相隔固定数目的数据点,不断重复上述步骤得到新样本。滑窗法需要确定2个参数的取值:窗口长度(积累数据段的长度)和滑动步长(相隔数据点的长度)。目前,RCS采样数据率和统计的滑窗参数对基于目标RCS统计特征的可分性影响研究很少,但上述参数在实际的雷达目标特性设计分析时却是必不可少的,需要优化上述参数完成空间目标的识别分类。本文利用基于距离的类别可分性判据,实验研究并分析了数据率和滑窗参数对空间目标可分性的影响,可以为目标识别雷达RCS数据处理设计提供参考与帮助。
1 基于距离的类别可分性判据
在模式识别理论中,可分性判据常用在特征选择和特征提取中来评价所选择特征对分类的有效性,利用距离判据既能反映同类样本的相似性,又能反映不用类别样本的差异度,具备直观的物理意义,且计算简便[9-10]。在Fisher线性判别确定最佳投影方向的可分性判决为:采用使样本投影后同类样本的距离离散度越小、类间离散度越大。基于此,在特征空间内,如果同一类别的样本聚集越集中,不同类别样本间的距离越远,就可以认为该样本集的样本可分性较强。
考虑一个包含两类别的样本集X,一类表示为![]() 另一类表示为
另一类表示为![]() 其中k=1,…,n1,l=1,…,n2,样本总数为n= n1+ n2。类内散布矩阵Sw和类间散布矩阵Sb定义为
其中k=1,…,n1,l=1,…,n2,样本总数为n= n1+ n2。类内散布矩阵Sw和类间散布矩阵Sb定义为
(1)
(2)
(3)
(4)
![]() 是i类样本集的协方差矩阵,它的迹
是i类样本集的协方差矩阵,它的迹![]() 是该类的特征方差的平均测度。类间散布矩阵的迹是每一类的均值和全局均值之间平均距离的一种测度。基于类间样本距离大,总的类内样本聚集(方差小)的原则,本文采用距离判据J2大小代表样本的可分性的强弱:
是该类的特征方差的平均测度。类间散布矩阵的迹是每一类的均值和全局均值之间平均距离的一种测度。基于类间样本距离大,总的类内样本聚集(方差小)的原则,本文采用距离判据J2大小代表样本的可分性的强弱:
(5)
2 数据实验与结果
2.1 实验条件
仿真实验数据的重复频率为50 Hz。RCS对观测角度的变化关系敏感,空间重点群和非重点群目标的RCS差异主要体现在群内部成员形状以及微运动特征上,空间重点类目标飞行过程中常常保持姿态稳定特性,而非重点类目标(包括碎片等目标)会产生翻滚等较为剧烈的姿态变化。
雷达目标RCS序列的常用统计特征有:1) 位置特征参数,描述了目标RCS时间序列的平均位置和特定位置,常用的有均值、极大/极小值、众数等;2) 散布特征参数,描述了目标RCS序列的离散程度,极差、方差以及变异系数等;3)分布特征参数,描述了目标RCS序列统计分布的总体密度函数的特征,标准偏度系数、标准峰度系数和多阶中心矩等;4) 变换域特征,把RCS数据变换到其他特征域后重新进行特征统计,提取新的特征以突出目标特性,例如,采用傅里叶变换后的统计特征:频谱均值、熵、低频能量比等。本文选取了4个典型RCS统计特征进行实验与分析,即{A,B,C,D},所述特征进行了归一化标准化数据处理,避免某一特征值过大或过小。
2.2 数据率
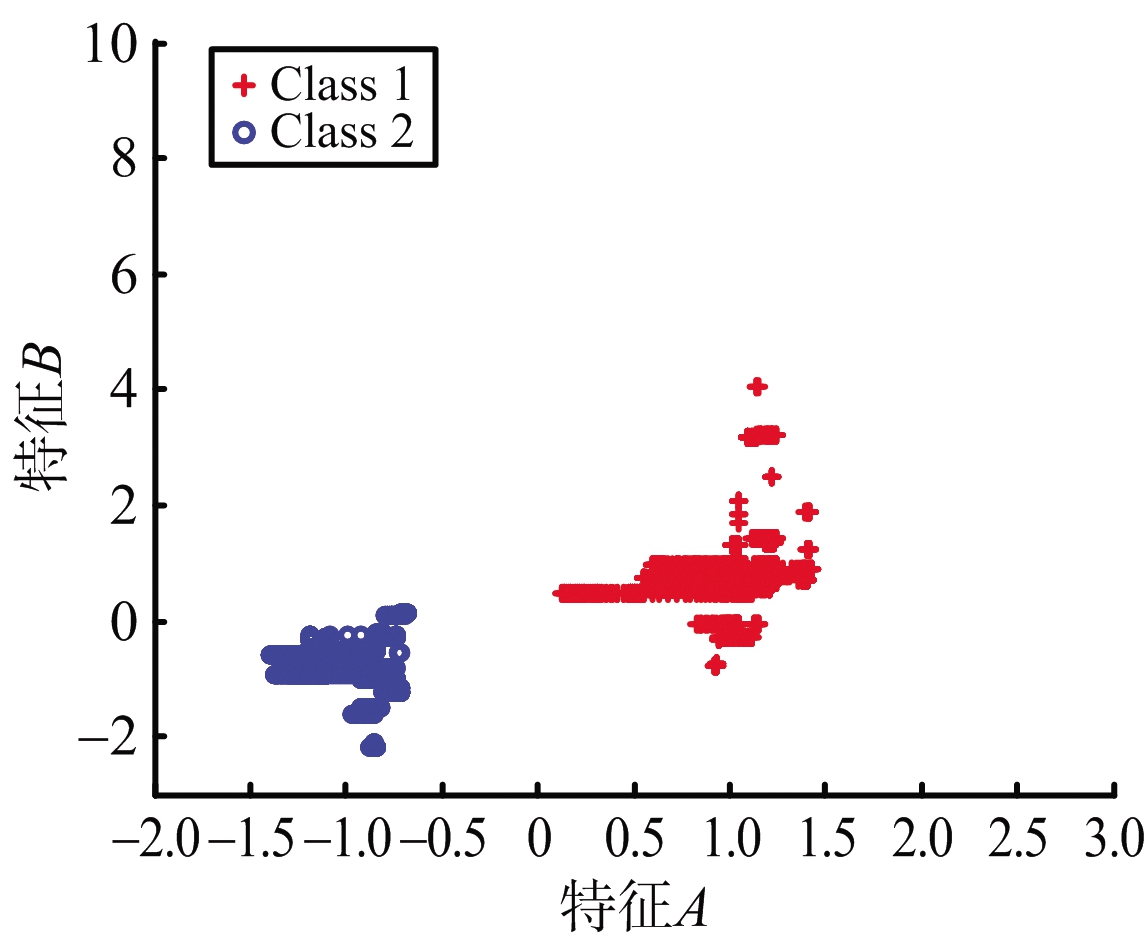
根据已有的50 Hz的RCS数据,采用隔点取样的方式,可以获得相应的低数据率下的RCS数据,例如:将50 Hz的RCS数据每隔1个点取1个点,取出的RCS数据可以认为是25 Hz数据率下的RCS数据。依此法,分别得到了1,2,5,10,25和50 Hz的RCS数据进行可分性对比研究。图1为不同数据率(1,2,5,10,25和50 Hz)下的二维特征样本分布图,此时二维特征集取为{A,B},窗口长度为3 s,滑动步长为1个数据点。
图1所示两类样本点分别用红色“+”(Class 1)及蓝色“o”(Class 2)表示。随着数据率的提升,两类点的类间距离不断增大,而同类点不断汇聚,也就意味着样本可分性不断增强。
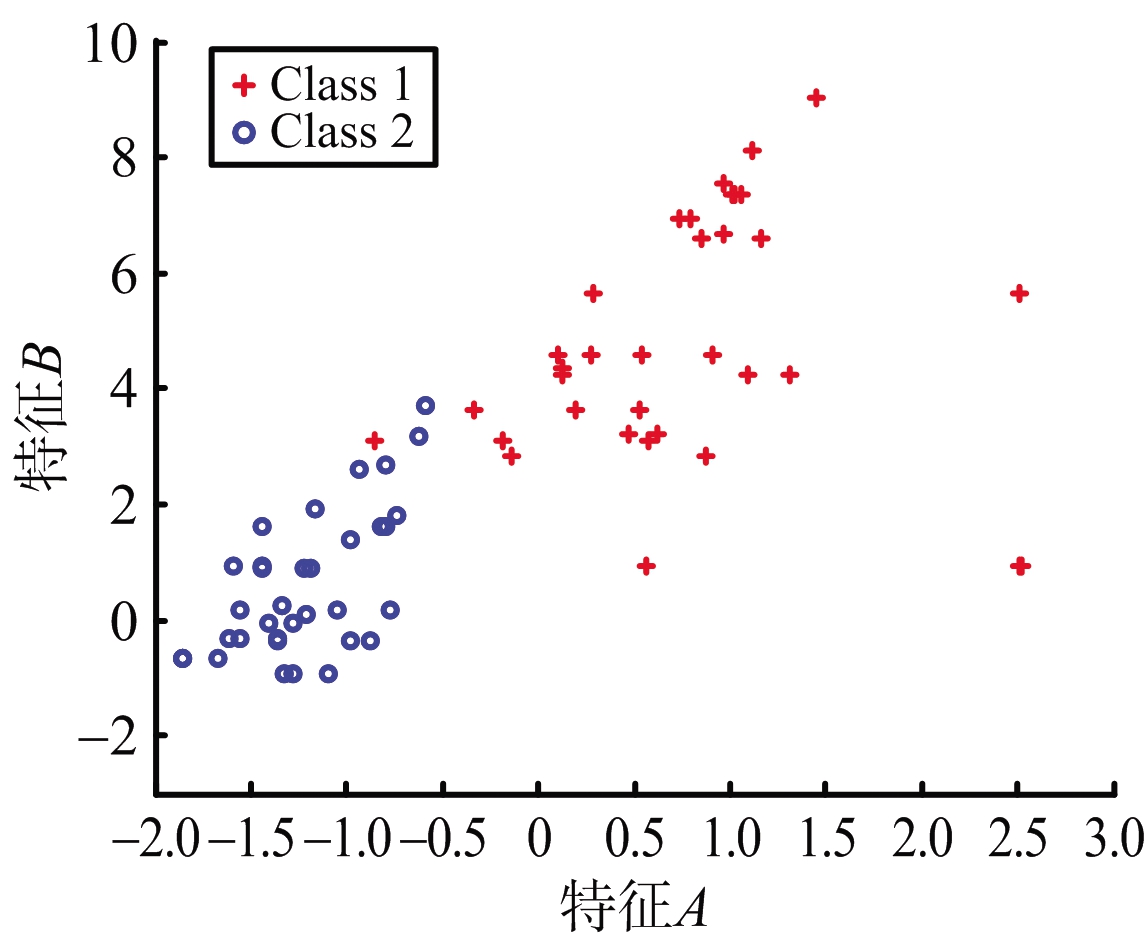
(a) 1 Hz
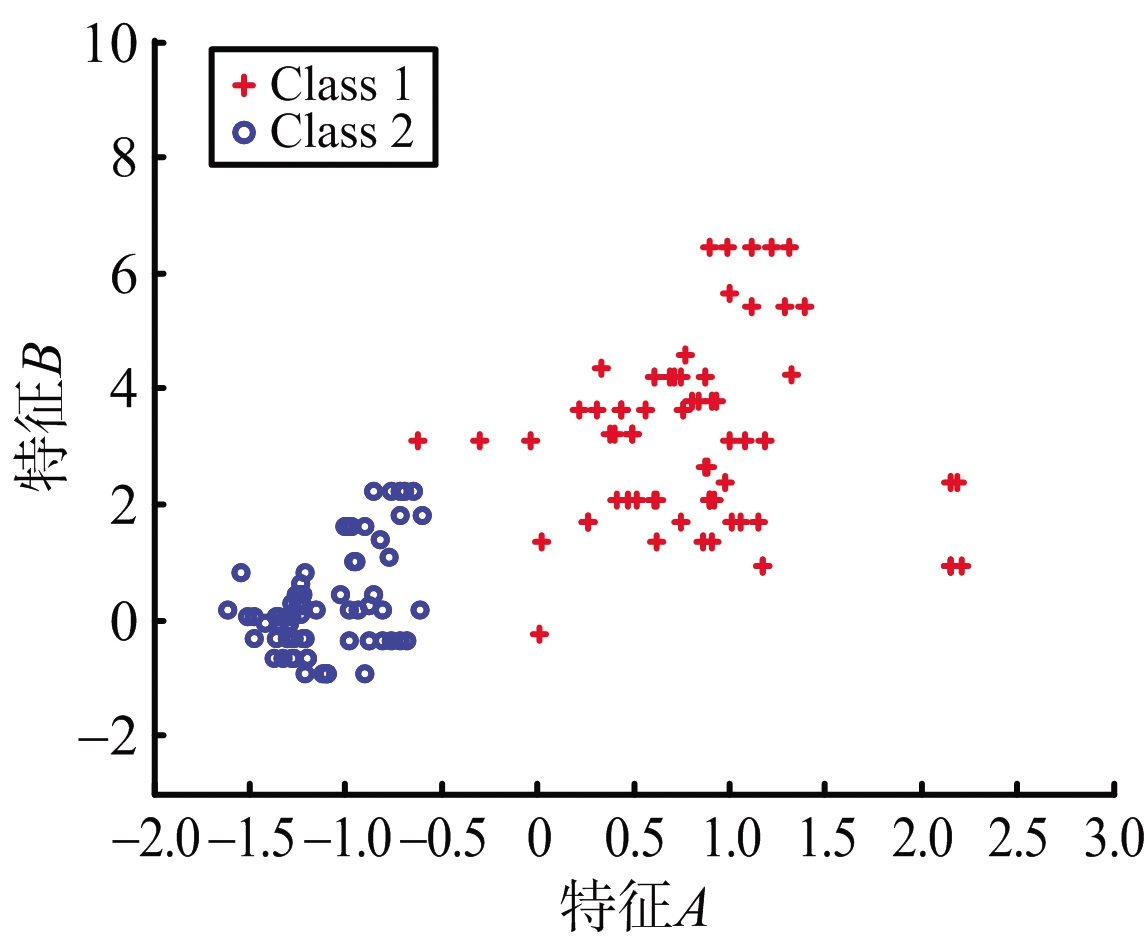
(b) 2 Hz
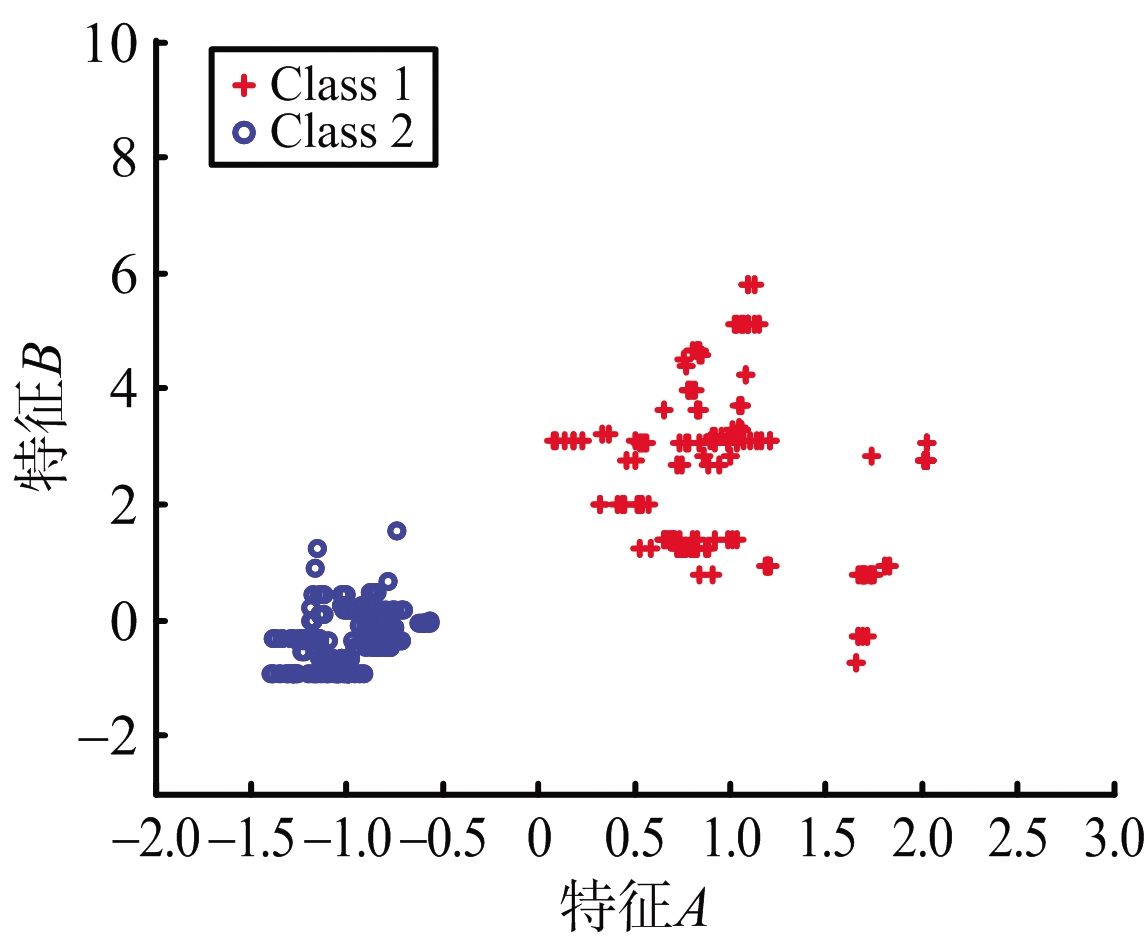
(c) 5 Hz

(d) 10 Hz
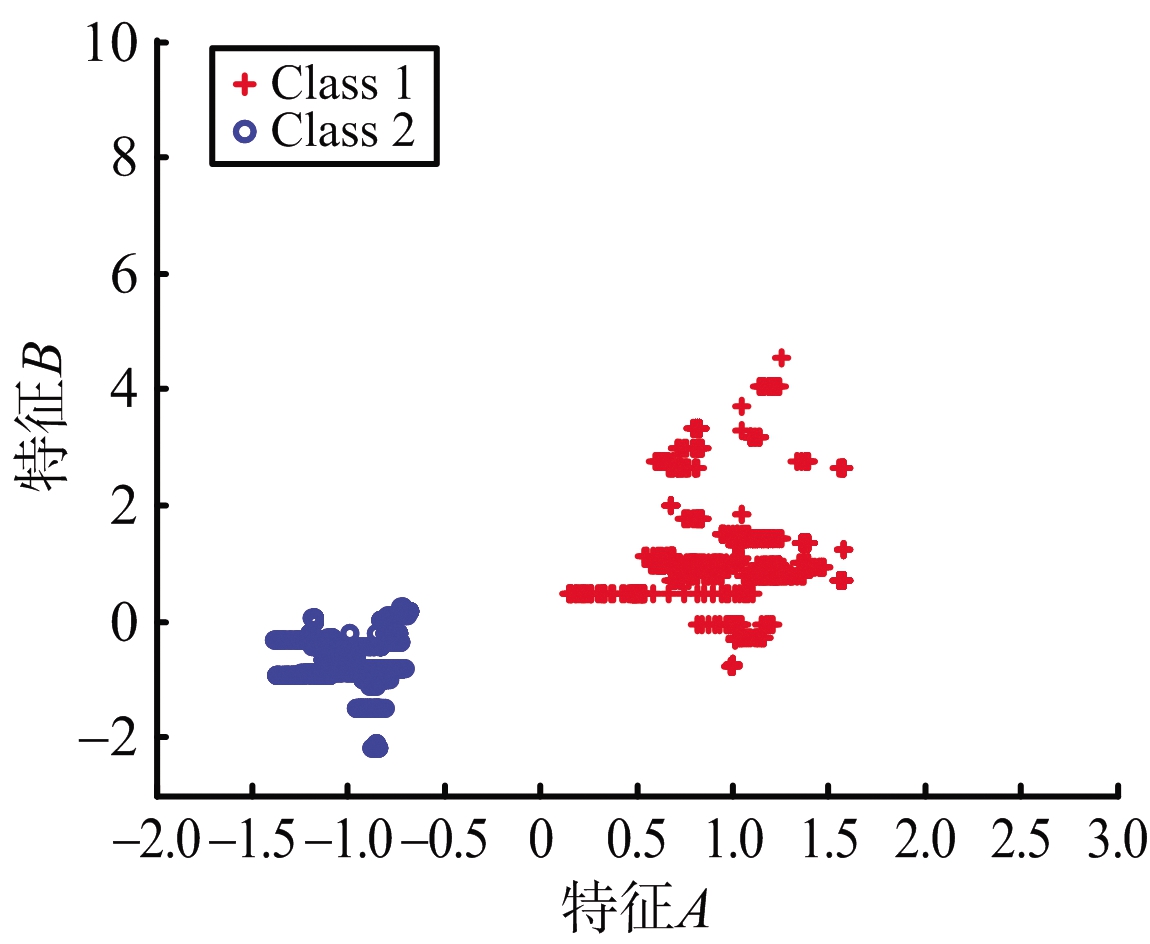
(e) 25 Hz
(f) 50 Hz
图1 不同数据率下特征集为{A,B}的样本分布
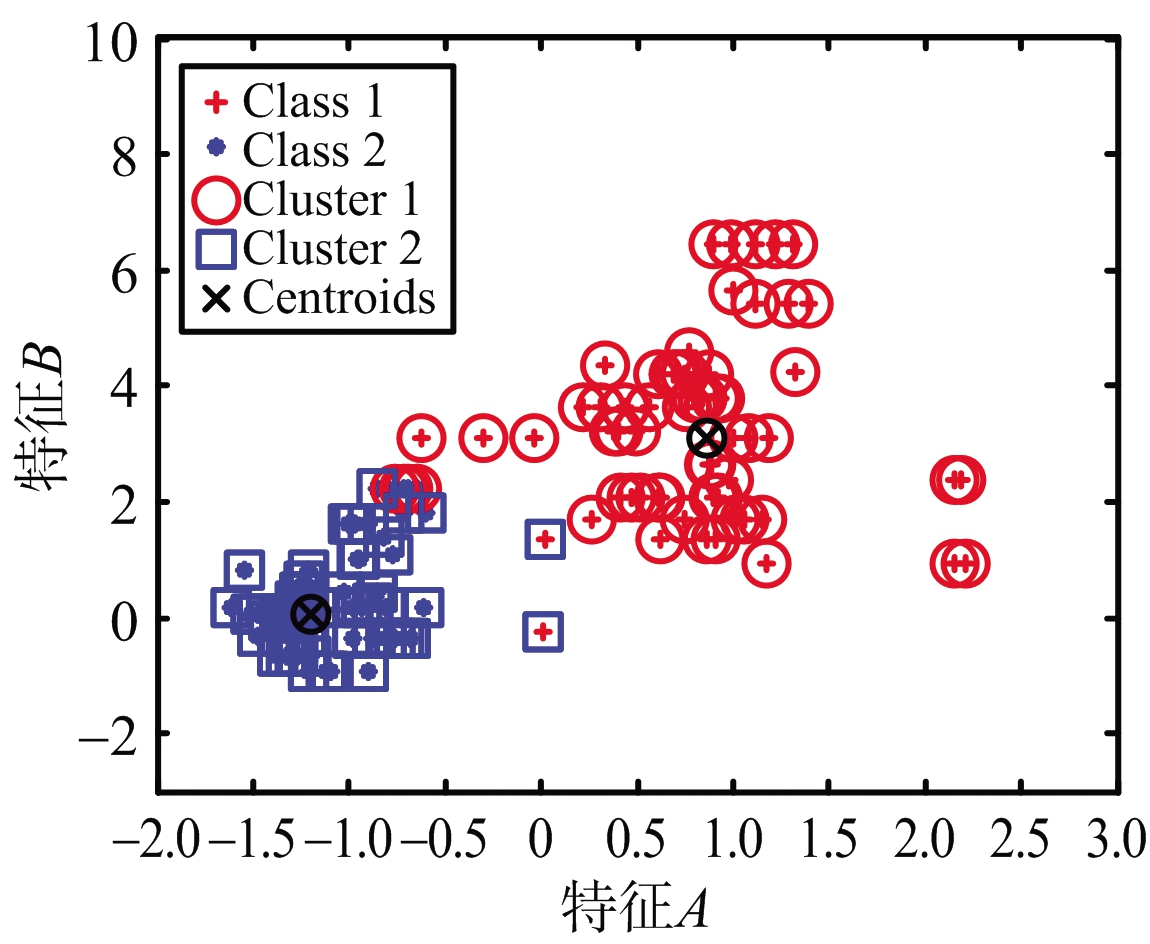
为了直观表明随着数据率对可分性的影响效果。利用K-means聚类方法,采用标准欧式距离标准对上述数据进行聚类分析,类别数设定为2。图2为不同数据率下特征集为{A,B}的K-means聚类结果。实际两类样本点分别用红色符号“+”及蓝色符号“*”表示,而聚类结果的两类点用红色圆圈和蓝色方圈表示。
(a) 2 Hz

(b) 25 Hz
图2 不同数据率下特征集为{A,B}样本的K-means聚类结果
图2(a)和(b)分别为数据率2 Hz和25 Hz的样本的聚类结果。在低数据率(2 Hz)下,图2(a)所示聚类的分类结果与实际样本分类结果有差异。而在较高频率(25 Hz)下,在图2(b)所示聚类的分类结果与实际样本分类结果一致。实验结果直观地表明:随着数据率的提升,最终分类效果会变好。
为了更好地分析参数影响,需要量化的样本可分性指标。利用上文所述的距离可分性判据J2,计算不同选择的特征集下J2随数据率变化曲线,如图3所示。
图3所示特征集{A,B}的J2曲线与图2散点分布图对应比较,二者结果相符合。观察图3,在大部分特征组合下,J2随频率增高而增大。J2随频率变化可以分为迅速增长区域与缓慢增长区域。在较低频率区域下,J2随频率增大而迅速增大,而高频率区域,J2随频率增高的增长率较慢,趋于饱和。低频与高频区域二者之间的交际区域大致为5~25 Hz。
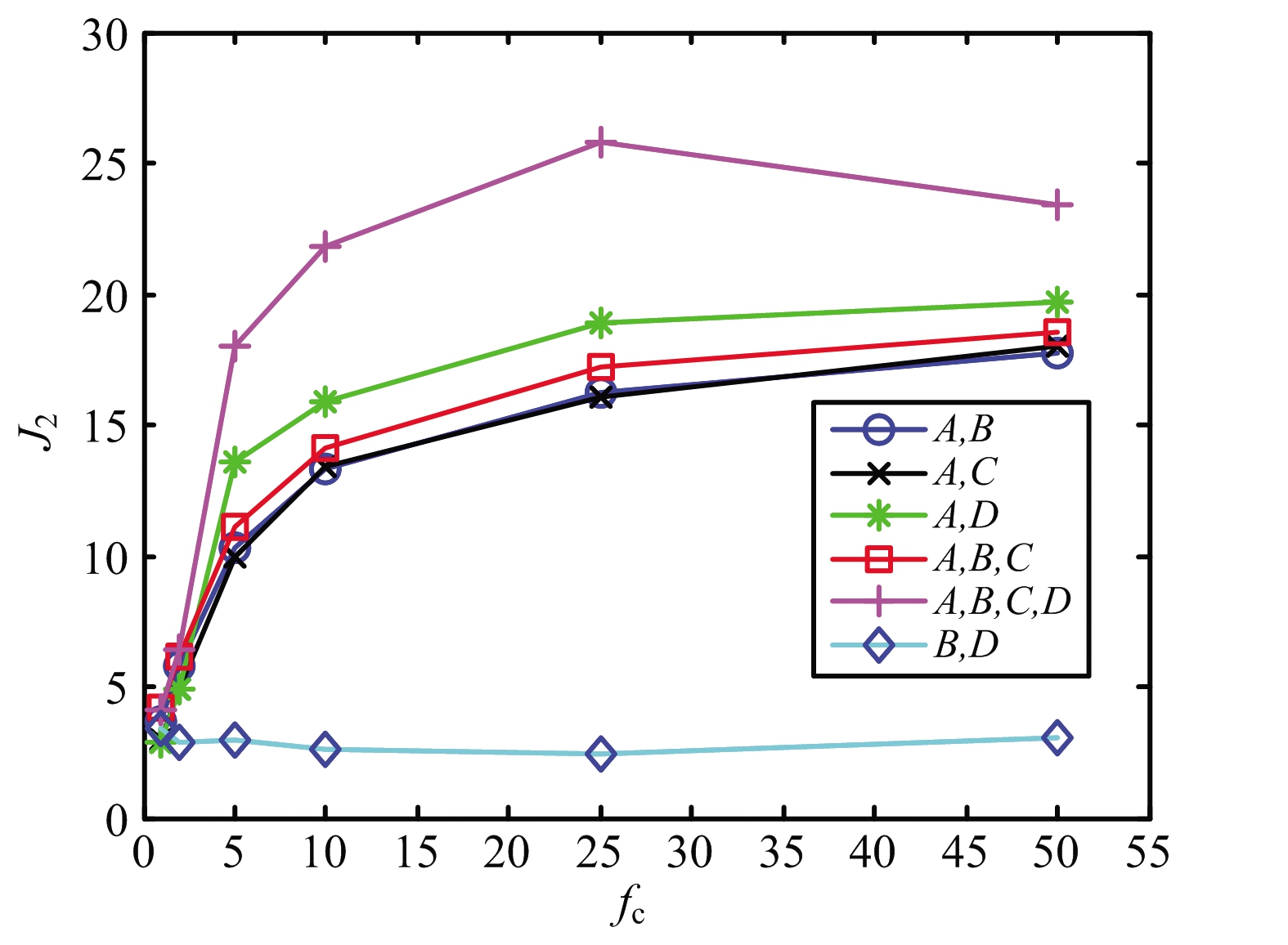
图3 不同特征集下J2随数据率变化曲线
在被雷达探测过程中,空间目标会随着运动存在姿态的变化,而且除了按轨飞行的正常平动状态外,还可能会存在翻滚等其他运动状态,故所对应的RCS也会呈现相当的起伏特性。如果数据率低,有可能得不到准确的RCS起伏数据,降低本来运动状态存在相当差异的目标分类性能。因此,提高数据率可以增强空间目标的可分性。而当频率增高到一定程度后,采样得到的RCS数据已经可以在一定程度上相当准确地反映其实际起伏情况,此时进一步增高数据率,空间目标的可分性缓慢提升直至趋于饱和。
(a) 2 Hz
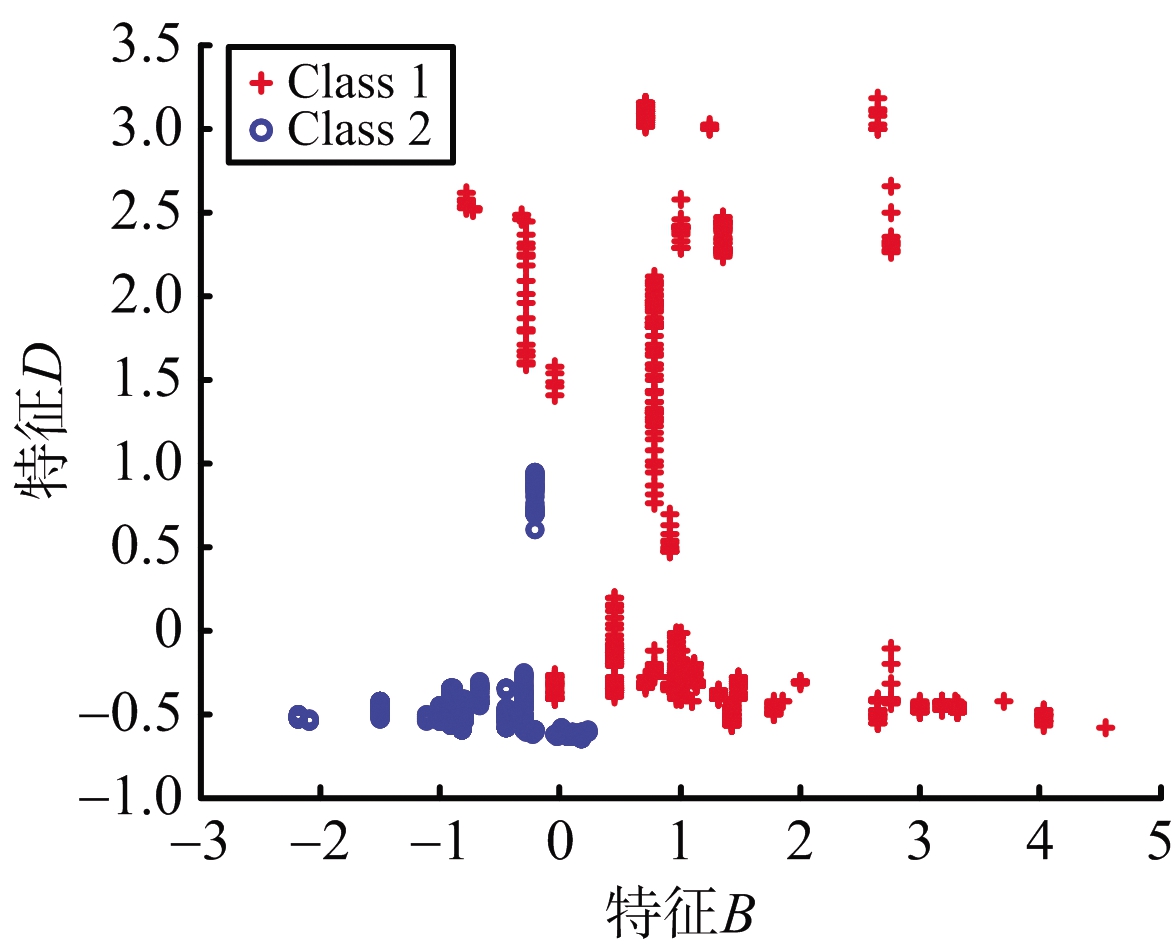
(b) 50 Hz
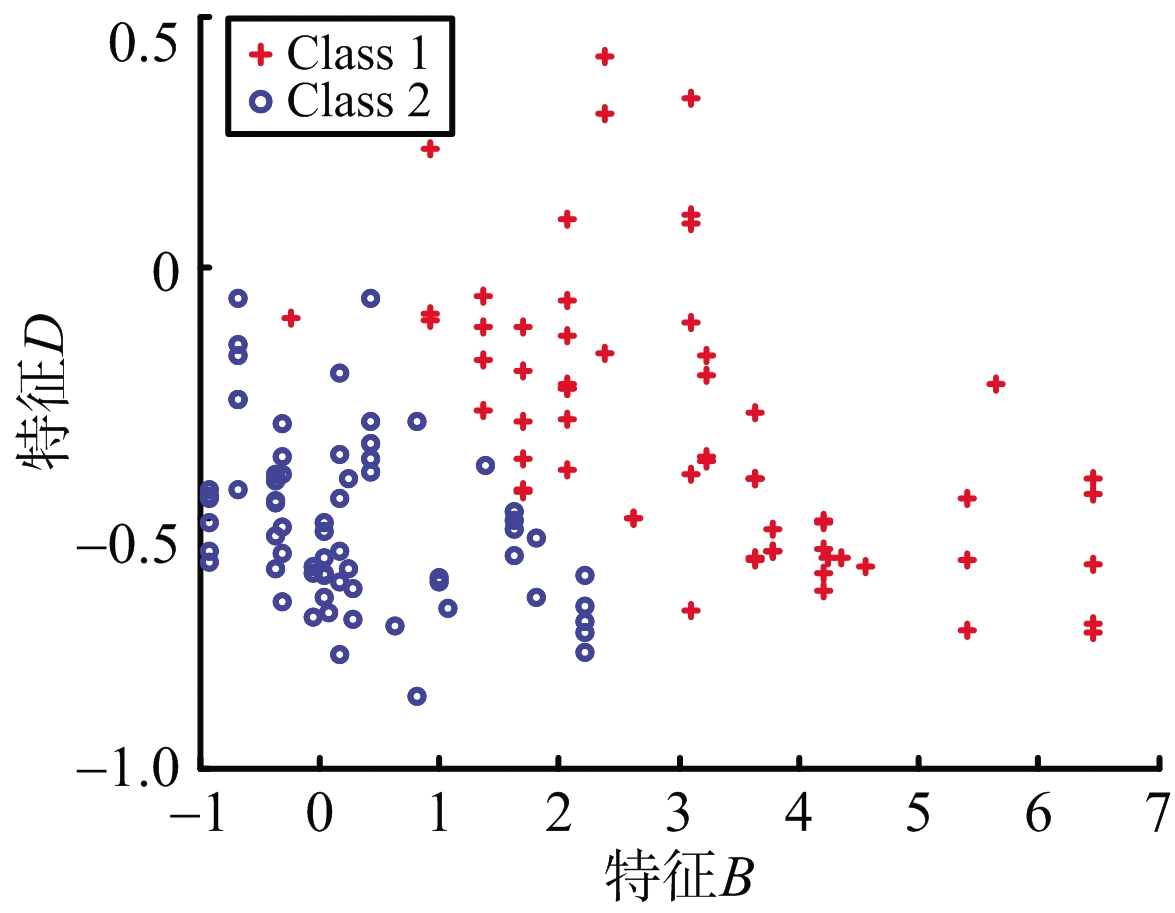
图4 不同数据率下特征集为{B,D}的样本分布
图3特征集{B,D}的J2曲线所示,该情况下J2随频率变化不大,数值也相对较小,反映了该样本数据的可分性不强。图4为不同数据率(2 Hz和50 Hz)下的二维特征{B,D}样本分布图,直观显示了该情形下空间目标RCS统计特征数据的样本分布情况。对比图4与图2的样本分布,无论从同类样本聚集情况还是不同类样本之间的距离比较,图4所示的样本分布的可分性弱于图2。
2.3 滑动步长
本节展示并分析滑动步长对J2的变化影响,此时窗口长度为3 s。图5为不同数据率下J2随滑动步长的变化曲线。图5(a)和(b)分别取2 Hz和50 Hz数据率,绘制了不同特征集J2随滑动步长的变化曲线。图5的实验结果表明:J2随滑动步长的变化较小。在本文的实验条件下,滑动步长基本对样本的可分性没有影响。
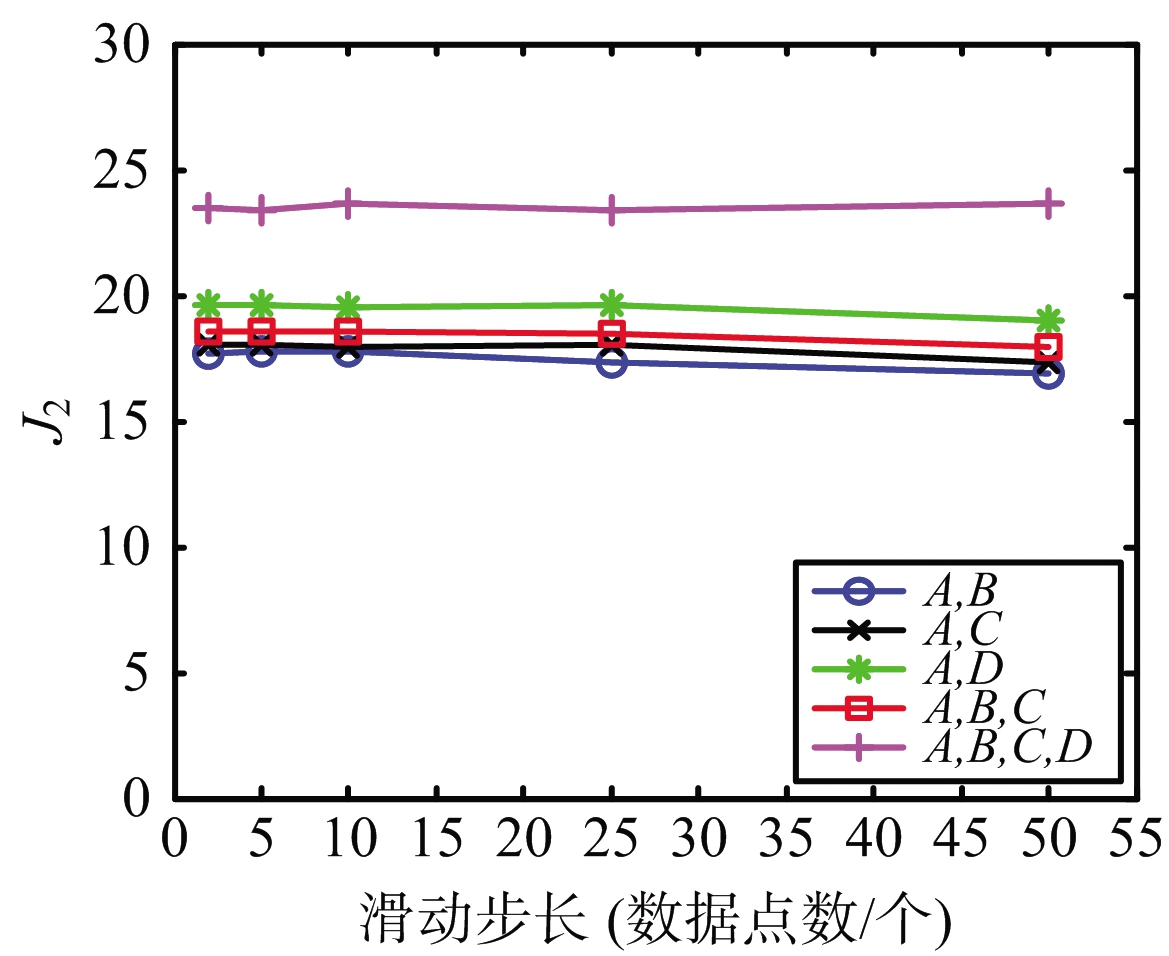
(a) 50 Hz
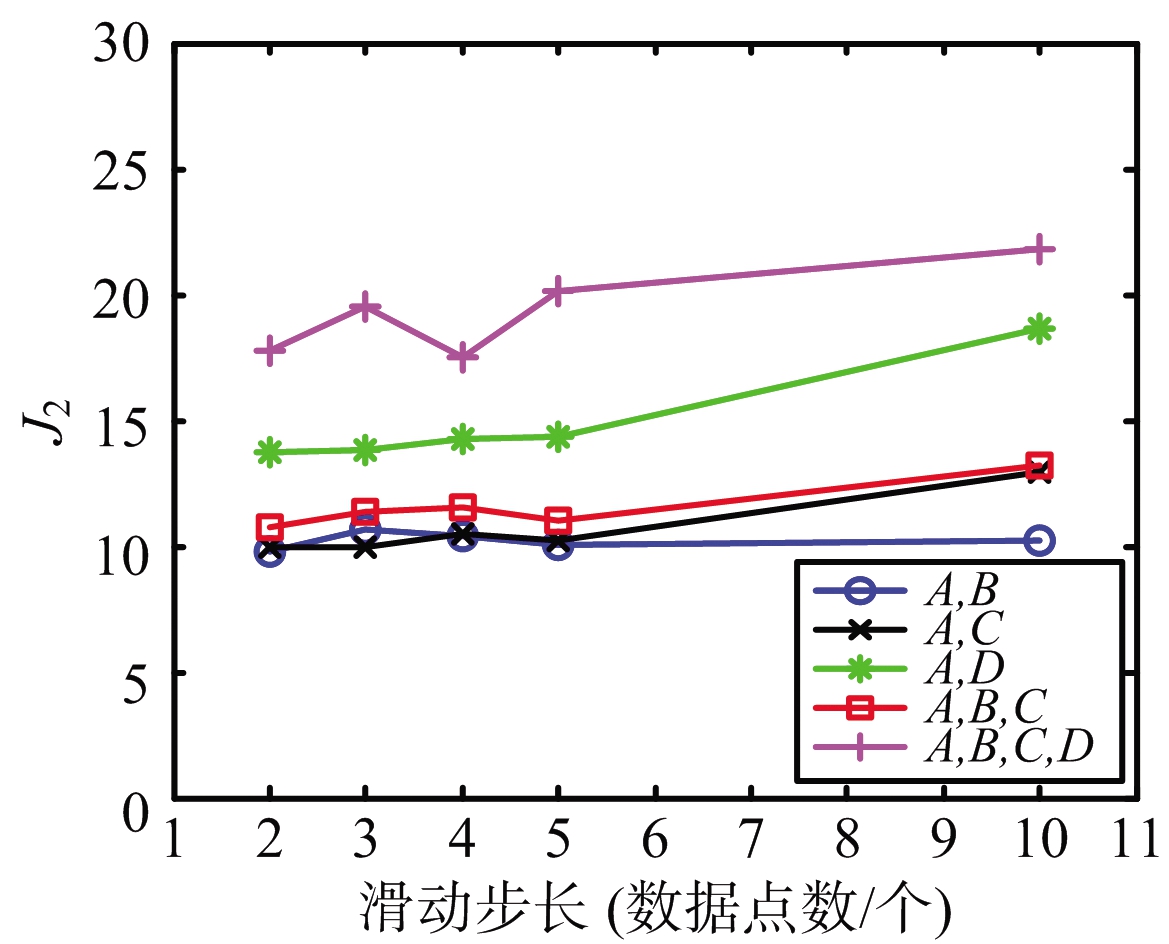
(b) 5 Hz
图5 不同数据率下J2随滑动步长的变化曲线
2.4 窗口长度
本节展示并分析窗口长度对J2的变化影响。滑动步长取1个数据点,RCS特征集取{A,B}。图6为不同数据率下J2随窗口长度变化曲线。数据率取值:2,5,10,25和50 Hz。窗口长度的单位分别取数据点数目和时间两个单位,图6(a)为不同数据率下J2随窗长数据点数目的变化曲线,图6(b)为不同数据率下J2随窗长时间(s)的变化曲线。
图6(a)结果表明:无论何种数据率取值,曲线都随着数据点数目的增多而快速增大,而且是一种超过线性增长率的增大方式。而若取相同窗长数据点数目,比较不同频率下的J2值,则频率越低的J2越大;换言之,若希望取得相同J2值,频率越低所需要的数据点数目越少。空间重点类目标一般要进行姿态控制,RCS呈现短时间内平稳,而空间非重点类目标则后自由运动,存在大的翻滚运动,使得其RCS统计特征与空间重点类的存在较大差异。数据点多,就意味着RCS统计的时间越长,测量误差带来的影响越小,空间目标的RCS统计特征的差异就越显著。基于此,图6(b)的横轴单位将数据点数目换算为时间,比较不同数据率下J2随滑动步长的变化曲线,在相同窗长时间下,数据率越高的J2越大。
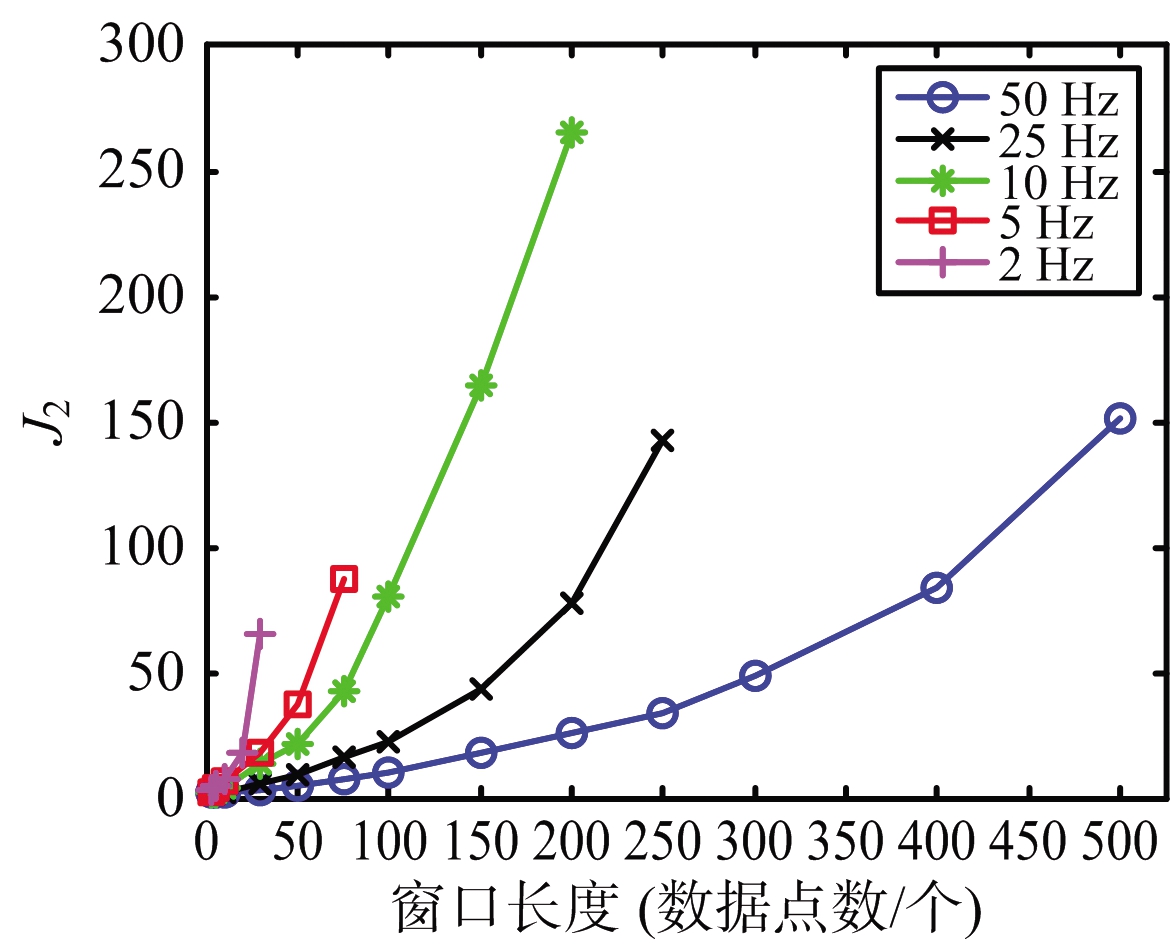
(a) 数据点数
(b) 时间单位
图6 不同数据率下J2随窗口长度变化曲线
3 结果分析与经验公式的提出
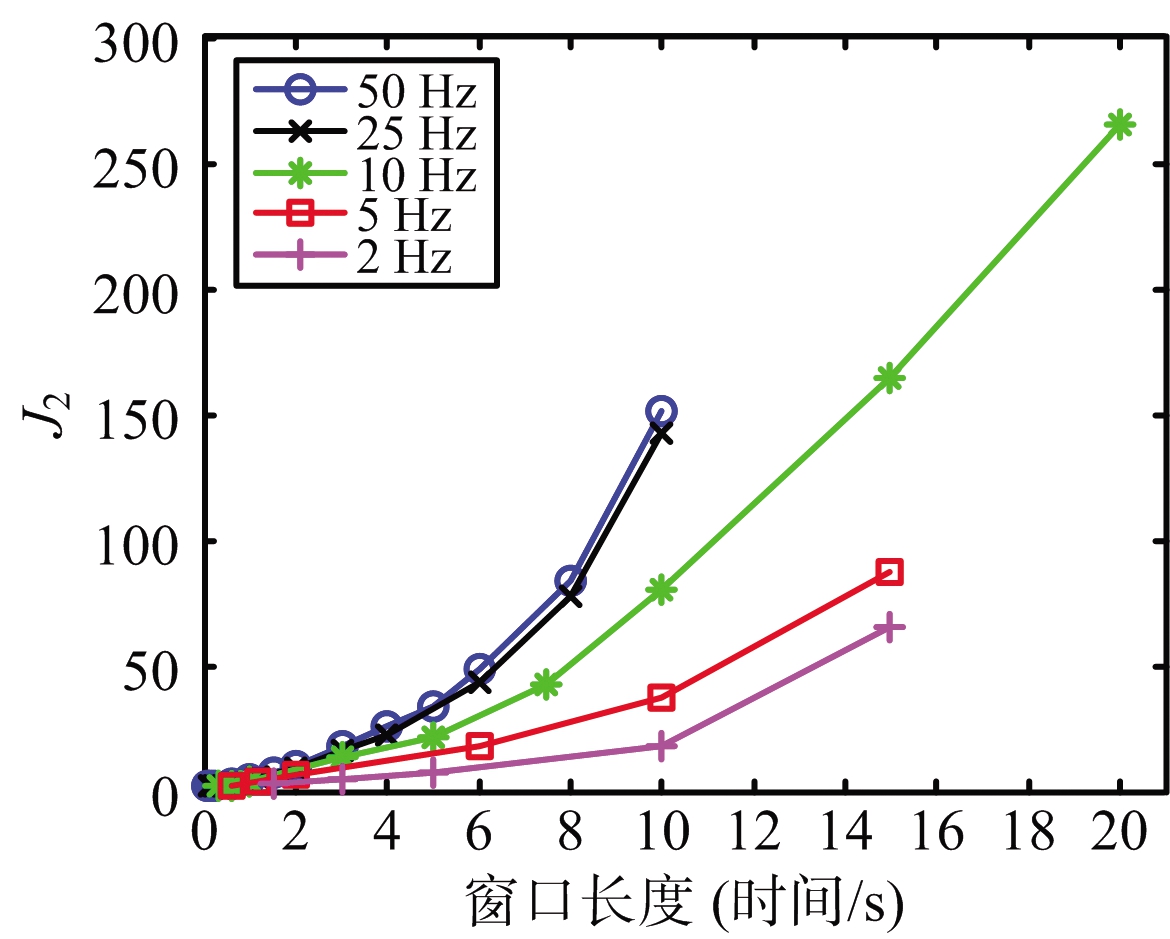
综上所述,随着数据率的增高,目标可分性呈现一个在低频区域(<5 Hz)快速增长,而在高频区域(>25 Hz)呈现一种趋于饱和的缓慢增长;目标可分性随滑动步长变化不显著;随着窗口长度的增长,目标可分性呈现非线性的快速增长趋势。基于此,绘制了不同窗口长度下J2随数据率变化的曲线,如图7所示。
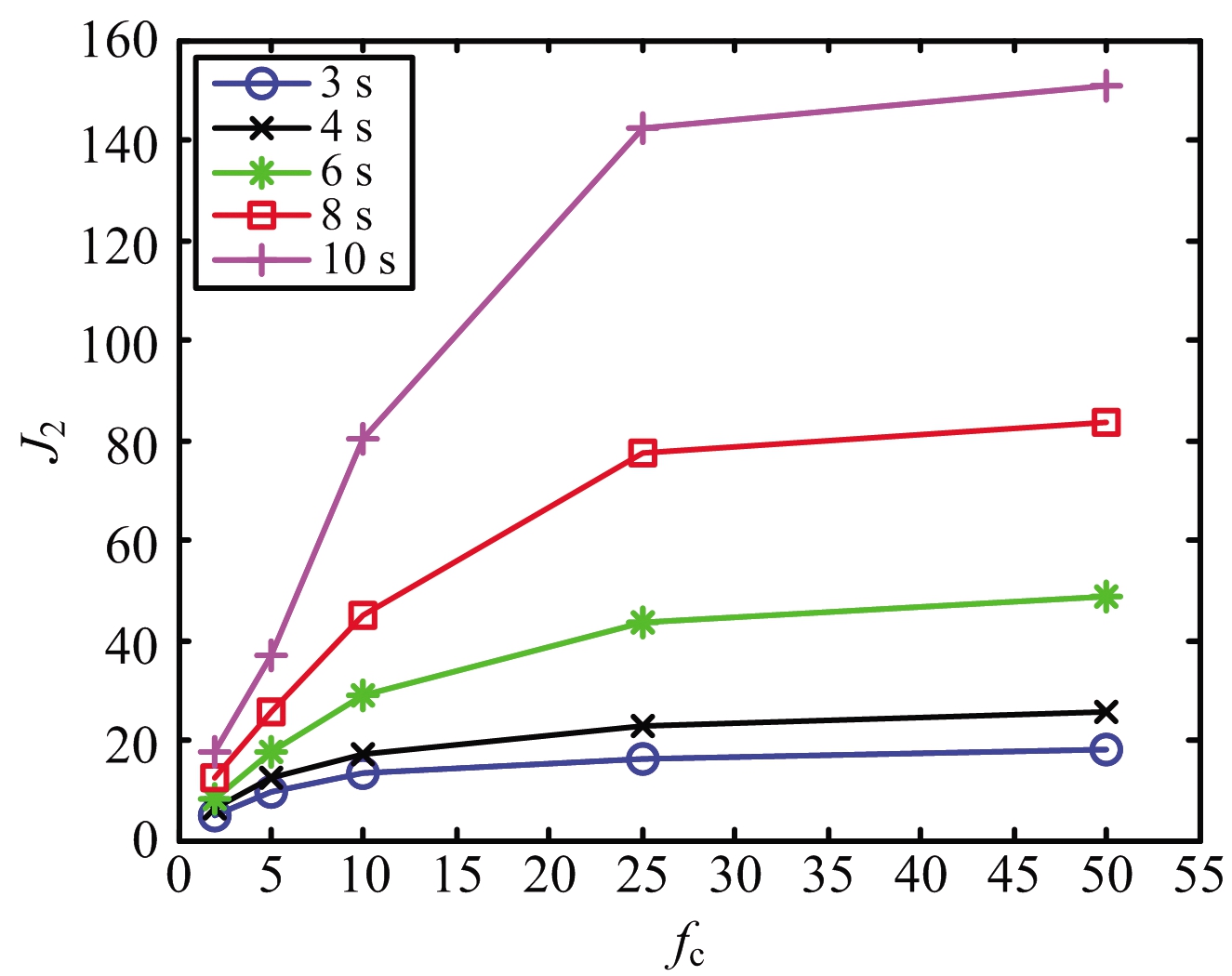
图7 不同窗口长度下J2随数据率变化的曲线
观察图7,考虑到物种数量增长常用的逻辑斯谛模型可以仿真先快速增长后趋于饱和这一物理形态,采用该模型希望获得经验公式:
(6)
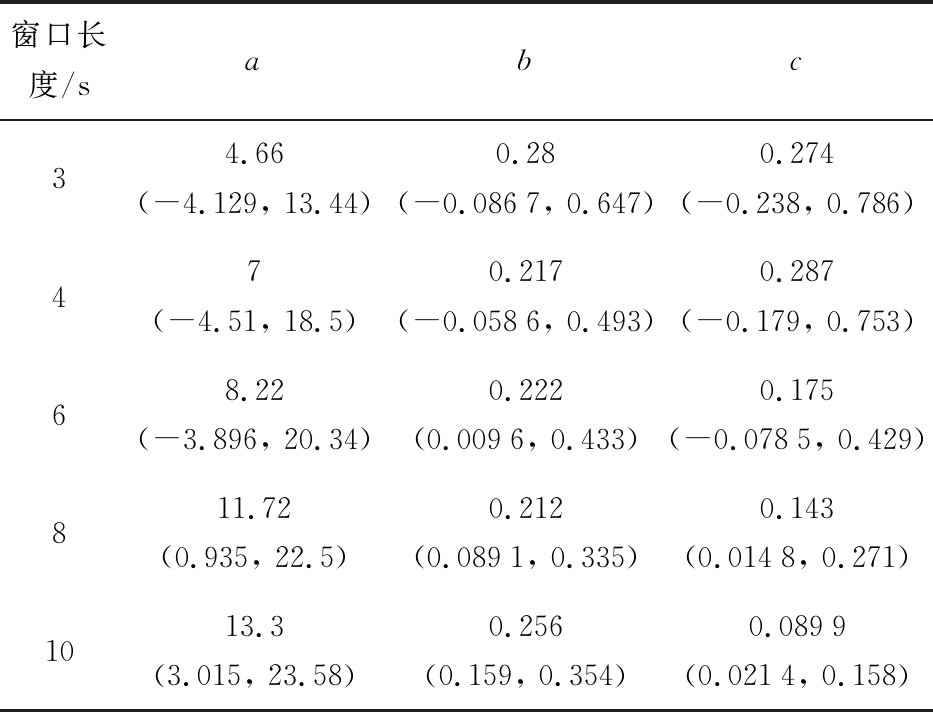
式中:a,b,c为系数,皆为正数;fc为频率。对图6不同窗口长度下随数据率的J2进行拟合。拟合结果如表1所示。
表1 逻辑斯谛模型拟合的参数取值
窗口长度/sabc34.66(-4.129, 13.44)0.28(-0.0867, 0.647)0.274(-0.238, 0.786)47(-4.51, 18.5)0.217(-0.0586, 0.493)0.287(-0.179, 0.753)68.22(-3.896, 20.34)0.222(0.0096, 0.433)0.175(-0.0785, 0.429)811.72(0.935, 22.5)0.212(0.0891, 0.335)0.143(0.0148, 0.271)1013.3(3.015, 23.58)0.256(0.159, 0.354)0.0899(0.0214, 0.158)
表1所示拟合的5条曲线的R_squre>0.96,拟合结果较好;更加让人感到有趣的是:b值在不同窗口长度下,最优取值保持在小范围区间 (0.21,0.28)范围。根据模型数学表达式(4),b值大小暗示了曲线弯折的位置与程度,即曲线从快速增长转到平稳阶段的过渡段的位置。当fc取值较大,fc=50 Hz时,exp(-bfc)接近于0,此时J2=a/c。将式(6)变换为
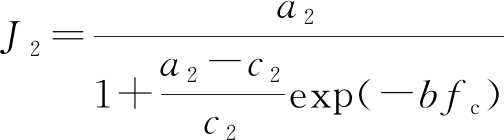
(7)
在式(7)常应用的生物学物种增长模型中,参数a2代表环境最大容纳量,参数b代表种族增长潜力指数,参数c2代表种族原始大小。如上文所述,取b=0.22,采用式(7)对不同窗口长度下J2随数据率变化的实验值进行拟合,获得a2,c2参数值与范围如表2所示。表2结果表明:系数a2随着窗口长度的增长而增大,系数c2也随着窗口长度的增长而增大。采用表2参数的依式(7)拟合与实验结果对比如图8所示。
表2 b=0.22逻辑斯谛模型拟合的参数取值
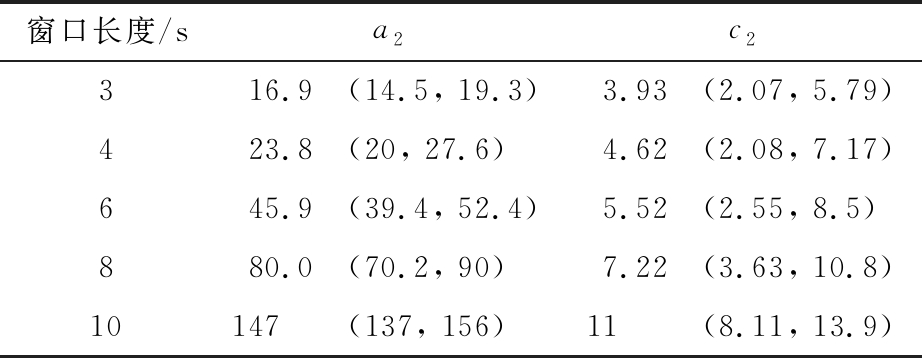
窗口长度/sa2c2316.9(14.5, 19.3)3.93(2.07, 5.79)423.8(20, 27.6)4.62(2.08, 7.17)645.9(39.4, 52.4)5.52(2.55, 8.5)880.0(70.2, 90)7.22(3.63, 10.8)10147.0(137, 156)11.00 (8.11, 13.9)
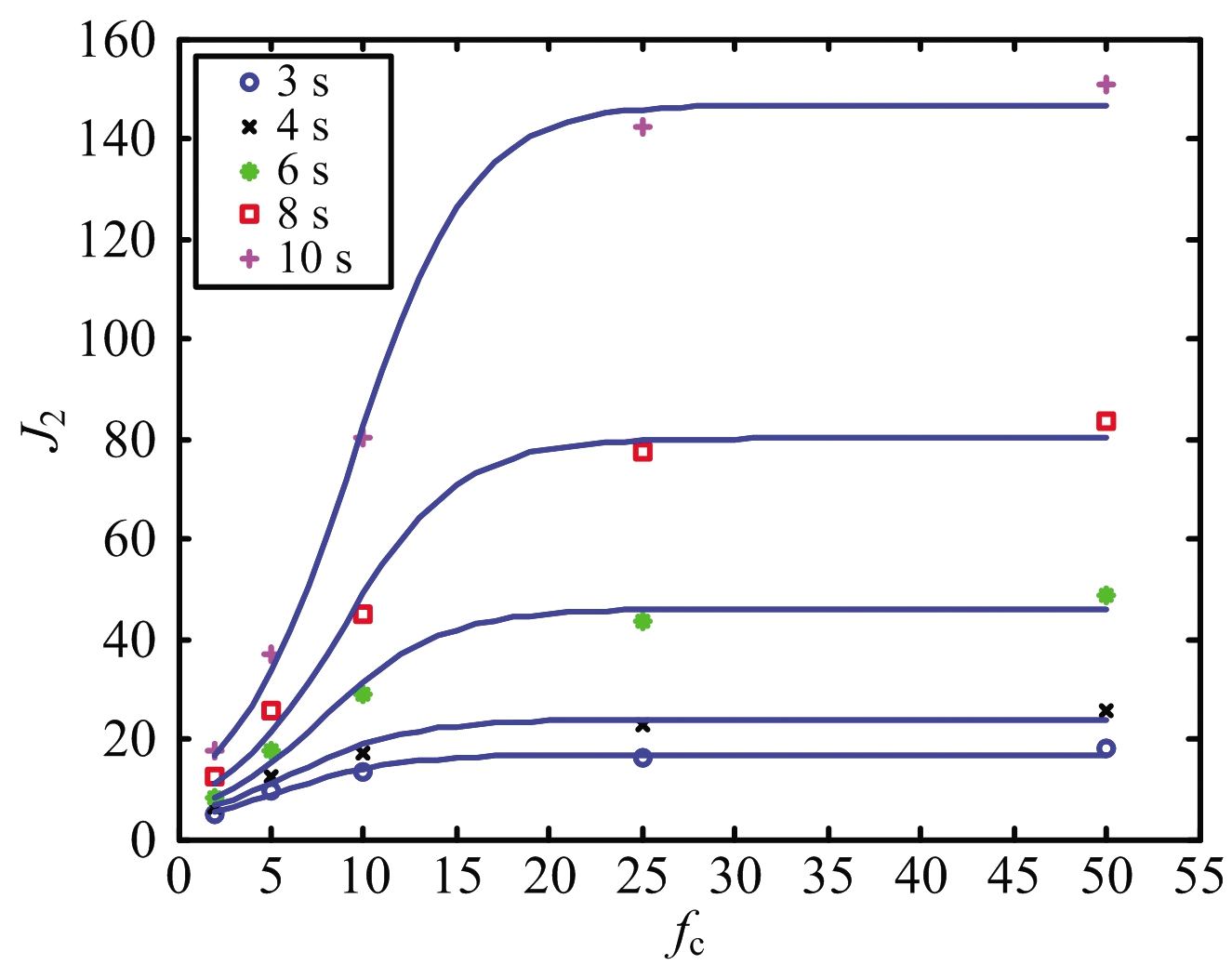
图8 拟合结果与实验结果对比图
逻辑斯谛模型的拟合方式存在两个不足之处:首先,如图8所示,虽然模型得到了较好的拟合效果,但尚存在误差,也许还存在更加恰当准确的数学模型;其次,数学模型与物理事实的解释预测性不强,例如,曲线饱和值是否和目标特性的关联性,雷达电磁波频率或者其他参数是否影响和如何模型参数变化。虽然存在上述不足,逻辑斯谛模型的拟合效果或许可以接受:在实际拟合中,指数项的参数b是常量,而a2代表了高数据率下RCS可分性指标J2的饱和值,c2则代表了低频率下的初始值。
4 结束语
本文研究了雷达采样的重复频率和滑窗参数(滑动步长和窗口长度)对空间目标RCS统计特征的可分性影响,利用类间、类内矩阵构建了基于距离的可分性测度J2来权衡样本类别可分性的强弱。采用50 Hz的RCS数据的实验结果,数据率的可分性的影响为:随着数据率的增高,目标可分性呈现一个在低频区域(<5 Hz)快速增长,而在高频区域(>25 Hz)呈现一种趋于饱和的缓慢增长。采用K-means对样本数据聚类,直观表现可分性对实际模式识别分类器的影响,结果验证了:在低数据率(2 Hz)下,聚类的分类结果与实际样本分类结果有差异;而在较高频率(25 Hz)下,聚类的分类结果与实际样本分类结果一致。滑窗参数的可分性影响为:目标可分性随滑动步长变化不显著;随着窗口长度的增长,目标可分性呈现非线性的快速增长趋势。最后,采用逻辑斯谛模型拟合不同窗口长度下J2随数据率变化曲线,虽然存在数学严谨性和物理解释相关性等方面的不足,但实际拟合得到的相关参数恒定或者具备一定的物理意义。未来工作将进一步拓展更多空间目标的数据进行研究,同时关注可分性指标的数学推导与物理解释,尝试得到可推广使用的经验公式或者半定量的经验方法。还将针对更多的特征,研究不同特征参数对可分性的影响;研究还将拓展更多的目标场景,特别是重点分析具备较弱可分性的空间目标RCS数据。
[1] 姚辉伟. 窄带雷达中段目标识别技术研究[D]. 长沙: 国防科学技术大学, 2014.
[2 ] 韩勋. 基于窄带微动特征的空间锥体目标识别方法研究[D]. 西安:西安电子科技大学, 2015.
[3] 董会方, 卞磊, 杨广平. 一种窄带雷达快速目标分类方法[J]. 国外电子测量技术, 2018, 37(2):105-111.
[4] 王曙光, 田西兰. 一种窄带雷达舰船目标分类的决策方法[J]. 雷达科学与技术, 2016, 14(2):159-162.
[5] 易晓柯. 支持向量机的全局局部特征融合目标识别[J]. 雷达科学与技术, 2011, 9(2):180-182.
YI Xiaoke. Target Recognition Based on Support Vector Machine (SVM) Features Fusion[J]. Radar Science and Technology, 2011, 9(2):180-182. (in Chinese)
[6] 陈志仁, 顾红, 苏卫民, 等. 改进的支持向量机低分辨雷达目标分类算法[J]. 系统工程与电子技术, 2017, 39(11):2456-2462.
[7] 纪永强, 刘通, 徐高正, 等.基于RCS统计特征的船舶目标识别方法[J]. 舰船科学技术, 2018, 40(13):129-132.
[8] 邵嘉琦, 曲长文, 李健伟. 卷积神经网络对SAR目标识别性能分析[J]. 雷达科学与技术, 2018, 16(5):525-532.
[9] 张学工. 模式识别[M]. 北京: 清华大学出版社, 2010:146-148.
[10] 王放.基于窄带RCS序列的低轨空间目标识别效果分析[C]∥第二届中国空天安全会议,大连:中国指挥与控制学会空天安全平行系统专业委员会,2017:74-78.
