0 引言
雷达辐射源识别是指对侦察得到的雷达信号进行分析，进而确定该辐射源体制、用途、工作状态、威胁等级等信息的过程，是雷达侦察的关键环节。近年来，机器学习作为一种数据分析的智能工具，具有强大的自学习能力。基于机器学习的雷达辐射源识别可以通过学习数据库样本的规律对新样本进行识别，是推动雷达侦察向智能化发展的关键举措，如美军陆航研制开发的AN/ALQ-211综合雷达对抗系统(SIRFC)、英国Selex公司为本国部队研制的“空中卫士2000”雷达告警系统、BAE系统(北美)公司为美国陆航部队研制的AN/APR-39A系列系统[1]等，都融合了机器学习的方法。然而，数据库的建立需要足够多的有标记的样本，样本的标记需要大量的人力和时间，这些都会导致机器学习的效率降低。并且，雷达信号采集时间和成本的限制将会导致：1)侦察样本数量有限而不足以支撑起雷达辐射源识别模型的训练；2)侦察样本多样性不足导致雷达辐射源识别模型泛化能力差或训练容易过拟合。
生成模型能学习有限样本的内在统计规律进而生成类似样本。常用的生成模型如受限玻尔兹曼机、深度置信网络、深度玻尔兹曼机、变分自编码器等涉及较高的计算复杂度，生成对抗网络(Generative Adversarial Network，GAN)是Goodfellow[2]在2014年提出的生成模型，在神经网络中引入对抗训练机制来解决上述问题且由于其能学习样本的真实分布，生成多样性样本而成为深度学习中的研究热点[3]。目前，GAN已成功应用于计算机视觉、自然语言处理等领域。此外，Santana利用GAN辅助自动驾驶，Schlegl[4]将GAN用于医学图像的异常检测，Wu利用GAN提高机器翻译质量，Hu利用GAN进行恶意软件的检测等都拓展了GAN的应用。鉴于其优良性质，本文在原始GAN基础上进行改进，提出了无监督的多样性最大化生成对抗网络(Maximum Diversity Generative Adversarial Network，MDGAN)，证明了是扩充数据集的有效方法。
1 改进的生成对抗网络
1.1 生成对抗网络(GAN)
GAN由两个卷积神经网络组成，分别作为生成器(G)和判别器(D)。其结构如图1所示。首先从先验分布PZ(z)(100维[-1，1]均匀分布)中采样出随机向量Z，即Z～PZ(z)，将Z作为G的输入，得到生成的假数据G(z)。接着，从真实数据分布Pdata(x)中采样出真实数据X(需要扩充的数据集里已有的样本)，即X～Pdata(x)。将G(z)和X作为D的输入，D对于输入G(z)时，应输出结果0，对于输入X时，应输出结果1，即对于真实数据D尽量给予接近1的输出，对于G产生的假数据尽量给予接近0的输出。同时，G的目标是使自己生成的假数据G(z)在D中的表现 D(G(z))和真实数据X在D中的表现D(x)尽量一致，以使得D无法正确区分数据真实情况。G和D根据各自的目的在对抗训练中不断优化提升能力，直到达到纳什均衡点。此时，D判别能力已经得到很大提升，但G也学到了真实数据的分布Pdata(x)能产生和真实数据相似的样本以至于D只能输出0.5，即无法正确判别数据来源只能随机猜测。将上述过程转化为各自的目标函数定义如下：
GAN判别器D目标函数：
maxVD=Ex～Pdata(x)logD(x)+
Ez～PZ(z)log(1-D(G(z)))
(1)
GAN生成器G目标函数：
maxVG=Ez～PZ(z)log(D(G(z)))
(2)
式中，E(·)表示计算期望值，D(x)表示D对真实数据X的真实程度的判断值，D(G(z))表示D对生成的数据G(z)的真实程度的判断值。D的目的是让D(x)接近1，D(G(z))接近0，所以希望式(1)最大。G的目的是让D(G(z))接近1，所以希望式(2)最大。D和G根据各自目标函数进行对抗训练，直到G能生成以假乱真的样本。
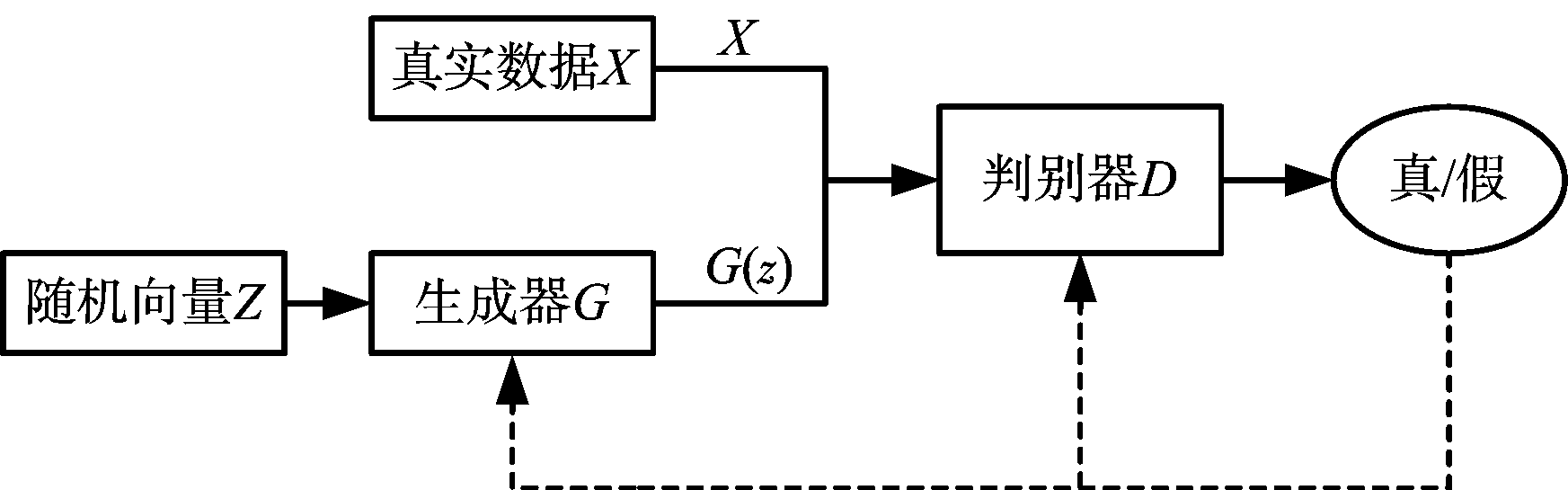
图1 GAN结构图
1.2 多样性最大化生成对抗网络(MDGAN)
GAN着重考虑了G生成样本的真实程度问题，希望生成与真实样本无差别的样本，会导致G为达到这一目的重复的生成某一个真实程度很高(D(G(z))值很大)的样本，这会使生成的样本的多样性程度锐减，即生成的样本特征单一[5]，无法满足数据集多样性的要求，尤其当采样的随机向量z1和z2很接近时，由它们生成的样本G(z1)和G(z2)也会很相似。为增加生成样本的多样性，本文在原始G的目标函数基础上增加了一个正则化项，提出MDGAN。新的目标函数定义如下[6]：
MDGAN判别器D目标函数：
maxVD=Ex～Pdata(x)logD(x)+
Ez1，z2～PZ(z)log(1-D(G(z)))
(3)
MDGAN生成器G目标函数：
maxVG=Ez1，z2～PZ(z)log(D(G(z)))+
Ez1，z2～PZ(z)·
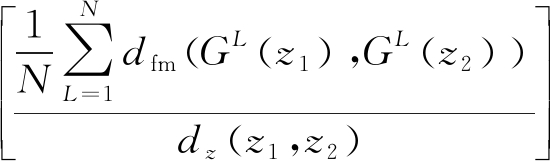
(4)
式中，z1，z2～PZ(z)表示从先验分布PZ(z)中采样出的两个随机向量，d(·)表示求归一化L1距离，则dz(z1，z2)表示求给定的两个随机向量z1，z2之间的归一化L1距离，N表示G的卷积层数量，GL(zi)表示随机向量zi输入G后在第L层生成的特征图，dfm(GL(z1)，GL(z2))表示两个随机向量z1，z2在G的第L层生成的特征图的归一化L1距离，
表示对所有层的归一化L1距离求平均。则通过最大化式(4)最右边的比值，可以保证在给定输入的随机向量z1，z2的条件下，使得G生成的样本的平均距离最大，即尽量生成差异较大的样本。综上，式(4)等号右边第一项保证生成的样本尽量真实，第二项保证生成的样本尽量拥有不同特征。
2 数据集有效性检验
本文利用起始分值(Inception Score，IS)[7]检验G生成的数据集的多样性，利用弗雷歇起始距离(Frechet Inception Distance，FID)检验G生成的数据集的真实性。IS计算公式如下：
(5)
p(y)=EX～PG(x)[p(y/x)]
(6)
式中，X～PG(x)表示G生成的样本，p(y/x)是X的条件类别分布，p(y)是类别边缘分布， DKL(·)是计算p(y/x)和p(y)之间的KL距离，E(·)是计算期望值。实际中，用平均值代替期望值，计算公式如下：
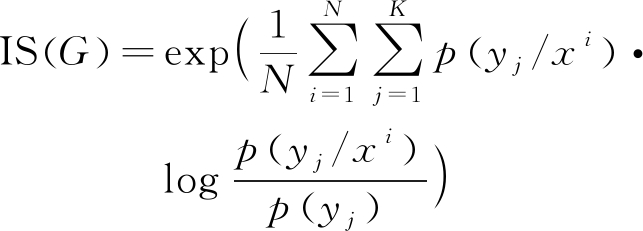
(7)
(8)
式中，N表示G生成的样本个数，K表示G生成的样本类别数。p(y/xi)=[p(y1/xi)，p(y2/xi)，…，p(yK/xi)]是一个K维的向量，表示将第i个生成样本xi输入Inception分类网络各个类别分别得到的概率值。p(y)=[p(y1)，p(y2)，…， p(yK)]是N个样本的各个类别概率的平均值。因为p(y/x)分布是一条含峰值的曲线(存在一个概率最高的值)，如果G生成的样本类别足够多， p(y)会向均匀分布靠拢，逐渐变为一条横线，则 p(y/x)和p(y)的KL距离会变大，所以利用IS值检验多样性，值越大多样性越好。式(5)只涉及生成样本，与真实样本无关，无法衡量生成样本的真实性，所以利用FID检验真实性[8]，计算公式如下：
FID(φ(x)，φ(G))=
(9)
式中，x表示真实样本，G表示生成的样本，
表示求L2距离，Tr(·)表示求矩阵的迹，φ(·)表示样本经过Inception网络的最后一个卷积层后提取的特征向量。将所有真实样本提取的特征向量建模为高斯随机变量，即φ(x)～N(μx，Σx)，μx，Σx分别是其均值和方差。将所有生成样本提取的特征向量建模为高斯随机变量，即φ(G)～N(μG，ΣG)，μG，ΣG分别是其均值和方差。则可利用式(9)求两个高斯分布之间的弗雷歇距离。生成的样本越真实，则生成样本的分布和真实样本的分布越接近，FID值越小。
3 仿真实验与分析
为验证本文提出的MDGAN网络用于扩充雷达辐射源数据集的有效性，采用6种雷达信号[9]：二进制相移键控(Binary Phase Shift Keying，BPSK)、线性调频(Linear Frequency Modulation，LFM)、二进制频移键控(Binary Frequency Shift Keying,BFSK)、非线性调频(Non Linear Frequency Modulation，NLFM)、多进制相移键控(Multiple Phase Shift Keying，MPSK)、连续波信号(Continuous Wave，CW)进行仿真实验。其中，BPSK采用7位巴克码；MPSK采用P4码；LFM带宽17 MHz，脉宽10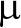 
s；NLFM采用正弦波调频；BFSK上边频10 MHz，下边频20 MHz；CW载频25 MHz，采样频率都取100 MHz。图2为6种雷达信号在无噪声条件下的时频图像(灰度图)，但在实际的雷达侦察中，截获的雷达信号都是受噪声影响的。因此，在信号中加入高斯白噪声，在信噪比为-4 dB条件下每种信号利用时频分析的方法产生100张时频图像模拟实际条件下建立的原始数据集[10-11]。本实验软件环境：操作系统Win10 64位，基于开源深度学习框架Tensorflow1.5-GPU搭建模型，VS2015+CUDA9+CUDNN7提供对GPU运算的支持并提高图形并行运算的速度。硬件环境：CPU：Intel i7-7700K @ 4.20 GHz，GPU:GTX TITAN X。训练参数[12]：Mini- Batch为64的随机梯度下降算法(SGD)进行训练，Adam优化器进行超参数调优，学习率0.000 2，动量β1为0.5，迭代轮数Epoch为50轮。
仿真1： 数据集扩增实验
将上述的原始数据集分别作为GAN、MDGAN的训练集，每种信号再生成100张时频图像作为扩增的数据集(为了保证样本有效，仅对原始数据集扩增一倍)。将原始的数据集、GAN生成的数据集、MDGAN生成的数据集进行对比展示，如图3至图8所示(每种信号仅展示3张样本)。其中，第一行为原始数据集样本，第二行为GAN生成的样本，第三行为MDGAN生成的样本。
图2 6种雷达信号的时频图像
图3 BPSK实验结果对比
图4 CW实验结果对比
图5 BFSK实验结果对比
图6 LFM实验结果对比
图7 MPSK实验结果对比
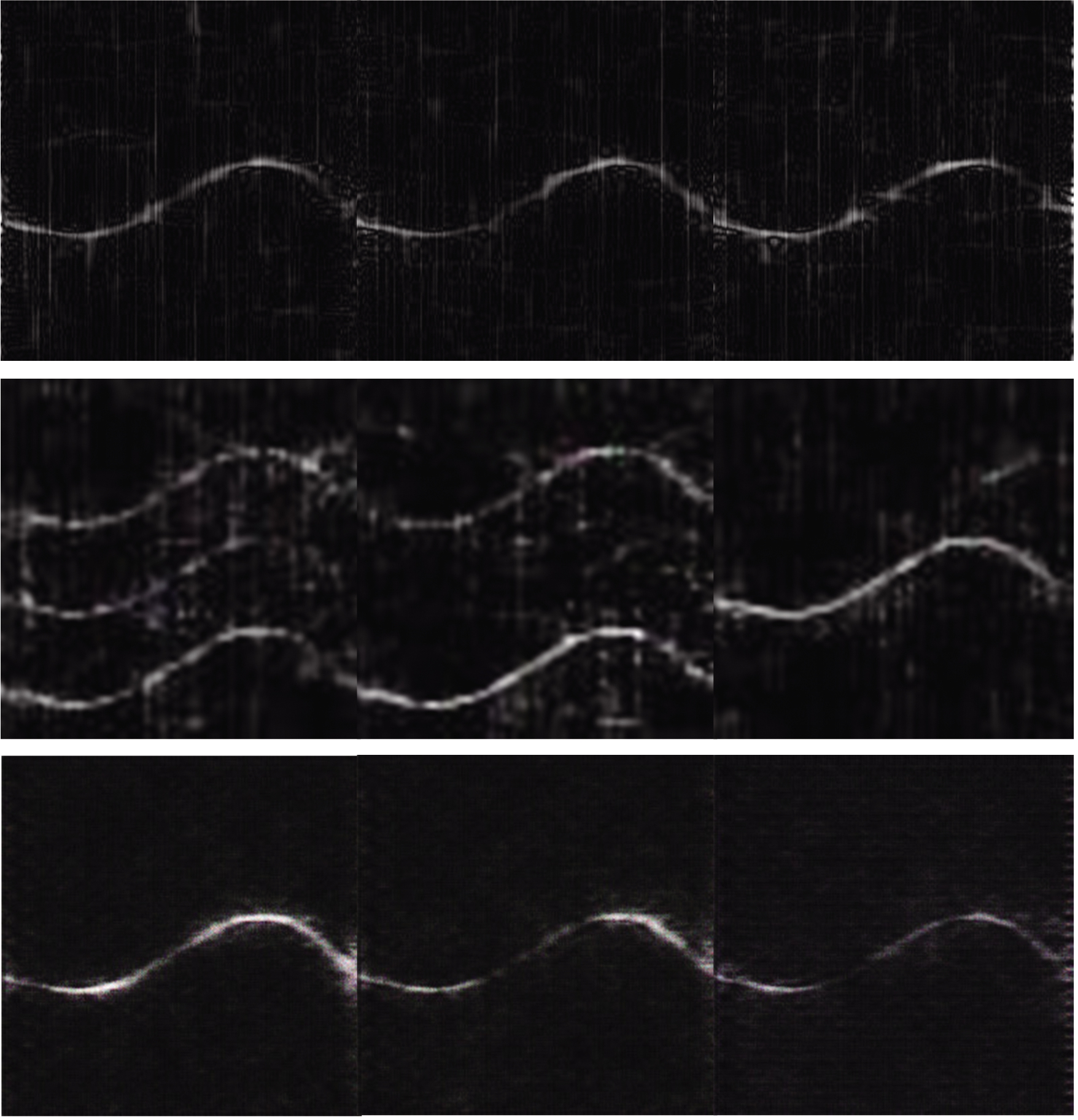
图8 NLFM实验结果对比
由图3至图8可以发现，受噪声影响，原始数据集中的时频图像存在毛刺、时频结构断裂、边缘模糊等情况，GAN将这种情况放大了，生成的时频图像背景噪声更大，有的样本甚至已经严重破坏了真实信号的时频关系，产生了根本不存在的时频特征或者时频特征局部消失，无疑是不能作为先验样本使用的。本文提出的MDGAN生成的时频图像具有以下优点：1)背景噪声被淡化，时频聚集性更好；2)生成的时频特征符合真实信号的时频关系，如BPSK的相位突变点、BFSK的频率跳变点、LFM的时频起止点、NLFM的调频宽度都被很好的刻画；3)在保证时频关系正确的前提下，每个样本具有不同的特征，如具有不同的时频分辨率，灰度值的强度变化关系不同，生成器重点生成的时频局部特征区域不同。因此，仅从视觉层面而言，本文提出的MDGAN能产生符合真实情况的样本，加入到生成器目标函数中的正则化项能提高生成样本的多样性。
仿真2： 数据集有效性检验实验
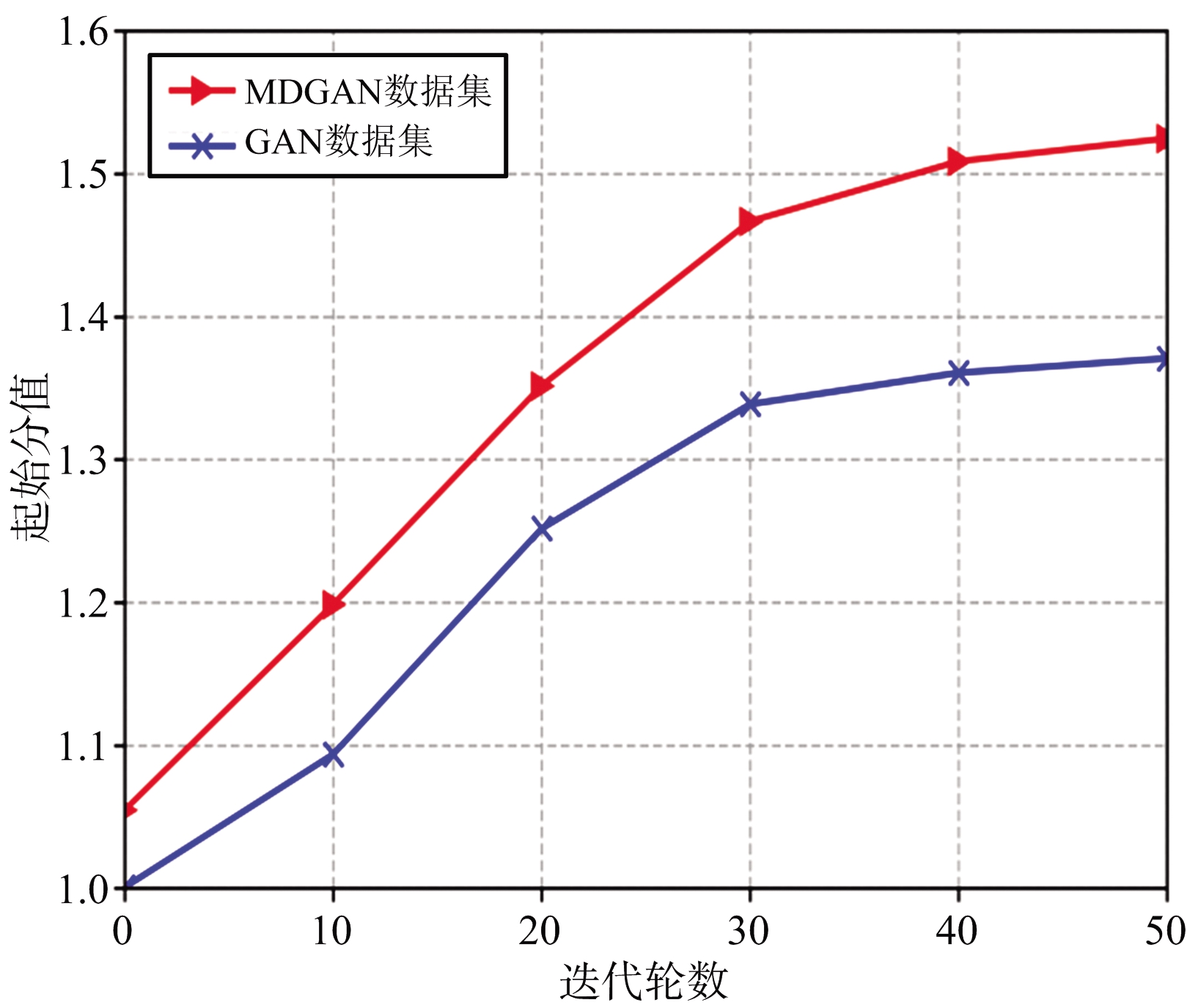
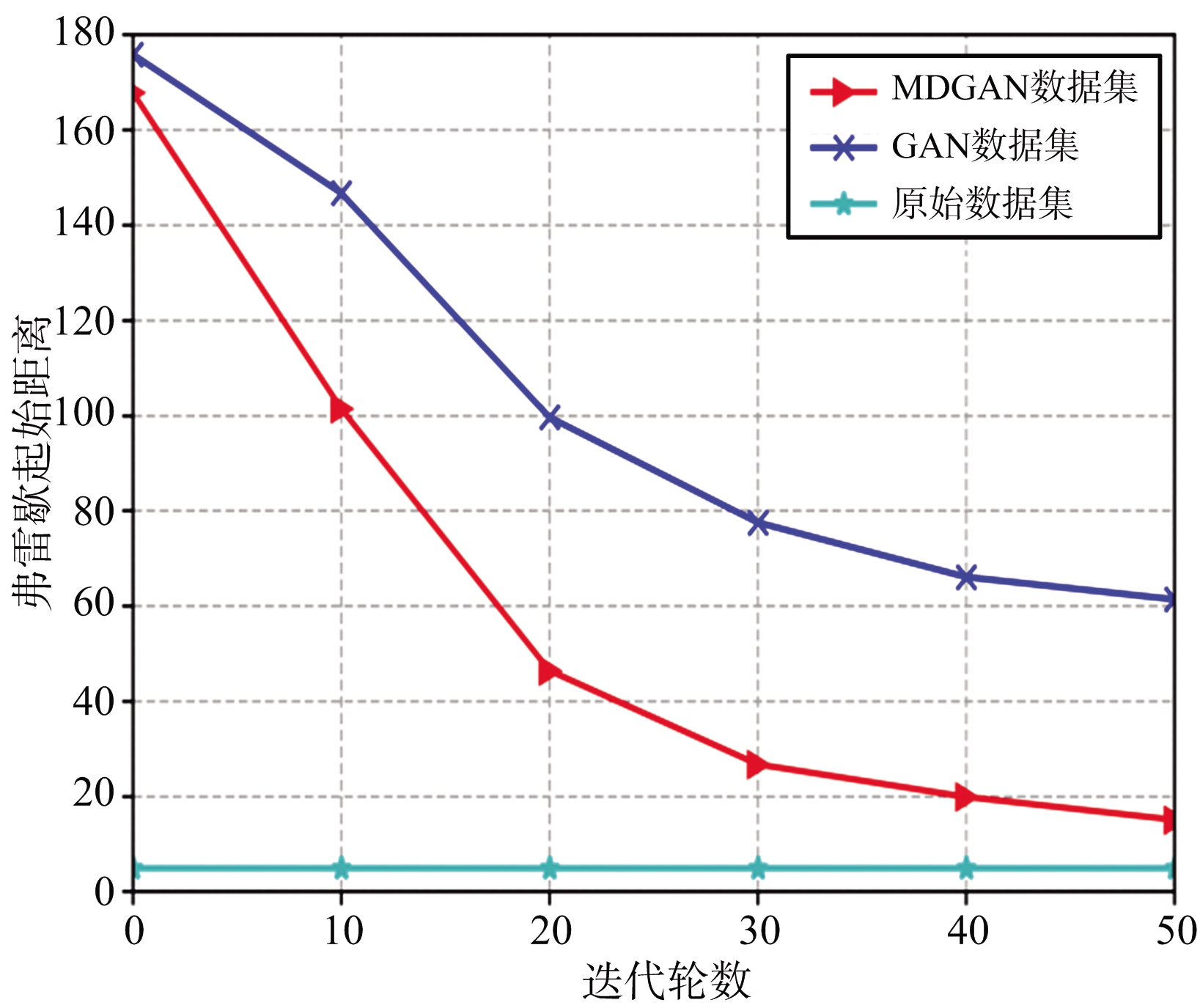
利用第3节方法，分别求取GAN、MDGAN在迭代轮数Epoch=0,10,20,30,40,50时生成的数据集的IS值和FID值，并将结果对比展示，如图9所示。并将MDGAN在Epoch=0，10，20，30，40时生成的样本进行可视化[13](Epoch=50在仿真1中已展示)，如图10所示。
(a) IS值
(b) FID值
图9 有效性检验结果
图10 生成样本可视化结果(从上到下依次为BPSK，CW，BFSK，LFM，MPSK，NLFM)
由图10可以发现，在Epoch=0时，此时生成的样本还只是从先验分布中采样的随机向量，并没有样本特征的生成。在Epoch=10时，此时生成的样本已经开始学习训练样本的特征，但主要是特征的整体轮廓，还不具备细节生成的能力。Epoch=30时，此时细节的刻画能力更强了，如BPSK的相位突变点已经开始显现。Epoch=40时，此时无论生成的整体特征还是局部特征都较为接近训练样本了。在这个过程中，随机向量在逐渐地向生成样本特征的方向靠拢，训练样本的背景噪声被忽视掉了。由图9可以发现，IS值：MDGAN>GAN，且整体都在上升，即随着对训练样本学习程度的加深，不同的特征都被挖掘出来，所以生成样本也不再是单一模式，多样性逐渐增加，且MDGAN比GAN能生成更多的不一样的样本。FID值：MDGAN 本文提出了一种无监督的由图像生成图像的网络—多样性最大化生成对抗网络(MDGAN)，MDGAN是GAN的衍生模型，它在生成器的原始目标函数的基础上引入了一个表示特征图之间距离与随机向量之间距离比值的正则化项，通过最大化这个比值，可以生成多样性样本。仿真实验证明了MDGAN相比原始GAN能生成更真实更多样的样本，是扩充雷达辐射源数据集的有效方法。同时，也存在一些问题需要继续考虑：本文提出的正则化项在提升效果的同时也会减缓模型收敛速度，能否对其进行简化；将生成的数据集用于雷达辐射源识别实验来更近一步说明样本的有效性；本文以-4 dB信噪比条件下数据集的扩充实验为主，模型在其他信噪比条件下的数据集生成效果如何；MDGAN作为一种数据生成模型，如何将它融入现有的雷达数据库系统中，提高系统的智能性。 [1] 王超, 陈为沛, 强勇. 雷达辐射源智能识别方法研究现状与展望[C]∥全国信号与信息处理联合学术会议,大连:[出版者不详],2007:233-235. [2] GOODFELLOW I, POUGET-ABADIE J, MIRZA M, et al. Generative Adversarial Nets[C]∥Proceedings of the International Conference on Neural Information Processing Systems,[S.l.]:[s.n.],2014:2672-2680. [3] 王万良, 李卓蓉. 生成式对抗网络研究进展[J].通信学报, 2018, 39(2):135-148. [4] SCHLEGL T, SEEBOCK P, WALDSTEIN S M, et al. Unsupervised Anomaly Detection with Generative Adversarial Networks to Guide Marker Discovery [C]∥International Conference on Information Processing in Medical Imaging,[S.l.]:[s.n.],2017:146-157. [5] SALIMANS T, GOODFELLOW I, ZAREMBA W, et al. Improved Techniques for Training Gans[C]∥Advances in Neural Information Processing Systems,[S.l.]:[s.n.],2016:2234-2242. [6] WANG T C, LIU M Y, ZHU J Y, et al. High-Resolution Image Synthesis and Semantic Manipulation with Conditional GANs[C]∥IEEE Conference on Computer Vision and Pattern Recognition (CVPR),[S.l.]:[s.n.], 2018:8798-8807. [7] SHMELKOV K, SCHMID C, ALAHARI K . How Good Is My GAN?[C]∥In European Conference on Computer Vision(ECCV),[S.l.]:[s.n.], 2018:213-229. [8] HEUSEL M, RAMSAUER H, UNTERTHINER T, et al. GANs Trained by a Two Time-Scale Update Rule Converge to a Local Nash Equilibrium[C]∥In Advances in Neural Information Processing Systems(NIPS),[S.l.]:[s.n.],2017:6626-6637. [9] 周志文, 黄高明，高俊.一种深度学习的雷达辐射源识别算法[J].西安电子科技大学学报(自然科学版),2017,44(3):77-82. [10] REN D, ZHANG T. Specific Emitter Identification Based on Intrinsic Time-Scale-Decomposition and Image Texture Feature[C]∥International Conference on Communication Software and Networks,[S.l.]:[s.n.], 2017:1302-1307. [11] 金秋. 基于深度学习的雷达辐射源识别方法研究[D].北京：航天工程大学,2018. [12] HE T, ZHANG Z, ZHANG H, et al. Bag of Tricks for Image Classification with Convolutional Neural Networks[C]∥In IEEE Conference on Computer Vision and Pattern Recognition(CVPR),[S.l.]:[s.n.], 2019:558-567. [13] 唐贤伦, 杜一铭, 刘雨微. 基于条件深度卷积生成对抗网络的图像识别方法[J].自动化学报, 2018, 44(5):855-864.4 结束语
