0 引言
雷达极化通常分为线极化和圆极化两类，对低分辨率雷达，复杂目标回波是各散射中心回波的相干合成，当使用线极化进行发射和接收时，目标的同极化回波比交叉极化回波要强，二者的功率比在4～10 dB之间；当使用圆极化进行发射和接收时，目标的交叉极化回波比同极化回波略强，二者的功率比在0～6 dB之间[1]。对于合成孔径雷达(SAR)，目标回波与雷达分辨单元对应，在二维分辨率足够高的情况下，各分辨单元目标回波散射中心一般可以近似看成是组成复杂目标的一些简单结构体，在极化SAR成像时，可获取与这些简单结构体极化散射特性相应的极化散射矩阵，利用不同简单结构体极化散射矩阵的处理分析，高分辨率多极化SAR图像不仅可识别目标的轮廓特征，还可以将目标散射分解为二面角、三面角(球、平板)、偶极子、圆柱体、窄二面角、左旋螺旋体、右旋螺旋体、1/4波振子等简单结构单元，实现雷达目标几何结构的初步反演，识别目标的结构组成[2]。
目前国内外研究开发的机载、星载极化SAR系统大多是线极化，目标的雷达极化散射特性和极化SAR目标识别分类研究也是以线极化为主，有关圆极化SAR文献主要与圆极化SAR系统技术、试验相关，圆极化SAR目标成像特性及检测、识别技术研究文献较少。文献[3]利用ALOS PALSAR卫星极化SAR数据仿真全圆极化(LL、LR、RL和RR)SAR成像，与线极化相比圆极化地物SAR图像更清晰。文献[4]介绍了一种L波段圆极化SAR系统车载试验以及微波暗室圆极化和线极化ISAR成像试验结果，从试验结果可以看出目标定向角对圆极化成像影响较小。文献[5]介绍了一种P波段圆极化SAR系统，并给出了机载飞行试验结果，结果表明线状目标圆极化比线极化有更好的成像效果，对于叶簇隐蔽以及沙土埋藏目标，圆极化比线极化有更好的探测性能。文献[6]给出一种超宽带(UWB)圆极化/线极化微波成像雷达系统穿墙成像试验结果，从中看出，同样信号带宽下，圆极化穿墙成像距离分辨率优于线极化穿墙成像距离分辨率。
本文将以目标线极化散射矩阵为基础，分析三面角、二面角、偶极子(线状体)、圆柱体等复杂人造目标基本构成单元的圆极化SAR成像特性，仿真计算圆极化轴比对不同目标圆极化散射特性的影响，给出圆/线极化机载SAR图像人造目标散射特性分析比较结果。
1 圆极化与线极化雷达散射矩阵变换
沿+z方向传播的平面电磁波电场矢量可以表示为
(1)
式中，
分别表示+x和+y方向的单位基矢量，Ex和Ey均为复数，是电场矢量在+x和+y方向的分量，φx和φy分别是Ex和Ey的相位。一般情况下，随着时间的变化，电场矢量
端点将处于一个椭圆之上，如图1所示。令φxy=φy-φx，当φxy等于0或π时端点将随时间在XY平面上的一条直线变化，此时称该电磁波为线极化波，若|Ex|=0或
端点将随时间分别在Y轴或X轴上变化，分别记为垂直线极化EV和水平线极化EH；当φxy等于
或
且|Ex|=|Ey|时，端点将随时间在XY平面的一个圆周上呈现左旋或右旋变化，此时称该电磁波为圆极化波，分别记为左旋圆极化EL和右旋圆极化ER。EL、ER和EH、EV之间可以通过式(2)、式(3)变换[1]。
(2)
(3)
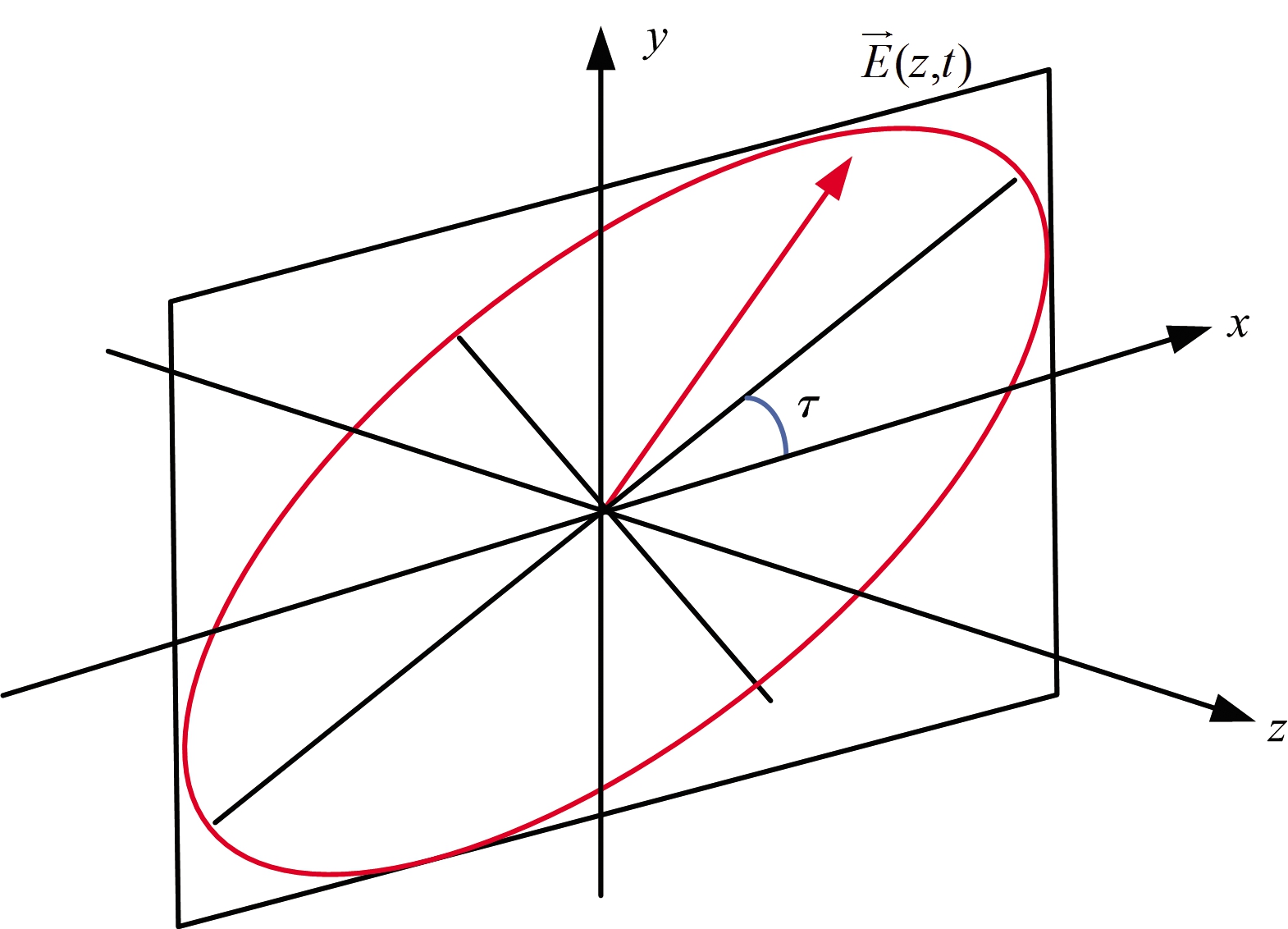
图1 平面电磁波电场矢量示意图
通常目标的雷达极化散射矩阵分为线极化基散射矩阵和圆极化基散射矩阵两类。式(4)给出了雷达发射到目标的水平与垂直极化入射场
与目标散射回波场
之间的关系，SLP是以水平极化和垂直极化为极化基的线极化散射矩阵。式(5)给出了雷达发射到目标的左旋与右旋极化入射场
与目标散射回波场
之间的关系，SCP是以左旋极化和右旋极化为极化基的圆极化散射矩阵。由式(2)、式(3)可知，左旋、右旋极化入射场与水平、垂直极化入射场之间的变换关系如式(8)、式(9)所示。考虑到目标散射回波与入射波传播方向相反因素，圆极化目标散射回波场与线极化目标散射回波场之间的变换关系如式(10)、式(11)所示。由式(4)～式(10)可推出SLP和SCP之间变换式(12)。式中SHH、SHV、SVH、SVV、SLL、SLR、SRL、SRR等均为复数。
(4)
(5)
(6)
(7)
(8)
(9)
(10)
(11)
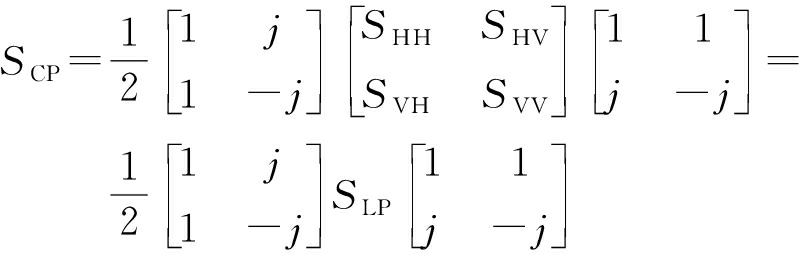
(12)
在实际工程中实现的圆极化波电场矢量旋转轨迹通常是一个倾角为τ的椭圆(如图1所示)，并用椭圆短轴与长轴比值ρ衡量椭圆度，ρ等于1时是理想圆极化波，ρ小于1时是椭圆极化波。不失一般性，设椭圆倾角τ等于0，椭圆极化波长轴位于x轴，短轴位于y轴，即垂直线极化EV位于短轴，水平线极化EH位于长轴，则
代入式(8)可得入射左旋椭圆极化、右旋椭圆极化波与线极化波之间变换式(13)。同理有
代入式(10)可得散射回波左旋椭圆极化、右旋椭圆极化波与线极化波之间变换式(14)。由式(5)、式(13)、式(14)可得式(15)，式中
因此式(15)是标准的线极化(水平极化与垂直极化发射信号、接收通道均衡)目标散射回波公式，由式(4)和式(15)可得式(16)，经矩阵运算可得轴比为ρ的椭圆极化目标散射矩阵与标准线极化目标散射矩阵之间的变换关系式(17)。
(13)
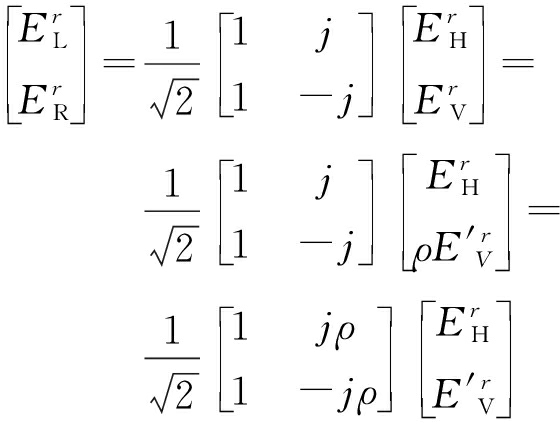
(14)
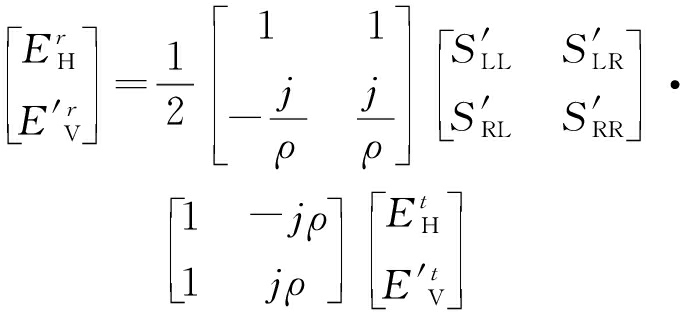
(15)
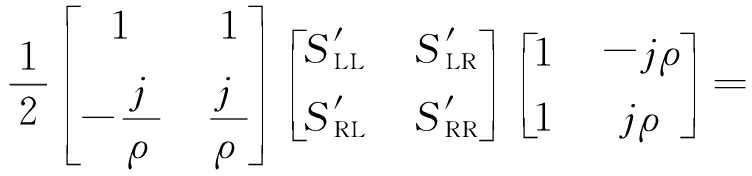
(16)
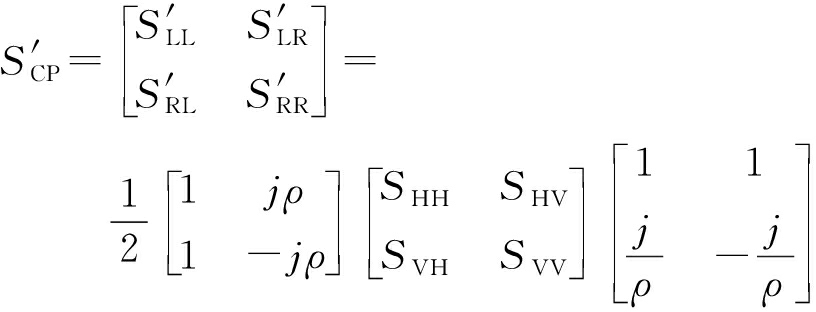
(17)
2 人造目标圆极化SAR散射特性分析
根据Cameron等人研究结果[2]，在高分辨率SAR图像中复杂目标散射可分解为二面角、三面角(球、平板)、偶极子(线状体)、圆柱体、窄二面角、左旋螺旋体、右旋螺旋体、1/4波振子等简单结构散射体，本文重点分析其中二面角、三面角(球、平板)、偶极子(线状体)、圆柱体等典型结构单元的圆极化SAR散射特性。
目标极化散射特性除了与目标形状、结构以及材料等因素有关外，还与目标相对于雷达视线的姿态有关，对于在垂直于雷达视线平面内绕雷达波入射方向旋转的目标，旋转角称为定向角，设式(6)为定向角0°时的目标线极化散射矩阵，则定向角为θ时目标的线极化散射矩阵为式(18)[1]。将三面角反射器、二面角反射器、偶极子以及圆柱体等目标定向角为0°时的线极化散射矩阵[2]代入式(18)可得这些目标在定向角为θ时的线极化散射矩阵，分别如式(19)、式(20)、式(21)、式(22)所示。由式中可以看出，三面角线极化散射矩阵中各极化复数散射幅度不随目标定向角变化，而二面角、偶极子、圆柱体等目标线极化散射矩阵中各极化复数散射幅度均随目标定向角变化，即不同定向角具有不同的线极化散射矩阵。
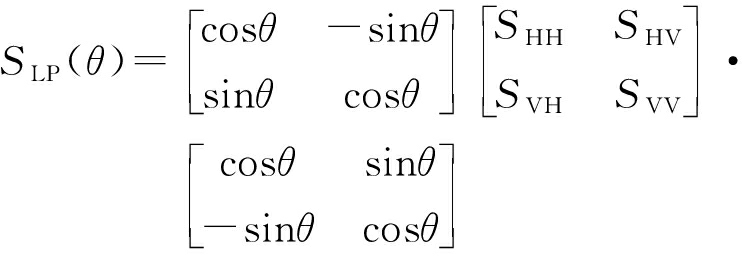
(18)
三面角：
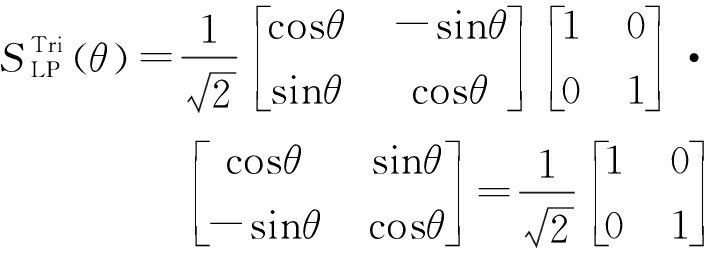
(19)
二面角：
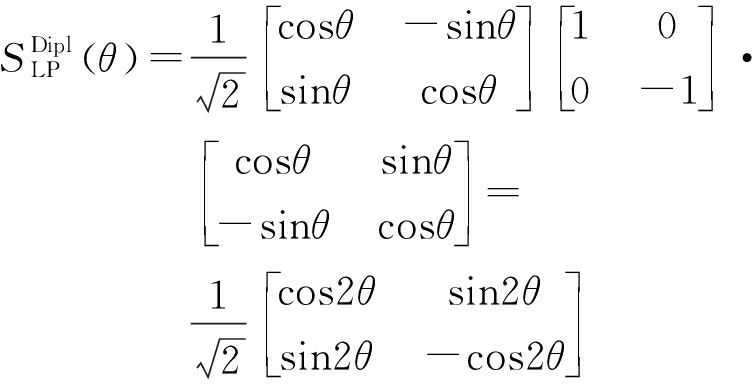
(20)
偶极子：
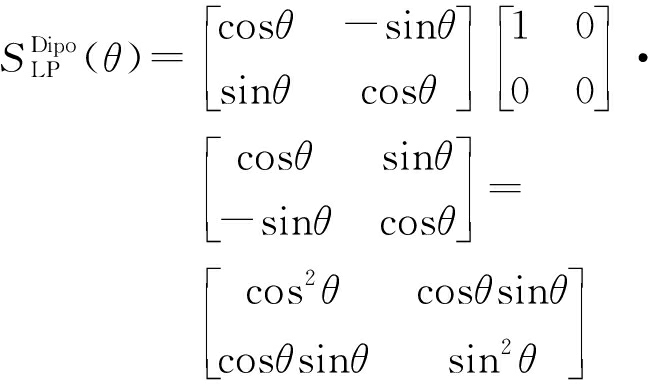
(21)
圆柱体：
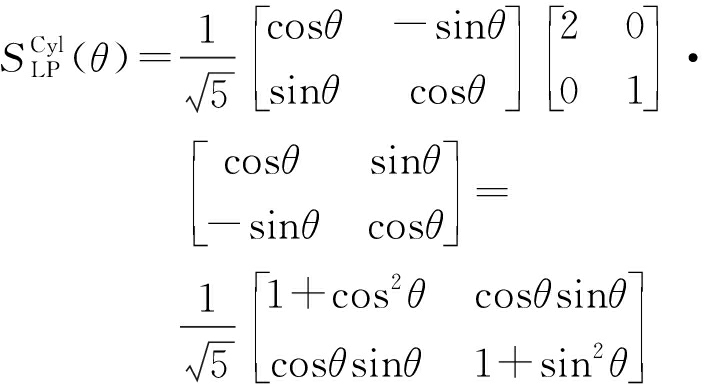
(22)
线极化波电场矢量随时间在垂直于雷达视线的一个固定方向变化，而圆极化波电场矢量随时间在绕雷达视线的一个圆周上呈现左旋或右旋变化，对于线极化、圆极化两种不同极化波雷达目标将呈现不同极化散射特性。将三面角、二面角、偶极子、圆柱体等目标线极化散射矩阵式(19)、式(20)、式(21)、式(22)分别代入式(17)可得相关目标的椭圆极化散射矩阵如式(23)、式(24)、式(25)、式(26)所示。从式中可以看出，三面角反射器轴比为ρ的椭圆极化散射矩阵与理想圆极化散射矩阵相同，不受极化轴比影响。在轴比ρ=1的理想圆极化情况下，二面角、偶极子、圆柱体等目标圆极化散射矩阵各极化分量复数散射幅度的幅值(绝对值)均不随目标定向角变化，仅同极化(LL、RR极化)复数散射幅度的相位随目标定向角变化，可见对于一些线极化雷达散射特性随定向角变化的目标，圆极化雷达具有较稳定的散射特性。比较式(23)、式(24)，三面角目标同极化(LL、RR极化)复数散射幅度的幅值为0，交叉极化(LR、RL极化)复数散射幅度的幅值为1，而二面角目标在轴比ρ=1时同极化(LL、RR极化)复数散射幅度的幅值为1，交叉极化(LR、RL极化)复数散射幅度的幅值为0，可见在圆极化雷达中三面角与二面角反射器极化散射能量呈现互补关系，一个交叉极化强，一个同极化强。而在线极化雷达中，三面角反射器极化散射能量是同极化强，交叉极化为0，二面角反射器极化散射能量只有在定向角45°时呈现交叉极化强、同极化为0，其他定向角情况下，同极化散射能量均大于0(定向角0°时达到最大)，从而与三面角散射特性重合。从式(25)中看出，在轴比ρ=1时圆极化雷达中偶极子(线状体)交叉极化(LR、RL极化)复数散射幅度的幅值与同极化(LL、RR极化)复数散射幅度的幅值相同，同极化与交叉极化具有相同的散射能量。从式(26)中看出，在轴比ρ=1时圆极化雷达中圆柱体交叉极化(LR、RL极化)复数散射幅度的幅值是同极化(LL、RR极化)复数散射幅度的幅值的3倍，交叉极化具有较大的散射能量。
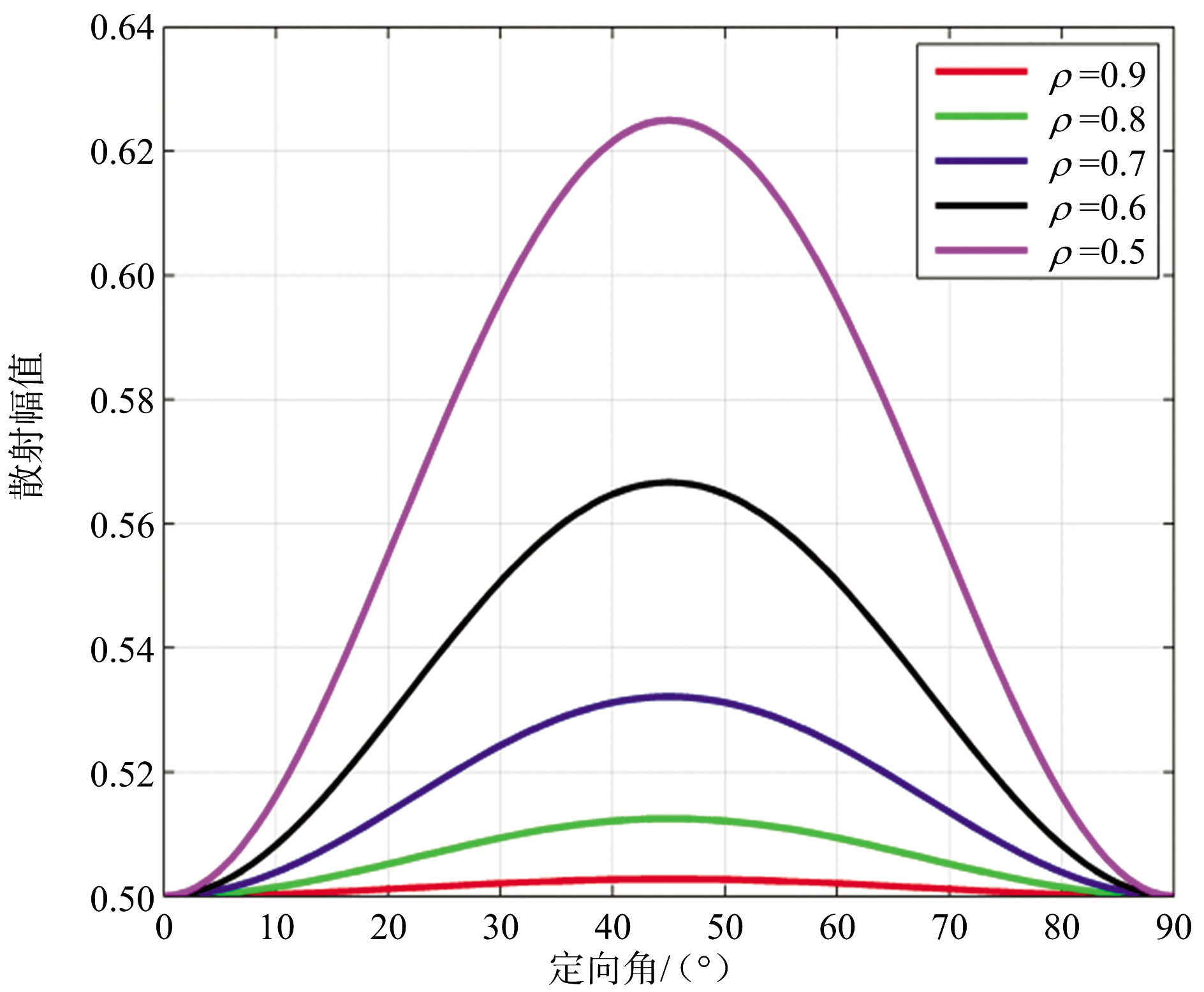
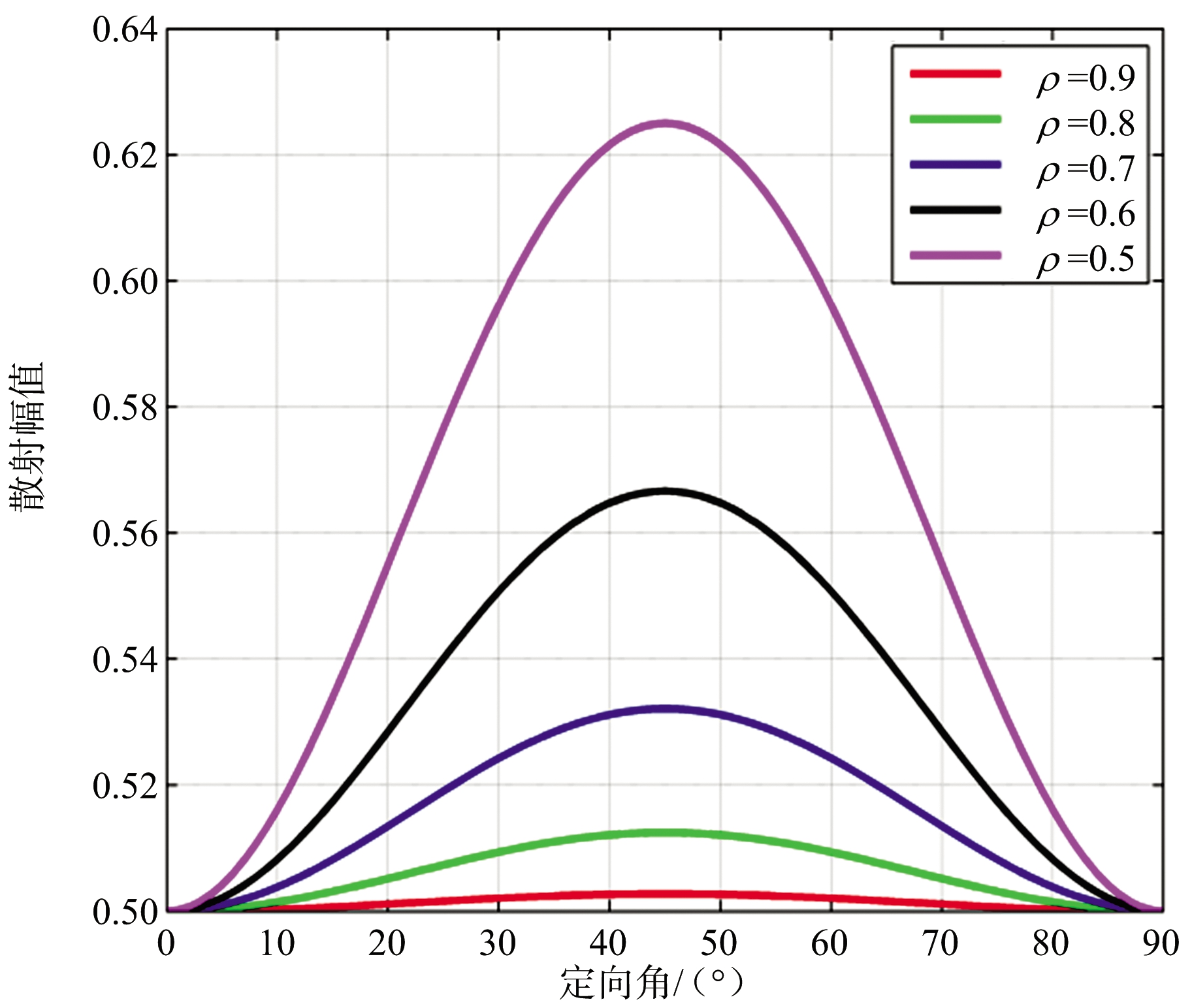
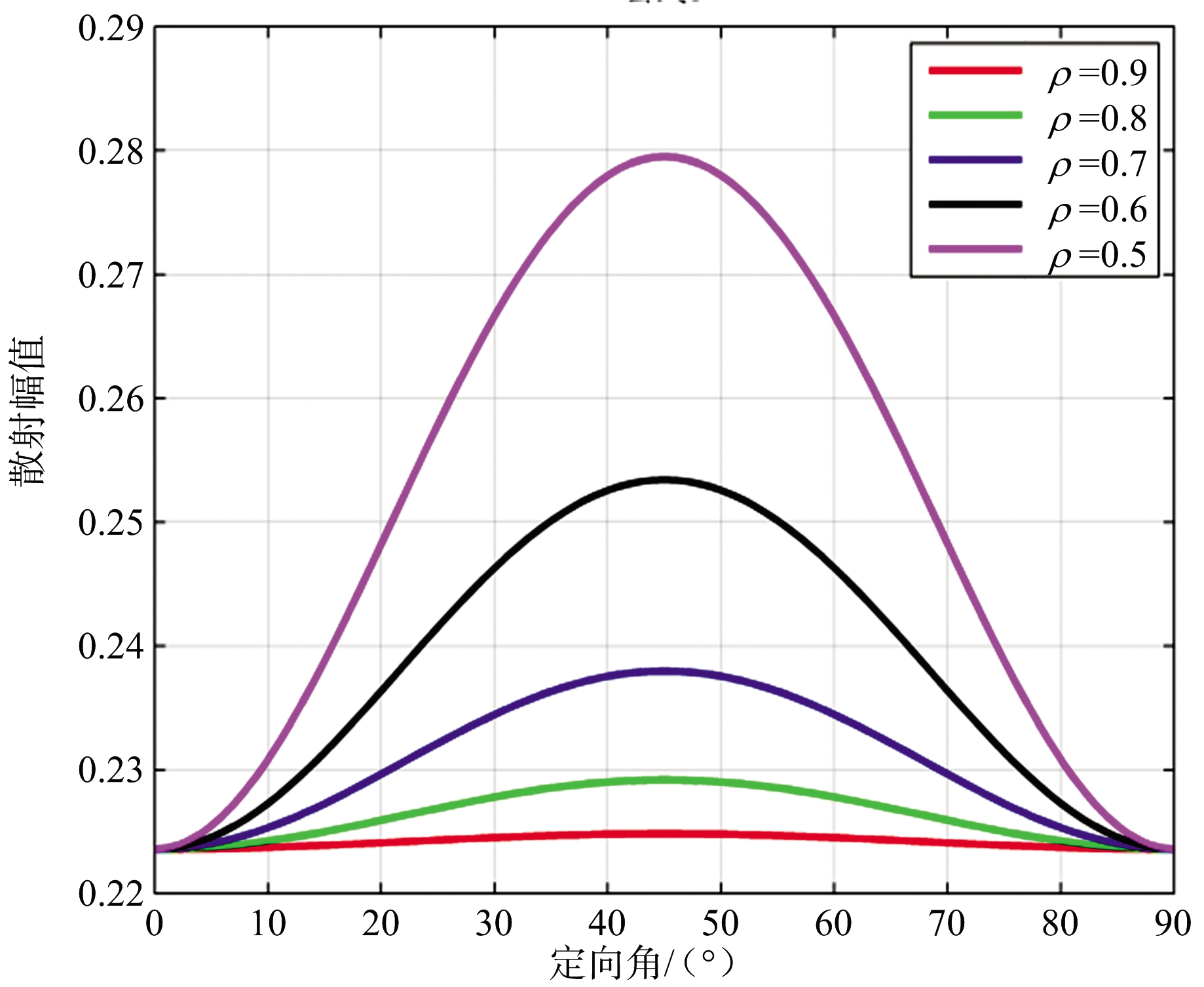
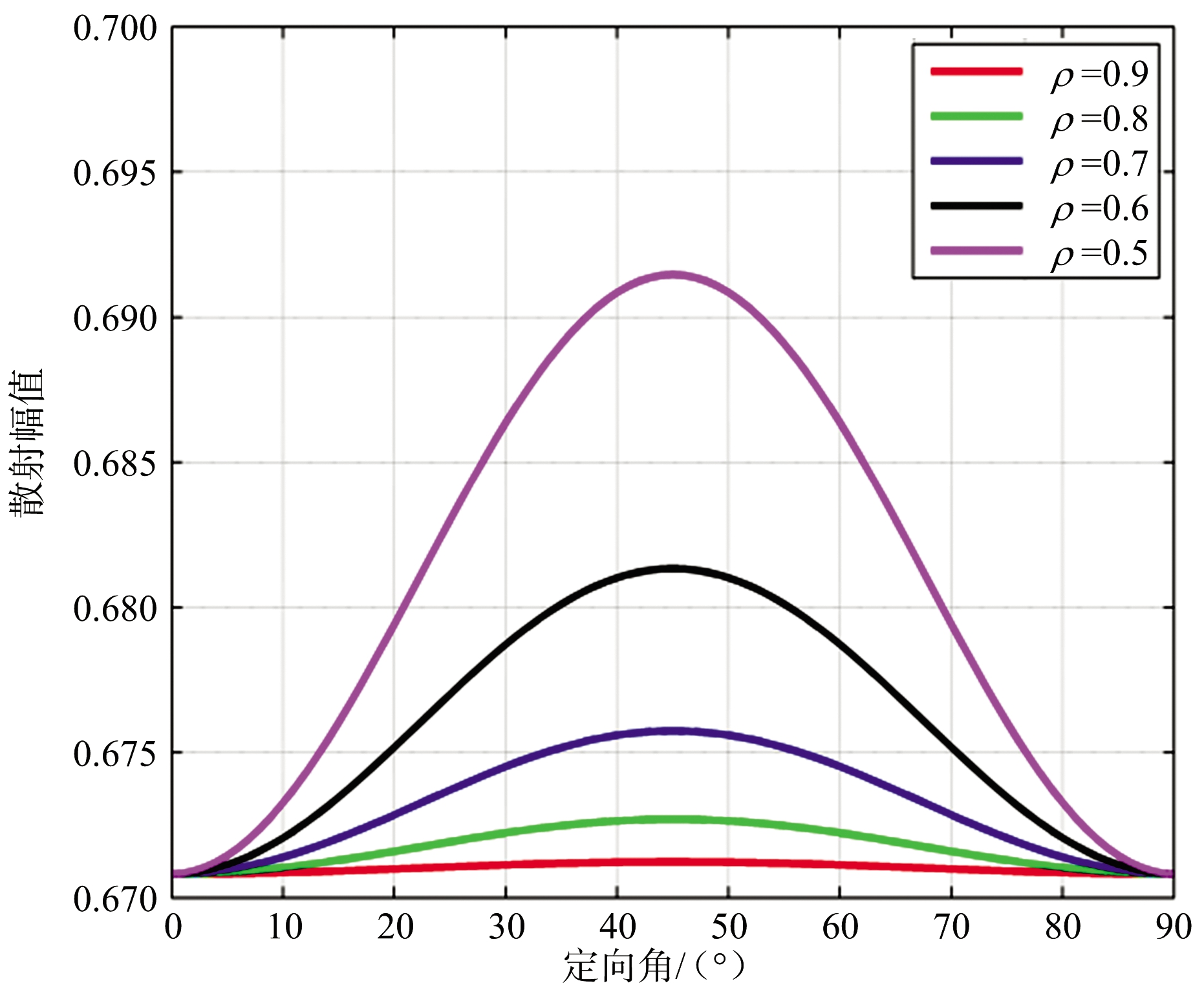
在轴比ρ小于1时，二面角、偶极子、圆柱体等目标椭圆极化散射矩阵中各极化复数散射幅度的幅值(绝对值)均随目标定向角和轴比变化，图2、图3和图4分别给出了二面角、偶极子、圆柱体等目标椭圆极化散射矩阵中各极化复数散射幅度的幅值(绝对值)随目标定向角、轴比变化曲线，从曲线图中可以看出，3种目标椭圆极化散射矩阵中各极化复数散射幅度的幅值(绝对值)随目标定向角变化的最大值均出现在45°定向角，当轴比大于0.7时，二面角LR、RL极化复数散射幅度的幅值随目标定向角变化最大值小于0.26，其他目标各极化复数散射幅度的幅值随目标定向角变化的最大值与轴比为1时幅值差均小于0.05，影响较小。
三面角：
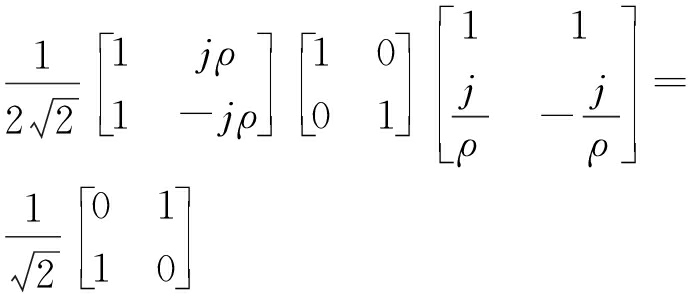
(23)
二面角：
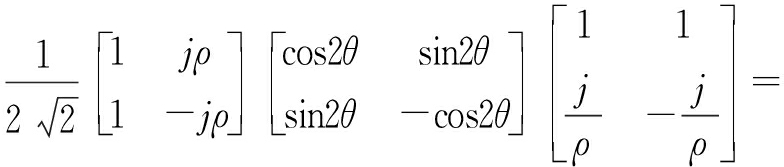
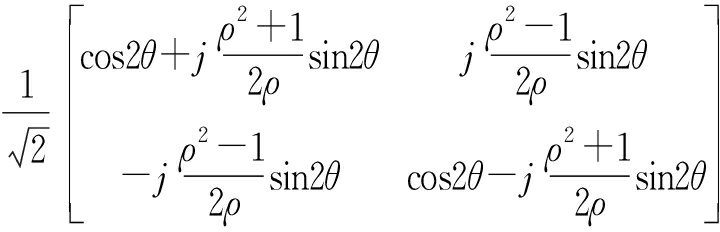
(24)
偶极子：
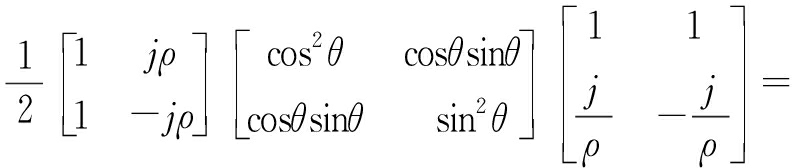
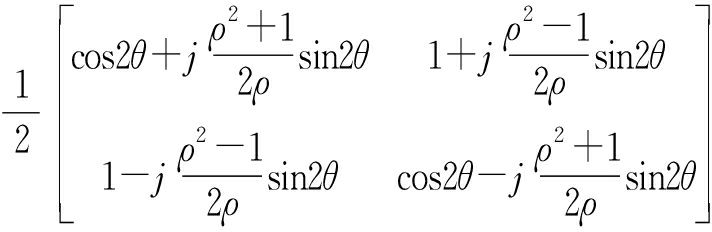
(25)
圆柱体：
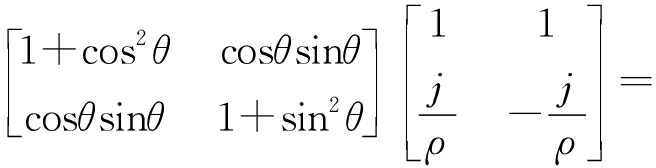
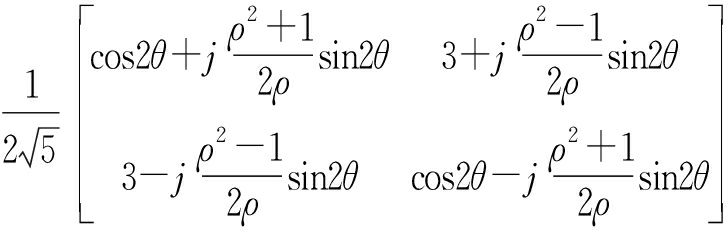
(26)
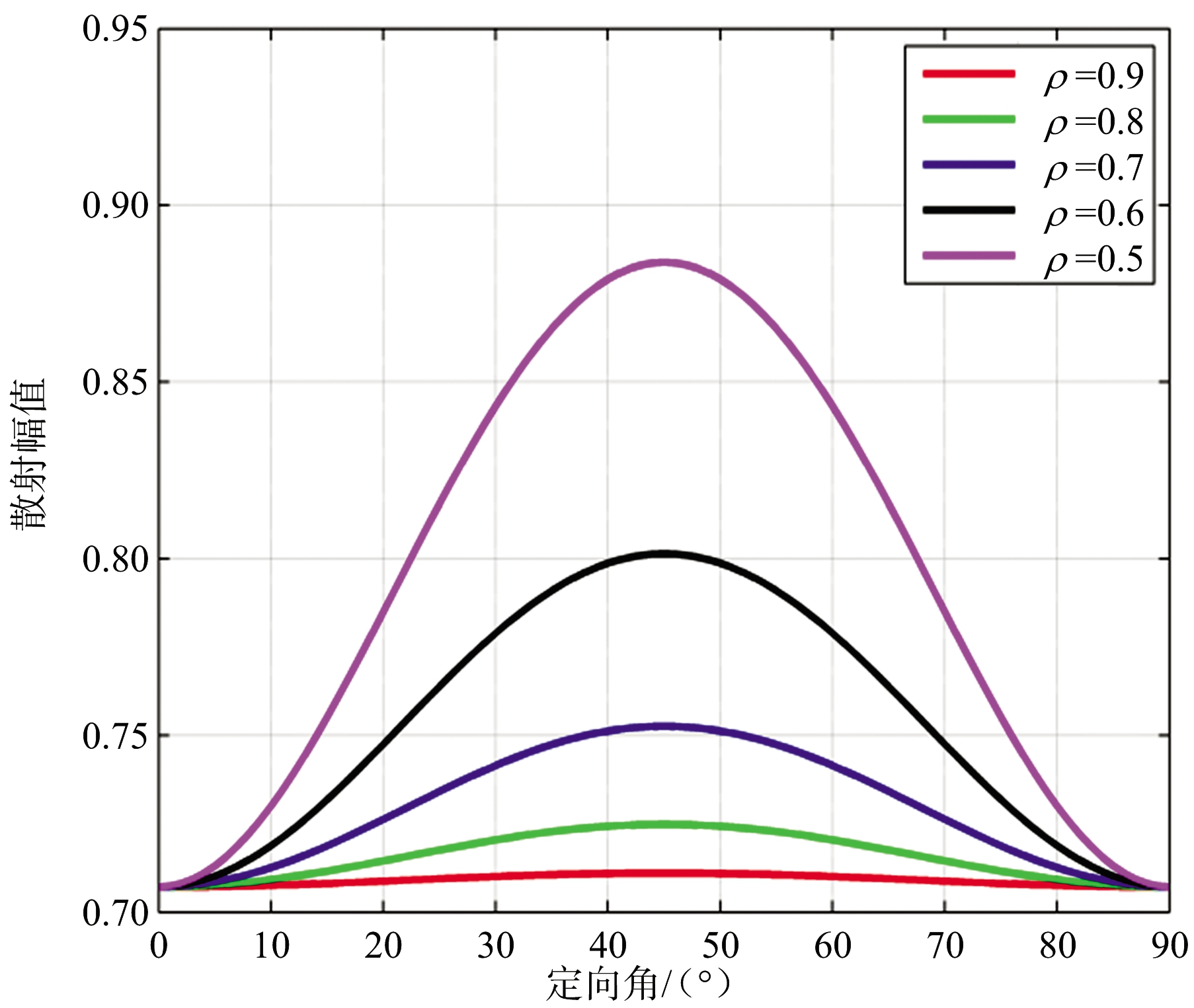
(a) LL、RR极化
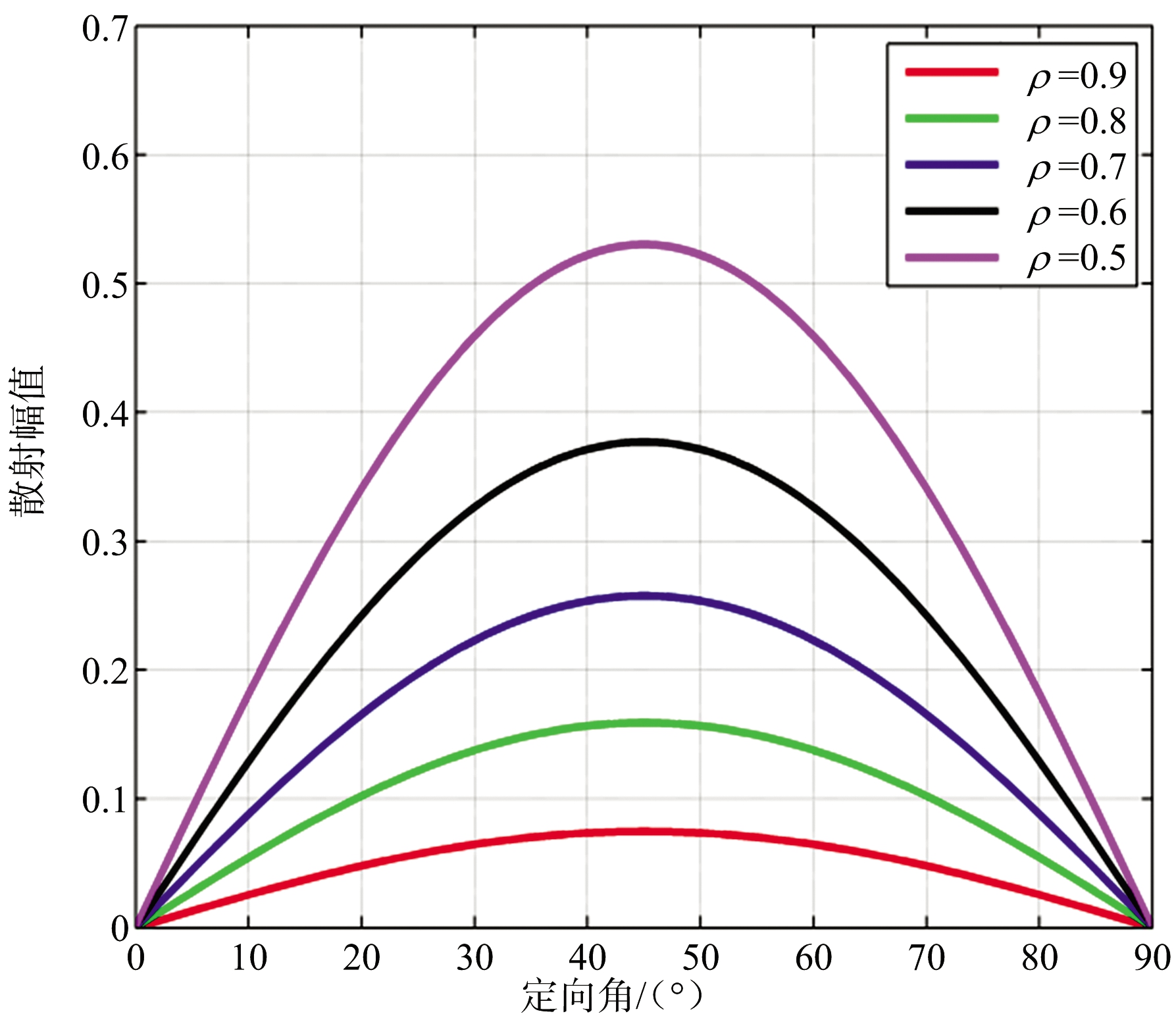
(b) LR、RL极化
图2 角复数散射幅度的二面幅值随目标定向角和轴比变化曲线
(a) LL、RR极化
(b) LR、RL极化
图3 偶极子复数散射幅度的幅值随目标定向角和轴比变化曲线
(a) LL、RR极化
(b) LR、RL极化
图4 圆柱体复数散射幅度的幅值随目标定向角和轴比变化曲线
3 圆/线极化SAR成像结果对比分析
图5～图8给出了圆极化SAR机载飞行试验成像结果，机载SAR系统工作于P波段，几何分辨率为1 m，具有线极化和圆极化成像能力，圆极化轴比大于0.8，根据前面分析结果，此时轴比对目标圆极化散射特性影响较小。
图5显示了一个公路斜拉索桥定向角在40°～70°范围内的斜拉索线极化SAR图像，从图像中可以看出，HH、HV、VV、VH 4个极化均显示出斜拉索图像，其中VV极化比HH极化显示出更多的斜拉索图像，这是由于大于45°定向角的斜拉索在VV极化中散射幅度比HH极化强，这与式(21)偶极子(线状体)线极化散射特性分析结果一致。图6是斜拉索桥圆极化SAR图像，从图中可以看出，LL、LR、RL、RR 4个圆极化图像中均显示出桥两边斜拉索图像，比线极化图像显示出更多的不同定向角斜拉索，这与式(25)偶极子(线状目标)圆极化散射特性分析结果一致。
图5 斜拉索桥线极化SAR图像
图6 斜拉索桥圆极化SAR图像
图7给出了一艘舰船线极化和圆极化SAR图像，由于甲板上面的舰楼结构中包含大量的二面角、三面角等强散射单元，因此在SAR图像中是舰船目标散射最强的区域。从图中可以看出，舰楼区域HH、HV、VV、VH 4个线极化均呈现连片的强散射特征，内部结构难以判读区分，由式(19)、式(20)分析可知，在同极化图像中舰楼结构中的三面角散射单元有强散射，而二面角散射单元在一定的定向角范围内交叉极化、同极化图像中均有强散射，两者叠加是造成舰楼区域线极化图像强散射连片的主要原因。而在LL、LR、RL、RR 4个圆极化图像中，舰楼同极化与交叉极化图像特征有较大区别，有利于舰楼结构特征判读识别。LL、RR极化舰楼周边散射较强，体现舰楼与甲板交界二面角散射特征；LR、RL极化在舰楼内有几个分散的强散射单元，体现三面角散射特征，与式(23)、式(24)分析结果一致。
图7 舰船目标线极化、圆极化SAR图像
图8是埋藏于沙堆下的圆柱目标圆极化SAR图像，其中圆柱目标由多个铁皮圆柱桶拼接而成，共拼接出5排分别埋藏于0～3 m深的沙堆下。由图中看出，LR、RL极化图像中最多可看到埋藏于1.8 m深沙堆中铁桶，而LL、RR极化图像中只能看到埋藏于1.2 m深沙堆中铁桶，LR、RL极化图像中圆柱体散射能量比LL、RR图像中圆柱体散射强，这与式(26)分析结果一致。
图8 埋藏于沙堆下的圆柱目标圆极化SAR图像
4 结束语
通过分析并经SAR成像试验验证表明，三面角、二面角、偶极子(线状体)、圆柱体等复杂目标结构组成单元在高分辨率圆极化SAR图像中各极化分量复数散射幅度的幅值(绝对值)不随目标定向角变化，其中偶极子(线状体)目标圆极化各极化散射分量幅值不仅不随目标定向角变化，而且各极化散射分量幅值、能量均衡，而在线极化SAR图像中偶极子(线状体)目标各极化散射分量幅值、能量均随目标定向角大幅变化，各极化散射分量幅值随定向角变化规律也不同；三面角与二面角反射器圆极化SAR极化散射幅值、能量呈现互补关系，一个交叉极化强，一个同极化强，而在线极化中三面角和二面角在一定的定向角范围内交叉极化、同极化图像中均有强散射，造成含有三面角和二面角结构的人造目标图像强散射点连片叠加，难以判读、识别；圆柱体圆极化SAR交叉极化(LR、RL极化)复数散射幅度的幅值是同极化(LL、RR极化)复数散射幅度的幅值的3倍，交叉极化具有较大的散射能量，而在线极化中圆柱体各极化散射分量幅值、能量均随目标定向角大幅变化。由此可见，与线极化SAR相比，高分辨率圆极化SAR图像更有利于复杂人造目标结构组成单元的检测以及图像判读、识别。
[1] 庄钊文，肖顺平，王雪松.雷达极化信息处理及其应用[M].北京：国防工业出版社，1999:49-294.
[2] CAMERON W L，LEUNG L K. Feature Motivated Polarization Scattering Matrix Decomposition[C]∥IEEE International Radar Conference, Arlington, VA, USA:IEEE,1990:549-557.
[3] TETUKO S S. Development of Circularly Polarized Synthetic Aperture Radar On-Board Unmanned Aerial Vehicle(CP-SAR UAV)[C]∥ 2012 IEEE International Geoscience and Remote Sensing Symposium, Munich, Germany:IEEE,2012:4762-4765.
[4] TETUKO S S, KOO V C, LIM T S, et al. Development of Circularly Polarized Synthetic Aperture Radar On-Board UAV JX-1[J].International Journal of Remote Sensing, 2017,38(8-10):2745-2756.
[5] ZHAO Ning，LU Jiaguo，GE Jialong，et al. Research of P Band Circular Polarization SAR [C]∥ 2016 CIE International Conference on Radar，Guangzhou, China:IEEE,2016:1-7.
[6] TORREALBA-MELENDEZ R, OLVERA-CERVANTES J L, CORONA-CHAVEZ A. Resolution Improvement of an UWB Microwave Imaging Radar System Using Circular Polarization[C]∥International Conference on Electronics, Communications and Computers， [S.l.]:[s.n.],2014:189-193.
