0 引言
作为阵列信号处理的研究难点与热点，宽带波束形成已广泛应用在雷达、无线通信、声呐和地质勘探等众多领域中。目前宽带波束形成最为流行的处理方法是空频处理和空时处理[1]。
空频方法是将宽带信号在频域划分子带，对每一个窄子带进行窄带波束形成后，再合为宽带信号[2]。此方法的优点是结构简单，但是需要在划分窄子带之前以及窄带频域处理后分别进行傅里叶变换(DFT)和反变换(IDFT)，缺点是需要同时处理数据块，不具有实时性。广义旁瓣对消(GSC)波束形成器和Frost空时波束形成器是空时处理常见的两种结构[3-4]，两者均可实现线性约束滤波，在波束形成与盲多用户检测中应用广泛。Frost[3]提出的线性约束最小方差(LCMV)自适应波束形成设计约束条件使期望信号无损失通过的同时，最大限度地抑制干扰与噪声。Compton[5]指出干扰抑制后的输出信干噪比(SINR)与抽头数和阵元数有关，空时维度越大则干扰抑制后输出SINR越大。
随着对抗干扰性能的要求增加，空时维度增加导致计算复杂度增大，难以保证信号实时性处理。稀疏布阵[6]与稀疏表示[7]问题得到广泛关注，从阵列中抽掉天线单元以降低其成本与计算量。但是宽带阵列信号稀疏问题并非线性，求解需要借助遗传算法，费时的同时不一定能求解出期望的最优解[8]。Compton的研究结果[9]表明，时域抽头数目一致时，SINR可达最大。基于该研究，在Frost结构基础上稍作改动构建一种高效的可行结构，抽头数减半，阵列个数保持不变，以降低空时维度，阵列分成奇、偶通道，奇、偶通道后的抽头延迟数目保持相同，根据通道的奇偶来选取奇偶延迟时间间隔。这种结构降低维度的同时能维持其抗干扰能力，即用较小的代价大大减轻了运算量的负担。
1 空时自适应干扰抑制结构
窄带信号情况下，纯空域滤波即可实现自适应波束形成。对于宽带信号，为满足权值和频率之间的关系，Frost[3]提出了空时自适应结构，如图1所示，在M个阵元后均接有N个抽头，Frost空时结构输出表达式为
(1)
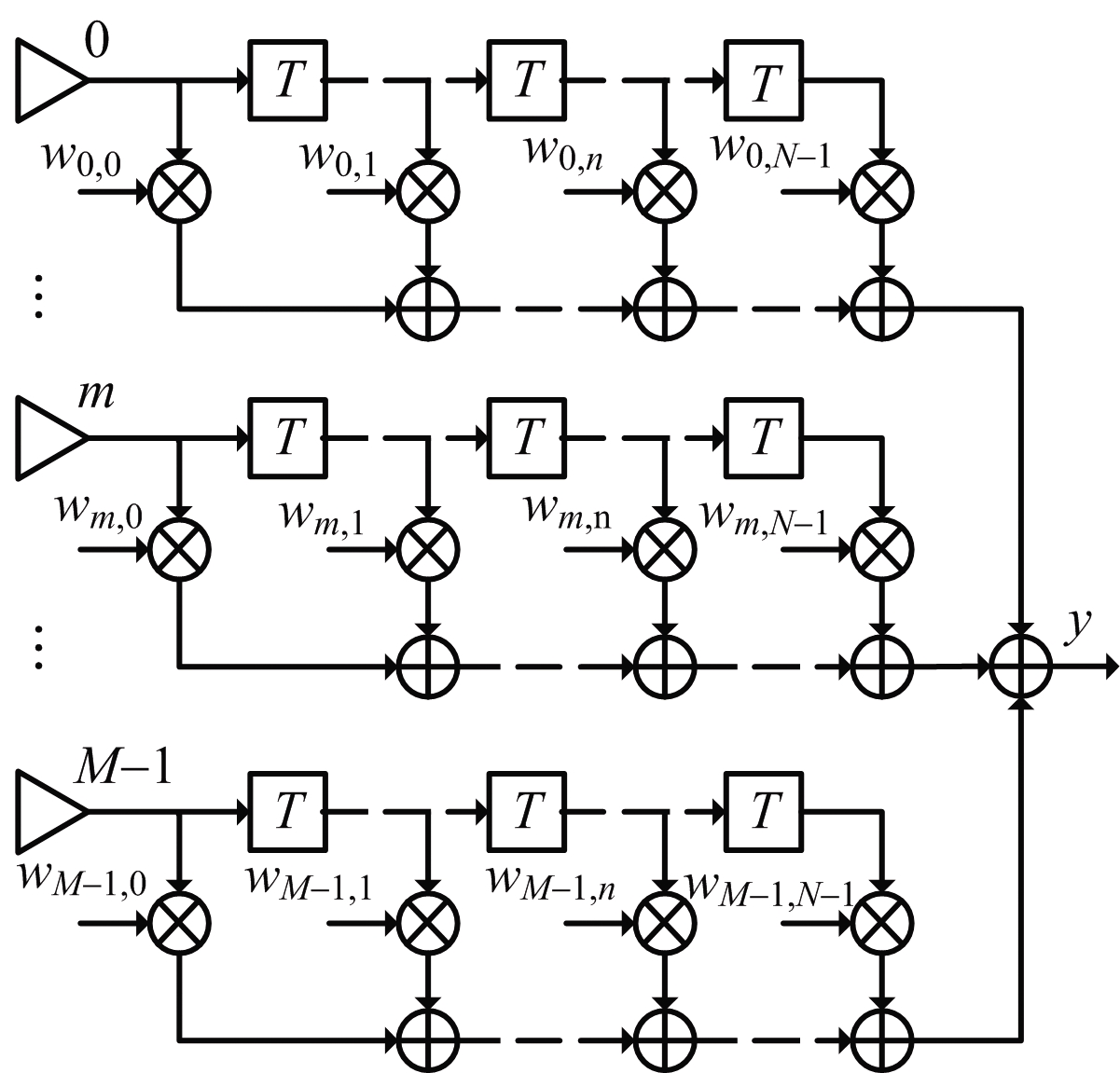
图1 Frost空时自适应波束形成结构
权值矢量w为MN维，定义为
(2)
式中，wk为第k阶抽头时延权值，wk=[w0k w1k … w(M-1)k]T，维度为N。
阵元接收信号为MN维，定义为
(3)
式中，xk(n)=[x0(n-k)x1(n-k)…xM-1(n-k)]T,k=0,1,…,N-1。
表达式(1)可写为
y(n)=wHx(n)
(4)
假设期望信号来自均匀线阵的正侧面，亦即入射角θ0=0。当此条件不满足时可通过机械旋转阵列或者数字时延等方式，将均匀线阵的法线方向对准期望信号，常见的实现方式是整数时延加分数阶时延滤波器(FDF)[10]。Frost结构最优化问题可描述为
(5)
式中，Rxx为MN×MN的信号相关矩阵，C为MN×N的线性约束矩阵[3]。当对准期望信号时，约束矩阵C则由向量1和0构成,约束向量f为N维的列向量：
f=[1,0,…,0]T
(6)
优化问题式(5)的最优自适应权值表达式为
(7)
2 改进的宽带自适应波束形成器
2.1 改进宽带自适应波束形成器结构
改进宽带自适应波束形成架构如图2所示，改进结构在常规Frost结构基础上抽头数减掉一半。改进结构共有M个阵元(M为偶数)，阵元的标号标为0,1,…,M-1；并按奇偶标号分为奇偶通道；偶通道阵元标号为0,2,…,M-2，奇通道阵元标号为1,3,…,M-1。横向FIR滤波器抽头数为常规Frost结构的抽头数的一半，即共有(N+1)/2个(N为奇数)。偶通道抽头延时为偶数倍时间间隔，分别为2T,4T，…,(N-1)T；奇通道的抽头延时为奇数倍时间间隔，分别为T,3T，…,(N-2)T。
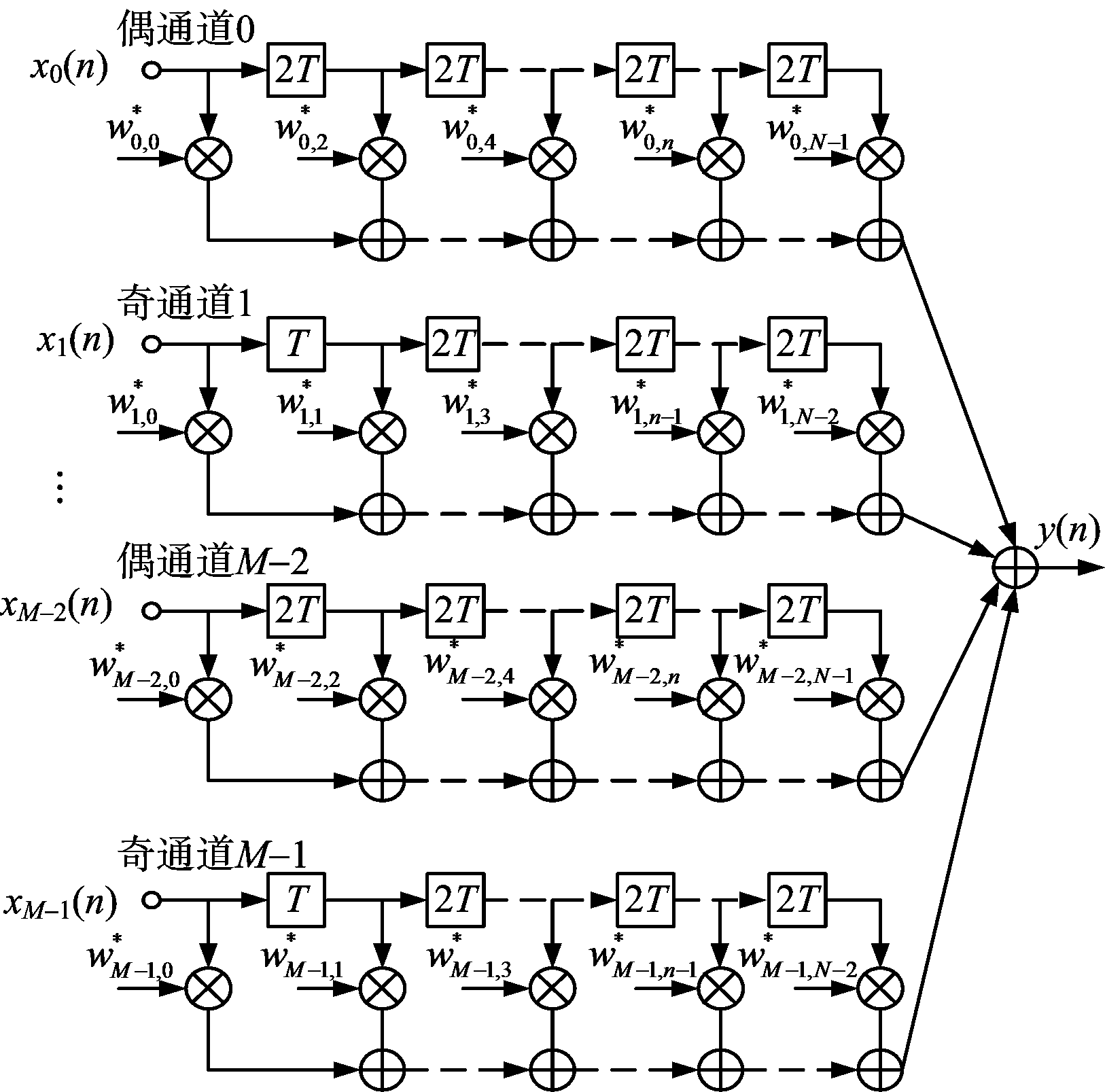
图2 改进空时波束形成结构
改进结构的变量用符号“-”以标示区分。所以改进结构自适应处理最终输出为
(8)
且m与k奇偶性一致。
改进结构优化问题描述如下：
(9)
为确保两种结构具有一致的频率约束性，令
但是因结构变化而导致约束矩阵发生变化，故需要重新构建。根据改进结构的特点将约束矩阵
重新构建为
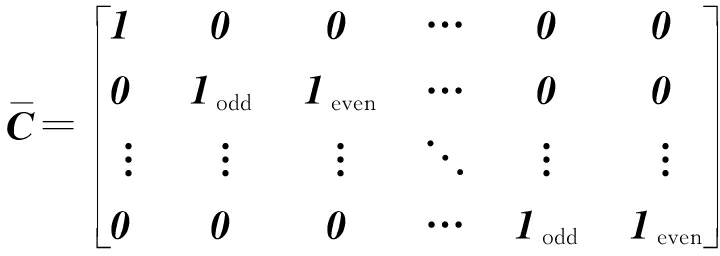
(10)
重构的线性约束矩阵维度为M(N+1)/2×N，其中1odd=[0 1 0 1 … 0 1]T，1even=[1 0 1 0 … 1 0]T，向量1与向量0同见文献[3]。
式(9)的最优解即改进结构的最优自适应权为
(11)
2.2 两种结构运算量对比分析
根据两种结构的最优权向量的表达式，式(7)和式(11)可以具体分析矩阵运算过程中的运算量；表1显示了Frost结构与改进结构分别所需的抽头个数、权值个数以及自相关矩阵维度、约束矩阵维度以及求逆的次数。
表1 Frost结构与改进结构的运算量比较
结构抽头个数权值个数矩阵Rxx维度矩阵C维度求逆次数Frost结构NMNMN×MNMN×N两次维度为MN×MN的矩阵求逆;一次维度为N×N的矩阵求逆改进抽头数减半结构N+1 /2MN+1 /2[MN+1 /2]×[MN+1 /2][MN+1 /2]×N两次维度为M(N+1)/2×M(N+1)/2的矩阵求逆;一次维度为N×N的矩阵求逆
由此可以看出，改进结构矩阵乘法运算与求逆运算的运算量明显低于常规Frost结构，故实时性也要优于常规Frost结构。
2.3 两种结构干扰抑制性能分析
改进结构在Frost结构的基础上进行了抽头数目减半能明显减小运算量并提高实时性，但是抑制干扰的能力是否减弱需要进一步分析。
阵元数为m快拍数为n时阵元接收信号表达式为
xm(n)=sm(n)+pm(n)+vm(n)
(12)
式中：sm(n)为期望信号，其中sm(n)=s(n- 2πf(m-1)dsinθ0/c)，θ0为期望信号的入射角，常规Frost结构一般假定θ0=0，故而sm(n)=s(n)； pm(n)为干扰信号，pm(n)=p(n)ejγm(θp)，θp为干扰角度；vm(n)为噪声信号。
将式(12)代入式(1)得到的波束形成输出为
y(n)=
(13)
令1=[1 1 … 1]T，β=[ejγ0 ejγ1 … ejγM-1]T，按照式(2)中权值向量wk的排列方式及定义，令
排列
与
可知a和b的维度均为N维，分别为
(14)
第n次快拍期望信号与干扰信号可表示为
s(n)=[s(n) s(n-1) … s(n-k) … s(n-(N-1))]T
p(n)=[p(n) p(n-1) … p(n-k) … p(n-(N-1))]T
(15)
如式(2)方式,重新排列噪声信号为
v(n)=[v0(n)Tv1(n)T … vN-1(n)T]T
(16)
且
vk(n)=[v0(n-k) v1(n-k) … vM-1(n-k)]T
(17)
阵列波束形成输出可表示为
y(n)=aHs(n)+bHp(n)+wHv(n)
(18)
输出信号的功率表达式为
P(θ)=E{|y(n)|2}=
E{y(n)yH(n)}=
aHE{s(n)sH(n)}a+
bHE{p(n)pH(n)}b+
wHE{v(n)vH(n)}w=
aHRssa+bHRppb+wHRvvw
(19)
式中，Rss维度为N×N，Rpp维度为N×N，Rvv维度为MN×MN。
SINR表达式为
(20)
由
的定义知道
常规结构约束条件
改进结构约束条件
又因约束一致性
综上
(21)
由此可知改进结构与Frost结构的期望信号功率是一样的，表达式为
(22)
Rss{1,1}表示Rss矩阵的第一行第一列元素。期望信号能量在单位时间内是恒定不变的，虽然改进结构抽头数减了一半，但是抽头数的数目并不会影响期望信号的能量，故改进结构期望信号的输出功率不变。
考虑权值不影响期望信号的情况下，优化问题理想化只使得干扰加噪声输出功率最小。由于干噪比通常比较大，故目标函数变为干扰噪声输出功率最小，式(5)的优化问题可转化为如下约束问题：
(23)
选取宽带白噪声作为干扰信号，fs=2B(fs为采样频率，B为信号的带宽)，式(23)可转化为
(24)
式中，
为干扰信号的功率。式(24)可转化为如下约束问题：
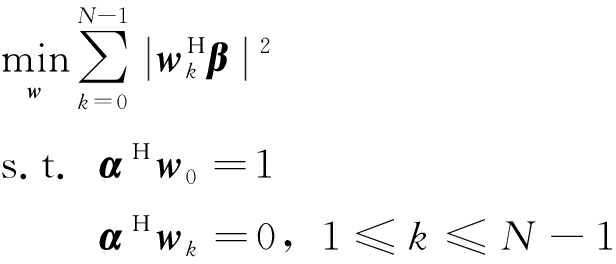
(25)
对约束条件分类，式(25)中约束问题进一步写为：
当k=0时，
(26)
当1≤k≤N-1时，
(27)
Frost结构的最优权为wopt k，0≤k≤N-1，有
改进结构
两种结构的干扰剩余功率相同需要N个线性方程组都有解。k=0时，
故
(28)
bopt 0=
(29)
式(28)为约束条件，式(29)为约束改进结构等于未改进结构的最小干扰值。满足M>2即有解。
当1≤k≤N-1时，由于改进结构分为奇偶通道，故以k=1(奇数阶)和k=2(偶数阶)为例，其他阶以此类推,k=1和k=2时得到下面的方程组：
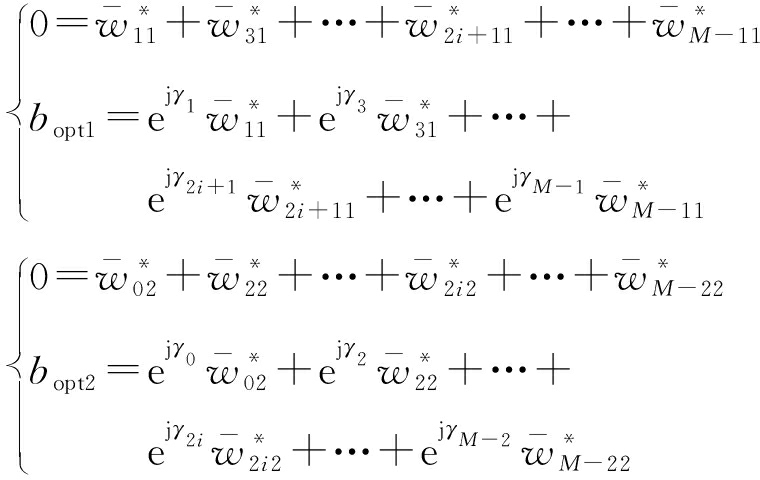
(30)
同样地M≥4时，式(30)表示的方程组才有解。综合上面方程组分析，当M≥4(M为偶数)且宽带干扰为噪声干扰时，两种结构具有一样的干扰剩余功率。宽带干扰为多个且不相关时，可根据式(28)、式(29)和式(30)类推。改进结构需要阵元数为2J来抑制J-1个干扰。
当存在单个宽带噪声干扰且M≥4(M为偶数)，改进结构与Frost结构具有相同的期望输出功率与干扰剩余功率，故两种结构在理论上的抗干扰能力是一致的，改进结构并没有因抽头数减半而导致抗干扰性能下降。
3 两种结构抗干扰性能对比仿真
仿真实验共分两组，两组实验的共同仿真条件：
阵列布阵方式为均匀布阵，阵元间距d=λ/2；期望信号：线性调频信号，θ0=0°，信噪比(SNR)为0 dB，载频f0=1.2 GHz，带宽B=400 MHz；干扰信号：宽带噪声信号，干扰角度θj=10°，干噪比(INR)为50 dB，带宽B=400 MHz；噪声信号：加性高斯白噪声，功率为0 dB。
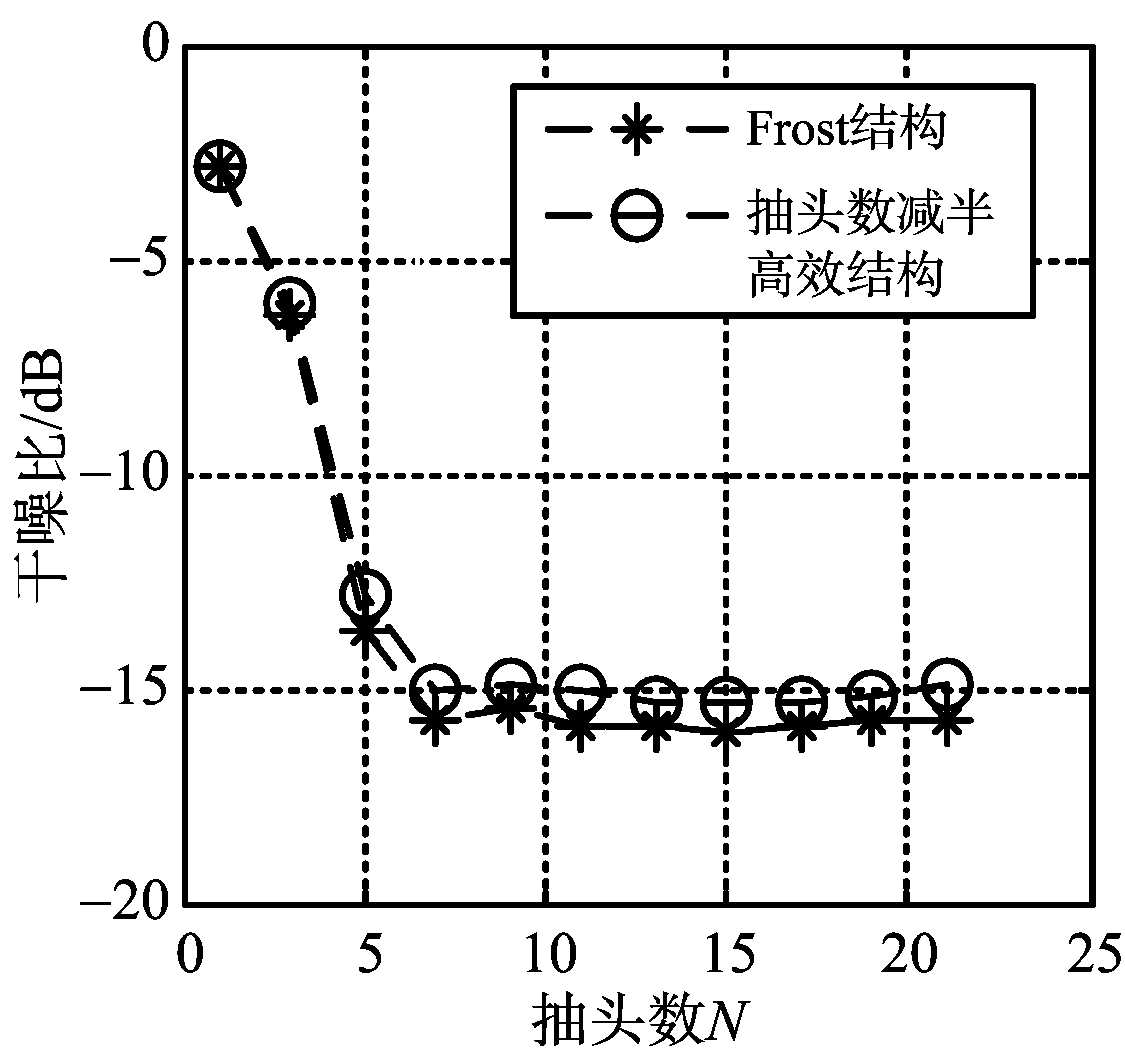
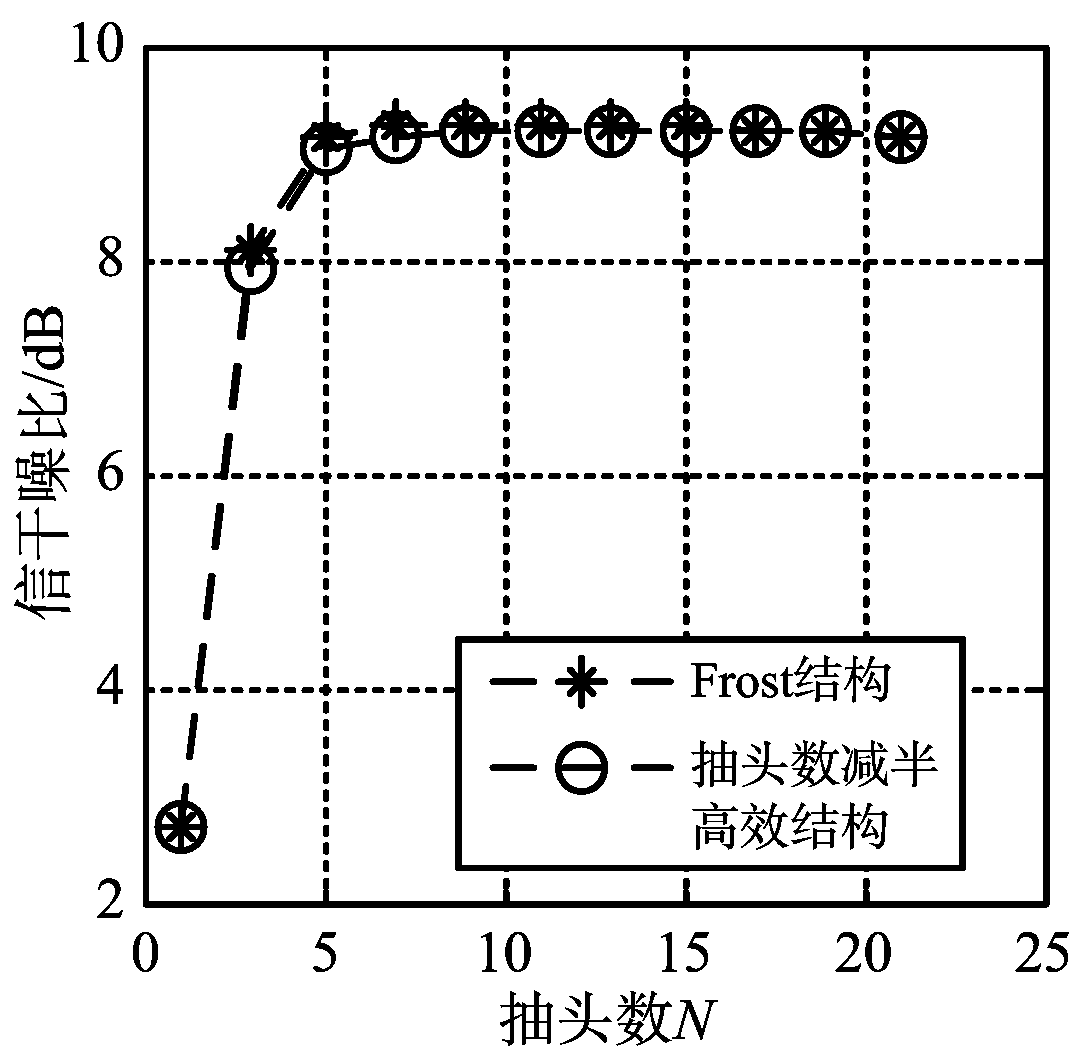
仿真实验一 对比两种结构抽头数对抗干扰能力的影响
保持阵元数不变，为M=12；分别选取奇数个抽头取值分别为1,3,…,21，测试不同抽头数在两种结构下抗干扰后的SNR(信噪比)、INR(干噪比)和SINR(信干噪比)，测试结果如图3所示。虽然两种结构抽头数不同，但表1显示矩阵
与
阶数依旧不变，为了便于对比依然记作N。
(a) 抽头数对信噪比影响
(b) 抽头数对干噪比影响
(c) 抽头数对信干噪比影响
图3 两种结构抽头数对抗干扰能力影响对比结果
实验表明，两种结构的信噪比(SNR)、干噪比(JNR)与信干噪比(SINR)测试结果均相差不大，这说明抽头数对两种结构干扰抑制性能大体相同，结构的不同导致之间存在微小的差别。
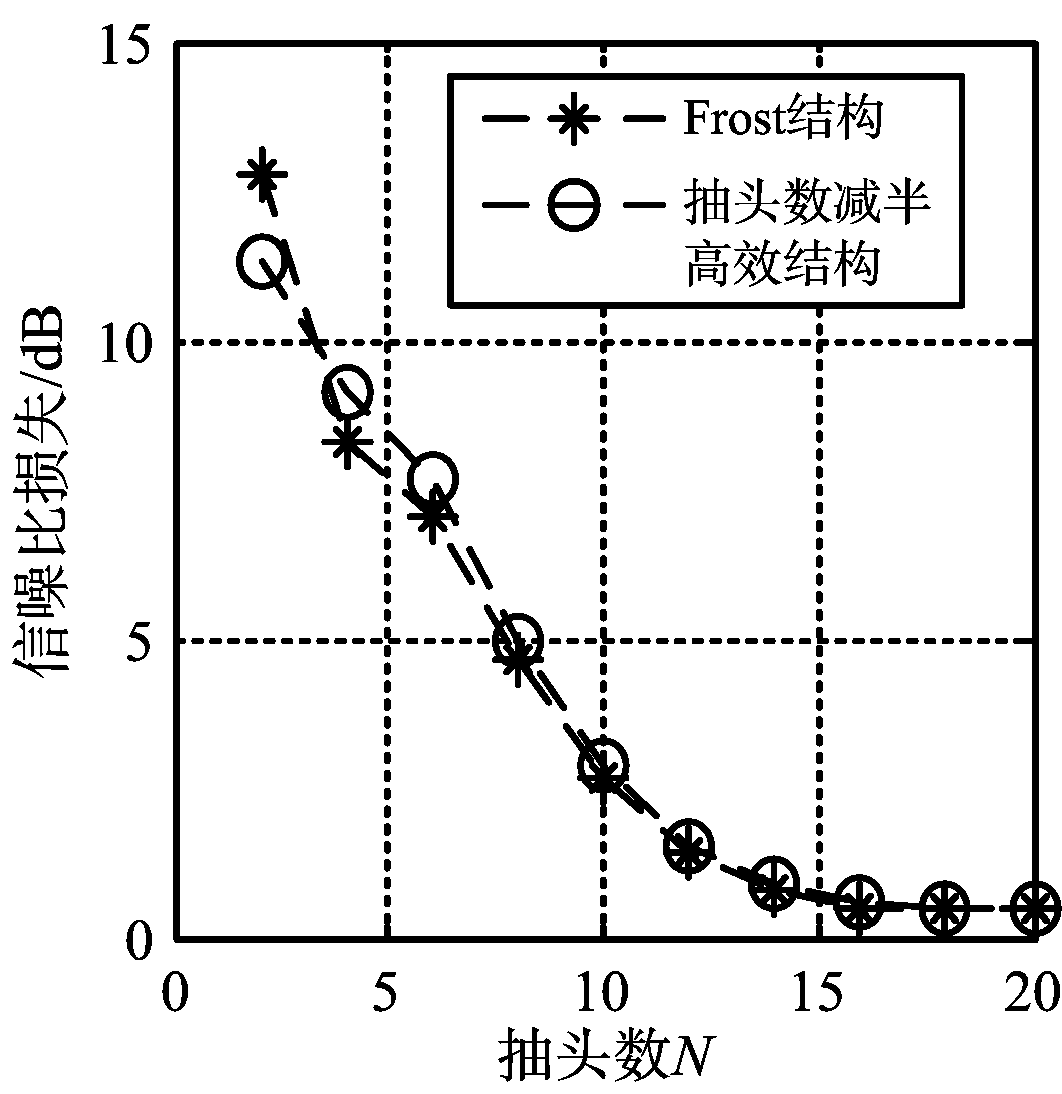
仿真实验二 对比两种结构阵元数对抗干扰能力的影响
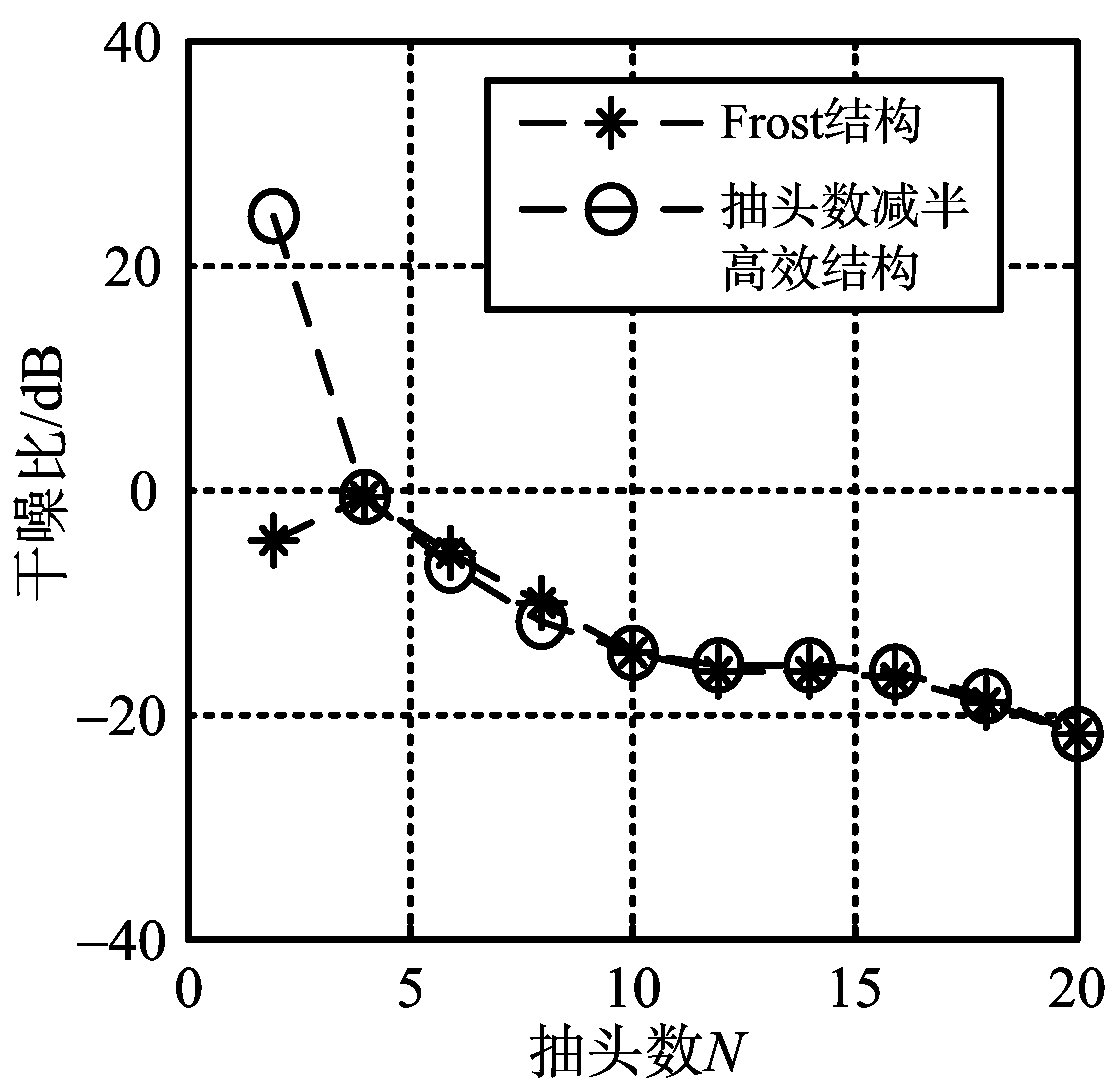
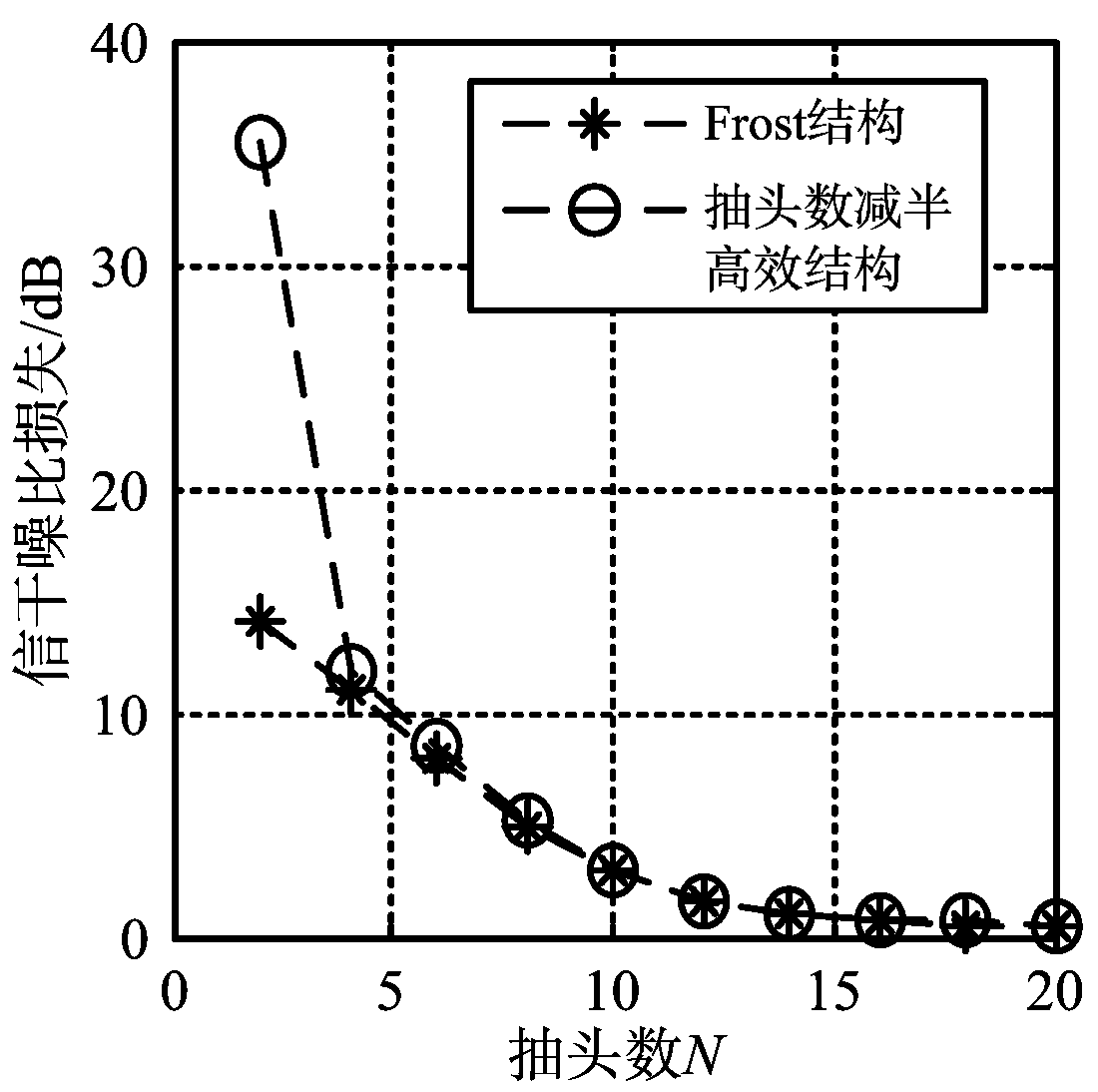
信噪比SNR与阵元个数M有关，测试时需要用信噪比损失和信干噪比损失来进行结果分析。信噪比损失等于不存在干扰时信噪比与存在干扰的信噪比之差，信干噪比为不存在干扰时信干噪比与存在干扰信干噪比之差。保持抽头数目不变，为N=7；分别选取M为偶数2,4,…,20，测试不同阵元个数在两种结构下抗干扰后的信噪比(SNR)损失、干噪比(INR)和信干噪比(SINR)损失结果,如图4所示。
(a) 阵元数对信噪比损失影响
(b) 阵元数对干噪比影响
(c) 阵元数对信干噪比损失影响
图4 两种结构下阵元数对抗干扰能力影响对比结果
图4(a)显示在不同阵元时Frost结构和改进结构的信噪比损失差异不大，证实了式(22)的正确性。常规结构和改进结构具有一样的期望输出功率，结构的不同导致了噪声抑制不同，故两者并不是完全重合。图4(b)显示M=2时常规结构远小于改进结构的干扰剩余功率，此时改进结构干扰抑制结果较恶劣，干噪比比较高，仍剩余24.03 dB的干扰；而当阵元个数M≥4时，两种结构干噪比几乎无差。图4(c)结果证实了式(28)、式(29)和式(30)的准确性，只是在M=2时，改进结构具有较差的抗干扰能力；M≥4时，抽头减半结构与Frost结构具有一样的剩余干扰功率。结构的不同导致了噪声抑制不同，故两者的干扰剩余存在轻微的差别。
通过两个对比仿真实验，当M≥4时，两种结构的抗干扰能力几乎无差，而改进结构在结构上减小一半抽头数目亦可实现与Frost结构一样的抗宽带噪声干扰能力，且运算量也大大减小。故而证实了该改进结构的可行性与高效性。
4 结束语
基于常规Frost空时结构，本文研究了一种改进的宽带结构，在结构上将抽头数目减至一半，权值数目与运算量可大幅下降。对改进结构抗宽带噪声干扰能力进行了理论推导，两种结构具有一样的输出期望信号功率，M≥4(M为偶数)时抗干扰之后具有一样的干扰剩余功率，细微差异是由于结构不同引起了噪声干扰抑制的不同。仿真对比结果显示改进结构并不会减弱抗干扰抑制性能，而是具有与Frost结构一样的抗干扰能力。故抽头减半的改进结构在保证抗干扰性能基础上降低了空时维度和运算量，可应用于空时处理中，具有一定的高效性和可行性，但是本文仅提出了一种高效的可降低维度与运算量的改进结构，并没有解决宽带结构的最优问题，今后可作进一步扩展研究。
[1] LIU Wei, STEPHAN W.Wideband Beamforming: Concepts and Techniques[M]. UK:John Wiley & Sons, 2010.
[2] CAO Yunhe, WANG Yu, WANG Shenghua, et al.Wideband Subarray Beamforming Based on Subband Decomposition[C]∥2014 IEEE China Summit & International Conference on Signal and Information Processing,Xi’an:IEEE, 2014:247-251.
[3] FROST O L.An Algorithm for Linearly Constrained Adaptive Array Processing[J]. Proceedings of the IEEE, 1972,60(8):926-935.
[4] GRIFFITH S L, JIM C. An Alternative Approach to Linearly Constrained Adaptive Beamforming[J]. IEEE Trans on Antennas and Propagation,1982,30(1):27-34.
[5] COMPTON R T. The Bandwidth Performance of a Two-Element Adaptive Array with Tapped Delay-Line Processing [J]. IEEE Trans on Antennas and Propagation,1988,36(1):5-14.
[6] HAMZA S A,AMIN M G. Optimum Sparse Array Receive Beamforming for Wideband Signal Model[C]∥2018 52nd Asilomar Conference on Signals, Systems, and Computers, Pacific Grove, CA, USA:[s.n.],2018:89-93.
[7] ZHAO Yonghong, ZHANG Linrang, ZHANG Juan,et al. Low Complexity Method for Wideband DOA Estimation Based on Sparse Representation Using Rotational Signal Subspace[C]∥2017 IEEE Radar Conference, Seattle, WA,USA:IEEE, 2017:460-463.
[8] HAWERS M B,LIU Wei. Sparse Array Design for Wideband Beamforming with Reduced Complexity in Tapped Delay-Lines[J]. IEEE/ACM Trans on Audio,Speech, and Language Processing,2014,22(8):1236-1247.
[9] VOOK F W, COMPTON R T. Bandwidth Performance of Linear Arrays with Tapped Delay-Line Processing [J].IEEE Trans on Aerospace Electron System, 1992, 28(3):901-908.
[10] JOHANSSON H, EGHBALI A. Two Polynomial FIR Filter Structures with Variable Fractional Delay and Phase Shift [J].IEEE Trans on Circuits and Systems I:Regular Papers, 2014, 61(5):1355-1365.
