0 引言
与相控阵相比，频率分集阵列(Frequency Diverse Array, FDA)在阵元间引入了很小的载频差(即频率间隔)，使得FDA可将波束指向相同角度、不同的距离单元，即会形成距离-角度耦合波束[1]，然而，由于FDA雷达的天线方向图在距离维上的周期性，导致在探测空间内很容易形成多个栅瓣，主波束空间能量分散严重，干扰落在栅瓣的几率大，极大地影响了其抗干扰的性能和目标探测能力。
当FDA采用对数[2]、平方或立方[3]、正弦[1]等非线性形式的频率间隔以及整数频偏策略[4]时，虽然可去除栅瓣，形成单峰值的“点”状波束，但这种波束的距离维副瓣很高，抗距离依赖性干扰性能和目标距离维估计精度都很差，且对于频率误差很是敏感。为此，Xiong等提出可采用遗传算法优化频率间隔的设置[5]，Wang提出了一种基于球函数的波束综合方法[6]，Shao和Gao等提出了一种多载频FDA雷达即各阵元发射频率为步进多载频信号的波束形成方法[7-8]，它们都能够在目标位置处形成点状单峰值波束，去除栅瓣，降低了副瓣，但形成的方向图的距离维主瓣宽度较大，计算量大，并且均只适用于发射，也没有得到其发射方向图的闭合表达式，对于回波的接收也没有展开深入研究。
考虑多输入多输出(Multiple-Input Multiple-Output, MIMO)雷达在目标探测、参数估计、空间分辨率等方面具有的许多优势[9]，本文结合FDA阵列与MIMO雷达，提出了一种基于子阵的频率分集多输入多输出(Multiple-Input Multiple-Output with Frequency Diverse Array, FDA-MIMO)雷达去栅瓣的方法，推导出基于子阵的FDA-MIMO雷达天线方向图闭合表达式，指出FDA-MIMO雷达采用子阵去除栅瓣和提高距离维分辨率的原理。仿真显示，与采用线性频率间隔的传统方法相比，该方法不仅去除了栅瓣，也使得距离维主瓣宽度更窄，提高了距离维分辨率。
1 FDA-MIMO雷达信号模型
假设FDA-MIMO雷达是采用N个阵元的等距线阵，d为阵元间距，假设传输的信号是远场窄带信号，其与阵列法线方向夹角为θ，选定第一个阵元为参考阵元，从散射点到第一个阵元的距离为r，其阵列模型如图1所示。
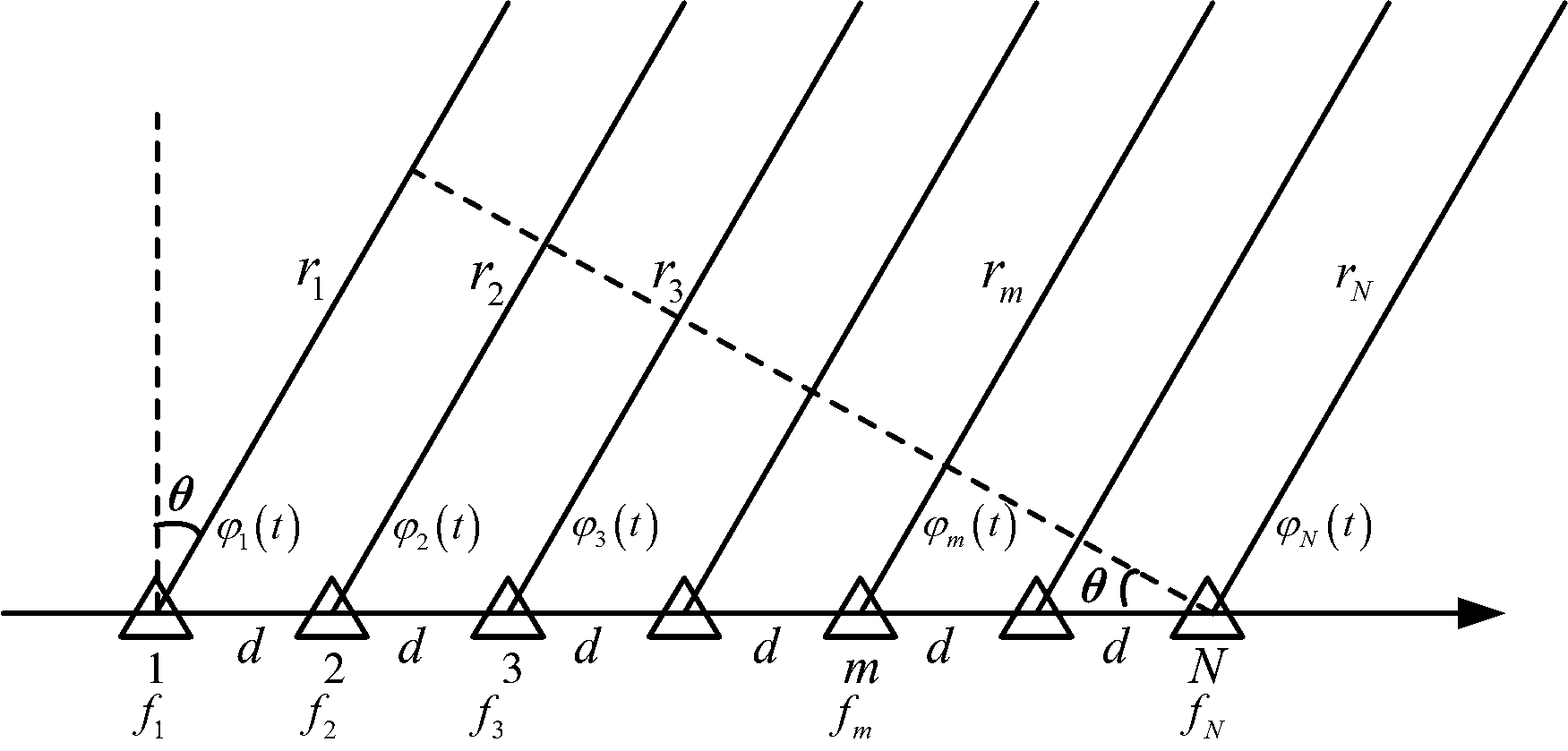
图1 FDA-MIMO信号模型
第m个阵元通道的发射频率为
fm=f0+(m-1)Δf m=1,2,…,N
(1)
式中,f0和Δf分别表示第一个阵元载波频率和相邻两个阵元之间的频率间隔。考虑为远场窄带信号，则第m个阵元与参考阵元的相位差为
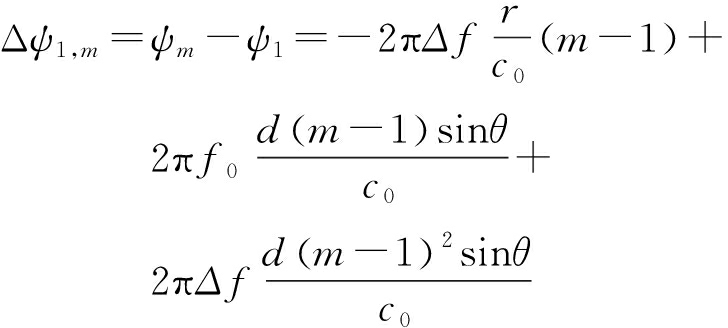
(2)
由式(2)可以看出，FDA-MIMO雷达发射信号的相位差不仅与空间角有关，同时与传播距离有关，因此，FDA-MIMO雷达天线方向图具有距离-角度依赖性。注意到，式中第3项为阵元数的二次函数，当频率间隔远小于载频，即NΔf≪f0时，相比较前两项带来的相位差可忽略不计。
由于FDA-MIMO雷达不同阵元发射信号的包络互相正交，则有
(3)
式中，φm(t)为第m个阵元发射信号的包络，T为脉冲发射持续时间，( )*表示共轭计算，τ为任意的延迟时间。
第m个阵元接收的频率为fn的信号可表示为
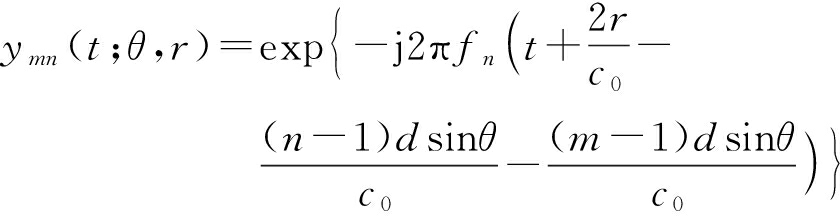
(4)
整个阵列接收的目标信号表示为
Y(θ,r)=ξ[y11,y12,…,y1N,y21,…，yNN]T=
ξb(θ)⊗a(θ,r,Δf)=ξv(θ,r,Δf)
(5)
式中，ξ为目标信号的幅度信息，上标T表示转置，⊗为Kronecker积，v(θ,r,Δf)为阵列导向矢量，a(θ,r,Δf)为发射导向矢量，b(θ)为接收导向矢量，具体表达式如下[10]：
a(θ,r,Δf)=aθ(θ)⊙ar(r,Δf)=
(6)
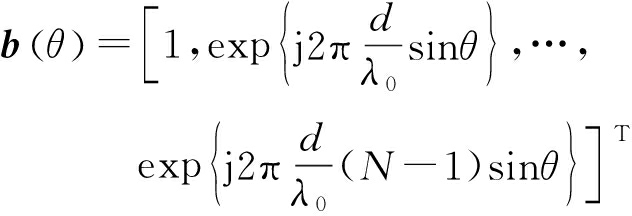
(7)
假如有一目标位于(θs,rs)，为了让FDA-MIMO雷达波束指向目标所在位置(θs,rs)，需要在FDA-MIMO雷达接收时进行波束加权，接收阵元通道加权矩阵为
(8)
式中，
(9)
为第m个阵元接收通道的第n个频率的加权值，有
(10)
此时，接收到的第m个阵元发射的第n个频率的信号可以表示为
(11)
不考虑幅度信息，最后形成的方向图可以表示为
Pr(t;θ,r)=wr(θs,rs)Hy(t;θ,r)=
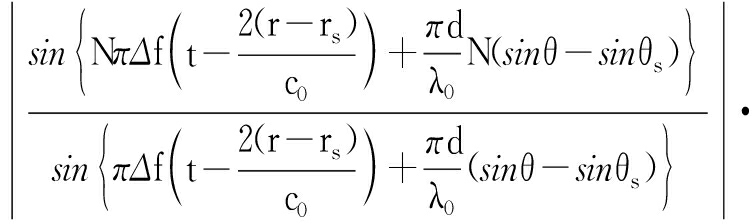
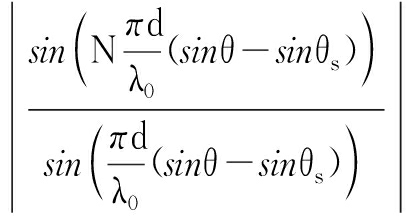
(12)
式中，y(t;θ,r)为到达目标位置处的信号矢量。
由式(12)取极值可得FDA-MIMO雷达双程方向图的峰值点，有下式：
(13)
式中，k,p为任意整数。
为避免角度维出现栅瓣，一般取d=λ0/2，使得
若扫描角与期望目标所在的角度稍有不同，就会很难满足条件
进而使得式(13)无解，此时在该扫描角上没有波束峰值，所以FDA-MIMO雷达波束峰值一定位于目标角度上。不考虑时间因素，进而可得
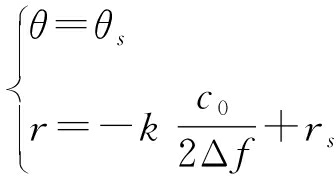
(14)
由上式可知，当d=λ0/2时，FDA-MIMO雷达波束在角度上与频率间隔Δf无关，没有周期性，即在角度维没有栅瓣，但在距离上具有周期性，即存在栅瓣，且栅瓣出现的距离周期为c0/2Δf，频率间隔越大，距离周期越短，在探测范围内形成的栅瓣越多，特别是当干扰落在栅瓣时，就会使得输出SINR急剧下降[11]。
根据栅瓣的距离周期性可以通过限制频率间隔的选取范围，使得FDA-MIMO雷达在探测范围内没有栅瓣[12]，有
Δf≤c0/2Rmax
(15)
式中，Rmax为FDA-MIMO雷达探测的最远距离。由上式可知，虽然可以解决距离维栅瓣的问题，但雷达探测越远，频率间隔选取的范围越小，而距离维主瓣宽度为c0/NΔf[13]，频率间隔越小，距离维主瓣宽度越大，距离维分辨率越低。
为解决这个矛盾，本文提出基于子阵的FDA-MIMO雷达去栅瓣的方法，在去除FDA-MIMO雷达栅瓣的前提下，提高了距离维分辨率。
2 基于子阵的FDA-MIMO雷达去栅瓣原理
如图2所示，假设FDA-MIMO雷达阵列为N个阵元组成的线阵，阵元间距为半个波长，整个阵列分成k个子阵，前N1个阵元构成子阵1，采用频率间隔Δf1；依次类推，中间Ni个阵元构成子阵i，采用的频率间隔为Δfi，最后Nk个阵元构成子阵k，采用的频率间隔为Δfi，且N=N1+…+Ni+…+Nk。
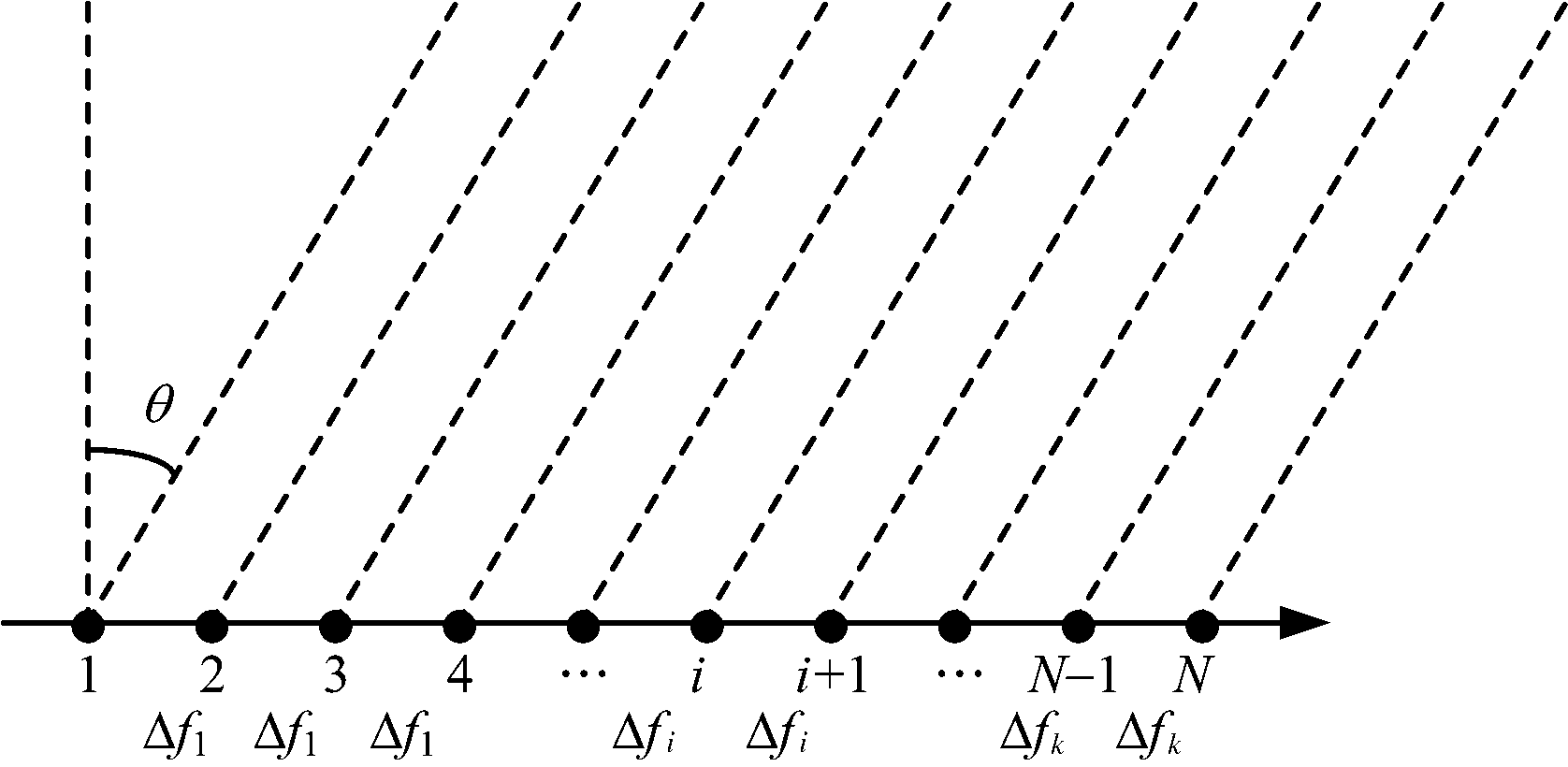
图2 FDA-MIMO雷达子阵模型
阵列带宽为
(16)
假设目标位于(θs,rs)，此时，不考虑时间和幅度因素，则整个阵列的双程方向图为
|P(θ,r)|=
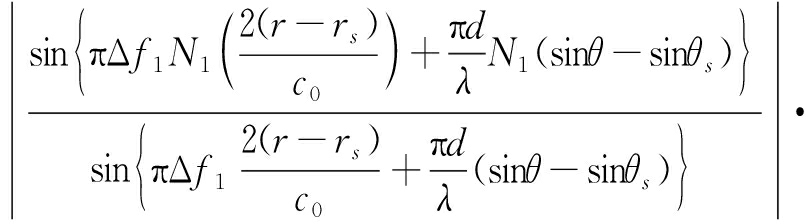
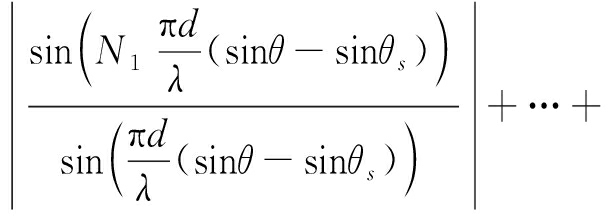
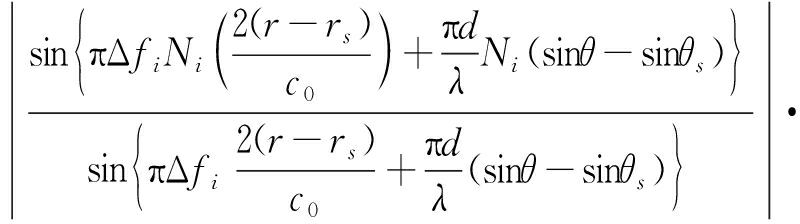
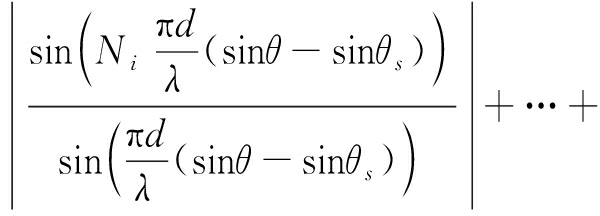
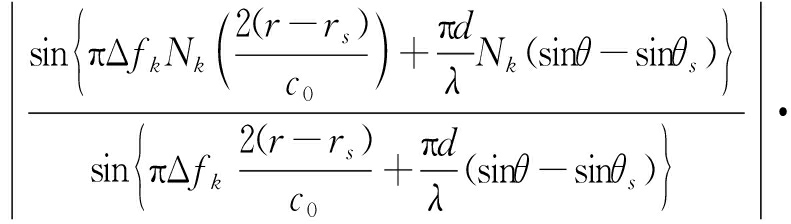
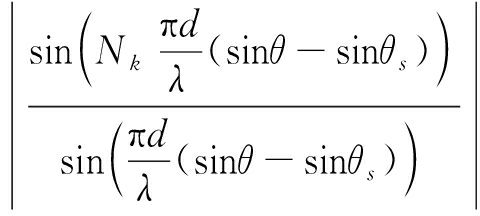
(17)
从上式很明显可以看出，最后合成的方向图是k个子阵方向图的叠加。可通过使所有子阵方向图的栅瓣位置尽量不重合来去除FDA-MIMO雷达大频率间隔产生的栅瓣，同时增大频率间隔来提高距离维分辨率。
以任意子阵i形成的方向图为例进行分析，有其方向图
|P(θ,r)|=
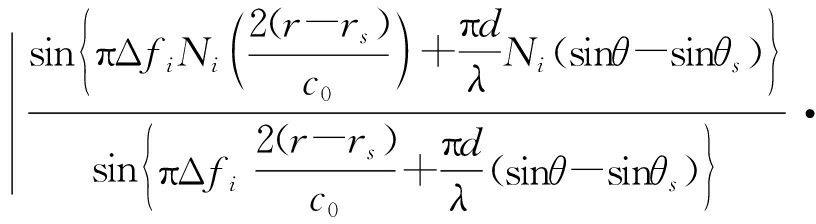
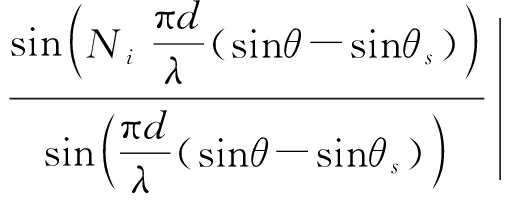
(18)
式(18)取极大值时，对应子阵i形成的方向图栅瓣，有
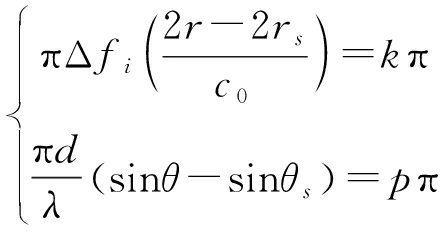
(19)
式中，k,p为任意非零整数。参照式(13)分析可知，子阵i方向图的栅瓣只能位于目标所在角度，距离维方向图栅瓣位置为
(20)
同理可知，任意子阵j的距离维栅瓣位置为
(21)
式中，q为任意非零整数。要使这两个子阵形成的栅瓣不能在同一个位置处叠加，有
(22)
化简可得
(23)
由式(23)可知，要使所有子阵方向图的栅瓣不重合是不可能的，但是可以通过选取互质的大频率间隔，来使得满足式
时，k和q取值都很大，此时重合的栅瓣与主瓣的距离就会大于最远探测距离，即
(24)
此时，虽然子阵的栅瓣会有部分重合，但重合的位置位于FDA-MIMO雷达探测范围外，即在探测范围内去除了栅瓣，不仅如此，由于采用的子阵频率间隔较大，所以合成的方向图距离维主瓣宽度更窄，距离维分辨率更高。
FDA-MIMO雷达距离维方向图主要是由阵元个数与频率间隔之积即带宽Bp确定的，带宽越大，距离维主瓣宽度越窄，距离维副瓣越低[13]。在FDA-MIMO雷达总阵元数一定时，若划分的子阵数越多，为满足子阵需采用互质大频率间隔的条件，会导致采取的频率间隔变多、变大，整个阵列带宽变大，合成的距离维副瓣电平会进一步降低。需要指出的是，由于子阵距离维副瓣电平本身较高，阵列合成的方向图副瓣是子阵方向图栅瓣与栅瓣或副瓣的叠加，所以整个阵列合成方向图的副瓣会随着子阵个数的增加降低到一定程度后，不会再降低。
3 仿真结果与分析
参数设置：FDA-MIMO雷达共有120个阵元，分成4个阵元数为30的子阵，假设探测最远距离为200 km，目标位于(0°,100 km)。子阵频率间隔依次为7，11，13，17 kHz；根据限定频率间隔选取范围去除栅瓣的方法(以下简称常规方法)，选取频率间隔Δf=c/2Rmax=750 Hz。两种方法的仿真图分别如图3和图4所示。
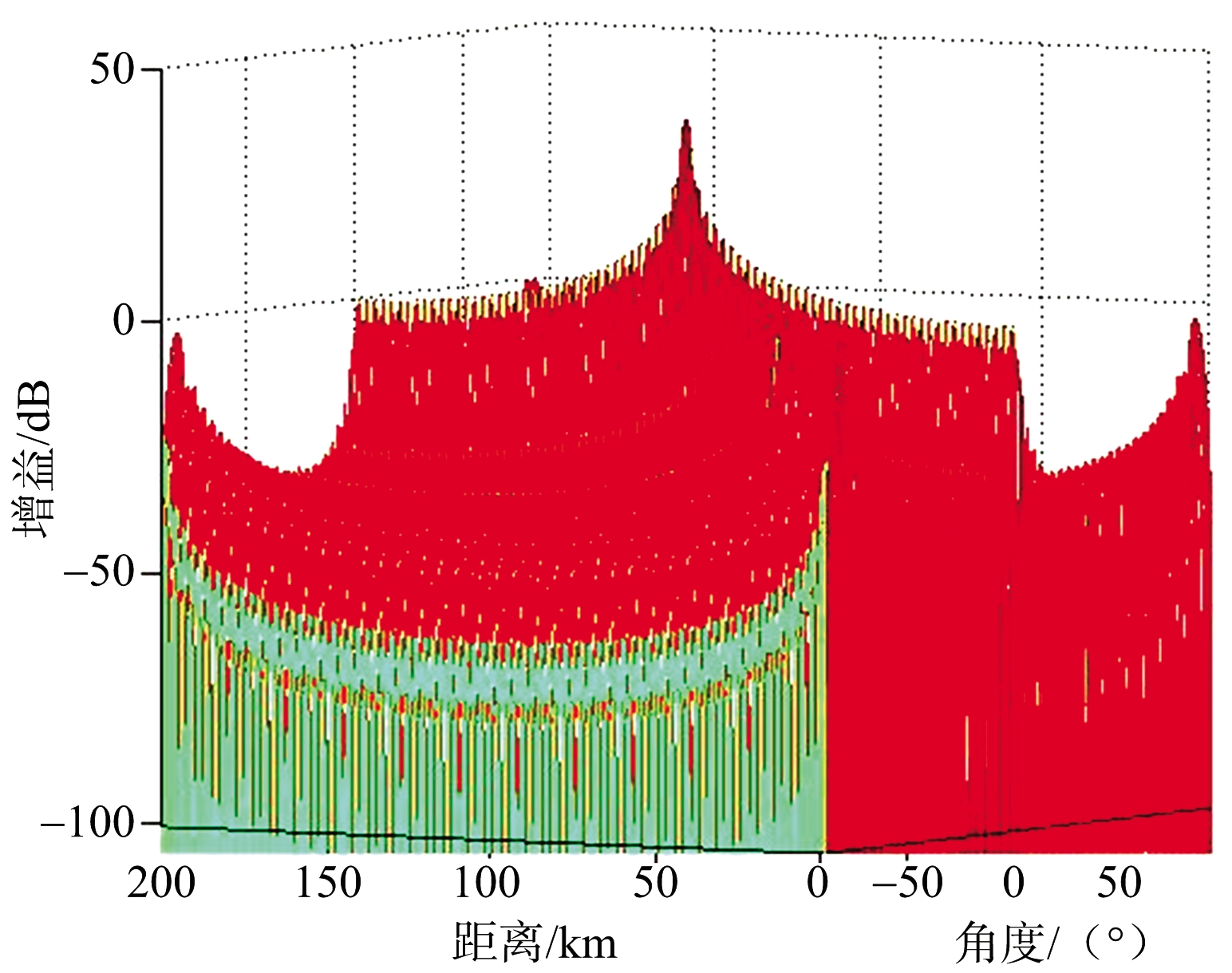
(a) FDA-MIMO雷达方向图
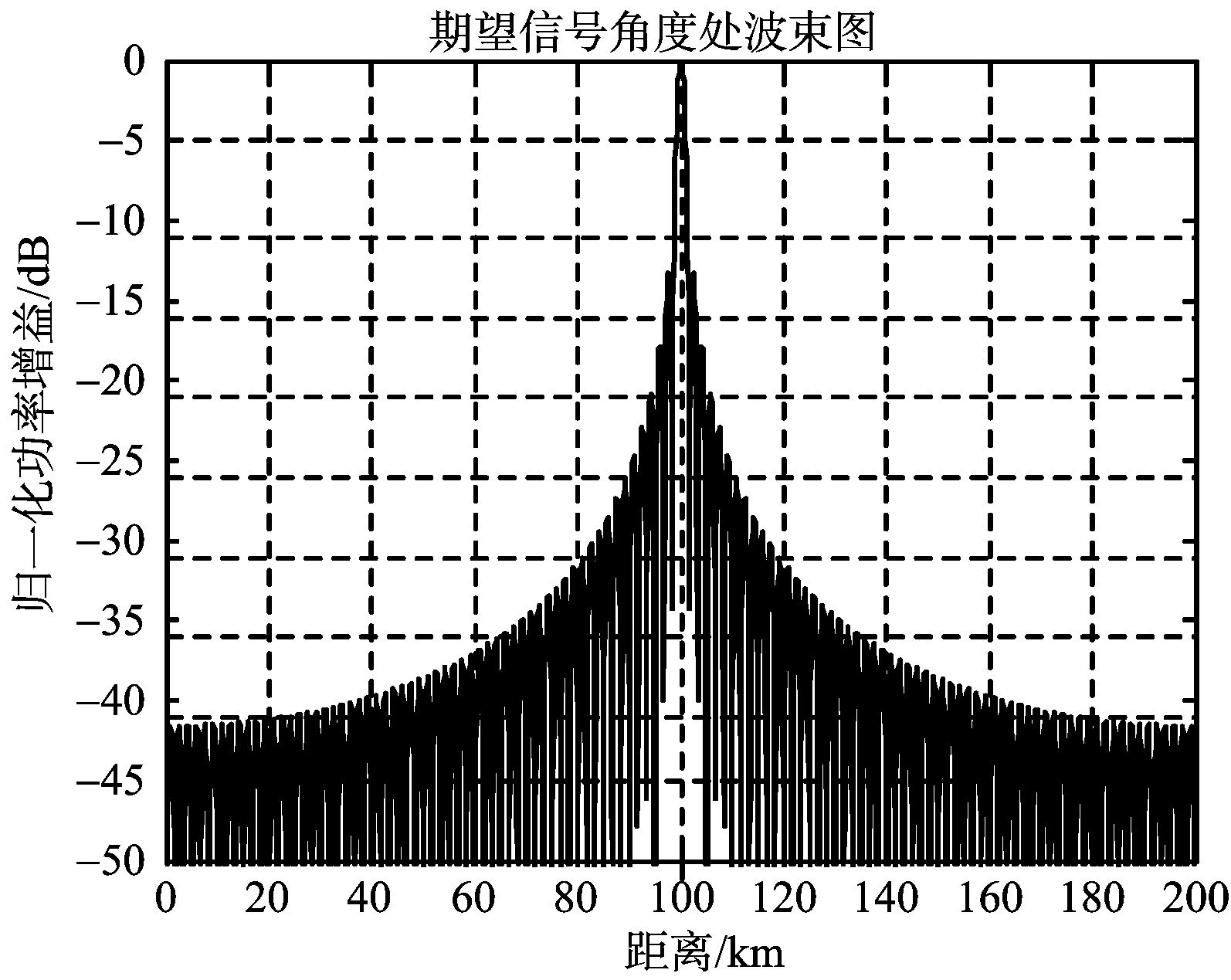
(b) 0°处切面(距离维)方向图
图3 常规方法仿真图
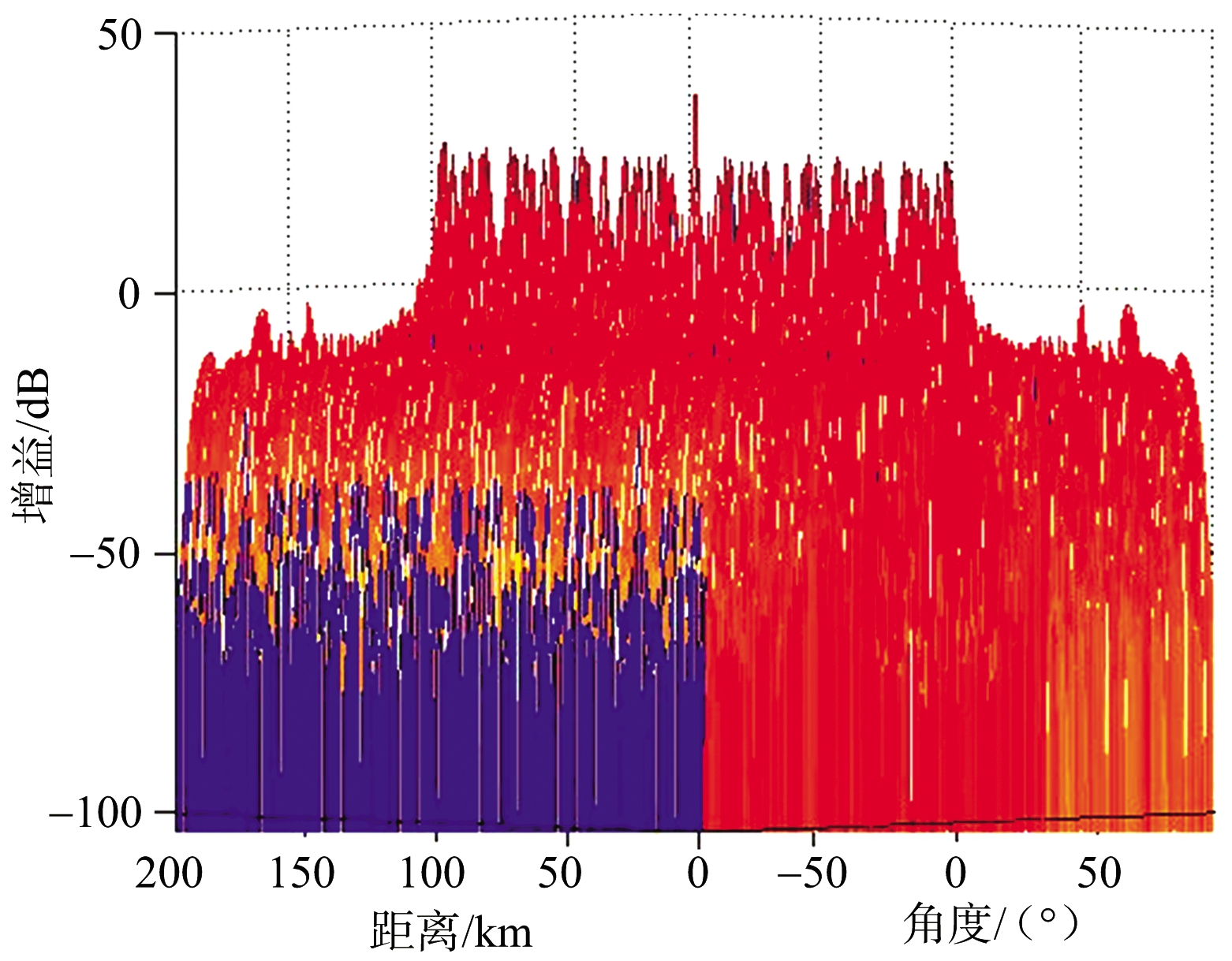
(a) FDA-MIMO雷达方向图
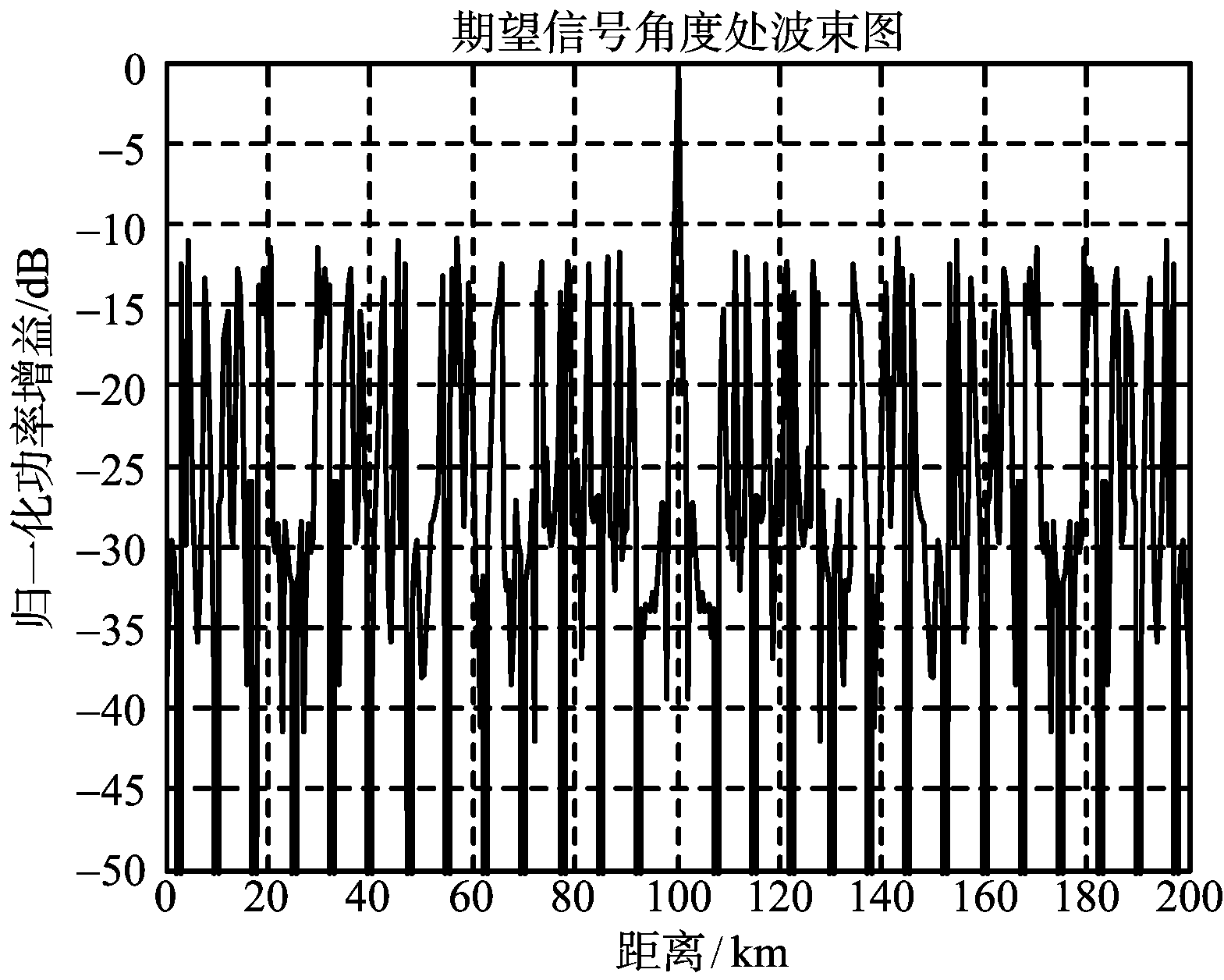
(b) 0°处切面(距离维)方向图
图4 基于子阵法仿真图
从图3和图4可以发现，本文提出的基于子阵去栅瓣的方法与常规方法均可以在探测范围内去除栅瓣，形成指向目标位置处的点状单峰值波束，而本文方法与常规方法相比，距离维主瓣宽度更窄，分辨率更高，但可以发现本文方法形成的波束副瓣在-12 dB左右，明显比常规方法形成的副瓣高。
改变FDA-MIMO雷达阵元为120个，分成6个子阵，子阵频率间隔改为7，11，13，17，19，23 kHz，其他参数不变，仿真图如图5所示。不改变参数设置，采用切比雪夫加窗(-30 dB)处理，两种方法0°处切面(距离维)方向图如图6所示。
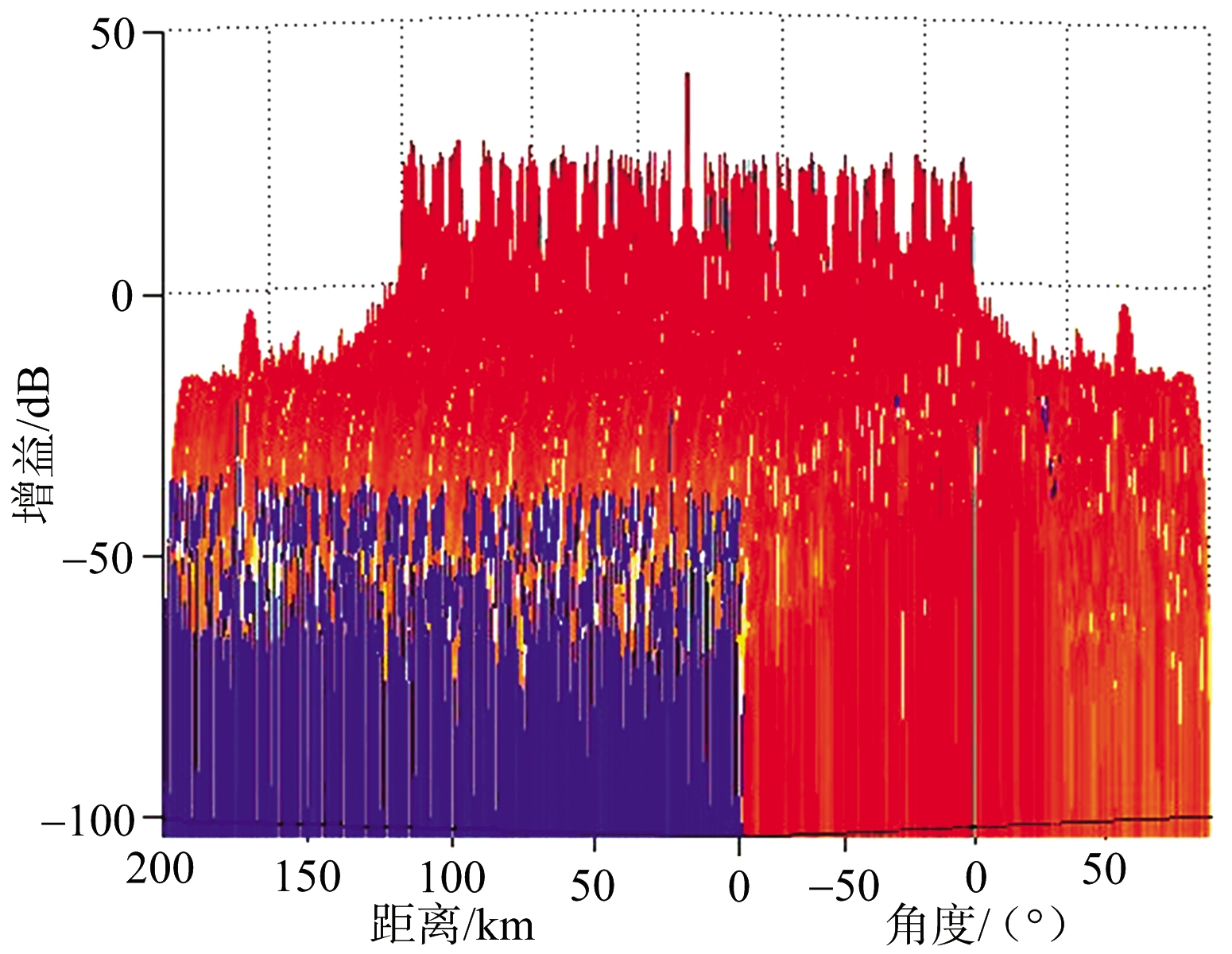
(a) FDA-MIMO雷达方向图
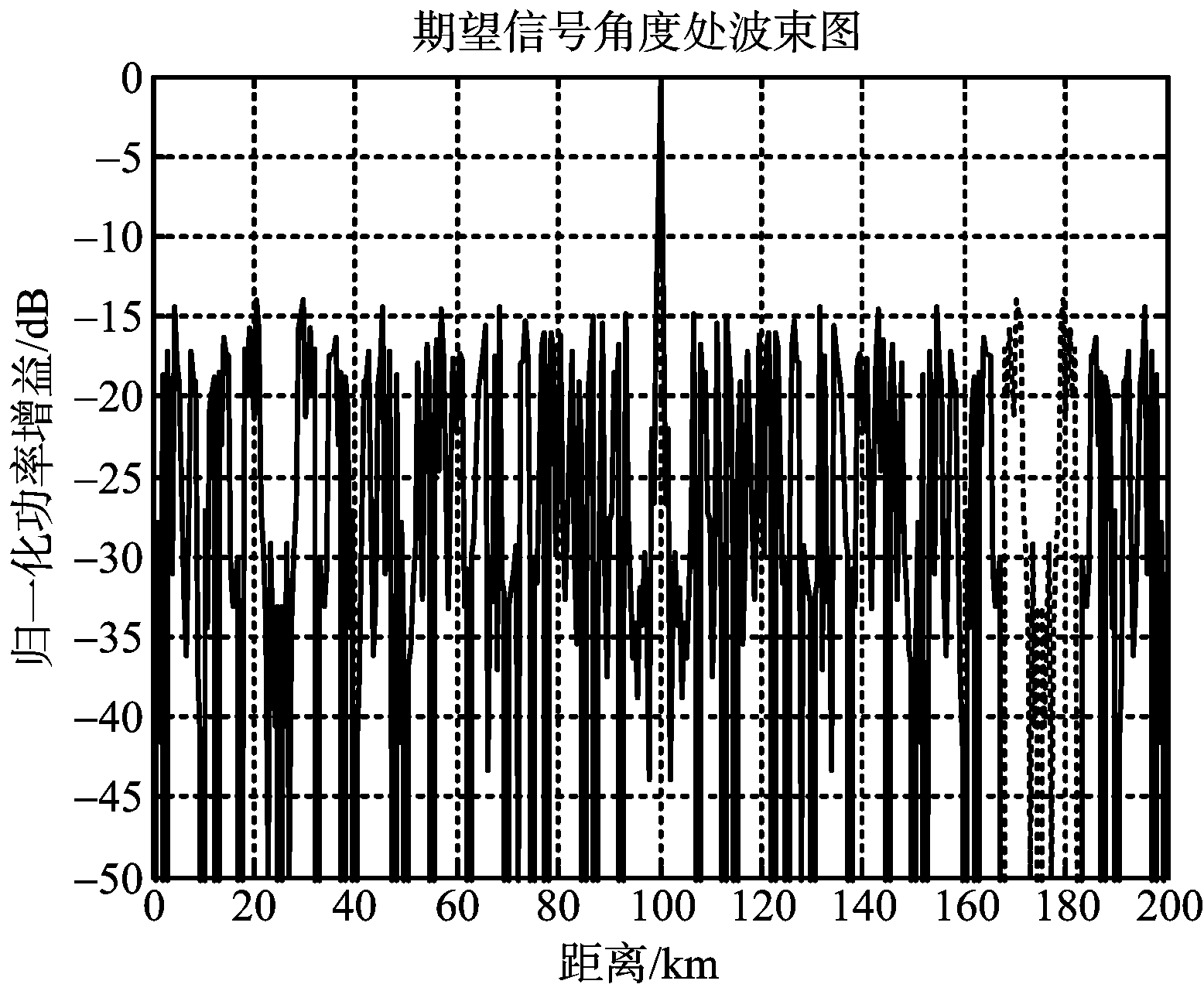
(b) 0°处切面(距离维)方向图
图5 基于子阵的去栅瓣方法仿真图
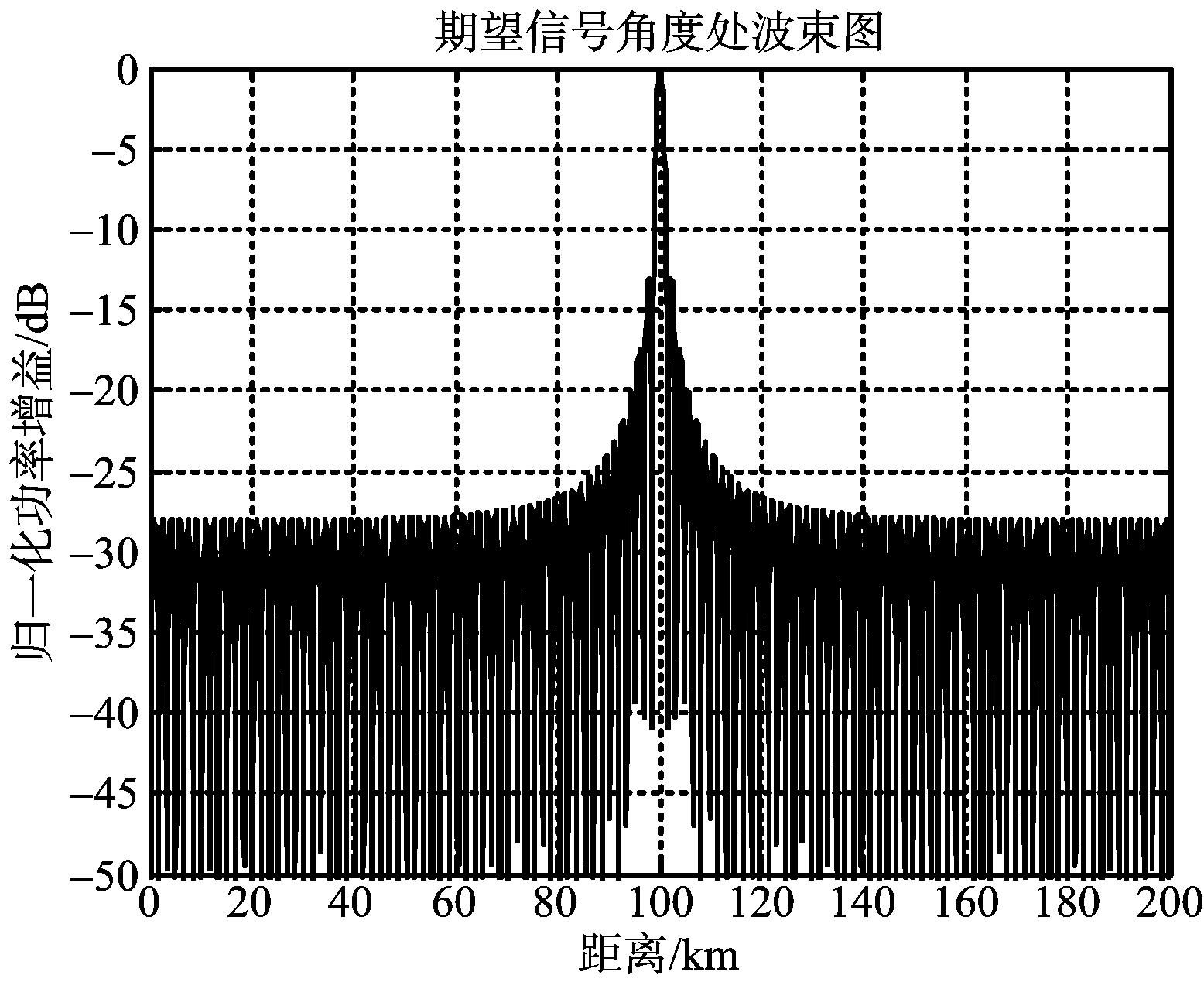
(a) 常规方法
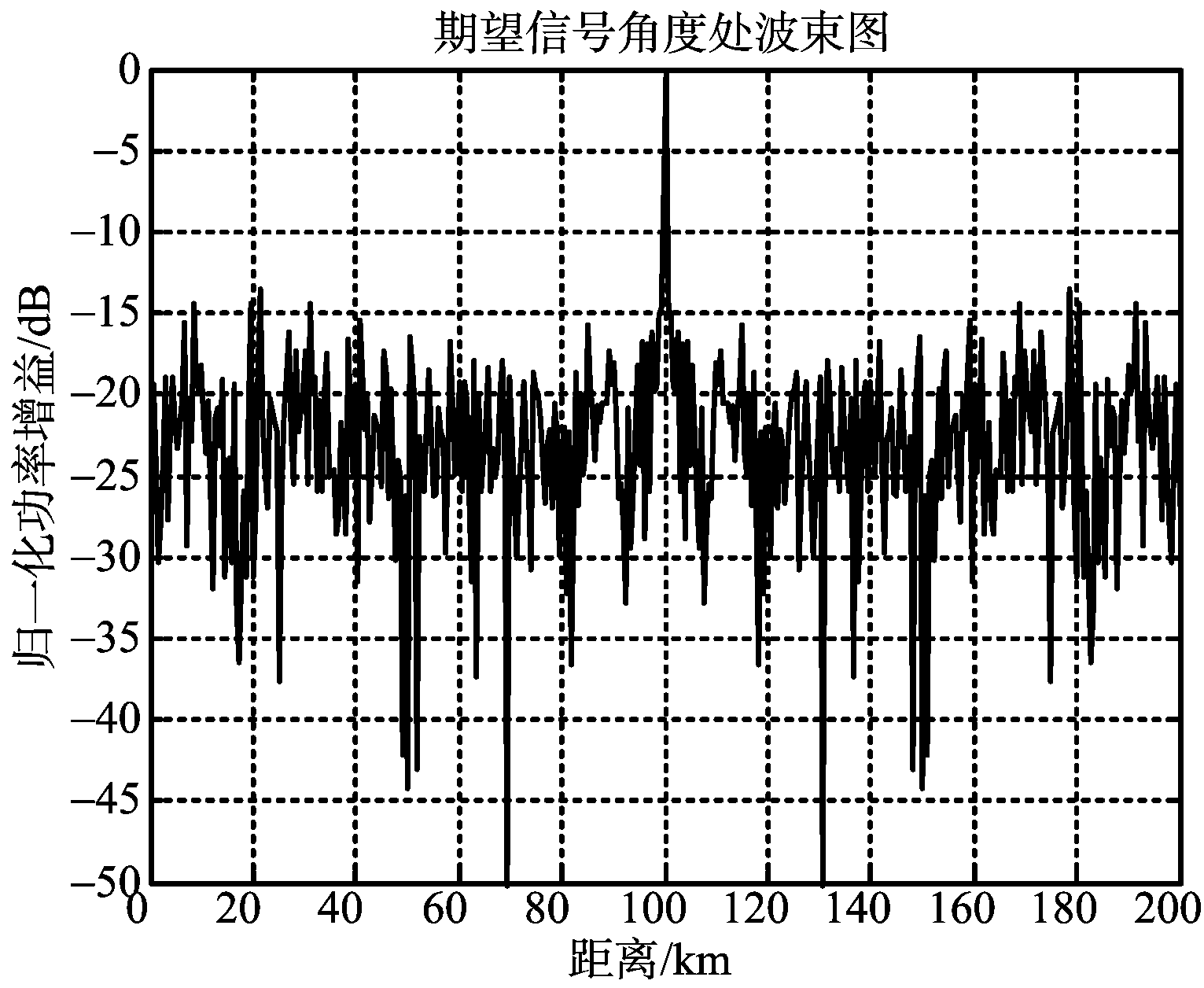
(b) 基于子阵法
图6 两种方法的0°处切面(距离维)方向图
对比图4(b)和图5(b)可以发现，本文提出的基于子阵的去栅瓣方法，副瓣会随着子阵个数的增加逐渐降低，且降低为-15 dB，并且随着子阵频率间隔的增大，距离维主瓣宽度会减小，距离维分辨率会进一步提高。对比图6(a)与图3(b)以及图5(b)与图6(b)可以发现，在采用加窗处理后，本文方法的距离维副瓣电平几乎没有任何变化，而常规方法的距离维副瓣明显下降。这主要是本文提出的基于子阵的去栅瓣方法形成的距离维副瓣，实质上是子阵方向图栅瓣与栅瓣或副瓣的叠加，采用加窗处理对栅瓣电平是没有影响的，所以叠加后距离维副瓣电平几乎没有影响。
4 结束语
本文在推导出基于子阵的FDA-MIMO雷达双程方向图闭合表达式的基础上，提出了一种基于子阵的FDA-MIMO雷达去栅瓣的方法，不仅去除了栅瓣，也提高了距离维主瓣分辨率。该方法提供了一种利用副瓣叠加去栅瓣的思路，不仅适用于FDA-MIMO雷达，也同样适用于FDA雷达，然而通过仿真可以发现此方法形成的方向图距离维副瓣仍然较高，采用加窗处理效果不明显，需进一步研究降低副瓣电平的方法。
[1] WANG Yuxi, HUANG Guoce, LI Wei. Transmit Beampattern Design in Range and Angle Domains for MIMO Frequency Diverse Array Radar[J]. IEEE Antennas and Wireless Propagation Letters, 2017, 16(99):1003-1006.
[2] KHAN W, QURESHI I M, SAEED S. Frequency Diverse Array Radar with Logarithmically Increasing Frequency Offset[J]. IEEE Antennas and Wireless Propagation Letters, 2015, 14:499-502.
[3] GAO Kuandong, WANG Wenqin, CAI Jingye, et al. Decoupled Frequency Diverse Array Range-Angle-Dependent Beampattern Synthesis Using Non-Linearly Increasing Frequency Offsets[J]. The Institution of Engineering and Technology, 2016, 10(8):880-884.
[4] BASIT A, QURESHI I M, MALIK A N, et al. Beam Sharpening of a Range-Angle-Dependent Pattern Using Non-Uniform Symmetric But Integer Frequency Offset[C]∥International Conference on Intelligent Systems Engineering, Islamabad, Pakistan：IEEE, 2016: 232-235.
[5] XIONG Jie, WANG Wenqin, SHAO Huaizong, et al. Frequency Diverse Array Transmit Beampattern Optimization with Genetic Algorithm[J]. IEEE Antennas and Wireless Propagation Letters, 2017, 16:469-472.
[6]WANG Wenqin. Range-Angle Dependent Transmit Beampattern Synthesis for Linear Frequency Diverse Arrays[J]. IEEE Trans on Antennas and Propagation, 2013, 61(8):4073-4081.
[7] SHAO Huaizong, DAI Jun, XIONG Jie, et al. Dot-Shaped Range-Angle Beampattern Synthesis for Frequency Diverse Array[J]. IEEE Antennas and Wireless Propagation Letters, 2016, 15:1703-1706.
[8] GAO Kuandong, WANG Wenqin, CHEN Hui,et al. Transmit Beamspace Design for Multi-Carrier Frequency Diverse Array Sensor[J]. IEEE Sensors Journal, 2016, 16(14):5709-5714.
[9] 赵永波, 刘宏伟. MIMO雷达技术综述[J]. 数据采集与处理, 2018, 33(3):389-399.
[10] 谭清莉,张艺乐,张伟,等. FDA-MIMO雷达主瓣欺骗干扰对抗方法[J]. 雷达科学与技术, 2017, 15(6):671-676.
[11] 陈浩, 李荣锋, 邵银波,等. FDA最优频率增量选取必要性分析[J]. 雷达科学与技术,2018, 16(6):650-655.
[12] 陈浩, 李荣锋, 周必雷，等. 基于加权模值的FDA最优频率间隔选取方法[J]. 现代雷达， 2019, 41(1):30-35.
[13] SAMMARTINO P F, BAKER C J, GRIFFITHS H D. Frequency Diverse MIMO Techniques for Radar[J]. IEEE Trans on Aerospace and Electronic Systems, 2013, 49(1):201-222.
