0 引言
基于相位差变化率的单站无源定位技术,利用空中观测平台上干涉仪测量目标辐射源到达信号的相位差,得到方位角变化率,结合目标的方位角,就可以计算出目标的位置(坐标)[1]。当观测平台为小型无人机时,大气湍流易使载机发生飞行姿态扰动[2],导致载机上的干涉仪基线矢量指向发生变化,对测量得到的相位差以及相位差变化率数据产生影响,针对这种情况,通常利用无人机导航数据中的姿态角数据对姿态变化后测量得到的相位差及其变化率数据进行补偿[3],以保证较高的定位精度。
这种补偿方法的前提是无人机在姿态变化时,得到的相位差变化率数据中需含有无人机姿态变化的信息。然而在实际应用中,相位差变化率既可以直接测量得到,也可以间接提取得到[4],不同的提取方法会导致相位差变化率中的姿态信息丰富程度不同,从而姿态补偿的效果也不同。经典的相位差变化率提取方法有差分法和卡尔曼滤波法[5],本文首先给出了这两种提取方法下的姿态补偿效果和定位精度,然后针对本文提出的基于差值定理的相位差变化率提取方法进行了对比分析,结果表明本文方法具有更好的姿态补偿效果和更高的定位精度。
1 单站无源定位姿态补偿方法
图1表示某时刻无人机定位态势,图中以地面某固定点为坐标原点建立固定坐标系Oxy,Ox轴指向正东,无扰动时默认无人机沿正东作匀速直线运动,出现风扰动时无人机将沿AB方向运动;A表示无人机位置,T表示目标位置,β表示目标方位角,θ表示偏航角,对于地面固定目标,当目标与载机距离较远时,可以忽略飞行高度的影响,等效至二维平面。
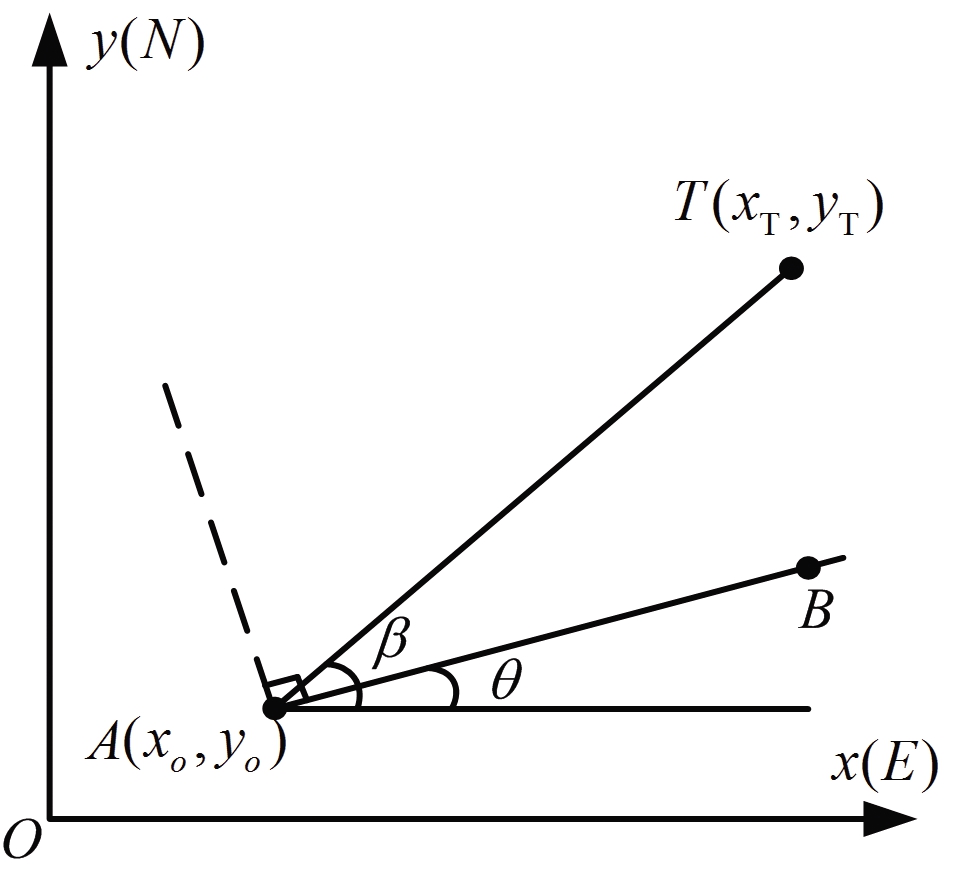
图1 某时刻定位态势示意图
无人机姿态可用欧拉角(偏航角、俯仰角和滚转角)描述。由于二维平面不考虑俯仰角,并且干涉仪位于无人机机身轴上,无人机发生滚转时不会对相位差及其变化率的测量产生影响,因此本文中无人机姿态只需考虑偏航角θ。根据空间关系,基于干涉仪得到的相位差及其变化率为 [6]
(1)
式中:φ和![]() 表示姿态变化时的相位差和相位差变化率,通过干涉仪测量和提取得到;
表示姿态变化时的相位差和相位差变化率,通过干涉仪测量和提取得到;![]() 和
和![]() 表示对应角的角变化率;k=2πdfT/c,其中d为干涉仪基线长度,c为光速,fT为目标辐射源载频,均为已知参数。
表示对应角的角变化率;k=2πdfT/c,其中d为干涉仪基线长度,c为光速,fT为目标辐射源载频,均为已知参数。
式(1)变形为
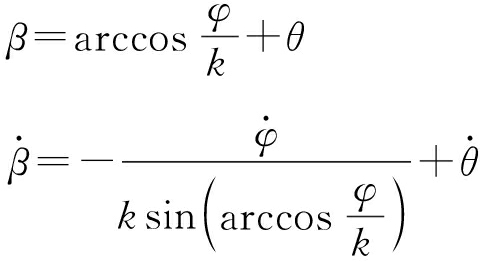
(2)
无人机无姿态变化,即θ=0时有
(3)
式中:φ1和![]() 表示无姿态变化时的相位差和相位差变化率。
表示无姿态变化时的相位差和相位差变化率。
将式(2)代入式(3)中,得
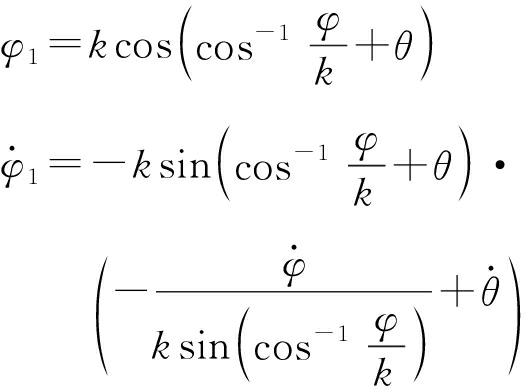
(4)
式(4)即通过无人机姿态角数据![]() 和姿态变化后的相位差及其变化率数据
和姿态变化后的相位差及其变化率数据![]() 求出姿态变化前的对应数据
求出姿态变化前的对应数据![]() 从而实现姿态补偿。
从而实现姿态补偿。
可以看出,利用姿态角数据进行无源定位精度补偿的前提是提取出的![]() 中含有丰富的姿态扰动信息,显然当
中含有丰富的姿态扰动信息,显然当![]() 中的姿态扰动信息较不完整时,补偿效果也会受到影响。因此需要提出一种能够较为完整保留无人机姿态信息的相位差变化率提取方法。
中的姿态扰动信息较不完整时,补偿效果也会受到影响。因此需要提出一种能够较为完整保留无人机姿态信息的相位差变化率提取方法。
2 基于经典方法提取相位差变化率的定位精度分析
提取相位差变化率的经典方法通常有差分法和卡尔曼滤波法,以下分析两种方法提取相位差变化率中姿态信息的保留情况,以及定位精度。
2.1 差分法提取相位差变化率
应用差分法提取相位差变化率数据的原理是利用(i-1)D~iD时刻内相位差数据的平均变化速度来近似iD时刻的相位差变化率[7]。即
(5)
式中,D表示差分运算时间间隔。用该方法提取相位差变化率较为简单。
2.2 卡尔曼滤波法提取相位差变化率
利用卡尔曼滤波法直接提取相位差变化率数据的基本思想是,一方面对输入的已解模糊相位差数据进行平滑,降低测量噪声,另一方面实时给出相位差变化率数据的滤波值[8]。由于该方法较为经典,滤波原理本文不作赘述。
2.3 两种方法的定位精度分析
下面通过仿真实验分析差分法和卡尔曼滤波法提取相位差变化率时的效果。
无人机基本仿真参数设置:如图1所示,无人机平行大地平面作匀速直线运动,飞行速度为150 m/s,无人机初始位置为(0,0)。另外在无人机运动学模型中引入传感器自身带来的测量误差,设为在横、纵向速度分量误差满足均值为0,方差为0.5 m/s的高斯分布。
无人机姿态扰动仿真设置:无人机姿态扰动一般是风扰动造成的,为了令仿真结果更贴合实际,本文引用Dryden大气紊流模型[9]模拟风扰动,近似认为风扰动对无人机姿态影响是线性的,即无人机在风扰动下的姿态角数据也服从Dryden模型,并根据实际情况设置姿态角变化最大不超过3°。模拟得到的姿态角数据片段如图3所示,图中横轴表示时间,纵轴表示偏航角大小。可以看出,模拟得到的偏航角数据既具有随机性又不失前后时刻相关性,更加贴合实际。
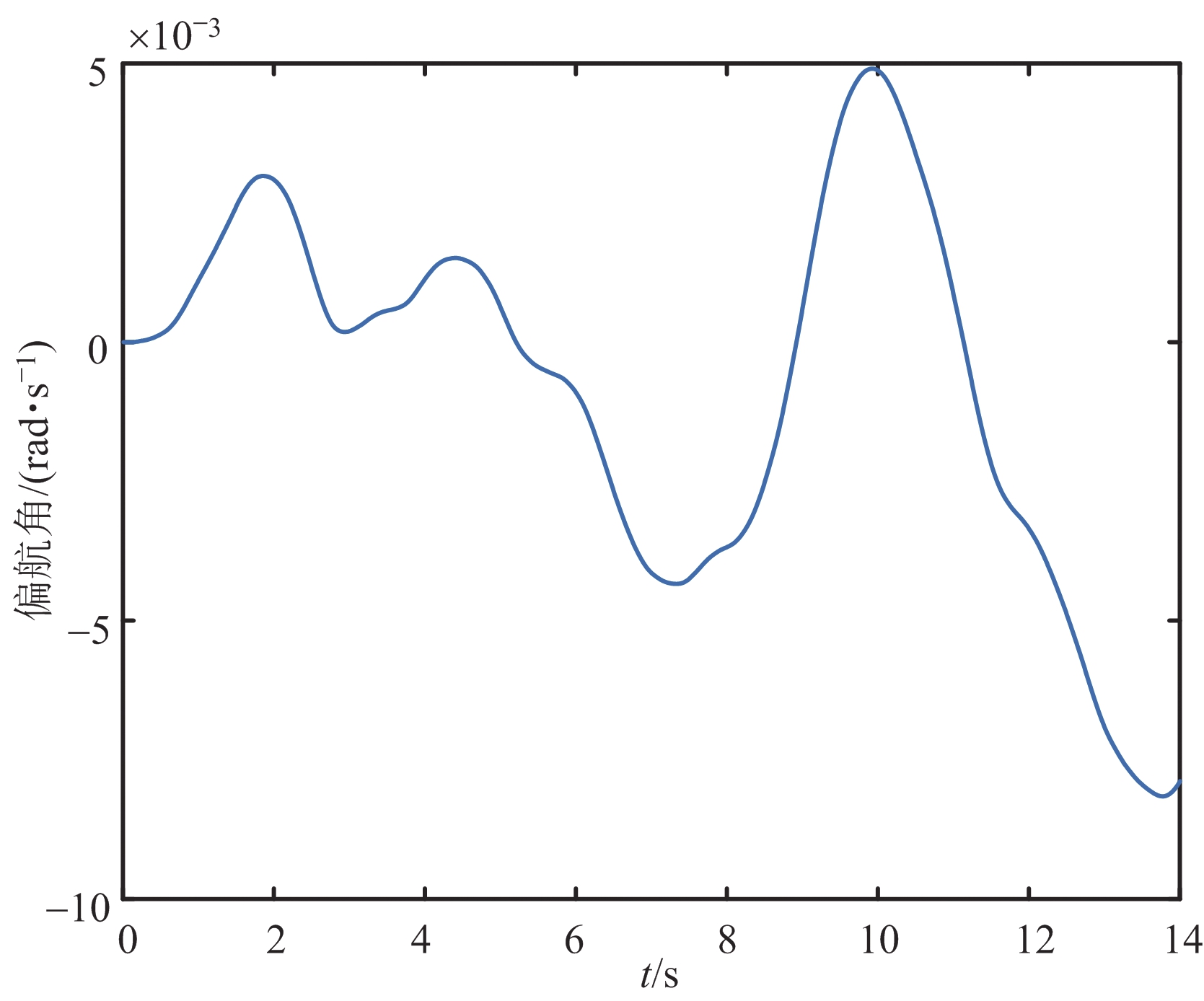
图3 无人机偏航角模拟片段
定位模型基本仿真参数如下:地面固定雷达目标工作频率fT=3 GHz,目标位置处于(100,50)km,目标雷达脉冲重复频率设置为500 Hz,即定位点采样间隔为2 ms,导航数据更新频率设置为20 Hz,干涉仪基线OA长度为1 m。
差分法参数设置:令D=20 ms为差分时间片间隔进行差分运算。
卡尔曼滤波法参数设置:实现卡尔曼滤波公式的递推过程,首先需要相位差数据初值U0和相位差数据的均方误差初值C0,并且初值的选取会影响卡尔曼滤波的收敛时间、预测精度等性能[10]。U0的确定采用随机选取一段相位差样本进行事先观测并取均值的方法确定,通过这种方法计算得到的一组初值为U0=50 rad;由于C0是误差初值,在没有误差经验值的情况下,一般认为U0的选取不存在误差,因此令C0=0。
仿真结果如图4所示。
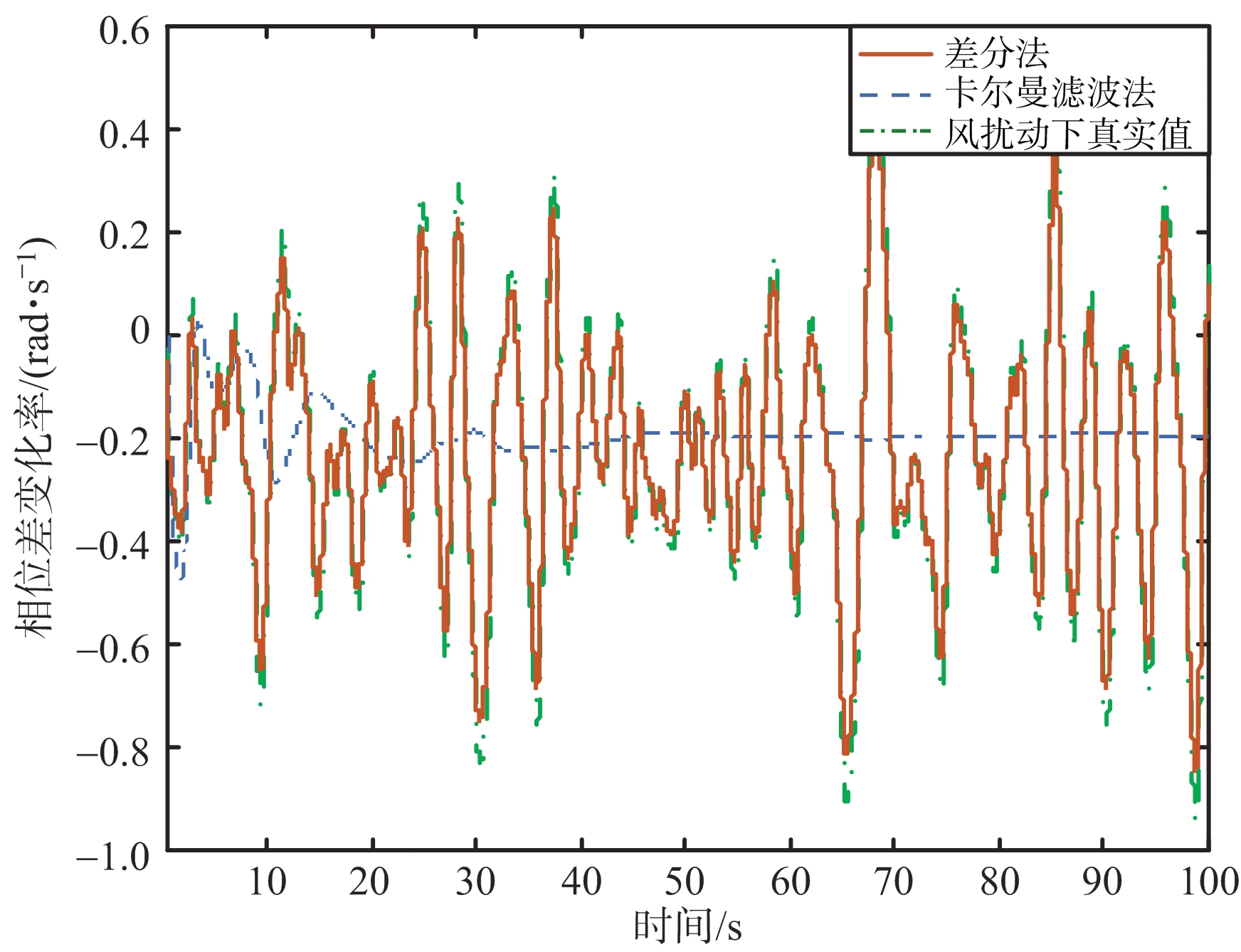
图4 两种提取方法的提前效果对比
可以看出,利用差分法提取得到的相位差变化率抖动明显,可以认为该方法能较好保留相位差变化率中的姿态信息;利用卡尔曼滤波法提取得到的相位差变化率在收敛后趋于平滑,即将无人机姿态抖动带来的影响视为噪声进行了滤波降噪处理,从而导致了相位差变化率中的姿态信息受到了较为严重的破坏。
为量化仿真结果,定义定位误差和平均定位相对误差如下:
(6)
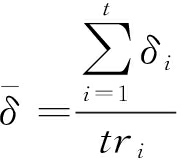
(7)
式中:xT,yT为目标真实位置的横、纵坐标;x′T, y′T为计算得到的横、纵坐标;ri为i时刻目标与无人机间的径向距离;t为无人机执行定位任务总时长。
当D、U0取不同值时,两种方法提取相位差变化率时的定位误差如表1所示。
表1 不同条件下两种方法定位误差对比
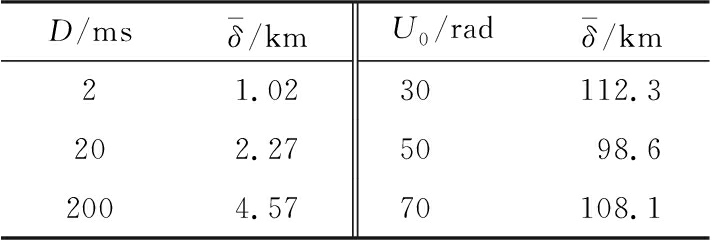
D/msδ-/kmU0/radδ-/km21.0230112.3202.275098.62004.5770108.1
从表1可以看出,D越小,定位误差越小,定位精度就越高。这是因为提取相位差变化率的过程实际上就是数值微分的过程,若期望提取出的相位差变化率中含有较为完整的姿态信息,则需要让数值微分的求解尽可能准确,显然当差分法中的D趋于无穷小时,数值微分的求解是趋于准确的,但是受目标雷达脉冲重复频率fPRF的限制,D最小只能取到1/fPRF;此外差分法的前提是认为在差分时间片间隔中,相位差变化率的值是恒定的,即在相位差变化率呈现线性或近似线性变化时,差分法提取方法较好[11]。但是在无人机姿态扰动时,相位差变化显然呈现非线性,因此无人机存在姿态扰动时,利用差分法提取相位差变化率存在一定的局限性。
从表1还可以看出,初值的选取对卡尔曼滤波的影响较大,并且经过计算得到的最佳初值为55 rad,并且初值的选取越靠近最佳初值,卡尔曼滤波的效果越好。但是卡尔曼滤波的平滑功能滤除了相位差变化率中本该含有的部分姿态信息,因此无论初值选取是否准确,在采用姿态补偿时,定位误差都非常大。
3 基于差值定理的相位差变化率提取方法
通过第2节的分析可知,要想令姿态补偿达到较好的效果就必须尽可能多地保留相位差变化率中的姿态信息,从数学的角度来说即要求对相位差的数值微分尽可能准确,而差值定理的提出将微分算法的效果从“无限逼近”提高到“理论上相等”。因此本文采用差值定理提取相位差变化率。
差值定理的基本内容是:设函数F(t)和f(t)在某定义域Ω内任一点均存在n阶导数,且G(t)=F(n-1)(t)-f(n-1)(t),则F(n)(t0)=f(n)(t0)⟺G′(t0)=0。
文献[11]中将差值定理的物理意义描述为:2个函数的n-1阶导数的差值的驻点是它们的n阶导数相等的点;2个函数差值曲线的驻点是它们的一阶导数相等的点。因此,在假设测量数据和拟合数据均满足处处可导的条件时,只需求出测量得到的相位差数据和拟合得到的相位差数据差的极值点,即可把拟合数据在极值点处的一阶导数作为该点的相位差变化率提取值。那么该方法的核心在于对相位差数据的拟合以及差值数据极值的判别。
3.1 对相位差数据的拟合
对于数据拟合,本文采用基于三阶多项式的最小二乘法滤波[12]进行拟合,即将相位差在不长的时间内的变化情况表示为
φ′(ti)=![]()
ti=-N,…,N
(8)
式中,φ′(ti)表示拟合得到的相位差,N表示滤波半径,i表示第i次滤波。
再根据最小二乘滤波的基本原理估计出系数[ai,bi,ci,di]即可。在应用过程中,令滤波半径不变,并以N为步长对相位差数据进行滑动滤波,将各步得到的相位差拟合数据拼接即完成了对相位差数据的拟合。
采用这种拟合方法最大的好处在于能够写出拟合数据的显式函数表达式,并且对其求一阶导数十分简单,即
![]()
![]()
ti=-N,…,N
(9)
式中,![]() 表示拟合相位差的一阶导数,即相位差变化率。
表示拟合相位差的一阶导数,即相位差变化率。
3.2 差值数据极值的判别
根据极大值和极小值的定义,第i点是极大值的充要条件:
(10)
第i点是极小值的充要条件:
(11)
式中,C(ti)=φ(ti)-φ′(ti),即相位差的差值函数,S表示误差限,即允许存在的最大测量误差,在要求高精度测量时,一般取S=0。
理论上通过以上极值判别方法即可判别出极值点,再将极值点代入式(9)即可得到较为准确的相位差变化率数据。然而由于拟合曲线与原数据曲线不完全匹配以及滤波半径的选取等原因,判别出的极值点数小于测量数据点数。令S=0,其他仿真条件不变时,改变滤波半径N时,得到的极值点情况如表2所示。
表2 滤波半径不同时的极值点求解情况

测量数据点数N=3时极值点数N=5时极值点数N=7时极值点数30000299632980126523
从表2可以看出,滤波半径改变虽然会影响求解的极值点的点数,但是求解得到的极值点数总是小于测量数据的点数,从物理意义来说,这会导致得到的相位差变化率数据在时间上不连续,不利于进行姿态补偿。
根据文献[11],可以采用系数调节法,使每个测量数据时刻点都成为驻点。即保持ai,di固定不变,令bi,ci满足如下关系式:
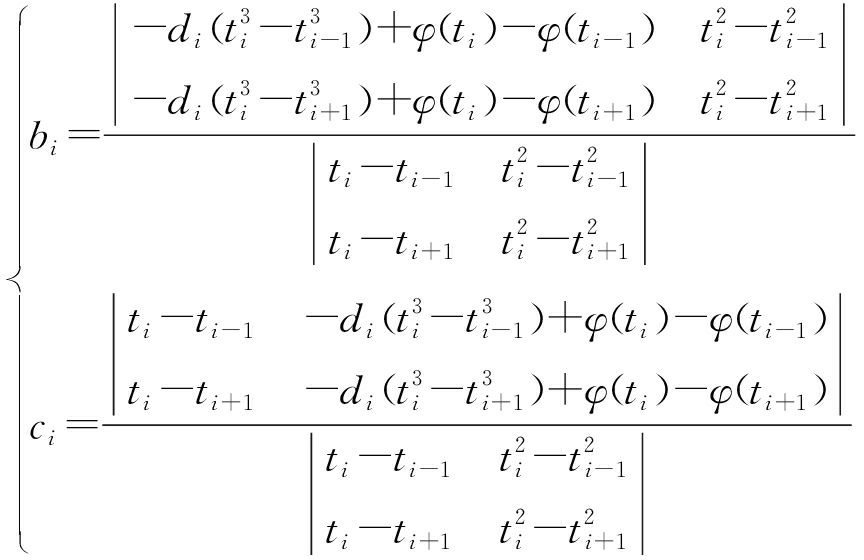
(12)
根据式(12)能够使相位差的拟合曲线与相位差测量曲线在极值点附近的曲率尽可能相等,即保证了解算出的极值点数等于测量数据点数,从而保证率求解出的相位差变化率的时间连续性。
3.3 相位差变化率提取流程
总结前文,基于差值定理的相位差变化率提取方法的步骤如图5所示。
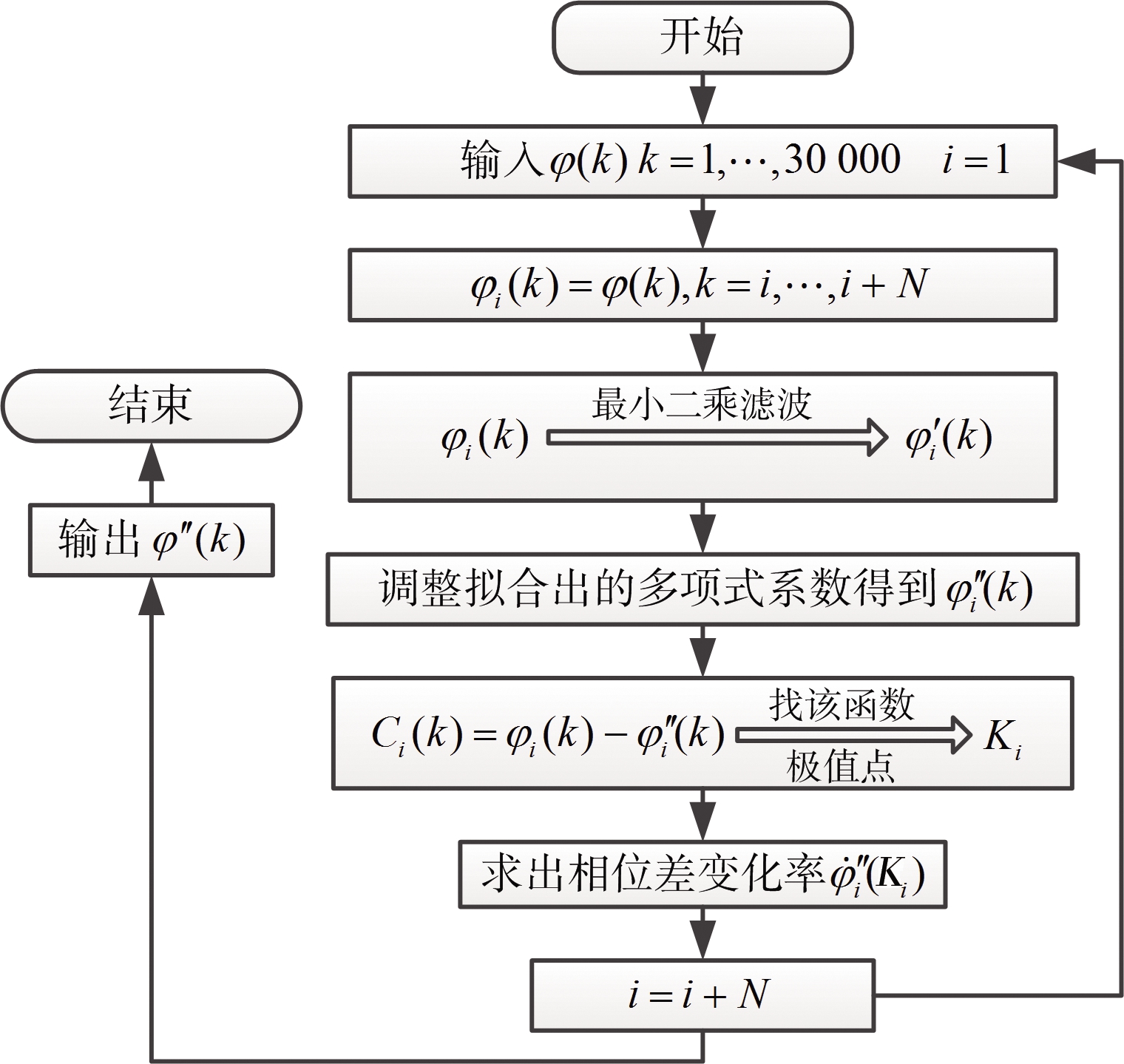
图5 相位差变化率提取新方法流程图
图5中,k表示离散时间变量,φ(k)表示相位差测量值,φi(k)表示第i次滑窗对应的长度为N的相位差测量值,φ′i(k)表示与φi(k)对应的相位差拟合数据,φ″i(k)表示调整多项式系数后的![]() 表示φ″i(k)对应求解的相位差变化率,Ki表示极值点的集合。
表示φ″i(k)对应求解的相位差变化率,Ki表示极值点的集合。
该方法的仿真参数设置为:拟合多项式阶数选取三阶,滤波半径选取N=5,并假设测量得到的相位差数据在时间上连续。该方法的相位差变化率提取效果片段如图6所示。
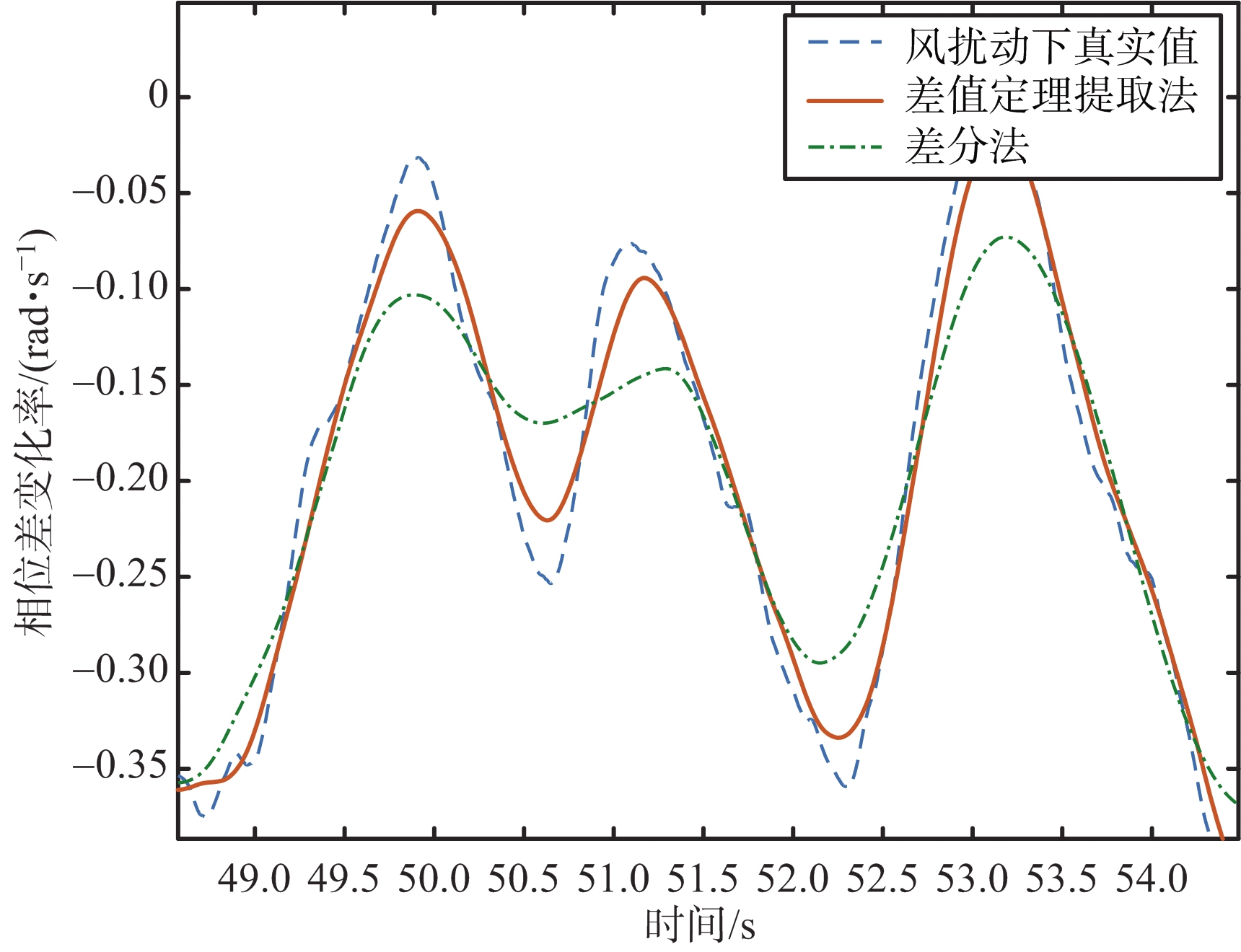
图6 不同方法提取效果对比示意图
从图6可以看出,与差分法相比,差值定理提取法提取得到的相位差变化率更加贴近风扰动下相位差变化率的真实值,与风扰动下相位差变化率的真实值相比,D=1 ms时差分法提取时的相位差变化率均方误差为0.084 rad/s,而差值定理提取时的误差为0.032 rad/s,说明了该方法的有效性。经过计算后的定位相对误差如表3所示。
表3 差值定理法定位误差对比

N定位相对误差/%差分法/T=1ms差值定理法3574.232.021.961.68
从表3可以看出,与差分法相比,在无人机姿态补偿时,利用差值定理法提取相位差变化率时的定位精度得到提高,定位误差基本保持在2%以内。
从运算时间看,在文中仿真条件下,相位差数据点数为50 000时,差分法、卡尔曼滤波法和差值定理法所需的时间分别为0.19,2.45和3.91 s,而根据文中设置,接收50 000个相位差数据点需要100 s,显然远大于这三种方法的计算时间,说明3种方法均具备很高的实时性。而本文方法更具高定位精度的优点。
4 结束语
本文针对现有相位差变化率提取方法提取得到的相位差变化率数据中观测平台姿态信息较少,导致利用观测平台姿态数据进行无源定位姿态补偿时精度较低的问题,提出了一种基于差值定理的相位差变化率提取方法,并对比分析了差分法、卡尔曼滤波法和本文方法提取相位差变化率时的姿态补偿精度。研究表明,本文方法能够提高单站无源定位的姿态补偿精度,对观测平台发生姿态扰动时单站无源定位性能的提升具有指导意义。
[1] 田明辉,马敏,李帅.基于相位差变化率的单站目标定位研究[J].雷达科学与技术,2014,12(5):522-526.
[2] 刘佳,方宁,谢拥军,等.姿态扰动情况下的目标动态RCS分布特性[J].系统工程与电子技术,2015,37(4):775-781.
[3] 单月晖,孙仲康,皇甫堪.变化姿态角下相位差变化率无源定位方法研究[J].电子学报,2002,30(12):1897-1900.
[4] 钟华,罗景青.相位差变化率的快速高精度测量及精度分析[J].火力与指挥控制,2016,41(8):133-136.
[5] 丁静.提取相位差变化率的一种新方法[J].无线电工程,2012,42(9):26-27.
[6] 马琴,朱伟强.航向角在相位差变化率定位中的影响分析[J].航天电子对抗,2007,23(6):57-60.
[7] 郭福成,贾兴江,皇甫堪.仅用相位差变化率的机载单站无源定位方法及其误差分析[J].航空学报,2009,30(6):1090-1095.
[8] 田明辉,马敏.基于相位差的机载单站无源定位算法[J].太赫兹科学与电子信息学报,2016,14(2):190-194.
[9] 郑黎明,杏建军,陈子昂,等.Dryden型大气紊流对平流层飞艇能量最优轨迹影响[J].航空学报,2017,38(1):118-132.
[10] 陆如华,徐传玉,张玲,等.卡尔曼滤波的初值计算方法及其应用[J].应用气象学报,1997,8(1):35-44.
[11] 梁红.差值定理在离散数据一阶导数解算中的应用[J].西北工业大学学报,2016,34(1):166-175.
[12] 张永涛,贾延明.最小二乘法中代数多项式曲线拟合的分析及实现[J].计算机与数字工程,2017,45(4):637-639.
