0 引言
为适应未来战争的防御需求,雷达系统需要有效提升探测能力和参数估计性能。采用更大孔径的均匀天线阵列可有效实现参数估计精度和覆盖范围的要求,然而,采用大孔径均匀阵列会使得系统成本骤增且阵元间耦合加剧。超稀疏阵列在提升阵列孔径的同时可大幅度减少阵元数目,有效地解决了系统成本和探测性能间的矛盾。
目前,针对稀疏阵列的研究主要分为两大类:一类是具有固定构造结构的稀疏阵列,例如互质阵列、嵌套阵列、最小冗余阵[1-3]等。这类阵列通常具有固定的构造方式,利用其特定的结构可等效重构出同孔径下均匀阵列对应的协方差矩阵进行参数估计,该类方法往往需要较大的快拍数,在雷达系统中往往无法满足,主要应用于天文探测这类观测时间长、快拍数多的应用场景。第二类是随机阵列结构,即通过构造特定的约束准则[4],优化求解满足约束的最优阵列分布。该类方法在雷达中具有良好的应用前景和实际价值,本文主要针对稀疏阵列综合的算法进行介绍讨论。
针对大孔径的稀疏阵列综合问题主要分为两种,一种是孔径和阵元数目受限条件下的副瓣电平优化算法,另一种是副瓣电平和孔径约束下的阵列最稀疏解问题。本文介绍的算法属于后者。此类问题的研究由于属于NP-hard问题,难以求得全局最优解,经典的算法往往采用智能优化算法[5-7],类似遗传算法、退火算法以及粒子群算法等进行随机优化搜索。该类方法在孔径较小时具有较高可行性,然而由于其运算量随着阵列孔径增大呈指数增长,因此在孔径较大时时间成本过高,无法进行优化。采用国外学者Nai提出的凸优化方法[8]可有效降低运算复杂度,但是在孔径较大时仍具有同样的困境。
本文针对大孔径稀疏阵列优化问题展开了研究,通过采用交替方向乘子[9]的优化思想进行快速初始化,并构建邻域空间进行二次优化,从而快速得到更优的稀疏解。仿真实验证明了算法的有效性。
1 算法原理
假设稀疏线阵孔径为L,分布于区间[0,L]上的N个阵元对应的位置矢量记为x=[x1,…,xN]T,初始位置矢量由远小于半波长的间隔d对区间[0,L]进行均匀采样得出,各阵元对应的权值为w=[w1,…,wN]T,因此,此时阵列方向图可表示为
(1)
式中,![]() 为自由空间下的波数,θ为方位角。
为自由空间下的波数,θ为方位角。
为了后续推导方便,式(1)中的方向图可用矩阵形式进行表示,即
F=Aw
(2)
式中,矩阵A中的元素为a(i,j)=ejκxjsin(θi)。
稀疏线阵最优稀疏解问题,即寻找满足主副瓣电平要求的最小阵元数N。则在上述模型的基础上,稀疏线阵稀疏化问题可建模如下:
s.t. |Aw|≤Mup
(3)
a0w=1
式中,||w||0表示w的l0范数,Mup为阵列方向图上界约束条件,a0为方向图主瓣方向所对应的导向矢量。
由于上式中的目标函数w的l0范数,为非凸优化问题,难以得到全局最优解。为了对式(4)中的问题进行求解,可采用l1范数进行如下近似:
s.t. |Awp|≤Mup
(4)
a0wp=1
其中,hp⊙wp为向量h和w的Hadamard积, ||q||1表示向量q的l1范数,上标p表示第p次迭代。每次迭代时的向量h由下式进行更新:
(5)
式中,ε为非常小的常量,可选为0.01。
通过式(4)和式(5)进行迭代求解,在小孔径时可快速有效地获得效果良好的可行解。然而,对于孔径较大的情况而言,采用上式进行优化的运算量将大幅提升,优化效果急剧恶化甚至失效。
利用交替方向乘子算法的思想,可将上述过程进行进一步优化改进。将各阵元位置进行拆分,即![]() 原问题可表述如下:
原问题可表述如下:
(6)
该问题可按照采用如下步骤进行优化:
第一步:设置w2为一初始值![]() 对w1进行优化
对w1进行优化
第二步:对第一步优化结果得到的![]() 代入原问题,对w2进行优化
代入原问题,对w2进行优化
第三步:构建新邻域进行二次优化。对第二步求解得到的P个位置的相邻域内加入K个邻域点,构成长度为KP的新位置矢量![]() 并对新的位置矢量进行二次搜索优化。
并对新的位置矢量进行二次搜索优化。
对于式(6)至式(8)的优化过程采用的分为两块进行求解,但是理论上在单步优化可行的前提下可对大孔径情况对应的搜索空间进行多次划分。
2 计算机仿真
仿真一:阵列孔径L=200λ的线阵综合结果。其副瓣电平要求不高于-20 dB(|θ|≥0.28°),主瓣指向0°,阵列初始间隔d=λ/10。优化得到的阵列方向图和阵元位置及权值分布如图1所示,其中图1(b)为图1(a)主瓣区域局部放大图。
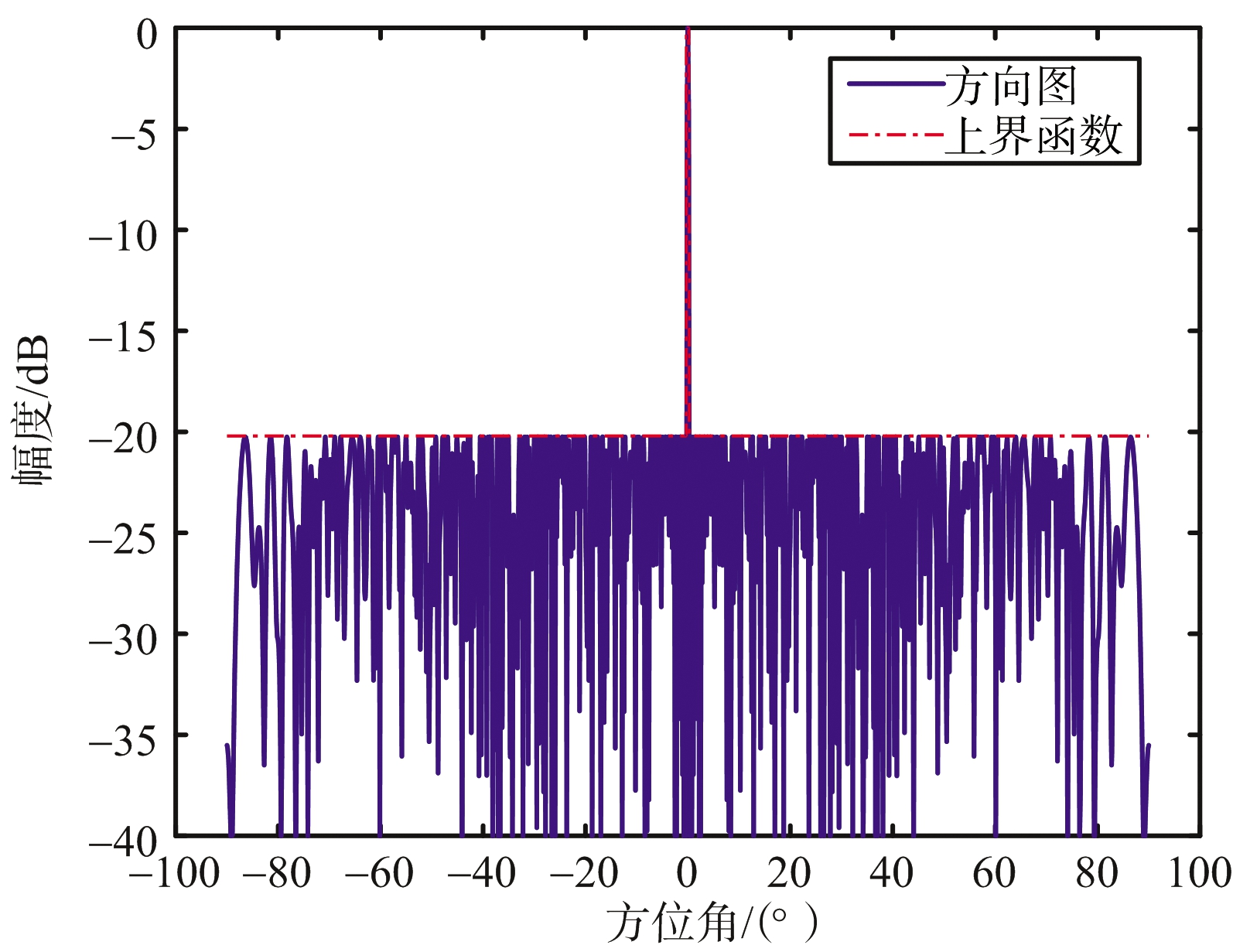
(a) 阵列方向图
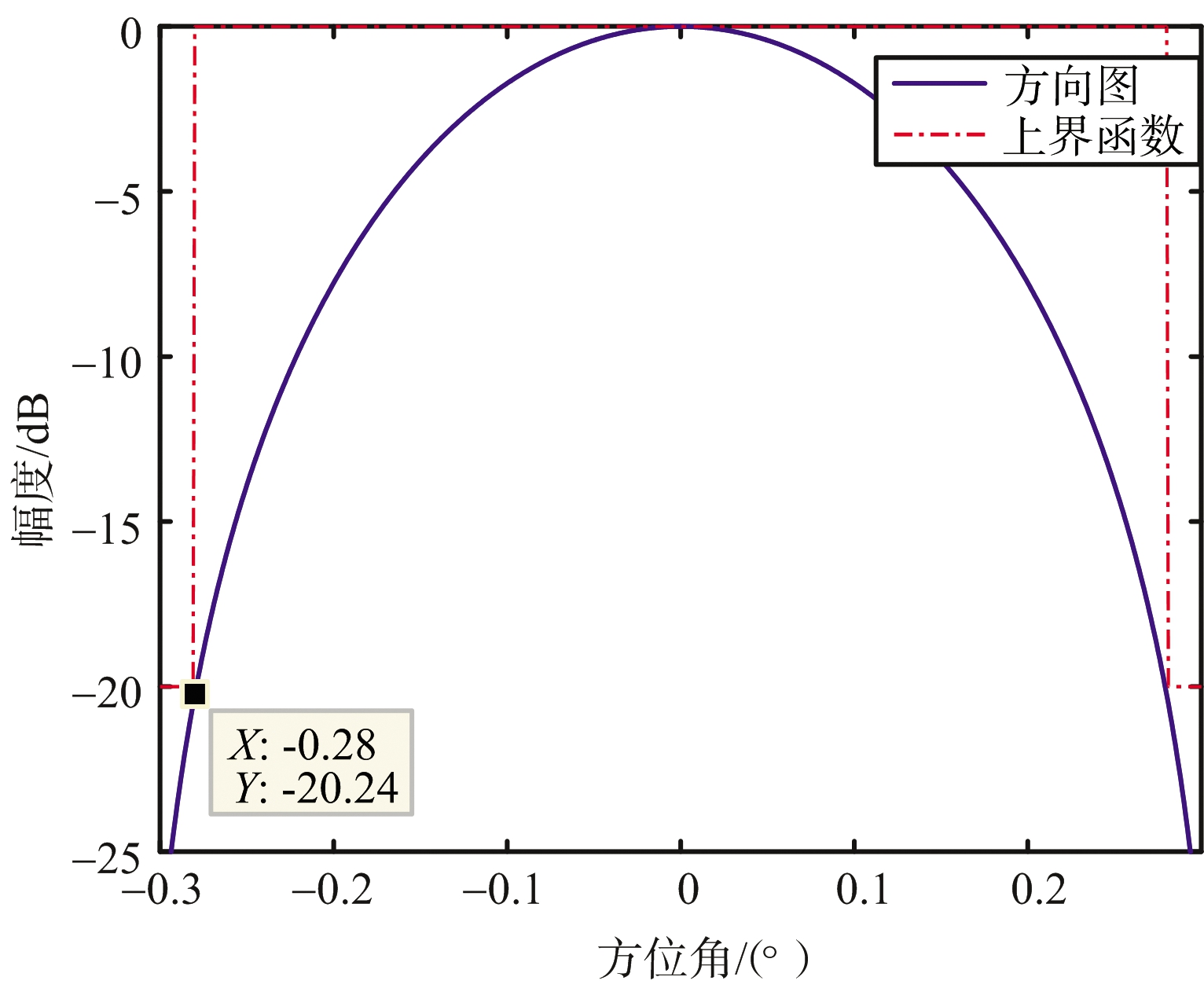
(b) 阵列方向图主瓣放大图

(c) 阵元位置及权值分布
图1 阵列方向图和阵元位置及权值分布
优化后阵元个数仅为129个,稀疏率为32.1%,且由图1可以看出,副瓣电平符合预期约束条件,且波束无展宽。
仿真二:阵列孔径L=400λ的线阵综合结果。副瓣电平低于-18.7 dB(|θ|≥0.17°),主瓣指向0°,阵列初始间隔d=λ/10。优化得到的阵列方向图和阵元位置及权值分布如图2所示,其中图2(b)为图2(a)主瓣区域局部放大图。
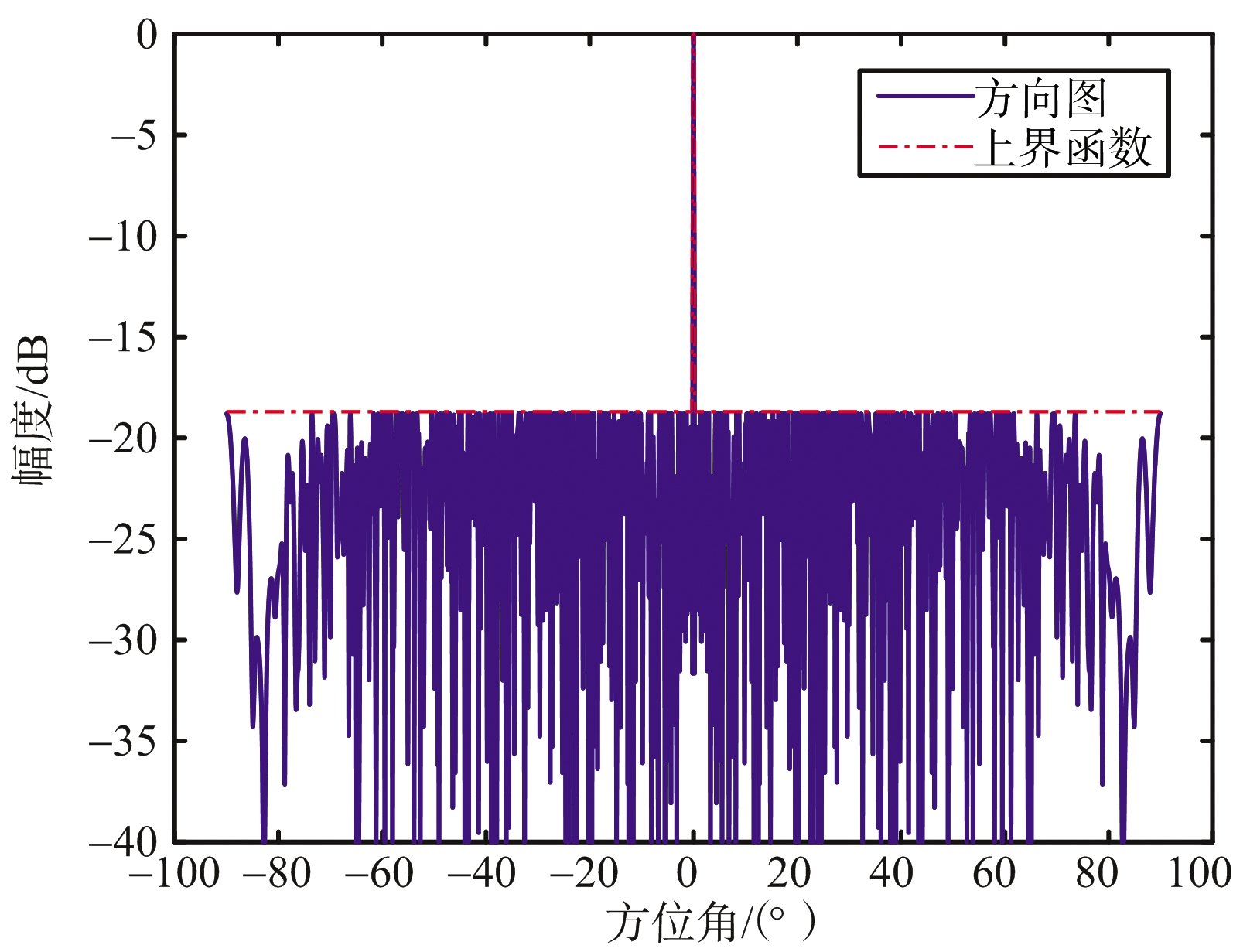
(a) 阵列方向图
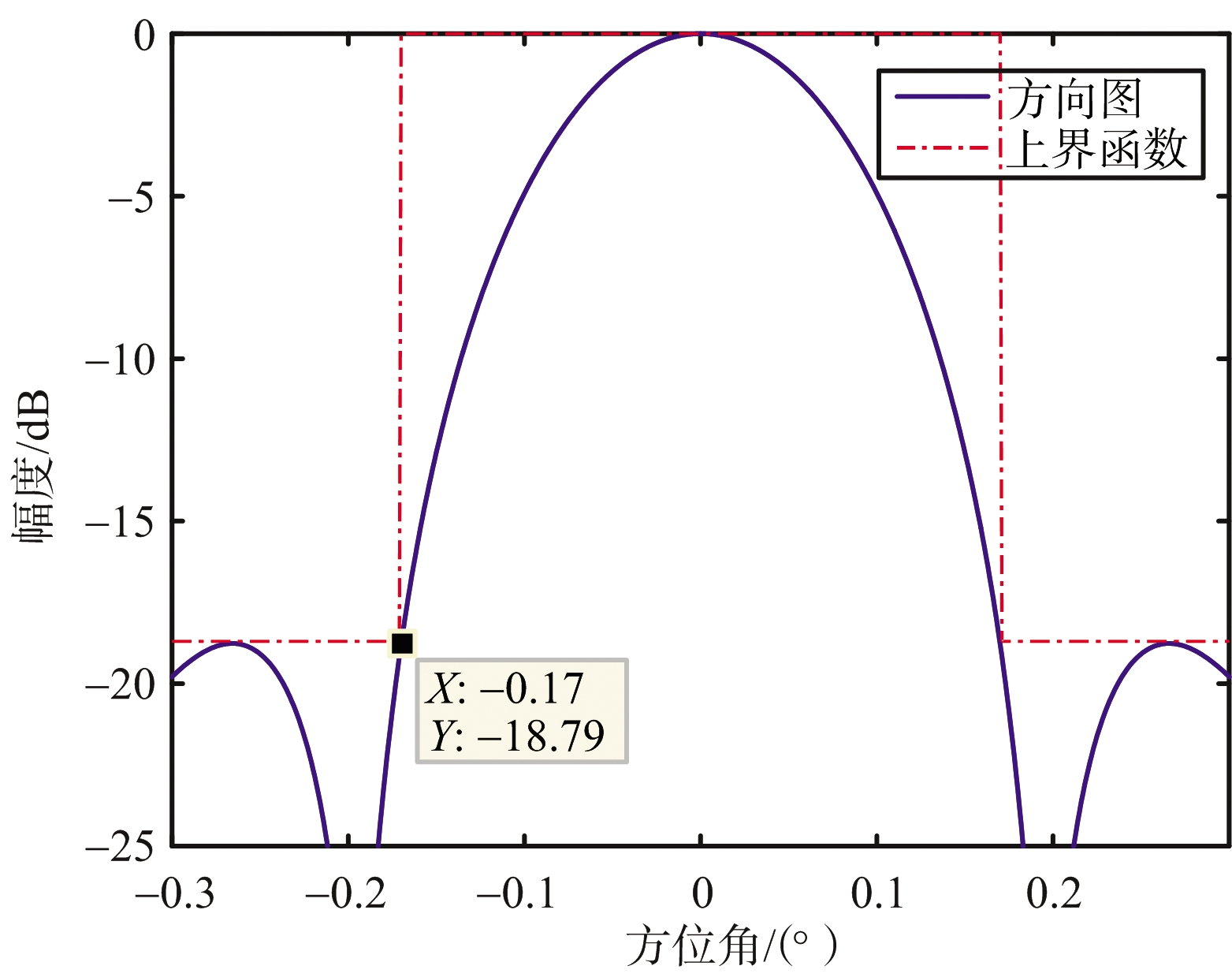
(b) 阵列方向图主瓣放大图
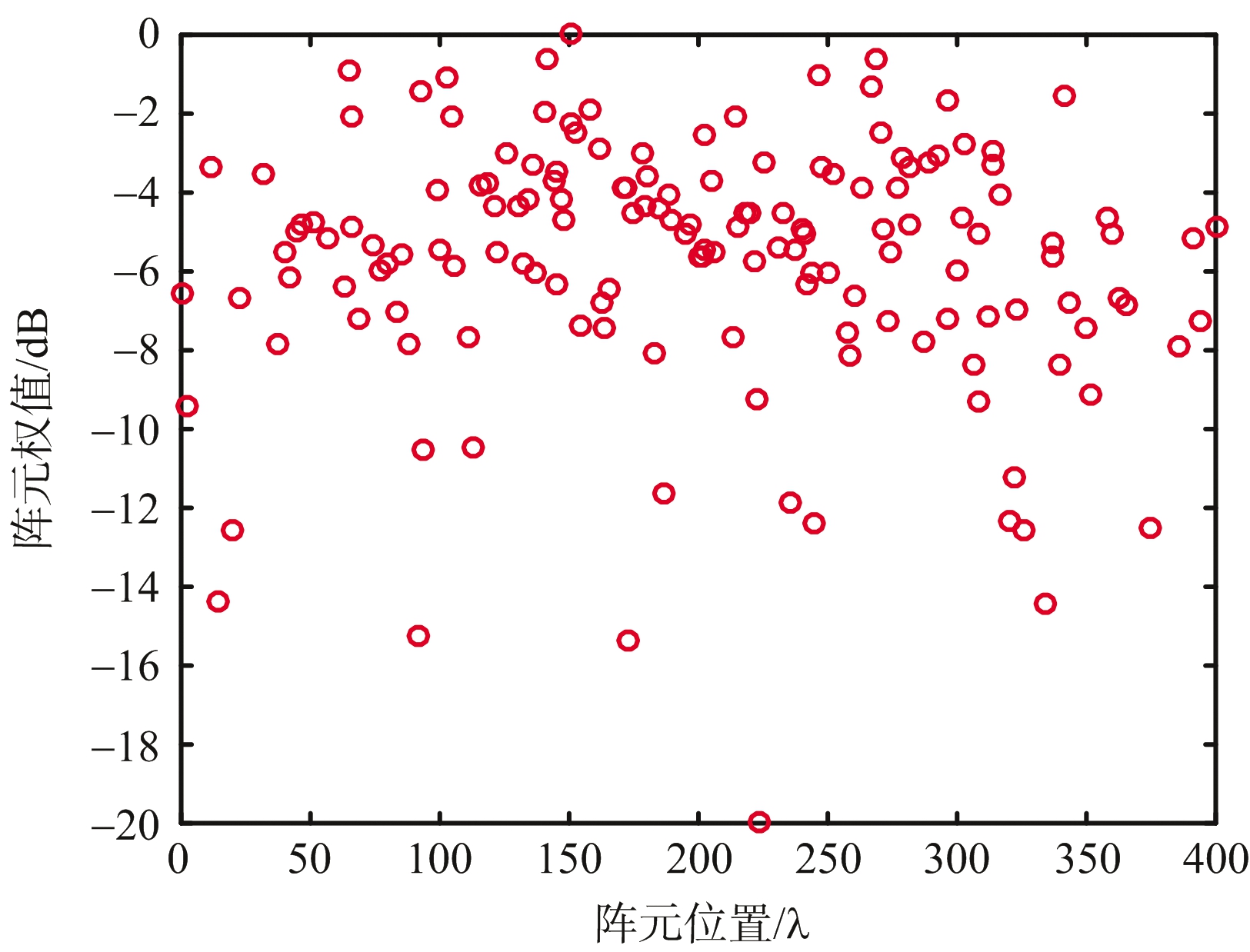
(c) 阵元位置和权值分布
图2 阵列方向图和阵元位置及权值分布
优化后的阵元个数为153个,稀疏率仅为19.1%。且由图2(b)可看出副瓣电平满足约束条件。
仿真三:阵列孔径L=500λ的线阵综合结果。副瓣电平低于-20.4 dB(|θ|≥0.114°),主瓣指向0°,阵列初始间隔d=λ/10。文献[10]对该条件下的阵列进行了优化,其优化结果如图3所示。
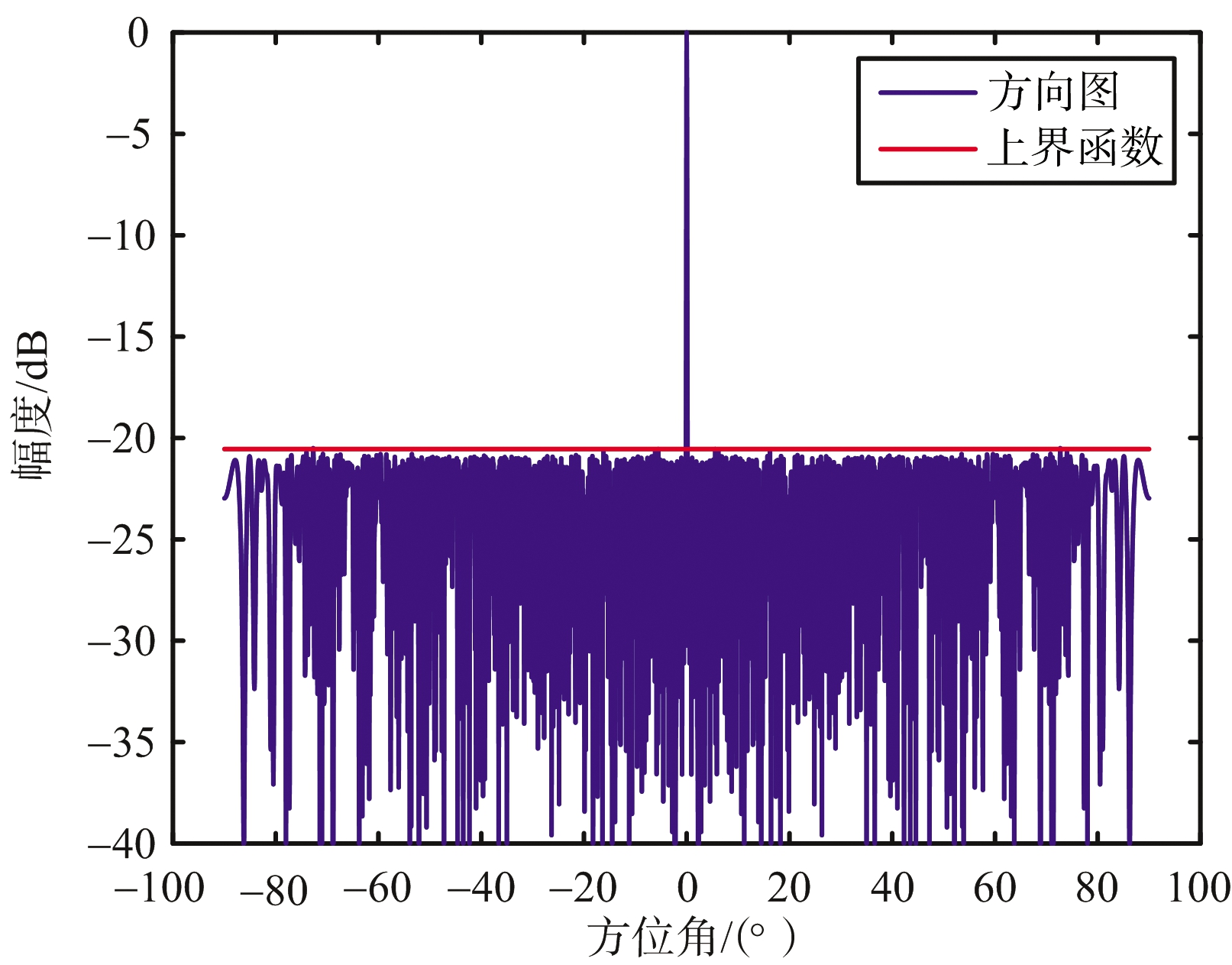
(a) 阵列方向图

(b) 阵元位置和权值分布
图3 阵列方向图和阵元位置分布图
而利用本算法优化后的结果如图4所示,其中图4(b)为图4(a)主瓣区域局部放大图。相较于文献[10],利用本文所提算法,阵元个数仅为188个,稀疏率为18.8%,且由主瓣区域放大图可以看出并无主瓣展宽,副瓣电平也符合预期目标。
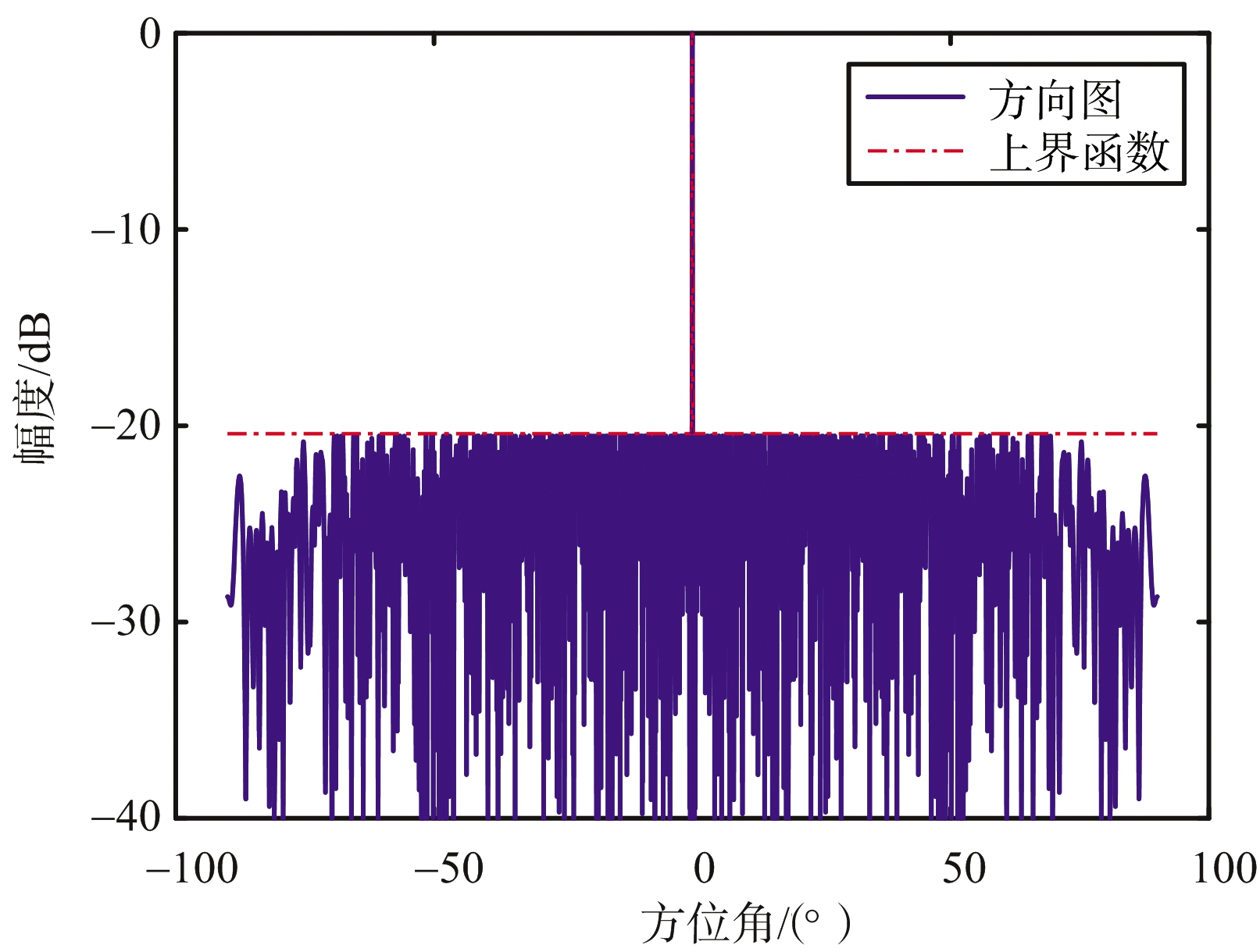
(a) 阵列方向图
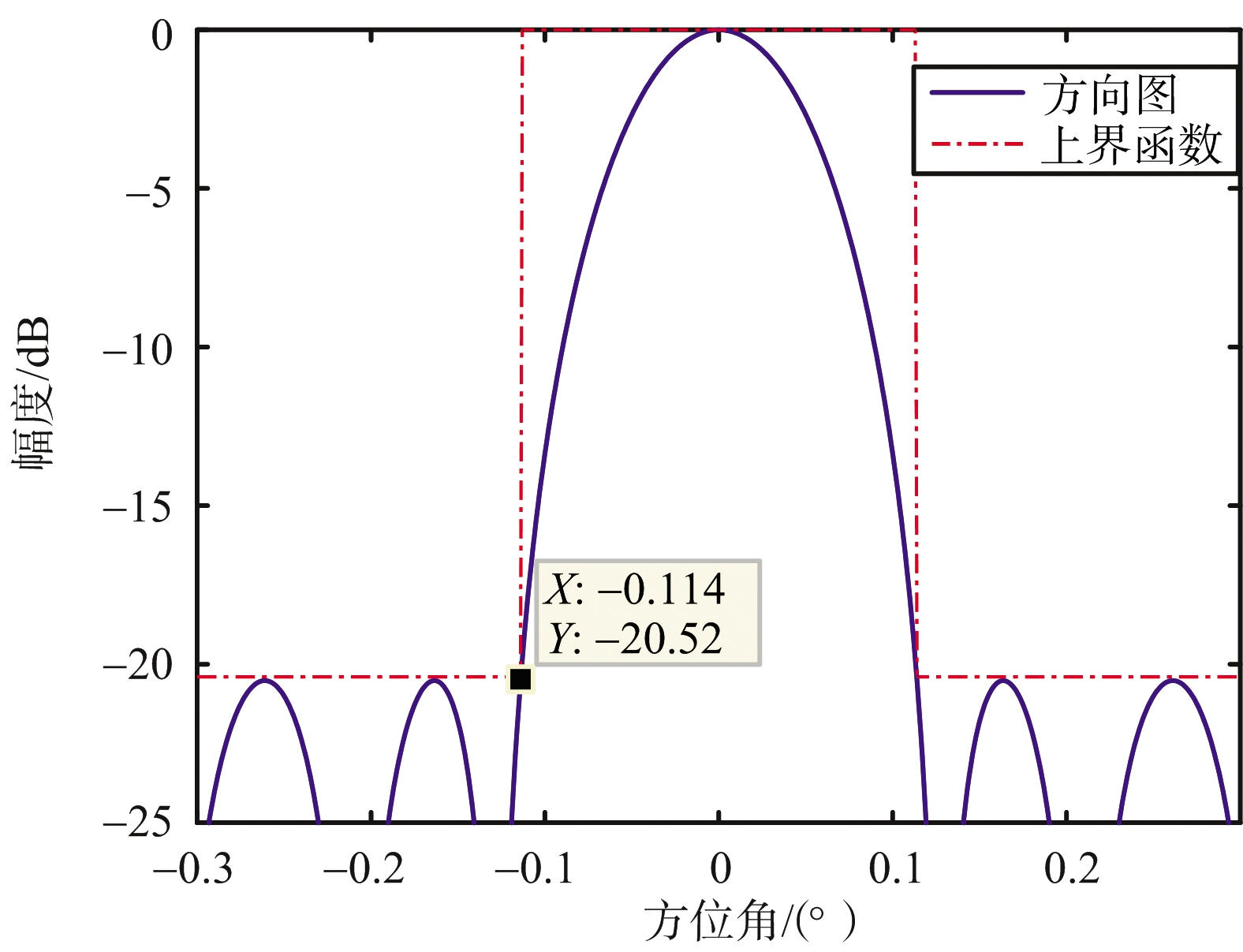
(b) 阵列方向图主瓣放大图
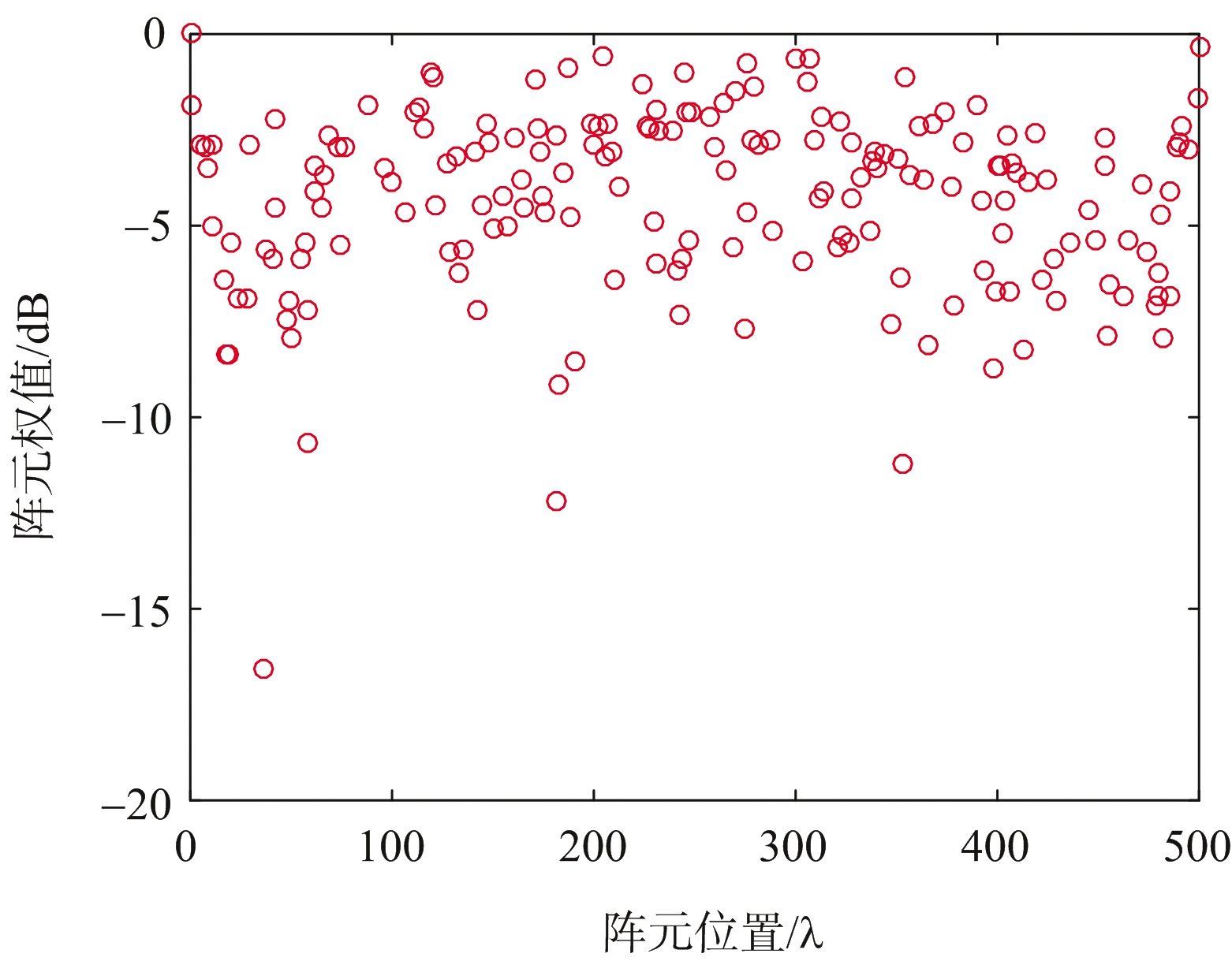
(c) 阵元位置及权值分布图
图4 阵列方向图和阵元位置及权值分布
3 结束语
本文提出了一种针对大孔径稀疏阵列综合的算法。通过利用交替方向乘子的思想使其快速得到初始可行解,并构建相邻域形成新的解空间进行搜索,从而求得更优的稀疏解。文中所提出的算法可有效地实现大孔径下的稀疏阵列的综合并得到相较传统算法更优的布阵结果。通过对若干不同孔径条件下的仿真实验,证明了算法的有效性。
[1] PAL P,VAIDYANATHAN P P. Coprime Sampling and the Music Algorithm[C]∥Digital Signal Processing and Signal Processing Education Meeting (DSP/SPE),Sedona, AZ, USA:IEEE,2011:289-294.
[2] PAL P,VAIDYANATHAN P P.Nested Arrays:A Novel Approach to Array Processing with Enhanced Degrees of Freedom[J].IEEE Trans on Signal Processing,2010,58(8):4167-4181.
[3] MOFFET A.Minimum-Redundancy Linear Arrays[J].IEEE Trans on Antennas and Propagation,1968,16(2):172-175.
[4] WANG Xiangrong,AMIN M,CAO Xianbin.Analysis and Design of Optimum Sparse Array Configurations for Adaptive Beamforming[J].IEEE Trans on Signal Processing,2018,66(2):340-351.
[5] HAUPT L R.Thinned Arrays Using Genetic Algorithms[J].IEEE Trans on Antennas and Propagation,1994,42(7):993-999.
[6] LANZA M,PEREZ J R,BASTERRECHEA J.Particle Swarm Optimization Applied to Planar Arrays Synthesis Using Subarrays[C]∥Proceedings of the Fourth European Conference on Antennas and Propagation,Barcelona, Spain:IEEE,2010:1-5.
[7] TRUCCO A.Weighting and Thinning Wide-Band Arrays by Simulated Annealing[J].Ultrasonics,2002,40(1):485-489.
[8] NAI S E,SER W,YU Z L,et al.Beampattern Synthesis for Linear and Planar Arrays with Antenna Selection by Convex Optimization[J].IEEE Trans on Antennas and Propagation,2010,58(12):3923-3930.
[9] LIANG J,ZHANG X,SO H C,et al.Sparse Array Beampattern Synthesis via Alternating Direction Method of Multipliers[J].IEEE Trans on Antennas and Propagation, 2018,66(5):2333-2345.
[10] PINCHERA D,MIGLIORE M D ,PANARIELLO G.Synthesis of Large Sparse Arrays Using Idea (Inflating-Deflating Exploration Algorithm)[J].IEEE Trans on Antennas and Propagation,2018,66(9):4658-4668.
