0 引言
近年来，穿墙雷达成像在军事和救援安全中具有广泛的应用，建筑物透视雷达技术得到了来自科研界和工业界的广泛关注和研究，并在这十多年间取得了快速的发展。现有穿墙雷达成像算法有后向投影(Back Projection，BP)成像算法，延时求和(Delay and Sum，DAS)和压缩感知稀疏成像算法。BP 算法[1]由于成像原理简单，易于实现，广泛应用于穿墙雷达成像领域。DAS[2]由于其快速、直观的实现，成为雷达应用中最常用的图像形成技术之一，其通过在特定像素点处将由所有通道引起的后向散射贡献累加，来估计该像素点的反射系数。然而BP算法和DAS算法都存在成像旁瓣多、分辨率低等问题。
由于在穿墙探测场景中目标相对于整个成像空间具有稀疏性，因此压缩感知被用于其成像。常用到的稀疏成像算法有贪婪类算法、凸优化以及贝叶斯算法。文献[3]提出了一种在贪婪类正交匹配追踪(Orthogonal Matching Pursuit，OMP)基础上改进的动态阈值弱正交匹配追踪算法，该方法成像的性能有所改善。然而贪婪类方法对弱目标的成像不太友好，BP成像中的栅旁瓣问题同样会出现在此类算法中[4]。文献[5]通过将前一雷达位置的测量值作为边信息加入到当前位置雷达处的场景重构中，有效地实现了隐藏在墙后的静态人体目标检测。然而该方法只是针对点目标的成像。考虑到实际场景中扩展目标更为常见，文献[6]采用可分离逼近结构稀疏恢复算法，充分利用扩展目标信号的结构稀疏先验对其进行稀疏成像重构。然而该方法面临着需要预先设置惩罚参数的问题。为了在保留扩展目标边缘特性的同时, 避免预先人工设置参数，文献[7]进一步提出全变分(Total Variation，TV)约束下的扩展目标稀疏成像方法，利用了目标的先验信息，通过“Integrate-out”方法得到扩展目标的最大后验(Maximum a Posteriori，MAP)估计，然后交替循环迭代至最优解。然而，在穿墙雷达稀疏成像中，由于字典矩阵的存在，成像过程中面临字典存储所占容量大、多次字典求逆和乘法运算导致计算复杂度高等问题。
针对以上问题，本文针对TV约束的MAP稀疏成像方法，考虑到字典矩阵的构建由发射信号和时延共同决定，通过对发射波序列进行变换，将迭代式中包含字典矩阵的所有项用线性卷积和哈希(Hash)表进行代替，从而将迭代循环中繁杂的计算过程进行简化。这种方法可以有效地减少运算时间，并在空间复杂度方面得到了改善，同时在成像质量性能上也得到了提高。
1 信号模型
使用L个收发共置天线单元合成线性阵列，对SOI(scene-of-interest)进行探测，阵列平行于墙体。将SOI离散化为N个像素点，堆叠L个天线的数据，得到雷达回波信号模型为
y=Ax+e
(1)
式中：x表示目标反射系数矢量，x∈CN×1，这里的N为像素点数；y表示回波数据矢量，y∈CML×1，这里的M为每个天线的采样点数；e表示噪声矢量；A表示字典矩阵，A∈CML×N，且
其中的Al用第l个天线构建，第m行第i列的元素为[8]
Al(m,i)=s(mTs-τli)
(2)
采用包含TV约束项的MAP成像模型来重构x，既保留了扩展目标边缘特性，又避免了LASSO问题中惩罚参数需预先人工设定参数问题[7]。假设噪声矢量e服从e～N(0,βI)，βI为噪声的协方差矩阵，则TV约束下关于x的MAP的目标函数为[7]
J(x,β)=
Nlog(‖Dx‖1)+MLlogβ
(3)
2 算法描述
首先对式(3)的前三项分别进行优化最小化(Majorize-Minimize，MM)替代[9]，然后对替代后的目标函数J(x,β)求解关于x和参数β的偏导数，并令其倒数为0，得到β和x的第i个元素xi的迭代式[10]，即
(4)
和
(5)
式中：
这里的nj是字典A的第j行中非零元素的数量；
从式(4)和式(5)可以看出，在计算β和x(包含
和Hi)都需要A的构造、存储和计算，因此需要的存储空间大，计算复杂度也高。接下来，结合文献[11]的思想简化β和x的计算，并在此基础上进行改进以适合任意超宽带波形。
2.1 β(t+1)的计算
在式(4)中，
只要求出Alx(t),l=1,2,…，L就可得到Ax(t)。令
并假设它的最小时延和最大时延分别为mmin和mmax，则有Alx(t)的第m个元素为
Alx(t)[m]=
m=1,2,…，M
(6)
记
gl[m]≜Alx(t)[m]
(7)
s(mTs)≜u[m]
(8)
利用冲激函数的抽样特性，得到
gl[m]=
(9)
令
则
(10)
可以看出，式(7)的运算转换为式(10)的pl和u的卷积计算，避免了A的构建、存储和计算。而且，这里的pl[n]通过将延时序列中满足{mli=n|mli=[ml1,ml1,…,mlN]}的第i个像素点所对应的
的值进行累加得到，其调用Hash表(即MATLAB的accumarray函数)就可以快速计算[11]。根据式(4)和式(10)，可得
(11)
的计算
将式(2)和式(7)代入
可得
(12)
令z[M+1-m]≜s(mTs)，则有
(13)
可以看出，的运算转换为z和(yl-gl)的卷积计算，也避免了A的构建、存储和计算。而且，通过对这里的s(mTs)用z[M+1-m]替换，使得式(13)对任何超宽带发射波形都可以将转换为卷积的计算，而不限于文献[11]所提到的对称的发射波。
2.3 Hi的计算
由式(2)可知，
Hi=
(14)
令f[M+1-m]≜s2(mTs)，则有
Hi=
(15)
同样，Hi的运算转换为nl(nl[m]表示Al的第m行中非零元素的数量)和f的卷积计算，也避免了A的构建、存储和计算。而且，通过对这里的s2(mTs)进行替换，使所提方法同样对任何超宽带发射波形都可以将Hi转换为卷积的计算，而不限于对称的发射波。
值得一提的是，如果要快速得到Hi，那么nl的计算是至关重要的。因为发射信号是超宽带信号，也就是时域为短时信号，所以对于长度为M的发射序列u[m](即s(mTs))而言，存在一个整数Q，当满足mTs≤QTs时，使得u[m]不为零。考虑矩阵Al的第i列为Al=[s(Ts-τli),s(2Ts-τli),…,s(MTs-τli)]T，则元素Al(m,i)非零当满足
1≤m-mli≤Q
(16)
且离散时延mli满足
mmin≤mli≤mmax
(17)
所以有
max(mmin,m-Q)≤mli≤min(mmax,m-1)
(18)
即
(19)
式中，φn={i=1,2,…,N|n=mli}表示第l个天线关于N个像素网格点的时延，它是满足{mli=n|mli=[ml1,ml2,…,mlN]}的mli的个数，可通过Hash表[11]求得。
3 复杂度分析
从前面的分析可知，若文献[10]采用100%回波数据重构，在迭代更新β时，它和本文的不同点体现在计算Ax上。文献[10]更新Ax所需乘法MLN次，所需加法为MLN-ML次，而采用本文方法需调用L次卷积函数和L次accummary函数(求pl[n]时用到)。文献[10]更新Hi的过程中涉及到求解字典矩阵A中每行非零元素个数，只能对字典A逐行搜索求解，则本文方法利用发射波的短时特性，只需调用L次accummary函数计算nj,j=1,2,…,ML。在已知nj的情况下，文献[10]更新全部的H=[H1,H2,…,HN]所需乘法为2MLN次，所需加法为MLN-N次，而采用本文方法需调用L次卷积函数，然后对不同的像素点i，取式(15)中L个卷积序列所对应的第γ个元素进行累加，即可得到所有的Hi。在迭代更新G时，更新全部的G=[G1,G2,…,GN]所需乘法为2MLN次，所需加法为2MLN-N次，而采用本文方法需调用L次accummary函数(求pl[n]时用到)，2L次卷积函数以及ML次加法运算，然后对不同的i，取式(13)中L个卷积序列所对应的第γ个元素进行累加，即可得到所有的Gi，降低了计算复杂度。
4 仿真及实验结果分析
4.1 仿真结果
仿真场景模型如图1(a)和图2(a)所示，距离天线1 m处长为3 m的墙体由均匀介质材料构成，其墙厚为0.2 m、相对介电常数为4.5、电导率为0.01 S/m。由GprMax电磁仿真软件产生仿真数据，仿真中采用发射波中心频率为1 GHz的窄高斯脉冲信号。仿真场景中，矩形目标体长均为0.5 m、宽为0.2 m，目标距墙体距离为1 m。
以单个目标为例，表1给出了文献[10]分别采用100%、50%和10%的回波数据以及本文方法在单次循环(即更新一次x和β)的时间(Per-Time)、总运行时间(Total Time)和分配的内存(Total Memory)3个方面的对比。从表1可知，对比文献[10]采用100%回波数据重构时的结果，本文方法的运算时间减少2/3左右，分配内存减少3/5左右；而相比文献[10]采用50%回波数据重构的结果，运算时间减少3/5左右，分配内存减少2/5左右；即使文献[10]采用10%的回波数据来重构，运算时间仍减少达2/5左右，分配内存也小到3/4左右。由此看来，本文方法有效地减少了运行时间和分配的内存。
表1 Per-Time、Total Time和Total Memory的比较
算法Per-TimeTotalTimeTotalMemory文献[10]100%采样17.619460s127.557s2642692.00Kbit文献[10]50%采样15.673452s96.028s1854984.00Kbit文献[10]10%采样14.557463s72.334s1372700.00Kbit本文方法11.056422s40.679s1036680.00Kbit
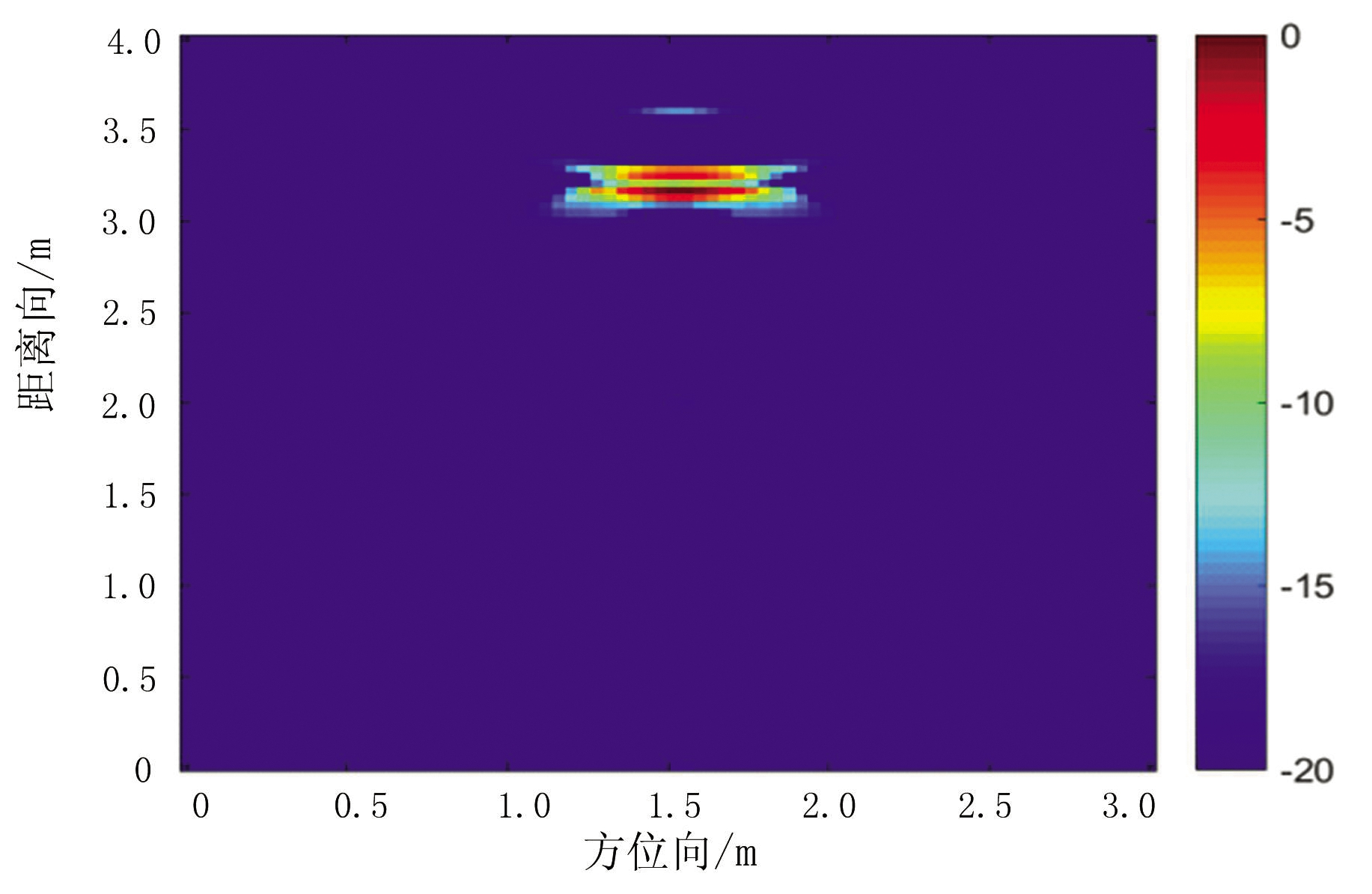
图1(b)到图1(f)分别为单个目标情况下采用BP算法和文献[10]100%、50%、10%的回波数据以及本文方法的重构结果。图2(b)到图2(d)给出了两个目标情况下BP算法、文献[10](采用100%的回波数据)以及本文方法的重构结果。可以看出，传统BP方法成像效果最差，杂波最多。本文方法成像最为清晰，且目标边缘轮廓明显。为了更直观地对重构质量进行对比，表2给出单个目标情况下其在TCR、ENT和MFOD三方面的对比，分别反映了目标杂波比、图像熵和目标的边缘轮廓特性。对比发现，本文方法和文献[10]方法的TCR都比BP成像大，ENT都比BP成像小，说明这两种方法的成像对比传统BP方法杂波少，图像清晰。本文方法的TCR最大，ENT最小，成像性能最优。文献[10]在采用3种不同的回波数据重构时，100%的回波重构时性能相对最好，而此时所提方法仍略优于文献[10]。MFOD反映了区域的平滑性，其值越小，目标的边缘轮廓特性越强，结合MFOD和表1中总运行时间对比可知，本文方法在减少运算时间的同时，并没有损坏扩展目标的边缘特性。
表2 TCR、ENT和MFOD的比较
算法TCRENTMFODBP方法3.13441.76300.1610文献[10]100%采样5.50091.05720.1416文献[10]50%采样5.39561.05870.1425文献[10]10%采样5.35641.06020.1426本文方法5.65370.90070.1410
(a)仿真场景
(b)BP成像
(c)文献[10]100%数据的重构结果
(d)文献[10]50%数据的重构结果
(e)文献[10]10%数据的重构结果
(f)本文方法的重构结果
图1 单个目标情况下成像结果对比
(a)仿真场景
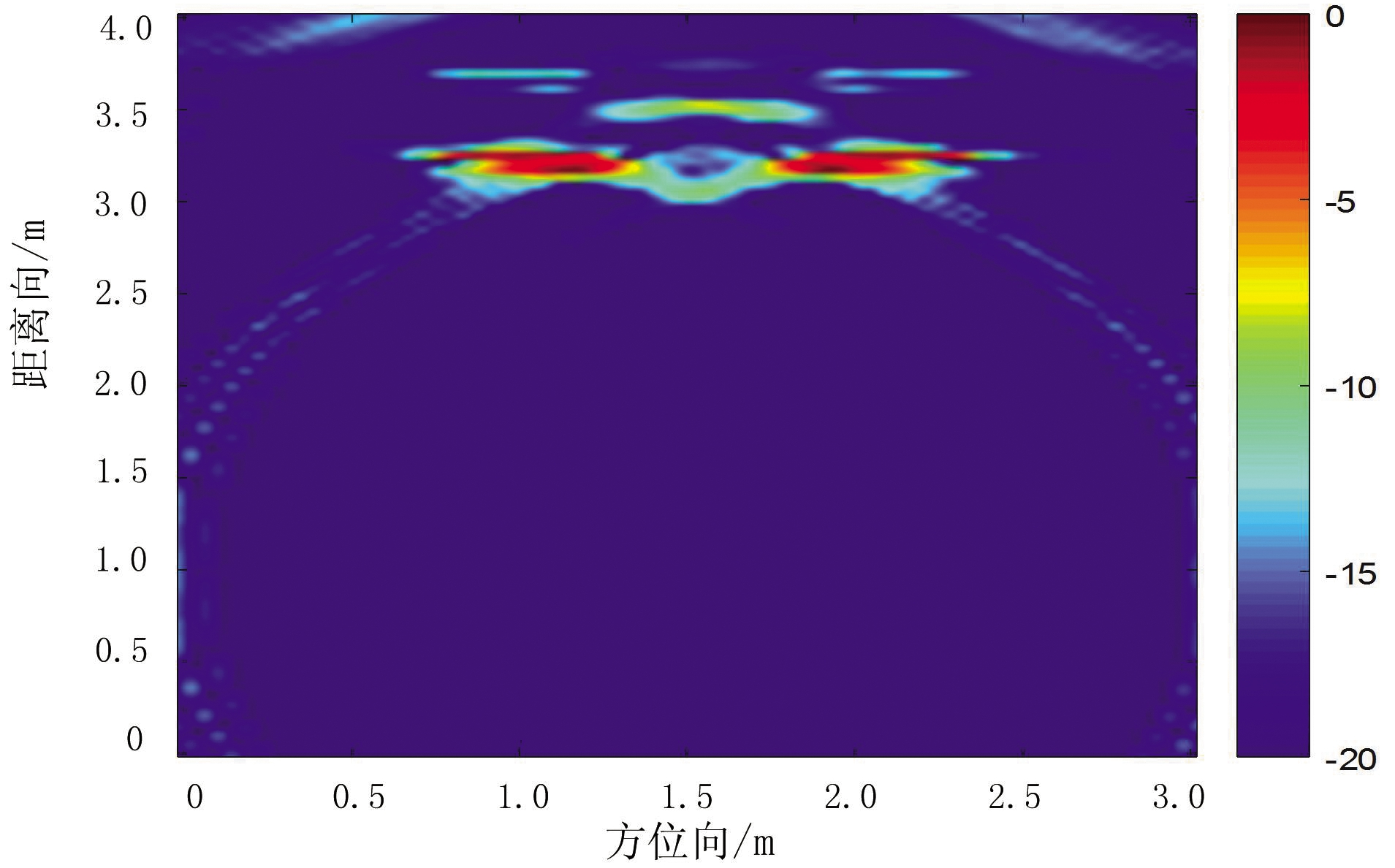
(b)BP成像
(c)文献[10]的重构结果
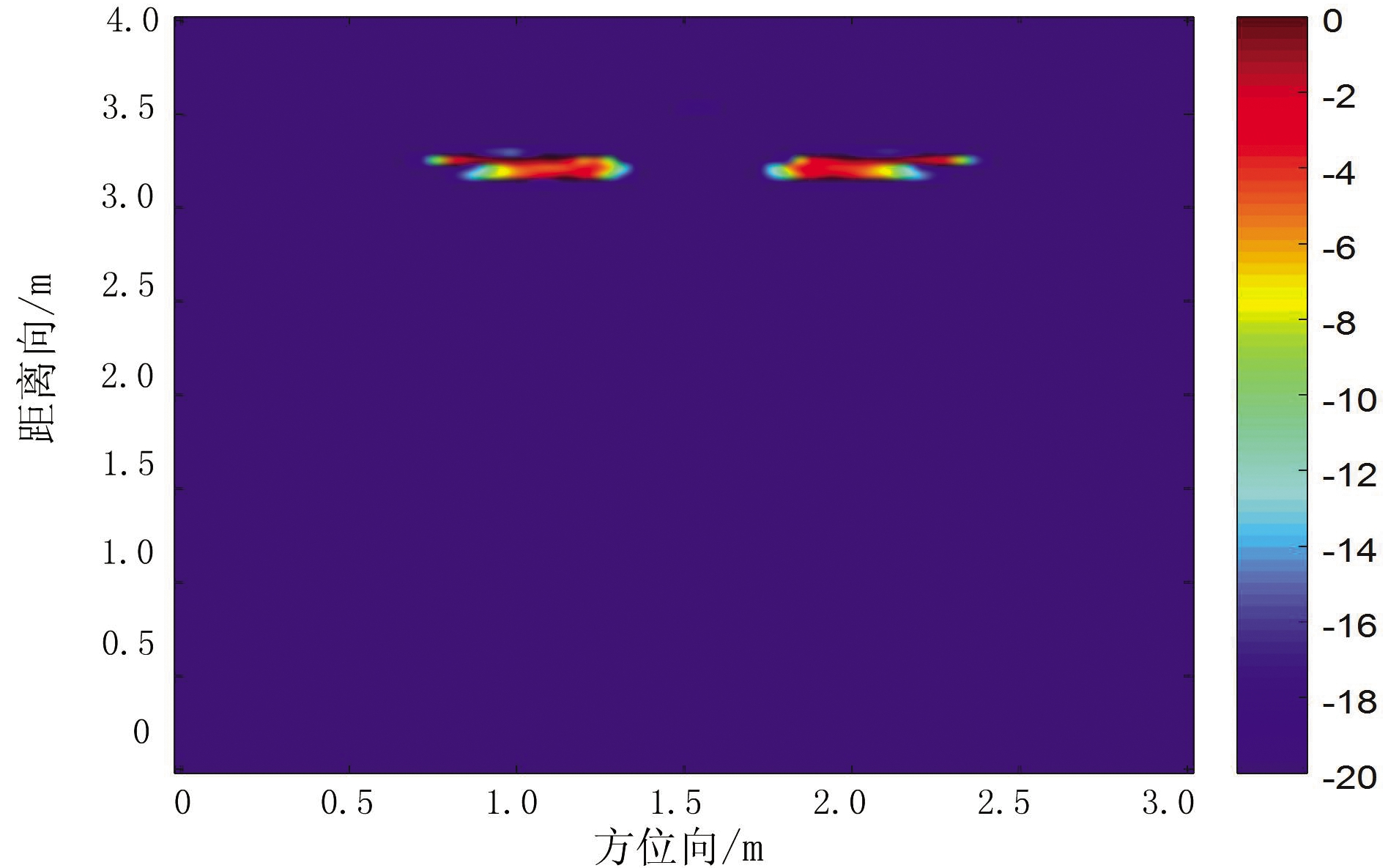
(d)本文方法的重构结果
图2 两个目标情况下成像结果对比
4.2 实测结果
实际探测场景如图3所示，实测数据集采用维拉诺瓦(Villanova)大学高级通信中心(CAC)与空军研究实验室(AFRL)合作收集得到的穿墙雷达成像实验数据集。数据使用型号为ENA 5071B的安捷伦网络分析仪收集。实验采用以2.5 GHz为中心的带宽为1 GHz的步进频率波形，步进间隔为5 MHz，文献[12]给出了场景的详细介绍。本文采用其中的一个场景进行实验验证，选取平面阵列中高度位于中心位置的一排天线所得到的数据进行二维平面成像。图4和图5分别为传统BP和本文方法成像结果，可以发现，后者重构结果杂波少。在运行时间上，采用BP重构、文献[10](采用100%的回波数据)重构和本文方法重构时间分别为3.339,121.346和38.473 s; 后两者在运行所需内存上分别为2 231 542 Kbit和914 623 Kbit。可以发现，对比文献[10]，本文方法有效地降低了运行时间和所需内存。
图3 实验场景
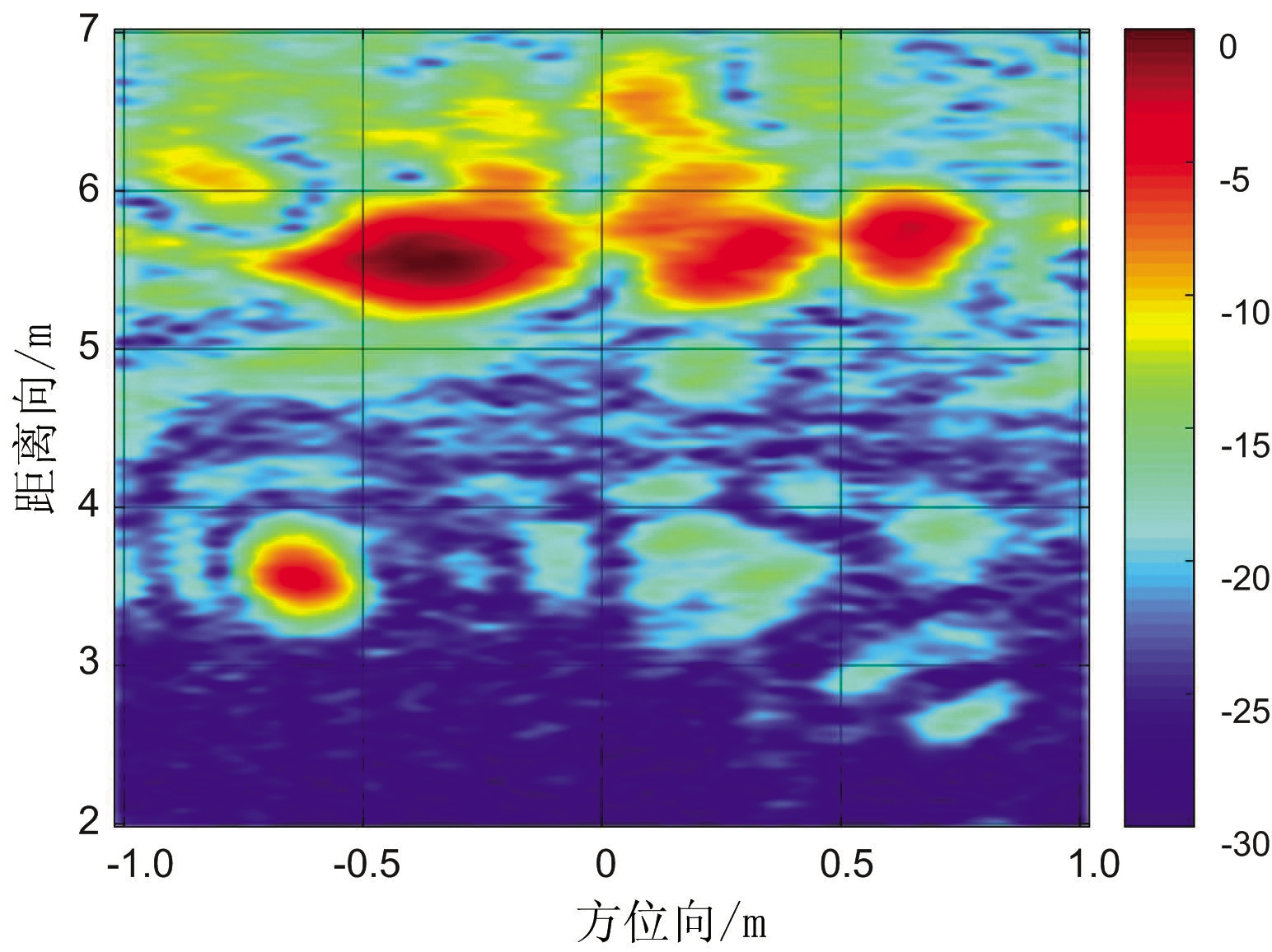
图4 BP成像
图5 本文方法的重构结果
5 结束语
本文提出一种在MM优化的TV约束MAP估计框架下，无需构建感知字典的超宽带穿墙雷达稀疏成像的快速实现方法。仿真结果和实验结果表明，通过与BP成像和文献[10]方法重构的图像相比，得到的图像有更少的噪声，能捕捉SOI内主要的散射点，有效抑制了旁瓣和栅瓣。而且，在提升运算速度和占用内存更少的同时，有效地保留了扩展目标的边缘特性。该方法为大数据量成像系统，如三维成像提供了重要的参考。
[1]CUI Guolong, KONG Lingjiang, YANG Jiangyu.A Back-Projection Algorithm to Stepped-Frequency Synthetic Aperture Through-the-Wall Radar Imaging[C]∥2007 1st Asian and Pacific Conference on Synthetic Aperture Radar, Huangshan, China:IEEE,2007:123-126.
[2]AHMAD F,AMIN M G,KASSAM S A.Synthetic Aperture Beamformer for Imaging Through a Dielectric Wall[J].IEEE Trans on Aerospace & Electronic Systems, 2005, 41(1):271-283.
[3]余杰,夏朝禹,杜江.基于CS-TWR的动态阈值贪婪算法成像研究[J].成都信息工程大学学报,2019,34(5):462-465.
[4]金添, 宋勇平.超宽带雷达建筑物结构稀疏成像[J].雷达学报, 2018, 7(3):275-284.
[5]BECQUAERT M, CRISTOFANI E, LAUWENS B, et al.Online Sequential Compressed Sensing with Multiple Information for Through-the-Wall Radar Imaging[J].IEEE Sensors Journal, 2019, 19(21): 4138-4148.
[6]戴耀辉, 晋良念.联合感知矩阵优化的穿墙MIMO阵列稀疏成像方法[J].现代雷达, 2018, 40(12):34-40.
[7]张燕,晋良念.结合TV约束的穿墙雷达扩展目标成像方法[J].雷达科学与技术,2017,15(3):229-235.
[8]WU H, WANG F.Parametric Sparse Recovery Method for TWR Imaging with Unknown Wall Parameter[C]∥ 2018 International Applied Computational Electromagnetics Society Symposium in China, Beijing, China:IEEE, 2018:1-2.
[9]ZHANG Qiping, ZHANG Yin, HUANG Yulin, et al.Sparse with Fast MM Superresolution Algorithm for Radar Forward-Looking Imaging[J].IEEE Access, 2019, 7:105247-105257.
[10]张燕.非均匀墙体下超宽带穿墙雷达成像方法[D].桂林:桂林电子科技大学,2017.
[11]NDOYE M, ANDERSON J M M, GREENE D J.An MM-Based Algorithm for l1-Regularized Least-Squares Estimation with an Application to Ground Penetrating Radar Image Reconstruction[J].IEEE Trans on Image Processing, 2016, 25(5):2206-2221.
[12]DILSAVORA R, AILESB W, RUSH P, et al.Experiments on Wideband Through-the-Wall Radar Imaging[EB/OL].(2005-05-19)[2020-01-19].https:∥spie.org/Publications/Proceedings/Paper/10.1117/12.607742?SSO=1.
