0 引言
主瓣干扰是指从雷达主瓣或近主瓣方向进入的干扰信号，能够获得雷达主瓣增益，对雷达探测性能影响十分严重[1]。在面对主瓣干扰时，传统的针对副瓣干扰的对抗措施不能继续生效，因此研究新的抗主瓣干扰方法具有重要意义。
当干扰从主瓣进入时，常规的自适应波束形成算法会在雷达主瓣波束方向上形成零陷凹口，导致主瓣产生畸变、旁瓣大幅抬高，性能损失严重。文献[2]发现在自适应波束形成的实现中存在协方差矩阵失配，并利用线性约束下的对角加载方法克服失配以及校正主瓣方向上的失真，但加载因子的计算较为复杂。文献[3]提出在自适应波束形成中用阻塞矩阵进行预处理，能够大幅降低计算复杂度。在此基础上，文献[4]提出一种新的阻塞矩阵方法，能够消除期望信号和主瓣干扰对协方差矩阵的贡献，从而避免了零陷凹口的产生。但构造阻塞矩阵需要知道精确的干扰方位角，方位角测量误差会较大影响最终的抗干扰效果。由于干扰信号和雷达回波信号可认为互相独立，文献[5]提出将盲源分离JADE方法应用于雷达抗主瓣干扰中，即将抑制干扰的过程看成信号分离的过程。
目前，噪声调频干扰是最常见的主瓣干扰形式之一。由于噪声调频干扰信号幅度起伏较小，可近似看作恒模信号，文献[6]提出了一种基于时域对消的干扰抑制方法，利用接收信号的幅度相位信息估计干扰信号，然后将接收信号和重构干扰信号对消，达到抑制干扰的目的。文献[7]在此方法基础上引入了滑动平均，以适应于幅度稍有起伏的主瓣干扰信号。然而该方法在对消干扰信号时，干扰信号依然有残留，会使目标位置附近距离旁瓣升高，影响小目标的检测。而且回波信号也有一定的损失，脉压峰值会降低6 dB。
本文通过进一步的数学推导，得到经干扰对消后的信号的具体形式，找到在一次对消后残余的干扰项。为补偿脉压峰值的6 dB损失，通过时变滤波法补偿了对消后的脉压能量损失。然后，在一次对消的基础上，对目标位置处剩余干扰作进一步修正，可使该位置旁瓣下降，临近小目标检测性能提升。最后通过MATLAB仿真实验验证，说明该算法的有效性。
1 时域对消算法
噪声调频干扰信号生成容易且干扰效果明显，是一种主要的雷达主瓣压制干扰方式。噪声调频干扰信号可表示为
J(t)=Ajexp(jωjt+2πkfm
un(t)dt+φ)
(1)
式中，Aj为干扰信号的幅度，ωj为干扰信号的中心频率，kfm为调频斜率，调制噪声un(t)为零均值带限高斯噪声，φ为[0,2π]上均匀分布的随机相位。
时域对消法通过接收信号的幅度信息和相位信息重构干扰信号，然后将接收信号和重构信号做差得到目标回波的估计。假设接收信号为
x(t)=s(t)+J(t)+n(t)
(2)
式中，s(t)=As(t)ejφs(t)为目标回波信号，J(t)=Ajejφj(t)为恒模的噪声调频信号，n(t)为加性高斯白噪声。当干扰信号功率很大时，n(t)的干扰效果会非常小，为了方便，将s(t)和n(t)合记为
s′(t)=s(t)+n(t)=A′(t)ejφ′(t)
(3)
则接收信号可以写成：
(4)
为叙述方便，将式(4)中括号内的第二项记为s1(t)。因为Aj≫A′(t)，对接收信号做取对数运算，近似得到
ln[x(t)]=ln(J(t))+ln[1+s1(t)]≈
ln(Aj)+jφj(t)+s1(t)
(5)
为将干扰信号的幅度信息和相位信息分离开，分别取其实部Rx(t)和虚部Ix(t)：
(6)
Ix(t)=Im{ln[x(t)]}=φj(t)+Im[s1(t)]-2kπ
(7)
注意此时的Ix(t)取值范围为[-π,π]。因为s1(t)可以认为是零均值信号，则可以估计干扰信号J(t)的幅值为
(8)
结合式(8)估计出的干扰幅度信息和式(7)中的干扰相位信息，重构干扰信号:
(9)
将重构信号从接收信号中减去，可得回波信号的估计为
(10)
对
进行匹配滤波，可以检测到目标。图1给出了时域对消算法流程。
图1 时域对消算法流程图
但是，该方法并不能完全对消掉干扰信号，且在对消后剩余信号中，回波信号也有一定的损失。
2 改进时域对消算法
2.1 信噪比损失推导
将式(10)展开，有
A′(t)ejφ′(t)
(11)
利用
整理为
-jA′(t)ejφj(t)sin(φ′(t)-φj(t))+
A′(t)ejφ′(t)
(12)
然而，式(12)中第一项为复数信号和正弦信号的乘积形式，其中复数项含有干扰信息，正弦项同时含有回波信息和干扰信息，不能明显地表现出对消后信号与真实回波信号的关系。为说明对消后得到的信号中究竟含有多少回波信息，我们对该项进行恒等变换，将只含有回波信息的部分从中提取出来。为表示方便，在计算时省略幅度项A′(t)：
-jejφj(t)sin(φ′(t)-φj(t))=
-j(cosφj(t)+jsinφj(t))(sinφ′(t)cosφj(t)-
cosφ′(t)sinφj(t))=
sinφ′(t)sinφj(t)cosφj(t)+j·cosφ′(t)sinφj(t)cosφj(t)-
j·sinφ′(t)cos2φj(t)-cosφ′(t)sin2φj(t)=
sin2φj(t)(j·cosφ′(t)+sinφ′(t))-j·sinφ′(t)cos2φj(t)-cosφ′(t)(1-cos2φj(t))
[cosφ′(t)-jsinφ′(t)]+cos2φj(t)[cosφ′(t)-
jsinφ′(t)]-cosφ′(t)=
(13)
将式(13)的结果乘以幅度项A′(t)，得到
-jA′(t)ejφj(t)sin(φ′(t)-φj(t))=
(14)
所以式(12)可整理成如下形式：
(15)
从式(15)可以看出对消后信号
中包含的回波信息与真实回波相比，幅度降低一半，不利于目标检测。
2.2 改进时变滤波算法
2.2.1 时变滤波器脉冲压缩
在式(15)中可见，回波位置处的残余干扰项与时间有关，且通过信号的匹配滤波器后没有增益，故脉压峰值将会有6 dB的损失。为补偿该损失，可采用时变滤波器作脉冲压缩，将对消后信号回波位置处的干扰残余项也作匹配处理。因为干扰项和回波项的幅度相等，且也为恒模信号，若经过匹配处理，恰好会补偿上6 dB的损失。
设发射信号的脉冲时长为T，回波延时为τ，则与时间区间[τ,τ+T]处的信号相匹配的信号应为
(16)
在脉冲压缩处理时，对所有的延时τ，都应使用与该时延处相匹配的时变滤波器作脉冲压缩，其中，在构造时变滤波器时，干扰的相位φj(t)可使用式(7)中的Ix(t)代替。则任意延时τ处的脉冲压缩结果应为
y(τ)=
(ej2Ix(t)e-jφs(t-τ)+ejφs(t-τ))dt
(17)
此时，由于残留干扰信号也得到了匹配增益，脉压峰值损失的6 dB得到了补偿。
2.2.2 修正目标位置干扰
对消后信号经时变滤波器脉冲压缩处理后，虽然增强了检测性能，但残留干扰项依然会使目标位置处距离旁瓣升高，所以，在强目标附近的小目标可能会被淹没从而造成漏警。为提取小目标，可在目标位置处进一步修正对消后信号
首先，需要计算出强目标位置处的真实回波幅度。由于脉压峰值损失已经得到补偿，则可认为目标处脉压峰值实际对应真实回波信号幅度。设由某延时τ位置处脉压峰值为yi,则该位置回波信号幅度Ai为
(18)
则该位置残留的干扰项可用下式近似替代：
(19)
在求得所有目标位置处的干扰残余项后，可修正对消后信号
(20)
将经修正后的信号s'(t)进行匹配滤波处理，可使目标位置处距离旁瓣下降，临近小目标能够被检测。
2.3 改进时域对消算法流程
本节给出改进的时域对消算法流程：
Step 1 将接收信号取对数并保存其实部和虚部：Rx(t)=Re{ln[x(t)]}, Ix(t)=Im{ln[x(t)]}；
Step 2 重构干扰信号：
Step 3 时域对消：
Step 4 时变滤波器脉压检测：
Step 5 计算时变滤波结果第i个峰值对应回波幅度Ai，并构造第i个目标位置处的干扰修正项：
Step 6 修正目标位置干扰，提取小目标：
Step 7 匹配滤波：
改进算法与原算法相比，额外计算量出现在时变滤波器的构造上。相比于匹配滤波，时变滤波需要计算的复数乘法次数增加一倍，但实时计算速度不会受很大影响，并能带来更好的检测性能。图2给出改进时域对消算法流程图。
图2 改进时域对消算法流程
3 仿真实验
设雷达发射信号为线性调频信号，时宽为100 μs，带宽为2 MHz。噪声调频干扰的调制噪声un(t)为带宽2 MHz，方差
的带限噪声，调频指数mfe=0.2。设噪声调频干扰幅度为20，回波幅度为1，回波延迟为200 μs，图3给出接收信号和对消后信号的时域波形和脉压结果对比。
(a)对消前处理结果
(b)对消后处理结果
图3 干扰抑制前后对比
可见，经时域对消后，大部分干扰信号被抑制掉，能够检测到原本被压制的目标。由式(15)知，在对消后剩余信号中，回波信号幅度仅为真实回波幅度的一半。对消后信号与真实回波信号相比，脉压峰值降低6 dB，如图4所示。
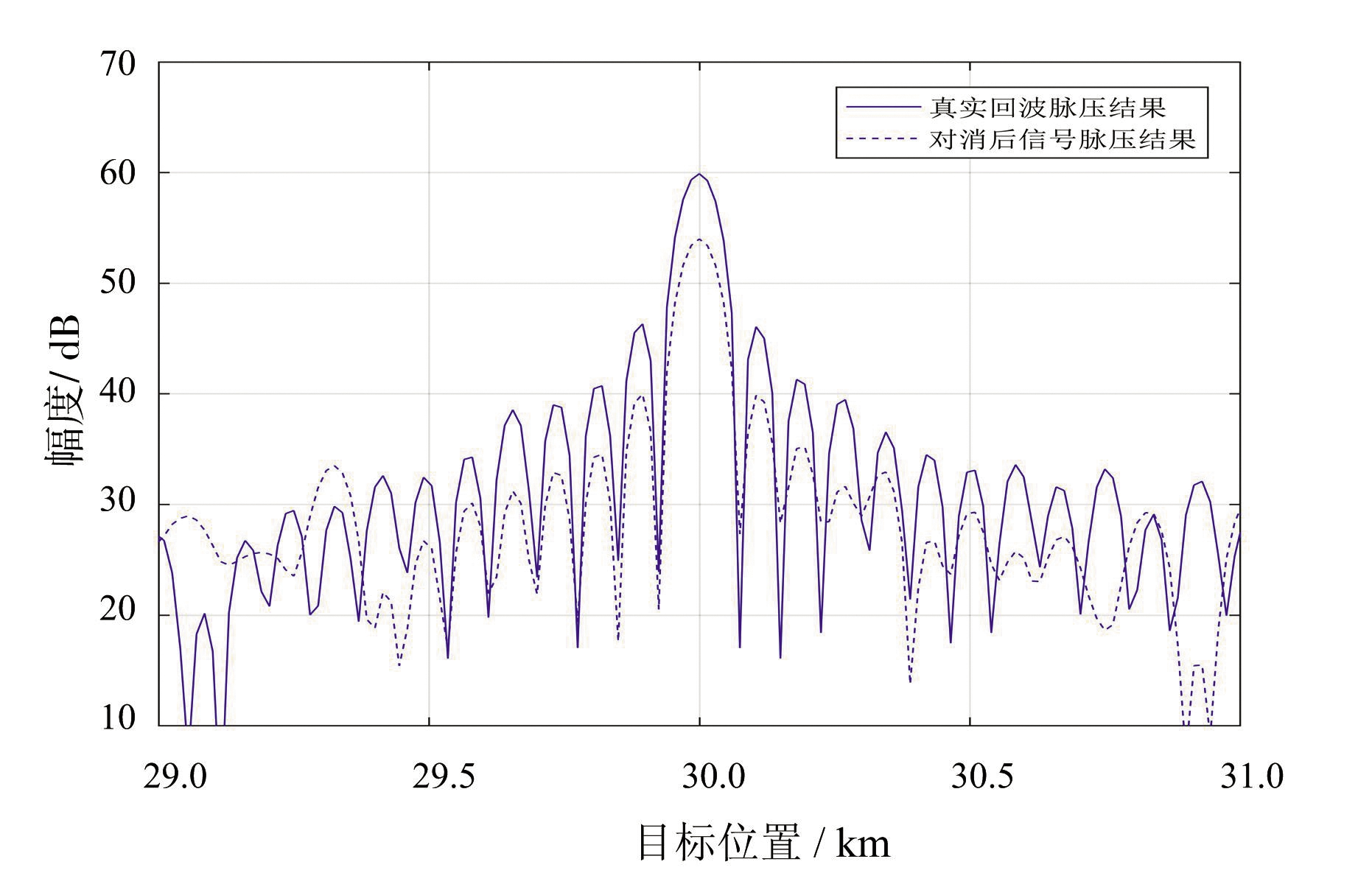
图4 对消后剩余信号与真实回波信号脉压结果对比
在相同仿真条件下，图5给出对消后信号经匹配滤波器脉压结果和经时变滤波器脉压结果的对比。可见，经时变滤波检测处理后，脉压峰值升高6 dB，信号损失得到补偿。
(a)匹配滤波处理结果
(b)时变滤波处理结果
图5 时变滤波与匹配滤波对比
图6给出临近目标的识别结果。其中主目标回波信号幅度为1，回波延迟为200 μs，临近小目标幅度为0.1，回波延迟为215 μs。可见，在修正目标位置干扰前，主目标的距离旁瓣将临近小目标被淹没，只能看到一个目标。通过对干扰二次修正后，主目标的距离旁瓣被明显抑制，使得临近小目标被提取，干扰抑制程度提升。
(a)二次修正干扰前脉压结果
(b)二次修正干扰后脉压结果
图6 修正目标位置干扰前后的对比
图7给出使用带宽为2 MHz的噪声调频连续波实测干扰数据进行验证：雷达中频带宽为 5 MHz，DDC后数据率为 20 MHz，重频周期为318.5 μs，干扰信号平均幅度为2 800。设发射信号为时宽100 μs，带宽2 MHz的线性调频信号，主目标幅度为600，回波延迟为50 μs，小目标幅度为120，回波延迟为35 μs。结果表明该方法有效。
(a)对消前脉压处理结果
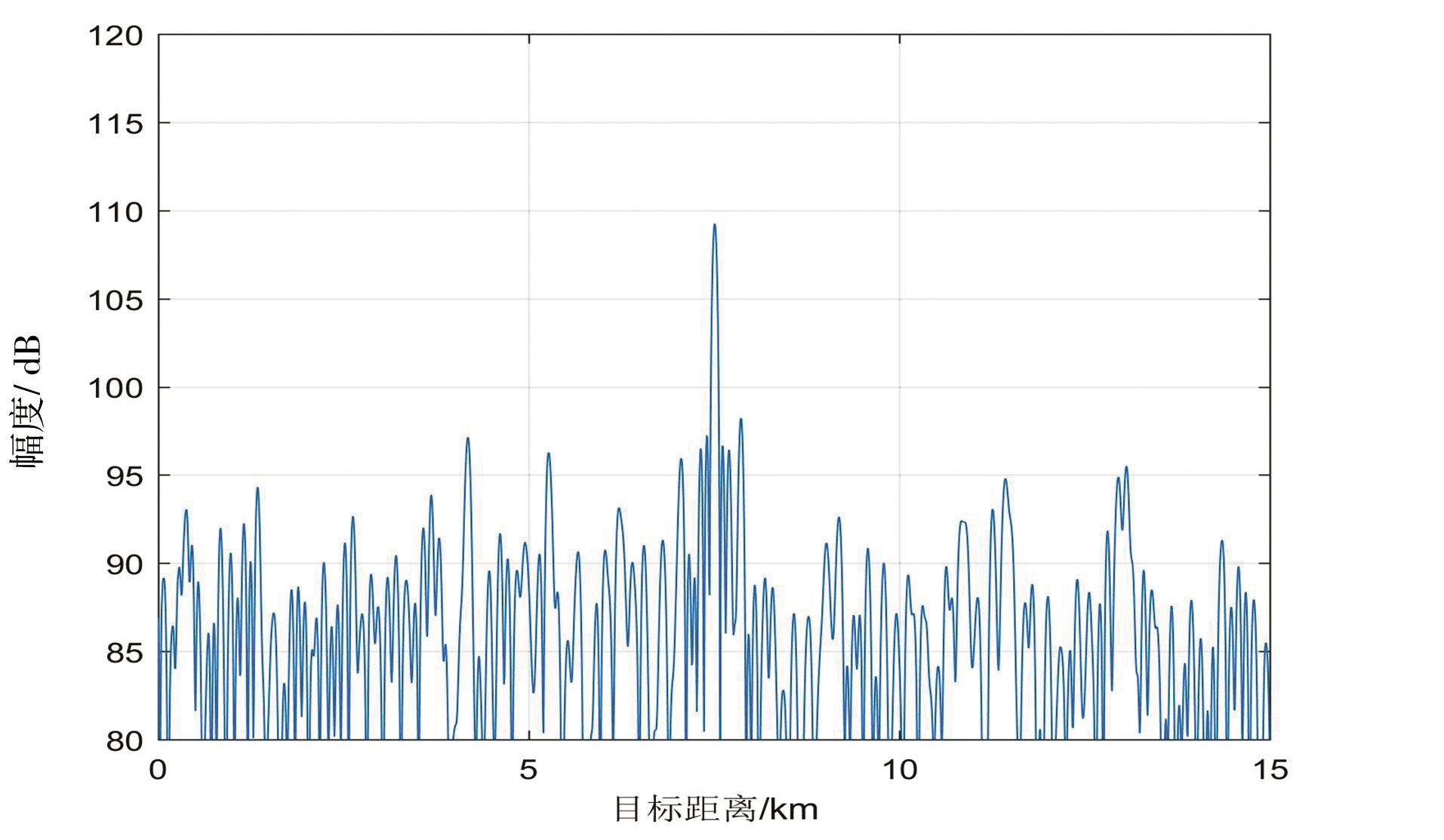
(b)对消后匹配滤波脉压结果
(c)对消后时变滤波脉压结果
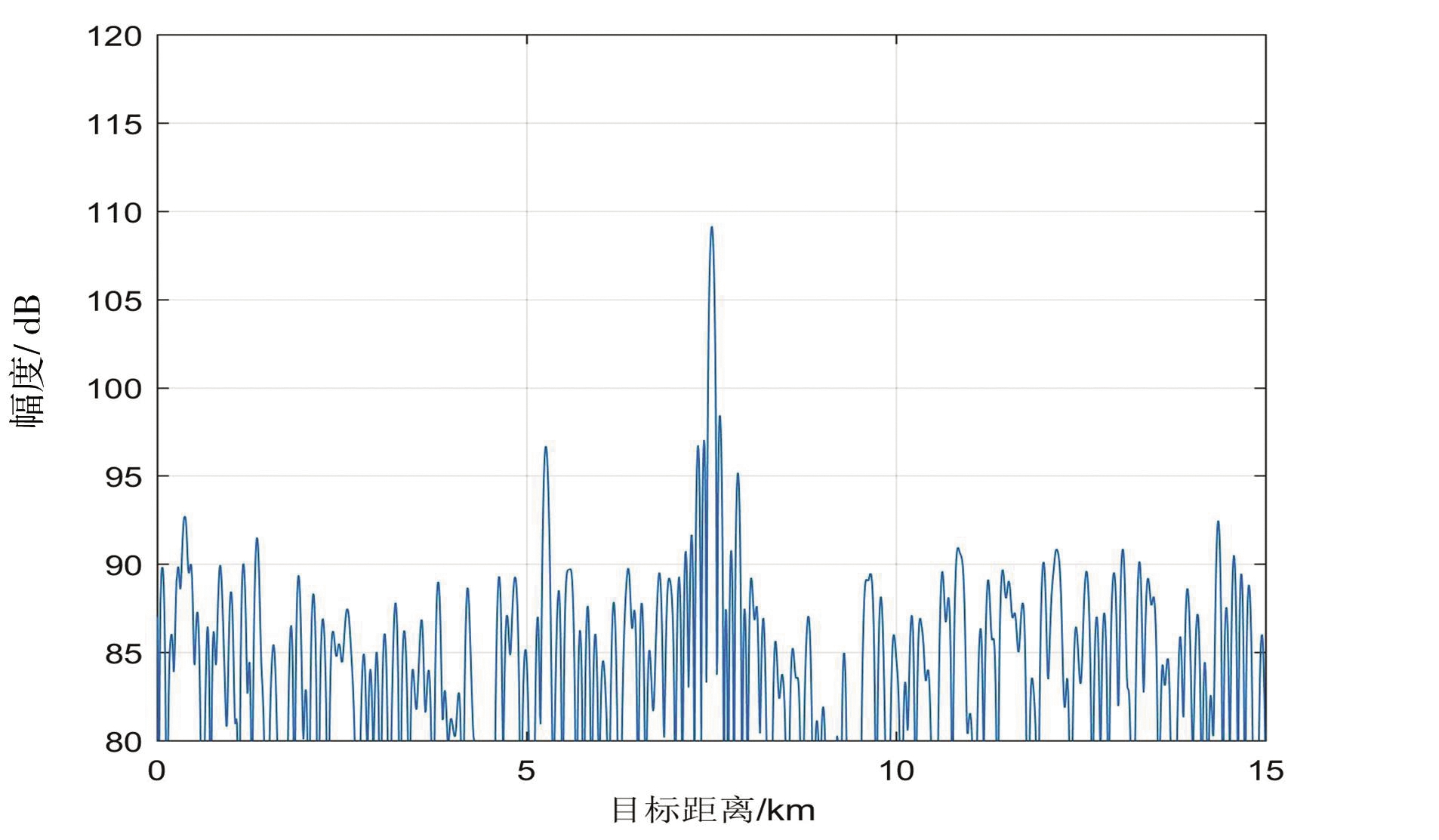
(d)二次修正后脉压处理结果
图7 实测干扰数据验证结果
4 结束语
本文在时域对消算法的基础上，推导了对消后剩余信号的具体表达式，找到了对消后剩余信号在脉冲压缩后峰值会损失6 dB的原因。通过设计时变滤波器补偿了这6 dB的损失，提升了目标检测性能。在一次对消后信号的目标位置处二次修正残余干扰项，可进一步提升干扰抑制效果。仿真结果表明，时变滤波处理补偿了脉压峰值的损失，二次修正目标位置处的残余干扰后，距离旁瓣大幅下降，使主目标附近的小目标能够显示。可见，改进时域对消算法提高了对恒模主瓣干扰的抑制性能。
[1]梁海珊.雷达反主瓣干扰的现状和趋势研究[J].火控雷达技术,2018,47(3):5-9.
[2]YANG Jie, LIU Congfeng.Improved Mainlobe Interference Suppression Based on Blocking Matrix Preprocess[J].Journal of Electrical and Computer Engineering,2015(3):1-8.
[3]YU S J, LEE J H.Efficient Eigenspace-Based Array Signal Processing Using Multiple Shift-Invariant Subarrays[J].IEEE Trans on Antennas and Propagation, 1999, 47(1):186-194.
[4]胡海涛,张剑云,李小波,等.基于阻塞矩阵预处理的抗主瓣干扰算法[J].探测与控制学报,2018,40(5):94-99.
[5]郭晓乐,邱炜,李向阳,等.基于JADE盲源分离的主瓣抗干扰算法研究[J].火控雷达技术,2018, 47(4):47-51.
[6]杜东平.雷达压制式干扰抑制算法研究[D].成都：电子科技大学，2008.
[7]魏迅,袁伟明,朱新国.改进的幅相重构算法抗主瓣干扰研究[J].电子测量技术,2017,40(1):26-29.
