0 引言
在敌方的侦察和作战行动中,新电磁装备的部署和原有电磁装备工作方式的变化意味着可能存在某种作战行动。而新电磁装备的部署和原有电磁装备工作方式的改变会引起电磁环境变化从而产生频谱异动[1]。如何准确、快速检测出电磁环境中的频谱异动对于开展雷达对抗侦察、提升预警能力和获取作战主动权有很大的战略意义。传统的雷达对抗侦察装备信息处理技术主要包括全脉冲数据和中频波形数据的生成、信号的分选识别、雷达的技战术指标推断以及无源定位等内容[2],缺乏对电磁频谱异动的检测。因此本文对电磁频谱异动检测展开研究,提出一种新的电磁频谱异动检测方法。
在雷达对抗侦察领域,公开的电磁频谱异动检测方法很少,只有文献[1]。该文献提出了一种检测异动电磁目标信号的方法。该方法构建了方位-频率二维划分模型,并提出了在一定检测概率的置信区间内生成频谱异动门限的方法对异动信号进行检测。该方法的本质为差值法,即通过当前频谱能量与历史频谱能量作差,差值超过门限处即存在异动信号。此方法只能处理简单场景,鲁棒性不强,门限设定过小时容易产生虚警,但该方法提出的方位-频率二维划分模型值得借鉴。
本文在文献[1]提出的方位-频率二维划分模型基础之上,提出一种新的频谱异动检测方法。该方法首先利用信号脉冲描述字(PDW),不需经过分选识别,建立频谱能量分布模型形成频谱图像;然后,由于设备的频谱使用情况具有周期性且以天为周期[3],即每天同一时间段的频谱图像理论上只存在微小差异,因此,可提取该时段的历史频谱图像的图像特征,对同一时段的频谱图像进行对比检测;最后,对于存在异动信号的频谱图像,在图像差值法[4]的基础上利用形态学图像处理[5]求得异动信号的坐标,从而可以引导装备对异动信号进行重点侦察。
1 频谱能量分布模型
文献[1]将侦察环境中电磁能量分布情况以单位方位Δθdiv和单位频率Δfdiv为基本单元进行划分,如图1所示,(Δθdiv,Δfdiv)为基本单元。
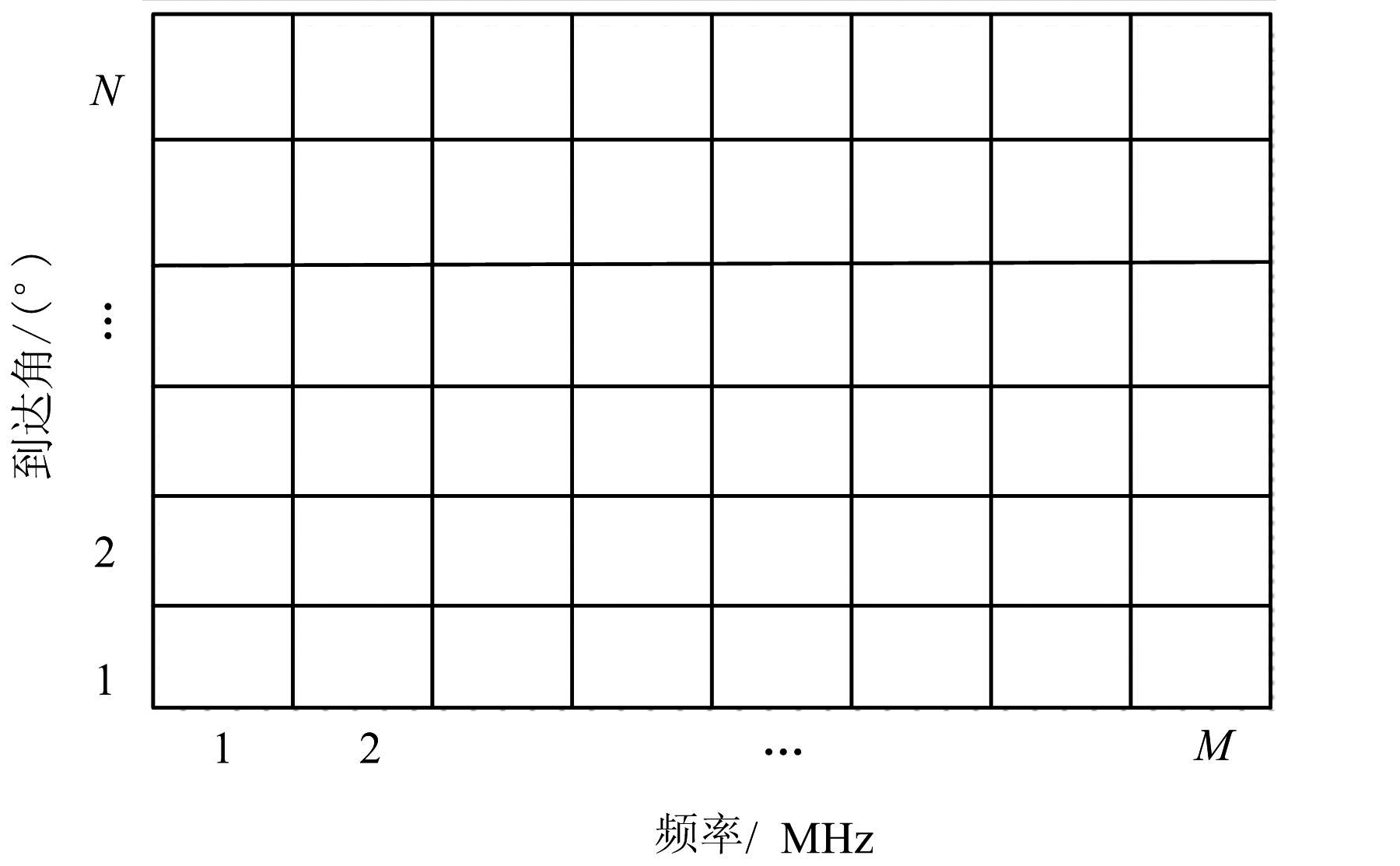
图1 方位-频率二维划分
令某个基本单元(i,j)的信号能量为Ei,j(t),在侦察作用范围内所有方位上和频率范围中的每个基本单元信号能量各不相同,形成了侦察信号环境频谱能量分布模型。基于PDW数据,该模型中基本单元(i,j)在t时刻的某一段积累时间Δt的能量为
Ei,j(t)=![]()
Antilog[(PA(θ,f)/10)]×
10-3dθdfdt
(1)
式中,PA(θ,f)表示基本单元(i,j)内信号PDW数据的幅度值(单位dBm),将该基本单元脉冲的幅度转化为以W为单位之后,再进行积分,即为该基本单元在时刻t,积累时间Δt内的能量量化值(单位J)。如图2所示为某情景下的频谱能量分布模型,将图2的三维频谱能量分布模型转化为二维频谱图像,如图3所示。
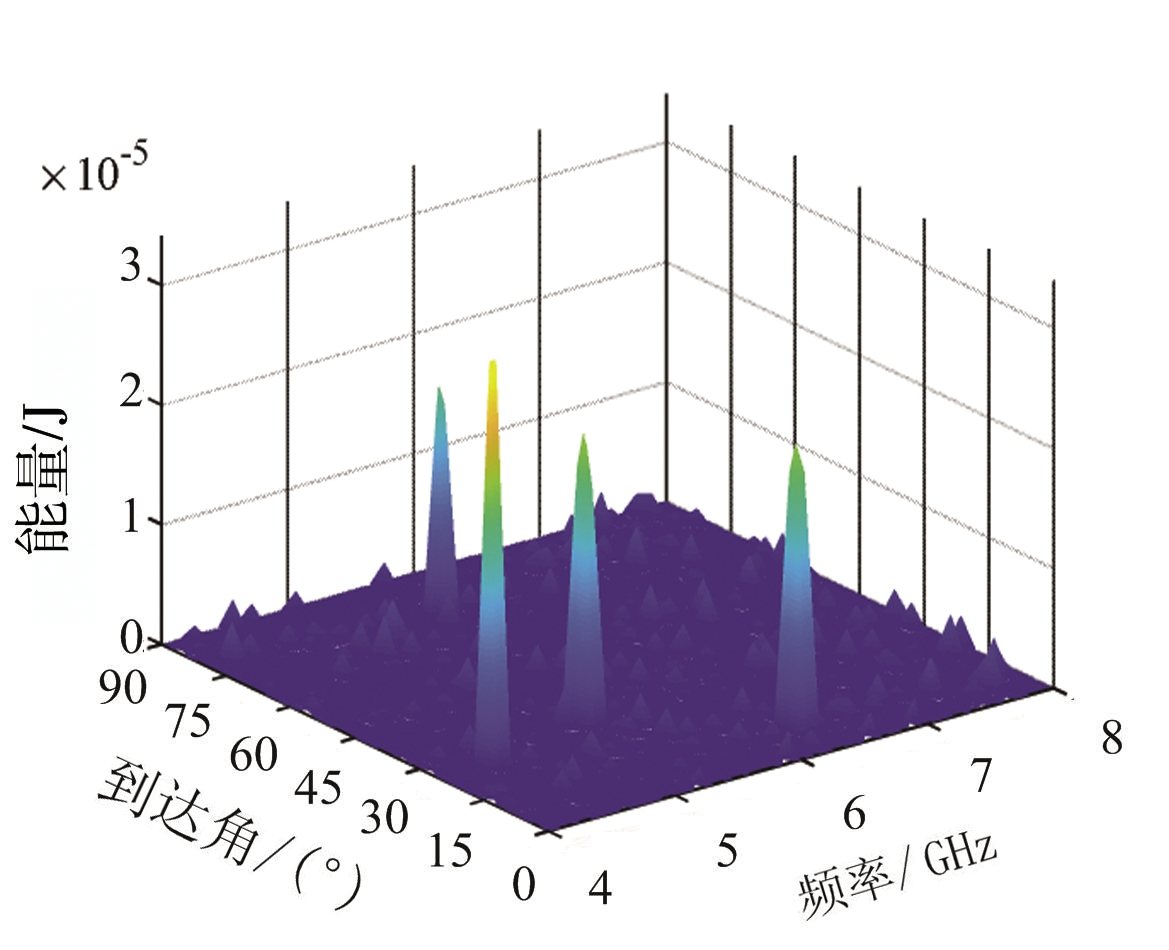
图2 频谱能量分布模型
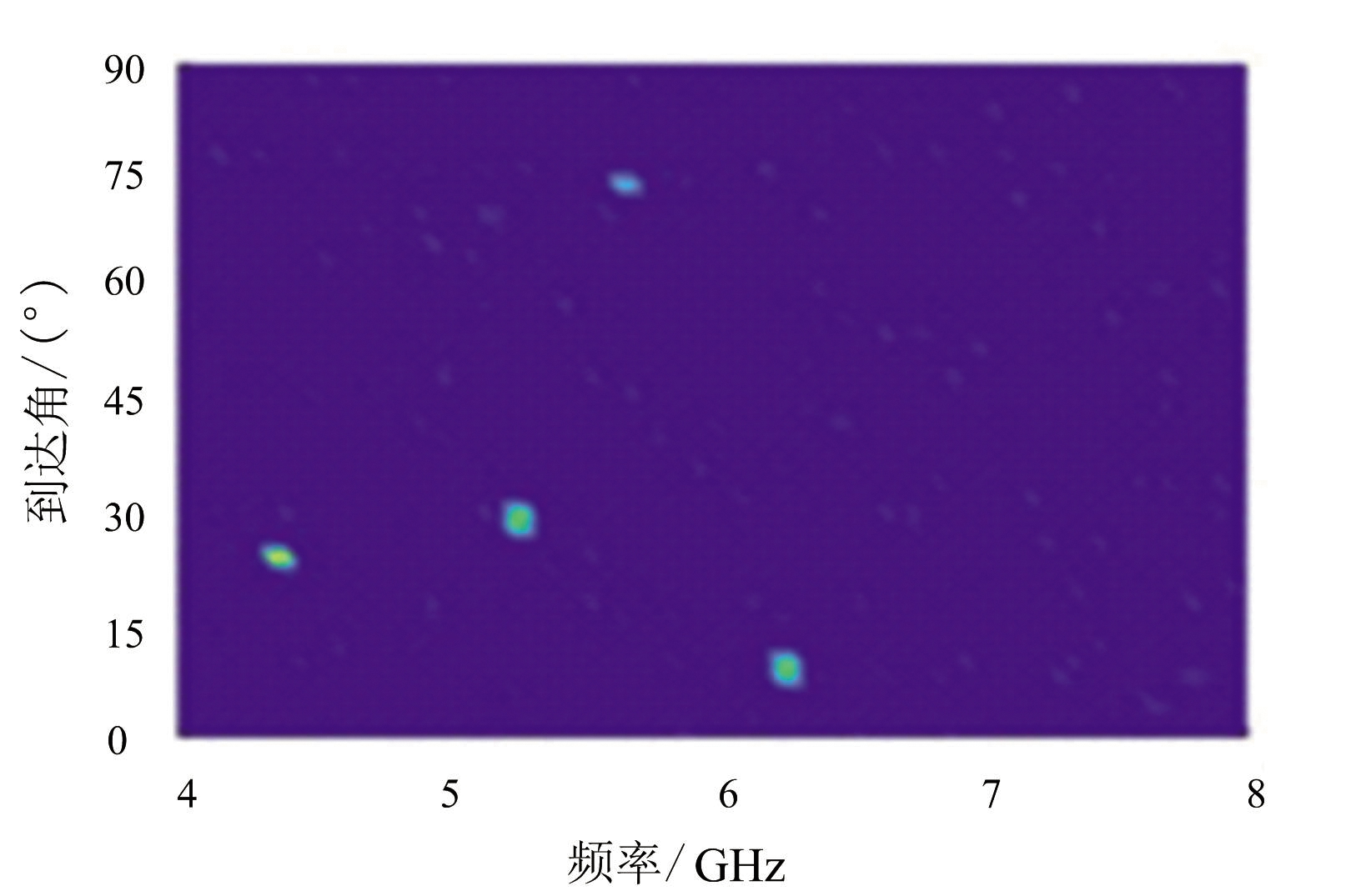
图3 二维频谱图像
2 频谱异动
电磁频谱异动主要分为2种情况:1)当前环境中出现新的目标信号;2)当前环境中,原有目标信号的工作方式(载频、脉冲重复周期、扫描方式等)发生变化[1]。
当环境中新的目标信号出现或原目标信号改变频点,且信号在其单元格(i,j)内积累能量足够大,频谱能量分布模型将突起“尖峰”,在二维频谱图像表现为出现新“亮斑”;当环境中,原有目标信号的工作方式发生变化(除频点变化外),频谱能量分布模型原“尖峰”的高度将升高或降低,在二维频谱图像表现“亮斑”变亮或变暗。如表1所示,给出了频谱异动对应的频谱图像变化情况。
表1 频谱图像变化情况

频谱异动频谱图像变化新目标信号出现新的“亮斑”出现原目标 信号载频变化新的“亮斑”出现其他工作方式改变“亮斑”亮度变化
3 基于图像亮度直方图的纹理描绘子的异动检测方法
对于异动检测的方法,容易想到的是对频谱图像求差值,即通过当前频谱能量与历史频谱能量作差,差值超过门限处即存在异动信号。结合文献[1]说明了此方法过于简单,鲁棒性不强,门限设定过小易产生虚警。因此,本文首先通过提取图像特征,设定距离门限对信号频谱图像进行检测,然后在图像差值法基础上利用形态学图像处理得到异动信号的坐标信息。
3.1 基于图像的亮度直方图的纹理描绘子
图像特征主要有图像的颜色特征、纹理特征、形状特征和空间关系特征。考虑到发生异动的频谱图像与正常频谱图像之间亮度存在差异,所以采用统计的方法提取频谱图像的亮度直方图的纹理描绘子[6-7]作为检测频谱异动的基础。如表2所示,给出了基于图像亮度直方图的一些纹理描绘子。
表2 基于图像亮度直方图的纹理描绘子

矩表达式纹理度量均值m=∑L-1i=0zipzi()平均亮度度量标准偏差σ=μ2z()平均对比度度量平滑度R=1-1/1+σ2()区域中亮度的相对平滑度度量第三阶矩μ3=∑L-1i=0(zi-m)3pzi()度量直方图的斜偏一致性U=∑L-1i=0p2zi()度量一致性熵e=-∑L-1i=0pzi()log2pzi()随机性度量
其中,zi是表示亮度的一个随机变量,p(z)是一个区域中的灰度级的直方图,L是可能的灰度级数量,均值的第n阶矩表示为
(2)
3.2 确定距离门限
用纹理描绘子形成向量描述一张频谱图像,可以计算频谱图像之间的欧氏距离(以下称距离)。本文用无异动信号的频谱图像之间距离{d1}生成门限dT,若待检测频谱图像到无异动信号的频谱图像距离{d2}的均值大于该门限则为频谱发生异动,即待检测的频谱图像中有异动信号。为方便讨论,假设距离{d1}服从正态分布。基于3σ原则[8],则门限dT取值为
dT=μ(d1)+3σ(d1)
(3)
式中,μ(d1)为距离{d1}的均值,σ(d1)为距离{d1}的标准差。以下为异动检测判断准则:
aveage(d2)>dT⟹异动
(4)
aveage(d2)≤dT⟹正常
(5)
式中,aveage(d2)为{d2}的均值。
3.3 异动信号坐标定位
确定待检测的频谱图像中有异动信号后,利用差值对异动信号坐标进行定位。由于接收机测量存在误差,没有异动信号处会产生小部分虚警点。理论上,虚警点处的差值相对异动信号处的差值是呈离散状分布,故在差值法基础上采取形态学图像处理:先对差值图进行腐蚀处理去除虚警点;再进行膨胀处理,恢复疑似异动信号处峰值;最后对处理后的差值图作峰值检测,计算所有峰值均值为门限,保留峰值大于门限的峰值即为异动信号的位置。
总结异动检测步骤,异动检测的具体流程如图4所示。

图4 异动检测流程图
4 半实物仿真结果与分析
4.1 数据采集
PDW采集工作为本文提供了数据支撑,同时利用PDW数据建立频谱能量分布模型得到频谱图像也是进行频谱异动检测的基础性工作。本次测量实验采用学院研制的侦察设备,于2019年12月22-26日在武汉某建筑物3楼进行了为期5天的PDW数据采集工作。前4天,每天16:20-16:30对环境信号进行接收产生PDW数据。第5天同一时间段,用信号发生器产生异动信号,通过天线对准侦察设备进行辐射。如图5(a)所示为设备的实物图,如图5(b)所示为信号发生器与天线的实物图。设备接收机灵敏度优于-55 dBm,可对所有方向信号进行接收,设备频段选择为1.8~4 GHz。经过10 min的接收,得到的数据量在1.2~1.3 GB之间。

(a)侦察设备

(b)信号发生器与天线
图5 设备实物图
4.2 建立频谱能量模型
在实际作战侦察时,异动检测是个实时问题,积累时间取值偏大,可以减少生成的频谱图像数量,降低数据库存储容量,其缺点是检测间隔过长,预警能力下降。但积累时间取值偏小会造成检测冗余。所以,积累时间取值应该适中,视具体情况而定。本文数据的实测时长为10 min,数据为事后处理。为方便计算机计算,本次仿真设积累时间为10 s,基本单元(Δθdiv,Δfdiv)为2°×50 MHz,用侦察数据建立频谱能量分布模型,形成频谱图像。
4.2.1 频谱无异动情况
前4天共生成240张频谱图像,分析所有频谱图像可知,忽略类间微小差异后,频谱能量分布模型可分为两大类。第1、3天为一类,如图6(a)所示;第2、4天为另一类,如图6(c)所示。图6(b)为第1、3天的频谱图像,记为类别1;图6(d)为第2、4天的频谱图像,记为类别2。类别1、2各120张。
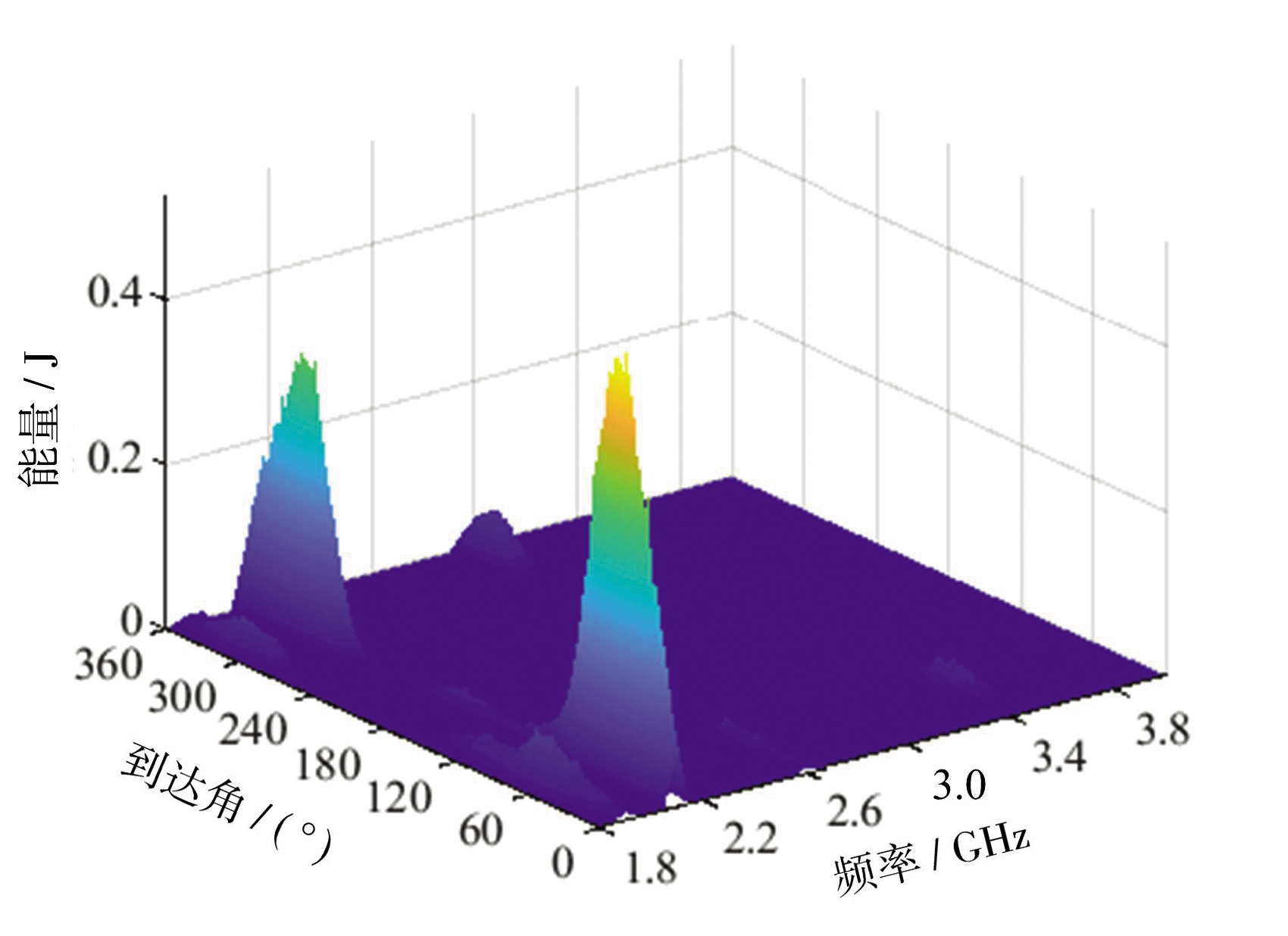
(a)类别1频谱能量分布
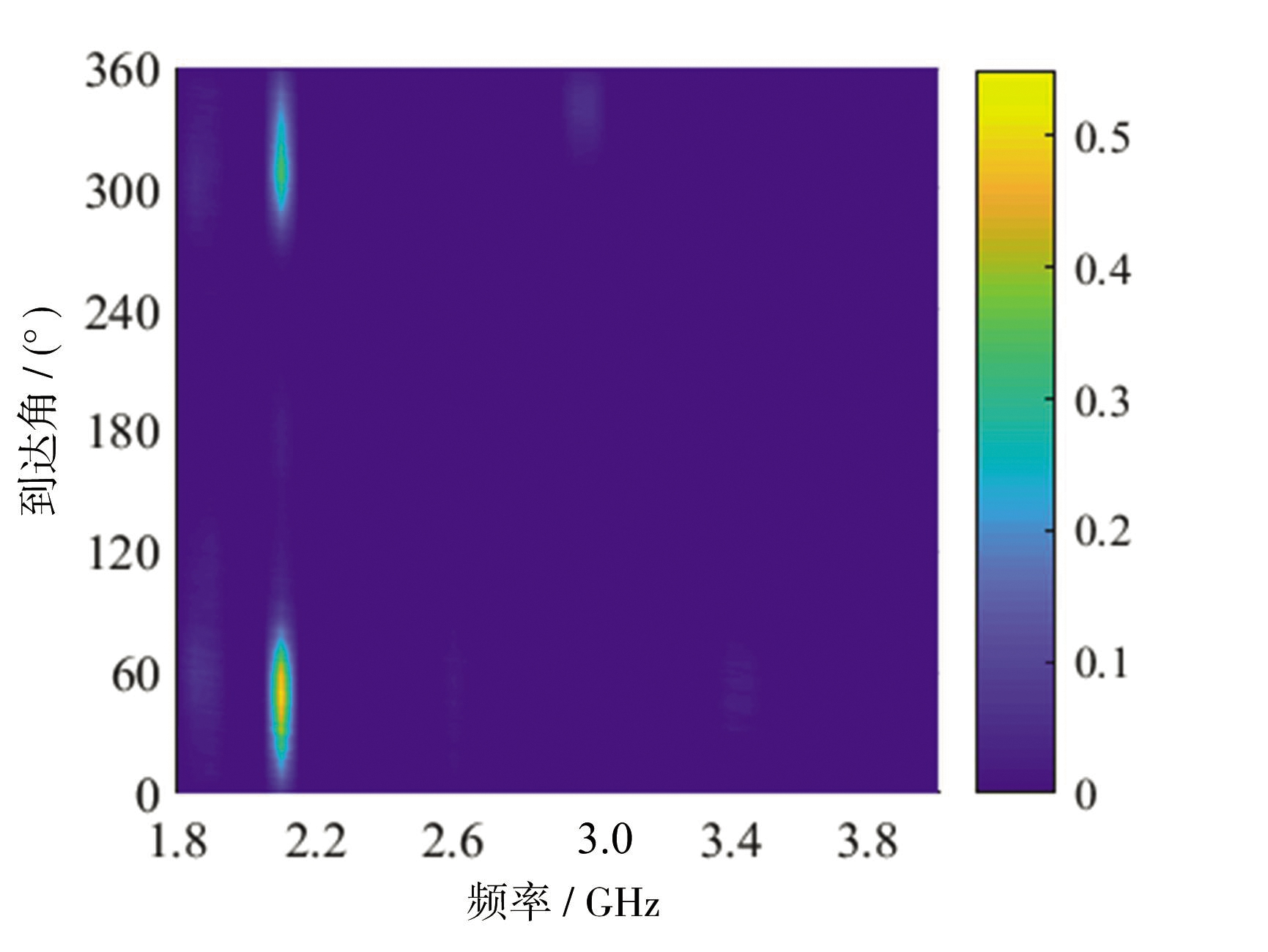
(b)类别1频谱图像
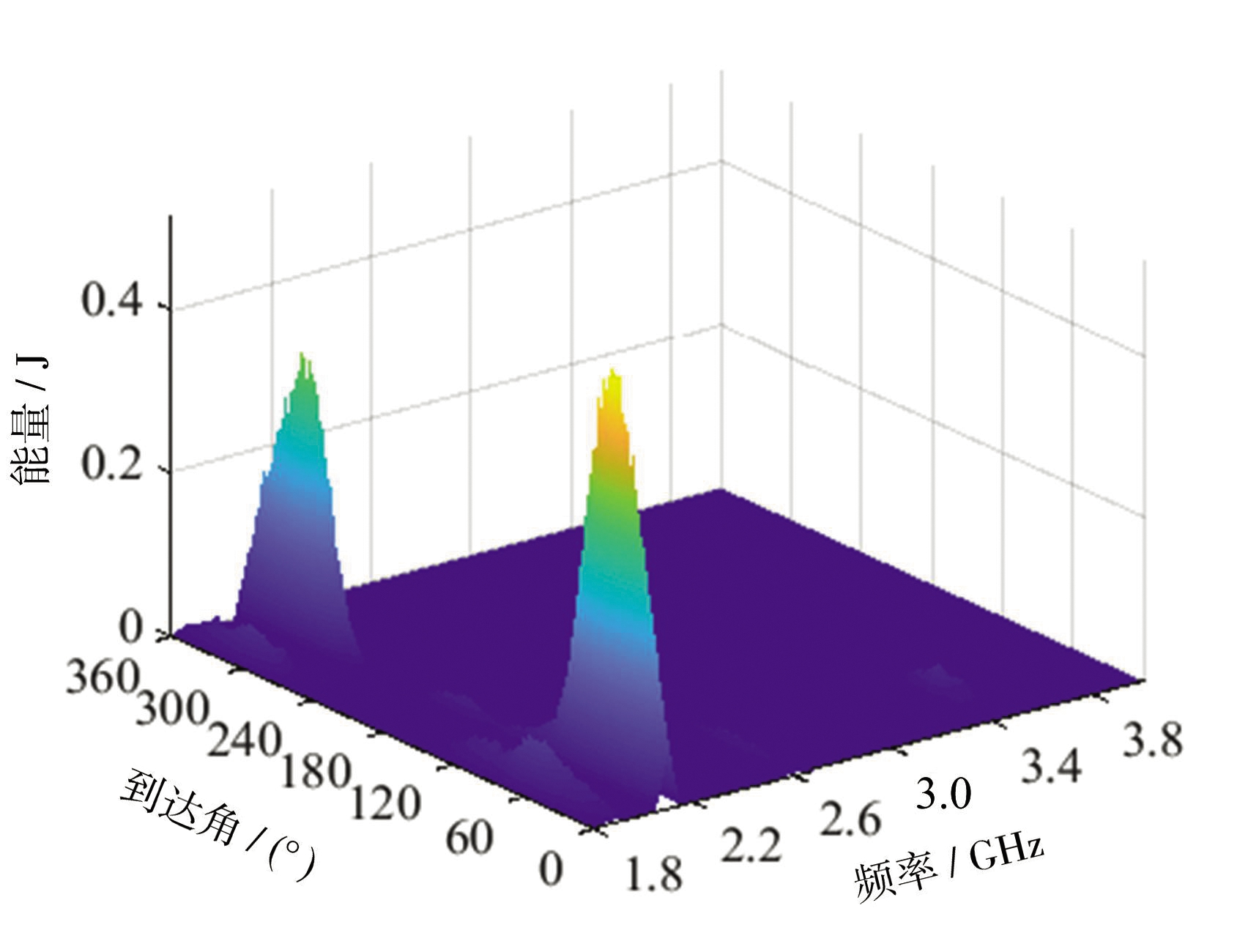
(c)类别2频谱能量分布
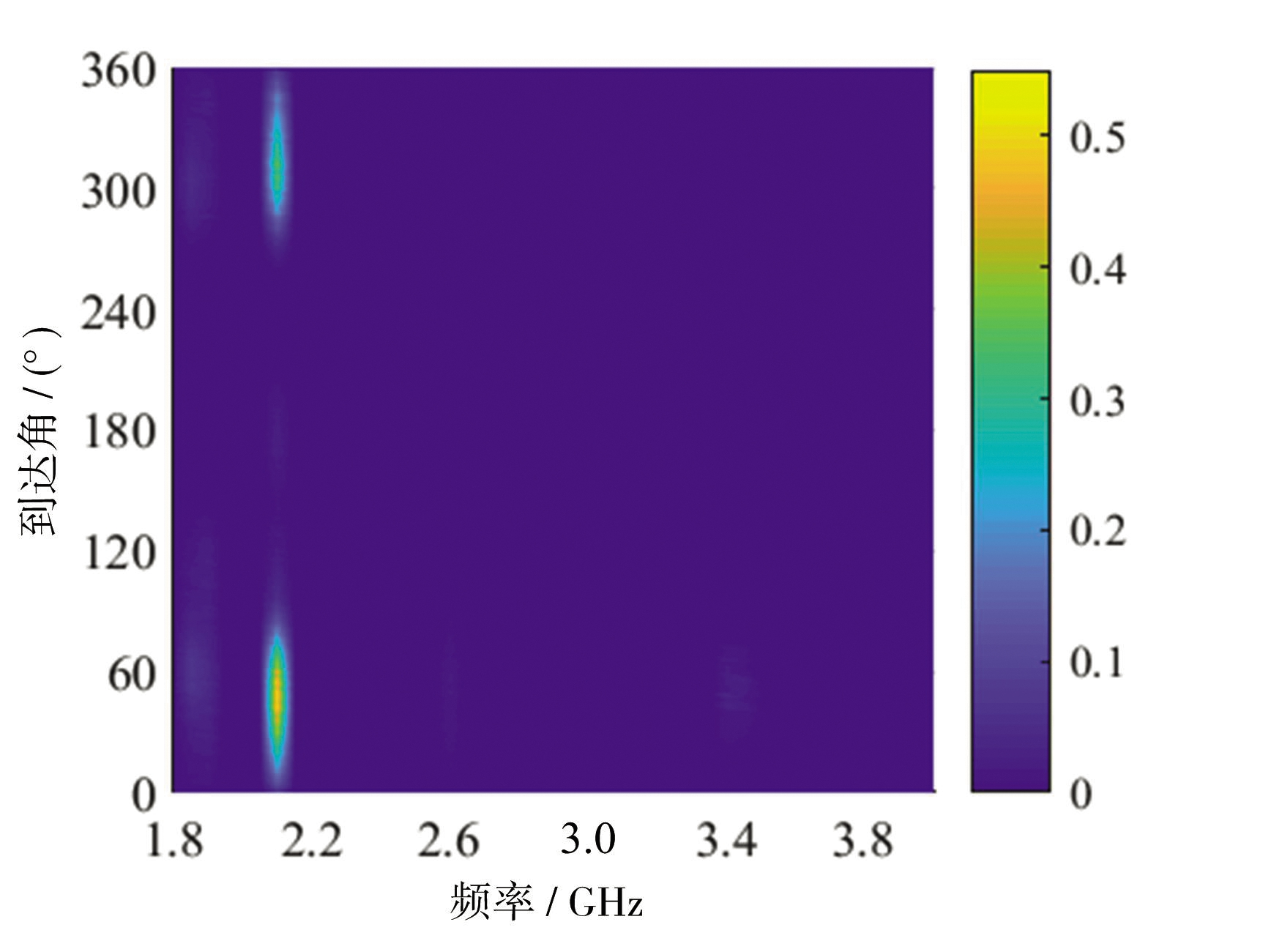
(d)类别2频谱图像
图6 第1~4天16:20-16:30频谱模型
以上为无异动目标时的两类频谱图像。分析频谱图像可知,在16:20-16:30时段,1.8~2.2 GHz内信号较多,且方位分布广泛。特别是2.0~2.2 GHz信号能量较大,这是因为环境中存在较多的移动通信基站信号。同时在2.6 GHz和3.5 GHz也存在信号。类别1相比于类别2来说,不同点在于类别1在频率3.0 GHz左右、方位角350°左右处存在信号。
4.2.2 频谱异动情况
本文在数据采集的第5天,用信号发生器产生异动信号,通过天线对准侦察设备进行辐射。信号发生器设置为常规脉冲信号,载频为2.8 GHz、功率为15 dBmW、脉宽为0.15 μs、重复频率为1 500 Hz;天线增益为15 dB。经接收机接收,产生频谱图像如图7所示,异动信号已用红框标出。
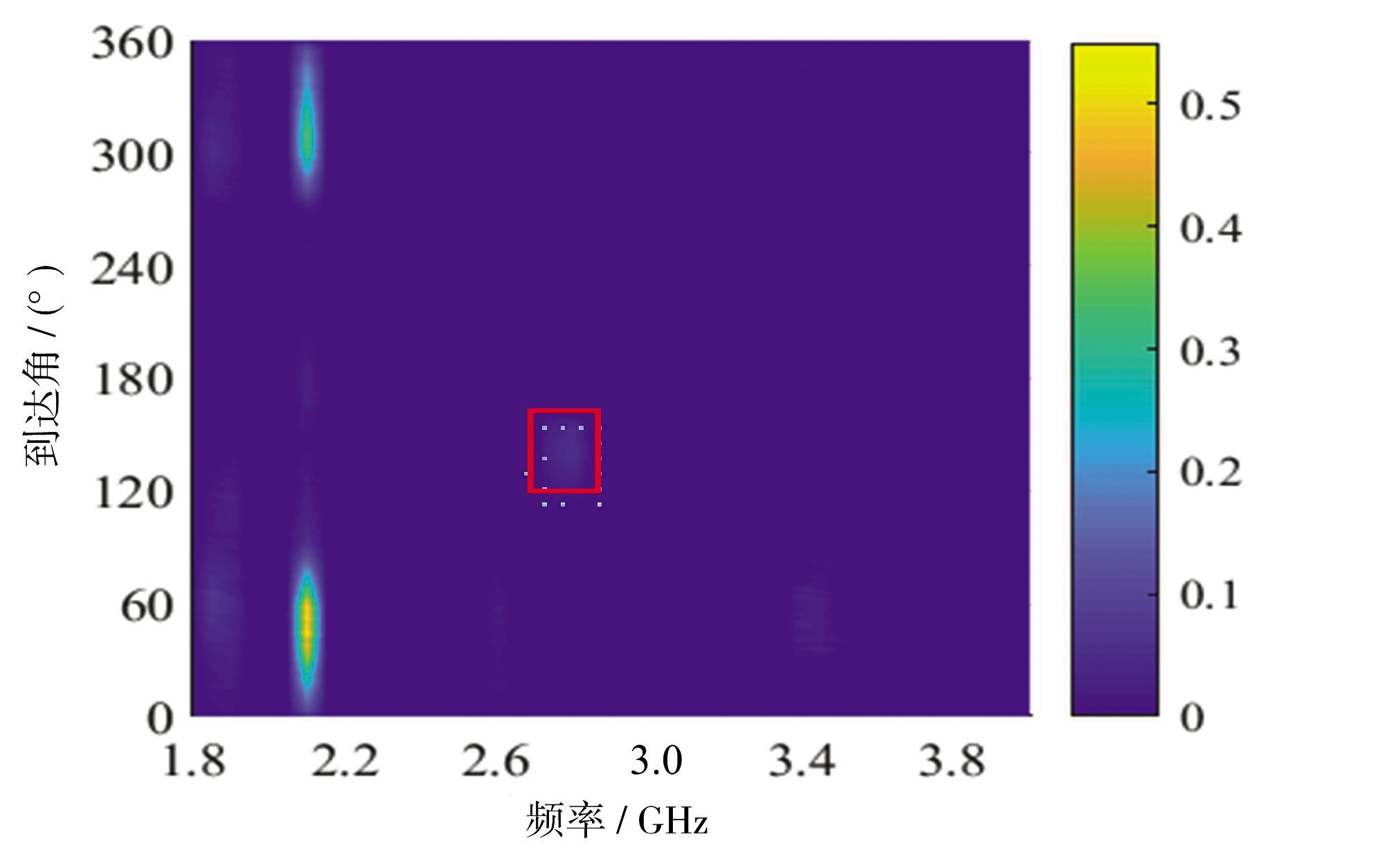
图7 第5天16:20-16:30频谱图像
对侦察数据修改可以得到几种典型频谱异动图像,如图8所示。在原侦察数据基础上对上述异动信号的方位、频率、幅度进行修改可以得到如图8(a)所示的异动频谱图像。将该目标信号侦察数据方位、频率、幅度进行修改并与类别1侦察数据融合可以得到如图8(b)所示的异动频谱图像。在类别1的侦察数据基础上对原信号脉幅进行修改可以得到如图8(c)、(d)所示的异动频谱图像。
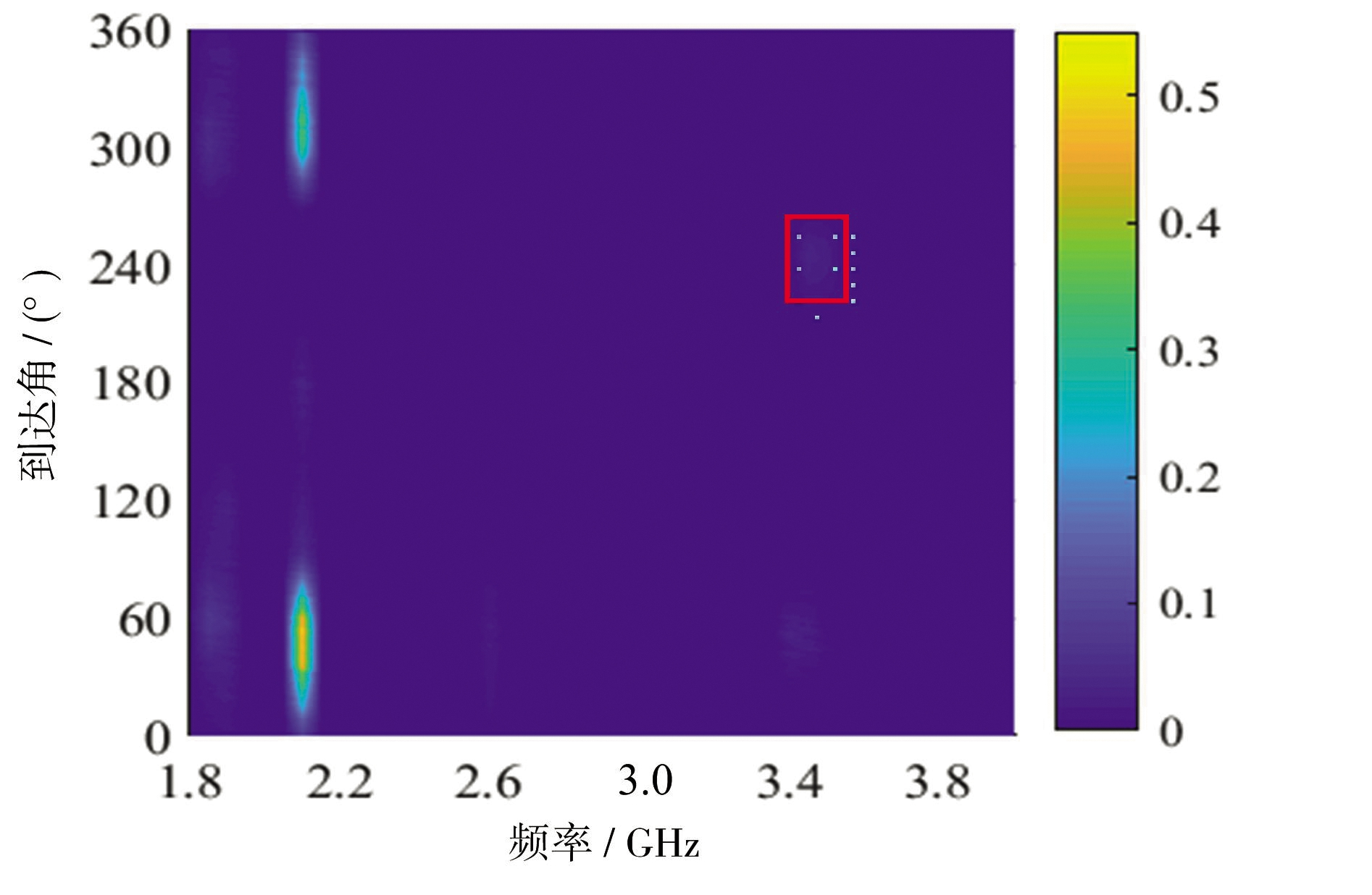
(a)典型异动频谱图像1
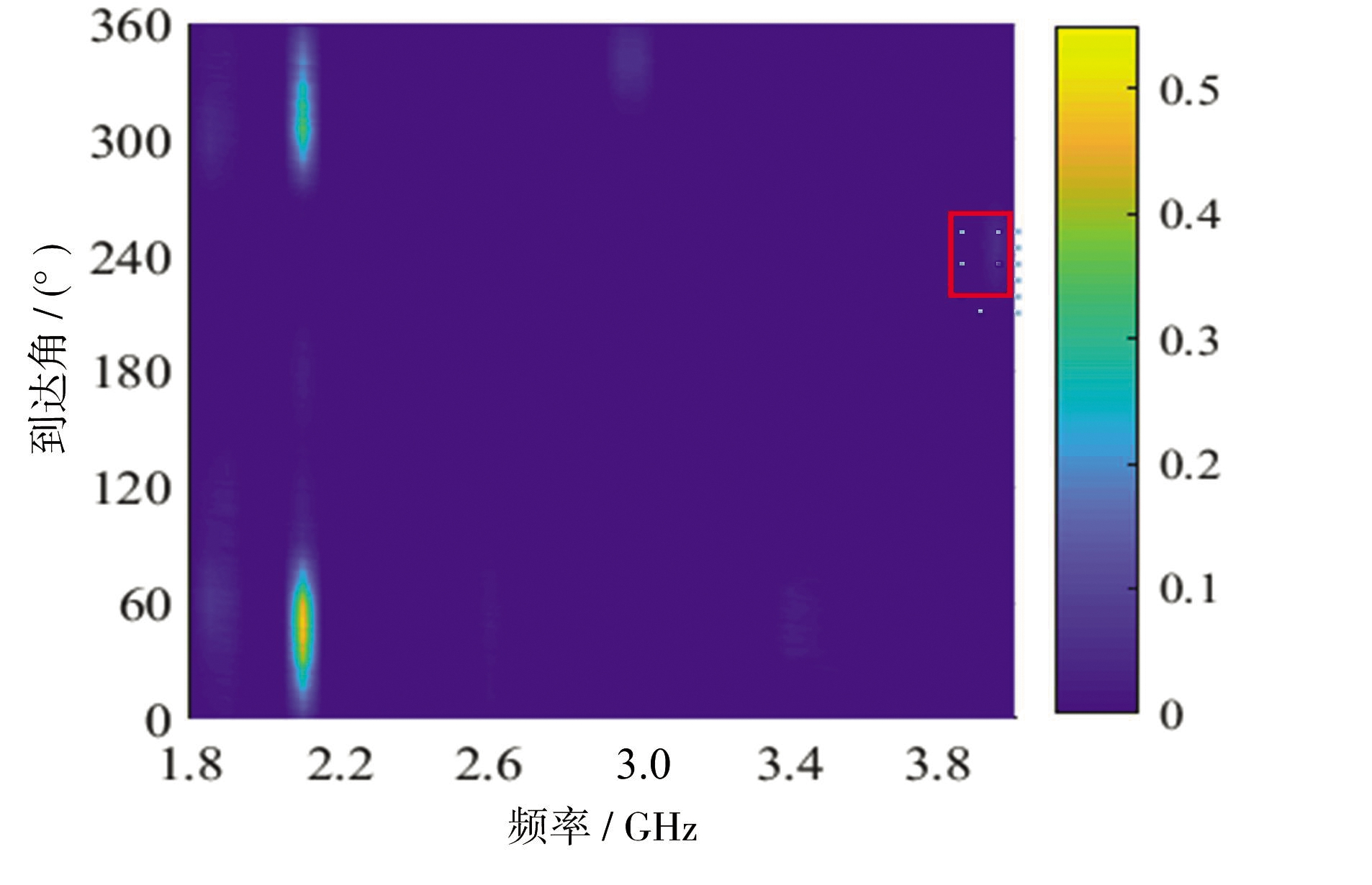
(b)典型异动频谱图像2
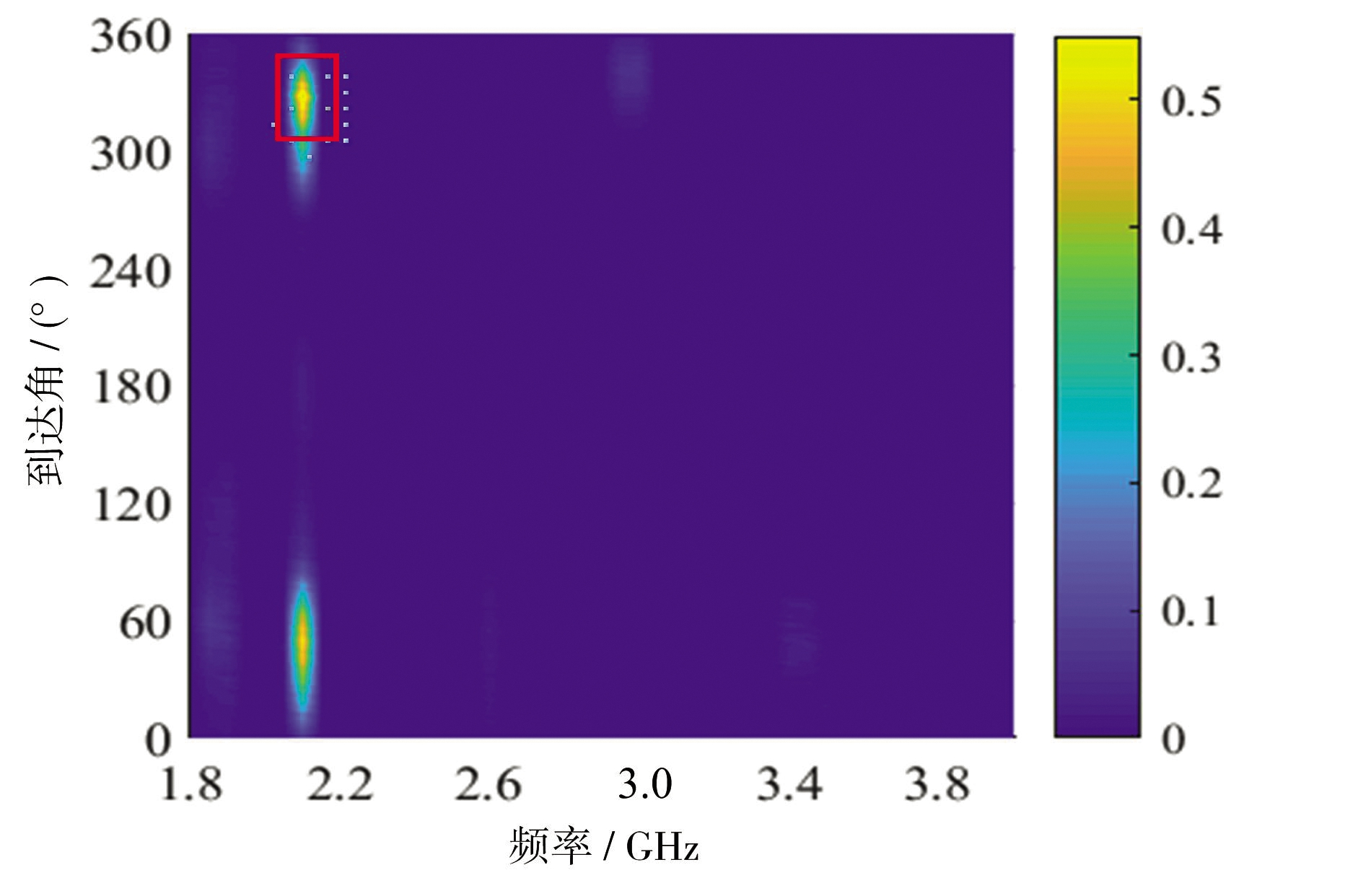
(c)典型异动频谱图像3
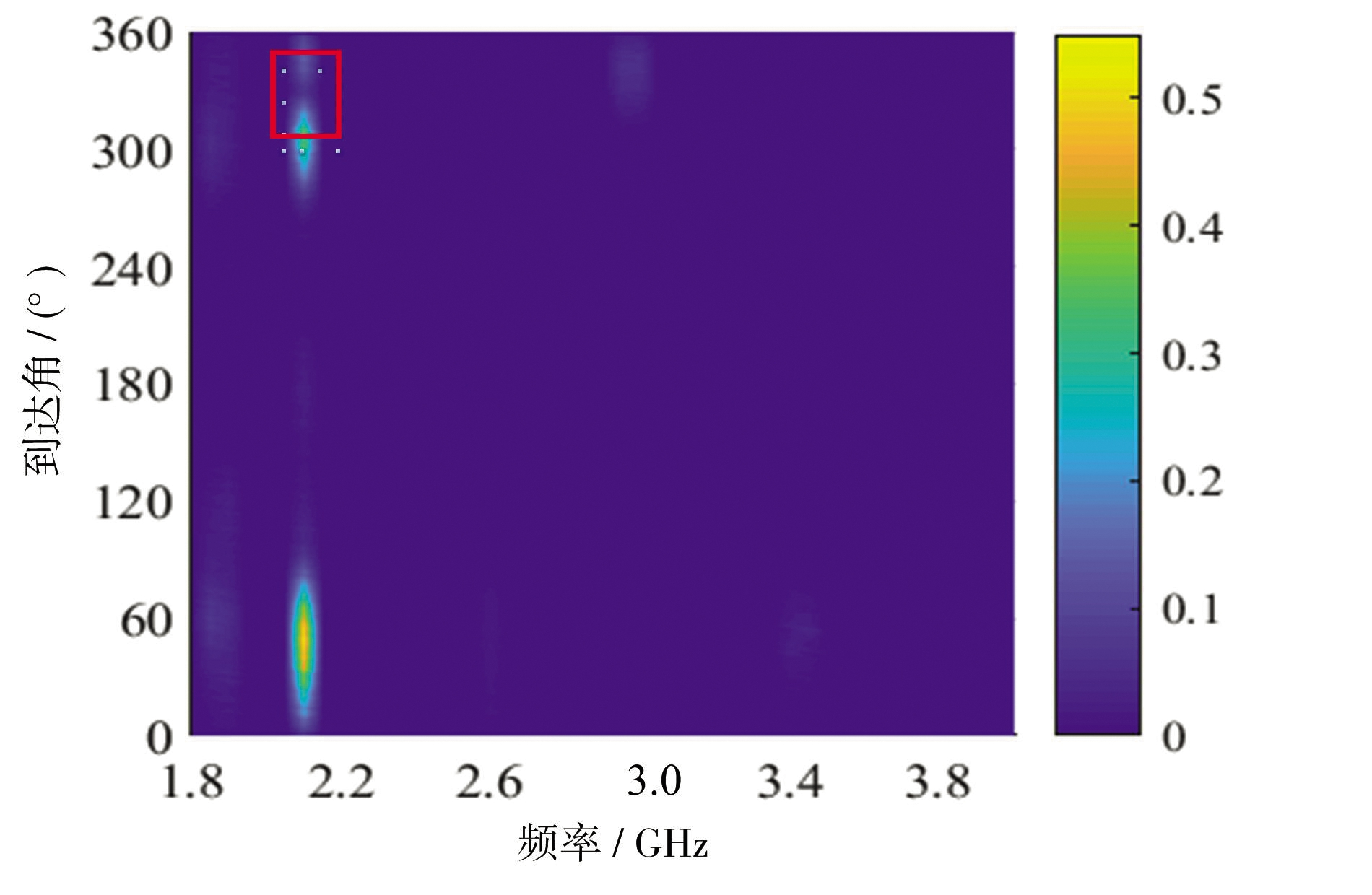
(d)典型异动频谱图像4
图8 异动频谱图像
4.3 异动检测仿真结果与分析
本节仿真对差值法,频谱图像纹理度量分析,新目标、原目标异动检测以及异动目标坐标定位进行了仿真分析,具体仿真结果及分析如下。
4.3.1 差值法
本小节用类别1频谱图像均值作为模板图,随机抽取一张类别1频谱图像与模板作差。像数亮度差值门限根据观察取值为5。结果如图9所示。
类别1频谱图像为无异动信号时的频谱,分析图9可知,使用差值法产生了大量的虚警点。显然,使用差值法进行频谱异动检测成功概率低,且鲁棒性不强。所以应当先对频谱图像进行检测,确定频谱图像确实存在异动信号,再利用差值等方法确定异动信号的坐标。
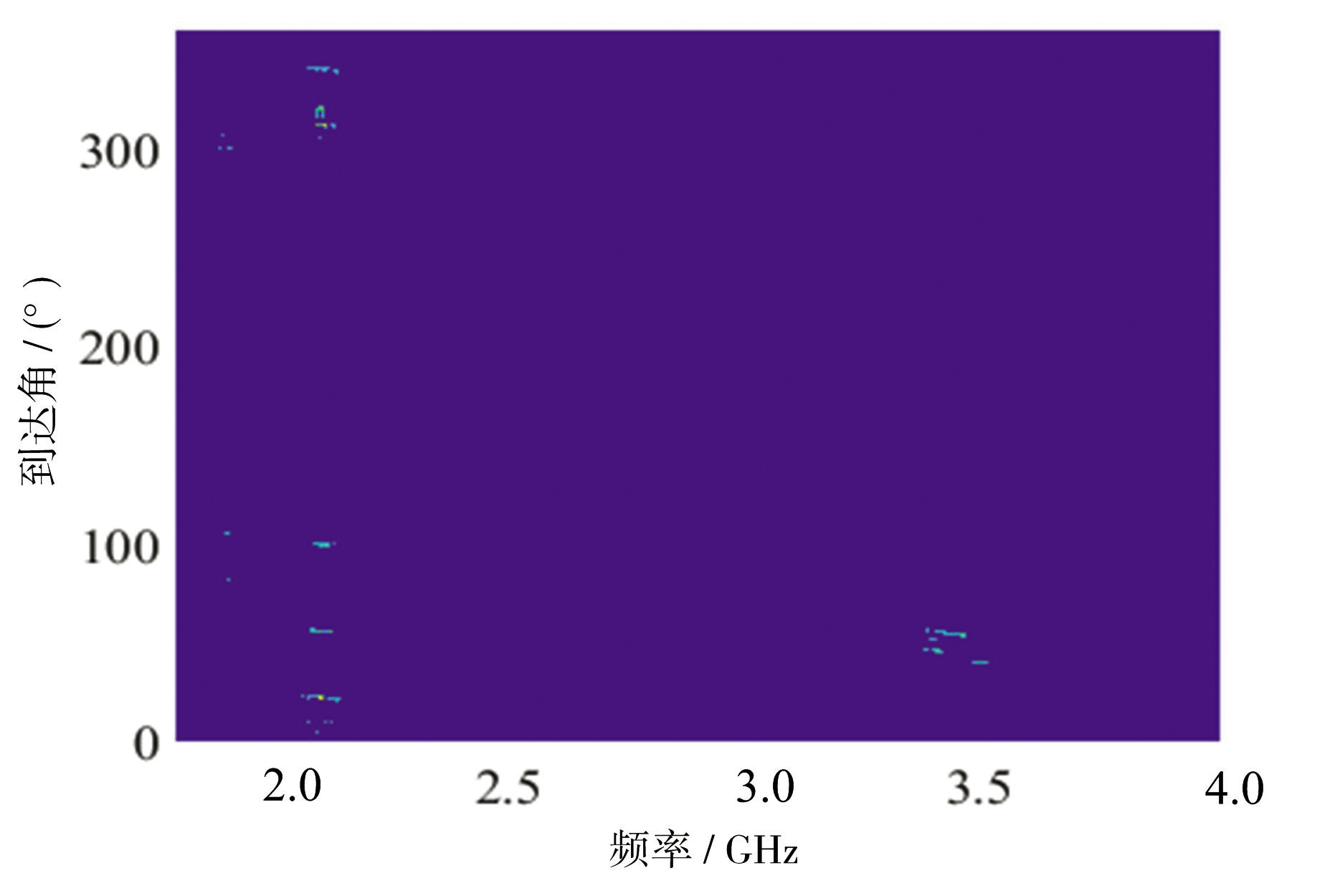
图9 差值法
4.3.2 频谱图像纹理度量分析
如表3所示,计算出了8张频谱图像的纹理度量。其中,图像1、2、3为类别1无异动信号下随机抽取的3张频谱图像,图像4为类别1有异动信号的频谱图像;图像5、6、7为类别2无异动信号中随机抽取的3张频谱图像,图像8为类别2有异动信号的频谱图像。仔细观察数据,可以得出频谱图像4与频谱图像1、2、3之间的差别体现在数值的小数点后第二位后(除平滑度度量外)。频谱图像5与频谱图像6、7、8之间差别同理。
表3 纹理度量
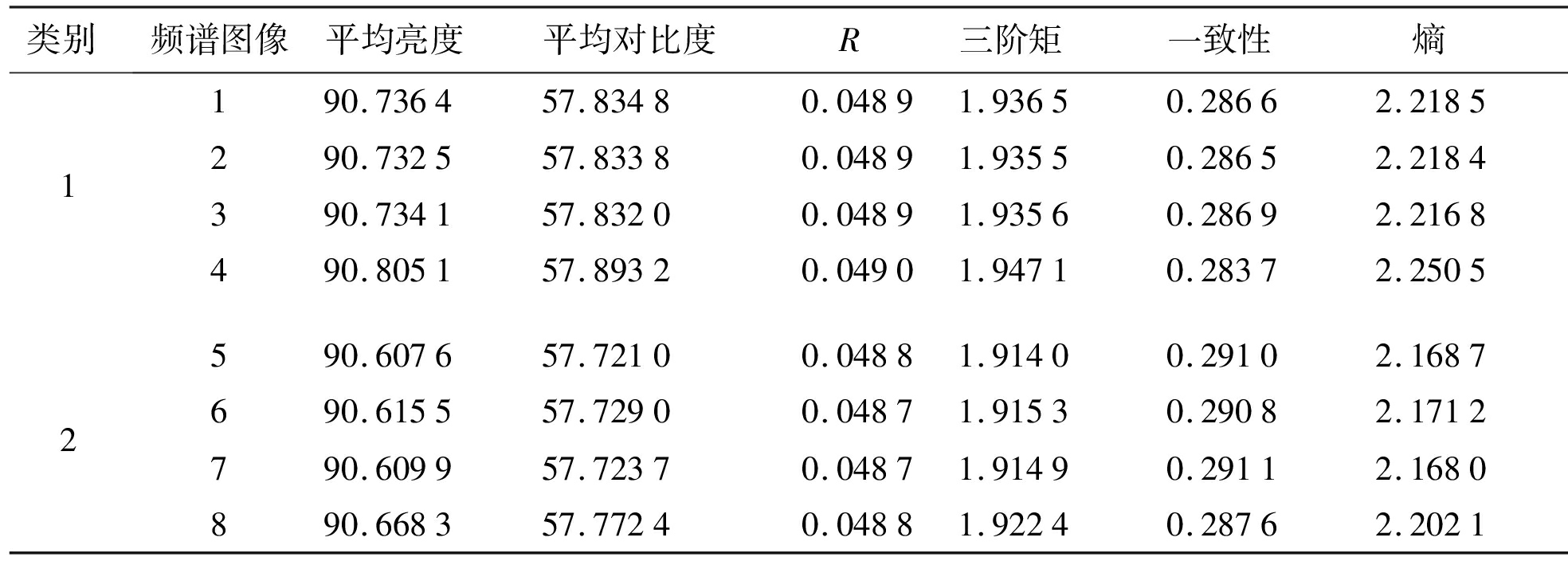
类别频谱图像平均亮度平均对比度 R三阶矩一致性 熵 1190.736457.83480.04891.93650.28662.2185290.732557.83380.04891.93550.28652.2184390.734157.83200.04891.93560.28692.2168490.805157.89320.04901.94710.28372.2505 2590.607657.72100.04881.91400.29102.1687690.615557.72900.04871.91530.29082.1712790.609957.72370.04871.91490.29112.1680890.668357.77240.04881.92240.28762.2021
由于平滑度度量差别相对较小,去除平滑度度量,用剩余5个纹理描绘子形成向量描述一张频谱图像,可以计算频谱图像之间的距离。如图10所示,给出了类别1无异动信号下60张频谱图像之间距离{d1}的频数和类别1有异动信号的某一频谱图像到该60张频谱图像之间距离{d2}的频数,该异动信号脉冲幅度为-40±2 dBm,重复频率为1 500 Hz。
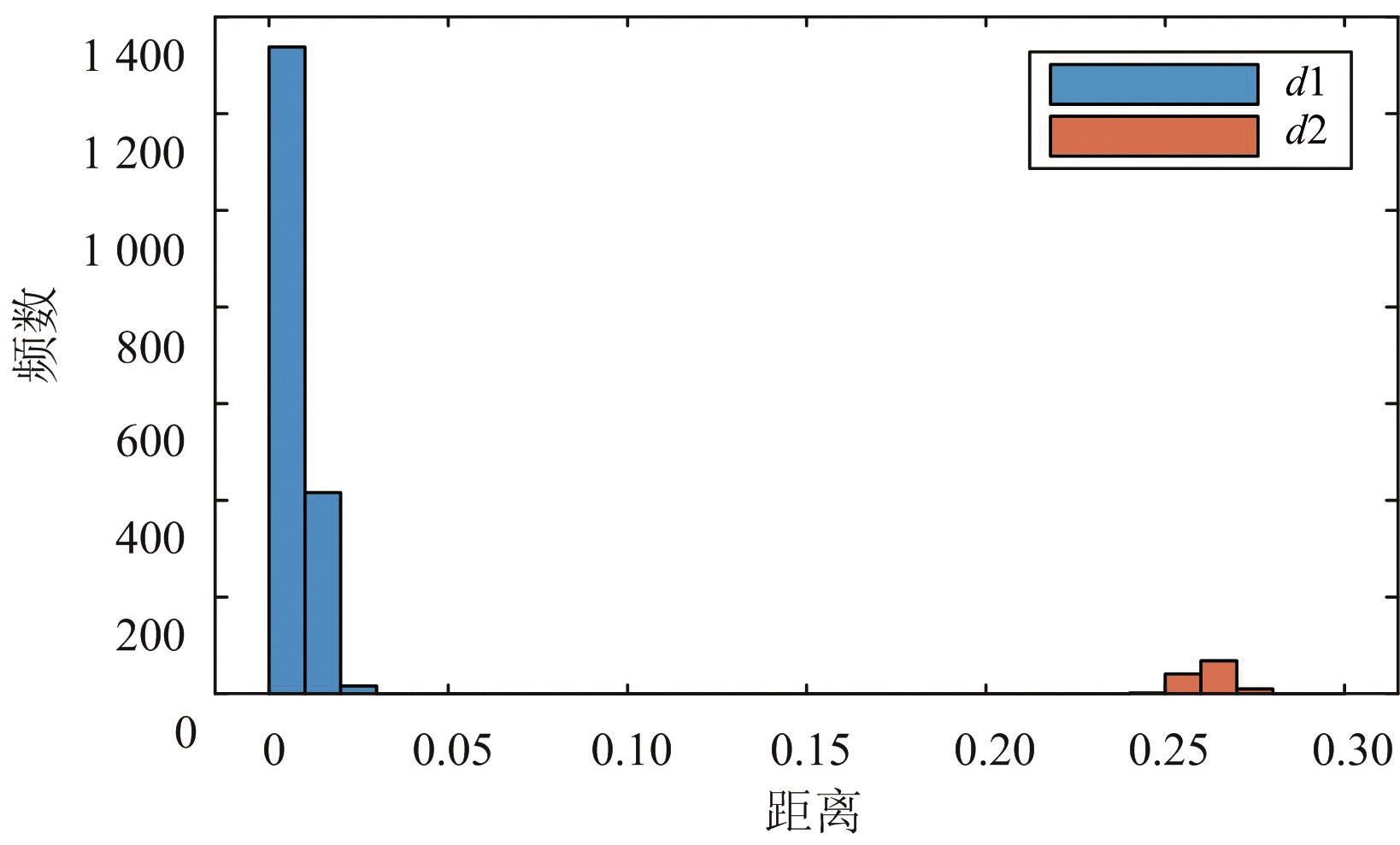
图10 距离频数图
由图10可知,存在异动信号的频谱图像到相应类别之间的距离会大于同一类别频谱图像之间的距离。因此设定距离门限可以检测出有异常信号的频谱图像。
4.3.3 对新目标信号异动检测实验
在PDW数据采集阶段,前4天共生成240张正常频谱图像,类别1、2各120张。本小节用类别1、2各60张频谱图像分别计算距离门限dT1、dT2,用剩余各60张频谱图像计算虚警概率。理论上,异动信号产生的“亮斑”亮度大小与脉冲幅度和重复频率正相关。脉冲幅度和重复频率越大,“亮斑”越亮,越容易被检测处异动。鉴于不方便从侦察数据上修改信号重复频率,本次仿真保持异动信号重复频率不变,修改其他侦察数据,使其方位、频率随机变化,脉冲幅度如表4所示,各参数在测量误差范围内变化,共得到500张异动频谱图像。
表4 待检测异动频谱图像数量

信号脉幅(±2dBm)类别1/张类别2/张-42dBm5050-44dBm5050-45dBm5050-46dBm5050-47dBm5050
实验结果如表5所示。
表5 对新目标信号异动检测实验结果

信号脉幅(±2dBm)检测概率-42dBm0.96-44dBm0.89-45dBm0.81-46dBm0.68-47dBm0.34
本次实验采用的设备接收机灵敏度优于-55 dBm,分析实验结果,本文提出的方法在积累时间为10 s,信号脉冲重复频率为1 500 Hz的情况下,对脉幅大于-46 dBm(±2 dBm)的异常信号具有较高的检测概率;对于信号脉幅小于-46 dBm(±2 dBm)的异常信号检测概率较低,这是因为其单元格内积累的频谱能量过小,大部分频谱图像没有亮斑形成或者形成的“亮斑”亮度低、面积小不足以被检测,这也是本文所提方法的缺陷所在。同时,基于3σ原则确定的距离门限对异动信号检测产生的虚警概率为0.008 3,结果在可以接受的范围之内。
4.3.4 对原目标信号异动检测实验
由于原目标信号的非合作性,本小节通过改变侦察数据中原基本单元格内信号脉冲幅度来实现异动检测实验。不改变其他参数,修改类别1中频率3 GHz、方位角350°处原信号的侦察数据使其脉冲幅度变化如表6所示,各参数在测量误差范围内变化得到300张异动频谱图像。
表6 待检测异动频谱图像数量
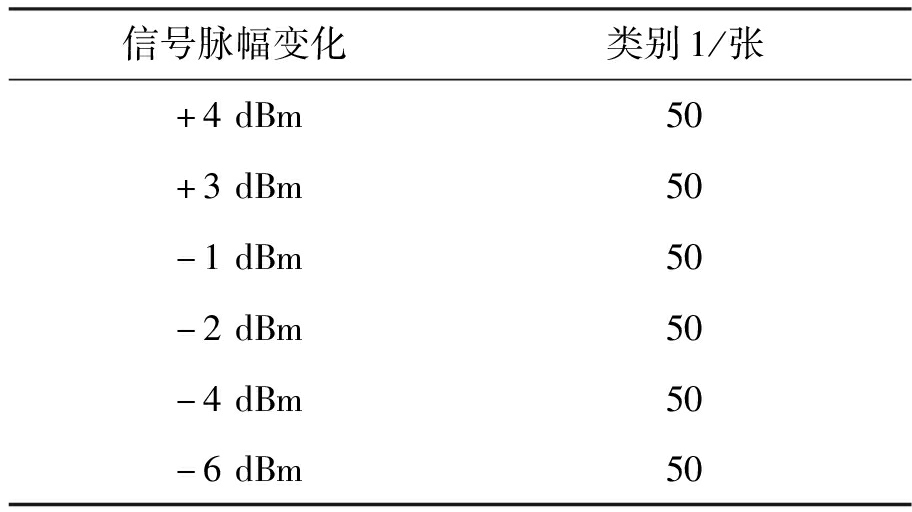
信号脉幅变化类别1/张+4dBm50+3dBm50-1dBm50-2dBm50-4dBm50-6dBm50
实验结果如表7所示。
表7 对原目标信号异动检测实验结果
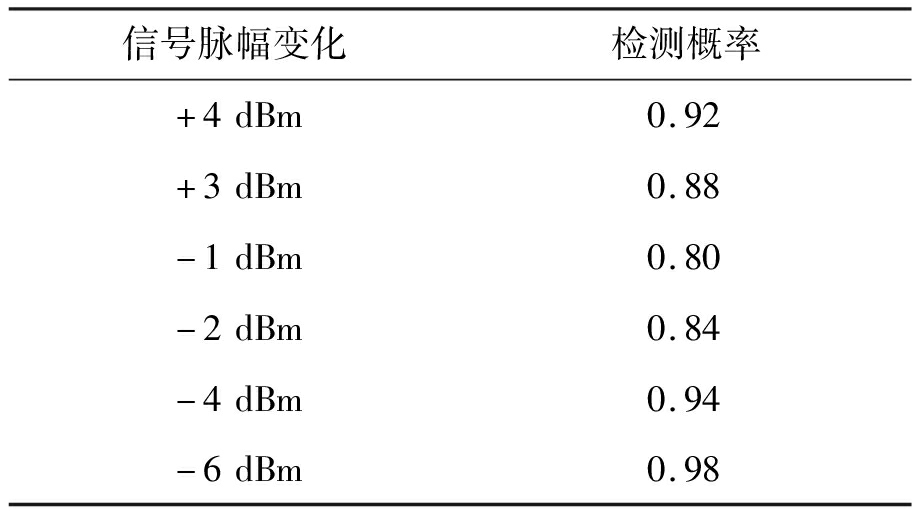
信号脉幅变化检测概率+4dBm0.92+3dBm0.88-1dBm0.80-2dBm0.84-4dBm0.94-6dBm0.98
在积累时间、脉冲重复周期一定的情况下,对于原目标信号异动,检测概率与脉冲变化程度大小有关,根据表7实验结果,脉冲幅度变化程度越大,检测概率越高。
4.3.5 异动目标坐标定位
本小节在差值法的基础上利用形态学图像处理对第5天的某一频谱图像进行异动目标坐标定位实验。用类别2频谱图像均值作为模板图,像素亮度门限根据观察取10。图11所示为差值法得到的图像,除异常信号处外其他位置产生虚警点。
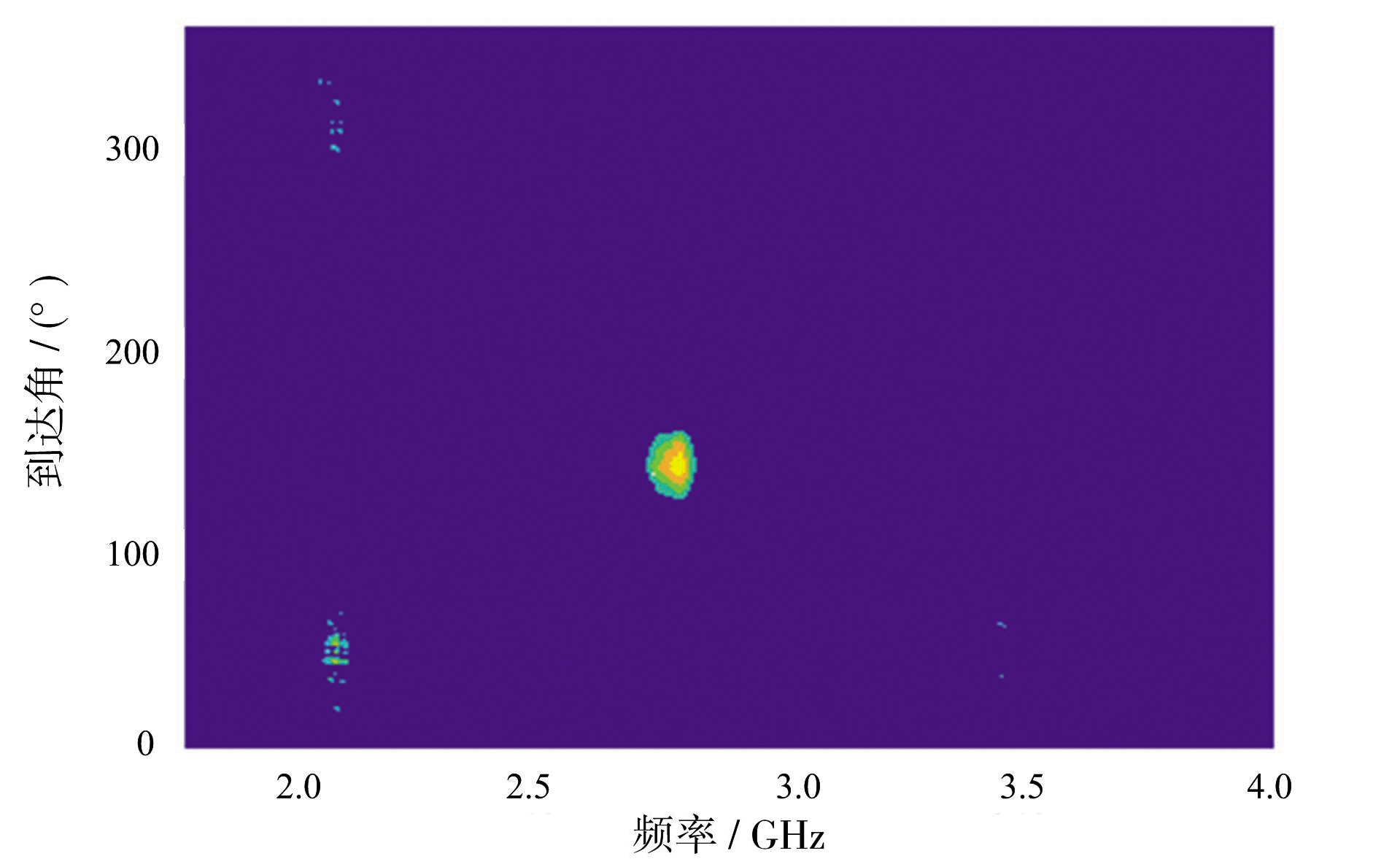
图11 差值法图
针对虚警点的离散特性,采用圆盘型结构元素对其腐蚀、膨胀处理。在腐蚀处理时,对于小于圆盘结构元素半径的区域将会被腐蚀掉。半径取值大小很重要,半径过小,去除虚警点的效果不佳;半径过大,异常信号区域也会被腐蚀。本文经多次实验,在半径取5的情况下,腐蚀效果较好,为恢复疑似异动信号峰值,膨胀半径也取5,处理结果如图12所示。
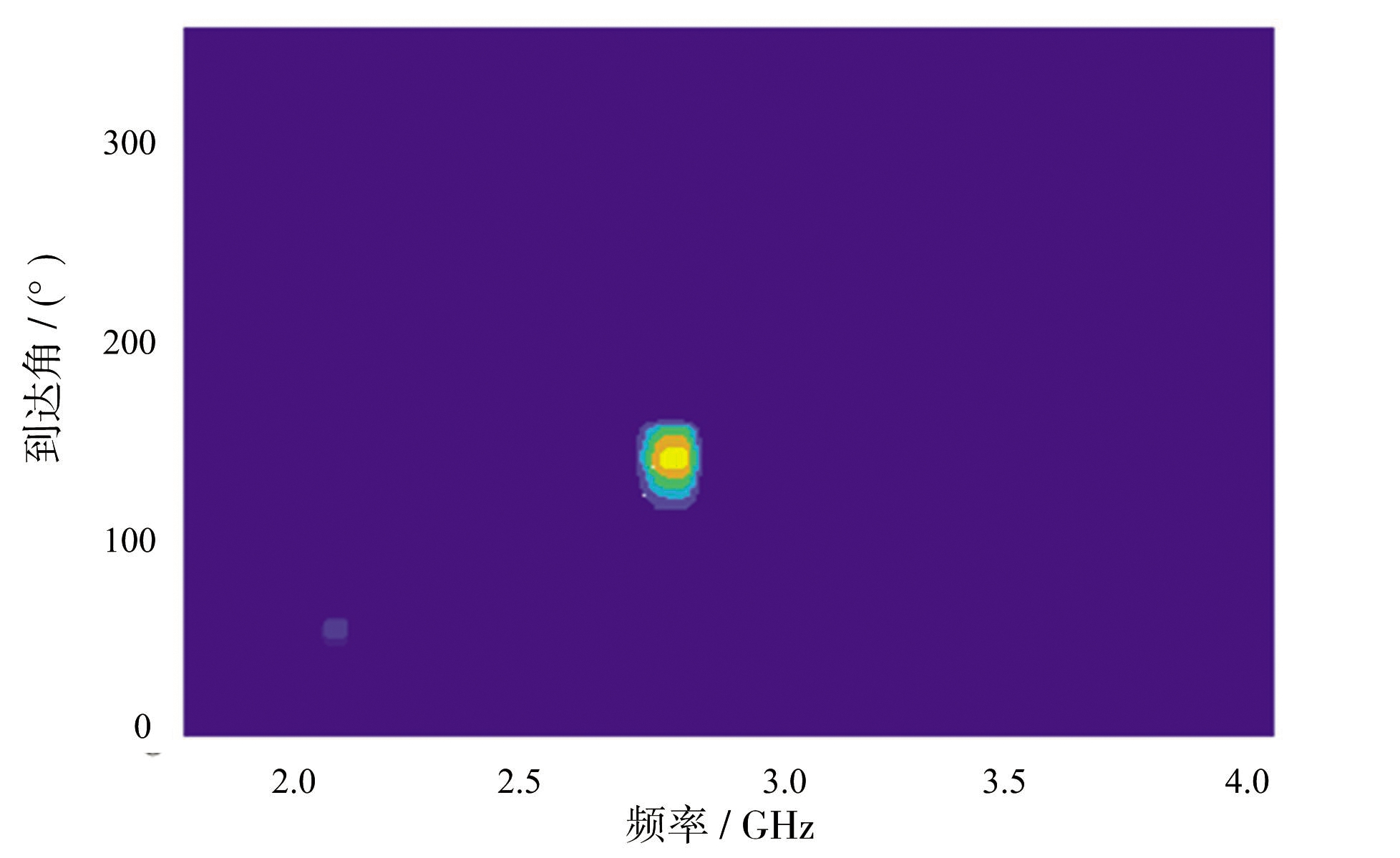
图12 形态学图像处理图
经腐蚀、膨胀处理后的差值图有两处疑似异动信号(频率2.1 GHz左右,到达角50°左右;频率2.8 GHz左右,到达角140°左右)。计算其峰值均值为门限,保留峰值大于门限的峰值即为异动信号的位置,如图13所示,经计算得到异动信号的位置信息,即频率2.75~2.85 GHz,到达角124°~156°存在异动信号。
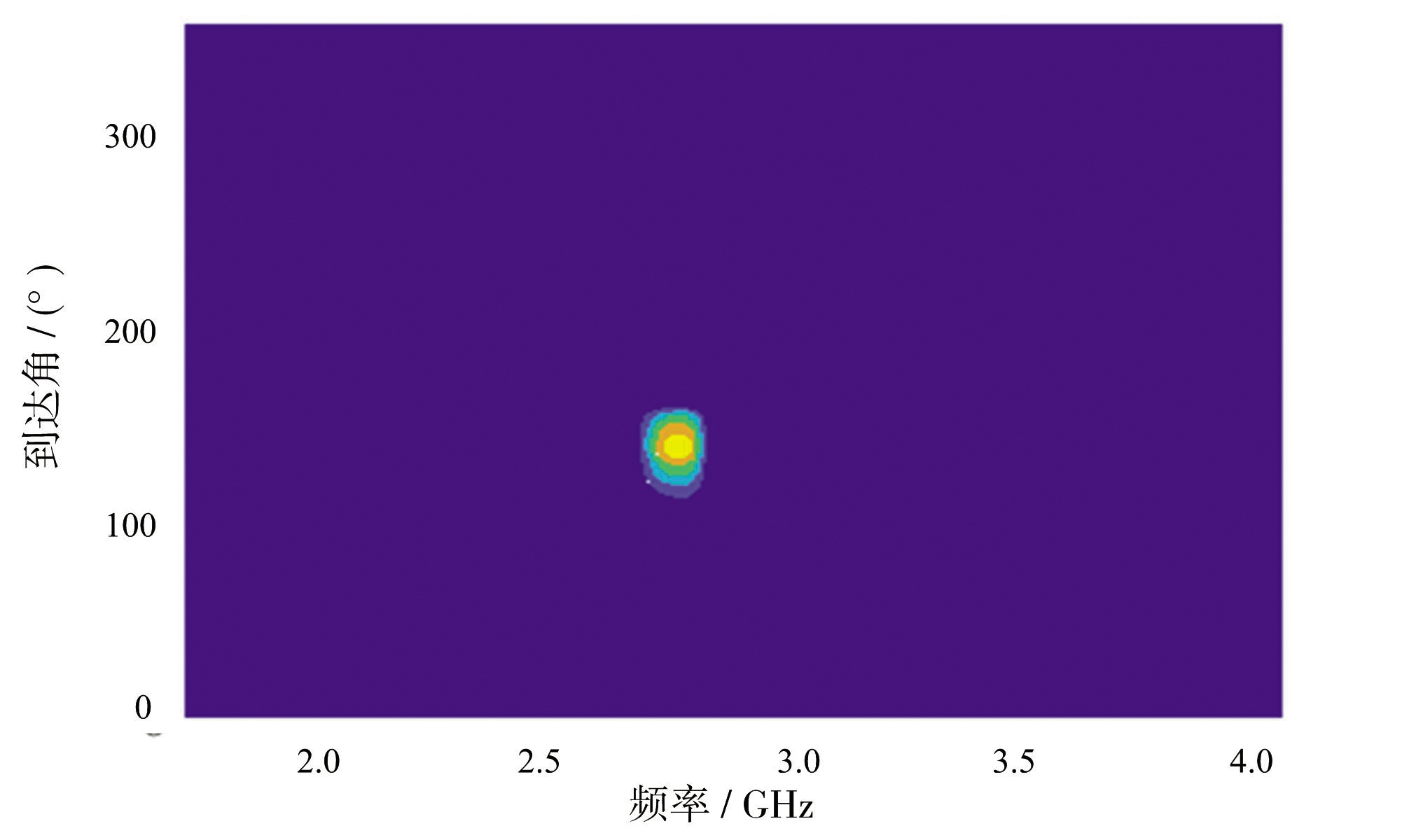
图13 峰值检测
5 结束语
本文在文献[1]提出的方位-频率二维划分模型基础之上,提出一种基于图像处理的频谱异动检测方法。该方法通过提取频谱图像特征,定义图像距离,设定距离门限对信号频谱图像进行异动检测,并在差值法基础上用形态学图像处理对异动信号坐标进行定位。仿真结果表明,通过该方法能有效检测频谱异动并定位异动信号坐标。但本文存在两点不足:一是对频谱能量小的信号检测能力差;二是腐蚀、膨胀半径是靠人工经验得出。为了更好地完善装备频谱异动检测性能,这将是本文后续进行优化的重点内容。
[1]吕进军,陈蓓,兰俊杰.一种监测异动电磁目标信号的方法[J].空军雷达学院学报,2011,25(6):408-411.
[2]何明浩.雷达对抗信息处理[M].北京:清华大学出版社, 2010:1-158.
[3]闫戈.基于大数据的频谱分析算法的研究[D].北京: 北京邮电大学,2018.
[4]刘海伟.图像分类与变化检测方法的研究与实现[D].北京:北方工业大学,2013.
[5]钱月.基于MATLAB的图像形态学处理技术与应用[J].内江师范学院学报,2019,34(10):51-55.
[6]张玉荣,陈赛赛,姜忠丽,等.基于图像处理的小麦容重检测方法研究[J].中国粮油学报,2015,30(3):116-121.
[7]PõDER E.Discrimination of Spatial Phase: The Roles of Luminance Distribution and Attention[J].Vision Research,2018,150:1-7.
[8]于航,刘阳,王海政,等.一种基于3σ准则与FCM算法相结合的光伏电站直流侧故障定位方法[J].太阳能,2019(2):50-55.
