0 引 言
相比单偏振雷达，双偏振雷达通过发射水平和垂直偏振电磁波不仅能探测到常规的多普勒参量，还能获取表征粒子相态和微物理特性的其他偏振参量。天气雷达的偏振参量对于确定雷达校准、地面杂波的消除、降水分类和雨滴谱参数估计等方面具有更大的优势[1]。相比C波段和S波段天气雷达，X波段天气雷达对弱气象目标的探测更敏锐，并且具有天线尺寸小、易于移动等特点。但由于降水区域会对天气雷达的回波信号产生散射干扰以及吸收，会导致接收到的数据与实际值相比会有衰减，特别是波长较短的X波段(中心波长3 cm)，其回波信号的衰减现象更为严重，这也是X波段天气雷达应用推广所面临的主要问题。
X波段天气雷达雨衰补偿相比C波段和S波段天气雷达的研究和发展较晚，因而对X波段天气雷达雨衰补偿研究的最开始阶段是借鉴了C波段和S波段气象雷达的相关方法以及研究结果[2]。2008年胡志群等人提出了差分传播相移率-衰减率(Kdp-Adp)方法，并通过对Kdp设置阈值，对水平反射率因子(ZH)进行衰减订正，该方法有一定的效果，但由于其没有考虑到Kdp的累积量在电磁波传播路径上会受到前向差分散射相移的影响，因而具有一定的局限性。2009年何宇翔等人引入卡尔曼滤波首先对差分传播相移(Φdp)进行滤波处理，进而对ZH进行衰减订正，该方法有效地减小了水平反射率因子的误差，但其处理过程是将降水区域视为线性关系，其具有一定的局限性。2014年魏庆等人采用线性滑窗、小波分析等方法对Φdp进行了衰减订正；2015年，孙跃、肖辉等人提出了线性拟合-递推法(LFRM)对Φdp进行质量控制。这些方法都能对Φdp进行一定程度的衰减订正，但这些方法的共同点都是将降水区域视为一个连续的线性区域，但由于天气雷达的回波功率只代表某一距离门的单位波束体积内N个降水粒子的回波功率平均值，不能理想的将天气雷达不同距离门的回波信号数据视为线性关系[3]，因而这些方法具有一定的局限性。
针对X波段天气雷达的偏振参量衰减订正，本文首先采用粒子滤波算法对Φdp进行滤波处理，在经过粒子滤波算法处理后，对数据利用卡尔曼滤波进行最优化估计，以达到对Φdp数据的精确估计订正。在得到Φdp滤波数据后，将Φdp数据作为参照量采用自适应算法，对ZH进行衰减订正处理。天气雷达的偏振参量回波数据是一个距离门内所有采样点的叠加值，常规的窗函数滤波等方法对所包含的噪声信号的滤除效果有限。粒子滤波能够利用偏振参量之间的关系建立合适的状态方程和观测方程，可以有效地进行数据的滤波处理，但由于粒子滤波的时间复杂度随着粒子数的增加而增加，于是引入卡尔曼滤波，能够对经过较少粒子数的粒子滤波处理后数据进行最优化估计，从而达到时间复杂度的平衡[4]。采用P-K算法能够得到更平滑和准确的Φdp，进而对水平反射率因子进行更精确的衰减订正。
1 基于P-K滤波的差分传播相移衰减订正
X波段双偏振雷达回波数据包含有ZH,Kdp，Φdp等偏振参量信息。在对ZH进行衰减订正之前需要先对Φdp进行衰减订正。
1.1 建立粒子滤波方程
直接从天气雷达回波数据中提取到的并不是差分传播相移而是包含了前向差分散射相移和后向差分散射相移的全差分相移(Ψdp)，其中后向差分散射相移也就是差分传播相移(Φdp)。单个距离门的全差分相移(Ψdp(k))定义为
Ψdp(k)=Φdp(k)+δhv(k)，k=1,…，K
(1)
式中：k表示传播路径电磁波到达的距离门，总共有K个距离单元；Φdp(k)表示第k个距离门的差分传播相移；δhv(k)表示第k个距离门的前向差分散射相移，它是单基地天气雷达回波信号中的有害高频噪声成分。X波段电磁波在小雨到中雨区域偏离瑞利散射很小，δhv(k)可以忽略，但对于较强的雨区，就可能产生较强的瑞利散射，因而不能被忽略，所以雨衰补偿的重点就是从全差分相移中将δhv(k)滤除。
从全差分相移中无法直接通过滤波等方式将前向差分散射相移滤除，Hubbert拟合得到的不同频率的雷达的δhv(k)与单个距离门的差分传播相移率Kdp(k)有如下关系[5]：
δhv(k)=c+bKdp(k)，k=1,…，K
(2)
式中，b和c的取值依赖于Kdp(k)(k=1,…，K)的取值[6]，当Kdp(k)≤2.5°/km时，b取2.37，c取0.054；当Kdp(k)>2.5°/km时，b取0.27，c取6.16。
将式(2)代入式(1)可得到Ψdp(k)与Φdp(k)及Kdp(k)之间的关系：
Ψdp(k)-c=Φdp(k)+bKdp(k)，k=1,…,K
(3)
而式(1)中的差分传播相移与差分传播相移率之间又有如下关系[7]：
Φdp(k+1)=Φdp(k)+2Δr·Kdp(k)，
k=1,…，K
(4)
式中，Δr表示相邻距离门之间的距离。
根据式(3)和式(4)即可建立如下的粒子滤波方程组[8]：
k=1,…,K
(5)
[Ψdp(k)-c]=
k=1,…,K
(6)
其中，式(5)为粒子滤波算法的状态方程，令
表示系统的状态向量，
为状态转移矩阵，εxk-1表示激励噪声。式(6)为粒子滤波算法的观测方程，令yk=[Ψdp(k)-c]表示观测向量，
为观测矩阵，εyk表示观测噪声。
根据粒子滤波算法流程，利用多项式方法[8]在第k个距离门得到xk的N个粒子的观测集
其中
的上标i表示第i个粒子，本文中设定N的值为1 000，并根据式(5)对第k个距离单元的每一个粒子的状态向量进行预测，如式(7)所示：
(7)
以观测量与预测状态之间的差值作为似然函数，计算公式如式(8)表示：
(8)
可以通过观测方程迭代更新重要性权值，更新步为
(9)
其中，初始的每个粒子的权重值
为1/N。
权值进行归一化可得
(10)
进而可以得到状态xk的估计为
(11)
即
(12)
1.2 建立卡尔曼滤波方程
粒子滤波通过寻找一组在状态空间的随机样本对概率密度函数进行近似，以后验概率密度所产生的N个独立同分布样本的均值代替积分运算，从而获得状态最小方差分布，但由于粒子数的增加会导致其运算量急剧增加，而较少的粒子又不能得到最优的最小方差状态值，因而建立卡尔曼滤波对数据进行再处理，从而得到结果值。
将式(12)得到的结果
作为卡尔曼滤波的观测向量，并将式(5)作为卡尔曼滤波的时间更新方程，可以得到Φdp与Kdp基于卡尔曼滤波估计的时间更新方程与观测更新方程，方程组如式(13)和式(14)所示：
(13)
(14)
其中，令
分别表示卡尔曼滤波观测矩阵和状态转移矩阵，uk表示激励噪声，vk表示观测噪声，uk与vk均服从0均值的正态分布，并用Q表示激励噪声协方差矩阵，G为观测噪声协方差矩阵，且假设uk与vk相互独立[9]。令
表示观测向量，
表示状态向量。
卡尔曼滤波主要包括预测和更新两个过程，预测过程如式(15)、式(16)所示[10]：
(15)
(16)
其中，
是根据第k-1个距离门数据迭代得到的状态向量的先验估计，
是第k个距离门的先验估计协方差矩阵。
更新过程是结合先验状态估计与当前距离门观测向量的数据进行后验估计过程，更新过程为
(17)
进而得到卡尔曼滤波估计方程为
(18)
而协方差更新方程为
(19)
卡尔曼滤波利用卡尔曼增益对系统状态和协方差矩阵进行数据修正；Pk是滤波后更新的协方差矩阵，也是下一次迭代的先验估计协方差矩阵；
为卡尔曼滤波估计后的估计值，也是本算法需要的最终值，即
(20)
2 基于自适应算法的水平反射率因子衰减订正
对差分传播相移的衰减订正是对水平反射率因子订正的基础，在利用P-K滤波算法得到误差更小的差分传播相移数据后，利用自适应算法，对反射率因子(ZH)进行衰减订正。
利用Bringi提出的自适应约束(self-consistent method with constraints)算法对ZH进行衰减订正[11]。ZH的衰减订正的关键就是确定雨区的衰减率AH，设定雨区的距离门范围为k0～k1，可得到第k个距离门的衰减率AH(k)的计算公式为[12]
AH(k)=
(21)
式(21)中的
其中AH(k)为单程衰减率，ZHa(k)表示订正前第k个距离门的反射率因子。根据文献[13]对雨滴谱的研究结果，本文β设定为0.78，α的取值范围为0.139～0.335 dB·(°)-1，步长取0.005。
每一个α值可以计算得到一个对应的AH(k)值，利用AH(k)计算出重构的差分传播相移
重构方程如式(22)所示：
(22)
其中，
表示对于一个固定的α所对应的第k个距离门的差分传播相移重构值，AH(i|α)表示对于一个固定的α值，第i个距离门的衰减率。以与利用K-P算法估计得到的Φdp(k)的最小差值作为约束条件，获得第k个距离门最优α值，接着将α代入式(21)计算得到最优化的AH(k)值。然后将结果代入式(23)中得到订正后的ZH(k)。
(23)
3 实验结果及分析
3.1 P-K滤波结果分析
本仿真实验的X波段气象回波数据来源于大气辐射测量气候研究中心(ARM)的网站。其数据包括了Φdp，Kdp，ZH等重要回波参数，每个径向上有400个距离单元，每个距离单元代表100 m。实验选用的X波段雷达于2018年7月3日11:00的回波数据。
一个径向上的Φdp数据经过不同方法的滤波效果与源数据效果对比如图1所示。
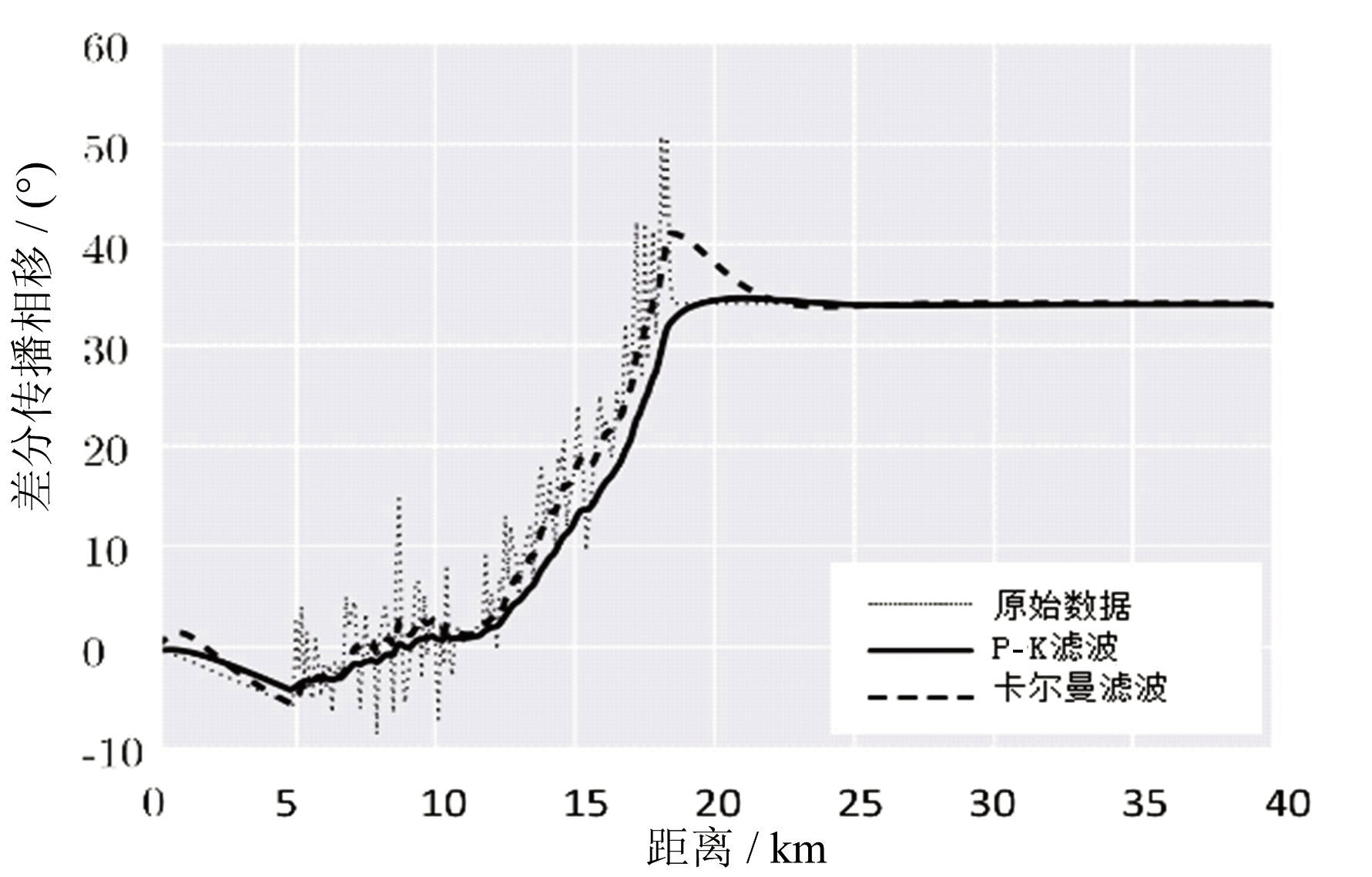
图1 同一径向不同方法的Φdp滤波效果图
由图1可以看出，相对比原始数据，卡尔曼滤波以及P-K滤波均能对反射率因子的波动和高频噪声进行抑制，保证了廓线的连续性和平滑度。但相比卡尔曼滤波，P-K滤波能够对数据进行更好的平滑处理。
如图2所示，为一个俯仰角的全径向PPI图对比，与卡尔曼滤波结果相比较，P-K滤波能更有效地将数据中的高频噪声部分剔除，且数据能呈现较好的非负性，更加符合真实气象特征[14]。
(a) 卡尔曼滤波
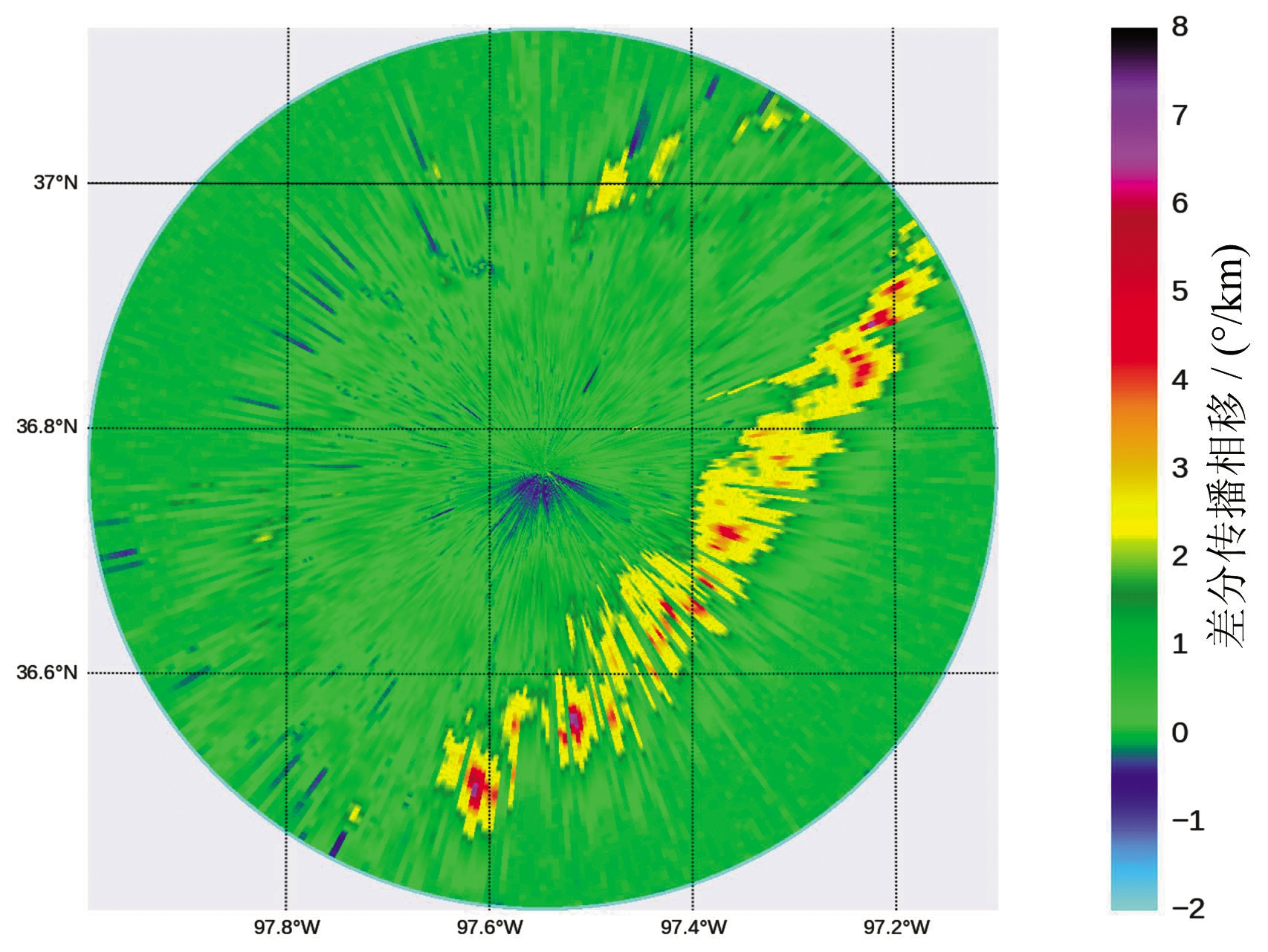
(b) P-K滤波
图2 同一俯仰角不同方法的ΦdpPPI效果图
3.2 水平反射率因子订正结果及分析
图3为衰减订正前后的ZH的一个径向距离廓线，由图可以看到相比与卡尔曼滤波，P-K滤波在衰减订正的同时，保留了更多的原始数据的轮廓细节。
图3 一个径向ZH订正结果显示
图4(a)是相同时间，相近地点的KVNX雷达的S波段的ZH图；图4(b)是衰减订正前的ZH数据的PPI图；图4(c)、(d)是应用卡尔曼滤波、P-K滤波处理后进行衰减订正后的ZH的PPI图。由于S波段的天气雷达其雨衰相对较小，因而可以当作参考，对比黑色方框区域可看到，P-K滤波的结果相对卡尔曼滤波结果，其雨衰补偿订正效果更好，与S波段KVNX 雷达的参考值更加接近。并且在雷达远端低SNR的条件下，依然具有良好的订正效果。
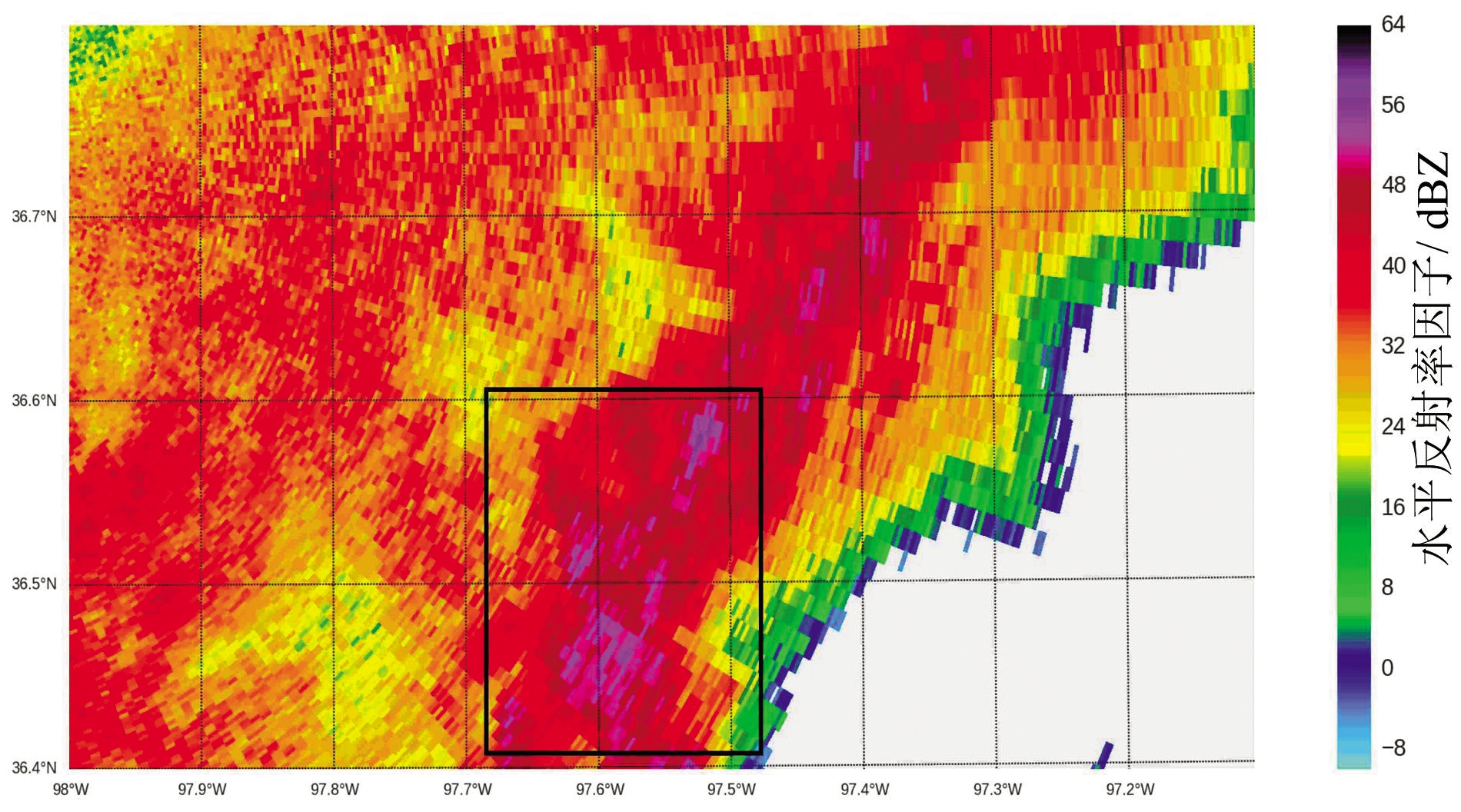
(a) S波段ZHPPI扫描图
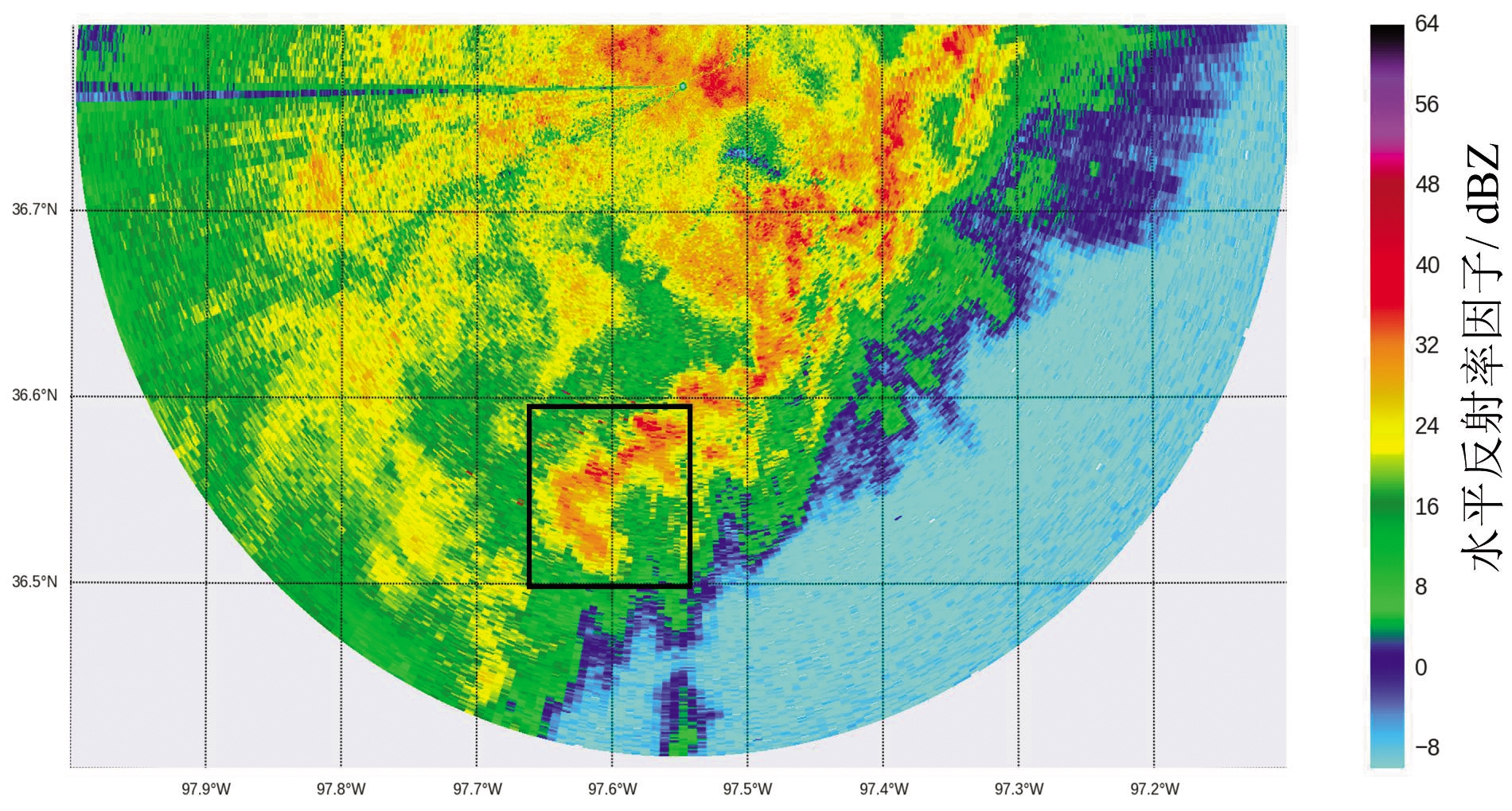
(b) X波段ZHPPI扫描图
(c) 卡尔曼滤波订正的ZHPPI扫描图
(d) 经过P-K滤波订正的ZHPPI扫描图
图4 订正前后ZH PPI比较图
通过散射模拟建立的偏振参量的经验关系验证衰减订正的效果，可以比较X波段订正前后的AH～ZH和ZH～Kdp之间的散点图特性。图5(a)、(b)分别为订正前后的ZH～Kdp的散点图，实线为Park通过散射模拟建立的ZH～Kdp的经验关系，由图5(a)可以发现，经过P-K滤波后订正的ZH～Kdp的散点分布与Park曲线更加接近。图5(c)、(d)分别为订正前后AH～ZH的散点图，由于全扫描的数据点过多，此处只显示50个距离门的数据。通过对比发现，P-K滤波后订正的散点图分布与Park的模拟曲线更加相似。由此可见，订正后的偏振参量与Park的散射模拟结果基本一致，进一步验证了本订正方法的有效性。
(a) 订正前Kdp与ZH的散点图
(b) 订正后Kdp与ZH的散点图
(c) 订正前AH与ZH的散点图
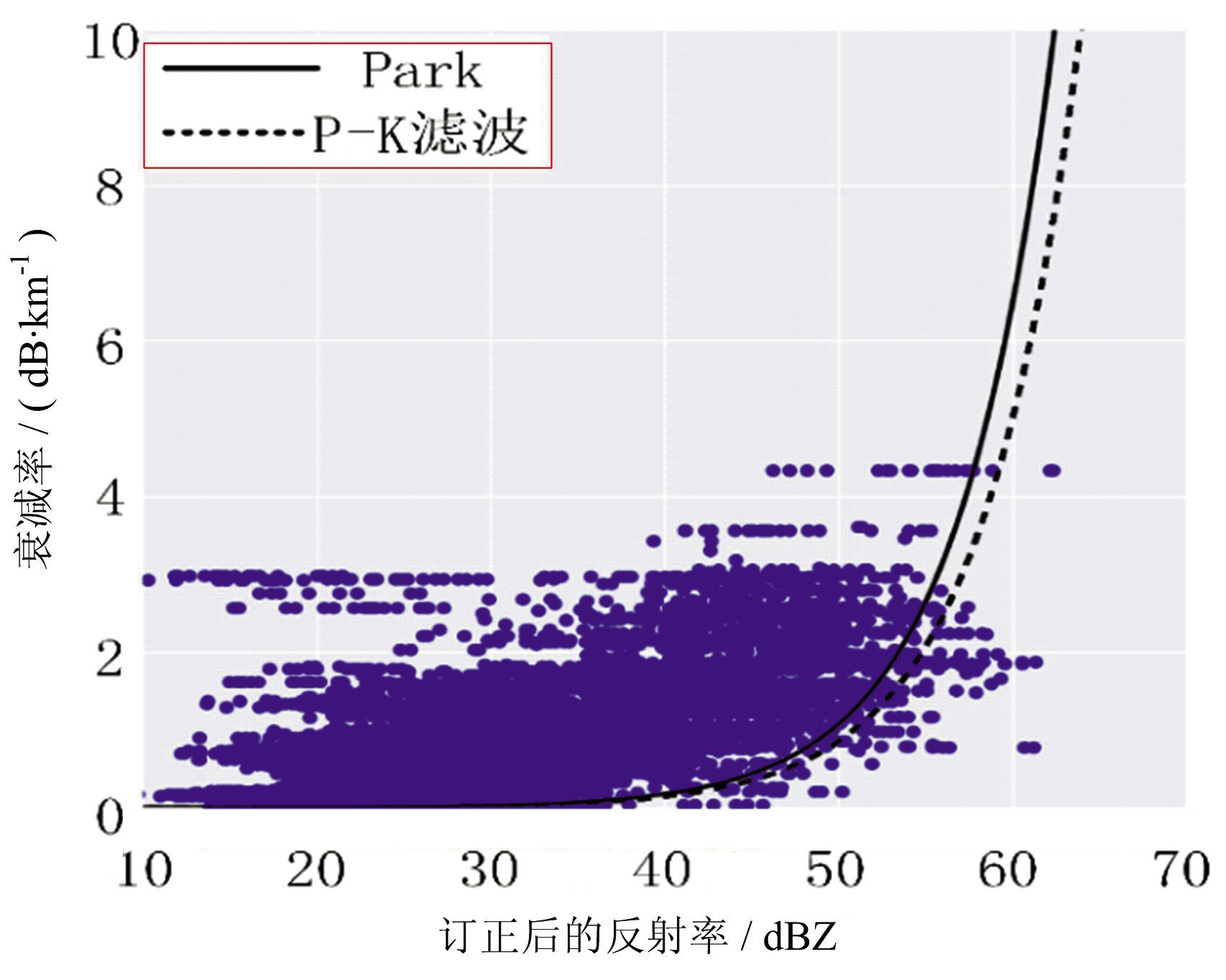
(d) 订正后AH与ZH的散点图
图5 P-K滤波后订正前后的偏振参量散点图
4 结束语
本文根据双偏振天气雷达偏振参量之间的相互关系，建立了适当的差分传播相移和差分传播相移率的状态方程和过程方程，利用粒子滤波-卡尔曼滤波的综合算法，首先对差分传播相移数据进行了效果显著的消噪和估计过程，并利用自适应算法，进行了反射率因子的衰减订正。对比了衰减前后以及只用卡尔曼滤波算法的订正结果。结果表明，本文采用的方法能够有效地进行衰减订正，能够使X波段的雷达偏振参量订正到一个良好的水平，这对降水量估计以及降水分类等有重要的作用，所以本方法具有一定的实际应用价值。
[1]吴欢,黄兴友.X波段双线偏振雷达回波强度衰减和地物回波识别订正[J].气象科学,2014,32(1):32-38.
[2]贺进瑞.C波段双偏振雷达衰减订正比对试验分析[D].南京：南京信息工程大学，2016.
[3]张培昌, 杜秉玉, 戴铁丕.雷达气象学[M].北京:气象出版社, 2001.
[4]王长元,张文强,薛鹏翔.粒子滤波和卡尔曼滤波组合的瞳孔跟踪方法[J].计算机与数字工程,2018, 46(4):739-742.
WANG Changyuan, ZHANG Wenqiang, XUE Peng-xiang.Pupil Tracking Method Combined with Particle Filter and Calman Filter[J].Computer & Digital Engineering, 2018,46(4):739-742.(in Chinese)
[5]HUBBERT J，BRINGI V N.An Iterative Filtering Technique for the Analysis of Copolar Differential Phase and Dual-Frequency Radar Measurements[J].Journal of Atmospheric and Oceanic Technology，1995，12(3)：643-648.
[6]SMITH A F M，GELFAND A E.Bayesian Statistics Without Tears: A Sampling-Resampling Perspective[J].The American Statistician，1992，46(2)：84-88.
[7]李海,崔爱璐,章涛,等.基于粒子滤波的差分传播相移估计方法[J].雷达科学与技术,2017,15(5):457-466.
[8]刘红红.粒子滤波算法的研究及其在目标跟踪中的应用[D].太原：太原理工大学, 2018.
[9]HUANG Hao，ZHANG Guifu，ZHAO Kun，et al.A Hybrid Method to Estimate Specific Differential Phase and Rainfall with Linear Programming and Physics Constraints[J].IEEE Trans on Geoscience and Remote Sensing，2017，55(1)：96-111.
[10]李爱双,夏宁.基于粒子滤波和卡尔曼滤波的室内定位方法研究[J].资源信息与工程,2019,34(3):163-164.
[11]BRINGI V N，KEENAN T D，CHANDRASEKAR V.Correcting C-Band Radar Reflectivity and Differential Reflectivity Data for Rain Attenuation: A Self-Consistent Method with Constraints[J].IEEE Trans on Geoscience and Remote Sensing，2001，39(9)：1906-1915.
[12]王晗,史朝,滕玉鹏.X波段双线偏振雷达反射率不同衰减订正法对比分析[J].成都信息工程大学学报,2016,31(4)：363-366.
WANG Han, SHI Zhao, TENG Yupeng.Comparison of Different Attenuation Correction Methods Using X-band Dual Polarimetric Radar[J].Journal of Chengdu University of Information Technology, 2016, 31(4):363-366.(in Chinese)
[13]ANAGNOSTOU E N，ANAGNOSTOU M N，KRAJEWSKI W F，et al.High-Resolution Rainfall Estimation from X-Band Polarimetric Radar Measurements[J].Journal of Hydrometeorology，2004，5(1)：110-128.
[14]ANAGNOSTOU M N，ANAGNOSTOU E N，VIVEKANANDAN J.Correction for Rain Path Specific and Differential Attenuation of X-Band Dual-Polarization Observations[J].IEEE Trans on Geoscience and Remote Sensing，2006，44(9)：2470-2480.
