0 引言
合成孔径雷达(Synthetic Aperture Radar,SAR)具有全天时、全天候、多波段、穿透性强等优点。星载SAR能够进行高分辨率成像,已成为军事战争中情报侦察的重要手段之一[1-2]。因此,如何有效地对抗SAR侦察是电子对抗领域的重要研究课题。目前,SAR干扰技术可分为欺骗干扰和压制干扰[3],而压制干扰根据干扰信号能否获得雷达的匹配压缩增益,又可分为非相干压制干扰和相干压制干扰[4]。相干压制干扰由于能够获得部分雷达匹配压缩增益,可以在干扰机发射功率较低的条件下实现有效的干扰,因此成为近年来的研究热点[5]。随着压制干扰研究的深入,研究学者提出了很多干扰算法。吴一戎等提出了距离调频率失配脉间去相干干扰算法[6]。黄洪旭先后提出了随机移频干扰、步进移频干扰[7]等干扰形式。吴晓芳等[8]提出了微动调制干扰。李田建立了基于幅度调制的SAR相干压制干扰模型,增加了干扰信号的随机性[9]。杨立波等从功率角度分析了雷达不同干扰算法的性能[10]。
目前,研究学者们所提出的干扰算法多为在距离向或方位向施加的一维相干压制干扰,经过雷达的匹配滤波后,只能形成沿距离向或方位向的线状干扰,无法对港口、机场等具有重要军事价值的面目标进行压制;且部分算法需要在获取敌方雷达参数的情况下进行干扰,会降低干扰的及时性、提高系统的复杂度。此外,目前关于干扰算法的相关文献中,鲜有学者采用雷达实测数据与干扰仿真信号结合的研究方法对干扰效能进行评估。针对以上算法及研究方式的不足,本文在微动干扰及噪声卷积干扰算法的基础上,提出一种基于微动调制的梳状谱灵巧噪声压制干扰算法,该算法使用数字射频存储技术存储雷达信号,无需对敌方雷达参数进行侦察与估计,可在距离向及方位向同时获得部分雷达压缩增益,形成面状干扰。此外,该算法可根据需要保护目标的大小、反射系数等特性,对梳状谱频点间隔、灵巧噪声方差等参数进行调节,控制干扰面积的大小。若目标区域回波较强,则可减小频点间隔和灵巧噪声的方差,使能量更加集中,同时提高干扰功率,达到压制的目的;若目标区域回波较弱,则可适当增加频点间隔和灵巧噪声方差,使干扰能量更为分散,形成较大的干扰面积。因此,该压制干扰算法能够对港口、城市、机场等重要军事目标提供保护,具有较大的应用价值。
1 基于微动调制的梳状谱灵巧噪声压制干扰算法
设雷达原始回波信号为s0(τ,η),其表达式为
s0(τ,η)=![]()
(1)
式中,A0为雷达信号的幅度,ωr及ωa分别代表距离向及方位向的时间窗,f0为雷达载波频率,Kr代表调频斜率,τ和η分别代表距离向快时间和方位向慢时间,ηc为波束中心穿越时刻。
基于微动调制的梳状谱灵巧噪声压制干扰信号表达式为
jcombine=![]()
(2)
式中,jamm=Amsin(2πfmη+φm)为方位向微动调制信号,记为式(3),Am为微动信号调制幅度,fm为微动信号调制频率,φm为微动信号的初始相位;![]() 为由N个频点组成的梳状谱调制信号,记为式(4),ai表示第i个频点的幅度,fi表示第i个频点的频率;n(τ,η)表示灵巧噪声干扰信号,⊗表示卷积。
为由N个频点组成的梳状谱调制信号,记为式(4),ai表示第i个频点的幅度,fi表示第i个频点的频率;n(τ,η)表示灵巧噪声干扰信号,⊗表示卷积。
微动指的是目标或目标的组成部分在相对于雷达径向方向上的小幅运动。微动理论指出,当目标的运动形式为简谐振动或匀速圆周运动时,目标会对雷达信号进行调制,使雷达信号增加一个指数项[11]。
经过雷达接收机的基带解调及距离压缩后,得到微动干扰信号的表达式为
sout(τ,η)=![]()
(5)
式中,sinc(·)为沿距离向的函数包络,B为发射线性调频信号的带宽。式(5)中的最后一项即为微动调制函数,记为smd(η),则有
(6)
对smd(η)进行傅里叶级数展开,得到
smd(η)=![]()
(7)
式中,n∈Z,Jn(βFM)为第一类n阶贝塞尔函数。上式在频域中表现为以零频为中心,左右对称展开的冲击串,间隔为fm。考虑到贝塞尔函数幅度的衰减,可忽略高阶分量。
对经过微动调制的信号进行仿真分析,结果如图1所示。图1(a)为未加干扰信号经过成像处理后得到的图像,图1(b)为微动调制的回波信号经过成像处理后得到的图像。对比图1(a)和(b)可知,经过成像处理后,未加干扰的信号被压缩为一个理想的点目标,而微动调制后的信号却在方位向出现了展宽,形成了线状目标。
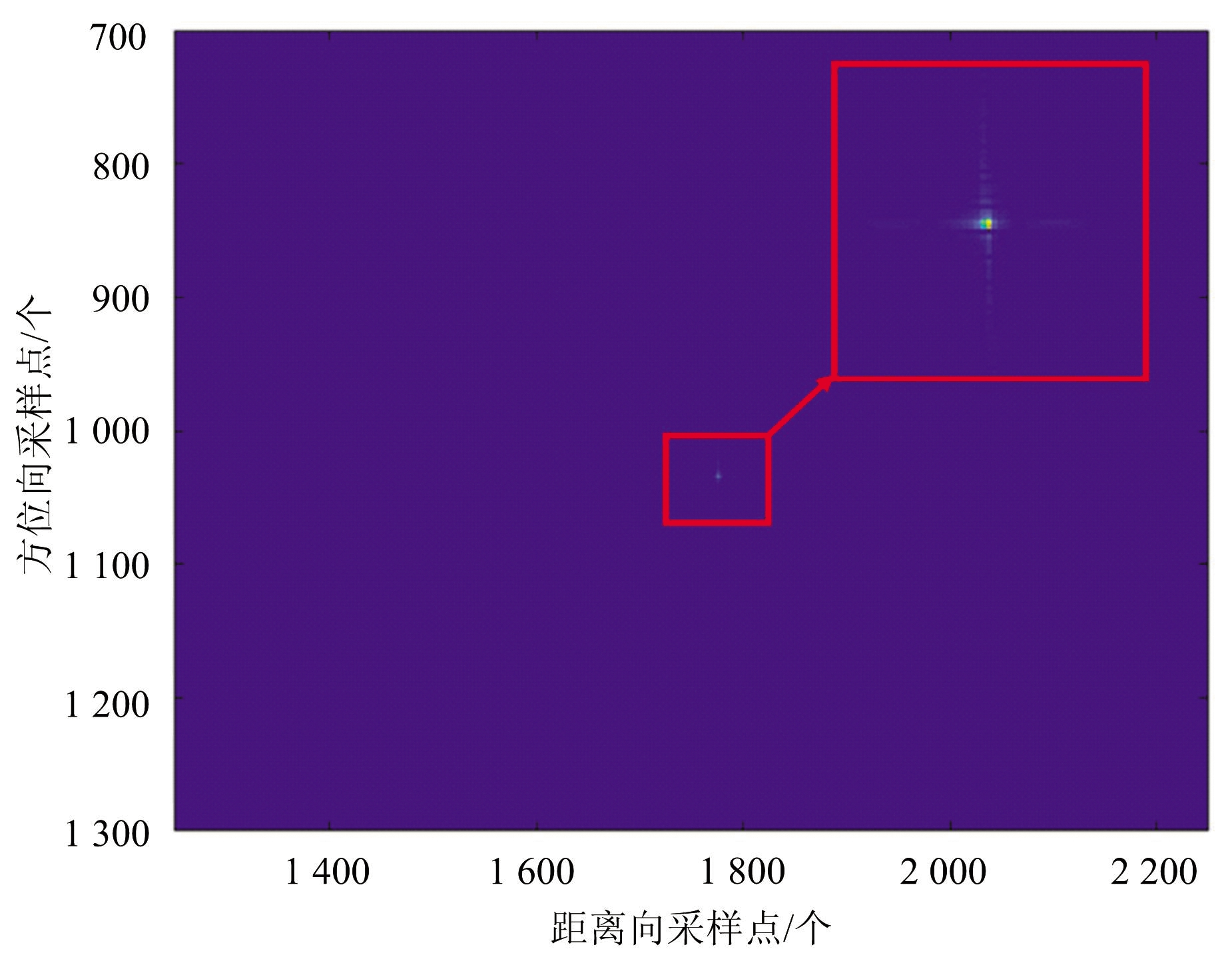
(a)未加干扰信号成像结果
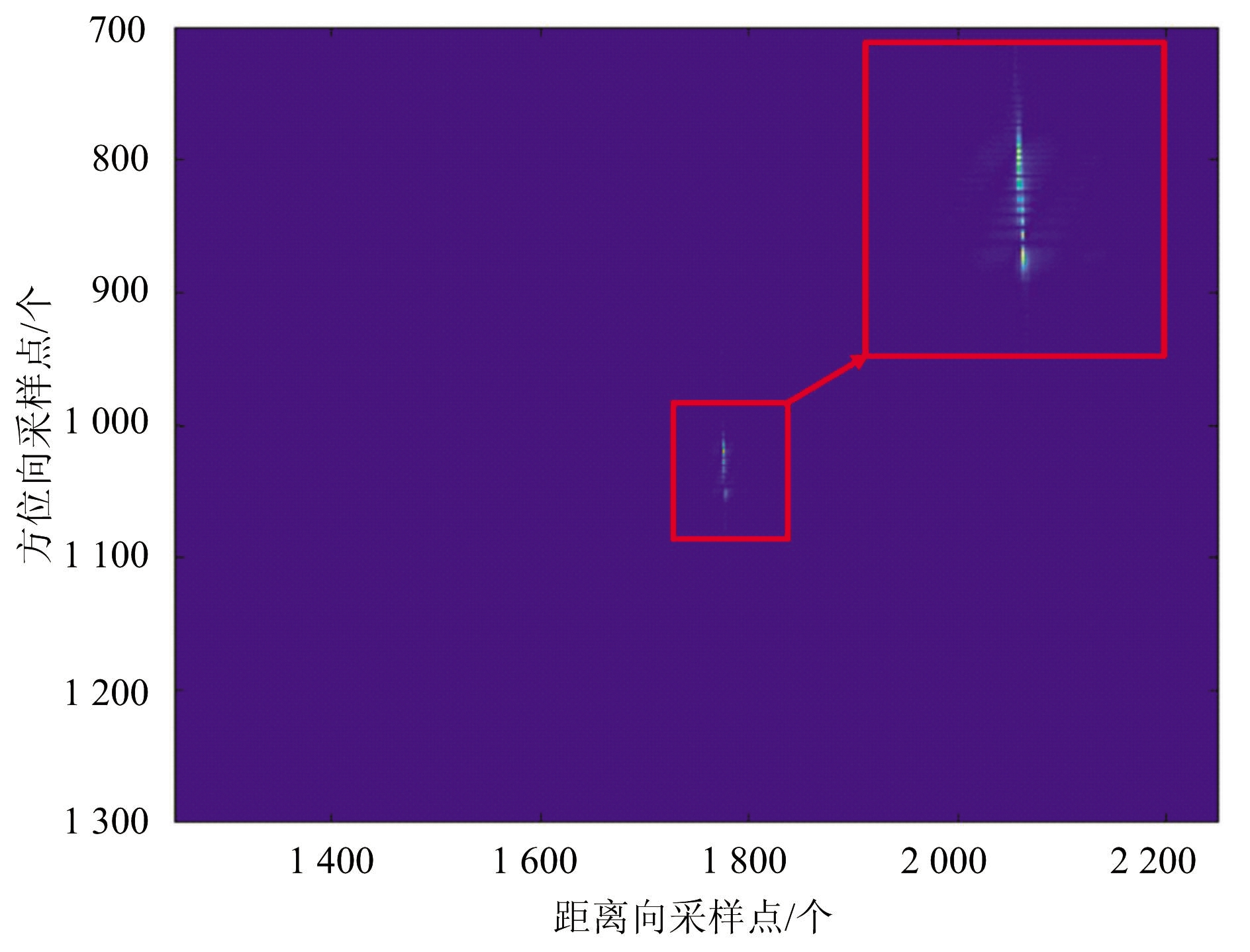
(b)微动调制回波信号成像结果
图1 未加干扰信号和微动调制干扰的信号成像结果
灵巧噪声卷积干扰指的是利用噪声信号对截获的雷达回波信号进行卷积调制后由干扰机发射的一种干扰算法。该算法克服了纯噪声干扰的弊端,由于干扰信号中包含雷达原始回波信号,因此可以获得部分雷达脉冲压缩增益,降低了干扰机的功率。灵巧噪声卷积干扰信号形式如式(8)所示:
jnoise(τ,η)=s0(τ,η)⊗n(τ,η)
(8)
出于压制干扰的目的,干扰信号应当满足以下两个条件:第一,在幅度上可以遮盖目标回波;第二,在时间上密集分布[12]。综合上述条件,若用时间t表示雷达回波信号的快时间和慢时间,即![]() 可以得出噪声信号的表达式为
可以得出噪声信号的表达式为
(9)
即为幅度、时延随机分布的脉冲串集合。其中,Ai,ti分别代表第i个冲击串的幅度和时延。考虑到需要满足时间上密集分布,因此ti服从均值为0,方差为σ2的正态分布。由于需要让干扰信号遮蔽大部分目标回波,因此考虑将幅度Ai设置为一常数,数值根据需要保护区域的雷达回波强度设置;方差σ2可根据需要保护区域大小设置,若所需保护区域较大且强散射点较少,则可适当增大σ2,若所需保护区域较小而强散射点较多,为了保证压制干扰效果,可减小σ2。
噪声卷积干扰结果如图2所示。图2(a)、(b)代表未加干扰回波信号成像结果以及使用噪声卷积干扰后的回波成像结果。对比图2(a)和(b)可知,经过灵巧噪声卷积干扰后,在距离向出现多个点目标,叠加形成沿距离向的亮线。
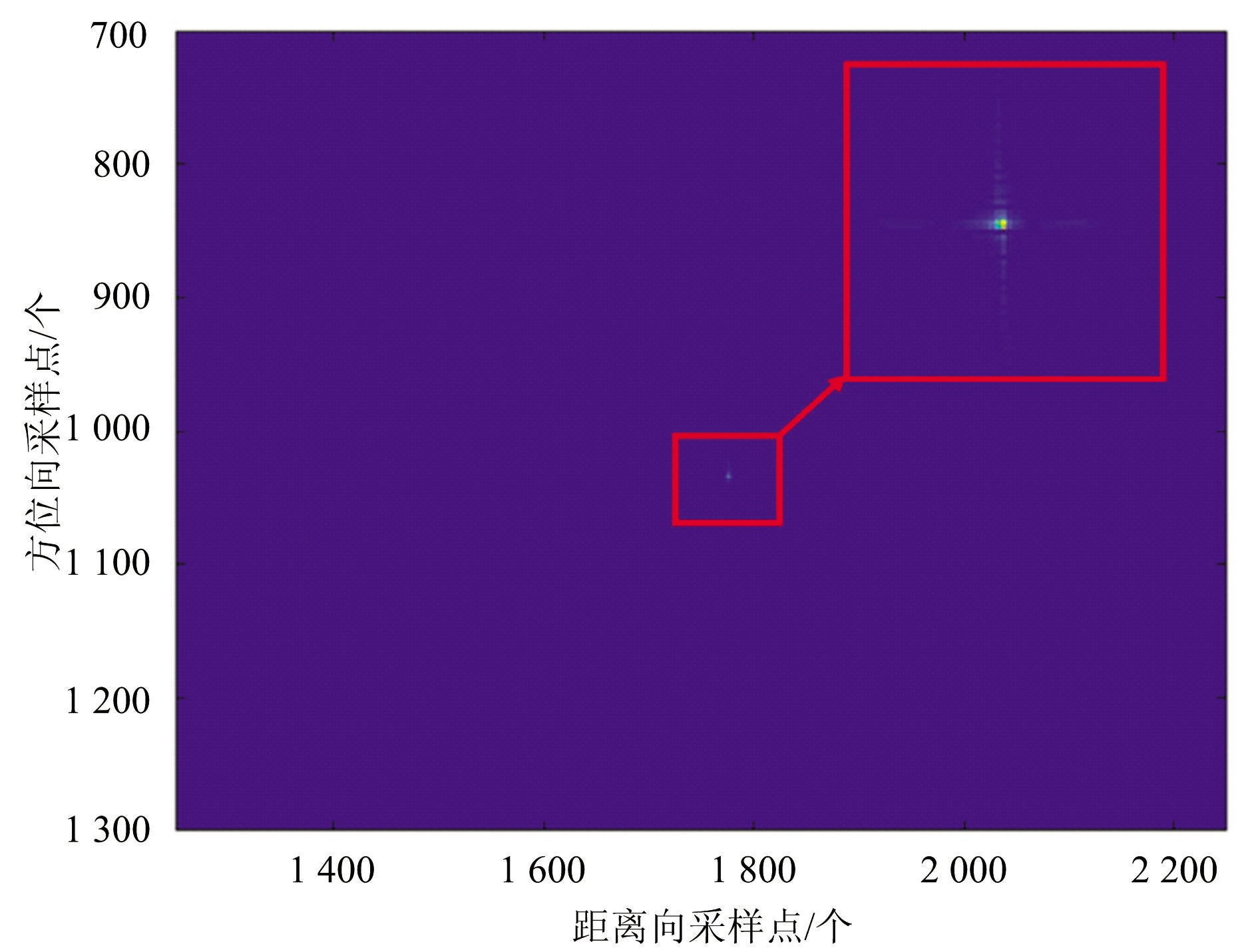
(a)未加干扰信号成像结果
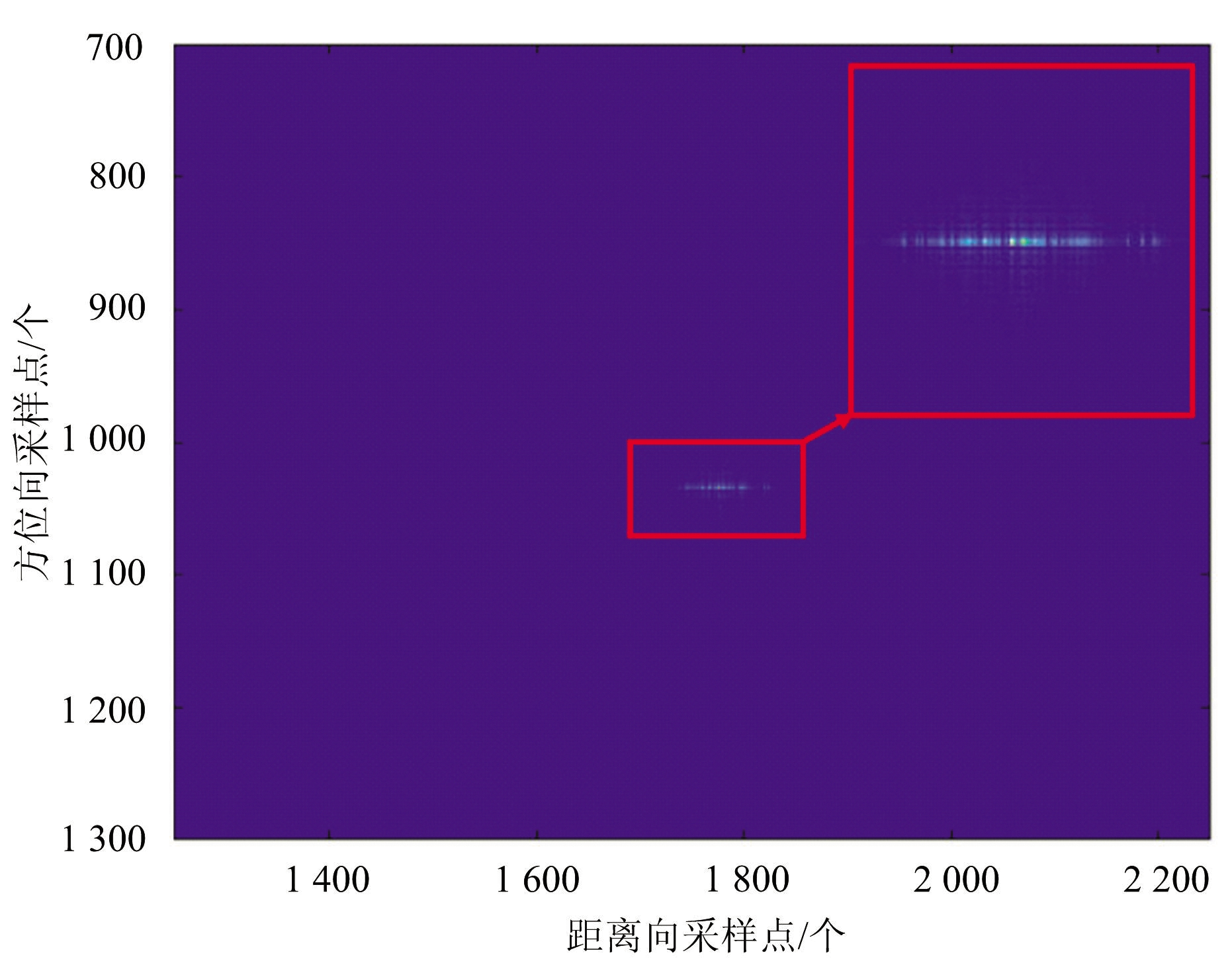
(b)灵巧噪声卷积干扰信号成像结果
图2 未加干扰信号和灵巧噪声卷积干扰的信号成像结果
梳状谱信号指的是包含一定数量频点的信号,表达式如式(4)所示。使用梳状谱信号对雷达回波信号进行调制,得到梳状谱干扰信号为
jcombsignal(t)=![]()
(10)
经过匹配滤波及傅里叶逆变换后,得到
joutcomb=![]()
(11)
由式(11)可知,梳状谱干扰信号经过匹配滤波后的输出为N个sinc函数加权之和,峰值出现在t=-fi/Kr处。因此,可以通过控制fi的正负,来控制干扰信号的超前或滞后。考虑到相邻频点出现的时间间隔Δt=(fi+1-fi)/Kr,且雷达的距离向分辨率为ρr=1/B=1/(Kr·T),因此当Δt>ρ,即Δf=fi+1-fi>1/T时,会形成在距离向上可以分辨的假目标,而当Δt<ρ,即Δf=fi+1-fi<1/T时,假目标之间无法完全区分,可以形成压制干扰效果[13]。图3(a)、(b)分别展示了在频点个数N=5时,Δt=4ρr以及Δt=0.5ρr时的仿真结果。根据结果可以看出,当Δt=4ρr时,形成了5个可明显分辨的假目标,而当Δt=0.5ρr时,假目标聚集在一起,无法分辨。该仿真结果与上述理论推导一致。若受保护目标区域回波较强,则可减少频点间隔,使能量更加集中;若目标区域回波较弱,则可适当增大间隔,形成更大的干扰面积。
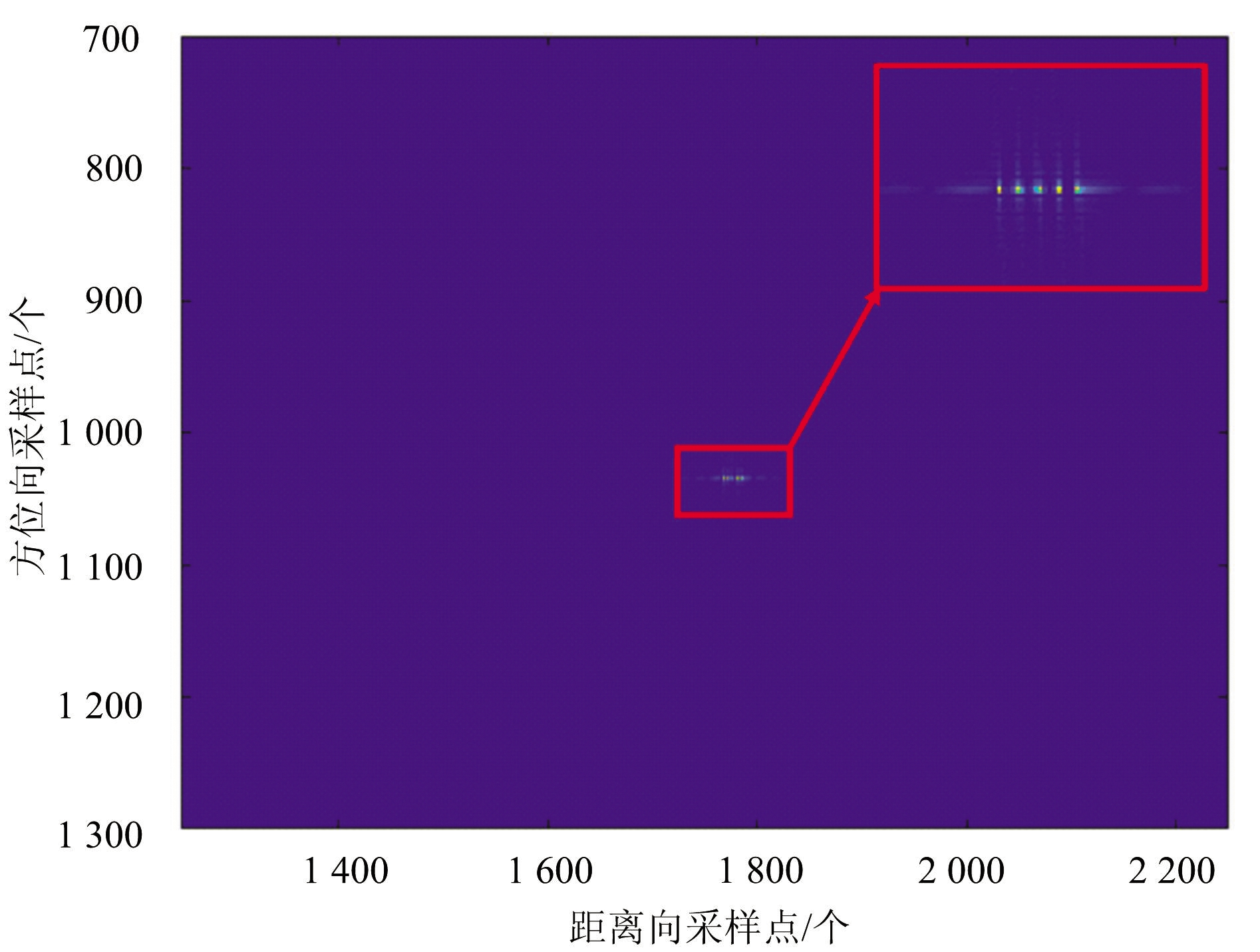
(a)Δt=4ρr时梳状谱干扰信号成像结果

(b)Δt=0.5ρr时梳状谱干扰信号成像结果
图3 不同频率间隔下的梳状谱干扰信号成像结果
根据上文分析和仿真结果可知,当单独采用微动调制干扰时,只能获得沿方位向展宽的一维压制干扰;而灵巧噪声卷积干扰或梳状谱干扰会形成沿距离向展宽的干扰信号,无法对面目标进行有效的压制;而如果将上述干扰方式的任意两种进行组合的话,无法获得较大的干扰面积,当对大型军事目标进行干扰时可能会出现无法完全遮蔽的情况。因此,本文提出一种基于微动调制的梳状谱灵巧噪声压制干扰算法,会造成距离向和方位向的失配,在距离向及方位向产生二维面状压制干扰。为了保证压制干扰效果,因此梳状谱干扰相邻频点间需满足Δt=0.5ρr,此时形成的压制面积较小,故需要使用灵巧噪声调制,扩展距离向的压制范围。此外,为了产生方位向压制,需要使用微动调制。此算法的优势在于能够产生比其他干扰算法更大的单点干扰面积,同时也保证了干扰的有效性。
结合上文分析可得,经过匹配滤波及傅里叶逆变换后的干扰信号为
jout=![]()
(12)
式中,![]() 代表灵巧噪声中第p个随机脉冲的时延。
代表灵巧噪声中第p个随机脉冲的时延。
图4(a)、(b)、(c)、(d)分别为采用微动干扰、灵巧噪声卷积干扰、基于微动调制的梳状谱干扰及本文所提出的干扰算法得到的干扰结果。由图可知,除本文所提出的方法之外,其余3种算法均只形成了线状干扰,而本文所提出的算法形成了大片干扰区域,在压制面积上优于其余3种算法。且该算法由于结合了噪声卷积干扰与梳状谱干扰的优势,因此可以通过对调整噪声信号冲击串时延的概率分布、梳状谱的相邻频率间隔等参数,实现对压制干扰区域能量分布及干扰面积大小的控制。
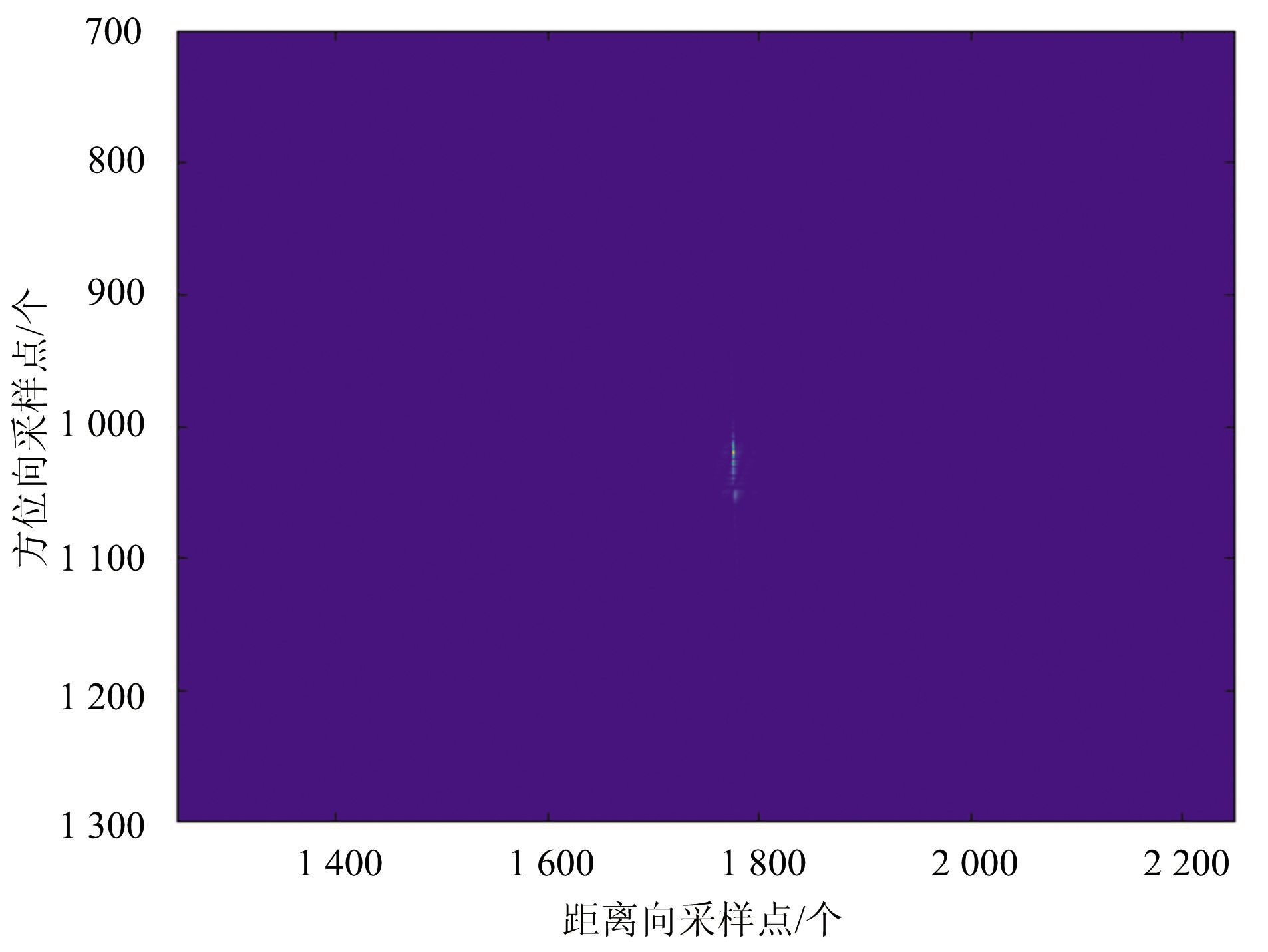
(a)微动干扰成像结果
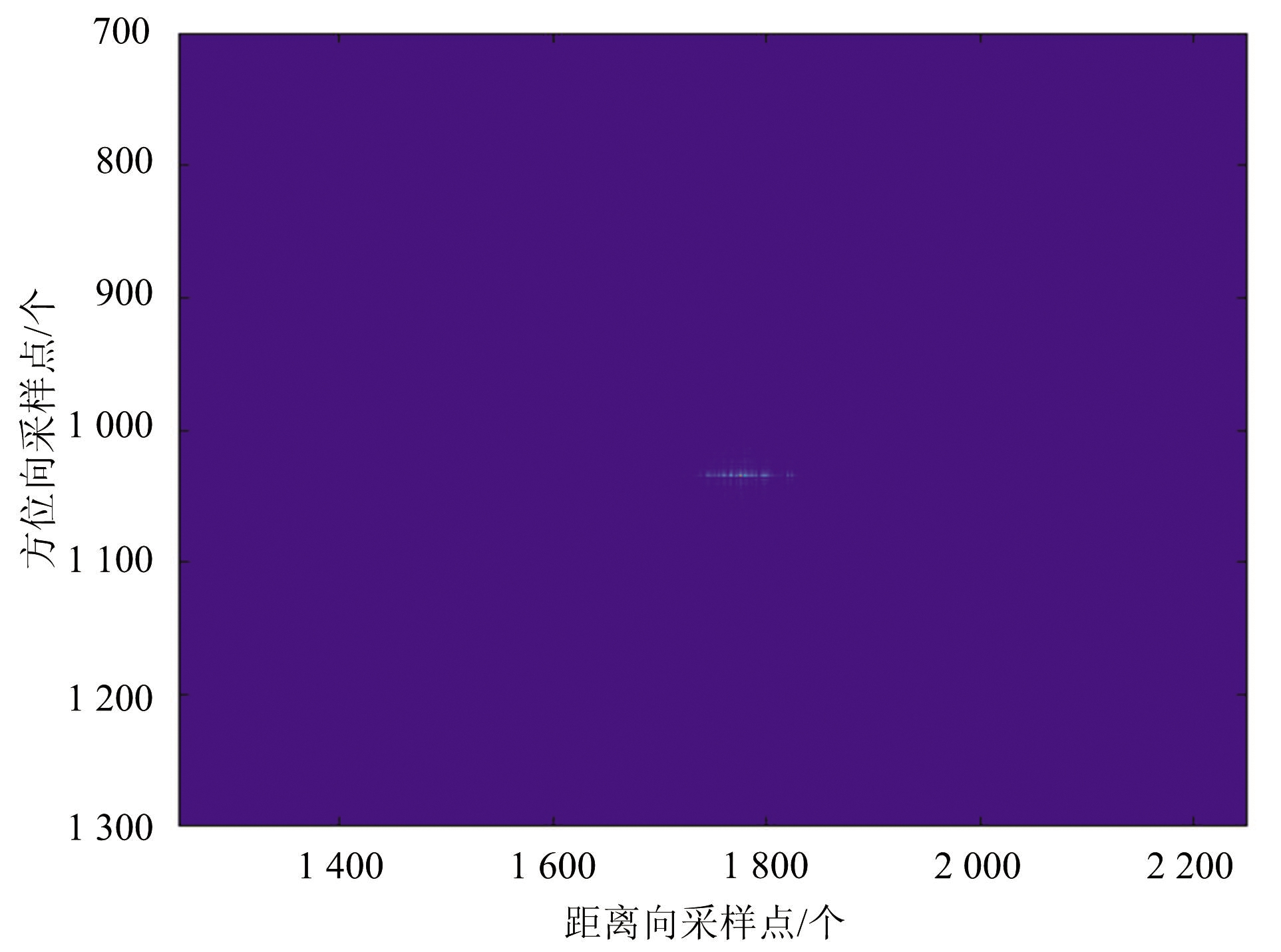
(b)灵巧噪声卷积干扰成像结果
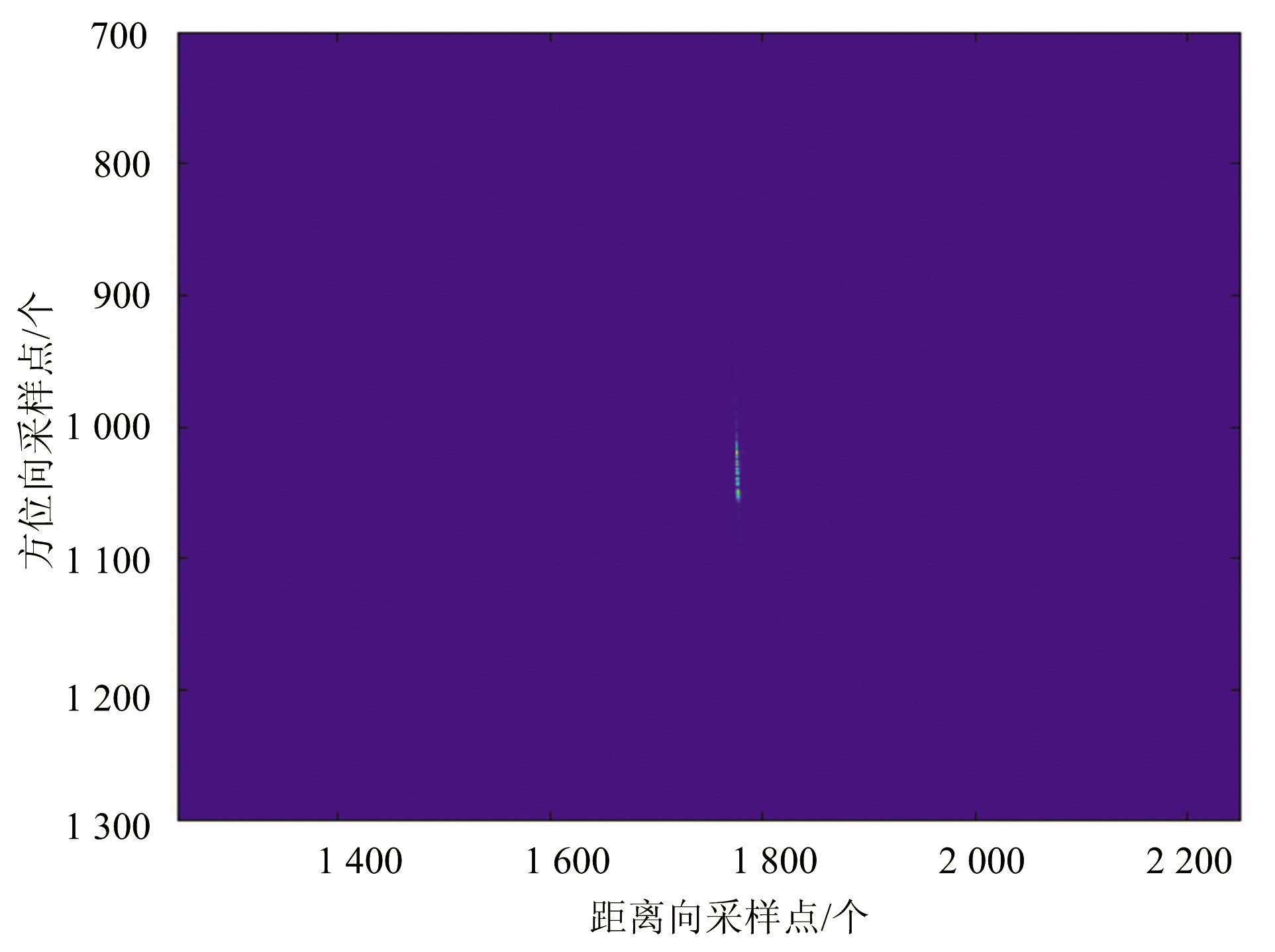
(c)微动调制的梳状谱干扰成像结果
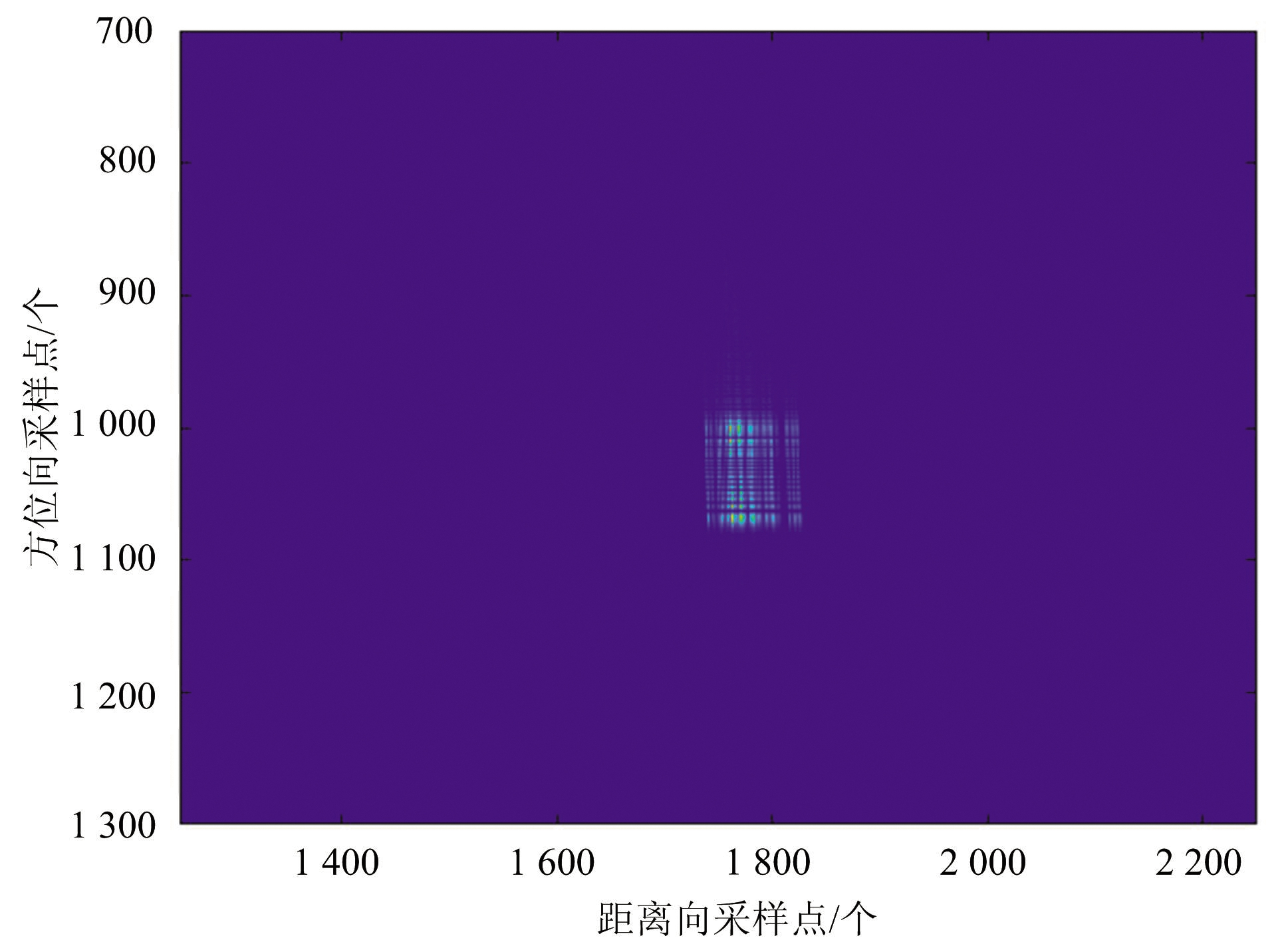
(d)本文所提算法成像结果
图4 不同干扰算法成像结果对比
2 仿真结果与分析讨论
2.1 仿真结果
使用RADARSAT-1雷达所获取的原始回波数据与干扰信号叠加,对算法进行仿真分析。为便于对比,本文在对基于微动调制的梳状谱灵巧噪声压制干扰算法进行仿真的基础上,还依次仿真了噪声非相干干扰及基于微动调制的梳状谱干扰等不同干扰算法。雷达参数如表1所示。
表1 RADARSAT-1雷达部分参数
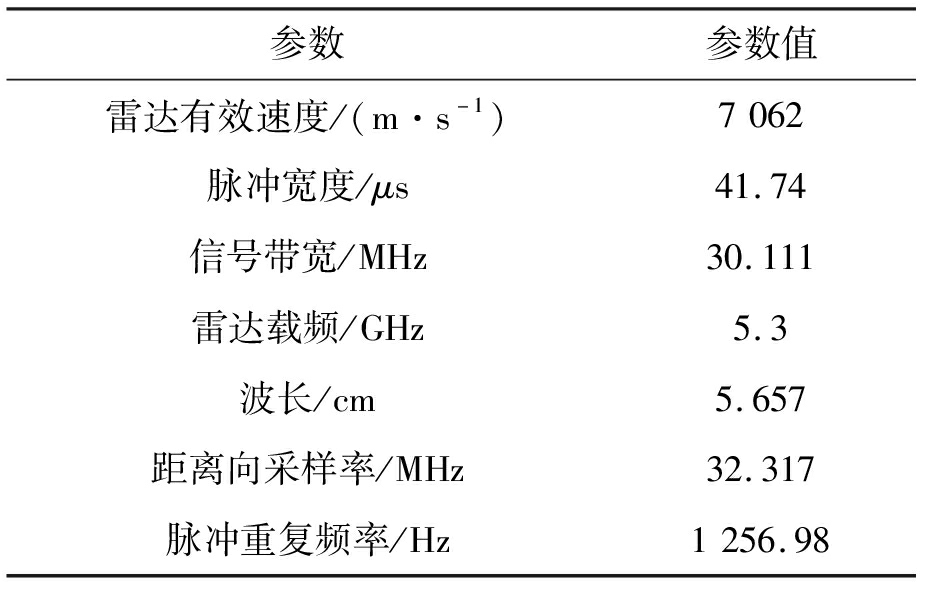
参数参数值雷达有效速度/(m·s-1)7062脉冲宽度/μs41.74信号带宽/MHz30.111雷达载频/GHz5.3波长/cm5.657距离向采样率/MHz32.317脉冲重复频率/Hz1256.98
在仿真中,使用不同干扰算法分别对城市、舰船等不同场景目标进行压制干扰,假设干扰区域为图中红色方框所示,干信比分别为5 dB及10 dB。图5为未加干扰信号时不同场景的成像结果。图6为使用本文所提出的压制干扰算法得到的仿真结果,其中图6(a)、(b)为干信比等于5 dB时的仿真结果,图6(c)、(d)为干信比等于10 dB时的仿真结果。

(a)无干扰城市成像结果

(b)无干扰舰船成像结果
图5 无干扰时的成像结果

(a)5 dB城市干扰结果

(b)5 dB舰船干扰结果

(c)10 dB城市干扰结果

(d)10 dB舰船干扰结果
图6 基于微动调制的梳状谱灵巧噪声干扰算法仿真结果
可以看出,当干信比为5 dB时,本文所提算法在压制城市等目标的效果较好,使该区域的大部分细节已经失去;由于舰船的回波较强,因此在干信比为5 dB时仍能辨认出其轮廓,在干信比增加到10 dB时,舰船轮廓变得模糊,近似无法辨认。
使用噪声压制干扰算法进行仿真,结果如图7所示。图7(a)、(b)为干信比等于5 dB时的仿真结果,图7(c)、(d)为干信比等于10 dB时的仿真结果。由图可知,不论噪声干扰信号的干信比为5 dB还是10 dB,干扰信号对图像均没有较大影响,图像的细节部分仍然可以辨认。由于噪声干扰信号无法获得距离向或方位向的压缩比,因此表现为在整幅图像上均存在的干扰信号,导致图像变模糊。

(a)5 dB城市干扰结果
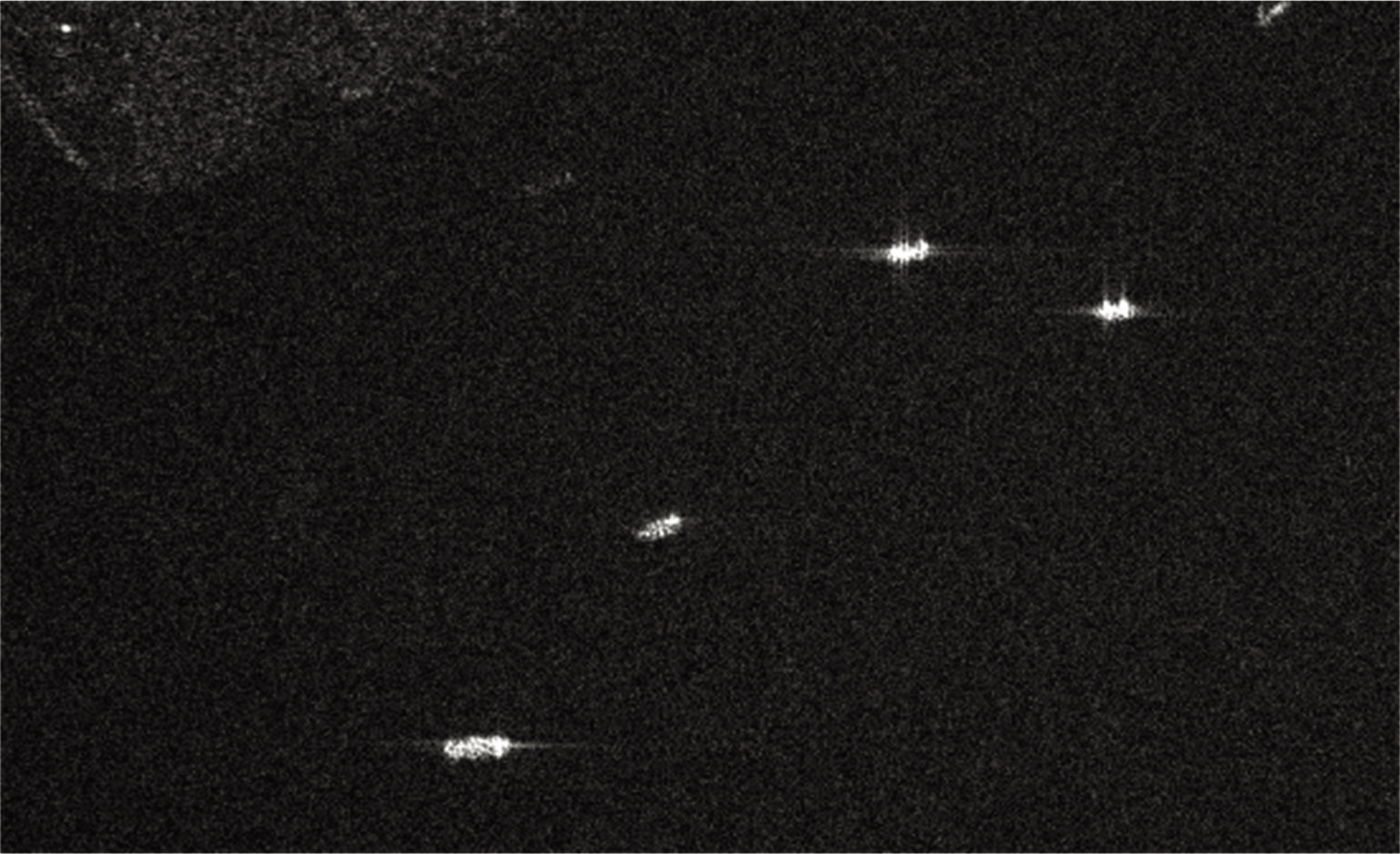
(b)5 dB舰船干扰结果

(c)10 dB城市干扰结果
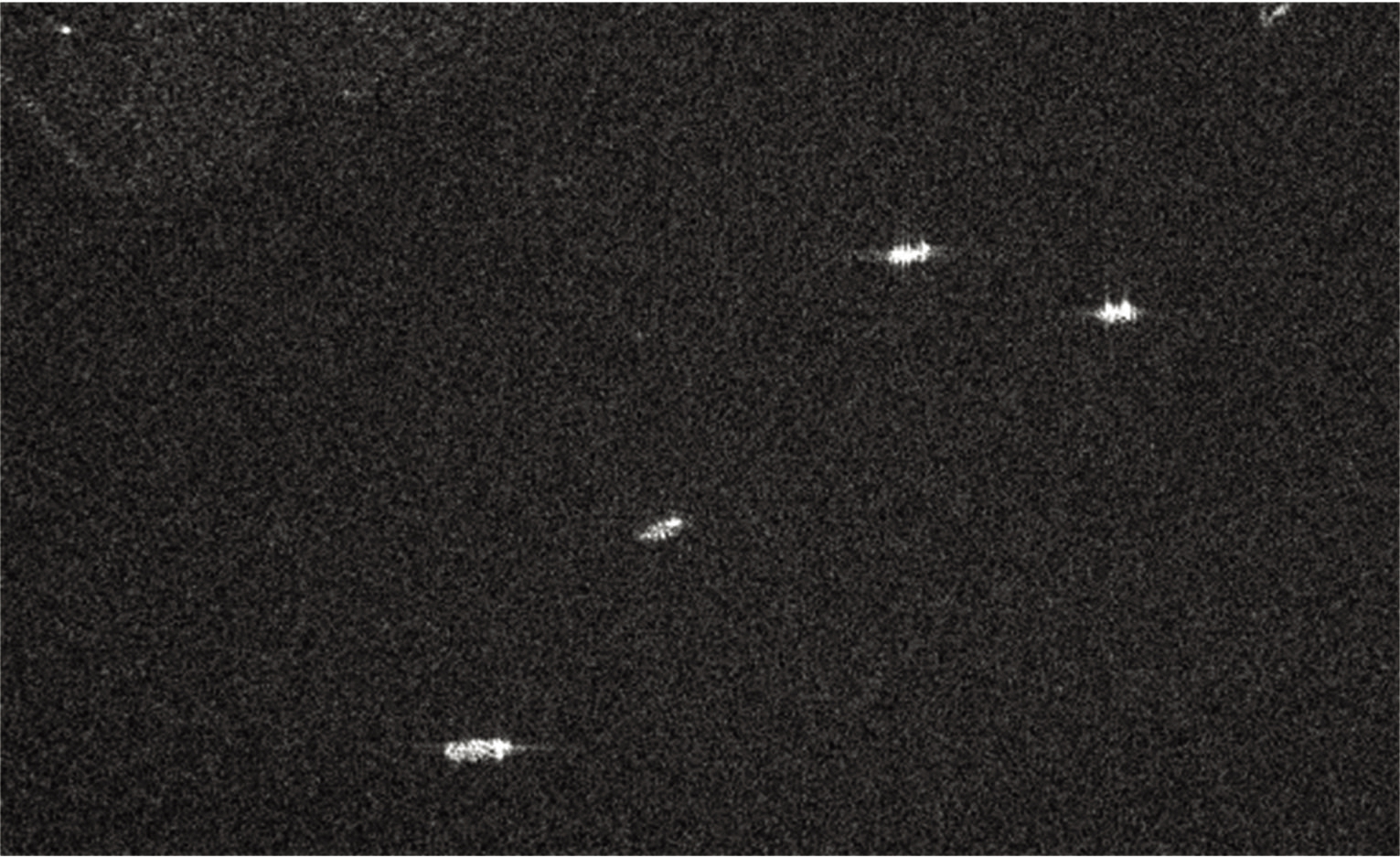
(d)10 dB舰船干扰结果
图7 噪声干扰算法仿真结果
使用基于微动调制的梳状谱干扰算法进行仿真研究,得到的结果如图8所示。图8(a)、(b)为干信比等于5 dB时的仿真结果,图8(c)、(d)为干信比等于10 dB时的仿真结果。根据上文分析可知,如果想要产生压制性干扰,则需要保证梳状谱相邻频点之间的频率间隔满足Δf=fi+1-fi<1/T,而当满足该条件时,压制面积会受到影响。图8的仿真结果验证了这一点,尽管使用基于微动调制的梳状谱干扰算法得到的干扰信号能量十分集中,但能量集中的代价为压制面积的大大减小。无论是压制城市,还是舰船等雷达回波较强的目标,均只能遮盖目标的局部,无法将目标完全覆盖。

(a)5 dB城市干扰结果
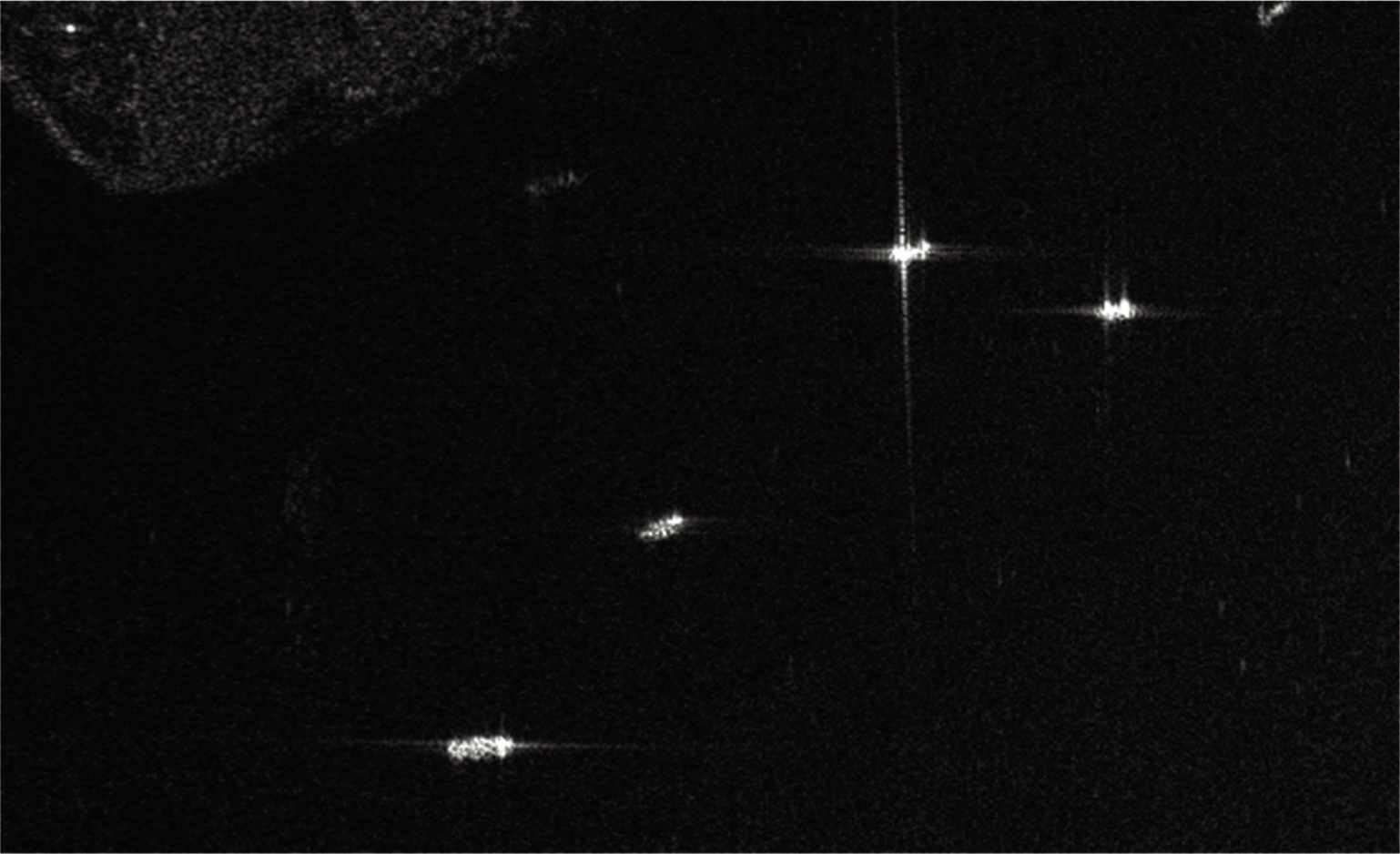
(b)5 dB舰船干扰结果

(c)10 dB城市干扰结果
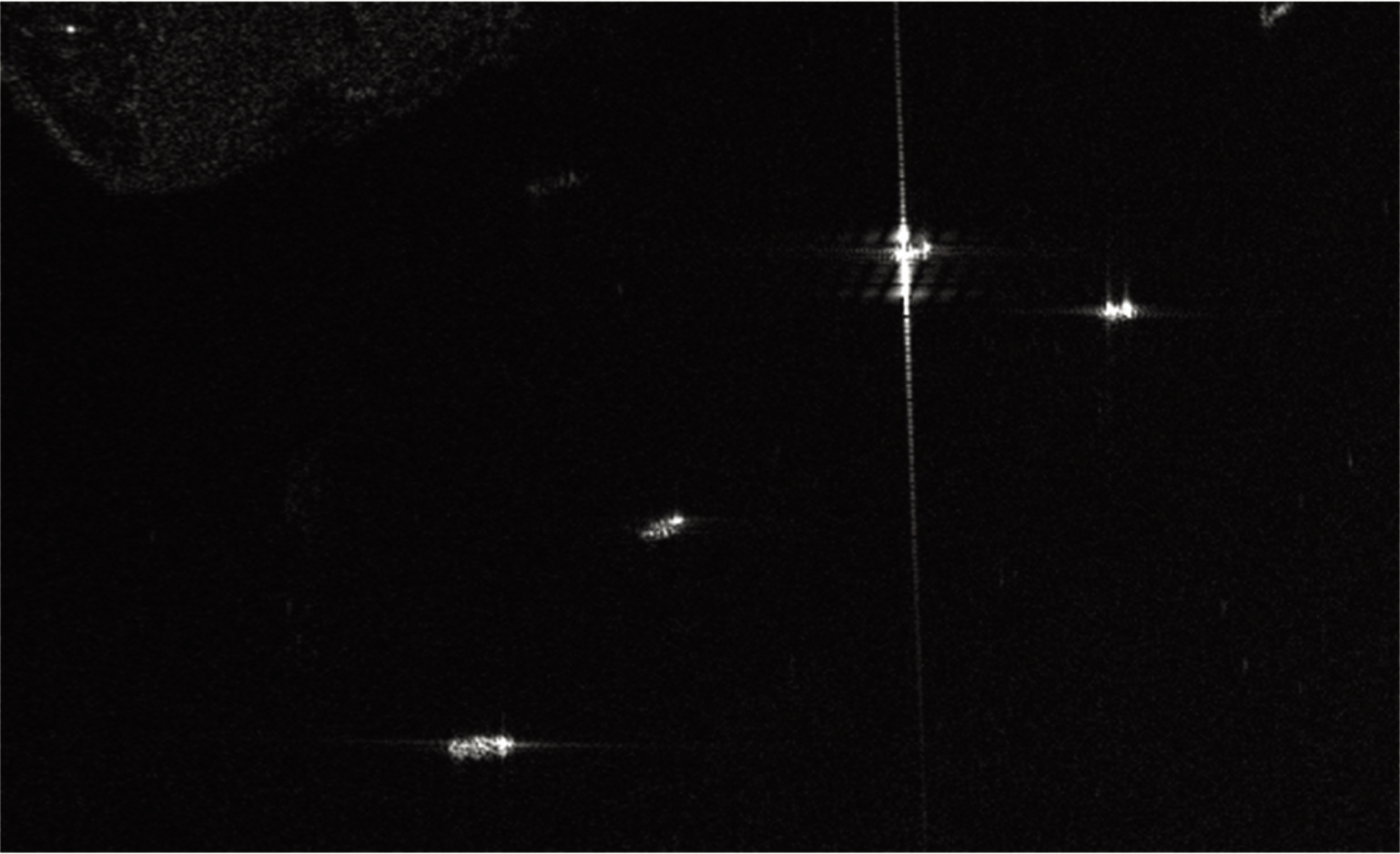
(d)10 dB舰船干扰结果
图8 微动调制梳状谱干扰算法仿真结果
2.2 干扰效果评估
在干扰效果评估方面,目前使用较多的为客观评估方法,例如基于干扰前后图像相似度的评估方法、干扰前后图像的均方误差等。但由于图像的最终阅读者是人,因此必须考虑人的视觉特性。故本文使用一种基于人眼视觉系统的主、客观结合的图像评估方法对干扰图像进行评估。在主观上,人的视觉系统通过小波分解、建立对比敏感度函数、空间位置函数等方式进行模拟。在客观上,评估指标采用图像干扰前后的均方误差。该评估方法首先使用哈尔小波基对干扰前、后的图像进行小波分解[14],形成子图像,模拟人眼的多通道特性;对于小波分解得到的子图像采用均方误差进行干扰效果评估;最后根据对比敏感度函数(Contrast Sensitivity Function, CSF)以及空间位置函数(Spatial Position Function,SPF)对每幅子图像得到的均方误差进行加权平均,计算出最终评估结果。
城市场景干扰图像的评估结果如表2所示。由表可知,在干信比为5 dB的情况下,噪声干扰、基于微动调制的梳状谱干扰以及本文所提干扰算法的干扰图像评估结果分别为1.770,2.437和25.561;而当干信比为10 dB时,评估结果分别为7.220,7.906和47.211。舰船场景干扰图像的评估结果如表3所示,在干信比为5 dB的情况下,噪声干扰、基于微动调制的梳状谱干扰以及本文所提干扰算法的干扰图像评估结果分别为12.734,8.610和85.654;而当干信比为10 dB时,评估结果分别为46.281,14.310和110.223。在舰船场景的干扰中,基于微动调制的梳状谱干扰算法表现较差,评估结果低于其他两种干扰算法,这可能是由于基于微动调制的梳状谱干扰的压制面积较小,近似为一个点目标,虽然干扰信号总功率高于原始回波信号,但仍会因失配而造成压缩比的损失。然而在所选取的干扰区域中,存在着回波较强的点目标,该点目标的回波经过匹配滤波后获得了距离向及方位向的压缩比,信号强度得以提升,将该干扰信号淹没。此外,根据评估结果可知,在城市及舰船场景干扰方面,本文所提出的干扰算法表现较好,评估结果均高于其余两种干扰算法,表明该算法具有一定的普适性。
表2 城市场景干扰图像评估结果

干信比噪声干扰基于微动调制的梳状谱干扰本文所提干扰算法5dB1.7702.43725.56110dB7.2207.90647.211
表3 舰船场景干扰图像评估结果

干信比噪声干扰基于微动调制的梳状谱干扰本文所提干扰算法5dB12.7348.61085.65410dB46.28114.310110.223
3 结束语
星载SAR干扰技术是雷达对抗领域的研究热点。针对目前压制干扰算法所存在的不足,本文提出一种基于微动调制的梳状谱灵巧噪声压制干扰算法,能够在距离向及方位向产生二维面状压制干扰。理论分析、仿真及实测结果表明,该算法在压制城市、舰船等不同场景的面目标时,表现均优于其他算法,具有一定的普适性。同时由于能够获得距离向及方位向的部分压缩比,因此可以大大降低干扰机的发射功率,在降低干扰机硬件要求、保护干扰机位置的同时达到了较好的干扰效果,能够有效对抗敌方星载SAR的侦察。此外,该干扰算法无需对敌方雷达参数进行精确评估,简化了干扰系统的设计,是一种有一定应用前景的算法。
[1]谢辉,赵强,曾祥能.合成孔径雷达技术应用于星载平台的现状与发展[J].舰船电子对抗,2019,42(1):6-9.
[2]张洋,杨超,谭世川,等.雷达干扰六要素[J].电子信息对抗技术,2016,31(5):57-61.
[3]JOSHI H D, KAUR R, SINGH A K, et al.An Improved Method for Deceptive Jamming Against Synthetic Aperture Radar[J].International Journal of Microwave and Wireless Technologies, 2018, 10(1): 115-121.
[4]梁文妍.合成孔径雷达智能干扰决策及干扰方法研究[D].成都:电子科技大学,2019.
[5]俞道滨,吴彦鸿,王宏艳.对合成孔径雷达不同干扰类型的功率分析[J].火控雷达技术, 2016, 45(1): 27-33.
[6]吴一戎, 胡东辉.一种新的合成孔径雷达压制干扰方法[J].电子与信息学报,2002, 24(11): 1664-1667.
[7]黄洪旭,黄知涛,吴京,等.对合成孔径雷达的步进移频干扰[J].宇航学报,2011,32(4):898-902.
[8]吴晓芳,代大海,王雪松,等.基于微动调制的SAR新型有源干扰方法[J].电子学报,2010,38(4):954-959.
[9]李田,彭世蕤,王广学,等.基于幅度调制的SAR相干压制干扰方法[J].现代雷达,2014,36(5):20-25.
[10]杨立波,高仕博,胡瑞光,等.合成孔径雷达相干与非相干干扰性能分析[J].系统工程与电子技术,2018,40(11):2444-2449.
[11]刘阳.基于微动特性的SAR干扰方法研究[D].长沙:国防科学技术大学,2012.
[12]邱杰.灵巧噪声干扰与旁瓣消隐技术关系探讨[J].现代雷达,2012,34(8):55-59.
[13]赖维柯,刘锋,李炳荣.基于梳状谱调制的LFM雷达噪声卷积干扰技术[J].海军航空工程学院学报,2018,33(6):513-517.
[14]韩国强,刘阳,李永祯.基于视觉加权处理的SAR干扰效果评估[J].雷达科学与技术,2011,9(1):18-23.


