0 引言
空时自适应处理(Space-Time Adaptive Processing, STAP)技术利用杂波在空间上和时间上的耦合性，进行空时二维域内的自适应滤波，使机载雷达杂波得到有效的抑制。STAP滤波器最优权的生成需要有大量二次回波样本用于估计杂波加噪声协方差矩阵(以下简称杂波协方差矩阵或协方差矩阵)。非均匀环境下，参考单元样本的非均匀性导致协方差矩阵估计的不准确，不同的非均匀杂波场景在不同程度上影响着STAP的输出性能。传统STAP方法无法从邻近距离单元中选取足够多的独立同分布(Independent and Identically Distributed,IID)参考单元样本来估计待检测单元(Cell Under Test,CUT)的杂波加噪声协方差矩阵，导致杂波抑制性能严重下降[1]。
针对非均匀杂波背景下空时处理性能下降的问题，作为认知雷达技术之一的知识辅助 STAP(KA-STAP)技术获得了广泛关注[2]。文献[3]借助先验信息构造杂波加噪声协方差矩阵，通过线性加权的方式将样本估计协方差矩阵与先验协方差矩阵同时用于空时滤波器的设计。对于利用先验知识的筛选算法，其性能依赖于先验知识的准确程度以及配准精度，而先验信息的不准确可能会导致算法性能下降[4]。
近年来，稀疏重构算法取得了很大的进展[5]，并已用于频谱估计。早期稀疏恢复STAP 算法侧重于单观测样本情况,但性能不甚理想[6-7]。基于数个样本的稀疏恢复算法有着更稳健的输出性能。文献[8]使用多快拍空时数据的稀疏贝叶斯重构方法得到杂波空时信息。
本文首先使用稀疏贝叶斯估计算法对参考单元样本数据进行稀疏表示；然后得到CUT单元的杂波协方差稀疏恢复矩阵，及噪声功率估计值；结合样本采样协方差矩阵进行空时处理。仿真结果表明，所提方法有着更稳健的STAP输出性能，在小样本非均匀杂波场景下的鲁棒性高于传统KA-STAP算法。
1 基于稀疏恢复的KA-STAP算法
1.1 信号模型
考虑工作于正侧视模式的N阵元均匀线阵机载相控阵雷达，载机速度为v，脉冲重复周期为Tr，阵元间距d为半波长。设一个相干处理间隔(CPI)内每个阵元接收脉冲数为K，则CUT单元的雷达接收回波数据可采用二元假设检验表示：
(1)
H0假设下的回波xcut∈
NK×1可表示为：xcut=xc+nc，其中xc,nc∈NK×1分别为CUT单元的杂波与噪声矢量。st∈NK×1为目标信号的空时导向矢量，b为未知的目标信号幅度。CUT单元的杂波加噪声协方差矩阵为
(2)
在最大化输出信杂噪比准则下的STAP滤波器空时最优权为[9]
wopt=μR-1st
(3)
式中，
实际应用中通常由其最大似然估计
代替R的真实值。xl为第l个不含目标且与CUT单元杂波回波信号满足IID条件的参考单元空时回波信号，L表示这些参考单元样本的总个数。
由RMB理论可知[10]，在满足IID条件的参考单元样本个数为两倍系统自由度的情况下，才能获得较最优值损失不超过3 dB的STAP滤波器输出性能。而在非均匀杂波环境中，需经筛选算法使参考样本尽量满足IID条件。筛选后的可用参考单元样本个数通常较少。针对该问题可采用KA-STAP方法设计协方差矩阵[11]，使估计得到的协方差矩阵尽可能逼近R的真实值，此时加载后的协方差矩阵可以表示为
(4)
式中，R0为辅助的先验协方差矩阵。通常情况下，R0由雷达工作参数、阵列流型等信息利用既定模型，如通用杂波模型(GCM)等构造而得。其整体性能主要受到杂波构建模型以及先验知识准确程度的影响，当雷达工作在非均匀杂波环境时，R0与理想协方差矩阵R的相似度会有所下降。本文拟用稀疏恢复的方法得到杂波协方差矩阵的估计值作为R0。一定程度上解决在非均匀环境条件下R估计不准导致STAP性能下降的问题。
1.2 基于稀疏贝叶斯恢复的空时协方差矩阵估计
由于杂波轮廓在角度多普勒域上是稀疏分布的[12]，本节使用基于复高斯分布的稀疏贝叶斯学习(Sparse Bayesian Learning，SBL)方法重构空时二维杂波回波信息。下面介绍其基本原理。
将归一化多普勒频率和归一化空间频率均匀地分成Nd，Ns份，由归一化多普勒频率和归一化空间频率组成的频点(fk,θi)，k=1,2,…,Nd；i=1,2,…,Ns处的空时导向矢量可表示为φ(fk,θi)∈M×1，M=Nd×Ns。则空时回波样本矢量x可用下式表示：
(5)
式中:矩阵Φ=[φ(f1,θ1),φ(f1,θ2),…,φ(fNd,θNs]为NK×M维空时导向字典(超完备基)；w=[w1,w2,…,wM]T代表x在角度-多普勒域(由空时导向字典Φ表示)上的稀疏表示也可称为角度-多普勒像(Angle-Doppler Profile，ADP)；n∈NK×1为复高斯噪声矢量。则回波信号x的稀疏恢复空时功率谱为
P=reshape(E[w⊙w*],Nd,Ns)
(6)
式中,⊙表示Hadamard积,(·)*表示共轭。
设β0为复高斯噪声n的方差，则观测样本矢量x的最大似然后验概率密度函数可表示为
p(x|w,β0)=CN(x|Φw,β0IN)=
(7)
假设w的先验概率服从零均值的复高斯分布，其任一元素wm的先验概率密度函数可表示为
(8)
式中，
为控制wm稀疏度的超参数。当αm=
时，wm趋于0。
则w的先验概率密度函数为
p(w|x,α,β0)=CN(w|μ,Σ)
(9)
式中，
(10)
(11)
其中，A=diag(α1,α2,…,αM)。当参数α,β0估得后，可得到w的最大后验估计
(12)
通过将边缘概率密度函数p(x|,α,β0)最大化，估计超参数α,β0就可以得到样本x稀疏表示的估计值。即有
{α,β0}=argmaxL(α,β0)
(13)
式中，L(α,β0)=logp(x|,α,β0)=-log|C|-xHC-1x，C=β-1I+ΦA-1ΦH。
分别对α,β0求最大边缘概率密度函数，即分别令
可得到α,β0的估计值：
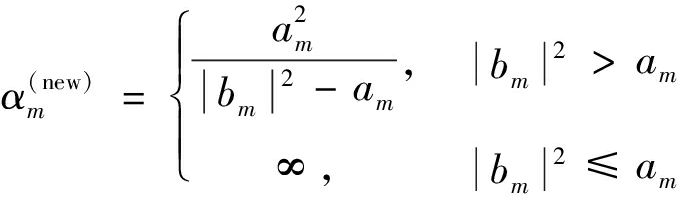
(14)
式中，
为Cm消除原子φm影响后的矩阵。
(15)
SBL是一种迭代算法，需要考虑参数向量w和噪声方差β0的初始化问题。最简单的方法是将超参数向量w的初始值设为全1向量。对回波信号噪声功率进行粗略估计，记估计值为
作为
通过式(14)、式(15)迭代α,β0更新参数向量w，利用式(10)、式(11)得到
再由式(12)可以得到w的估计值。
综上，稀疏恢复过程总结如下：
1)构建完备集Φ；
2)设置初始值
及最大迭代次数NL；
3)由参考单元样本集合中样本xl迭代更新超参数
筛选w(n)中元素，直至收敛(或循环次数达NL)，得到wc；
4)由3)步得到的wc非零元素对应的
为wc非零元素个数)构成的支撑集Φc，对样本xcut进行迭代更新超参数直至收敛(或循环次数达NL)，最终得到wcut。
则CUT单元的回波稀疏表示为
稀疏恢复的杂波加噪声协方差矩阵为
(16)
式中，对角阵INK∈NK×1。
值得注意的是参考单元样本集中不包含样本xcut，因此所估计出的杂波支撑集不会将待检测单元中的目标空时信息包含进去，可有效防止检测时的目标自相消。
在得到稀疏恢复杂波协方差矩阵后，式(4)表示的加载矩阵可重写如下：
(17)
对于加载系数λ的确定，这里用一个以杂波协方差矩阵大特征值个数为权重的方法实现。设
的特征值为
特征值
大于特征值门限rth的为大特征值。重写特征值向量为
NK×1，向量
中的元素有
(18)
则加载系数λ可表示为
(19)
式中，|·|0为求向量的L0范数，γsr为Rsr重写后的特征向量。
理想情况下，杂波的大特征值个数Nr=βc(N+K-1)，其中βc为杂波折叠系数，有βc=2v·Tr/d[13]。大特征值门限rth可由较充足回波样本情况下，采样协方差矩阵较大的Nr个确定。尽管这些样本可能不是均匀样本，但所确定出的门限对及Rsr的影响是相同的。rth也可由感兴趣的经验值确定。
用此方法得到的加载系数可确保在小样本情况下，采样协方差矩阵与估计协方差矩阵中任一个可逆性较差时，所得加载矩阵构建空时权矢量时有稳定的可逆性。
2 计算机仿真
本节将通过计算机仿真来验证算法的有效性。仿真参数设置如下：
正侧视均匀线阵机载相控阵雷达，阵元个数N=8，脉冲个数K=8。阵元间距为半波长，杂波折叠系数为1。目标的归一化空间频率为0，信噪比SNR=0 dB。构造两种杂波类型，其中类型Ⅰ每一个杂波块的杂噪比为25 dB，脉冲间起伏系数采用预处理后的IPIX实测数据构造，预处理低通滤波器通带频率参数为ωp=0.02，阻带频率参数为ωs=0.006；类型Ⅱ的杂噪比为30 dB，谱宽通带频率参数为ωp=0.06，阻带频率参数为ωs=0.01。设CUT单元的杂波属于类型Ⅰ，即类型Ⅰ样本为均匀样本。
STAP滤波器的输出性能由输出信杂噪比损失给出：
(20)
估计最优权用到的真实协方差矩阵R由5 000个均匀样本估计得到。稀疏恢复的迭代次数NL=1 000。
CUT单元得到的稀疏恢复功率谱如图1所示，可以看出稀疏恢复的方法较好地估计出正侧视时高精度的杂波功率谱轮廓。
图1 稀疏恢复空时功率谱
图2展示了稀疏恢复得到的协方差矩阵Rsr、采样协方差矩阵及真实协方差矩阵R的特征值。其中稀疏恢复协方差矩阵的杂波支撑集与采样协方差矩阵均使用8个样本进行估计。由图可以看出，在样本个数较少的情况下，稀疏恢复得到的杂波协方差矩阵特征值中，表征杂波特征的大特征值(即前Nr个特征值)与真实协方差矩阵R的更为接近。
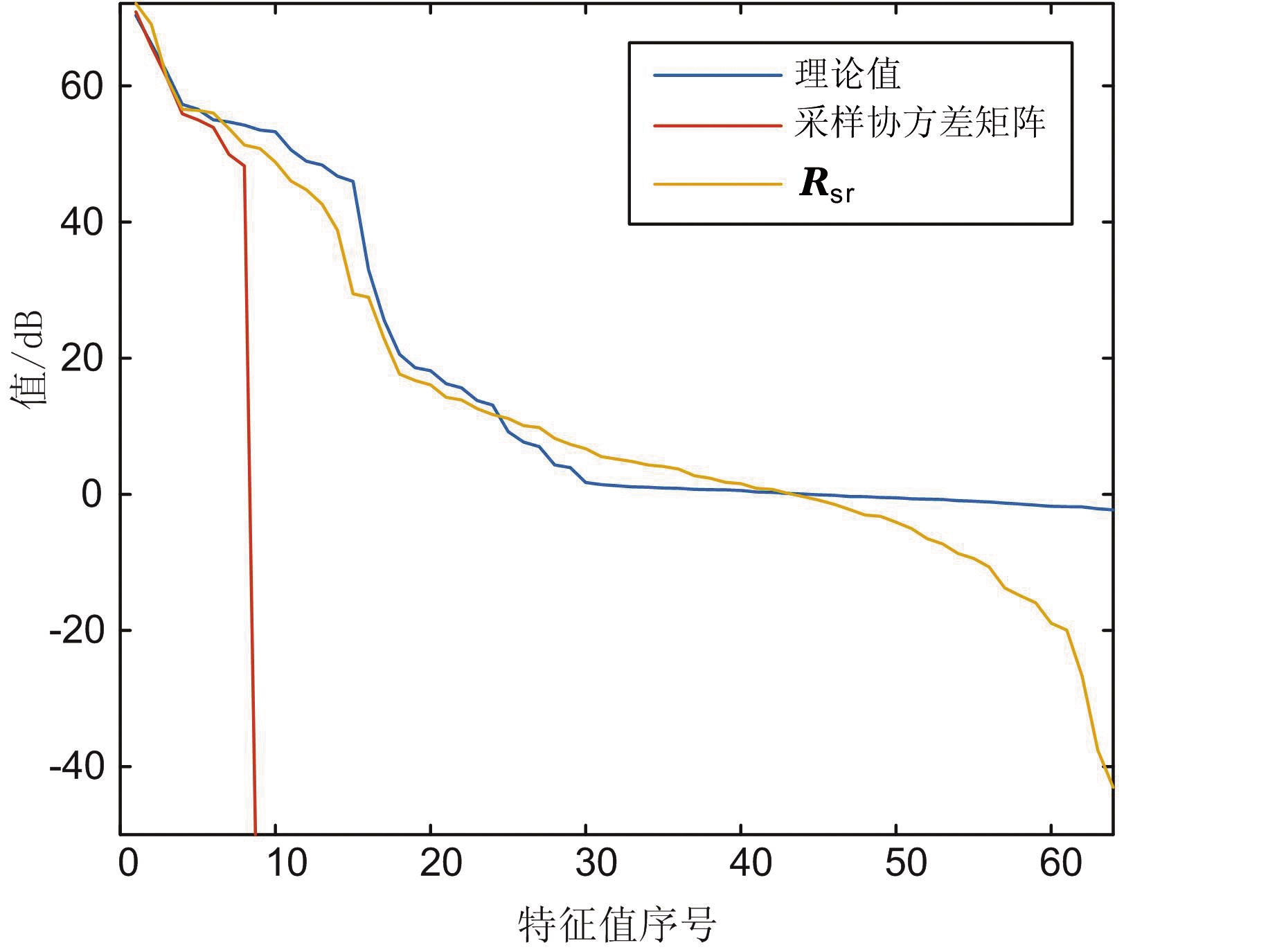
图2 不同协方差矩阵特征值比较
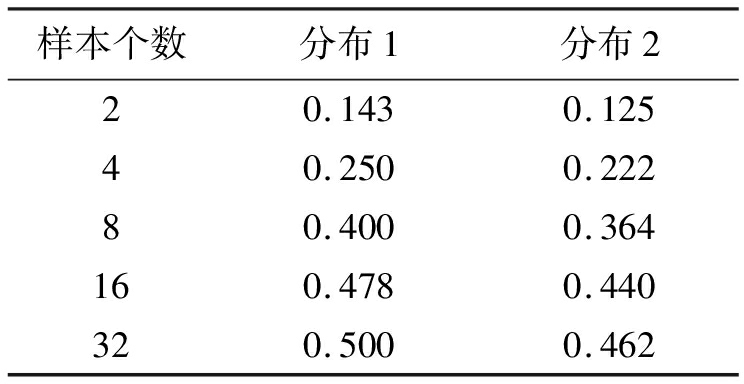
表1考虑两种杂波分布模型下(分布1为瑞利分布，分布2为对数正态分布)，随着用于估计采样协方差矩阵及稀疏恢复协方差矩阵Rsr的杂波支撑集的参考单元样本个数变化，加载系数λ的变化情况。由表可以看出两种分布下均有在样本数较少时，Rsr在估计最终加载协方差矩阵
时占主要比重，随着样本数增多两个协方差矩阵所占的比重变得相当。
表1 不同杂波分布下的加载系数值
样本个数分布1分布220.1430.12540.2500.22280.4000.364160.4780.440320.5000.462
图3给出了3种算法的SCNRloss曲线，分别为本文所提出的KA-SBL算法、经典KA-STAP算法和对角加载算法。图4(a)与图4(b)分别为用于估计的可用均匀样本个数为32个与16个时的情况。STAP理想输出性能的SCNRloss曲线也由虚线给出。经典的KA-STAP算法中先验协方差矩阵R0由CMT锥化矩阵杂波模型产生，且模型中含有类型Ⅱ杂波，以此来构造一种先验信息失配的场景。
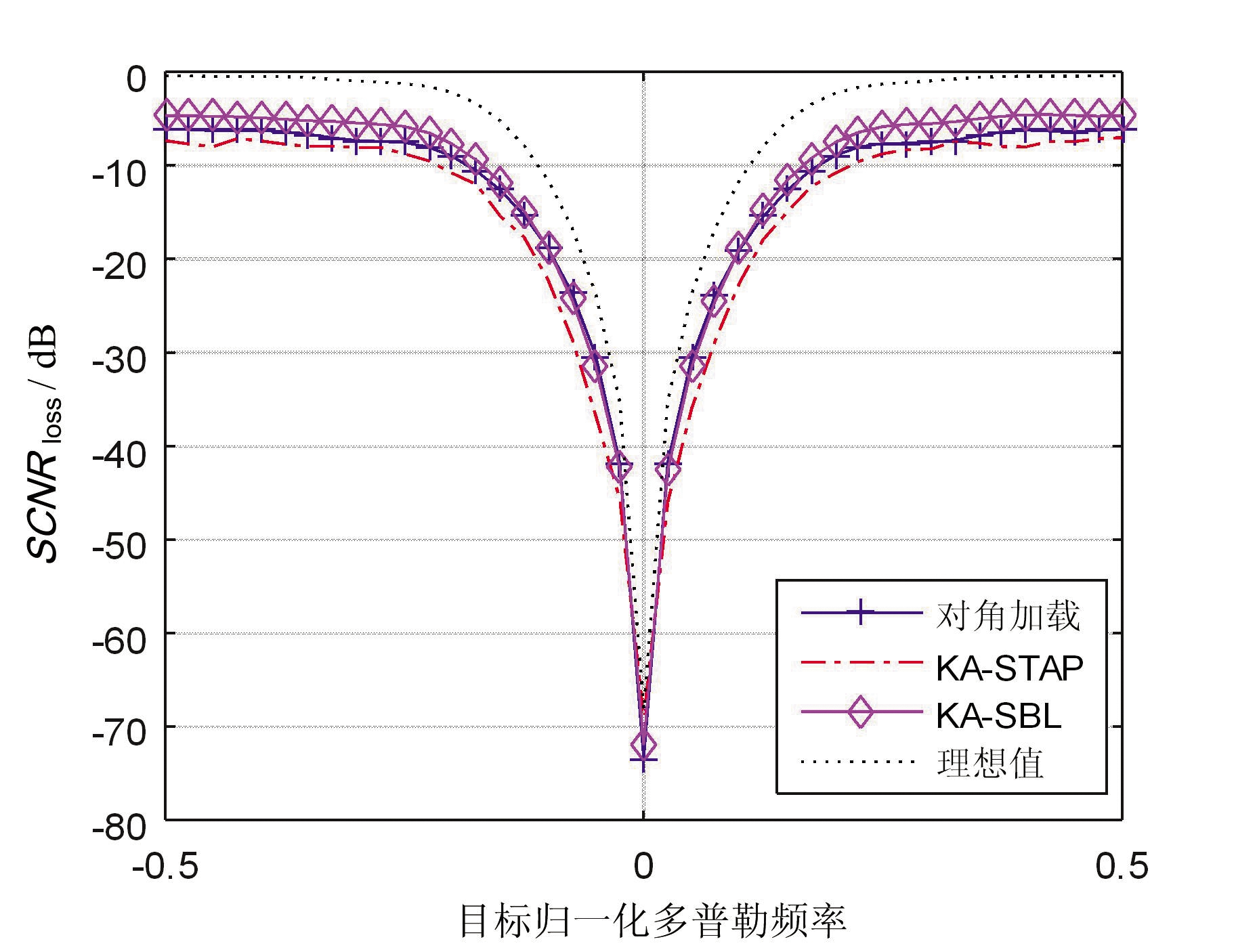
(a)均匀样本个数为32个
(b)均匀样本个数为16个
图3 输出信杂噪比损失曲线
图3(a)展示了在先验信息失配时，样本数量较少情况下KA-STAP算法性能甚至劣于对角加载算法，KA-SBL算法在低速区优于KA-STAP约5 dB，在高速区优于KA-STAP约3 dB；图3(b)展示了在样本数量很少时，KA-SBL算法在低速区优于KA-STAP约4 dB，在高速区优于KA-STAP约3 dB，对角加载算法因不能估计出杂波特征导致输出性能较最优值下降约20 dB。两种情况下KA-SBL算法均有优于KA-STAP算法的全局输出性能。因此，在非均匀杂波环境下，可使用的均匀样本数量较少时KA-SBL算法输出性能有良好的稳定性。
3 结束语
本文提出了一种基于贝叶斯稀疏恢复技术的空时处理算法。该算法不依赖先验信息，通过少量参考单元回波样本恢复出稳健的杂波协方差矩阵，再与采样协方差矩阵相结合构造出真实杂波协方差矩阵估计值。仿真结果表明，在非均匀杂波环境下有优于传统KA-STAP算法的输出性能，一定程度改善了均匀样本数量较少时STAP算法的鲁棒性。
[1]ZHANG Wei , AN Ruixue , HE Ningyu , et al.Reduced Dimension STAP Based on Sparse Recovery in Heterogeneous Clutter Environments[J].IEEE Trans on Aerospace and Electronic Systems, 2020, 56(1):785-795.
[2]侯静，胡孟凯，王子微.一种改进的知识辅助MIMO雷达空时自适应处理方法[J].电子与信息学报，2019，41(4):795-800.
[3]BERGIN J S, TEIXEIRA C M, TECHAU P M, et al.STAP with Knowledge-Aided Data Pre-Whitening[C]∥Proceedings of the IEEE Radar Conference, Philadelphia, PA, USA:IEEE, 2004:289-294.
[4]段克清，袁华东，许红，等.稀疏恢复空时自适应处理技术研究综述[J].电子学报，2019, 47(3):748-755.
[5]SAHOO S K, MAKUR A.Signal Recovery from Random Measurements via Extended Orthogonal Matching Pursuit[J].IEEE Trans on Signal Processing, 2015, 63(10):2572-2581.
[6]COTTER S F，RAO B D，ENGAN K，et al.Sparse Solutions to Linear Inverse Problems with Multiple Measurement Vectors[J].IEEE Trans on Signal Processing，2005，53(7):2477-2488.
[7]WIPF D P，RAO B D. An Empirical Bayesian Strategy for Solving the Simultaneous Sparse Approximation Problem[J].IEEE Trans on Signal Processing，2007，55(7):3704-3716.
[8]WU Qisong, ZHANG Y D, AMIN M G, et al.Space-Time Adaptive Processing and Motion Parameter Estimation in Multistatic Passive Radar Using Sparse Bayesian Learning[J].IEEE Trans on Geoscience and Remote Sensing,2016,54(2):944-957.
[9]GUPTA S , BHAMRE P.GMTI STAP Performance Under Space-Time Impaired Clutter Environment[J].IET Radar,Sonar & Navigation,2019,13(10):1836-1841.
[10]ZHANG Wei , HAN Minghua, HE Zishu, et al.Data-Dependent Reduced-Dimension STAP[J].IET Radar, Sonar & Navigation, 2019 , 13(8):1287-1294.
[11]YANG Zhaocheng , LI Xiang , WANG Hongqiang , et al.Knowledge-Aided STAP with Sparse-Recovery by Exploiting Spatio-Temporal Sparsity[J].IET Signal Processing, 2016, 10(2):150-161.
[12]胡进峰，李健萍，林涛.一种基于稀疏降维的STAP方法[J].雷达科学与技术,2019，17(4):421-425.
HU Jinfeng，LI Jianping，LIN Tao.A STAP Method Based on Sparsely Reduced-Dimension[J].Radar Science and Technology, 2019,17(4):421-425.(in Chinese)
[13]谢文冲, 段克清, 王永良.机载雷达空时自适应处理技术研究综述[J].雷达学报, 2017,6(6):575-586.
