0 引言
对空间目标的地面观测手段主要有地基雷达和自适应光学望远镜等,是空间态势感知系统SSA[1](Space Situation Awareness)重要组成部分。雷达观测属于主动探测,可全天时、全天候工作,主要用于中低轨道目标探测;光学观测属于被动观测,具有分辨率高、灵敏度高和探测距离远的特点,可用于中高轨目标及低轨小目标的搜索及跟踪测量,二者互为补充、相辅相成。
观测数据的变化反映空间目标姿态特征,可估计其稳定方式、受控状态等,对于掌握空间目标状态具有十分重要的意义。地基雷达获取的空间目标特性数据主要是RCS数据(Radar Cross-Section,雷达反射截面积,反映目标电磁波反射能量,单位是m2或者dBsm),该数据是随时间或观测角度变化的一维曲线。
尽管影响空间目标RCS 值变化的因素众多、测量噪声较大,但对于一个固定的观测参量(如雷达观测视角)来说, 其RCS 的变化可认为是一平稳随机过程,且其中蕴含的空间目标运动规律性也不会被随机噪声所掩盖,利用RCS特性可以对目标姿态进行判别[2]。文献[3]利用非参数统计学中的随机游程理论,对绕质心自旋和非旋转(翻滚)两种姿态特征进行了识别,仅能判定目标是三轴稳定或翻滚,对于自旋稳定无法判定。文献[4]利用傅里叶变换与小波变换相结合的分析方法,基于RCS时间序列对自旋稳定卫星和三轴稳定卫星进行识别,但并未给出具体标准,也无法区分三种运动状态。文献[5]提出了基于目标实时光学特性状态和正常状态的差分处理,利用短时傅里叶变换进行时频分析,通过比较低频能量和高频能量占比来判定目标姿态:如果低频能量(频谱20%以内的低频)占优,则判定目标为稳定,如果高频能量(频谱高频80%的能量)占优,则判定目标为翻滚。此方法需要实现获取目标正常工作状态,仅可用于合作目标或仿真数据分析,对于基于实测数据的非合作目标难以实施。
综上,目前的研究主要集中在讨论目标是否翻滚上,而不能从本质上对空间目标三轴稳定、翻滚和自旋稳定运动状态进行区分。本文基于RCS序列满足平稳随机信号的假设,利用功率谱估计精确测定RCS序列中蕴藏的固定频率信号,通过对滚转状态的判断实现对目标运动状态的准确估计。
1 运动状态估计流程
基于RCS的空间目标运动状态判别主要由数据预处理、数据分段、功率谱估计和运动状态判定等流程组成,总体流程如图1所示。
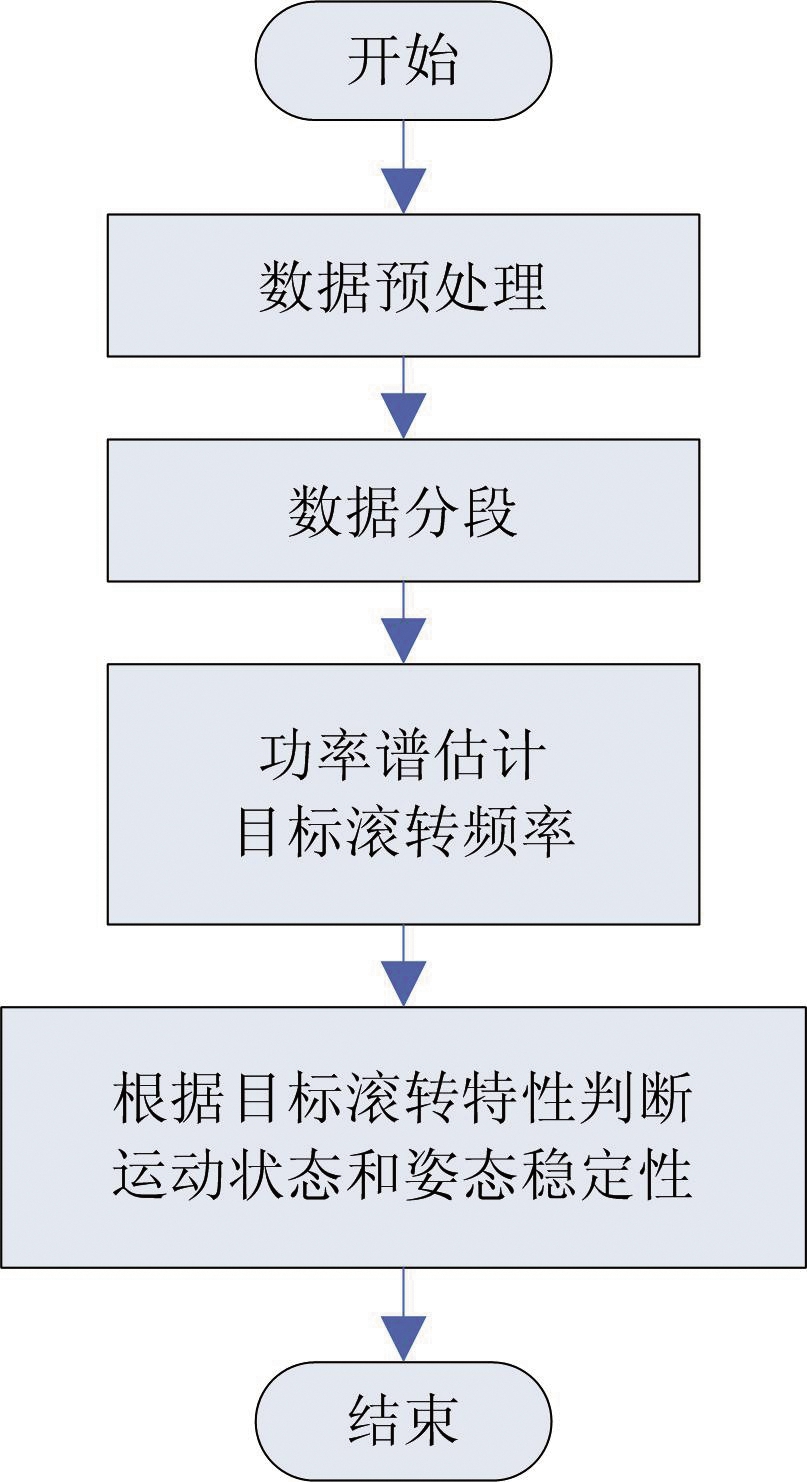
图1 基于RCS的空间目标运动状态判定流程
(1)数据预处理
由于噪声的影响,RCS数据存在一些野值,野值会给后续处理带来干扰,需要首先进行去野值预处理。
根据“大数”定理,自然界及工程中大量的随机现象都是服从或近似服从正态分布的。RCS是通过雷达测量物体电磁反射特性的物理量,可以是一种随机信号,我们假定RCS数据服从正态分布,可利用正态分布的“3σ准则”对数据进行去野值预处理。正态分布示意图如图2所示。
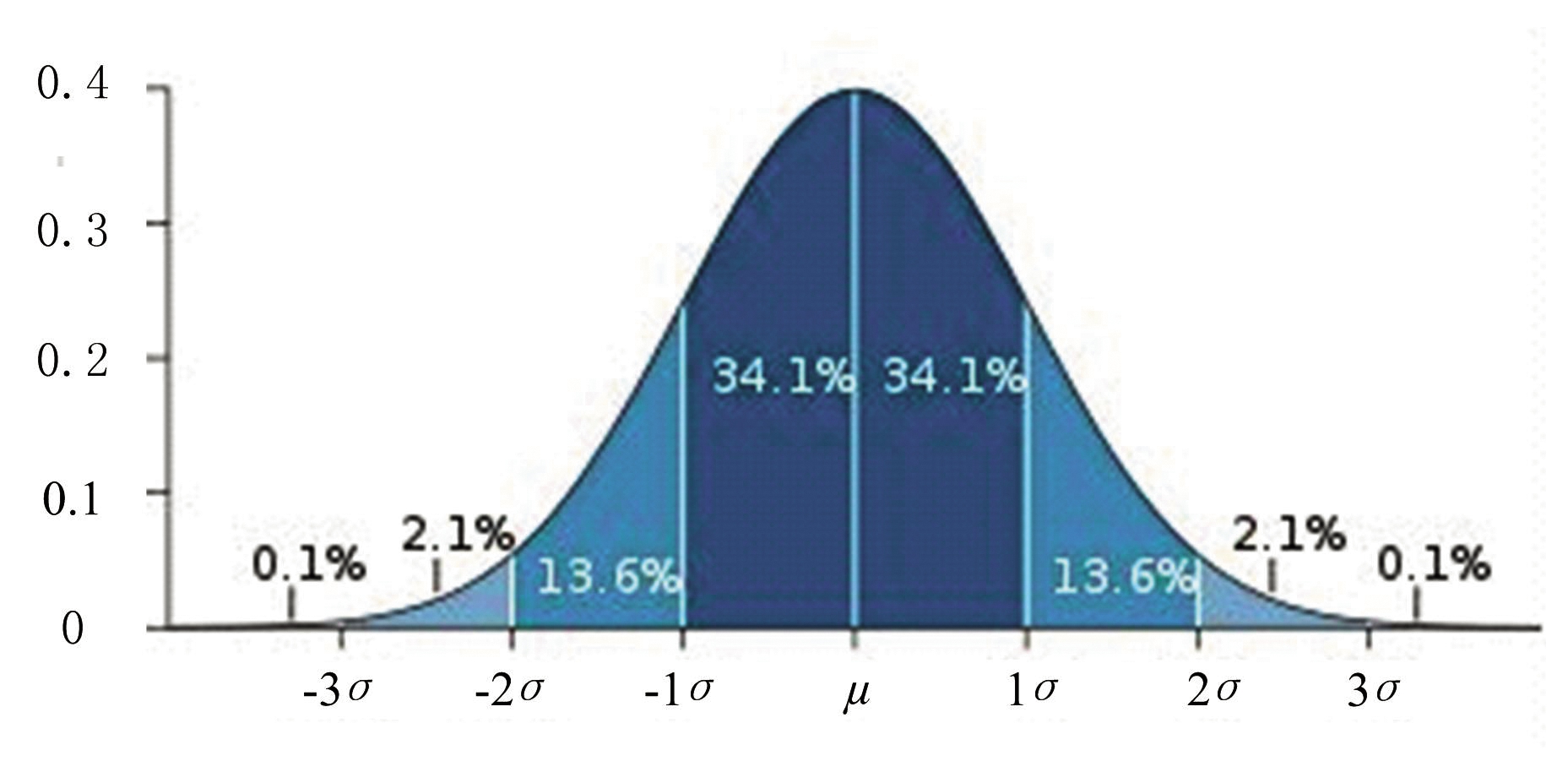
图2 正态分布示意图
如图2所示,在正态分布中,距平均值小于一个标准差、二个标准差、三个标准差以内的概率分别是68.27%,95.45%和99.73%。可以认为,一个正态分布的数据集的取值几乎全部集中在(μ-3σ,μ+3σ)区间内,超出这个范围的可能性仅占不到0.3%,即为3σ准则。因此,在RCS去野值处理中,基于3σ准则,对于μ±3σ范围之外的数据采用均值代替,实现去野值处理。
(2)数据分段
根据数字信号处理理论[6],对于均值和方差不随时间变化的随机信号,可视为平稳随机信号,可通过功率谱估计的方式估计信号频率。对于数据长度较短的RCS序列,可视作平稳随机信号直接进行功率谱估计;对于观测时间较长的RCS序列,可能属于非平稳随机信号,不能直接进行功率谱估计。此时,可通过加窗处理方法对数据进行分段,分段后的数据观测时长较短,可视为平稳随机信号而采用功率谱估计方法进行处理。
数据加窗处理方法较多,可以采用矩形窗、汉明窗或汉宁窗等,可叠加也可不叠加。这里,为了处理方便,本文采用无叠加矩形窗对数据进行加窗处理。矩形窗的宽度根据功率谱估计的分辨率确定,设频率分辨率Δf=0.001 Hz,数据率为fs,则窗长M为
M=fs/Δf
(1)
若数据长度为L,则可以划分的数据段数为
(2)
(3)功率谱估计
如前,数据分段后视为平稳信号,可采用经典功率谱估计方法进行信号的谱估计。经典功率谱估计[6]有Bartlett法、Welch法和Nuttall法等,这里采用Bartlett法。
采样数据xL(n)加窗分成N段后,第i段数据为
![]() xL[n+(i-1)M]d1[n+(i-1)M]
xL[n+(i-1)M]d1[n+(i-1)M]
0≤n≤M-1,1≤i≤N
(3)
式中,d1(n)是长度为M的矩形窗口。
Bartlett法分别计算每一段的功率谱![]() 即
即
(4)
把![]() 对应相加,再取平均,得到平均周期图
对应相加,再取平均,得到平均周期图![]() 即
即
![]()
![]()
(5)
(4)运动状态判别
正常工作的空间目标如卫星等,其状态按照姿态稳定方式的不同可以分为:自旋稳定、三轴稳定、重力梯度稳定等。①自旋稳定是利用陀螺的定轴性原理,通过绕自转轴高速旋转使卫星保持惯性空间的定向稳定,优点是实现简单,缺点是星上质量必须保持对称,载荷受限,姿控和轨控比较麻烦,如我国的“东方红”1号、“实践”1号、“东方红”2号和“风云”2号等卫星都采用了自旋稳定控制方式。②三轴稳定就是卫星基本不旋转,本体在X、Y、Z三个方向上均保持稳定,依靠姿态控制系统使卫星本体坐标系与某一参考基准保持一定的姿态关系,能够适应大多数卫星应用,易于满足载荷定向要求,轨控较易实现,但需要增加姿控系统(姿控推力器、动量轮等),控制系统较复杂。目前绝大多数应用卫星或科学探测卫星都采用三轴稳定姿控控制方式,如著名的hubble太空望远镜、clementine月球探测器等。③重力梯度稳定是在地球重力场的作用下,转动物体的转轴逐渐达到平衡状态,与重力梯度方向一致,保持姿态稳定。这种控制方式简单、实用,但控制精度较低,一般试验性小卫星采用这种控制方式,如英国Uosat-1小卫星采用的就是重力梯度稳定。由于重力梯度稳定只保持重力方向稳定,可看作是三轴稳定的简化。
就地面观测而言,自旋稳定的卫星滚转频率在100 r/min左右,典型的FY-2卫星[7]以100 r/min的转速在其定点位置高速旋转,原理类似于陀螺,实现空间的姿态定向稳定;三轴稳定卫星相对于地面几乎处于“静止”状态,仅需要根据阳光角度缓慢调整太阳帆板的朝向,或者卫星的姿态控制装置对卫星姿态飘逸进行适当调整,总体滚转频率在1 r/min以内,重力梯度稳定与三轴稳定类似;空间碎片和失效卫星,由于不具备姿态控制功能,表现为失控状态,最终会以翻滚姿态在轨道上运行[8],这类目标滚转频率要么介于三轴稳定和自旋稳定之间,要么超过自旋稳定频率。
因此,可根据估计出的信号频率(即目标滚转频率),设定一定的区间,对目标的姿态稳定性进行判别。如对于三轴稳定卫星滚转频率设定为0.9 r/min以内,即频率上限为0.015 Hz;对于旋转稳定卫星,可设定滚转频率区间为90~120 r/min,即频率为1.5~2 Hz;其他情况可认为是翻滚状态:

(6)
2 试验分析
基于不同观测时长和数据率的某地基空间监视雷达空间目标RCS特性实测数据,进行了空间目标运动状态判别试验。这里仅列举3种典型运动状态的空间目标RCS序列及分析判断结果,以简要说明问题。
(1)典型三轴稳定状态
获取的某空间目标RCS数据有158点、数据率为1 Hz,数据长度较短不作加窗处理,功率估计的滚转频率为0.008 Hz,根据式(6)可判定为三轴稳定状态,如图3所示。

(a)RCS数据

(b)功率谱
图3 典型三轴稳定空间目标RCS数据和功率谱
(2)典型旋转稳定状态
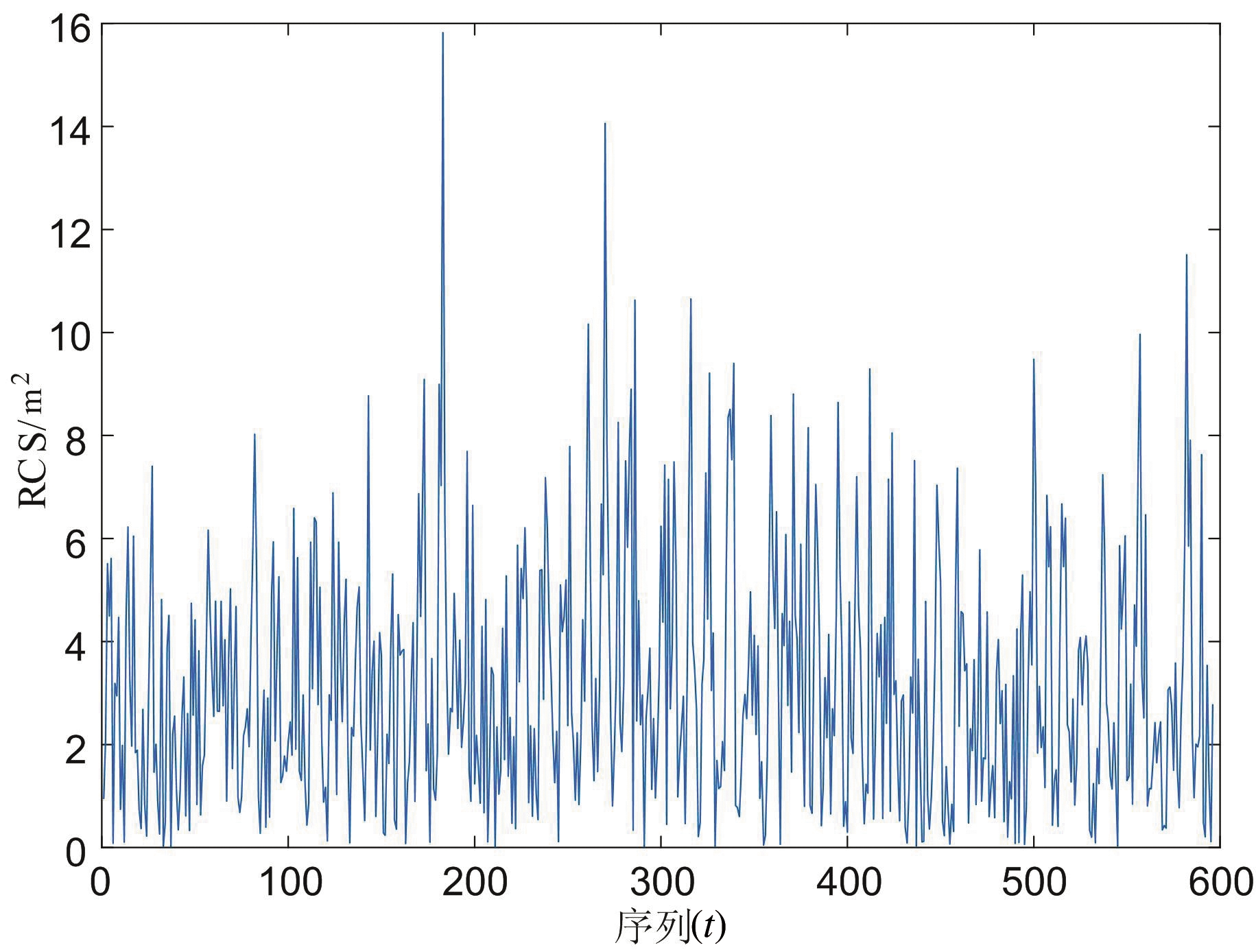
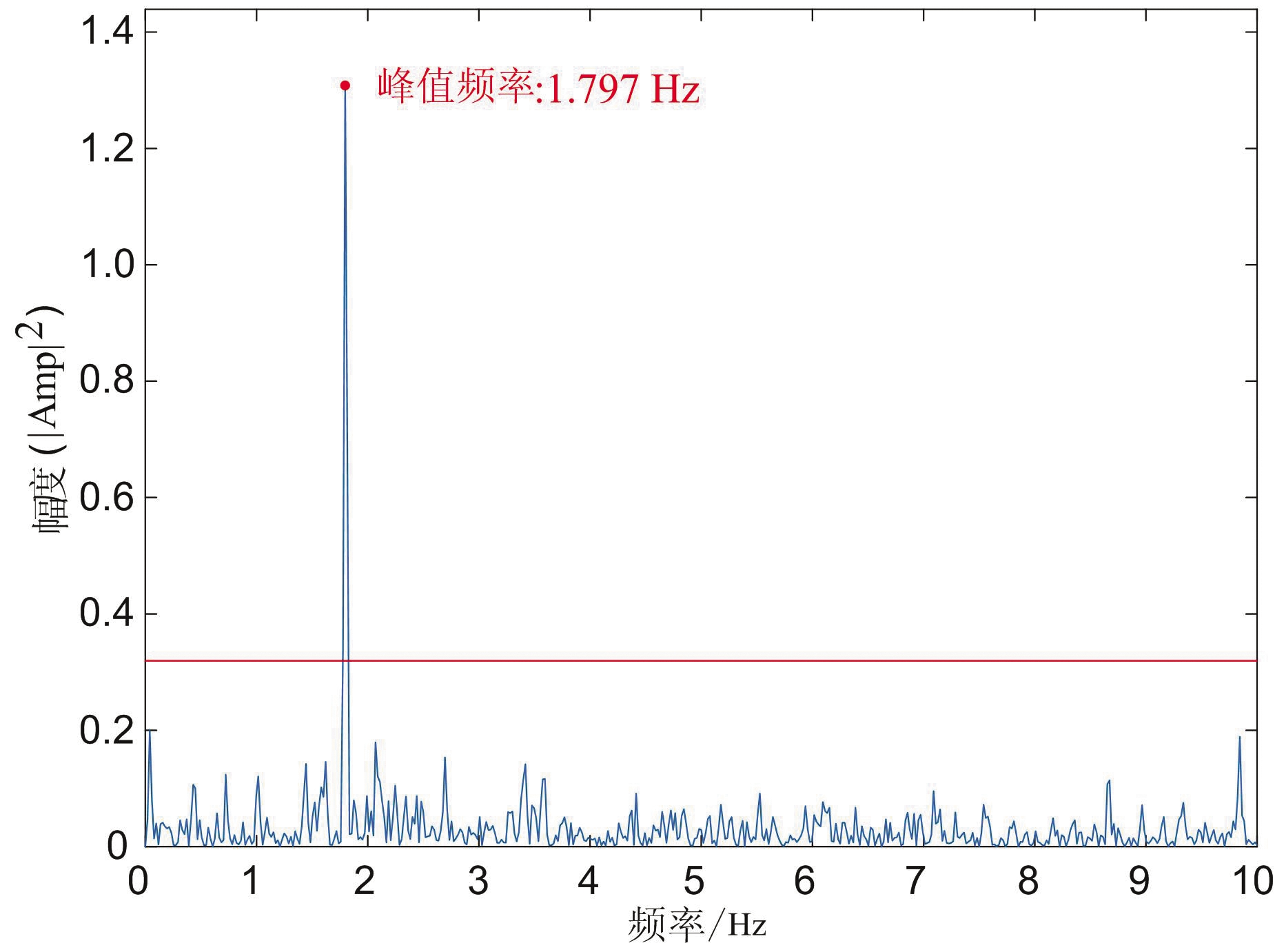
获取的某空间目标RCS数据为596点、数据率为20 Hz,不作加窗处理,功率估计的滚转频率为1.797 Hz,根据式(6)可判定为旋转稳定状态,如图4所示。
(a)RCS数据
(b)功率谱
图4 典型自旋稳定空间目标RCS数据和功率谱
(3)典型翻滚状态
获取的某空间目标RCS数据为942点、数据率为20 Hz,不作加窗处理,功率估计的滚转频率为4.609 Hz,根据式(6)可判定为翻滚状态,如图5所示。

(a)RCS数据

(b)功率谱
图5 典型翻滚空间目标RCS数据和功率谱
(4)关于功率谱估计的进一步讨论
上述为单个峰值的典型功率谱估计,由于噪声信号相关性低、功率能量小且频谱较宽,此时可采用3σ准则在功率谱中确定一个阈值,将功率谱值大于阈值的分量视为待估计频率信号,小于阈值的分量看作噪声,功率谱中红线为采用3σ准则设定的阈值线。工程实际中,功率谱图可能存在多个满足阈值的频率分量,此时应统计功率值大于峰值功率的50%的频率分量,并将满足要求的最高频率分量作为运动状态判断的依据,否则仍取峰值功率对应的频率作为判断依据。如果功率谱中没有满足阈值的频率,则应视为随机噪声信号,直接判定为三轴稳定状态。
3 结束语
本文提出的基于RCS的空间目标运动状态估计方法,具有物理概念清晰、方法简洁、精度较高、易于工程实现且无需额外辅助信息等特点,对没有更多先验信息的非合作目标运动状态估计方面时具有显著优势。此外,对于基于光度的空间目标运动状态估计,由于信号特点与RCS类似,该方法也同样适用。
当然,由于空间攻防的需要,部分空间目标还需进行机动变轨运动,其运动状态也不仅限于自旋稳定、三轴稳定和翻滚,再加上测量噪声对状态估计的干扰,空间目标真实运动状态估计是一个复杂的科学技术问题。文中讨论的空间目标运动状态的判定准则,是建立在纯数据处理和大概率估计基础上,主要反映空间目标的正常工作运动状态。在此基础上,附加轨道、电磁特性等测量信息,则可以对空间目标运动状态进行综合研判,实现更精准识别。此外,在有更多合作目标和先验信息基础上,还可以建立空间目标运动状态数据库,通过支持向量机或深度学习等机器学习方法进行深度挖掘,则可以进一步提高空间目标运动状态的识别精度。
[1]王建立.空间目标地基光电探测与识别技术的发展[J].飞行器测控学报,2015,34(6):489-499.
WANG Jianli.Development of Technologies for Detection and Identification of Space Objects with Ground-Based E-O Systems[J].Iournal of Spacecraft TT & C Technology, 2015,34(6):489-499.(in Chinese)
[2]杨嵩,丁宗华,许正文,等.曲靖上空空间碎片姿态、分布和散射特性的统计分析[J].电波科学学报,2018,33(6):648-654.
[3]全备,戴征坚,胡卫东,等.两类空间目标的非参数姿态判别方法[J].中国空间科学技术,2000,20(3):4-7.
[4]卜正明,李相迎,黄顺东.基于小波功率谱估计的空间目标RCS特性分析[J].现代雷达,2004,26(2):47-49.
[5]樊志鹏.基于时序光度信号的空间目标物性参数反演方法[D].哈尔滨:哈尔滨工业大学,2017:17-31.
[6]胡广书.数字信号处理:理论、算法与实现[M].2版,北京:清华大学出版社,2003:512-519.
[7]陈博洋,郭强,常翔,等.FY-2 自旋稳定气象卫星动态月球观测与图像配准[J].传感技术学报,2017,30(5):703-707.
[8]马君国,付强,肖怀铁,等.雷达空间目标识别技术综述[J].现代防御技术,2006,34(5):90-94.
MA Iunguo, FU Qiang, XIAO Huaitie, et al.Survey of Radar Space Target Recognition Technology[J].Modern Defence Technology, 2006,34(5):90-94.(in Chinese)
