0 引言
随着制导武器的迅速发展以及雷达技术的大量运用,现代战场的电磁环境日趋复杂,新体制雷达不断被研发出来,导致从复杂密集的电磁信号环境中快速地分选识别出威胁雷达信号日趋艰难。
雷达信号分选利用信号参数的相关性来实现分选,表征雷达的特征参数有频域参数、空域参数、时域参数、幅度参数等[1]。雷达信号分选的方法主要有基于脉间五参数的方法、基于脉内细微特征的方法和基于波形匹配的方法[2]。目前广泛使用的是基于脉间五参数的方法:首先用载频、脉宽、到达角参数进行预分选,然后基于脉冲重复间隔(PRI)去交错方法进行主分选。典型的PRI去交错方法有动态关联法[3]、直方图法[4-7]、PRI变换法等[8-10]。目前,众多学者提出了多种基于脉间五参数的常规雷达信号分选算法,但这些算法运算量较大。同时,这些方法在信号丢失严重或者脉冲密度大的情况下易出现增批、漏批等问题,导致分选效果差,虚警和漏警多,从而影响作战人员对战场形势的判断。
针对上述问题,本文提出一种基于时序匹配及变长滑窗的雷达信号分选算法,首先,利用载频、脉宽两个参数对待分选脉冲进行粗筛选,将待分选脉冲稀释;然后,利用重频值在时域上对待分选脉冲进行更进一步的抽取,从而获取符合该辐射源模板的脉冲序列。在此算法基础上,本文提出了一种新的分选流程:首先,将待分选脉冲分为若干个数据段;然后,对每一段数据先用之前处理的结果作为已知辐射源模板进行本文算法处理,再用常规分选算法处理剩余脉冲,重复进行上述步骤,直到完成大数据量脉冲的快速分选。实验结果表明,本文算法结合常规分选算法能有效提高雷达的分选精度及速度。
1 基于时序匹配及变长滑窗的信号分选方法
1.1 时序匹配
在脉冲的5个参数中,到达时间(TOA)在雷达分选领域中是一个非常重要的参数,在雷达信号分选的主分选算法中一般都是用TOA来计算雷达的脉冲重复间隔(PRI),然后用PRI进行主分选[11]。
我们利用PRI参数,用待分选脉冲序列计算出脉冲重复间隔prii,用雷达模板的prij值和给出的pri容差ε计算出pri窗口:[prij*(1-ε),prij*(1+ε)],若prii落入该窗口,则认为匹配成功,将prii对应的脉冲保存下来。
1.2 变长滑窗
关于子序列匹配问题,Christos提出了一种新技术—滑动窗口,在提取特征的时候只对窗口内的序列进行提取,不用对整个脉冲进行特征提取,极大地提高了信号分选的效率[12-13]。陈国泰提出了一种基于变长的滑窗技术用于译码工作[14],在该研究的基础上,本文提出一种变长滑窗的方法用于雷达信号分选,即根据模板的PRI值确定pri的容差范围[PriMin, PriMax],将滑窗长度与容差范围比较:(1)若窗口长度小于PriMin,则增加窗口长度;(2)若滑窗长度在PriMin和PriMax之间,则时序匹配成功,将滑窗起点移向当前的滑窗终点,将滑窗终点向后移动一条脉冲;(3)若滑窗长度超过PriMax,则将滑窗起点向后移动一条脉冲,将脉冲终点移向滑窗起点的下一条脉冲。
1.3 处理流程设计
本文提出的分选流程如图1所示:对于待分选脉冲序列,先用雷达参数模板的载频RF和脉宽PW进行粗筛选,使得剩余脉冲都和模板的RF、PW匹配,然后初始化滑窗起点为第一条脉冲,滑窗终点为第二条脉冲,根据1.2节所述方法移动滑窗,进行时序匹配,直到滑窗移到最后一条脉冲。

图1 算法流程设计图
1.4 常规分选算法结合本文算法处理流程
常规分选算法在处理海量脉冲数据时,由于计算机资源有限,无法一次处理过大数据,需要对数据进行截取,分段进行分选。由此会导致增批问题的产生,并且这样的分段分选,使得后一段的分选无法应用前一段的分选结果,无法利用各个数据段之间的时间关系。常规的雷达信号分选算法结合本文算法则可有效解决此问题,处理流程如图2所示:(1)对待分选脉冲数据进行切分之后;(2)对第一段脉冲进行常规脉冲;(3)用第一段脉冲的常规分选结果作为已知雷达参数模板,对第二段脉冲进行本文算法处理,然后对第二段剩余脉冲进行本文算法处理;(4)用之前数据段的分选结果作为雷达参数模板,重复步骤3,直到完成对最后一段数据的处理。
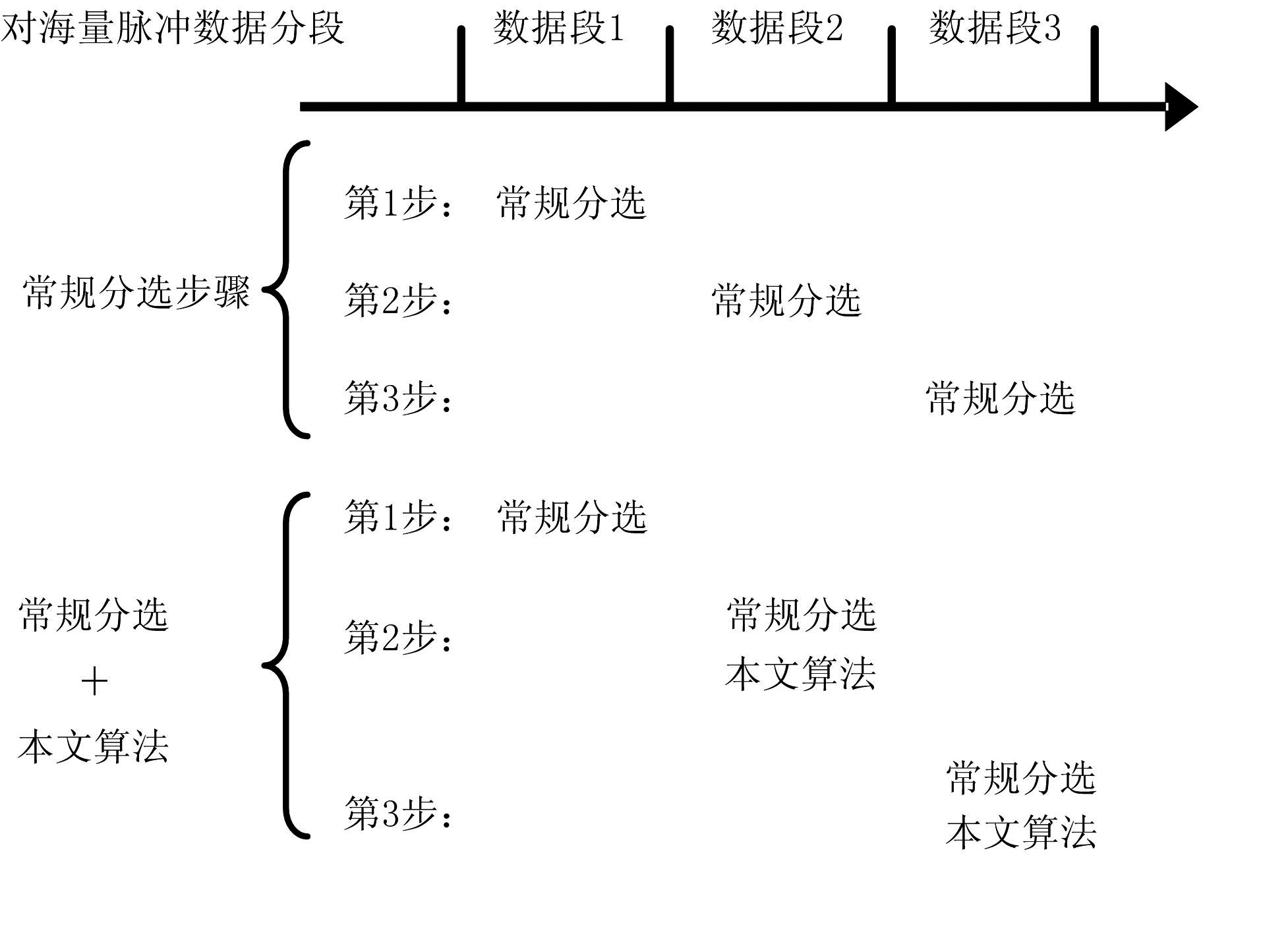
图2 常规分选结合本文算法处理流程
1.5 复杂度分析
本文的算法主要耗时在窗口长度的变化及窗口的移动。由于窗口的长度最大为PriMax,在长度超过PriMax时,窗口长度不再变化,因此窗口长度的变化是常量级的。而窗口的移动则要从第一条脉冲滑动到最后一条脉冲,属于线性级。因此本文算法的时间复杂度为O(n)。
2 仿真实验验证
2.1 仿真数据描述
算法采用仿真数据进行测试,在本文的仿真实验中,仿真数据包含10部雷达辐射源的混合全脉冲数据,脉冲数分别为9 487,967,3 806,9 531,6 642,9 469,9 486,7 607,9 525,18 989,噪声脉冲数为4 266。
在仿真试验中观测时间为0~25 579 ms,观测时间内共有10个目标,每个目标在观测时间内的分布如图3所示。为模拟常规分选在处理大文件情况下的文件切分,本文将数据分为四段:(1)0~3 840 ms中有雷达1,2,3,4;(2)3 840~12 670 ms中有雷达3,4,5,6;(3)12 670~16 600 ms中有雷达5,6,7,8;(4)16 600~25 579 ms中有雷达7,8,9,10。

图3 雷达目标在时序中的分布
考虑到真实情况雷达脉冲会有丢失现象,本文仿真数据的丢失率设置为5%。为更加真实地模拟战场情况,本文在仿真数据中加了10%的高斯噪声脉冲,噪声的分布均值为真实参数,方差为真实参数的20%。其中每个目标的样式特征如表1所示,参数分布如图4所示。
表1 雷达目标的样式特征

序号RF类型RF典型值PRI类型PRI典型值PW类型PW典型值DOA典型值1固定3226组变423,291,346,379,474(16)组变39,26,32,35,45802固定3007固定2697固定1.892.53脉组捷变2950#2996#3020#3046(19)固定2483固定10.587.34固定2837组变1132#1359(21)固定3580.55固定3125参差1518/1669/1584/1649/1540/1625/1560/1604固定1685.56脉间捷变3005/3011/3016固定1212固定1586.57固定2780抖动1050(3%)固定3593.58固定9800抖动1560(2%)固定1087.59固定9776组变41#49#61#53(24)固定2.59010固定9721固定10.5固定0.893

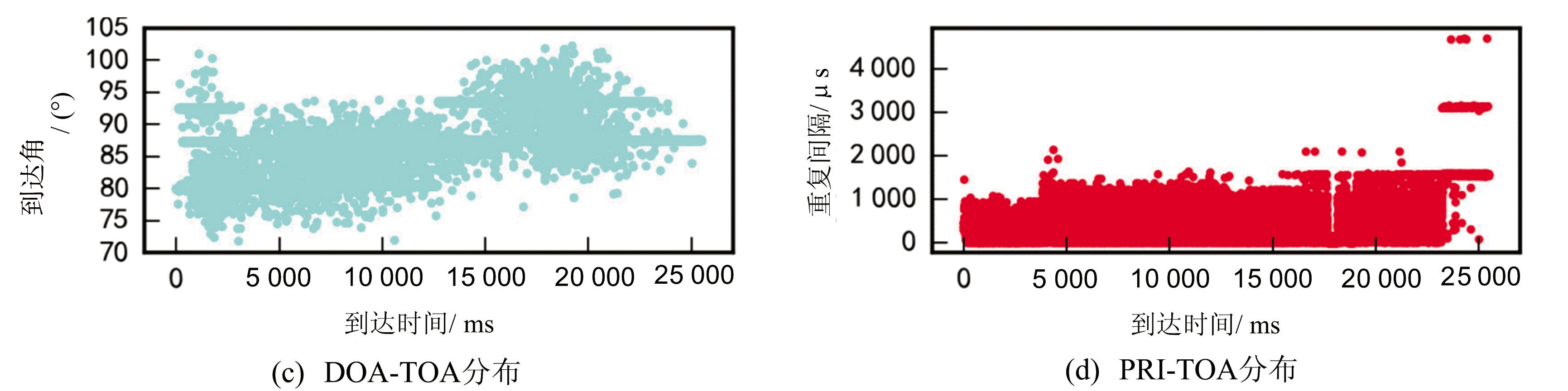
图4 雷达参数分布
2.2 仿真实验一
为验证本文算法对常规分选的提升效果,本实验的仿真数据使用2.1节所示雷达数据,在仿真数据上分别对单独的常规分选算法和常规分选算法结合本文算法进行实验。常规分选算法以基于CDIF的分选算法为代表,常规分选结合本文算法处理流程如图2所示,实验结果如表2所示。
表2 CDIF算法和CDIF结合本文算法对比
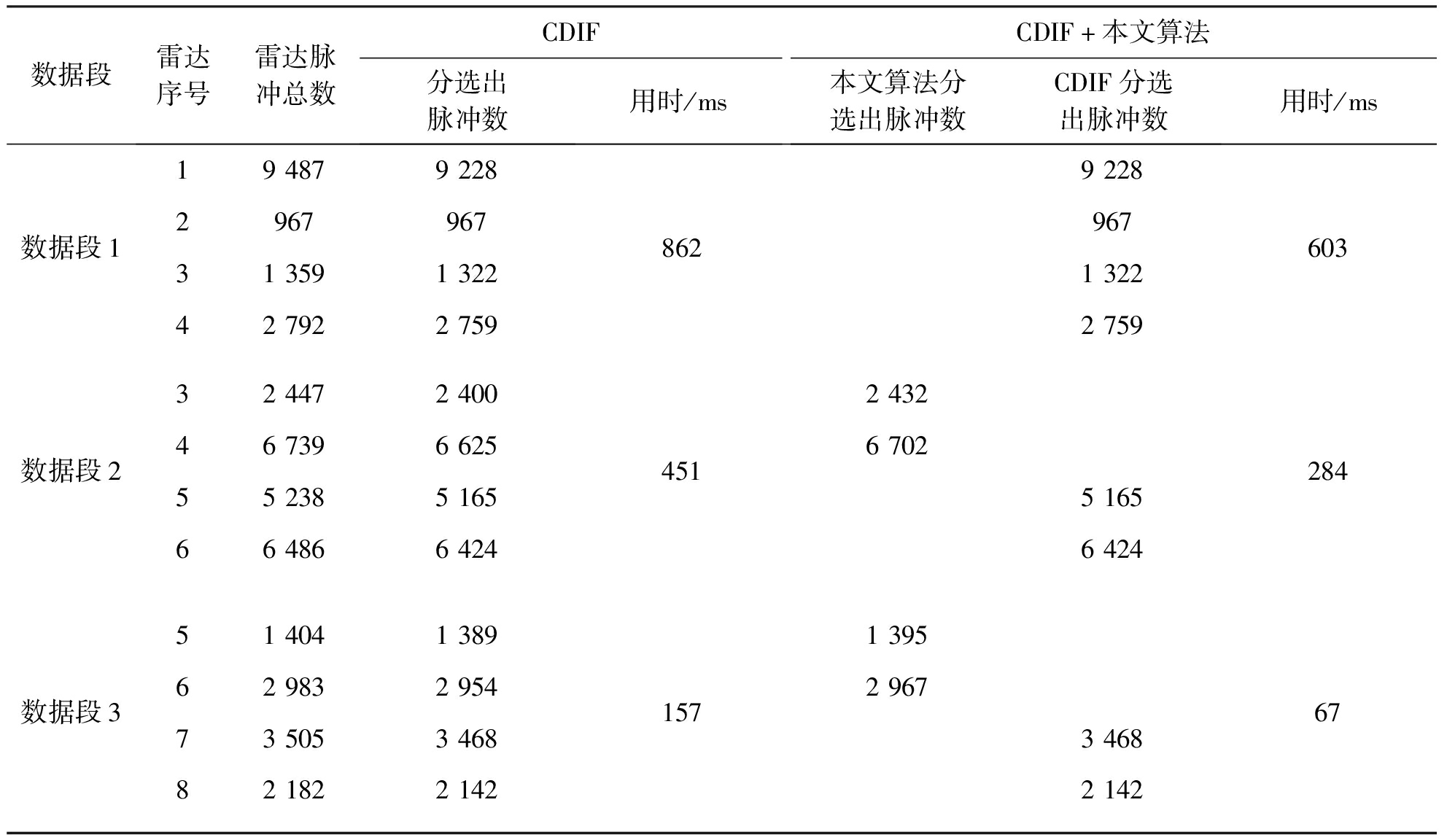
数据段雷达序号雷达脉冲总数CDIF分选出脉冲数用时/msCDIF+本文算法本文算法分选出脉冲数CDIF分选出脉冲数用时/ms数据段11948792282967967313591322427922759862922896713222759603数据段23244724004673966255523851656648664244512432670251656424284数据段3514041389629832954735053468821822142157139529673468214267
续表2

数据段雷达序号雷达脉冲总数CDIF分选出脉冲数用时/msCDIF+本文算法本文算法分选出脉冲数CDIF分选出脉冲数用时/ms数据段4759815940854255320995259099101898918550292859385388909918550521脉冲总数85509 83752 83946 准确率0.979452455 0.981721222
从表2中数据可以看出,在仿真数据集上,一共有10部雷达,共发射雷达脉冲85 509条,基于CDIF的常规分选算法可分选出83 752条脉冲,准确率为97.94%,共用时4 398 ms。而常规分选算法结合本文算法则可分选出83 946条脉冲,准确率为98.17%,共用时1 475 ms。实验表明结合本文算法在保证分选准确率稍优的基础上,能有效缩短分选时间。其中在数据段4上由于利用数据段3的分选结果事先将目标7和目标8的脉冲抽取出来,分选效率甚至提高5倍。
2.3 仿真实验二
为验证本文算法可以有效解决常规分选算法的增批问题,我们分别对0~3 840 ms,3 840~12 670 ms,12 670~16 600 ms和16 600~25 579 ms四段数据进行基于CDIF的常规分选和本文所述算法的对比实验。常规分选算法会产生16个目标,如表3所示:数据段1、2都会识别出目标3和目标4,数据段2、3都会识别出目标5和目标6,数据段3、4都会识别出目标7和目标8。为解决增批问题,在传统的分选算法之后,需要增加雷达信号融合算法,判断分选的结果中是否有目标可以融合,该过程会大大降低分选识别的速度。
表3 常规分选结果

数据段序号分选结果数据段1目标1目标2目标3目标4数据段2目标3目标4目标5目标6数据段3目标5目标6目标7目标8数据段4目标7目标8目标9目标10
如果结合本文的算法,对于待分选脉冲序列,截取其中的一部分用来进行CDIF,然后用CDIF的结果作为已知辐射源,对剩余脉冲使用本文算法进行分选。即对数据段1进行传统分选,用数据段1的分选结果对数据段2使用本文算法进行二次分选,从数据段2中分选出目标1和目标2的脉冲,然后对数据段2中剩下的脉冲进行传统分选;对数据段3和4也进行同样的分选步骤。对仿真数据进行实验,得到10个目标,如表4所示。
表4 结合本文算法的分选结果

数据段序号分选结果数据段1目标1目标2目标3目标4数据段2目标5目标6数据段3目标7目标8数据段4目标9目标10
由于本文的算法是一种基于已知辐射源的分选算法,因此文件的切分不会造成增批问题;而且充分利用了各数据段在时间维度上的关系,减少了之后常规分选的脉冲密度。因此在大数据量脉冲的情况下,本文算法可以有效解决文件切分导致的增批问题,提高分选速度。
2.4 仿真实验三
由于真实环境中在捕获雷达信号时存在脉冲丢失情况,为测试在此情况下本文算法的适应性,在仿真数据上进行了不同漏脉冲比例下的实验。不同漏脉冲比例下算法的分选精度如图5所示。

图5 漏脉冲比例对算法的影响
分析实验可知:本文算法对漏脉冲的鲁棒性特别高,即使有20%的漏脉冲,本文算法的准确率仍然可以达到86.94%,甚至在有50%的脉冲丢失的情况下,本文仍然可以准确分选出来49.74%的脉冲。
2.5 仿真实验四
为测试TOA的测量误差对本文算法的影响,本次实验设计了7个样本,每个样本10万条脉冲,漏脉冲比例为5%,样本之间只有TOA测量误差不同,分别为[0.001, 0.005, 0.01, 0.02, 0.03, 0.04, 0.05]。同时在这些样本上,进行4次仿真实验,每次实验的重频容差分别为0.5%、1%、2%、3%(重频容差表示算法对重频的容忍度,即变化小于该值则认为属于同一个重频值)。实验结果如图6所示。

图6 TOA测量误差对算法的影响
分析可知,在分选算法中重频容差范围确定的情况下(例如0.5%),当TOA测量误差较小时,抽取成功率维持在较高水平。随着TOA测量误差增大,分选成功率会急剧降低。但是随着重频容差范围的提升(从0.5%到3%),算法对TOA测量误差的适应性逐渐加大(重频容差范围在0.5%情况下,TOA测量误差超过0.5%即会急速降低;重频容差范围在1%时,TOA测量误差超过1%才会下降;在重频容差范围为3%时,TOA测量误差则要超过3%才会降低)。由实验结果可知,本文算法的重频容差范围和TOA测量误差存在类似线性的关系,在实际分选过程中,可根据设备的TOA测量误差来设定本文算法的容差范围。
3 结束语
针对复杂电磁环境中雷达信号常规分选算法计算量大、识别速度慢、增批漏批等严重问题,本文提出了一种基于时序匹配及变长滑窗的分选算法,对载频、脉宽两参数过滤后的脉冲进行时域参数的匹配,匹配过程中窗口的大小根据脉冲间的到达时间差来动态确定。仿真实验结果表明,本文算法能有效提高常规分选算法的准确率和效率,并且在处理海量脉冲的情况下可有效解决常规分选算法产生的增批问题,在复杂的电磁环境下仍然保持在较高的识别准确率,适应能力强,在实际环境中具有较高的实用价值。
[1]王怡宁.复杂雷达信号分选技术研究[D].西安:西安电子科技大学,2019.
[2]刘嗣勤,李秀平.雷达信号分选关键技术研究[J].电脑编程技巧与维护,2019(10):147-149.
[3]黎聪.雷达的信号分选技术研究[D].成都:电子科技大学,2015.
[4]MARDIA H K.New Techniques for the Deinterleaving of Repetitive Sequences[J].IEE Proceedings F-Radar and Signal Processing, 1989, 136(4):149-154.
[5]MILOJEVIC D J , POPOVIC B M.Improved Algorithm for the Deinterleaving of Radar Pulses[J].IEE Proceedings F-Radar and Signal Processing, 1992, 139(1):98-104.
[6]梁徵羽.密集复杂环境下信号分选算法研究[J].信息通信,2019(5):38-40.
[7]陈骄阳.一种低截获概率雷达信号分选方法研究[J].科技与创新,2019(11):98-99.
[8]石荣,吴聪.基于PRI信息的雷达脉冲信号分选技术研究综述[J].电讯技术,2020,60(1):112-120.
[9]NISHIGUCHI K , KOBAYASHI M.Improved Algorithm for Estimating Pulse Repetition Intervals[J].IEEE Trans on Aerospace and Electronic Systems, 2000, 36(2):407-421.
[10]牟皓,高由兵,郑坤.复杂电磁环境下同型雷达信号的分选方法[J].电子信息对抗技术,2018,33(5):12-15.
[11]刘正成,齐永梅,姚志均.一种快速重频参差信号分选方法[J].舰船电子对抗,2017,40(5):70-73.
[12]FALOUTSOS C, RANGANATHAN M , MANOLOPOULOS Y.Fast Subsequence Matching in Time-Series Databases[J].Acm Sigmod Record, 2000, 23(2):1-11.
[13]POVINELLI R J.Time Series Data Mining: Identifying Temporal Patterns for Characterization and Prediction of Time Series Events[M].USA:Marquette University, 1999.
[14]陈国泰,余轮,陈长汶,等.基于变长滑窗的turbo码译码[C]∥第十届全国青年通信学术会议论文集,四川绵阳:中国通信学会,2005:7.
