0 引言
天波超视距雷达因其探测距离远，覆盖范围大，单位面积所需成本低，抗隐身能力强等优点，在国内外得到广泛关注与应用。与常规雷达的目标探测不同，天波超视距雷达探测目标是依靠电离层对短波信号的反射来实现的，对目标的定位则通过P-D转换和目标的方位角来完成。由于电离层的倾斜、虚高的测不准、P-D转换的误差和目标方位分辨率较低的影响，使得天波超视距雷达目标定位精度不高，严重制约了其应用。为了提高目标定位精度，需要增加电离层观测设备，以改善电离层虚高测量精度；通过增大接收天线阵口径，来提高目标方位分辨率；通过在目标区设置一定数量的应答机或利用无源信标[1]，来修正系统定位误差。但是，以上方法都无法克服由于电离层虚高测不准和目标方位角误差所带来的目标定位误差，无法使目标的定位精度得到较大提升，因此最根本的解决办法是目标的定位不能依赖于电离层的虚高和目标的方位角。基于以上思想，本文针对海面目标提出了一种多站联合定位的方法，通过建立发射站、接收站、电离层和目标之间的几何模型，利用多个接收站测得的目标距离和信息，建立目标定位方程组，对目标位置进行解算，消除电离层虚高和目标方位角对定位的影响，从而大大提高目标的定位精度。
1 天波超视距雷达单站定位原理
1.1 单站目标定位方程
天波超视距雷达通常由1个发射站、1个接收站和若干电离层诊断设备组成。发射站与接收站相隔100 km左右，以保证发射与接收足够的信号隔离度。电离层诊断设备广泛布置于系统覆盖区适宜位置处，为系统目标探测提供最佳的工作参数。天波超视距雷达工作时，发射站所发射的短波探测信号，经电离层反射后照射到目标上，被目标反射后的短波探测信号再经电离层反射后被接收站接收，通过接收站的信号处理和目标检测，获得目标到发射站和接收站的射距和，以及目标的方位角；根据发射站、接收站、电离层和目标的几何关系，建立包含电离层虚高和目标方位角的定位方程组，通过解方程组，实现对目标的定位。
在地球面球面电离层情况下，假设电离层对短波信号的反射是同地心镜面反射，接收站、目标、地球和电离层形成如图1所示的几何关系[2]，发射站、目标、地球和电离层之间也存在相同的几何关系。
图1 接收站、目标、地球与电离层的几何关系示意图
图1中，A为接收站位置，M为目标位置，C为探测信号经电离层反射的等效反射点，CB为电离层虚高hA，O为地心。设地球半径为R，A到M的地面大圆距离为RD，AC与CM之和为接收站到目标的射距RA，则可以得到
R2+(R+hA)2-
(1)
同上可以得到发射站到目标的射距公式(2)。
R2+(R+hT)2-
(2)
式中，RT为发射站到目标的射距，R′D为发射站到目标的地面大圆距离，hT为发射站到目标的电离层反射虚高。当发射站与接收站相距较近时，hT与hA近似相等都为h。
设接收站测得的目标方位角为α，目标经度为LongM，纬度为LatM,，接收天线阵法线与地理北的夹角为β，可以建立如图2所示的球面三角形，其中N(0°，90°)为地理北极，A(LongA，LatA)为接收站位置，T(LongT，LatT)为发射站位置，M(LongM，LatM)为目标位置，O为地心，
为接收站正北方向矢量(经过A点，且与过接收站和北极点的地球大圆相切)，
为目标相对于接收站的方向矢量(经过A点，且与过接收站和目标点的地球大圆相切)，
为接收天线阵法线方向矢量(处于和确定的平面上)。
图2 接收站、目标和地理北极的位置关系示意图
利用平面三角形定理，可以得到式(3)和式(4)所示，利用球面三角形定理可以得到式(5)。
arccos(sin(LatA)sin(LatM)+
cos(LatA)cos(LatM)cos(LongA-LongM))
(3)
arccos(sin(LatT)sin(LatM)+
cos(LatT)cos(LatM)cos(LongT-LongM))
(4)
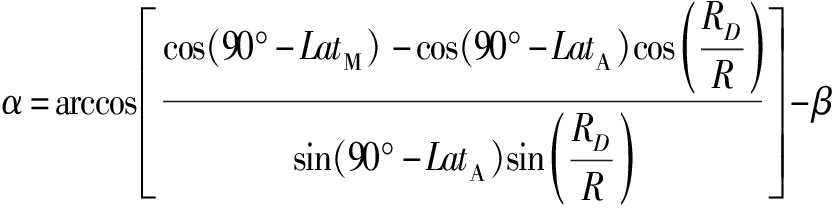
(5)
由式(1)、(2)、(3)、(4)和(5)建立关于目标经纬度的方程组，如式(6)所示。
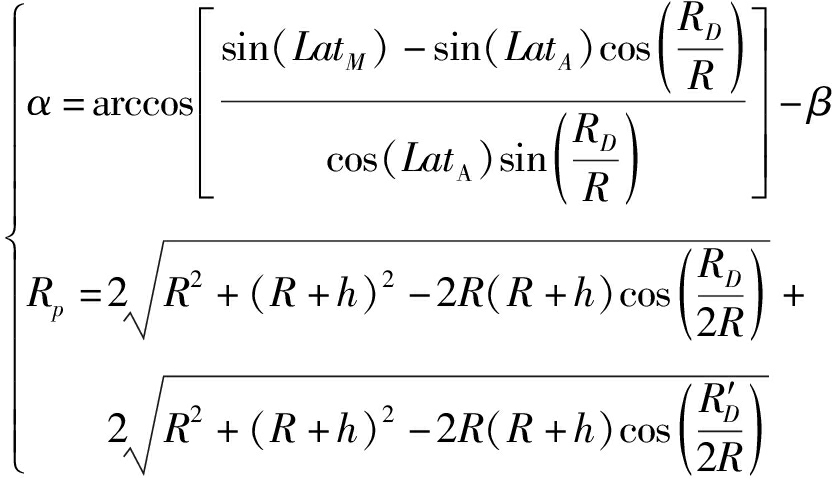
(6)
方程组(6)中，Rp为发射站射距RT与接收站射距RA之和，且α，β，Rp，R，h，LatA，LongA，LatT，LongT为已知量，LatM和LongM为待求量，通过解方程，可以获得LatM和LongM的数值解。
1.2 影响目标定位精度的因素
天波超视距雷达的目标定位精度受多种因素的影响，包括电离层虚高测不准、目标方位角误差、收发站坐标误差、射距Rp的测量误差等，其中电离层虚高的测不准和目标方位角误差是影响天波超视距雷达单站定位的主要因素。
1)电离层虚高测不准
电离层是一种不均匀的、各向异性的、随机色散的介质，由太阳高能电磁辐射、宇宙射线和沉降粒子作用于地球高层大气，使其大气分子发生电离而形成。它具有统计的规则变化和随机的不规则变化特性，对同一频率的短波信号，在空间同一位置，不同的时间，其影响的状态也是不同的[3]。
要将电离层对不同频率，不同空间，实时准确的描绘出来是不可能的。通常对电离层的描绘是采用统计的方法，其实时性和精确性都较差。在建立较好的电离层诊断系统后，电离层虚高的测量误差也只能做到十几千米。
2)目标方位角误差
天波超视距雷达接收天线阵一般为均匀线性阵列，当按-35 dB水平方位副瓣考虑时，其水平波束按汉明窗函数加权后波瓣将展宽1.38倍，与接收天线阵口径有(7)式的关系：
(7)
式中，D为天线阵口径，λ为工作波长，φ为水平面波束宽度。当工作频率为15 MHz时，天线阵口径按1.4 km计，天波超视距雷达接收天线阵水平波瓣宽度将达到1°，根据工程经验，目标方位角误差为0.4°左右。当目标距离接收站2 000 km时，其方位误差将会产生14 km距离误差。
1.3 单站目标定位仿真与分析
假设发射站坐标为(114.0°，35.5°)，接收站坐标为(113.0°，35.0°)，目标坐标位于(133.0°，27.0°)的海面上，目标方位角α为-5.12°，接收天线阵法线方向β为114.7°，电离层虚高为200 km，地球半径为6 370 km。根据以上条件，计算得到发射站与接收站的射距和为4 266.55 km。按照方位角误差σα为0.4°，电离层虚高测量误差σh为15 km，产生测量误差按标准正态分布的目标方位角和电离层虚高模拟数据，进行目标定位仿真。
仿真分3种情况进行，即仅存在目标方位角误差情况下的仿真、仅存在电离层虚高测量误差情况下的仿真和二者都存在情况下的仿真。3种情况下各进行了500次的仿真，仿真结果如图3所示。
(a)存在电离层虚高误差时的目标定位仿真结果
(b)存在方位角误差时的目标定位仿真结果
(c)同时存在电离层虚高和方位角误差时的目标定位仿真结果
图3 3种不同情况下目标定位的仿真结果
统计计算电离层虚高测量误差引起的目标定位均方差为8.2 km，方位角误差引起的目标定位均方差为13.7 km，二者共同作用带来的目标定位均方差为16.2 km。由仿真结果可以看出，在单基地天波超视距雷达定位时，目标方位角误差是影响目标定位的主要因素。
2 天波超视距雷达多站目标定位原理
2.1 多站联合目标定位方程
单站天波超视距雷达在进行目标定位时，需要电离层虚高和目标方位角参与目标地理位置的求解，因此电离层虚高和目标方位角的测量误差对目标定位带来较大影响。为消除两者带来的影响，根本的办法是使目标的定位不依靠电离层虚高和目标的方位角。基于此，提出了一种多站联合目标定位的方法。该方法采用“1发3收”技术体制，即用1个发射站和3个接收站组成多基地天波超视距雷达系统，通过协同工作，系统可以同时获得目标的3个射距和测量数据，利用这3个数据，通过发射站、接收站与目标的几何关系，构建目标联合定位方程组，直接求解目标地理位置坐标。
在进行多站联合目标定位时，按照单站定位的地球与电离层的假设关系以及发射站、接收站与目标的几何关系，可以得到发射站和接收站的射距方程如式(8)和式(9)所示。
R2+(R+hAi)2-
i=1,2,3
(8)
R2+(R+hT)2-
(9)
式中，RAi为接收站到目标的射距，RTi为发射站到目标的射距，RDi为接收站到目标的地面大圆距离，R′D为发射站到目标的地面大圆距离，hAi为接收电离层反射虚高，hT为发射电离层反射虚高，R为地球半径。
根据发射站、接收站、目标的地理位置关系，利用平面三角形定理可以得到式(10)和(11)。
arccos(sin(LatAi)sin(LatM)+
cos(LatAi)cos(LatM)cos(LongAi-LongM))
(10)
arccos(sin(LatT)sin(LatM)+
cos(LatT)cos(LatM)cos(LongT-LongM))
(11)
当发射站与接收站相距较近时，发射电离层虚高hT与各接收电离层虚高hAi近似相等都为h。由式(8)、(9)、(10)和(11)可以建立“1发3收”多站联合目标定位的方程组如式(12)所示。
(12)
式中，RP1,RP2,RP3分别为发射站和3个接收站到目标的射距和。
2.2 多站联合目标定位仿真分析
假设发射站坐标为(114.0°，35.5°)，接收站1坐标为(113.0°，35.0°)，接收站2坐标为(113.3°，36.0°)，接收站3坐标为(115.0°，35.7°)目标坐标位于(133.0°，27.0°)的海面上，电离层虚高为200 km，地球半径为6 370 km。根据以上条件，计算可得发射站到接收站1、接收站2和接收站3的的射距和分别为4 266.55 km、4 281.26 km和4 128.49 km。因为多站联合定位方程组中不包含目标方位角，因此无须进行目标方位角的计算。按电离层虚高测量误差σh为15 km，产生标准正态分布电离层虚高模拟数据500组，进行目标定位仿真。仿真结果如图4所示。
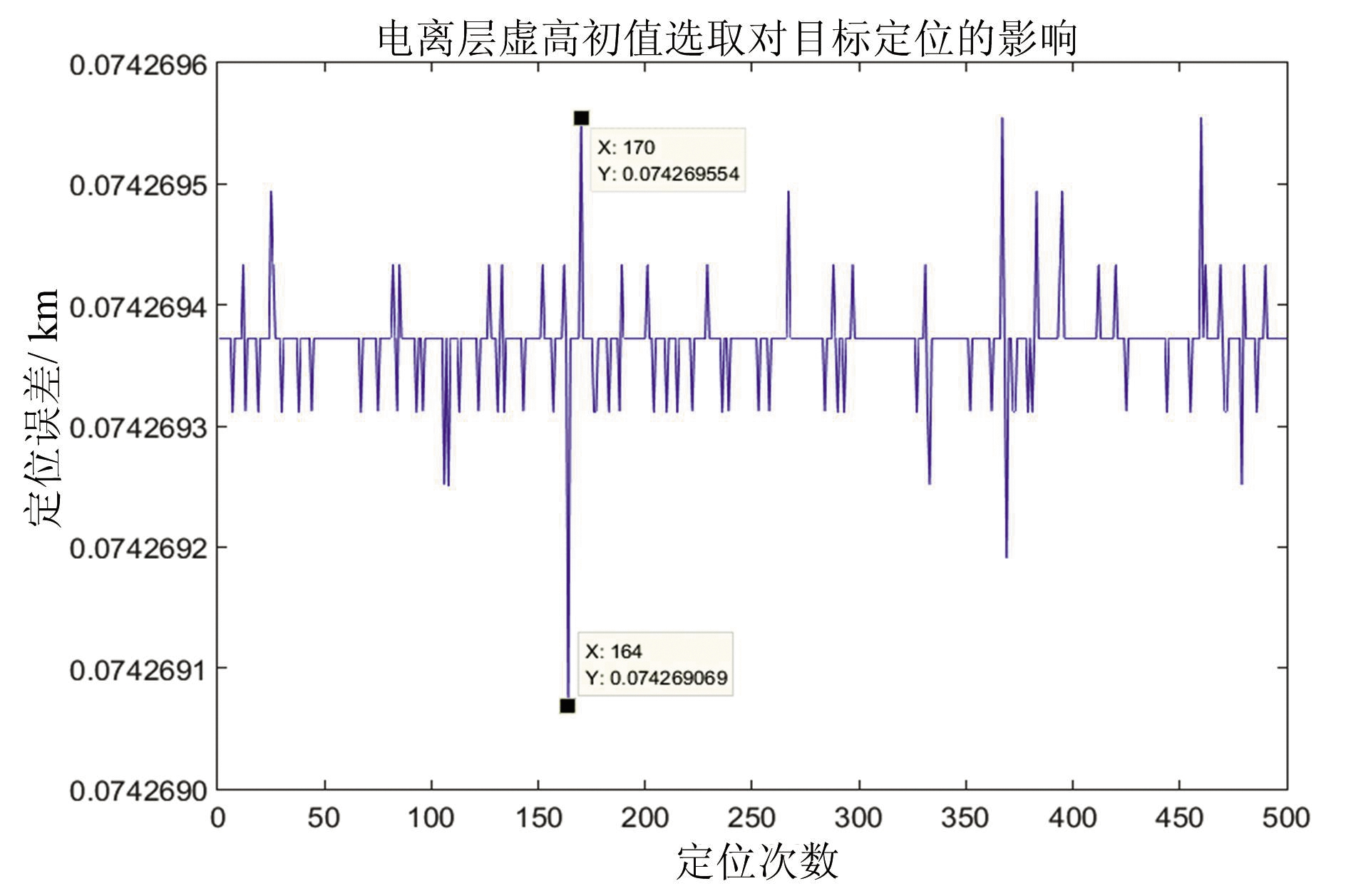
图4 “1发3收”多站联合目标定位仿真结果
经仿真计算，多站联合目标定位的定位均方差为0.074 km。在多站联合目标定位中，由于目标的方位角不参与目标位置解算，电离层虚高仅作为未知参数参于方程组的解算，因此目标方位角的测量误差不会影响目标定位误差，电离层虚高的变化也不会影响目标的定位误差。由仿真结果图4可以看出在多次定位中，目标定位误差基本保持不变，从而说明了多站联合目标定位能够消除电离层虚高和目标方位角测量误差的影响，减小目标定位误差，大大提高目标定位的精度。
2.3 初值选取对目标定位解算的影响
多站联合定位方程组为非线性方程组，需要通过迭代法求解[4]，以获取方程组的最优数值解。在迭代解算过程中，初值的选取非常重要，不仅影响迭代运算的收敛速度、解算的误差，甚至影响到方程组能否获得数值解。多站联合定位方程组的初值包括3项即电离层虚高、目标的经度和纬度，当初值选择不当时，解算的位置坐标将出现较大的误差。分别对电离层虚高初值、目标经度初值和目标纬度初值的不同变化所引起的目标定位误差进行了仿真，仿真结果如图5、图6和图7所示。
图5 电离层虚高初值对目标定位的影响
图6 目标经度初值对目标定位的影响
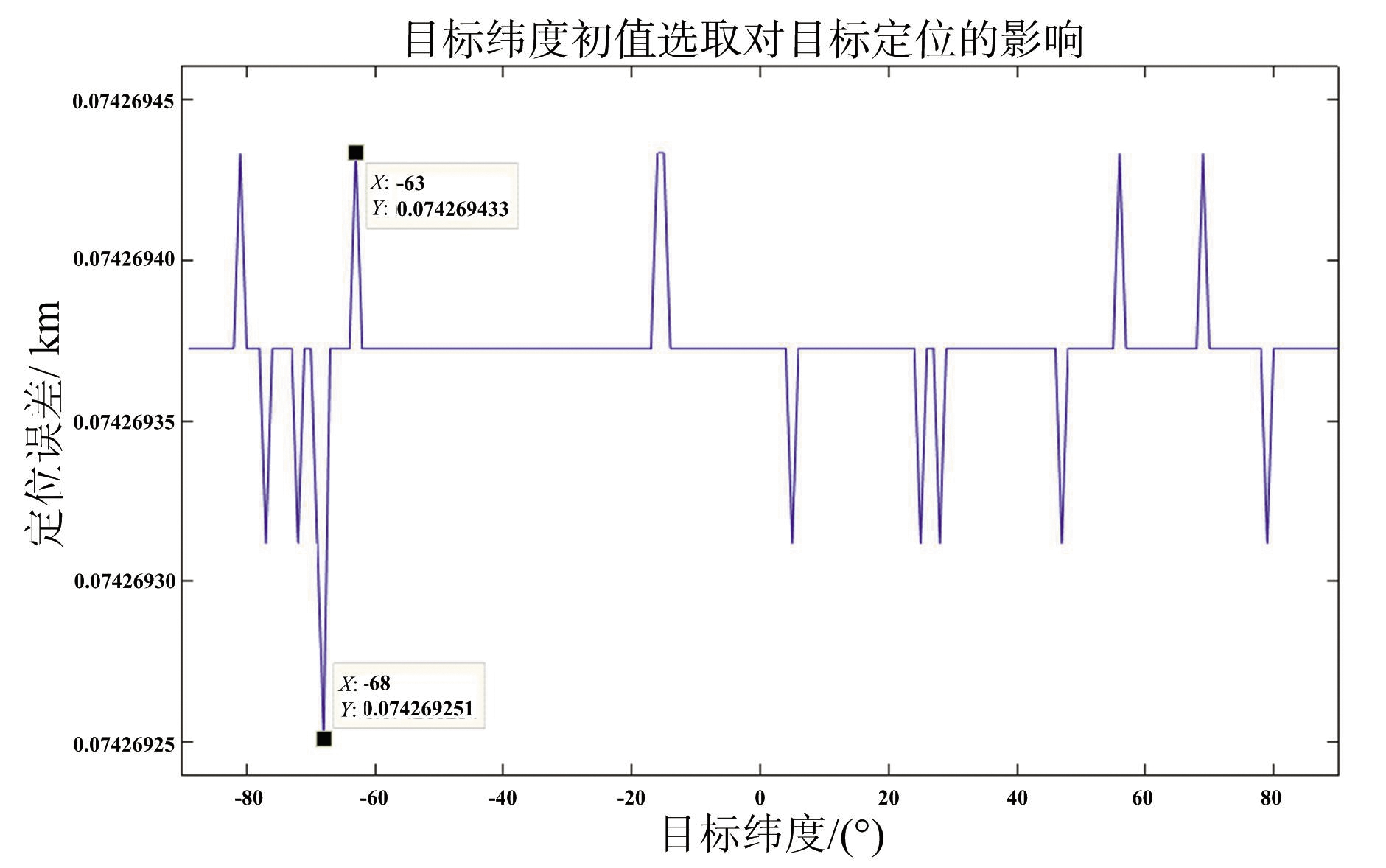
图7 目标纬度初值对目标定位的影响
由仿真结果可以看出，当电离层虚高初值小于87 km时，解算得到的位置误差将由0.074 km增大为74.656 km，因此电离层虚高初值选取应大于87 km；当目标经度初值小于52°或大于255°时，解算得到的位置误差将由0.074 km增大为74.656 km，因此目标经度初值应在(52°，255°)之间选取；目标纬度初值在-90°至90°内变化，不会影响定位结果。实际工程中，用迭代法求解目标位置时，电离层虚高、目标经纬度初值的选取随目标所处的不同区域有所不同，可以事先经过仿真计算得到。
3 结束语
本文提出的多站联合定位方法，在建立多站联合定位方程组时，对各站所用到的电离层虚高作了相等的假设，而实际中各站的电离层虚高并不一定相等，由此产生多站联合定位的模型误差，其相当于在各接收站的射距和测量值上增加了额外的测距误差。为了减小模型误差的影响，可以通过优化布站几何构形[5-6]，调整各站之间的距离，使各站的电离层等效反射点保持在一定范围内，减小各站电离层虚高的差异，从而获得较高的对目标定位的精度。但是当各站距离增大，各站电离层等效反射点相距较远，电离层虚高相差较大，此时再假设各站电离层反射点虚高相等将会对定位误差带来很大的影响。
[1]韩彦明.天波超视距雷达无源信标修正方法研究[D].南京：南京理工大学，2010:7-9.
[2]周文瑜，焦培南.超视距雷达技术[M].北京：电子工业出版社,2008：348-356.
[3]焦培南.雷达环境与电波传播特性[M].北京：电子工业出版社，2007：245-317.
[4]雷文英.多站被动超视距雷达时差定位及相关问题研究[D].西安：西安电子科技大学，2014：17-32
[5]王敏.一种多站定位方法研究[J].通信对抗,2005(1):42-45.
[6]唐小明,王贞杰,张涛.四站无解及模糊问题的增站处理方法[J].现代雷达,2012,34(7):16-19.
