0 引言
近些年来,随着无人驾驶领域的兴起,毫米波雷达相关技术也随之飞速发展,其中77 GHz FMCW雷达更是成为了业界的主流。由于毫米波雷达具有高探测精度等特点,使得其在除辅助驾驶之外,还能应用于人体动作识别领域。相比于利用摄像机来进行人体动作识别,毫米波雷达不仅具有不受视距和光线影响等特点,还能在很大程度上保护用户的个人隐私[1]。
利用毫米波雷达来进行人体动作检测的关键在于从雷达采样数据中处理得到微多普勒特征。针对利用微多普勒特征来进行动作识别,国内外相关研究者作了许多研究。已有研究者[2]将人体动作雷达采样数据通过短时傅里叶变换后,直观地从微多普勒谱图中提取相关标量指标来作为特征,但其提取的特征主观性太强,不适合部分复杂动作检测。文献[3]将频谱质心、带宽、频谱图的熵、SVD分解后所求得的统计量作为特征来进行动作识别,但其经分类器分类后的识别准确率不高。也有研究者[4]从微多普勒谱图的3D图形着手,使用点描述算法来得到一些谱图三维形状的标量属性,以此作为特征。其算法较为复杂,且提取的特征不够直观。将深度学习和人体动作微多普勒谱图相联系来进行研究[5]也是当前比较流行的一种方式,尽管其分类准确率高,但对大量训练数据集的要求及对计算机的性能需求也不容小觑。
针对上述问题,提出一种基于77 GHz FMCW雷达的人体复杂动作识别方案。首先,基于FMCW信号模型采用一种以RDM(Range Doppler Map)向速度维投影的方式,逐帧构建微多普勒谱图。再结合雷达实测数据深入分析,并从各类动作产生的微多普勒谱图中提取用于表征整个动作频谱相关信息的特征矢量。最后,利用经贝叶斯超参数优化后的支持向量机来进行分类验证,并筛选得到最优的特征矢量组合。实验结果表明,从动作谱图中所提取的各个特征矢量对人体动作的正确分类有很大的贡献,经筛选得到的最优特征矢量组合能在最大程度上提高分类准确率。
1 FMCW信号模型及建立微多普勒谱图
1.1 FMCW信号模型
FMCW雷达采用连续波体制,拥有较大的带宽、几乎不存在测距盲区、高距离分辨率以及低发射功率等特点,完全可应用于近距离检测人体动作实验。假设其发射锯齿形线性调频连续波,其发射信号[6]可表示为
(1)
式中,AT表示发射功率,fc表示Chirp的起始频率,B表示Chirp的带宽,Tc表示Chirp的持续时间,φ(t)表示相位噪音。
相应地,雷达将接收到该延时的,且经缩放后的发射信号,即回波信号,其公式为
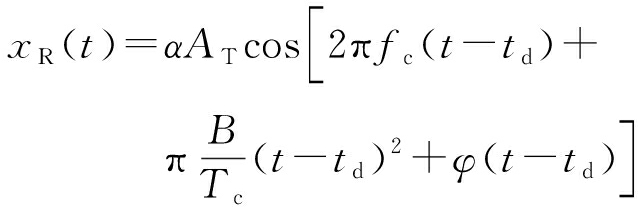
(2)
式中,td=2R(t)/c,用以表示信号在与距离雷达R(t)处的目标之间的往返时间,α则与回波损耗有关。将如上xT(t)及xR(t)混频后再结合I/Q信号分析,其差拍信号可近似表示为
y(t)=ARej(2πfbt+φb(t)+Δφ(t))
(3)
此处差频fb=2BR(t)/(cTc),AR表示接收功率,相位φb(t)=2πfctd+πBtd2/Tc。在近距离检测人体动作的实验中,上述的残留相位噪音 Δφ(t)可近似忽略。相应地,φb中的πBtd2/Tc项由于在实际状况下很小,亦可将其忽略。
综上,最后可将该差拍信号描述为雷达采样数据矩阵的形式:
(4)
式中,n表示快时间采样轴上对应的标号,m表示慢时间采样轴上对应的标号,Tf表示快时间采样轴上的ADC采样时间间隔,Ts表示慢时间采样轴上的采样时间间隔。
1.2 构建微多普勒谱图
针对上文所描述的雷达采样数据矩阵Y,包含该FMCW雷达于单帧状况下的所有采样数据。现对其于快时间维上的所有列数据加上汉宁窗,执行Range FFT[7],继而在慢时间维上的所有行数据加上汉宁窗后执行Doppler FFT并将零频分量搬至频谱中心,从而得到相应的RDM(Range Doppler Map),该RDM可直观地描述对应帧下所有人体散射点的距离、速度相关信息。此处用 RD(i,j,t)来表示在t帧下位于RDM中第ith距离门、jth速度门下的信号功率值。
本文仅针对单个人体目标进行研究,将所得每帧下的RDM向距离维投影并按列逐帧积累,可得到单目标运动轨迹图,如图1所示。横轴表示对应的帧标号,纵轴表示其距离门标号对应的目标距离雷达的径向距离。其计算公式为
(5)
从单目标运动轨迹图中可得到其目标在运动中距离雷达的最小/最大径向距离所对应的距离门标号,此处记为imin及imax。据此提取目标运动范围内的RDM,并进一步将提取的RDM向速度维投影并按列逐帧积累,则可得到目标运动产生的微多普勒谱图,如图2所示。横轴代表对应的帧号,纵轴表示其速度门标号对应的速度值,正值表示远离雷达,负值表示接近雷达。其具体公式为
(6)
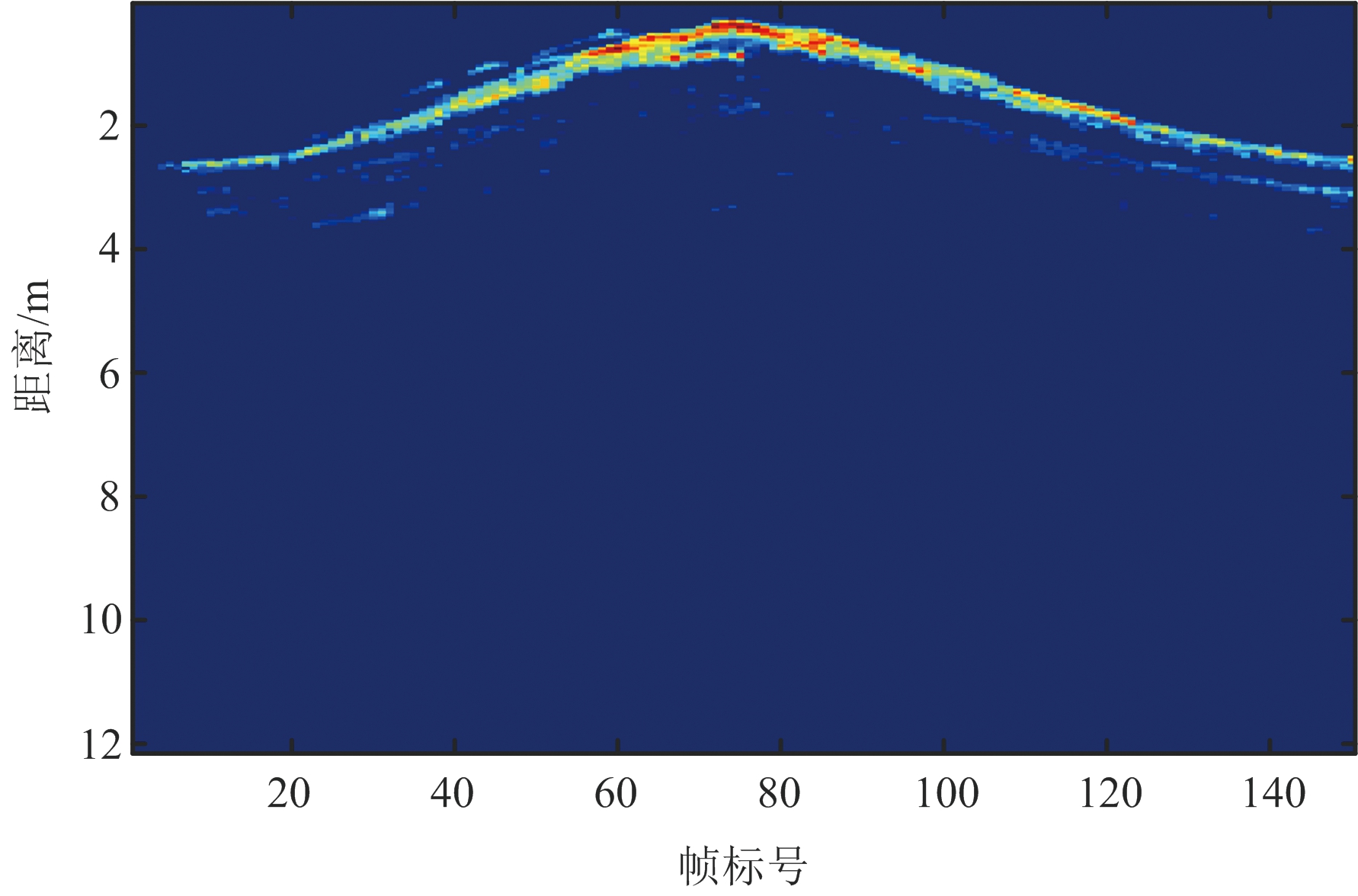
图1 单目标运动轨迹示意图
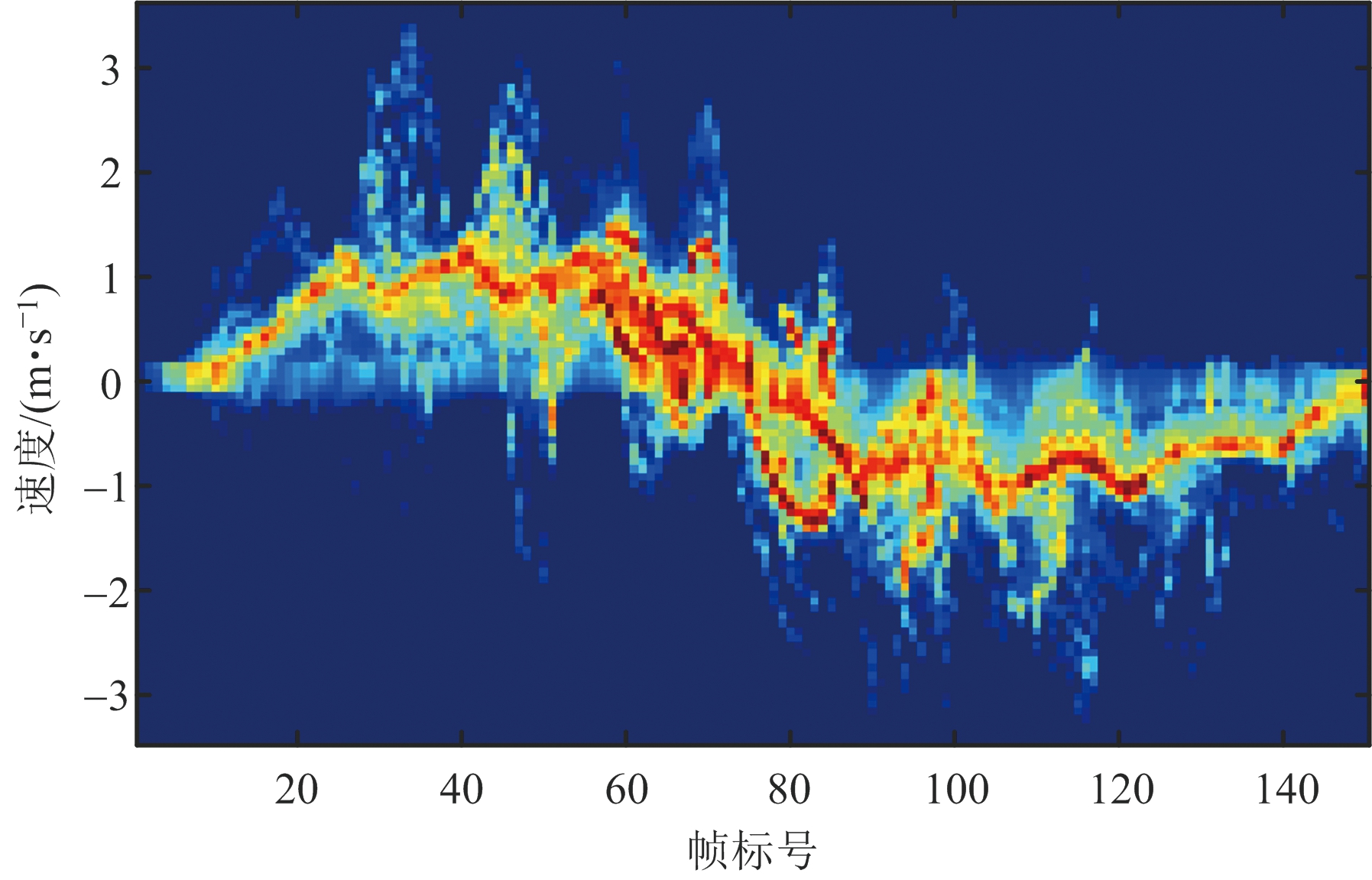
图2 微多普勒谱图示意图
从FMCW雷达收发信号到微多普勒谱图的构建的整个流程图如图3所示。

图3 微多普勒谱图构建流程
2 微多普勒特征矢量提取
引入公式v=λ/(2MTc)×j,其中v表示速度门标号j对应的实际速度值,λ表示雷达工作频率对应的波长,M表示单帧下的Chirp总数,Tc表示发送的相邻Chirp间的时间差。由此可将公式(6)中的DP(t,j)转变为DP(t,v),以便于后续描述。
2.1 躯干微多普勒特征矢量
从图2中的微多普勒谱图示意图中观测可得,零速度层附近颜色较深的曲线,可表征为躯干微多普勒曲线。本文用速度质心[8]序列来近似描述该躯干微多普勒曲线vtorso(t),将该序列作为从谱图中所提取的躯干微多普勒特征矢量,其公式为
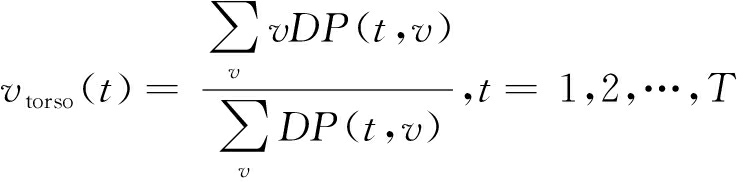
(7)
2.2 肢体微多普勒特征矢量
相应地,可观察到谱图中,许多速度分量基于躯干微多普勒曲线向四周延伸,可表征为肢体微多普勒曲线。本文提出如下公式来近似描述该肢体微多普勒曲线vlimb(t),将该序列作为从谱图中所提取的肢体微多普勒特征矢量:
vlimb(t)=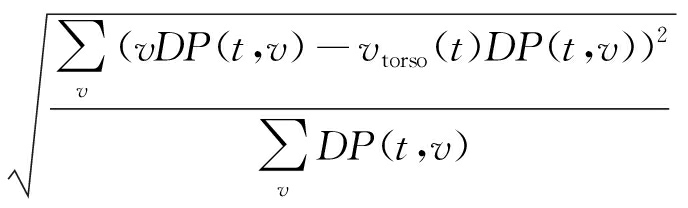
t=1,2,…,T
(8)
2.3 微多普勒谱图SVD分解
对微多普勒谱图运用SVD分解[9],可将其谱图中包含的人体动作频率相关信息、时间相关信息解耦并投影到左右奇异矢量上,使对应的左奇异矢量表示频率相关抽象信息,而右奇异矢量表示时间相关抽象信息。其分解公式为
DP=USVT
(9)
式中,U代表左奇异矩阵,S代表奇异值对角矩阵,V代表右奇异矩阵。
本文选取U矩阵和V矩阵中的前三个奇异矢量来作为从微多普勒谱图中所提取的用于表述时间、频率相关抽象信息的特征矢量,将这些特征矢量分别记为U1,U2,U3,V1,V2,V3。
3 实验结果与分析
3.1 信号采集与处理
实验中用于进行人体动作信号采集的设备为Texas Instruments公司所研发的AWR1642BOOST雷达传感器模块以及DCA1000EVM数据采集适配器模块。设定该雷达传感器的工作起始频率为77 GHz、带宽为4 GHz,单位Chirp下的采样数为256,单位帧下的Chirp数为128,帧周期为30 ms,每个动作下捕获150帧数据。于该配置下,速度分辨率为0.071 m/s,最大无模糊速度可达±4.564 m/s,每次固定采集数据时长为4.5 s。
本次实验于室内进行,在雷达的扇形扫射面内除测试者外无其他运动目标。将雷达置于距离地面0.8 m的桌面上,且测试者在雷达正前方1.5~4.0 m范围内执行动作。共有12名志愿者参与本次数据采集,测试者中身高跨度为1.53~1.85 m,体重跨度为41~83 kg,年龄均在23岁左右。实验过程中共采集了9类动作,测试者将每类动作各重复执行8次,则一共测得864组数据。将所采集的数据通过图3所示过程构建微多普勒谱图,此处为了消除信号在幅值上的敏感性,将微多普勒谱图中所有点的幅值都映射至[1,100],且最终得到的所有数据样本大小均为101×150。如图4所示,为实验中的9种动作描述。对所采集的数据进行处理后,各动作对应的微多普勒谱图如图5所示。
3.2 特征矢量提取
图5所示的人体动作微多普勒谱图形态会由于测试者的性别、身高、健康状态等因素而存在少许差异,但这并不会改变其整体的走向,故所提取的微多普勒特征矢量将能很好地表述一个动作的发生。

图4 9种实测人体动作描述
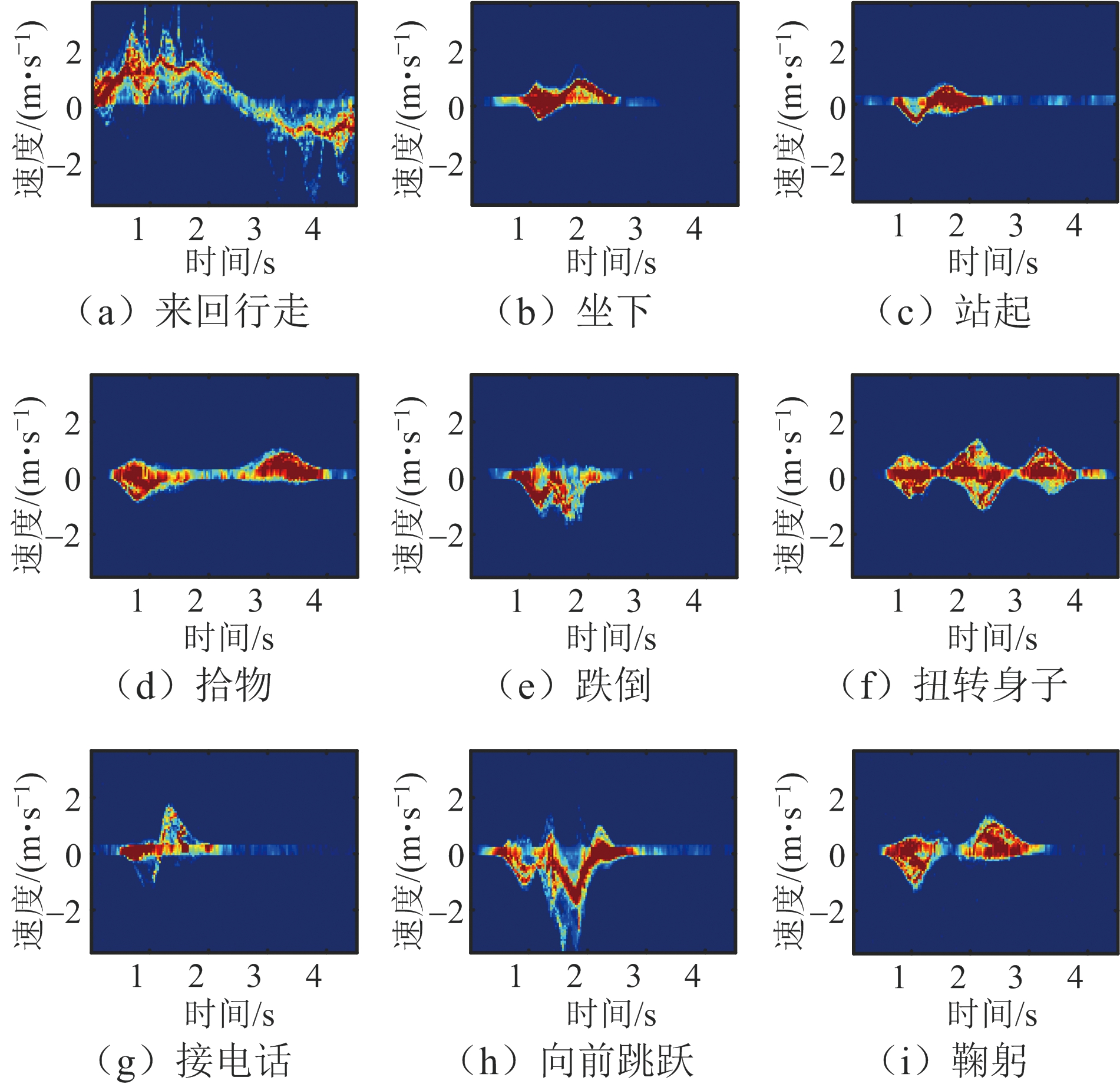
图5 9种实测人体动作微多普勒谱图
此处取图5(a)所示的来回行走微多普勒谱图作为示例来阐述从中提取的特征矢量,结果如图6所示。
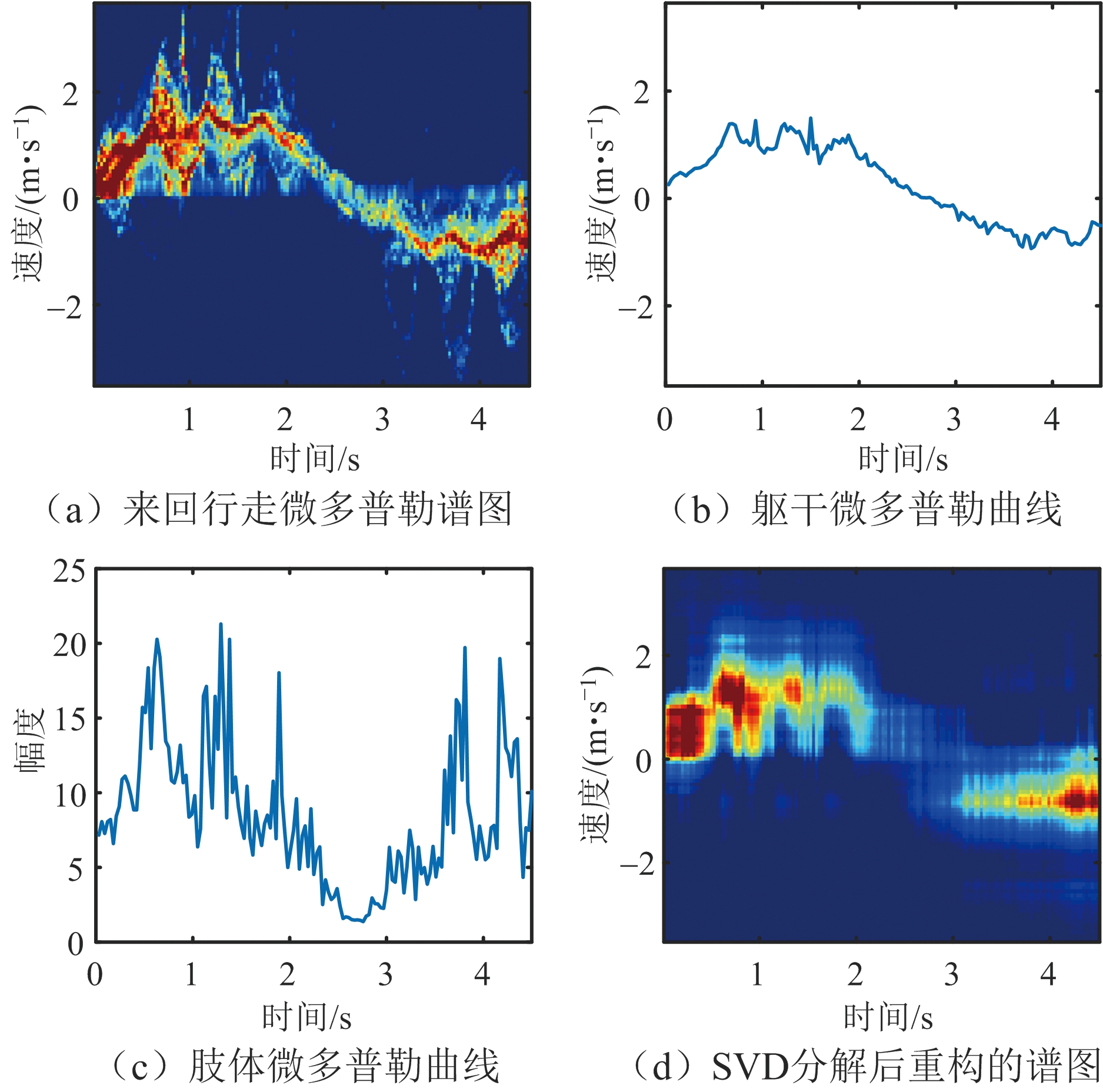
图6 人体动作微多普勒特征矢量描述示意图
图6(a)表示所示例的来回行走微多普勒谱图,根据公式(7)从该微多普勒谱图中提取躯干微多普勒特征矢量,其表述的曲线如图6(b)所示。同理,根据公式(8)从谱图中提取肢体微多普勒特征矢量,其表述的曲线如图6(c)所示。将微多普勒谱图经公式(9)所表述方式分解为U、S、V矩阵,取U、V矩阵前三个奇异矢量及S矩阵前三个奇异值来重构微多普勒谱图,所得到的重构谱图如图6(d)所示,不难看出,U、V矩阵前三个奇异矢量实则包含了大量谱图中的时间、频率相关信息,已基本上可以用来表征原始的微多普勒谱图。
综上,结合实验中所配置的雷达参数,可以得到各特征矢量的长度,如表1所述。
表1 所提取的特征矢量长度描述
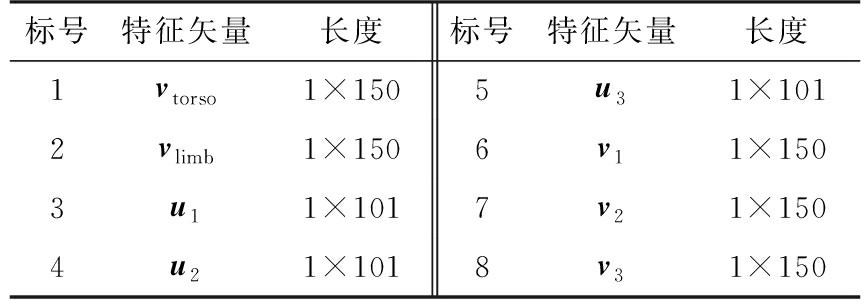
标号特征矢量长度标号特征矢量长度1vtorso1×1505u31×1012vlimb1×1506v11×1503u11×1017v21×1504u21×1018v31×150
3.3 利用支持向量机进行分类
3.3.1 数据集划分及分类策略拟定
将实验所测得的所有动作数据样本通过处理得到微多普勒谱图,并在此基础上提取特征矢量后,按如下两种方式划分为训练集和测试集:
1) 方案1:描述对已知个体的预测性能。将各个测试者所执行的每类动作中的随机6组数据样本作为训练集,剩余2组数据样本作为测试集。
2) 方案2:描述对未知个体的预测性能。将随机9个测试者所执行的所有动作数据样本作为训练集,剩余3个测试者所执行的所有动作数据样本作为测试集。
支持向量机(SVM)是建立在统计学习理论基础上一种机器学习方法,在训练集样本较少的情况下也能进行良好的统计和预测学习。其中,针对核函数的选取不同,其分类的性能也会发生较大的差异。
针对利用SVM进行如上9类动作的分类问题,采用高斯径向基核函数,构建9个二分类器,将各个分类器所对应的动作类别设置为正类,而其他8种动作类别则设置为负类,最终将置信度最大的类别判决为最终分类结果。为了进一步提升SVM分类性能,本文采用贝叶斯超参数调整[10]来选择最优框约束参数和核尺度参数。贝叶斯超参数调整基于目标函数的历史评估结果来建立新的概率模型,用以将目标函数值最小化,此处的目标函数即为所构建的SVM模型在调用当前调试的超参数下的五折交叉验证损失。
3.3.2 特征矢量筛选
从微多普勒谱图中所提取的8种特征矢量,均能从各个方面来表述谱图相关信息,对动作分类都能发挥一定的作用。然而,直接将每个样本所提取的8种特征矢量进行组合作为输入来训练SVM,则会产生以下结果:1) 8种特征矢量组合最终产生的向量维数过高,降低运算效率。2) 8种特征矢量中必定存在冗余特征矢量,这将产生过拟合现象,降低模型的泛化性能。
综上,分别研究将单个特征矢量作为分类器输入时以及将各特征矢量进行组合来作为分类器输入时对总体分类准确率的影响。如图7(a)所示,描述了数据集在如上两种不同划分方案下各单特征矢量与总体样本分类准确率之间的关系。图7(b)描述了8种特征矢量的247种组合与总体样本分类准确率之间的关系。输出结果表明,特征矢量vtorso、U1、U2对各动作的正确分类具有较大的贡献,而剩余5个特征矢量所作出的贡献相对较低,特别是V2、V3特征矢量可能对动作正确分类所起到的作用不大。分析图7(b)所示的特征矢量组合结果可得,不论是以方案1还是方案2方式对数据集进行划分,均在第29个组合位置处产生最高总体准确率,该组合下的特征矢量分别为躯干微多普勒特征矢量vtorso、肢体微多普勒特征矢量vlimb、U1特征矢量。值得一提的是,从该图中可以看到总体分类准确率随组合标号呈现类似周期性的波动,其产生的原因是:组合中包含U1特征矢量时将处于峰值位置,组合中包含V3特征矢量时将处于谷值位置。此处结合图7(a)综合分析可得,单特征矢量分类状况下相对较差的特征矢量在与其他特征矢量进行组合时,可提高总体分类准确率。
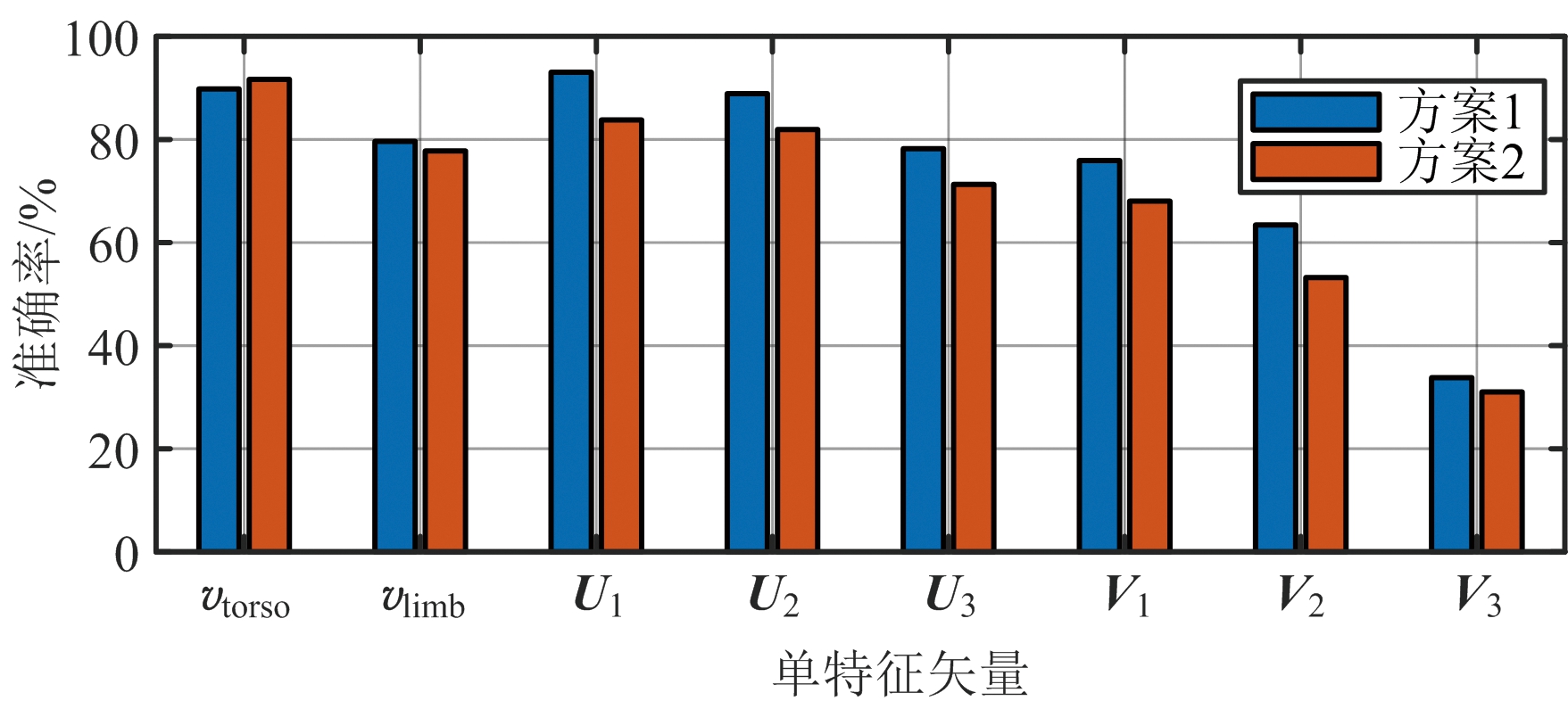
(a) 单特征矢量与总体分类准确率关系直方图
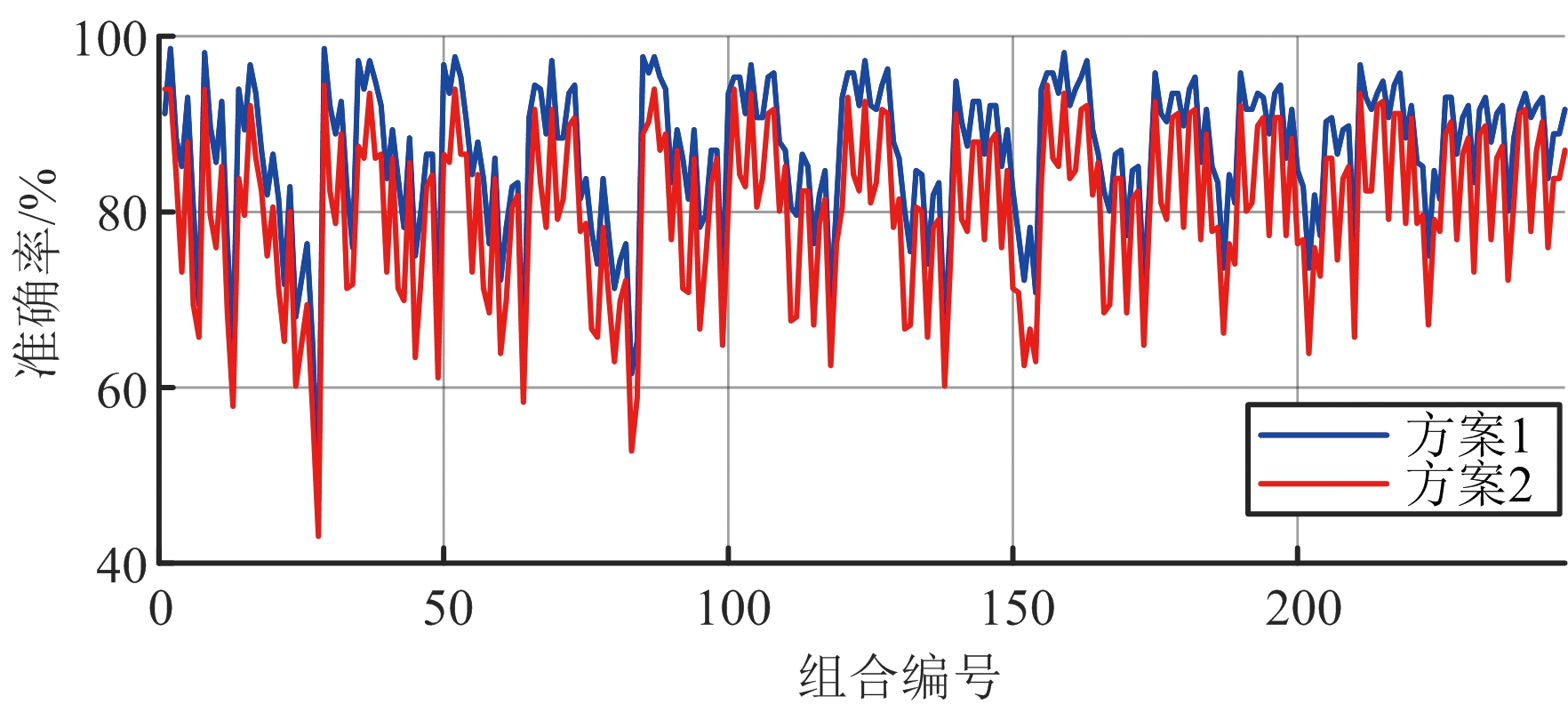
(b) 各特征矢量组合与总体分类准确率关系图
图7 单特征矢量及各特征矢量组合总体分类
准确率相关图
3.3.3 人体动作识别结果
基于上述的特征矢量筛选,已取得优异的特征矢量组合,即躯干微多普勒特征矢量vtorso、肢体微多普勒特征矢量vlimb、U1特征矢量组合。现针对上述的数据集划分方案1及方案2,利用该优异特征矢量组合,来进行对测试集中的各数据样本进行识别测试。图8(a)表示根据方案1的数据集划分方式所得到的各动作混淆矩阵图。图8(b)则是根据方案2的数据集划分方式得到的结果。各混淆矩阵纵轴表示如图4所描述的各类动作的真实归属类别,横轴表示各动作的预测类别,矩阵中的值表示将真实类别判定为对应预测类别的百分比,例如0.96则代表96%。结果表明,对已知个体的各动作识别总体准确率高达99.07%,对未知个体的各动作识别总体准确率为96.76%。且除向前跳跃和鞠躬动作外,其他动作的分类准确率均为100%,说明本文方法不管对已知个体还是未知个体的动作都能有较好的识别准确性。

(a) 对已知个体的各动作识别混淆矩阵
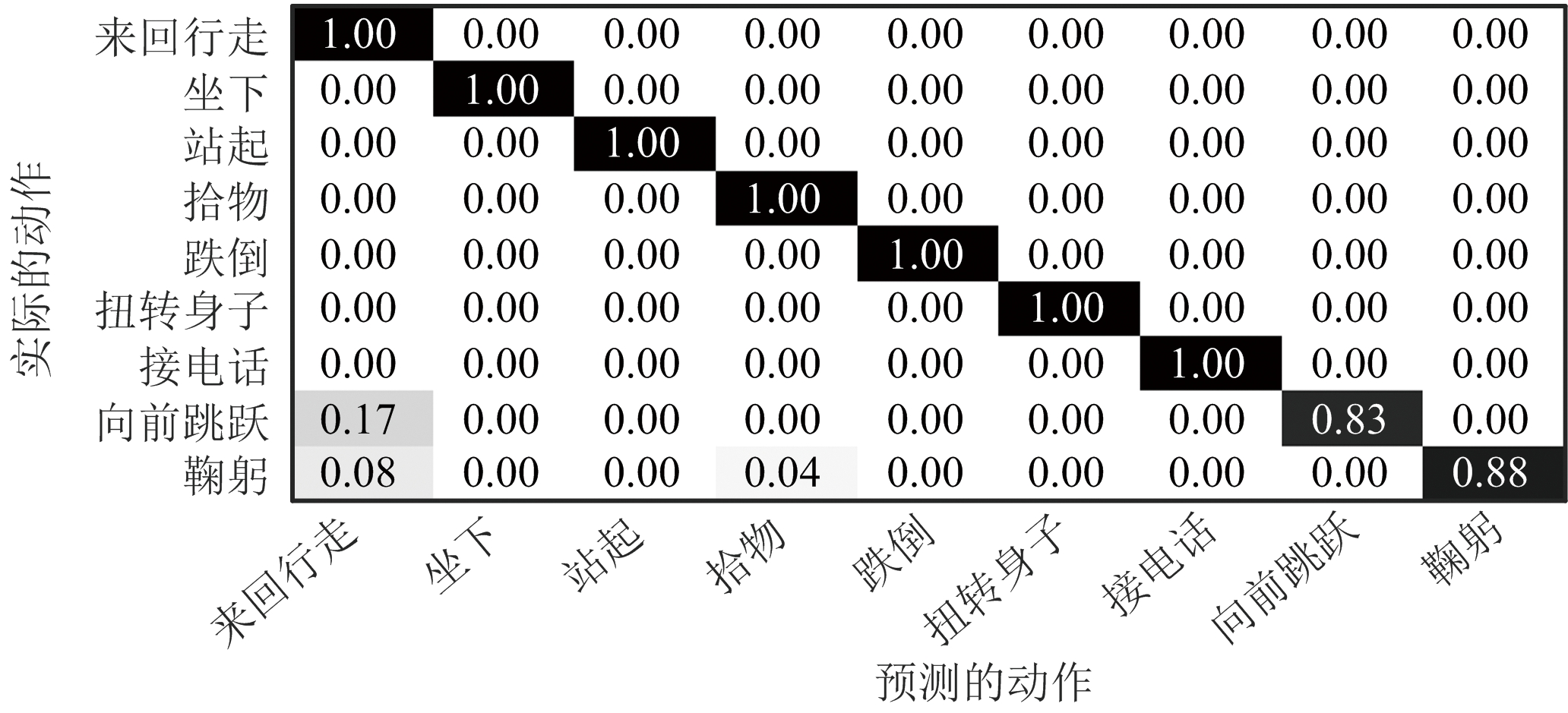
(b) 对未知个体的各动作识别混淆矩阵
图8 两种数据集划分方案下的混淆矩阵图
3.3.4 算法比对
为了检验本文所提出的基于谱图特征矢量的动作分类方法是否优于其他方案,则与英国格拉斯哥大学最新提出的用于检测动作发生的雷达微多普勒标量特征组合方案[11]进行比对。具体对比方式为:在本文实测数据集处理得到的微多普勒谱图中复现并提取该文献所提出的20个微多普勒标量特征,分类策略同本文一致。所得的对比结果如表2所述。
表2 基于本文算法与文献算法的各动作准确率比对表
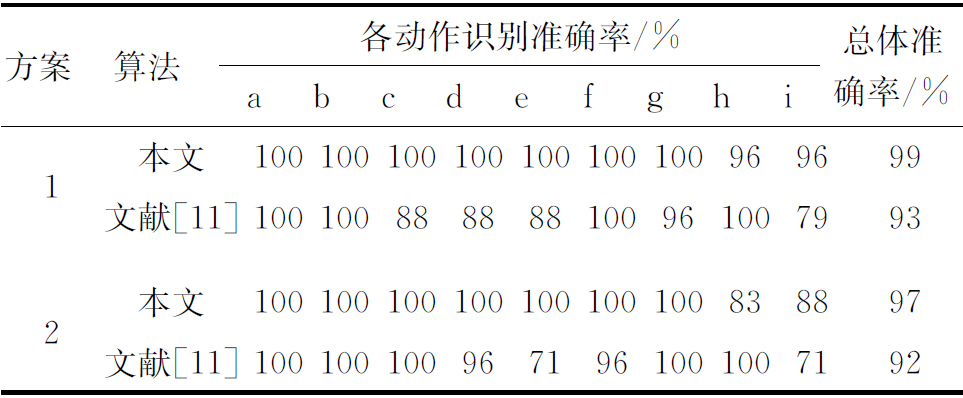
方案算法各动作识别准确率/%abcdefghi总体准确率/%1本文100100100100100100100969699文献[11]1001008888881009610079932本文100100100100100100100838897文献[11]1001001009671961001007192
对实验结果进行对比分析,可知不管是方案1还是方案2的数据集划分方式,本文算法在对各种动作进行分类上准确率更高,能更好地从人体动作微多普勒谱图中提取出本质特征。
4 结束语
本文提出一种基于77 GHz FMCW雷达的人体复杂动作识别方案。该方案从各个动作产生的微多普勒谱图中提取相应的躯干微多普勒特征矢量、肢体微多普勒特征矢量,以及经SVD分解后的用于表征谱图时间、频率相关信息的6个特征矢量,继而通过比对各种特征矢量组合经SVM分类后所得的准确率,甄选出最好的一组特征矢量组合。实验结果表明,从谱图中所提取的特征矢量都能较好地表述一个动作的发生,且最后所筛选出来的特征矢量组合(vtorso、vlimb、U1)能最大程度上对各类动作进行正确分类,其中对已知个体的各动作识别总体准确率高达99.07%,对未知个体的各动作识别总体准确率为96.76%,并将其与其他文献方案进行了对比分析,证明了本文方案的有效性。
[1] 蒋留兵,魏光萌,车俐.基于字典学习的77 GHz雷达人体动作识别[J].科学技术与工程,2020,20(6):2317-2324.
[2] 李万福.一种基于支持向量机的人类动作分类方法[J].中国新通信,2019,21(9):75-76.
[3] LI Haobo,SHRESTHA A,FIORANELLI F,et al. Multisensor Data Fusion for Human Activities Classification and Fall Detection[C]∥2017 IEEE SENSORS,Glasgow,UK: IEEE,2017:1-3.
[4] 陈亦望,靳秀海,张品,等.使用微多普勒信息识别伪装人体目标动作的新方法[J].解放军理工大学学报(自然科学版),2012,13(5):505-510.
[5] KIM Y,MOON T. Human Detection and Activity Classification Based on Micro-Doppler Signatures Using Deep Convolutional Neural Networks[J]. IEEE Geoscience and Remote Sensing Letters,2016,13(1):8-12.
[6] AHMAD A,ROH J C,WANG D,et al. Vital Signs Monitoring of Multiple People Using a FMCW Millimeter-Wave Sensor[C]∥2018 IEEE Radar Conference,Oklahoma City,OK,USA: IEEE,2018:1450-1455.
[7] SONG M,LIM J,SHIN D J. The Velocity and Range Detection Using the 2D-FFT Scheme for Automotive Radars[C]∥2014 4th IEEE International Conference on Network Infrastructure and Digital Content,Beijing: IEEE,2014:507-510.
[8] LIEN J,GILLIAN N,KARAGOZLER M E,et al. Soli: Ubiquitous Gesture Sensing with Millimeter Wave Radar[J]. ACM Trans on Graphics,2016,35(4):1-19.
[9] DE WIT J J M,HARMANNY R I A,MOLCHANOV P. Radar Micro-Doppler Feature Extraction Using the Singular Value Decomposition[C]∥2014 International Radar Conference,Lille,France: IEEE,2014:1-6.
[10] 李斌,王卫星.NCA降维和贝叶斯优化调参对分类模型的改进[J].计算机应用与软件,2019,36(8):281-287.
[11] LI Haobo,SHRESTHA A,HEIDARI H,et al. Bi-LSTM Network for Multimodal Continuous Human Activity Recognition and Fall Detection[J]. IEEE Sensors Journal,2020,20(3):1191-1201.
