0 引言
中段防御是导弹防御的关键阶段,因为它具有防御面积大、拦截时间长、弹道相对固定[1]的优点。然而当导弹在中段释放诱饵后,由于弹头、诱饵、残骸、假目标等组成包含真假目标的威胁目标群,并且以大致相同的速度和轨迹在大气层外做惯性飞行,很难用轨迹和速度上的差别来区分各目标;此外,其他各种先进突防手段的采用,也使得中段拦截导弹在目标识别上面临极大的挑战,这已经成为弹道导弹防御系统发展的一个瓶颈。但是由于弹头目标的特殊结构在特定的受力作用下会产生微动,所谓微动是指目标或目标的组成部分除了质心平动以外的振动、转动、翻滚和加速运动等微小运动。因为此运动状态常常是独一无二的,反映了目标的精细特征,所以可以用来作为目标识别的重要依据。因此,很多学者提出利用中段目标的微动特征来区分真假弹头[2-13],微动参数估计的主要途径[2]有基于时频图[3]、ISAR(Inverse Synthetic Aperture Radar)图像[4-5]、RCS(Radar Cross Section)[6-7]、高分辨距离像[8-14]等。
雷达高分辨距离像包含了目标径向的空间结构信息[15],在雷达光学区内能够较好地描述目标的散射特性,在弹道中段,因受弹头进动的影响[16-17],由多幅连续高分辨距离像构成的一维距离像序列上的散射中心位置将会发生周期性走动,其包含着目标的进动调制信息,因此可利用目标的一维距离像序列来估计目标的进动参数和形状参数。文献[8-13]以锥体目标为研究对象,其中文献[8]在利用目标一维距离像序列变化估计进动参数过程中需要已知目标的一些结构参数,而这些参数实际中是很难获取的;文献[9-10]利用散射中心在雷达视线上投影距离之间的相关性实现目标进动特征的提取;文献[11]对目标散射中心的一维投影距离进行建模,采用非线性拟合的方法估计进动和结构参数;文献[12-13]通过雷达视角的变化来实现目标进动特征的提取,其中文献[12]从时间-距离像数据实现锥体弹头散射点三维空间位置的重构,并在此基础上进行目标进动特征的提取,文献[13]利用多视角观测一维距离像序列联合获得弹道目标各个散射中心的绝对坐标;文献[14]以旋转对称锥柱体目标为研究对象,基于静态电磁散射数据,利用雷达观测视角内锥柱体各散射中心的一维距离像序列中各散射中心间的相对位置变化的极值与目标参数之间的关系来进行目标进动和结构参数的估计,不过仅从区域Ⅱ(α<β<π/2)进行考虑,且在参数估计过程中未考虑参数耦合问题。
本文从宽带雷达体制出发,以锥体目标为研究对象,针对缺少目标结构参数等先验信息及估计过程中参数耦合问题,基于高分辨距离测量提出了一种能同时估计出空间锥体目标进动参数和形状参数的方法,仿真表明该方法可行、有效。文中第二部分对锥体目标的进动模型进行分析,得出目标姿态角随时间变化的关系式,进而得出目标径向长度序列与姿态角关系式;第三部分对如何从回波信号中提取径向长度序列作了详细介绍;第四部分给出了本方法的具体实现步骤及推导过程;第五部分通过仿真计算验证了该方法的可行性和有效性。
1 锥体目标进动模型
弹道导弹的弹头外形一般较常见的有平底锥弹头、球底锥弹头、平底锥柱弹头及球底锥柱弹头4种,本文主要对平底锥弹头进行分析,其结构如图1所示,其中α为目标半锥角,b为目标斜边长度,R为底面半径,1、2、3表示弹头目标的3个散射中心。
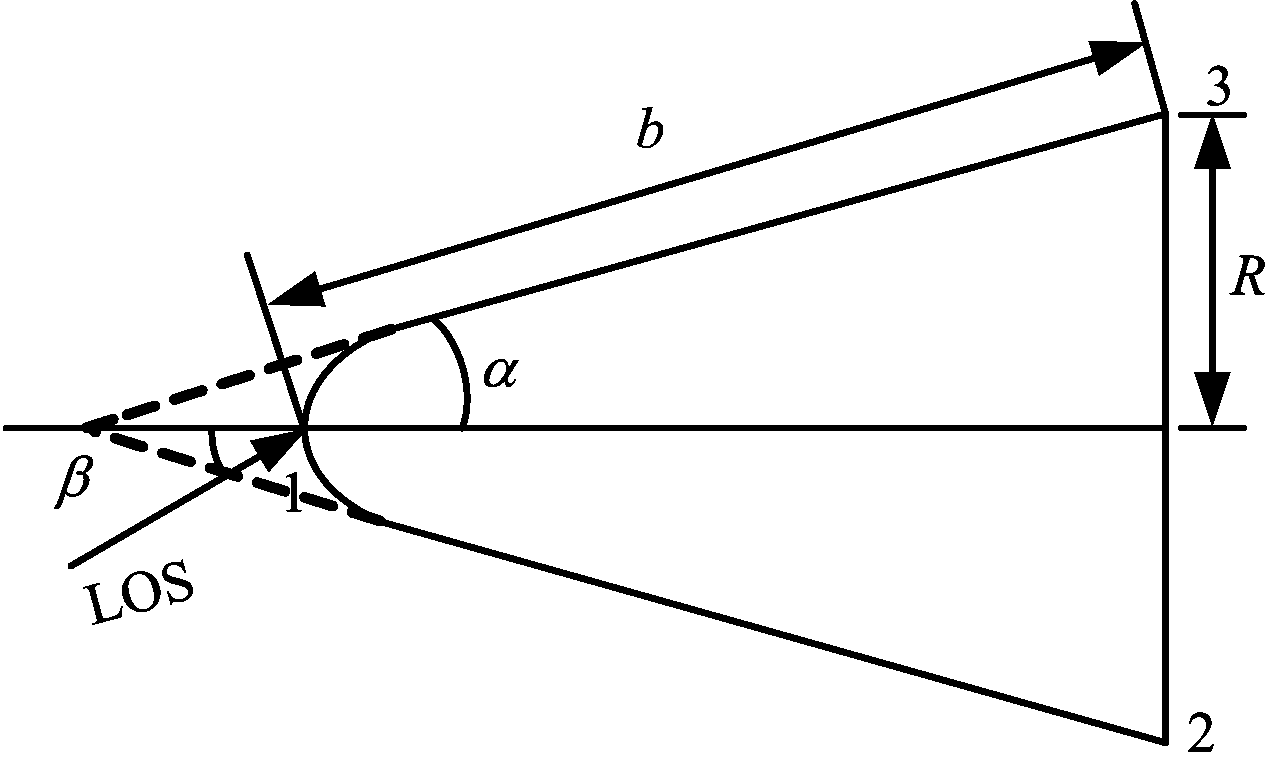
图1 锥体目标结构图
在弹道导弹飞行过程中,为了保证飞行的平稳性和命中的精度,弹头目标会采用自旋的方式定向,而在诱饵释放、弹箭分离时,弹头目标不可避免地会受到横向扰动,进而产生进动,称为微动。由于诱饵、假目标、残骸等其他空间目标无姿态控制系统,故不会具有规律的微动特性。弹头目标的规律微动特性导致姿态角,即雷达视线与目标自旋轴的夹角,呈现周期变化。姿态角的变化规律同目标的进动参数有关,但是姿态角一般不易直接测量得到。另一方面,如果不考虑目标的平动,姿态角的周期变化会导致空间进动锥体目标的径向长度序列呈现规律变化,其变化规律同锥体目标的形状参数和进动参数有关,其中,某次观测中锥体目标的径向长度序列,是指通过该次观测中的各次回波计算出的锥顶散射中心和锥底散射中心的径向距离的差值,并由这些差值组成的序列。因此可以利用弹头目标特有的微动特性来提取弹头目标的进动参数和形状参数。
根据以上分析,可建立弹道中段锥体目标进动模型[9]如图2所示,Oxcyczc坐标系为平动坐标系,Oxsyszs坐标系为随体坐标系,弹头绕其对称轴Ozs以角速度Ω作自旋运动,同时轴Ozs绕轴Ozc以角速度ω进动,进动角为θ,故zs为自旋轴,zc为进动轴,γ为雷达视线与进动轴夹角,即俯仰角,ω为进动角频率,β为雷达视线与自旋轴夹角,即姿态角,LOS是指雷达视线方向。根据图2所示的锥体目标的进动模型,可以得到第k次观测锥体目标的姿态角随时间t变化的表达式为
βk(t)=arccos[cosθkcosγk+
sinθksinγkcos(ωt+φk)]
(1)
式中,γk为第k次观测的俯仰角,θk为第k次观测的进动角,φk为第k次观测的进动初相角,k=1,2。
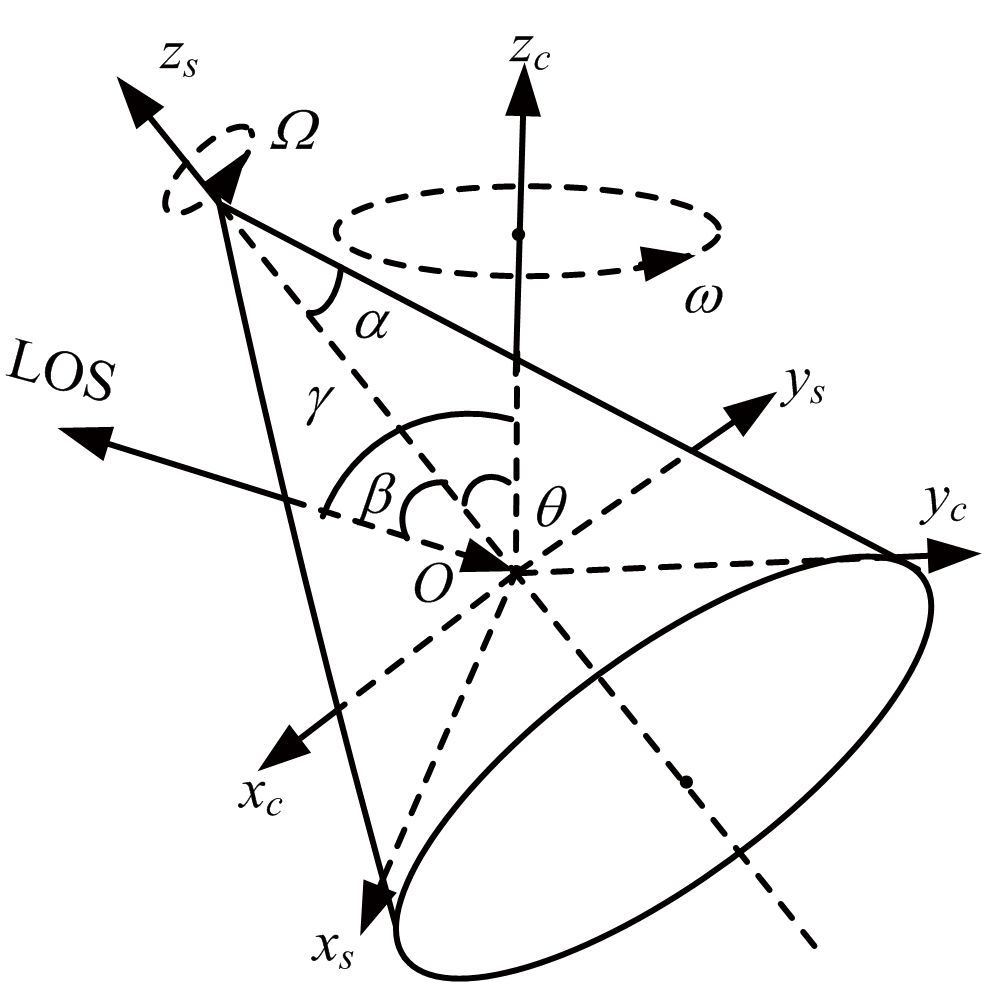
图2 锥体目标进动模型
实际雷达探测目标时一般迎着锥顶照射锥体目标,且锥形弹头和诱饵的半锥角较小,一般取 5°~15°,此时可认为锥体目标进动时姿态角β< π-α,在这一角度范围内,钝头锥对应散射中心1与2均一直可见[9]。根据上述姿态角随时间变化的表达式,可以求出第k次观测中锥体目标的径向长度序列的表达式为
Lk(n)=bcos(βk(tkn)+α)
(2)
式中,tkn表示第k次观测第n个回波的时刻,n=1,2,…,N,N为每次观测的回波数目。
2 径向长度序列提取
当目标运动速度不高时,可以认为在一个脉冲持续时间内,目标到雷达站的距离不变,即所谓的“停-跳”假设;但对于高速机动目标,如导弹目标,上述假设不再成立,此时应当首先估计每次观测时目标的轨道运动信息。令第k次观测中第i个回波时,目标到雷达站距离的表达式为
Rki(t)=Rki0+fki(t)
(3)
式中,Rki0为参考时刻目标距雷达站的距离,fki(t)为第k次观测第i个回波中目标的轨道运动表达式。下面对所获得的宽带回波信号进行平动补偿,具体方法如下:
令第k次观测中第i个回波对应的雷达发射信号的表达式为
ski(t)=pki(t)ej2πf0t=|pki(t)|ejφki(t)ej2πf0t
(4)
式中,k=1,2,i=1,2,…,N,f0为载频,c为电磁波的传播速度,pki(t)为发射信号的复包络,|pki(t)|为pki(t)的幅度,φki(t)为pki(t)的相位,|·|表示求模运算。则该次回波信号解调后的表达式为
srki(t)=Apki(t-τki(t))e-j2πf0τki(t)=
A|pki(t-τki(t))|ejφki(t-τki(t))e-j2πf0τki(t)
(5)
式中,τki(t)=2Rki(t)/c,A为该次回波信号的幅度。将目标到雷达站的距离表达式代入式(5),则该次回波的表达式可以写作:
srki(t)=Apki(t-τki(t))e-j2πf0τki(t)=
A|pki(t-τki(t))|ejφki(t-τki(t))·
e-j2πf0τki(t)=
![]() ·
·
A|pki(t-τki(t))|ejφki1(t)·
(6)
式中,ejφki2(t)为![]() 中与目标平动信息有关的项,ejφki1(t)为
中与目标平动信息有关的项,ejφki1(t)为![]() 中与目标平动信息无关的项,ejφki2(t)和ejφki1(t)的具体表达式取决于发射信号的形式。对该次回波进行平动补偿,即将该次回波解调后的信号相位中和目标平动信息有关的项抵消掉,即对srki(t)乘上e-jφki2(t)·
中与目标平动信息无关的项,ejφki2(t)和ejφki1(t)的具体表达式取决于发射信号的形式。对该次回波进行平动补偿,即将该次回波解调后的信号相位中和目标平动信息有关的项抵消掉,即对srki(t)乘上e-jφki2(t)·![]() 令scki(t)为该次回波平动补偿后的信号,则
令scki(t)为该次回波平动补偿后的信号,则
(7)
至此,完成了对宽带回波信号的平动补偿,下面依次对各信号用MUSIC算法[16]作参数估计,提取强散射中心的距离,并形成散射中心距离历程图(一维距离像序列),其中,散射中心距离历程图是指横坐标为各次回波的时刻,纵坐标为各次回波中强散射中心的距离的图像。然后运用图像边缘检测方法[17],从散射中心距离历程图提取各次回波时刻锥顶散射中心和锥底散射中心的径向距离的差值,这些差值组成的序列即为锥体目标的径向长度序列,并将第一次观测的径向长度序列记为L1(n),第二次观测的径向长度序列记为L2(n),其中,n=1,2,…,N。
3 参数估计
对所观测到的一维距离像序列进行散射中心提取后,假设已经把散射中心1与2对应散射中心关联起来,得到它们之间的位置差估计![]() 将
将![]() 的最大值记为limax,最小值记为limin(i=1,2)。下面设第一次观测时,雷达视线方向在平动坐标系中的俯仰角是γ1,第二次观测时,雷达视线方向在平动坐标系中的俯仰角是γ2,目标的半锥角为α,进动角为θ。根据三角关系,可知当目标雷达视线方向在平动坐标系中的俯仰角大于目标的进动角,即γ>θ时,有以下关系式成立:
的最大值记为limax,最小值记为limin(i=1,2)。下面设第一次观测时,雷达视线方向在平动坐标系中的俯仰角是γ1,第二次观测时,雷达视线方向在平动坐标系中的俯仰角是γ2,目标的半锥角为α,进动角为θ。根据三角关系,可知当目标雷达视线方向在平动坐标系中的俯仰角大于目标的进动角,即γ>θ时,有以下关系式成立:
l1max=bcos[(γ1+α)-θ]=
bcos(γ1+α)cosθ+bsin(γ1+α)sinθ
(8)
l1min=bcos[(γ1+α)+θ]=
bcos(γ1+α)cosθ-bsin(γ1+α)sinθ
(9)
l2max=bcos[(γ2+α)-θ]=
bcos(γ2+α)cosθ+bsin(γ2+α)sinθ
(10)
l2min=bcos[(γ2+α)+θ]=
bcos(γ2+α)cosθ-bsin(γ2+α)sinθ
(11)
进一步有以下关系成立:
l1max+l1min=2bcos(γ1+α)cosθ
(12)
l1max-l1min=2bsin(γ1+α)sinθ
(13)
l2max+l2min=2bcos(γ2+α)cosθ
(14)
l2max-l2min=2bsin(γ2+α)sinθ
(15)
为进一步推导方便,令a11=l1max+l1min,a12=l1max-l1min,a21=l2max+l2min,a22=l2max-l2min。所以有
(a11sinθ)2+(a12cosθ)2=4b2sin2θcos2θ
(16)
(a21sinθ)2+(a22cosθ)2=4b2sin2θcos2θ
(17)
因此可以解得
(18)
(19)
(20)
若根据雷达对目标的跟踪信息,可以估计得到![]() 则可进一步估计得到
则可进一步估计得到![]() 如果没有利用跟踪信息得到的
如果没有利用跟踪信息得到的![]() 也可用其他方法进一步估计
也可用其他方法进一步估计![]() 和
和![]() 具体方法将稍后给出。然而当目标雷达视线方向在平动坐标系中的俯仰角小于目标的进动角,即γ<θ时,情况变得较为复杂。在这种条件下有以下关系式成立:
具体方法将稍后给出。然而当目标雷达视线方向在平动坐标系中的俯仰角小于目标的进动角,即γ<θ时,情况变得较为复杂。在这种条件下有以下关系式成立:
l1max=bcos[(θ+α)-γ1]=
bcos(θ+α)cosγ1+bsin(θ+α)sinγ1
(21)
l1min=bcos[(γ1+α)+θ]=
bcos(θ+α)cosγ1-bsin(θ+α)sinγ1
(22)
l2max=bcos[(θ+α)-γ2]=
bcos(θ+α)cosγ2+bsin(θ+α)sinγ2
(23)
l2min=bcos[(θ+α)+γ2]=
bcos(θ+α)cosγ2-bsin(θ+α)sinγ2
(24)
进一步有以下关系成立:
l1max+l1min=2bcos(θ+α)cosγ1
(25)
l1max-l1min=2bsin(θ+α)sinγ1
(26)
l2max+l2min=2bcos(θ+α)cosγ2
(27)
l2max-l2min=2bsin(θ+α)sinγ2
(28)
为进一步推导方便,令a11=l1max+l1min,a12=l1max-l1min,a21=l2max+l2min,a22=l2max-l2min。所以有
[a11sin(θ+α)]2+[a12cos(θ+α)]2=
4b2sin2(θ+α)cos2(θ+α)
(29)
[a21sin(θ+α)]2+[a22cos(θ+α)]2=
4b2sin2(θ+α)cos2(θ+α)
(30)
因此可以解得
(31)
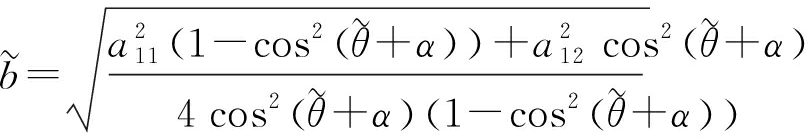
(32)
(33)
(34)
通过以上分析可知,当雷达视线方向在平动坐标系中的俯仰角γ大于目标的进动角θ时,可以估计得到![]() 但目标的半锥角α与γ耦合在一起;而当γ<θ时,可以估计得到
但目标的半锥角α与γ耦合在一起;而当γ<θ时,可以估计得到![]() 而α与θ耦合在一起。而且在实际中,我们并不能事先知道是γ>θ还是γ<θ成立,因此需要采用进一步的处理来完成对目标进动和形状参数的完整估计。在以上的两种情况下,都可以获得目标斜边长度的估计
而α与θ耦合在一起。而且在实际中,我们并不能事先知道是γ>θ还是γ<θ成立,因此需要采用进一步的处理来完成对目标进动和形状参数的完整估计。在以上的两种情况下,都可以获得目标斜边长度的估计![]() 根据式(2)可获得雷达视线在目标随体坐标系中的姿态角变化规律。
根据式(2)可获得雷达视线在目标随体坐标系中的姿态角变化规律。
(35)
由于估计中存在半锥角α,在估计其他两个角参数时希望去掉它的影响,而对![]() 求一阶导数就可以去掉α。
求一阶导数就可以去掉α。
(36)
且![]() 为了方便进一步的推导,不直接对
为了方便进一步的推导,不直接对![]() 进行运算,而是对它的平方进行运算。令辅助函数h(t)=
进行运算,而是对它的平方进行运算。令辅助函数h(t)=![]() 则
则
(37)
令x=cos ωt,则有
(38)
以下来分析h的变化规律:
1) 当x=±1,即ωt=kπ时,h取最小值0。
2) 下面分析h何时取得极大值。根据求极值原理可知当h对x的一阶偏导为0时h可以取得极大值。
令a(x)=sin2γsin2θ(1-x2),b(x)=1-![]() ,则
,则![]() 时h取得极大值,那么
时h取得极大值,那么![]() 进而可得
进而可得![]() 时,h(t)取得极大值。其中h(t)的极大值是可以根据观测得到的,根据以上的分析,γ>θ时可以得到
时,h(t)取得极大值。其中h(t)的极大值是可以根据观测得到的,根据以上的分析,γ>θ时可以得到![]() 而γ<θ时可得到
而γ<θ时可得到![]() 那么只要得到h(t)取得极大值时的x,就可以得到另一个未知参数的估计。因为目标的进动周期是容易估计得到的[11,13],而且也已分析过ωt=kπ时 h(t)取得极小值0,所以根据h(t)取极大值和0值之间的时间长度,就可估计h(t)取极大值时的x=cosωt的取值,进而估计得到另一个未知参数,也就可以进一步估计出目标的半锥角α,下面以
那么只要得到h(t)取得极大值时的x,就可以得到另一个未知参数的估计。因为目标的进动周期是容易估计得到的[11,13],而且也已分析过ωt=kπ时 h(t)取得极小值0,所以根据h(t)取极大值和0值之间的时间长度,就可估计h(t)取极大值时的x=cosωt的取值,进而估计得到另一个未知参数,也就可以进一步估计出目标的半锥角α,下面以![]() 为例给出目标进动角、半锥角和斜边长度的估计表达式。
为例给出目标进动角、半锥角和斜边长度的估计表达式。
如果![]() 则
则
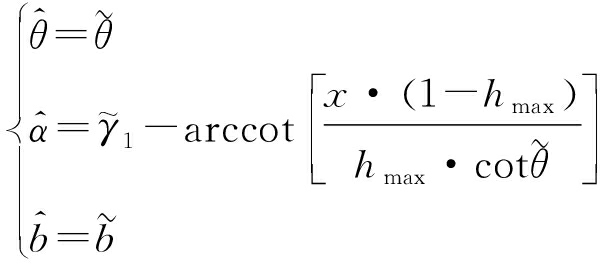
(39)
如果![]() 则
则
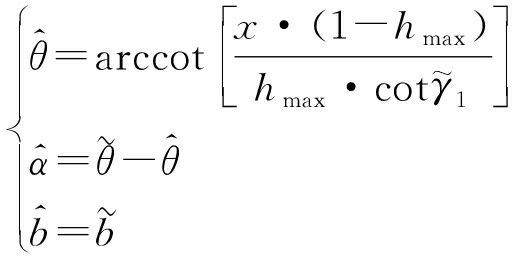
(40)
至此,我们完成了对目标进动角、半锥角及斜边长度的估计,其计算流程如图3所示。
4 仿真与分析
实验所观测的锥体目标如图1所示,其形状参数为:目标半锥角α=14°,目标斜边长度b=1 m,底面半径R=0.25 m;进动参数为:进动角θ=10°,进动角频率ω=31.4 rad/s。第一次观测的俯仰角γ1=37°,第二次观测的俯仰角γ2=37.2°。实验所用数据为空间进动锥体目标电磁仿真数据,测量频带为9~11 GHz,频点间隔为0.02 GHz。假定目标回波中的观测噪声为高斯白噪声,观测信噪比SNR的定义为
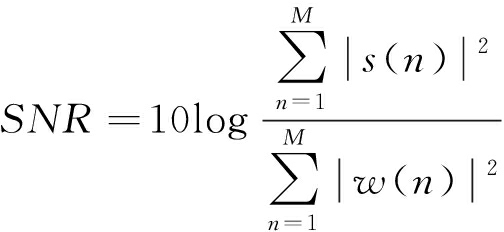
(41)
式中,![]() 为目标回波中的信号分量,
为目标回波中的信号分量,![]() 为目标回波中的噪声分量,M为每次回波的采样点数。
为目标回波中的噪声分量,M为每次回波的采样点数。
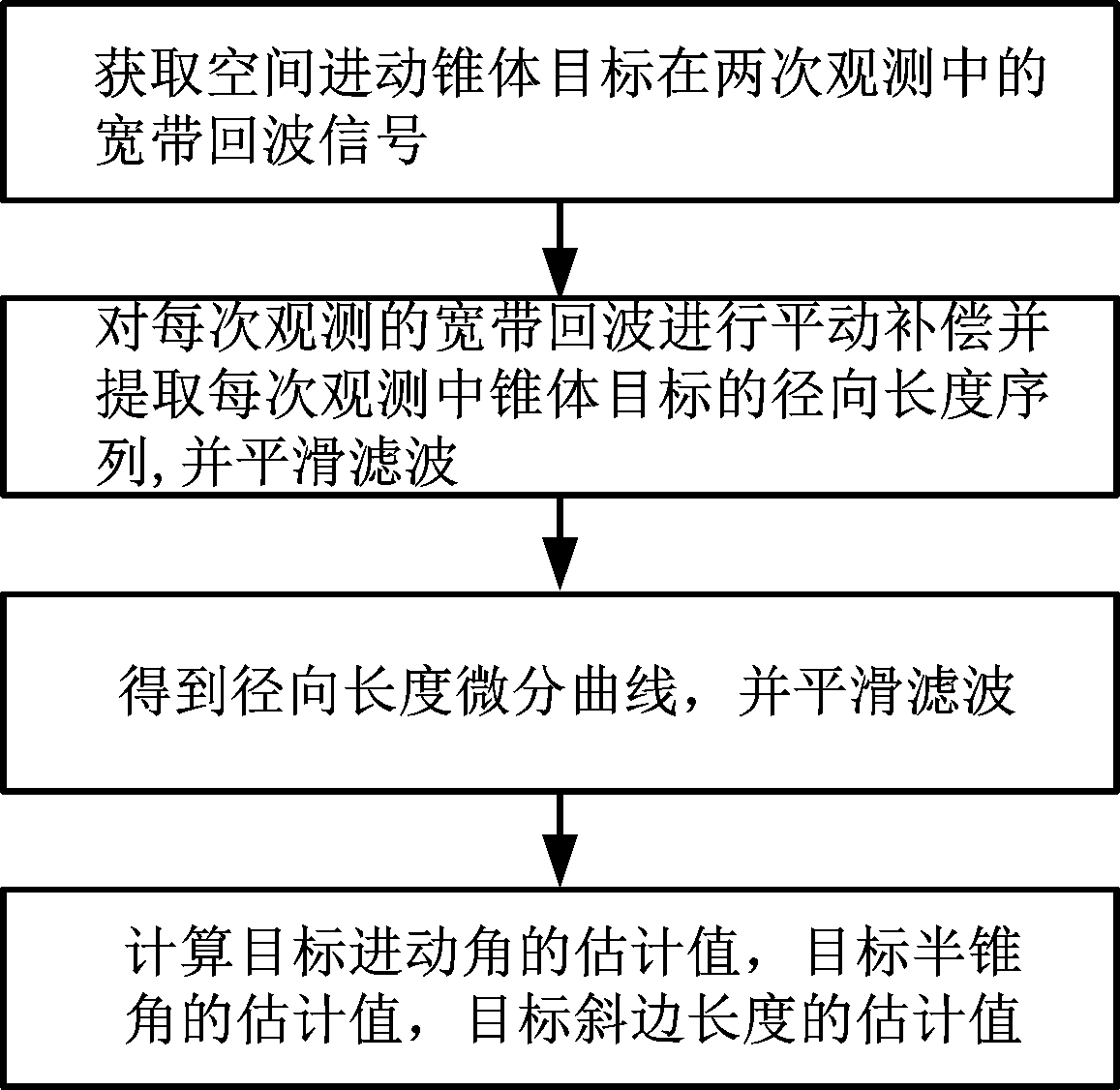
图3 方法流程图
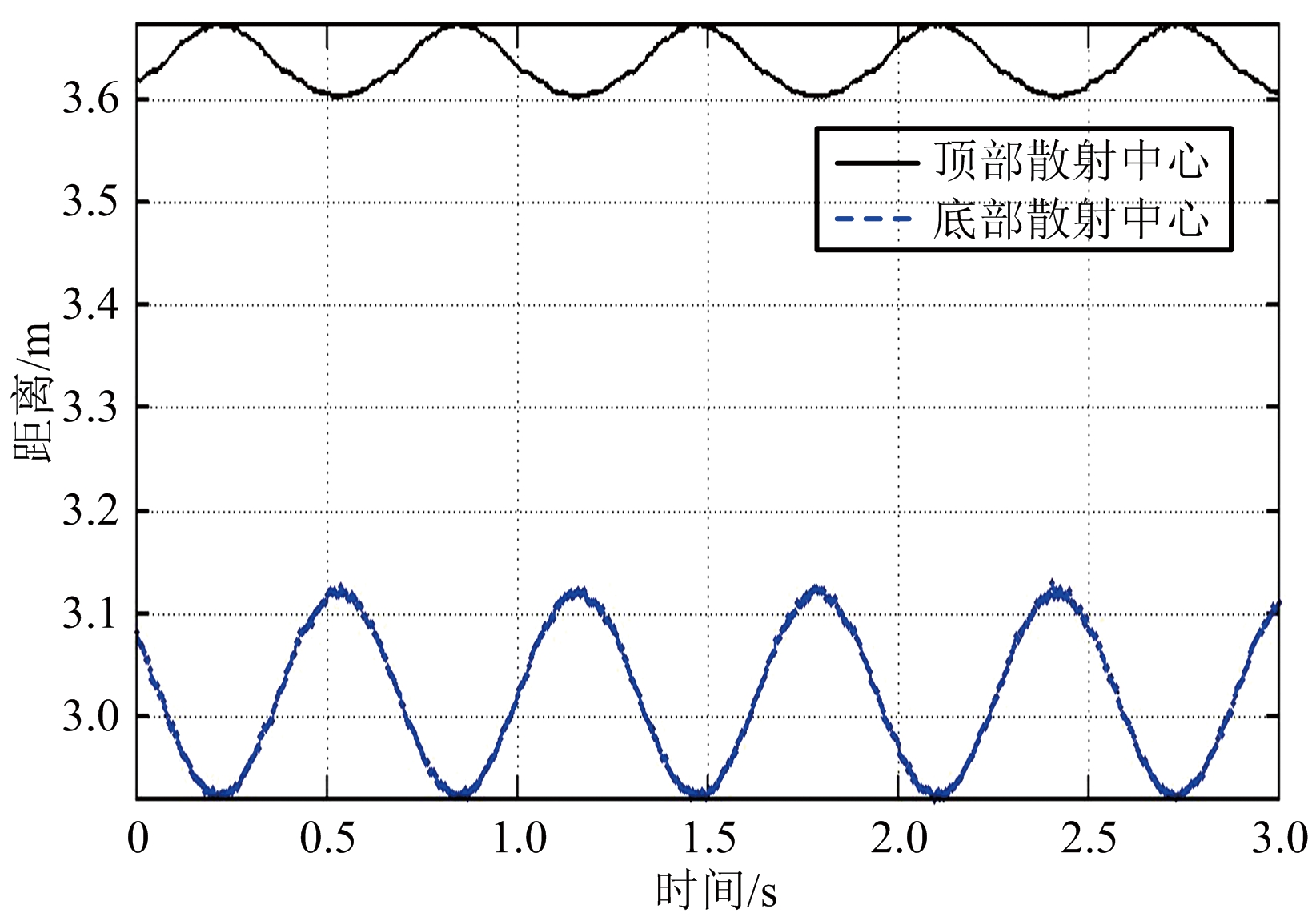
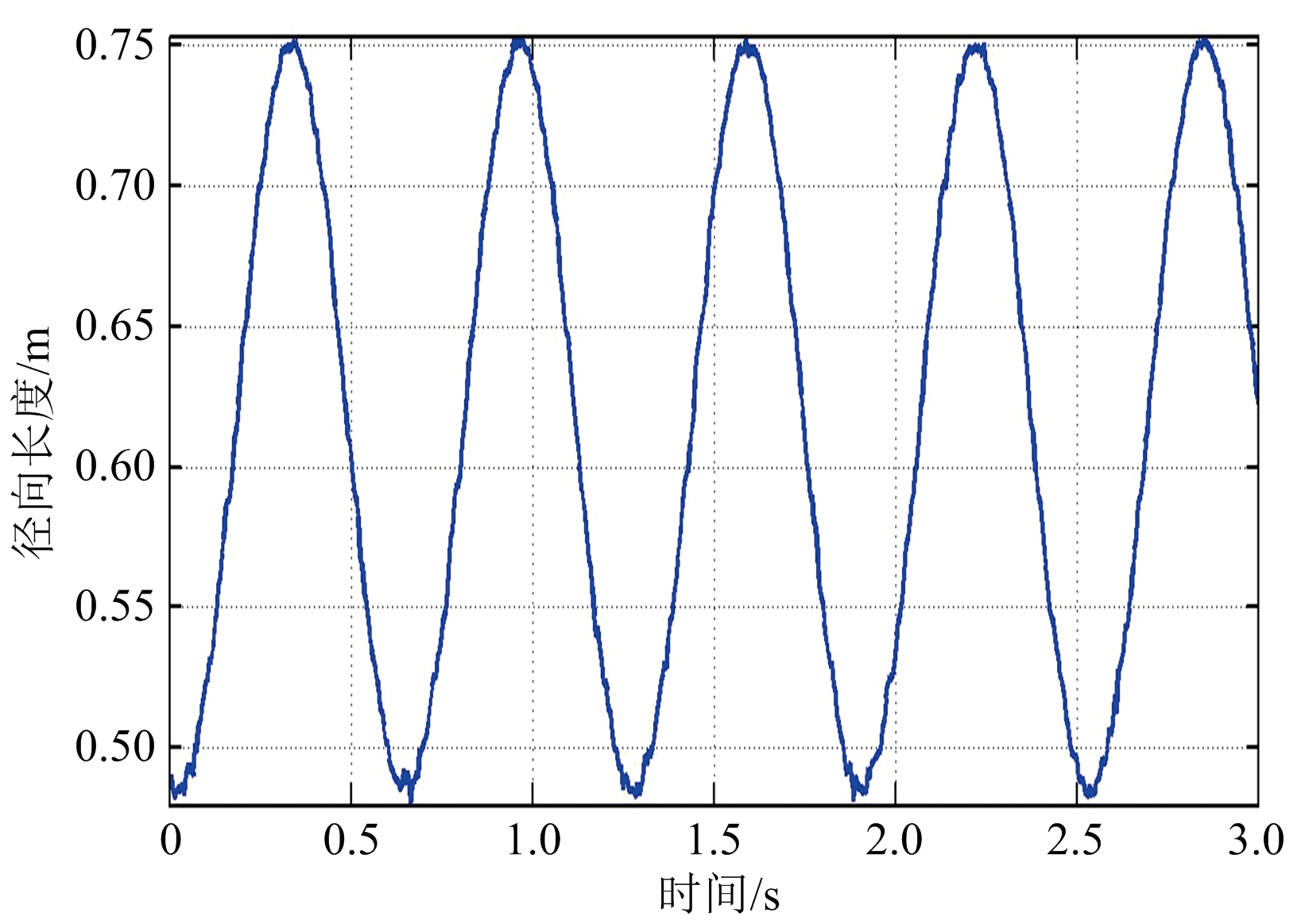
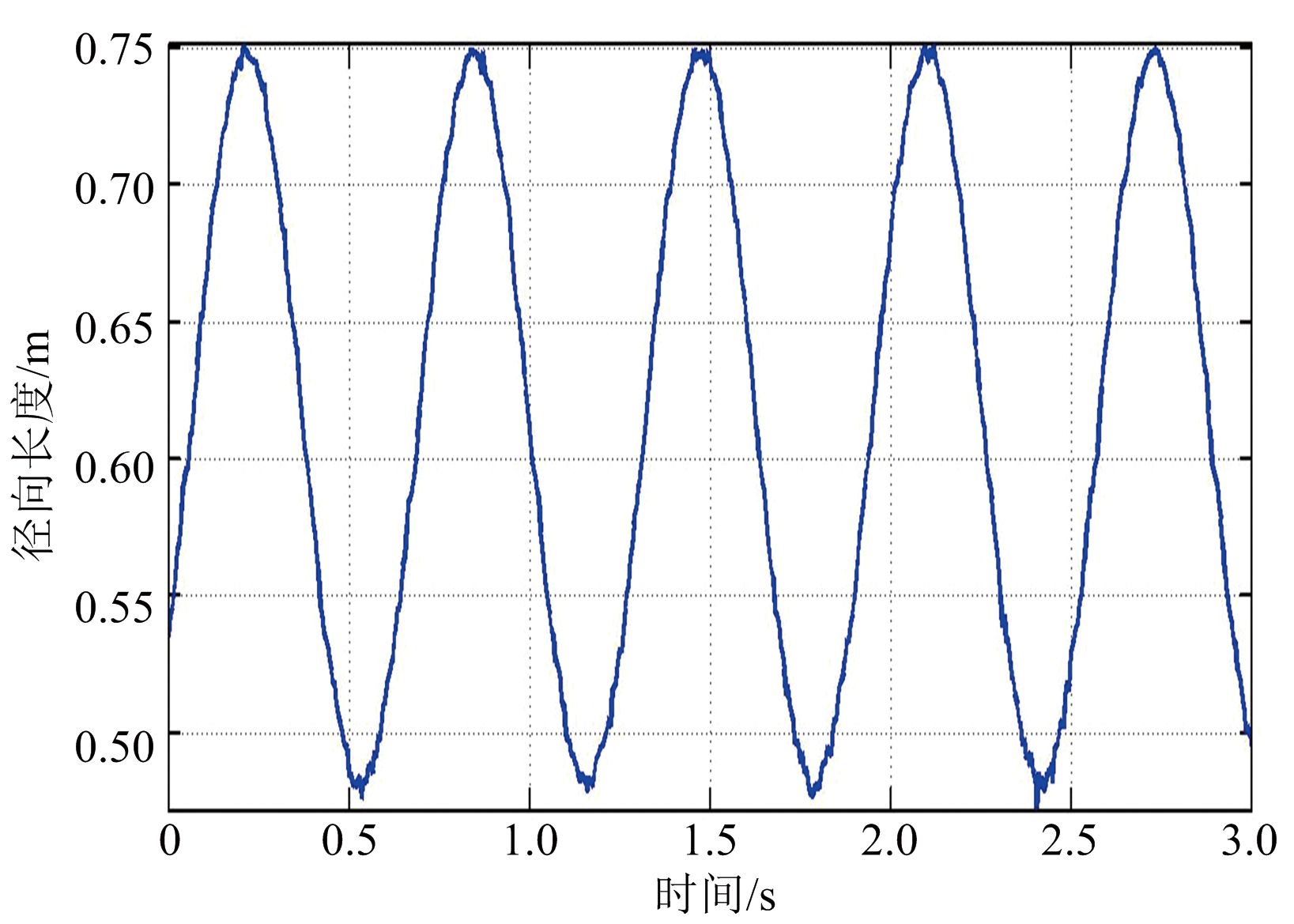
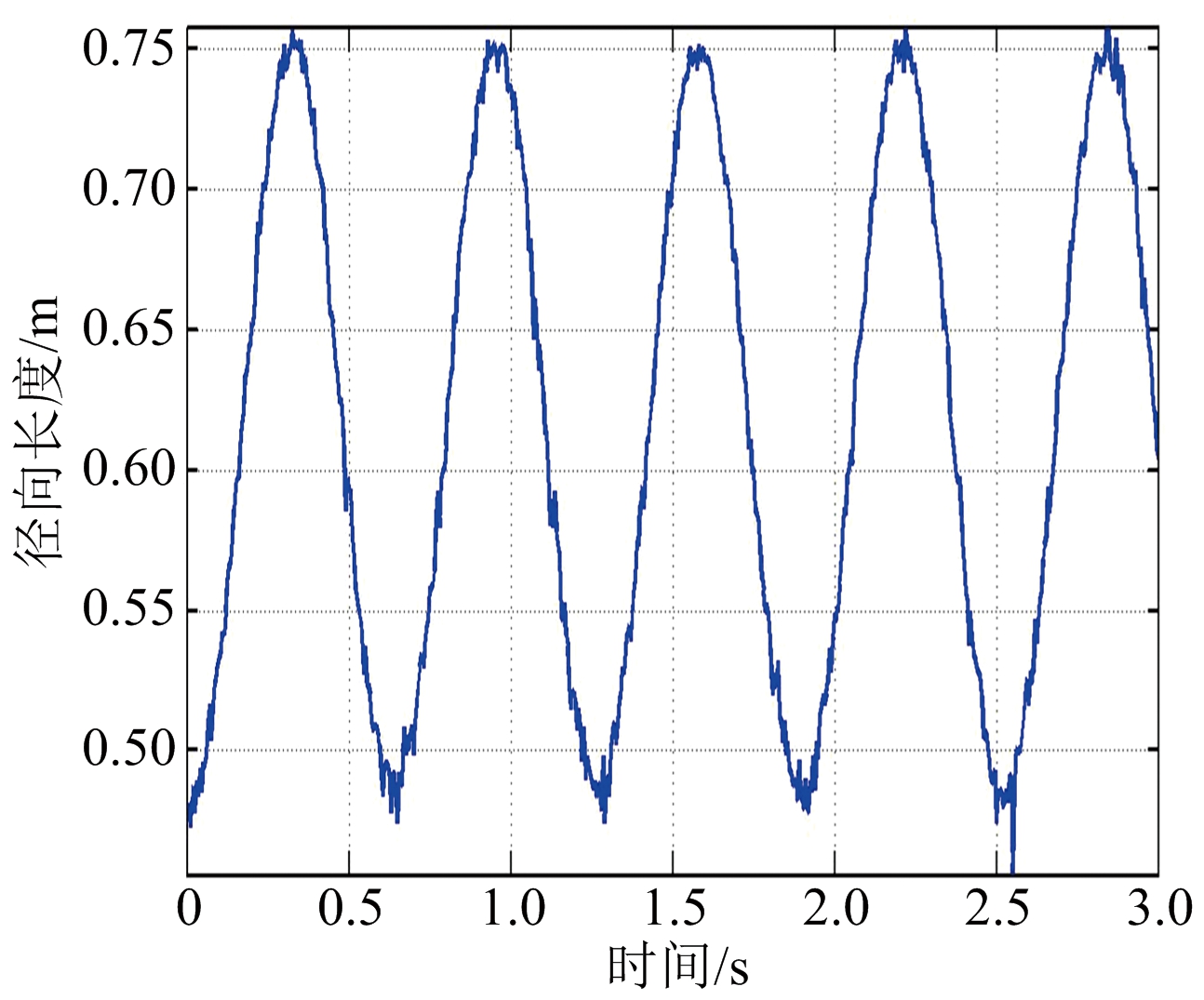
首先在观测信噪比20 dB条件下进行仿真实验,得如下结果:图4(a)为第一次观测所得的目标锥顶、锥底散射中心的一维距离像序列,图4(b)为第二次观测所得的目标锥顶、锥底散射中心的一维距离像序列,图4(c)、(d)分别为第一、二次观测所得的锥体目标径向长度序列。从图中可以看出,散射点对应的一维距离像序列与径向长度序列均呈正弦规律变化,且频率一致,这与前述分析一致,故可通过这种规律性变化来进行目标形状和进动参数估计;另外,从图中还可以看出此时所得的径向长度序列曲线有毛刺,并且信噪比越低,毛刺越多,即抖动越大,这是因为信噪比较低时,距离估计精度比较差。图5以第一次观测为例,给出了不同信噪比条件下目标径向长度序列曲线。
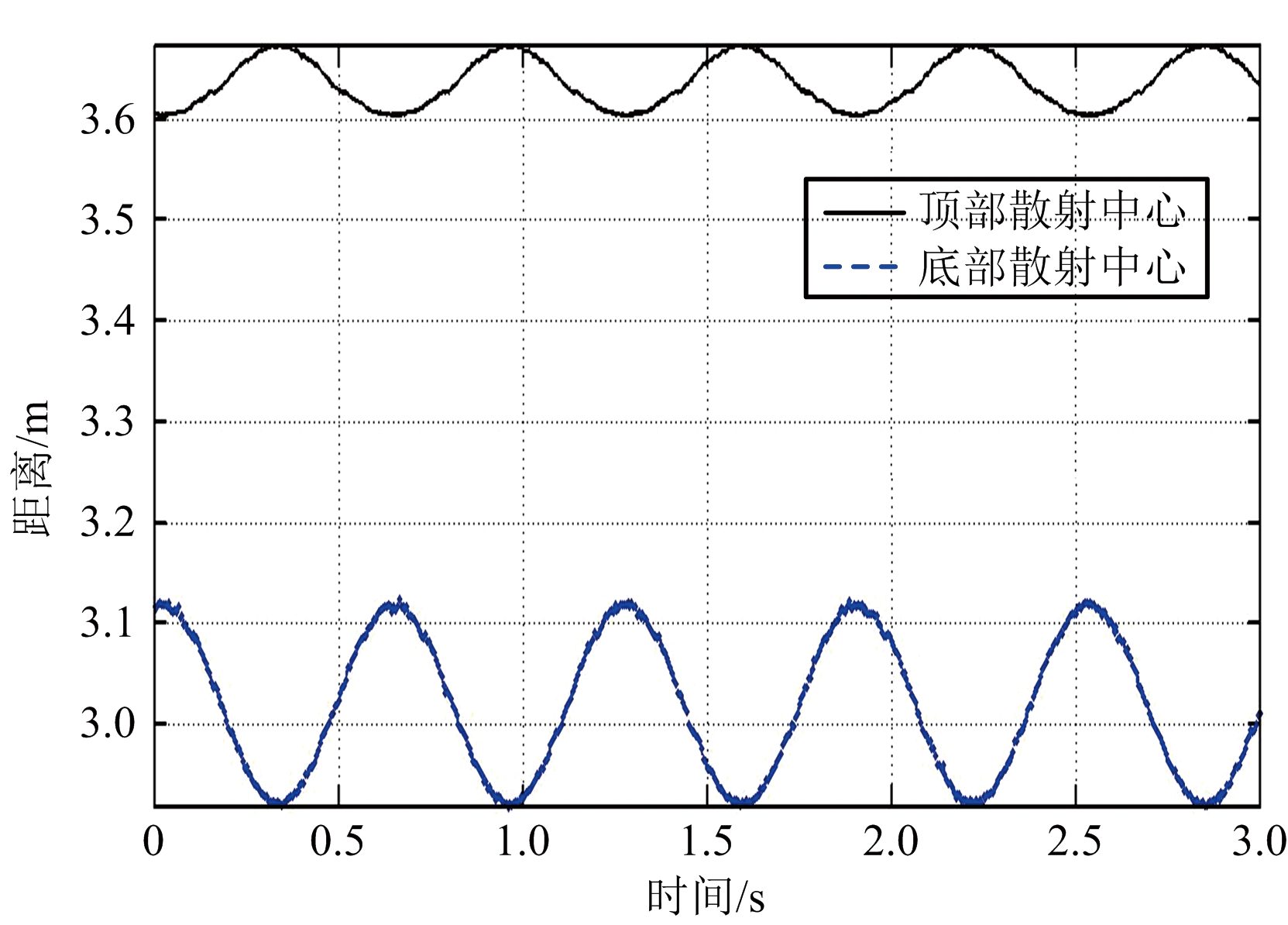
(a) 第一次观测得到的散射中心一维距离像序列
(b) 第二次观测得到的散射中心一维距离像序列
(c) 第一次观测得到的径向长度序列
(d) 第二次观测得到的径向长度序列
图4 锥体目标一维距离像及径向长度序列
(a) SNR=15 dB
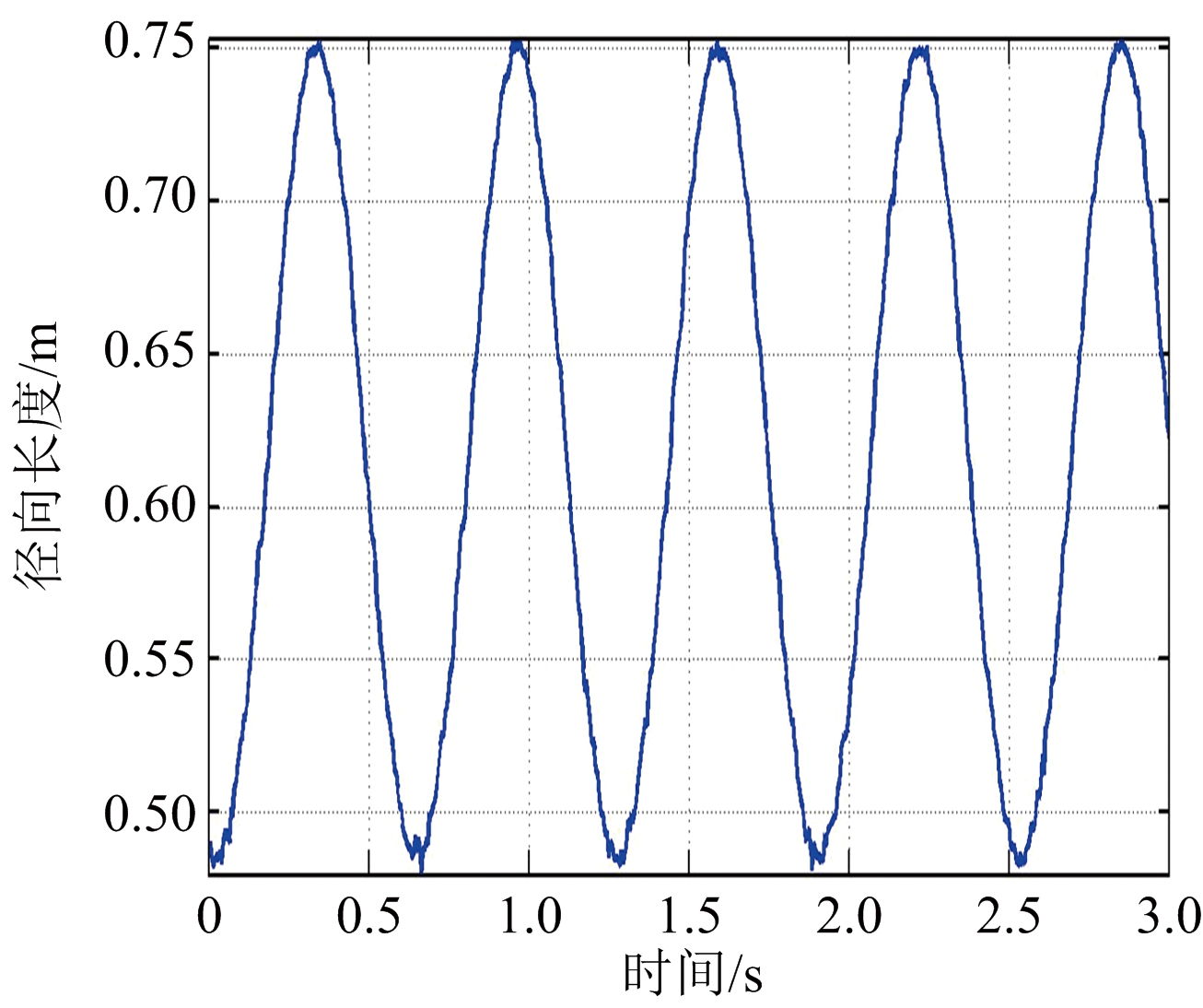
(b) SNR=20 dB
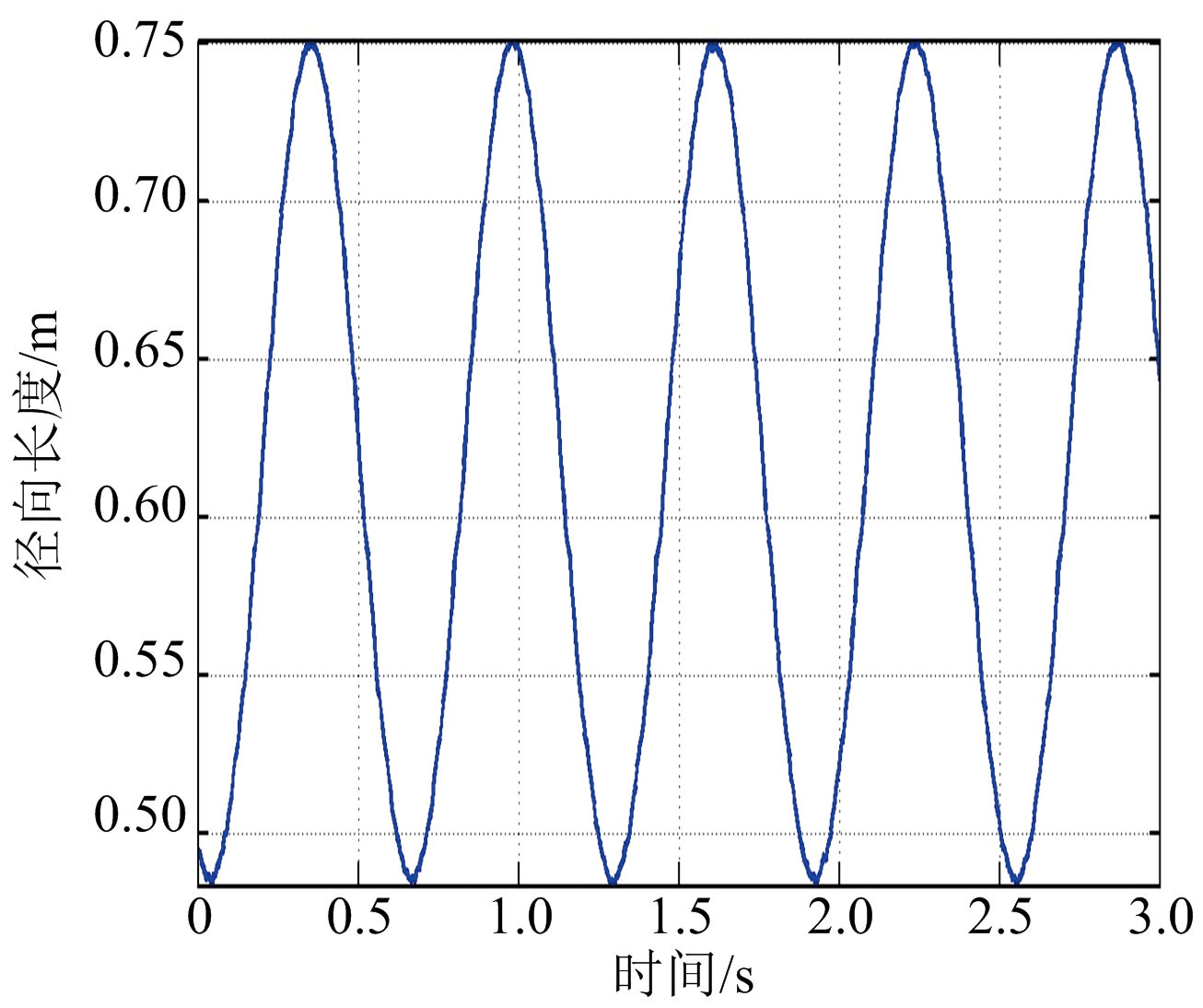
(c) SNR=25 dB
图5 不同信噪比下的径向长度序列曲线
针对径向长度序列毛刺问题,可采用低通滤波器对其进行平滑处理,所得结果如图6所示,其中图6(a)为第一次观测时锥体目标的平滑滤波后的径向长度序列曲线,图6(b)为第二次观测时锥体目标的平滑滤波后的径向长度序列曲线。图7(a)为锥体目标径向长度微分曲线,图7(b)为锥体目标径向长度微分曲线平滑滤波后的结果图。最后由式(39)、式(40)得到观测信噪比为20 dB时目标进动角、半锥角和斜边长度分别为:![]()
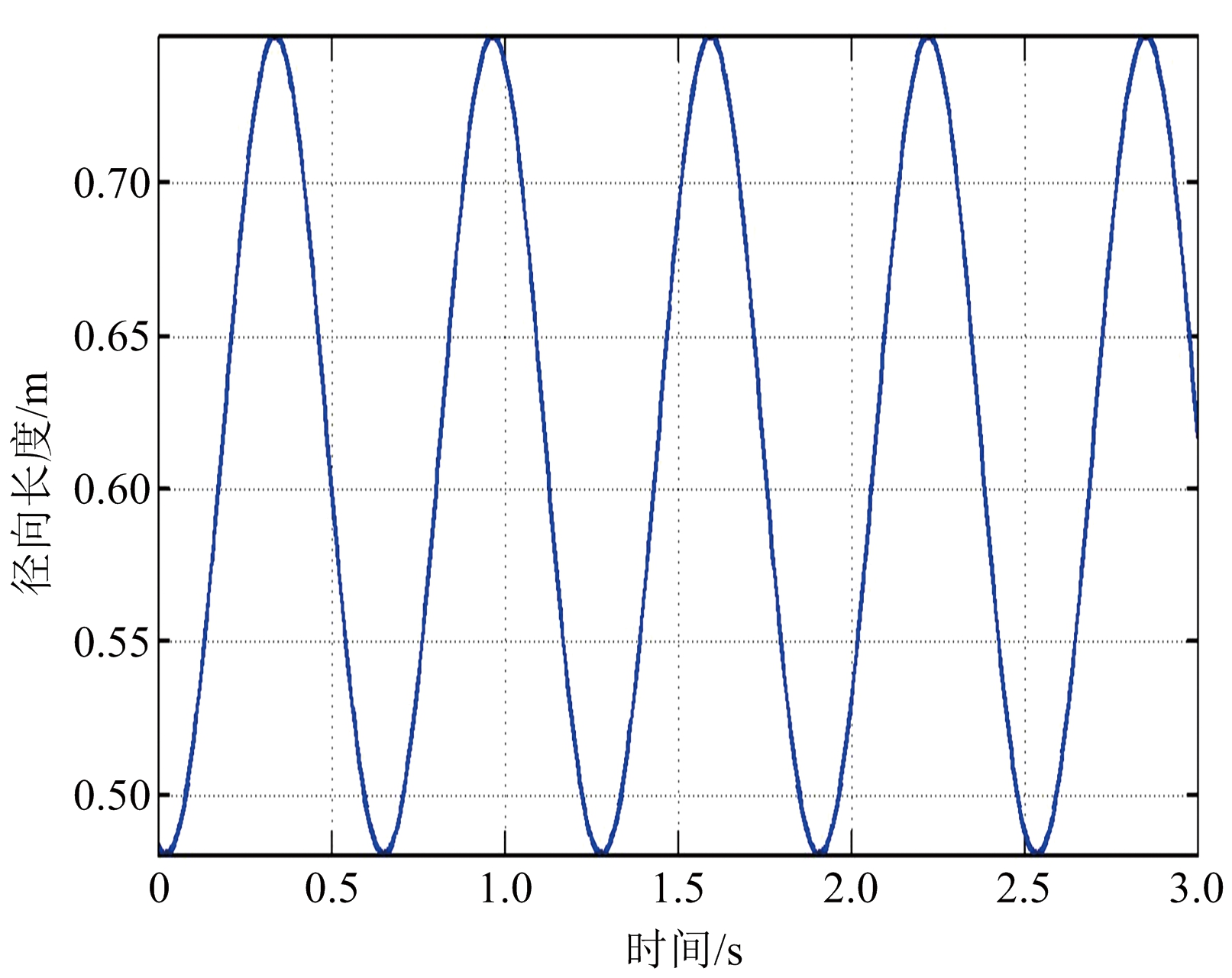
(a) 第一次观测得到的平滑滤波后的径向长度距离曲线
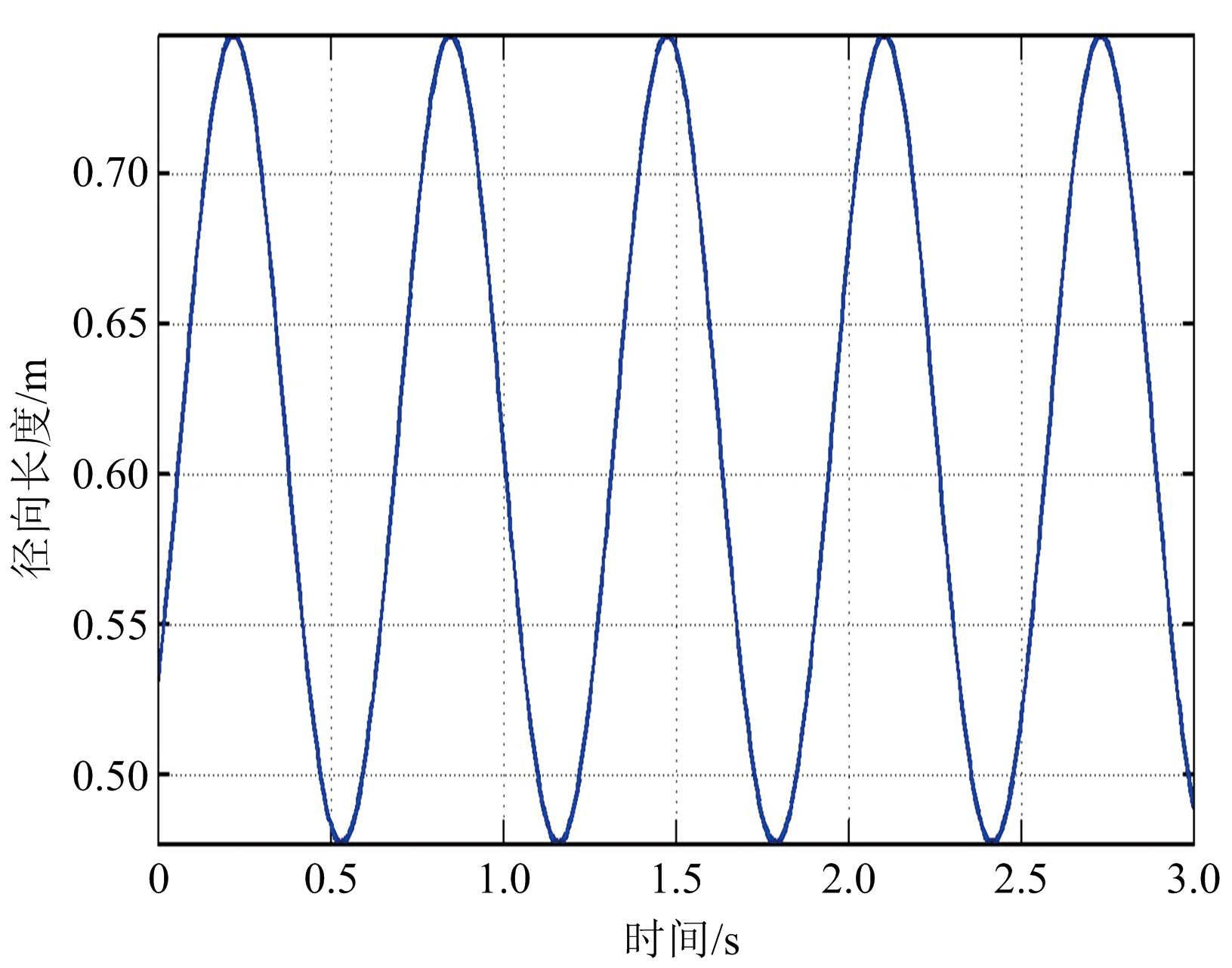
(b) 第二次观测得到的平滑滤波后的径向长度距离曲线
图6 平滑滤波后的径向长度序列曲线
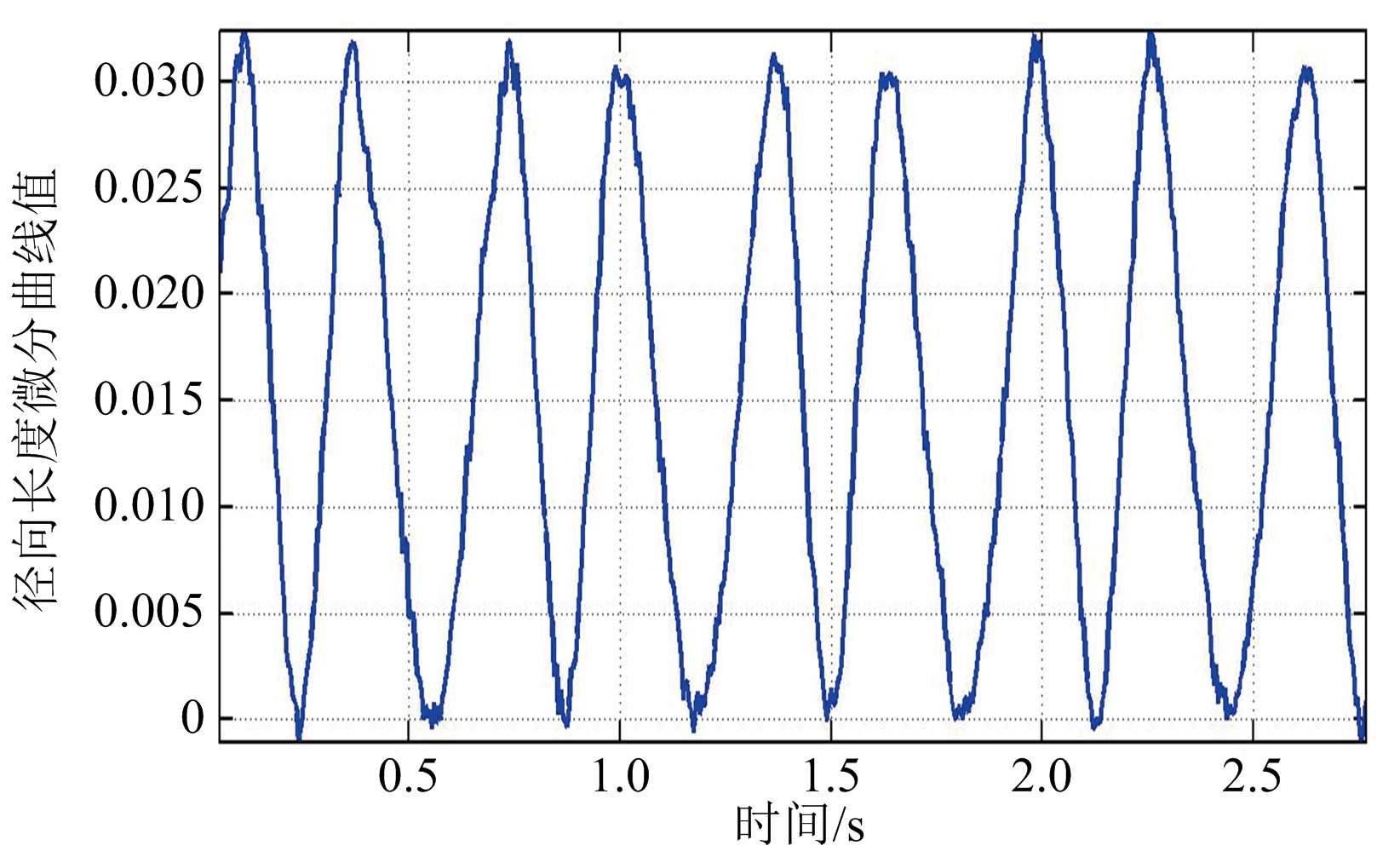
(a) 锥体目标径向长度微分曲线
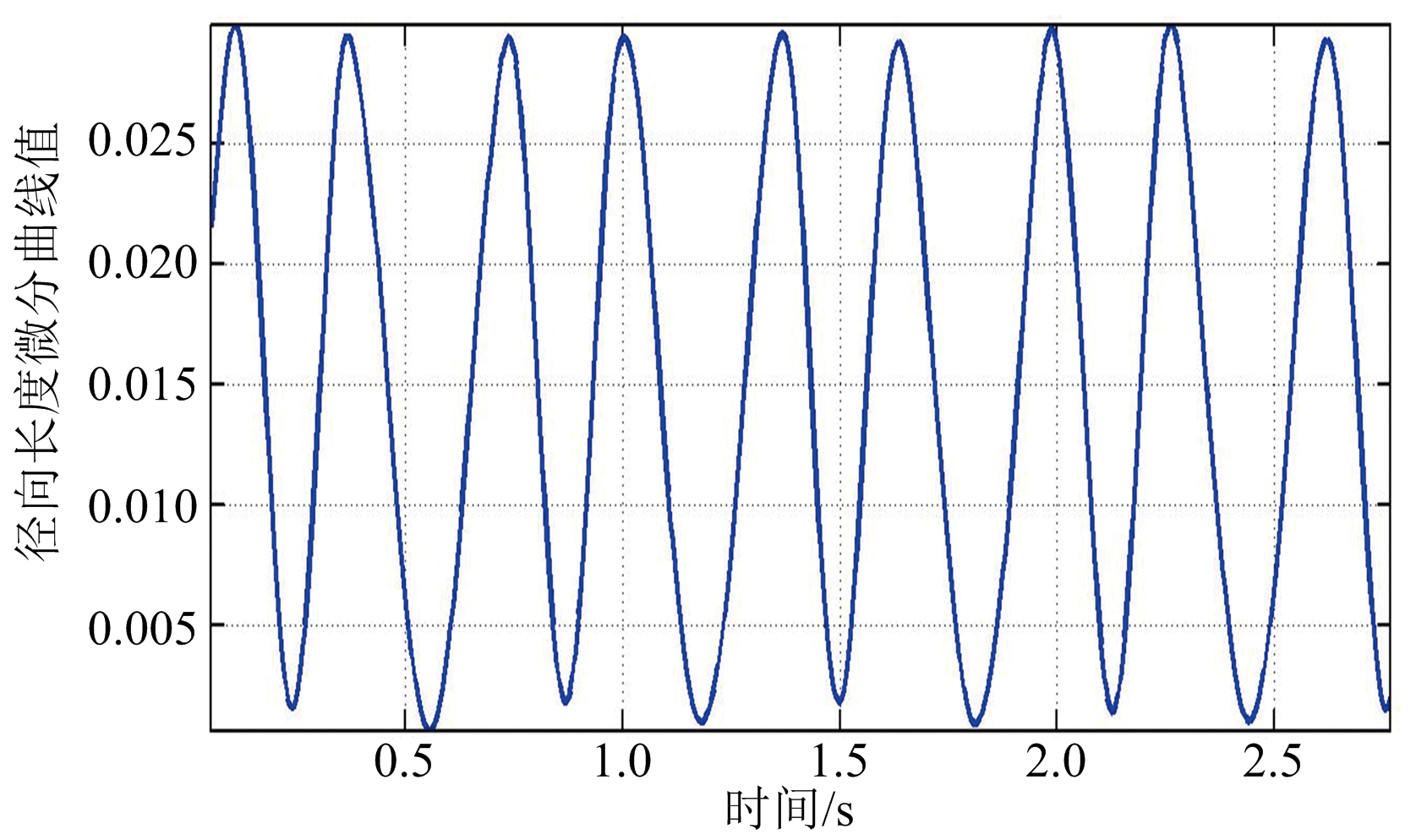
(b) 平滑滤波后的锥体目标径向长度微分曲线
图7 锥体目标径向长度微分曲线
下面分析不同信噪比对估计性能的影响,在观测信号信噪比为16,16.5,17,…,29.5,30 dB时,各进行100次Monte Carlo仿真实验,每次仿真实验在相应观测信号信噪比下,计算目标进动角的估计值![]() 目标半锥角的估计值
目标半锥角的估计值![]() 目标斜边长度的估计值
目标斜边长度的估计值![]() 取各次仿真结果的平均值作为最终参数的估计值,并计算各估计值的估计误差,结果分别如图8、图9和图10所示,其中,图8是目标进动角的估计误差随观测信号信噪比的变化曲线,图9是目标半锥角的估计误差随观测信号信噪比的变化曲线,图10是目标斜边长度的估计误差随观测信号信噪比的变化曲线。从3个图中可以看出,该方法对空间锥体目标的进动和形状参数有较高的估计精度。
取各次仿真结果的平均值作为最终参数的估计值,并计算各估计值的估计误差,结果分别如图8、图9和图10所示,其中,图8是目标进动角的估计误差随观测信号信噪比的变化曲线,图9是目标半锥角的估计误差随观测信号信噪比的变化曲线,图10是目标斜边长度的估计误差随观测信号信噪比的变化曲线。从3个图中可以看出,该方法对空间锥体目标的进动和形状参数有较高的估计精度。
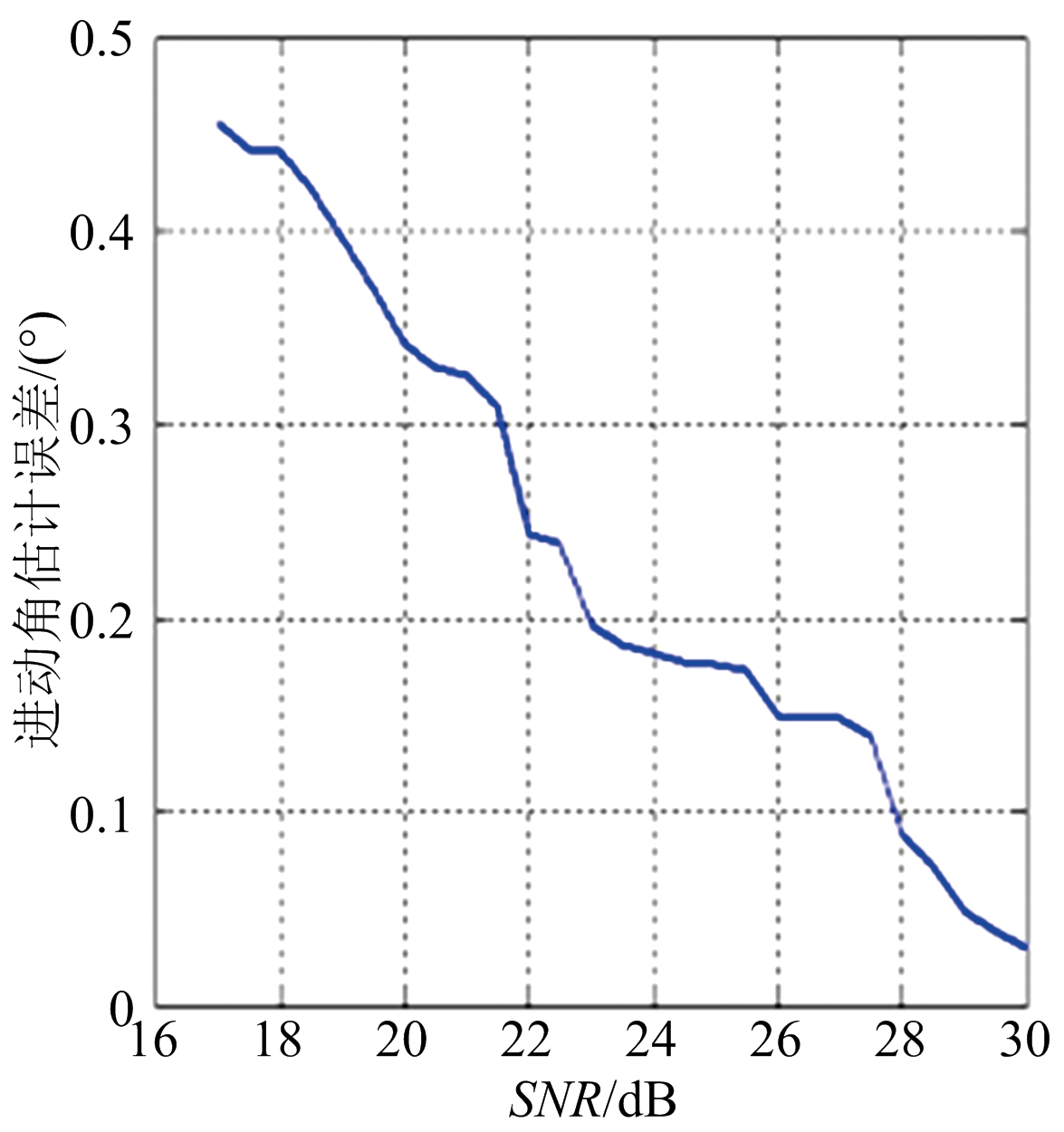
图8 进动角估计误差
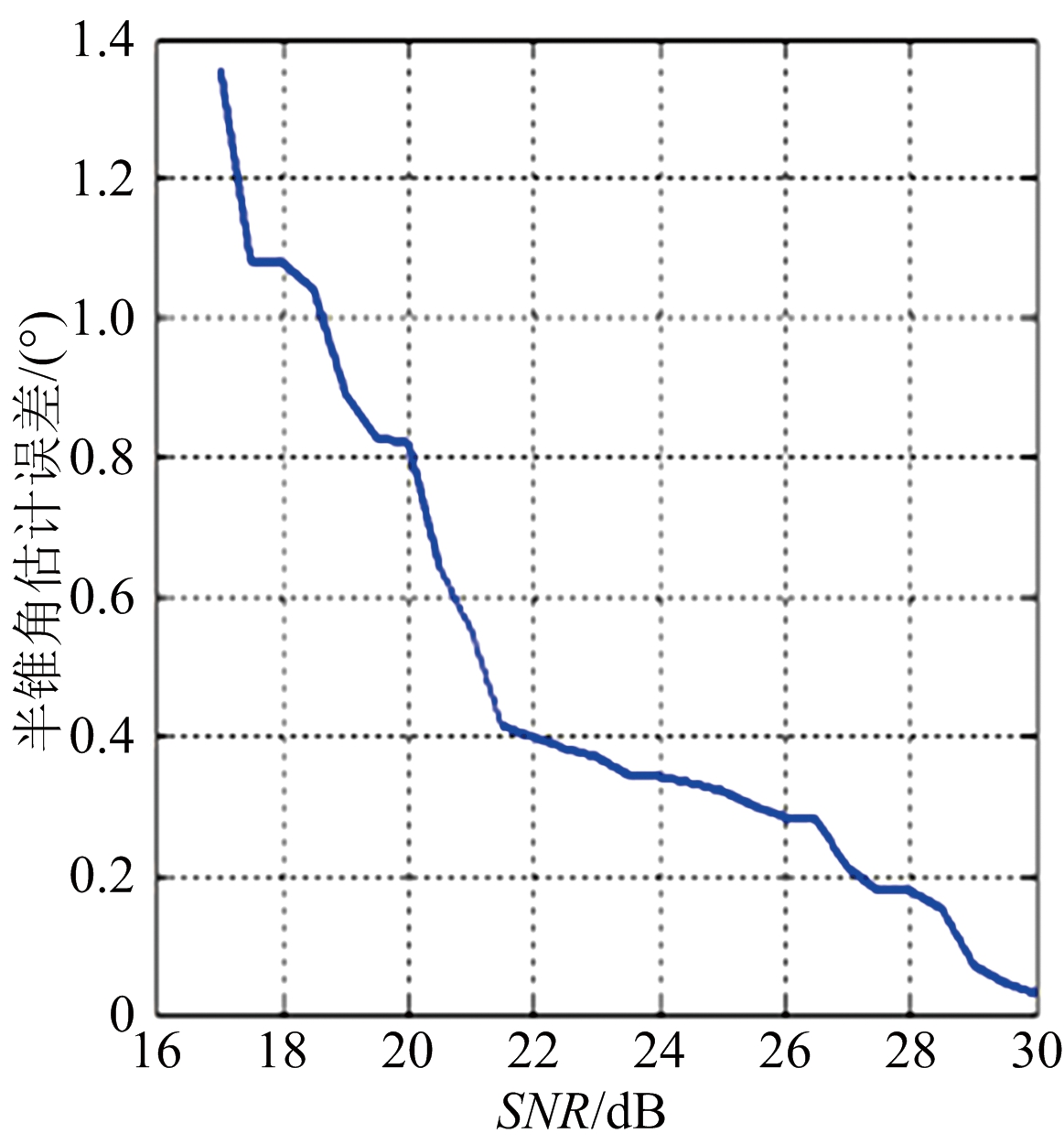
图9 半锥角估计误差
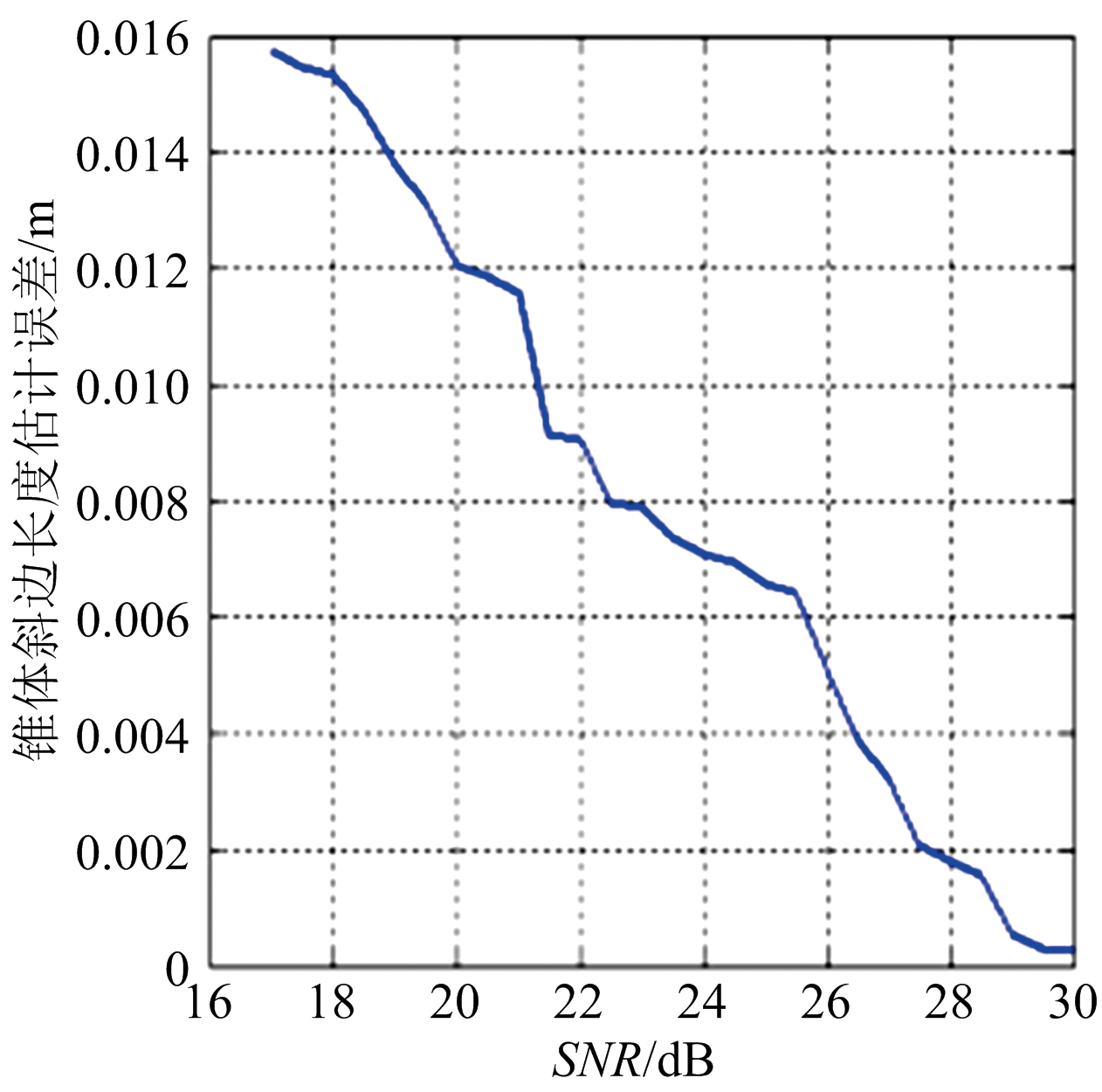
图10 斜边长度的估计误差
5 结束语
本文从宽带雷达体制出发,以空间锥体目标为研究对象,针对缺少目标结构参数等先验信息及估计过程中参数耦合问题,通过对其进动模型的分析,根据锥顶和锥底散射中心径向距离变化曲线,利用点散射中心间相对位置的极值变化信息,提出一种基于高分辨距离测量的中段弹道导弹目标进动参数和形状参数估计方法,并给出了详细推导步骤,仿真结果表明此方法可以同时估计出空间进动锥体目标的形状参数和进动参数;另外,该方法充分利用了空间进动锥体目标的径向长度序列、进动参数和形状参数的关系,且不使用非线性曲线拟合的方法估计目标的进动参数,从而提高了参数估计方法的可实施性,改善了参数估计过程的稳定性。
[1] 高乾,周林,王森,等. 弹道导弹中段目标特性及识别综述[J]. 装备指挥技术学院学报,2011,22(1):79-82.
[2] 刘永祥,李康乐,黎湘,等. 雷达目标微动特性研究[J]. 科技导报,2011,29(22):76-77.
[3] 鲁逸杰,宫志华,张群,等. 基于变分模态分解的进动目标微多普勒特征提取方法[J]. 探测与控制学报,2019,41(4):30-35.
[4] WANG Chao,YEH Chunmao,WEN Shuliang,et al. Precession Parameter Estimation Method of the Cone-Shaped Target Based on Inverse Synthetic Aperture Radar Image Sequence Analysis[J]. IET Radar,Sonar & Navigation,2019,13(8):1242-1248.
[5] 王超,叶春茂,文树梁. 低重频宽带雷达中小幅微动目标的周期估计[J]. 系统工程与电子技术,2018,40(9):1945-1952.
[6] CHEN Jian,XU Shiyou,HU Pengjiang,et al. Precession Period Extraction of Axisymmetric Space Target from RCS Sequence via Convolutional Neural Network[C]∥2018 Progress in Electromagnetics Research Symposium,Toyama,Japan:IEEE,2018:1-8.
[7] 张瑞国,李春雨,郝云胜. 一种RCS序列多周期估计方法[J]. 现代雷达,2020,42(2):40-45.
[8] 朱玉鹏,王宏强,黎湘,等. 基于一维距离像序列的空间目标微动特征提取[J]. 宇航学报,2009,30(3):1133-1140.
[9] 周代英,张瑛,冯健. 利用一维像序列时域差分估计目标进动频率[J]. 航空学报,2018,39(S1):69-74.
[10] AI Xiaofeng,XU Zhiming,ZHAO Feng. Feature Extraction of Micro-Motion Targets via Time-Range Distribution[J]. IEEE Access,2019,7:118889-118897.
[11] 苏楠,戴奉周,刘宏伟. 基于HRRP序列的钝头倒角锥目标微动特性分析及参数估计[J]. 电子与信息学报,2019,41(7):1751-1757.
[12] 雷腾,刘进忙,杨少春,等. 基于三站一维距离像融合的弹道目标特征提取方法研究[J]. 宇航学报,2012,33(2):228-234.
[13] SU Nan,DAI Fengzhou,LIU Hongwei,et al. Three-Dimensional Absolute Attitude Reconstruction of a Rigid Body Based on Multi-Station HRRP Sequences[J]. IEEE Access,2020,8:27793-27806.
[14] 姚汉英,孙文峰,马晓岩. 基于高分辨距离像序列的锥柱体目标进动和结构参数估计[J]. 电子与信息学报,2013,35(3):537-542.
[15] 刘宏伟,杜兰,袁莉,等. 雷达高分辨距离像目标识别研究进展[J]. 电子与信息学报,2005,27(8):1328-1333.
[16] STOICA P. Spectral Analysis of Signals[M].US: Prentice Hall,2005:161-171.
[17] 肖志河,任红梅,袁莉,等. 弹道导弹防御的雷达目标识别技术[J]. 航天电子对抗,2010,26(6):14-16.
