0 引言
随着雷达发射机自由度的增加，雷达可以通过改变发射脉冲波形来增强其对抗复杂干扰能力。此外，相比于单一发射波形，捷变波形能提供更好的探测性能。模糊函数是分析雷达波形探测性能的重要工具，可以反映出雷达信号的距离-多普勒二维分辨率。因此，雷达波形设计问题往往可以描述成模糊函数设计问题。常用的模糊函数性能指标有积分旁瓣电平(ISL)和峰值旁瓣电平(PSL)，皆为待设计信号的四次函数。
针对波形设计问题，He给出了用于设计模糊函数的Multi-CAO算法[1]，Arlery给出了基于梯度下降的模糊函数设计算法[2]，但所设计信号均为连续相位调制信号。Boyd提出了交替方向乘子法(Alternating Direction Method of Multipliers,ADMM)适用于大规模凸优化问题[3]，随后Liang使用ADMM方法求解带约束二次型最优化问题，给出了一种设计具有低自相关旁瓣的连续相位调制信号方法[4]。在二次型优化问题中，ADMM更新公式可以给出闭式解，但在四次型优化问题中，闭式解难以获取。Hunter和Lange提出的MM算法是一种迭代求解最优化问题的算法，通过构造并求解形式更为简单的辅助函数，逐渐逼近原问题的最优解[5]。Song给出了一种基于MM算法的模糊函数设计方法，其中辅助函数为目标函数上界的二次型[6]。
本文基于离散相位调制信号(Discrete Phase Coded Signal,DPCS)，以脉冲串模糊函数平均ISL为目标函数，将波形设计问题建模为带约束四次型最优化问题，并给出基于MM算法的求解方法。其中，辅助上界函数的求解采用ADMM算法。最后，给出MM-ADMM算法流程。仿真结果表明，该方法计算速度快，收敛趋势明显。
1 模型建立
设脉冲-多普勒雷达发射设含N个脉冲的脉冲串信号，可表示为
(1)
式中：sn(t)为第n个发射脉冲的复包络，并满足sn(t)=0,∀t⊄[0,T]，T为发射脉冲长度；Tr为脉冲重复间隔(Pulse Repetition Interval,PRI)。发射信号采用相位编码调制方式，则第n个发射脉冲可表示为
(2)
式中，s(n,m),n=0,1,…,N-1,m=0,1,…,M-1为相位编码调制序列，pm(t)表示矩形赋形脉冲：
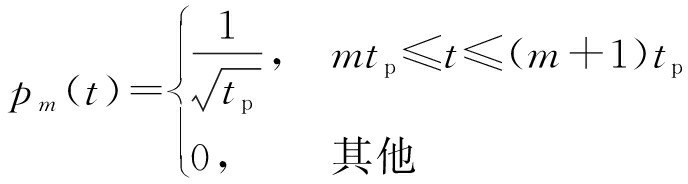
(3)
式中,tp为发射脉冲中每个调制相位对应的时宽，满足关系T=Mtp。
为表示方便，记列向量sn=[s(n,0),s(n,1),…,s(n,M-1)]T表示第n个发射脉冲的调制序列，且满足
s(n,m)=
0≤φ(n,m)≤K-1
(4)
式中，K为离散相位数。在脉冲-多普勒体制雷达中，我们只关注脉冲串模糊函数的中心条带部分，即所有发射脉冲自模糊函数的叠加。若采用离散模糊函数(Discrete Ambiguity Function,DAF)的形式，在时间轴上选取τ=ltp的点，在多普勒频率轴上选取f=p/NTr的点，并简
sn(ltp,p/NTr) 
sn(l,p)，则sn的模糊函数可写为
(5)
其中矩阵Hlp=Jl·Dp,Jl为转移矩阵，其定义为
(6)
Dp为对角矩阵，其定义为
(7)
则脉冲串离散模糊函数中心条带可表示为
(8)
我们期望得到图钉型的模糊函数，即中心位置为一窄峰，其他位置近似为零。对于DPCS信号，模糊函数主瓣峰值为定值，所以可将近主瓣区域内模糊函数ISL作为优化目标。在离散距离-多普勒域内，设集合Φ={(l,p)|-a≤l≤a,-b≤p≤b,0<a<M,0≤b<N}表
center(l,p)的中心区域，则该区域内ISL为
(9)
记列向量
表示待优化的脉冲串的调制序列，矩阵
则有
(10)
至此，上述离散相位调制脉冲串模糊函数设计问题可写为
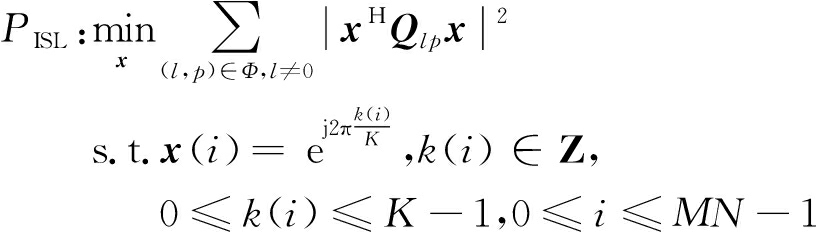
(11)
其中k(i)和φ(n,m)的关系为k(nM+m)=φ(n,m),n=⎣i/M」,m=mod(i,M)。该问题是非凸约束条件下的四次型优化问题，对于带约束优化问题，通常选择构造带惩罚项的增广拉格朗日函数进行求解，ADMM方法是一种求解增广拉格朗日函数的方法。由于四次型较为复杂难以优化，另一种思路是将高次型进行降次，针对这种思路，本文提出一种基于MM算法的求解方法，将四次型优化问题转化为二次型进行求解。
2 算法设计
2.1 MM算法介绍
MM(Majorization-Minimization)算法是一种通过迭代逼近求解最优化问题的算法。在每次迭代中，首先原函数上某一点出发，构造一个位于目标函数上界的辅助函数，且辅助函数与原函数相交于该点。然后，求解辅助函数的最优值点。一般来讲，构造的辅助函数要求形式简单，易于求解。最后，将解得的辅助函数最优值点作为新的出发点，进行下一次迭代。经过若干次迭代后，辅助函数最优值点将收敛到原问题的最优值点，算法完成。下面简要介绍MM算法的流程。设最优化问题为
(12)
选取某一出发点xk，构造一个新函数g(x|xk)，在xk处与f(x)相交，其他位置上皆在f(x)的上界，即满足关系：
(13)
然后求解辅助函数g(x|xk)的最小值：
(14)
易得
f(xk+1)≤g(xk+1|xk)≤g(xk|xk)=f(xk)
(15)
这样每一次迭代都可以使目标函数值下降，直到辅助函数极值收敛到原函数极值。图1给出了MM算法的示意图。
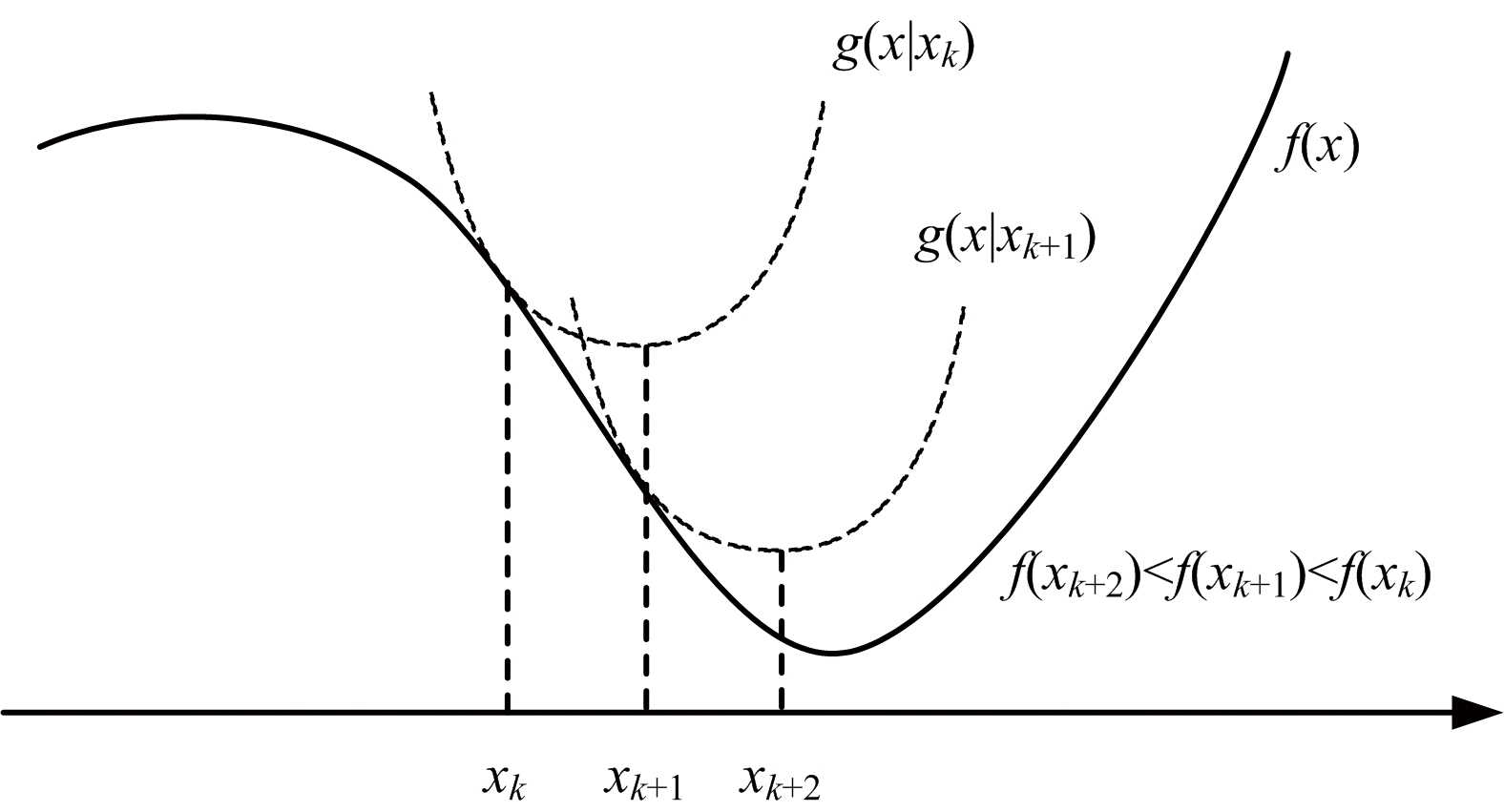
图1 MM算法示意图
2.2 ADMM算法介绍
ADMM算法是一种求解优化问题的计算框架,通过将原优化问题分化两个子问题交替求解，缩小了问题的规模。ADMM框架的基本模型为
(16)
将式(16)写成增广拉格朗日函数，ρ为惩罚项系数，有
Lρ(x,z,λ)=f(x)+g(z)+λT(Ax+Bz-c)+
(17)
则ADMM更新公式为
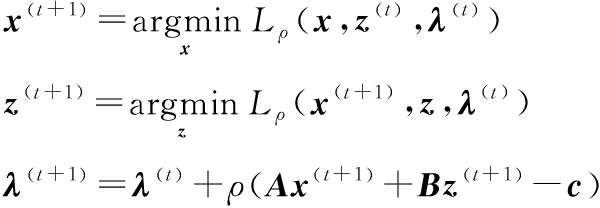
(18)
判断收敛的条件为x(t+1)-z(t+1)<δ，δ为一个较小的正数，作为收敛门限。
2.3 辅助函数构造
因为xHQlpx=tr(QlpxxH)，其中tr(·)表示矩阵的迹，记矩阵X=xxH，则有
vec(Qlp)H·vec(X)=
vec(Qlp)H·vec(X)
(19)
式中，vec(·)为矩阵向量化符号，表示将矩阵按列排成的列向量。
引理：设L和M为两个不同MN阶Hermitian矩阵，并满足关系M≥L，则对∀x0∈CMN×1，存在以下关系：
证明：将xHLx在x0处泰勒展开，有
xHLx=
(x-x0)HL(x-x0)≤
(x-x0)HM(x-x0)=
xHMx+2Re(xH(L-M)x0)+
(20)
当x=x0 时，式(20)中不等关系取等。
由此，将Hermitian矩阵∑l,pvec(Qlp)·vec(Qlp)H记为L，设L的最大的特征为λmax，可求得λmax=MN，记M=λmaxI=MN·I，易得M≥L。将引理1代入式(19)，可得
vec(X)HLvec(X)≤
vec(X)HMvec(X)+2Re(vec(X)H(L-M)vec(X0))+
vec(X0)H(M-L)vec(X0)
(21)
在约束条件下，式(21)的第一项和第三项为常数，所以只要考虑第二项即可。其中第二项可以记成：
Re(vec(X)H(L-M)vec(X0))=
(22)
在MM算法迭代过程中，设第k次迭代后求得的脉冲串为xk，并记
(23)
容易看出Pk为Hermitian矩阵，Tk为半正定Hermitian矩阵，则式(22)中取实部符号Re(·)可以去掉。在下式的xHTkx项上再次套用式(20)，可得
xH(Pk-Tk)x=
(x-xk)HTk(x-xk))≤
xHPkx-2(MN)2Re(xHxk))+(MN)2
(24)
综上，有
const+xHPkx-2(MN)2·Re(xHxk)
(25)
至此，辅助函数已经构造完成，即每次MM迭代中，需要求解的问题为
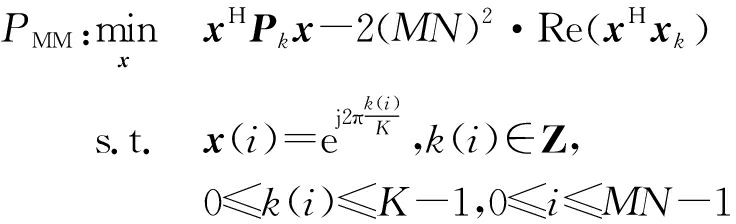
(26)
2.4 ADMM算法求解辅助函数
问题式(26)中包含二次项xHPkx和一次项2(MN)2·Re(xHxk)，通过引入辅助变量z和约束x=z，可将该问题写成如下等价形式：
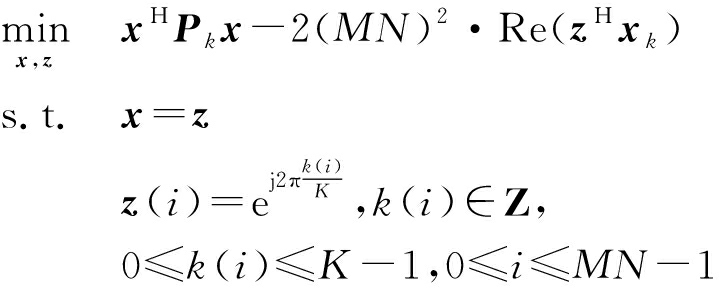
(27)
形如上式的带约束优化问题可用ADMM框架求解，根据式(27)写出增广拉格朗日函数：
Lρ,k(x,z,λr,λi)=
xHPkx-2(MN)2Re(zHxk)+
(28)
记u=(λr+jλi)/ρ，则式(28)可写为
Lρ,k(x,z,u)=xHPkx-2(MN)2Re(zHxk)+
(29)
由于ADMM迭代嵌套在MM迭代中，记第k次MM迭代中，经过t次ADMM迭代后的值为
和u相应的记为
并将MM迭代中的当前值xk作为ADMM迭代的初值
则该问题的求解可按照如下步骤进行：
1) 更新x，此时
和
看作已知量：
(30)
2) 更新z，此时设
和看作已知量：
(31)
s.t. 
0≤k(i)≤K-1,0≤i≤MN-1
由于式(31)是一个线性问题，且z中的元素彼此独立，则可以将其分解为MN个子问题，为表示方便，记
第i个子问题可表示为
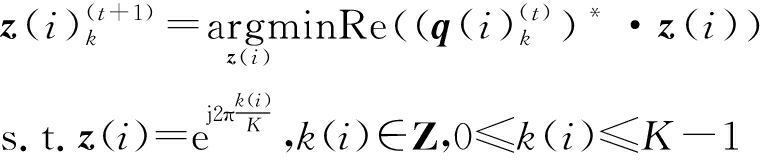
(32)
若将复数
和z(i)看成复平面上的向量，则有
(33) 
由于
为定值，在约束条件下，
也为定值，则式(32)转化为
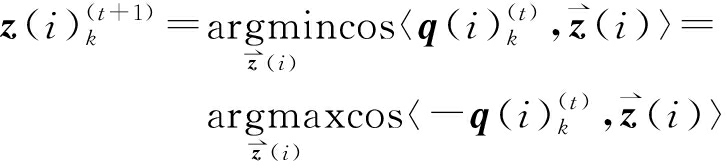
(34)
式(34)的几何意义为，求0到K-1之间的整数k(i)，使向量
和z(i)之间的夹角最小。k(i)的解为
(35)
3) 更新u
(36)
重复步骤1) 到3) 直至算法收敛，判断收敛的条件为x(t+1)-z(t+1)<δ，δ为一个较小的正数，作为收敛门限。
下面给出MM-ADMM算法求解中心区域低副瓣脉冲串模糊函数流程：
Step 1 记k为MM算法迭代次数，初始化k=0，δ=0.001，给随机初值x0；
Step 2 记t为ADMM算法迭代次数，初始化t=0，给初值
Step 3 进行ADMM迭代：
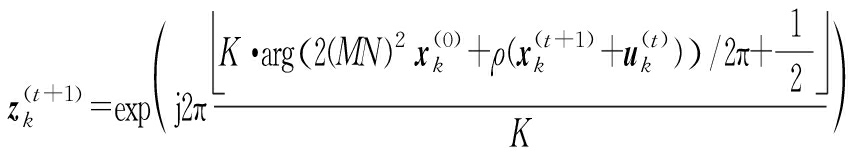
Step 4 t←t+1，若
则完成ADMM迭代，否则回到Step 3；
若收敛则完成算法，否则回到Step 2。
3 仿真分析
设相干雷达系统在一个CPI中有N个发射脉冲，每个发射脉冲中有M个子脉冲。目标区域Φ的参数为a=M/2，b=N/4，即Φ={(l,p)|-M/2≤l≤M/2,-N/4≤p≤N/4}，则可定义脉冲串模糊函数中心条带的中心区域平均副瓣为
(37)
收敛门限δ=0.001，二次惩罚项系数ρ=2M2N2，初值使用随机离散相位序列。图2给出了MM-ADMM算法所设计的离散相位调制脉冲串在不同的相位数K下的模糊函数中心条带(M=50,N=16)。随调制相位数K增多，目标区域AISL明显下降。
图3给出了MM-ADMM算法所设计的离散相位调制脉冲串在不同子脉冲数M时的模糊函数中心条带(K=8,N=16)。随子脉冲数M增多，目标区域AISL明显下降。
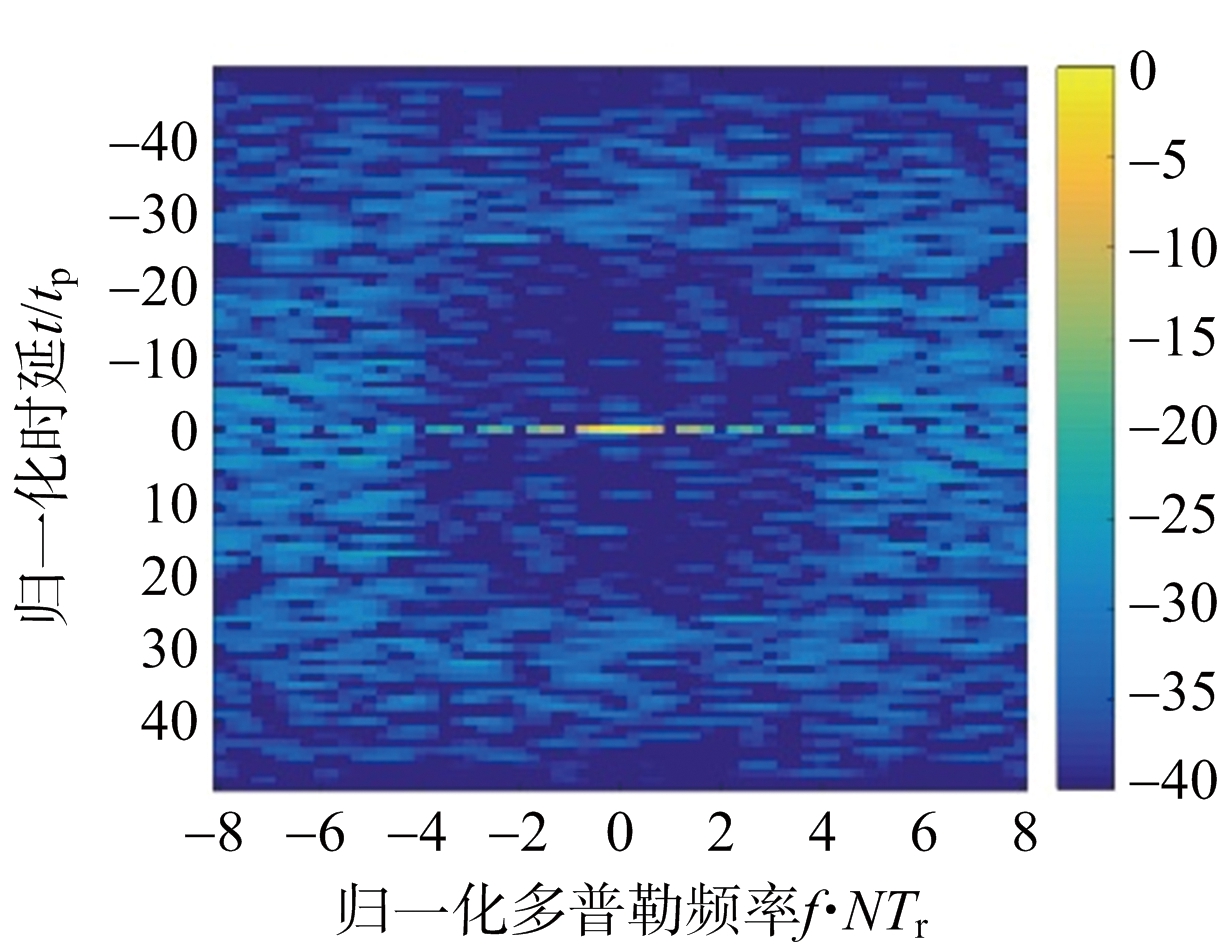
(a) K=4
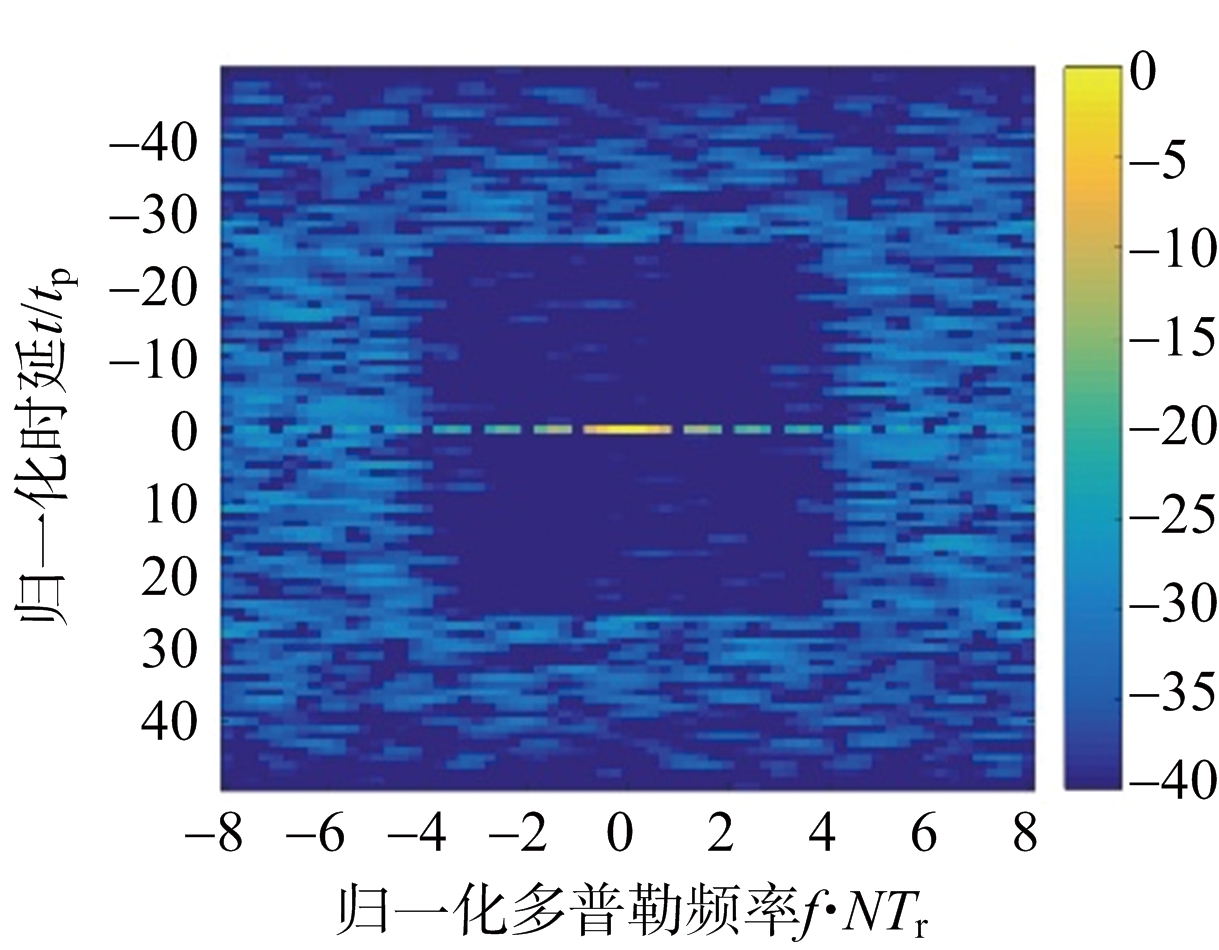
(b) K=8
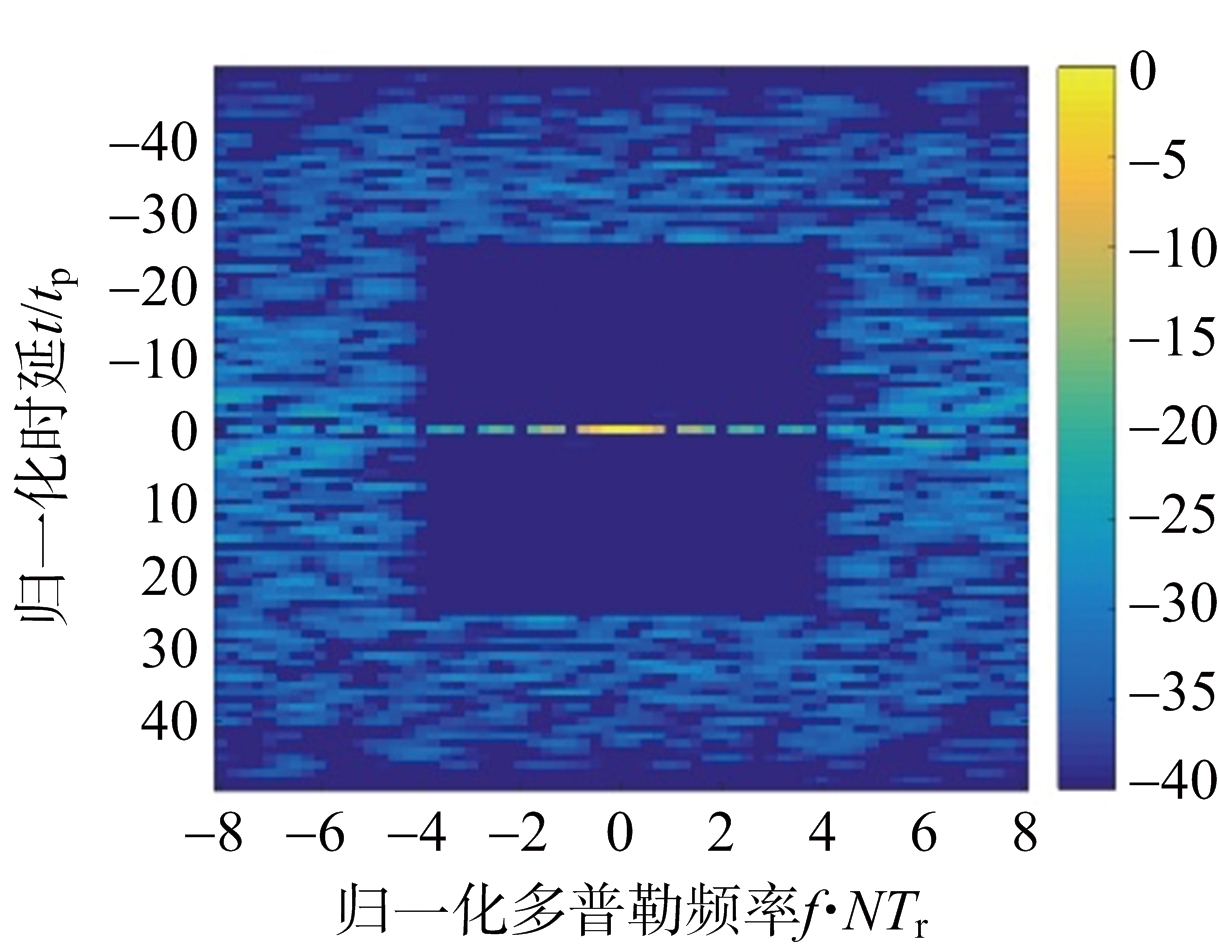
(c) K=16
图2 不同相位数K下的MM-ADMM方法设计脉冲串模糊函数
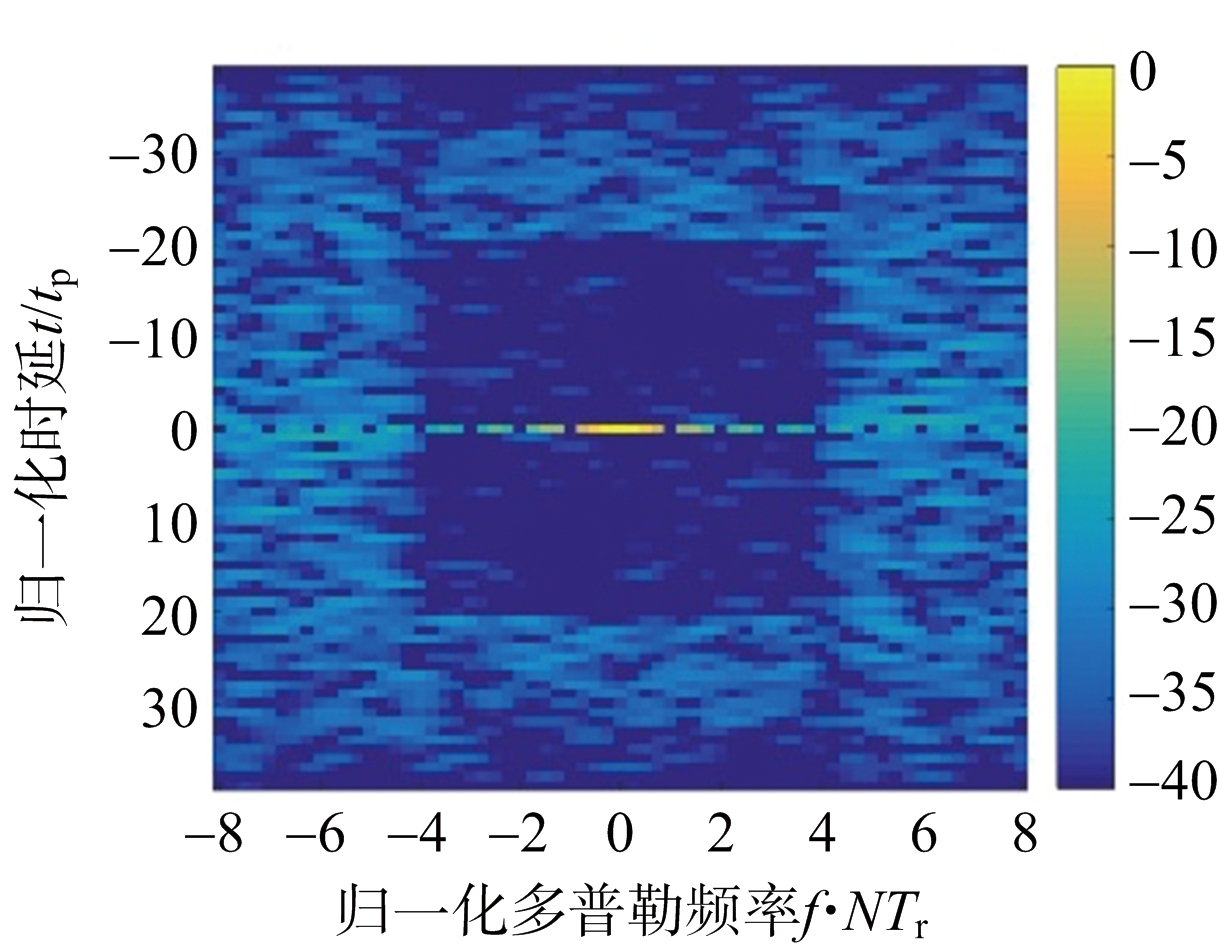
(a) M=40
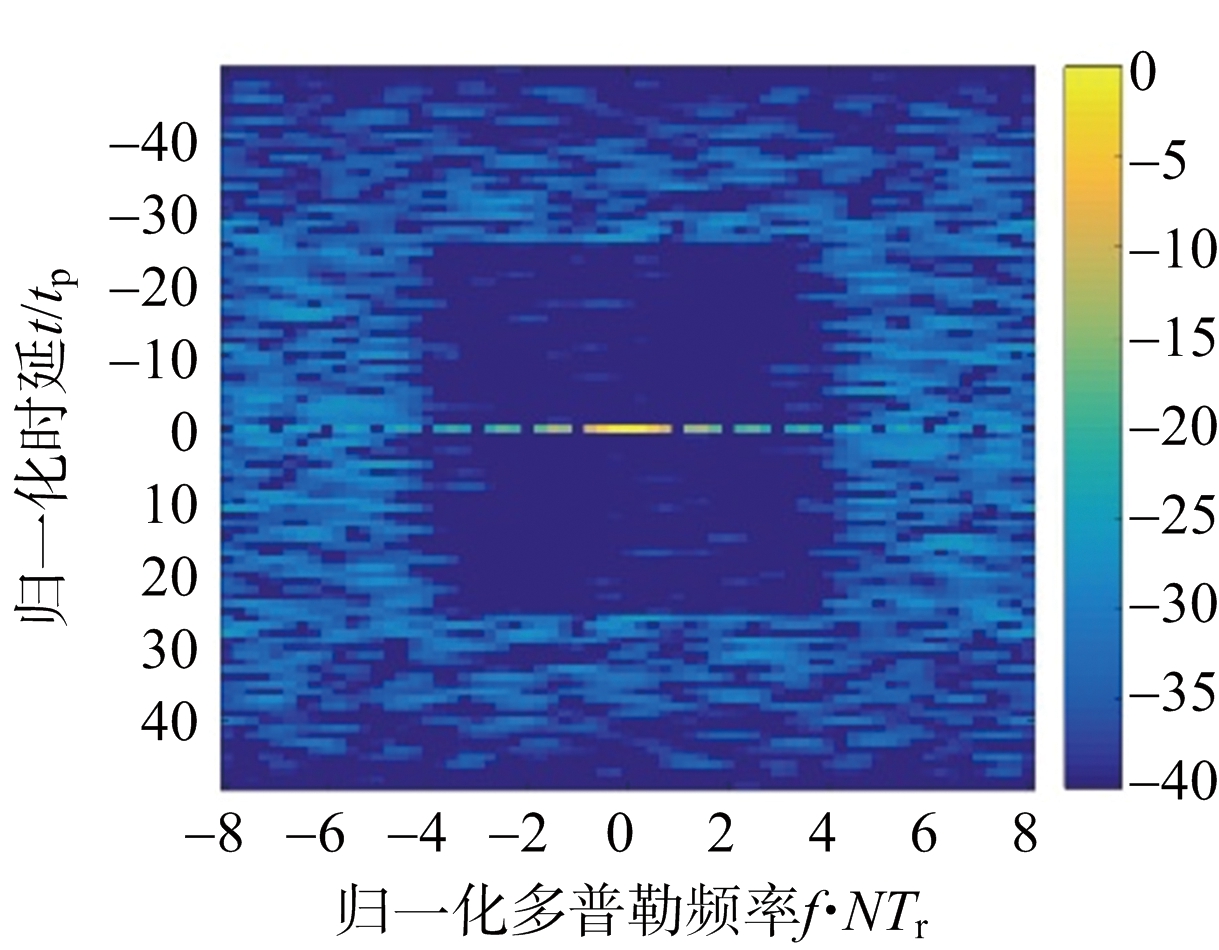
(b) M=50
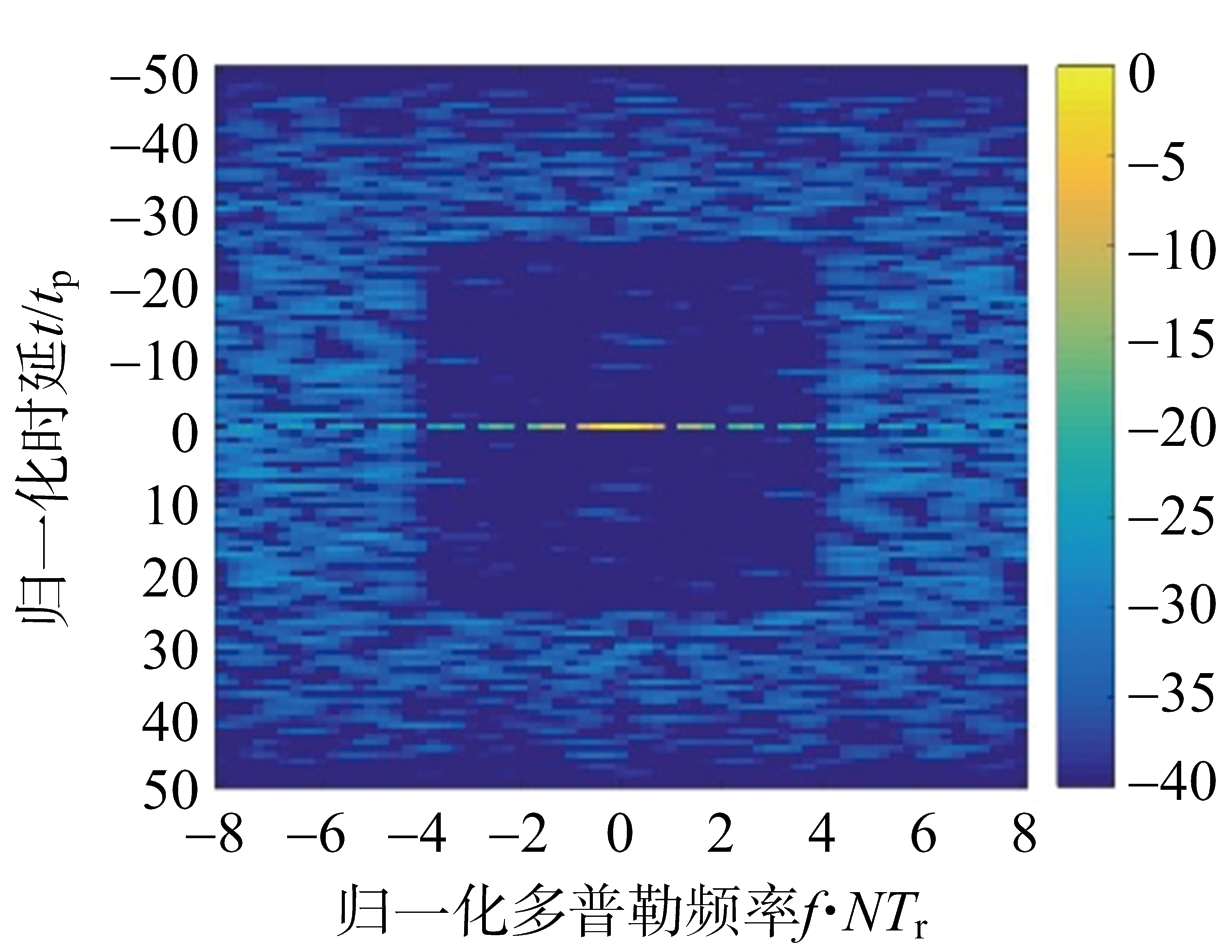
(c) M=60
图3 不同子脉冲数M时的MM-ADMM方法设计脉冲串模糊函数
由于MM算法通过求解形式更为简单的辅助函数，显著降低了运算量。现将MM-ADMM算法与用拟牛顿法求解四次型最优化问题的ADMM算法对比，仿真平台为Intel i5-7300HQ处理器，8 G内存计算机。表1～表4分别给出了两种算法在不同子脉冲数M和不同调制方式K的情况下的AISL值(100次蒙特卡罗实验取平均)和在所需的运算时间。
表1 MM-ADMM算法不同情况下的AISL
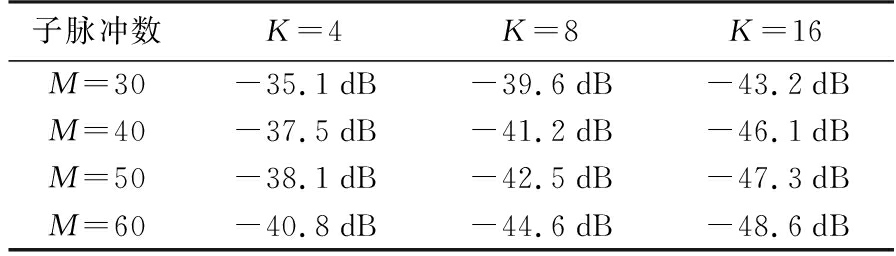
子脉冲数K=4K=8K=16M=30-35.1dB-39.6dB-43.2dBM=40-37.5dB-41.2dB-46.1dBM=50-38.1dB-42.5dB-47.3dBM=60-40.8dB-44.6dB-48.6dB
表2 ADMM算法不同情况下的AISL
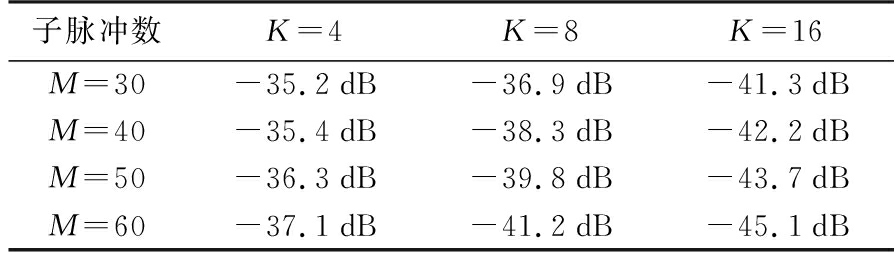
子脉冲数K=4K=8K=16M=30-35.2dB-36.9dB-41.3dBM=40-35.4dB-38.3dB-42.2dBM=50-36.3dB-39.8dB-43.7dBM=60-37.1dB-41.2dB-45.1dB
表3 MM-ADMM算法不同情况下的计算时间
子脉冲数K=4K=8K=16M=305.8s7.4s9.8sM=407.2s11.8s14.4sM=508.8s14.2s21.4sM=6023.4s30.1s33.1s
表4 ADMM算法不同情况下的计算时间
子脉冲数K=4K=8K=16M=30569s433s339sM=40650s485s394sM=502406s1871s1440sM=604108s3232s2358s
可以看出，目标区域AISL均随着子脉冲数M或调制相位数K增多而逐渐降低，计算时间逐渐增多。相比于ADMM算法，MM-ADMM算法的AISL略优于ADMM算法，且运算量大幅减小，运算速度显著提升。
图4给出了两种算法的收敛情况(M=50,N=16,K=8)，可见在约15次迭代后，AISL相比于随机脉冲串下降了10 dB并趋于收敛，且下降趋势明显。
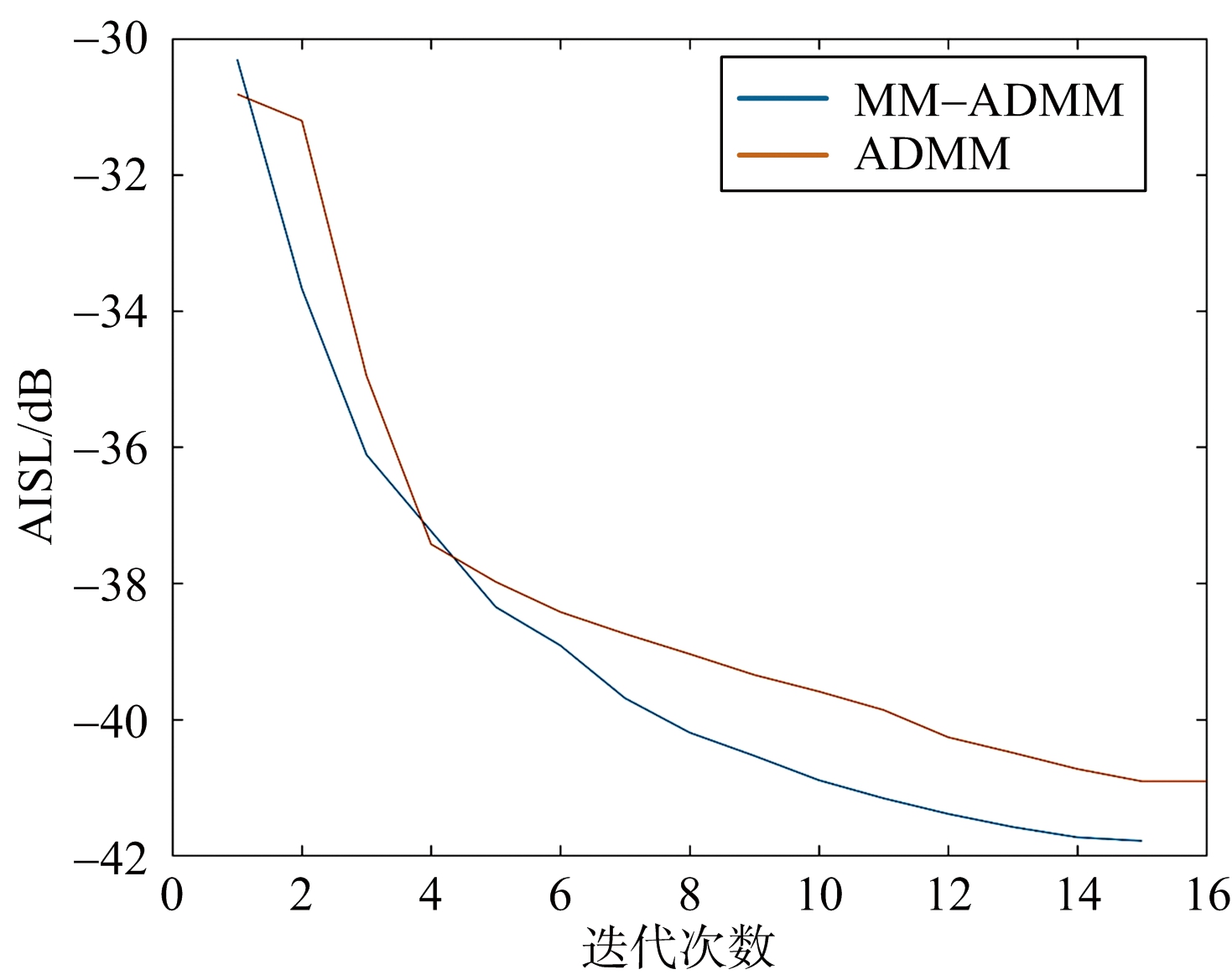
图4 MM-ADMM算法与ADMM算法的收敛曲线
4 结束语
本文主要介绍了具有目标区域低旁瓣模糊函数的离散相位编码脉冲串信号的设计方法。该问题实际上是带约束的四次型优化问题，难以直接求解。为此，引入了MM算法，将四次型优化问题转化为二次型优化问题，进行迭代逼近求解。仿真结果表明，MM-ADMM算法所设计信号性能满足要求，运算速度快，收敛趋势明显。
[1] HE H,LI J,STOCIA P. Waveform Design for Active Sensing Systems: A Computational Approach[M]. UK:Cambridge University Press,2012:49-53.
[2] ARLERY F,KASSAB R,TAN U,et al. Efficient Optimization of the Ambiguity Functions of Multi-Static Radar Waveforms[C]∥2016 17th International Radar Symposium,Krakow,Poland:IEEE,2016:1-9.
[3] BOYD S,PARIKH N,CHU E,et al. Distributed Optimization and Statistical Learning via the Alternating Direction Method of Multipliers [J]. Foundations & Trends in Machine Learning,2010,3(1):1-122.
[4] LIANG J L,HING C S,LI J. Unimodular Sequence Design Based on Alternating Direction Method of Multipliers [J]. IEEE Trans on Signal Processing,2016,64(20):5367-5381.
[5] HUNTER D R,LANGE K. Quantile Regression via an MM Algorithm [J]. Journal of Computational & Graphical Statistics,2000,9(1):60-77.
[6] SONG J X,BABU P,PALOMAR D P. Sequence Design to Minimize the Weighted Integrated and Peak Sidelobe Levels[J]. IEEE Trans on Signal Processing,2016,64(8):2051-2064.
