0 引言
航天发射场测量数据的精度在很大程度上取决于测控设备的跟踪精度,但提高设备跟踪精度的成本较高,且受制于设备生产的工艺水平和其他因素,有其固有的极限。目前,广泛采用的处理策略是通过先进、可靠的数据预处理方法来弥补设备精度的不足[1]。测量数据误差的估计与分离是外测数据预处理中的一项重要工作,无论是无线电测量、光学测量或其他测量手段,由于测控设备本身或数据传输、记录和处理过程中周围环境的影响,都不可避免地存在误差。如果对测量数据序列中的误差不予以分离和消除,将给数据处理结果带来很大的偏差,严重影响外测数据处理的精度[2]。
对测量数据而言,系统误差影响真实信号的准确度,随机误差影响真实信号的精密度。要获得高精度的外弹道测量数据,必须准确分离系统误差,同时要正确地揭示随机误差的统计特性。本文针对航天发射场外测数据预处理中的传统方法难以对测量数据的随机误差和系统误差进行准确估计与分离的难题,提出采用小波非线性滤波和回归匹配诊断两种新方法,有效提高了参与融合求解的测元数据质量和外弹道参数精度。
1 随机误差分离方法
目前,在外测数据处理中最常用的观测数据随机误差的方法是差分法和最小二乘拟合残差法,由于受数据采样间隔、误差统计特性、差分阶次和截断误差等多种因素的影响,两种方法的处理结果常常出现不一致性[3]。通过对测控数据的深入研究和分析,认识到外测数据随机误差性质十分复杂,如果再应用这两种常用和简单的统计方法,已经难以准确统计数据随机误差的数字特征。小波变换则是一种比傅里叶变换还要灵活的信号处理工具,在时域、频域同时具有良好的局部化性质,而且由于对高频采取逐渐精细的时域或频域步长,可以聚焦到分析对象的任意细节,把对象中存在的任何变化表现出来[4]。本文将小波变换方法用于分离雷达测量数据的随机误差,再通过与具有更高精度的设备进行数据比对,得到该雷达的总误差,两者相减便可得到当前雷达的系统误差。
1.1 小波变换去噪原理
小波变换去噪基于如下基本假设,即携带信息的原始信号在频域或小波域的能量相对集中,表现为能量密集区域的信号分解系数的绝对值比较大,而噪声信号的能量谱相对分散,所以其系数的绝对值小,这样我们就可以通过作用阈值的方法过滤掉绝对值小于一定阈值的小波系数,从而达到降噪的效果。
一个含噪声的一维信号的模型可以表示成如下形式,即
(1)
式中,f(t)为真实信号,e(t)为噪声,σ为噪声强度,S(t)为含噪声的信号。如果以一个简单的噪声模型加以说明,即认为e(t)为高斯白噪声N(0,1),则σ=1[5]。在实际的工程应用中,有用信号通常表现为低频信号或是一些比较平稳的信号,而噪声信号通常表现为高频信号,因而,可以应用门限阈值等形式对小波系数进行处理,然后对信号进行重构即可达到消噪的目的。对信号S(t)消噪的目的就是要抑制信号中的噪声部分,从而在 S(t)中恢复出真实信号f(t)。一般情况下,一维信号的消噪过程可按照图1所示的流程来进行。
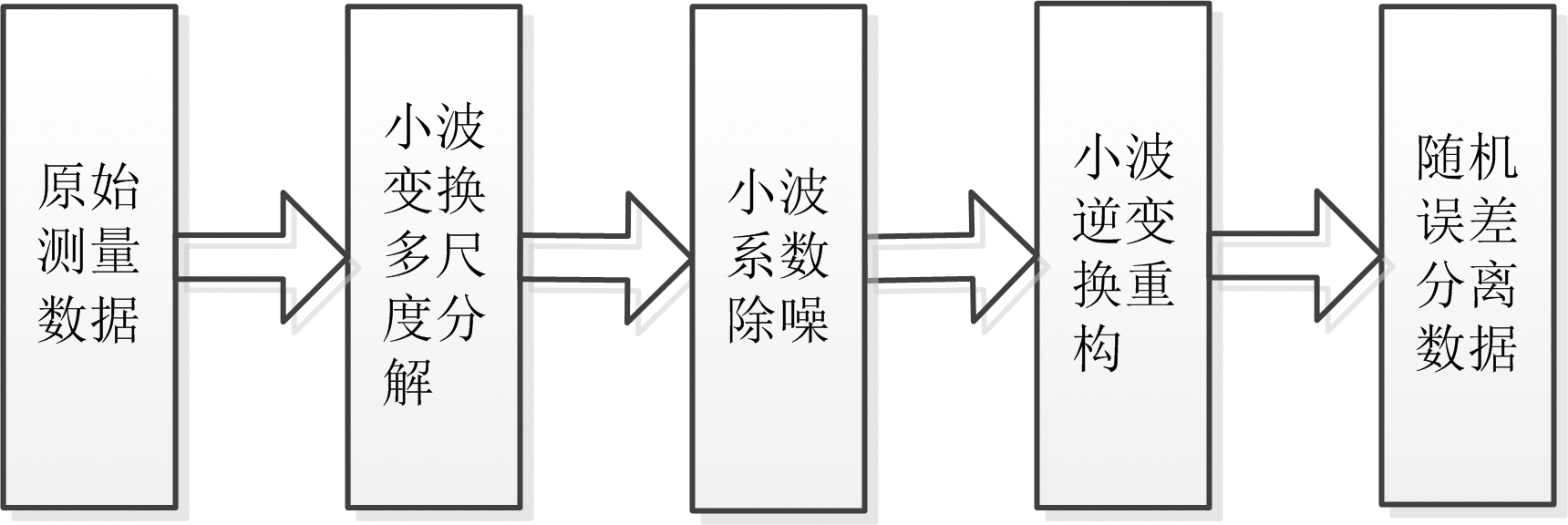
图1 小波变换除噪流程图
一维信号利用小波进行除噪的步骤如下:
1) 对含噪信号进行预处理,便于后续处理。
2) 一维信号的小波分解。选择一个小波并确定一个分解层次N,然后对信号S进行N层分解。
3) 小波分解高频系数的阈值量化。对第一层到第N层的每一层高频系数,选择一个阈值进行软阈值或硬阈值量化处理。
4) 一维小波的重构。根据小波分解的第N层的系数和经过量化处理后的第一层到第N层的高频系数,进行一维信号的重构。
小波分解是把信号分解到不同的频段上,噪声主要在高频段,信号主要在低频段。噪声对应相对较小的小波系数,信号对应相对较大的小波系数。选择一个合适阈值处理小波系数,认为小于此阈值的小波系数主要由噪声引起,将其去掉,用剩下的小波系数重建信号。从去噪原理看出,在小波去噪过程中,噪声能量估计是确定噪声和信号分界点的关键。阈值的选择即噪声和信号分界点的确定,对去噪效果有较大影响。
根据噪声的特点,小波分析消噪主要采用前两种处理方法。第一种是强制消噪处理方法。该方法把小波分解结构中的高频系数全部为零,即把各尺度或某几个尺度的部分全部滤掉,然后再对信号进行重构处理。这种方法比较简单,重构后的信号也比较平滑,但容易丢失原信号中有用的高频分量。第二种是门限消噪处理方法。该方法要根据经验或某种依据设定阈值,对信号小波分解中的最高频系数用阈值处理,即大于阈值的部分保留,低于阈值的系数变为零。这种处理符合噪声在高频部分均匀密集的特点。对其他各尺度的高频系数改变阈值处理,随着分解层次的增加,阈值可大约按照乘以2倍到0.5倍减小,这种阈值消噪处理方法在很多实际应用中取得了良好的效果[6]。
针对最小尺度上的小波系数估计噪声能量,即依靠最小尺度上的小波系数估计噪声的方差。在最小尺度上,分辨率最高,信噪比很小,可以认为这一层次主要是噪声。根据方差定义,其在最小尺度上的估计值为
(2)
式中,n为第J尺度上小波系数的个数,d为某一尺度上高频小波系数,J为尺度,i为某一尺度上小波系数序号。美国著名学者Donoho提出在小波域中噪声标准方差的估计公式[7],即
![]()
![]()
(3)
式中:MAD为最小尺度上小波系数的中值;d(J-1)为最小尺度上的小波系数的向量;![]() 分别为d(J-1)的分量和均值。
分别为d(J-1)的分量和均值。
1.2 应用效果
本文采用了Donoho等人提出的小波非线性滤波方法分离靶场测量数据的随机误差,与传统方法相比,不需要噪声先验知识,噪声强度可以通过高频波分解系数进行估计,在实际应用中取得了较好的效果,其可分为以下3个主要步骤:
1) 对带随机误差的发射场外弹道测量数据 y(ti),i=1,2,…,N进行多尺度分解,获得各尺度的小波分解系数dj,k;
2) 取阈值![]() 用非线性阈值函数sgn(dj,k)(|dj,k|-λ)作用于小波分解系数,得到新的估计小波系数dj,k;
用非线性阈值函数sgn(dj,k)(|dj,k|-λ)作用于小波分解系数,得到新的估计小波系数dj,k;
3) 采用新的小波系数进行信号重构,得到去噪的测量数据。
其中,σ为测元理论随机误差指标,n为第j尺度上小波系数的个数,d为某一尺度上高频小波系数,k为某一尺度上小波系数序号。
该方法的原理依据是N个具有独立同分布的标准高斯变量中的最大值小于t1的概率随着N的增大趋于1。若被测信号含有独立同分布的噪声时,经小波变换后,其噪声部分的小波系数也是独立同分布的。如果具有独立同分布的噪声经小波分解后,它的系数序列长度N很大,则根据上述理论可知:该小波系数中最大值小于t的概率趋于1,即存在一个阈值t,使得该序列的所有小波系数都小于它。小波系数随着分解层次的加深,其长度也越来越短,根据t的计算公式,可知该阈值也越来越小。当噪声强度已知时,可直接采用此方法滤波,在实际应用中噪声强度是未知的,这时可以计算出该噪声的强度,然后采用Donoho方法进行滤波[8]。
采用具有较好对称性及正则性的Daubechies(dbN)小波基系列中的db4小波基对某脉冲雷达测量数据求解的弹道参数进行了随机误差分离。图2为随机误差分离前后时的误差对比曲线,由图可见,对该脉冲雷达测量数据求解的弹道参数采用小波分离随机误差后,弹道参数的光滑性与平稳性得到了明显改善。
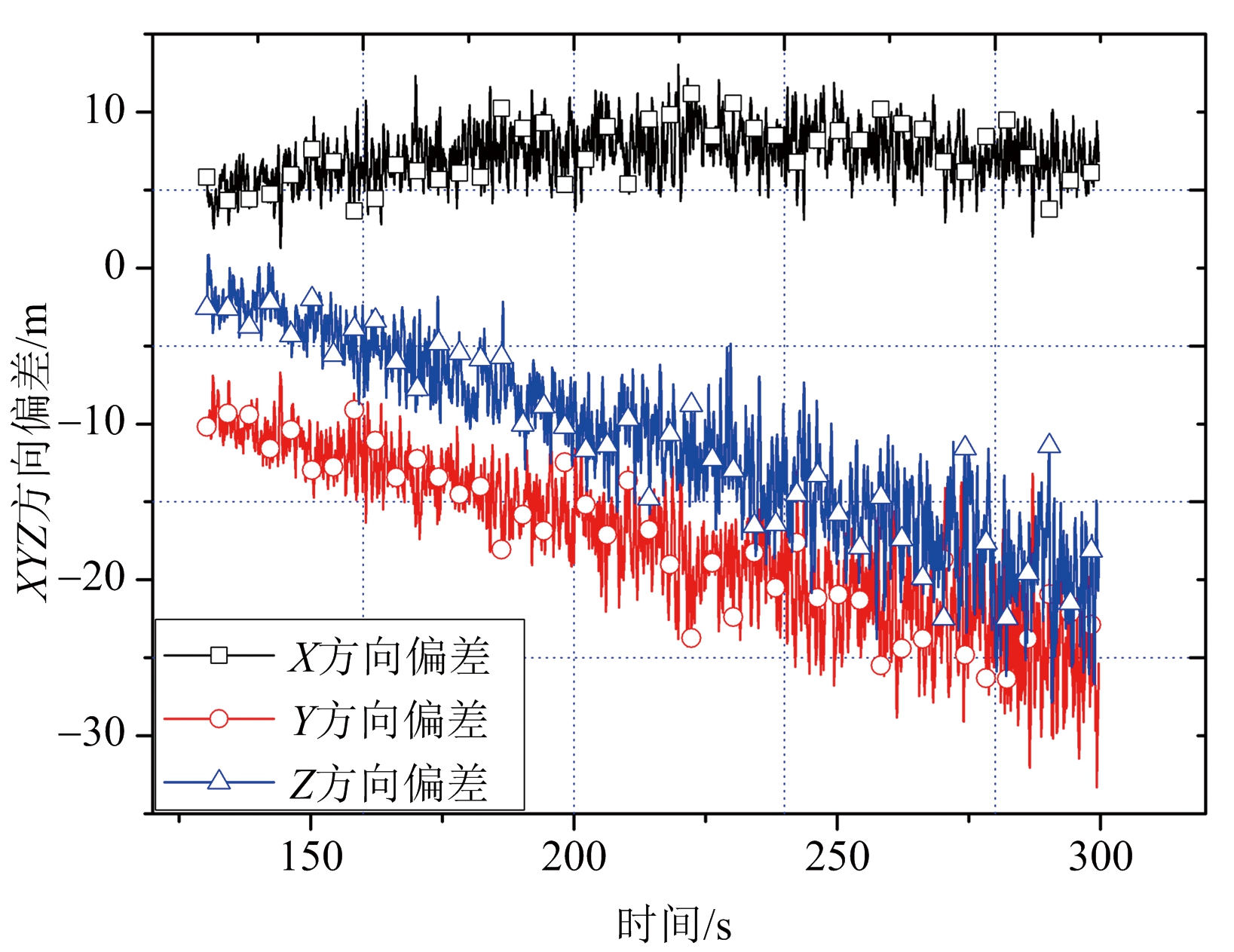
(a) 随机误差分离前
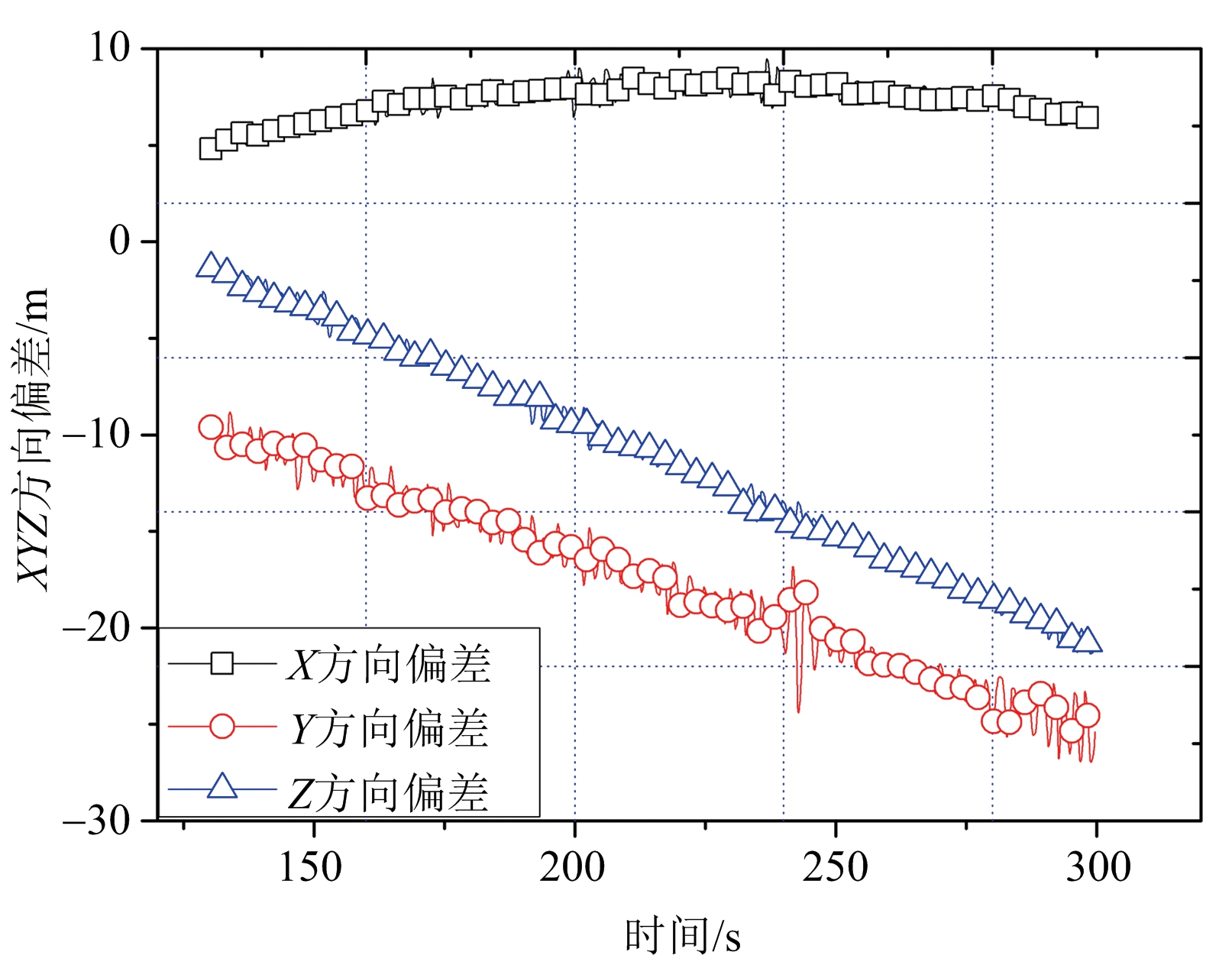
(b) 随机误差分离后
图2 采用小波方法分离随机误差前后弹道参数误差曲线
实践证明,靶场外测数据随机误差性质复杂,用简单的模型不能准确统计出随机误差的数字特征。传统方法只能统计随机误差的大小而不能对其有效分离,平滑滤波器可以将部分随机误差分离但不能对其值进行估计。采用小波变换的方法可以高精度地分离靶场测量数据的随机误差,且不需要噪声先验知识,噪声强度可以通过高频波分解系数进行估计,有效提高了弹道参数的精度和平稳性。
2 系统误差诊断方法
传统的靶场测量数据系统误差处理,通常采用与高精度数据作差后的残差平均值作为测控设备的固定偏差并进行扣除,这种方法对消除复杂的系统误差,如时间、光机、光电、动态滞后等误差应用效果较差。本文依据可匹配的测元系统误差成分建立测控设备误差回归分析模型,通过模型辨识确定最优,然后利用回归分析方法对系统残留误差进行分离。
2.1 系统误差模型分析和诊断方法
脉冲测量雷达在卫星发射、导弹试验的上升段、自由段、再入段按时段接力方式承担外弹道跟踪测量任务,作为靶场测控体制下的常规定位设备,在数据处理中占有重要的地位,对其测量数据的挖掘和应用具有深远的意义[9]。一方面,通过研究和分析脉冲雷达系统误差特性,可为设备准确查找误差源提供依据;另一方面,经过多个子样的统计和比对,找到误差变化的规律,力图采用先进、可靠的数据处理方法来弥补设备精度的不足。因此,本文以脉冲雷达的系统误差特性和参数估计方法为例进行分析,光学等其他外弹道测量设备的系统误差特性可由此借鉴。
作为一种数理统计方法,回归分析主要用于处理各变量之间的相关关系。对脉冲雷达建立一个误差分析模型,其中的误差系数作为未知数。根据不同弹道、不同目标,突出某些误差因素,忽略另外一些误差因素,以便确定这些待定系数,对系统残差进行估计和研究。根据测量误差模型和误差影响函数,省略其中的微小量,经过合并与化简,可导出如式(4)的脉冲雷达误差原始回归分析模型[10]。
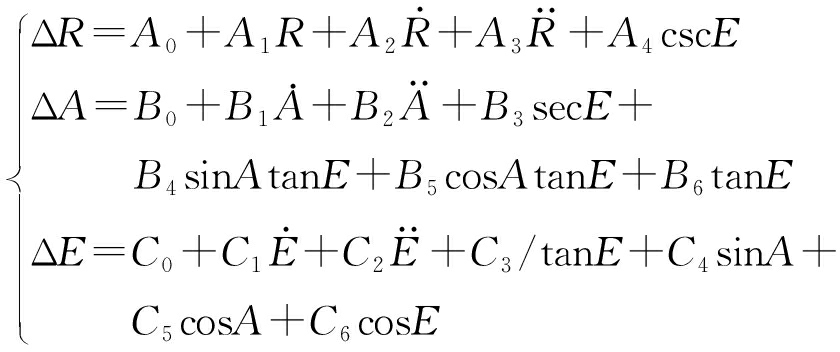
(4)
式中:ΔR为脉冲雷达测距系统误差;ΔA为脉冲雷达方位角系统误差;ΔE为脉冲雷达俯仰角系统误差;A0,B0,C0为零值;A1为比例误差系数;A2,B1,C1为时间误差系数;A3,B2,C2为动态滞后误差系数;A4为角度相关误差系数(包含折射残差);B3为对准误差系数(包含光机轴和光电轴误差);C3为俯仰角折射残差系数;B4,B5,C4,C5为大盘不水平误差系数;B6为不正交误差系数;C6为天线重力下垂误差系数。
从这些系统误差的基函数可以看出,部分误差项可能存在相关性。因此,在估计系统误差时总是假设没有系统误差,即系统误差项尽量少,估计过程中丢掉影响较小(通常为数值较小)的系统误差项。如有高精度标准数据,如卫星精轨或弹载GNSS数据,可以使用最小二乘估计方法直接给出这些系统误差估计值。将一组观测数据和所对应的系统误差带入式(4)的回归分析模型中,上述问题可归结为求解下列线性方程组。假设m个观测数据y1,y2,…,ym与n个待估系数x1,x2,…,xm有如下线性关系式[11-12]:
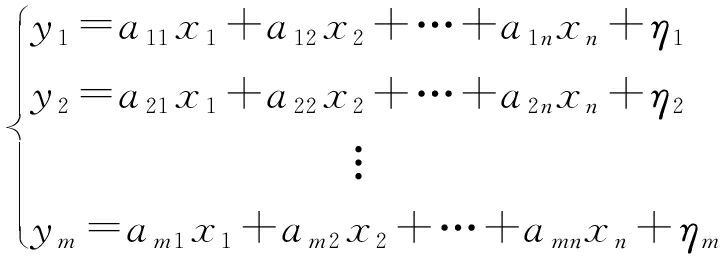
(5)
式中:{aij}为已知脉冲雷达的观测数据,{ηi}为观测数据的随机误差,满足
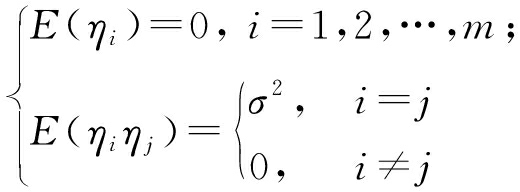
(6)
用矩阵形式来表示方程组(6),有
Y=AX+η
(7)
式(4)中:rankA=n,E(η)=0,E(ηηT)=σ2I。当m>n时,即观测子样个数多于未知系数个数时,经典的最小二乘估计为
(8)
上述系统误差模型中,某些误差项影响很小,当测量元素较多,待估的误差源过多,加上众多误差源之间可能存在相关性,会造成矩阵的病态。此时必须通过系统误差模型辨识、压缩和筛选影响很小的误差项,合并相关性较强的误差项。由于引入的误差模型已近似为线性模型,因此可以应用线性模型假设检验方法对实测数据系统误差模型进行辨识,辨识内容有如下3项[13]。
1) 系统误差模型的准确性检验(或称显著性检验);
2) 系统误差模型的紧致性检验(或称有效性检验);
3) 系统误差模型的稳定性检验。
显著性检验的目的在于检验系统误差是否明显存在,检验引入的误差模型与实际情况是否相吻合。如果假设检验成立,则误差模型可以接受。模型中每个误差源对测量数据的影响各不相同,有的影响很小,有些误差源之间则存在相关性。在综合处理中,如果待估的误差源过多,会影响它们估计的精度。因此,在估计系统误差时总是假设没有系统误差,即系统误差项尽量少,估计过程中丢掉数值较小的系统误差项。必须对误差源进行筛选,使误差模型紧致。在跟踪飞行器飞行的过程中,不同弧段上外测系统误差模型会发生变化,为检验模型稳定性,可将观测数据分成两组(或多组),检验各组误差向量是否一致。
2.2 应用效果
典型单脉冲雷达系统误差分离的具体步骤为:
1) 根据原始模型和误差特性分析结果建立初始回归模型;
2) 对所建立的回归模型进行模型辨识,判断其正确性;修改模型并重复模型辨识过程直至确定最优模型;
3) 依据最优模型进行回归分析,分离系统误差。
在靶场某雷达精度鉴定过程中,采用本文提出的方法通过测距系统误差估计分析出设备存在约-26 ms的时间误差。为了检验误差模型的正确性,分别使用全程数据和部分数据进行估计,结果如表1所示,统计结果显示系统误差模型可以有效估计设备的时间误差。
表1 某脉冲雷达跟踪卫星的时间误差估计结果

段落时间段/sΔt/msσtAll46656~46942-26.0480.004146656~46800-29.1670.012246800~46942-26.1860.011
使用全程数据扣除系统误差前后的测距残差序列如图3所示,估算的测距零值为-15.8 m,扣除零值和时间误差后的残差序列的均值为0 m,标准差为8.0 m。
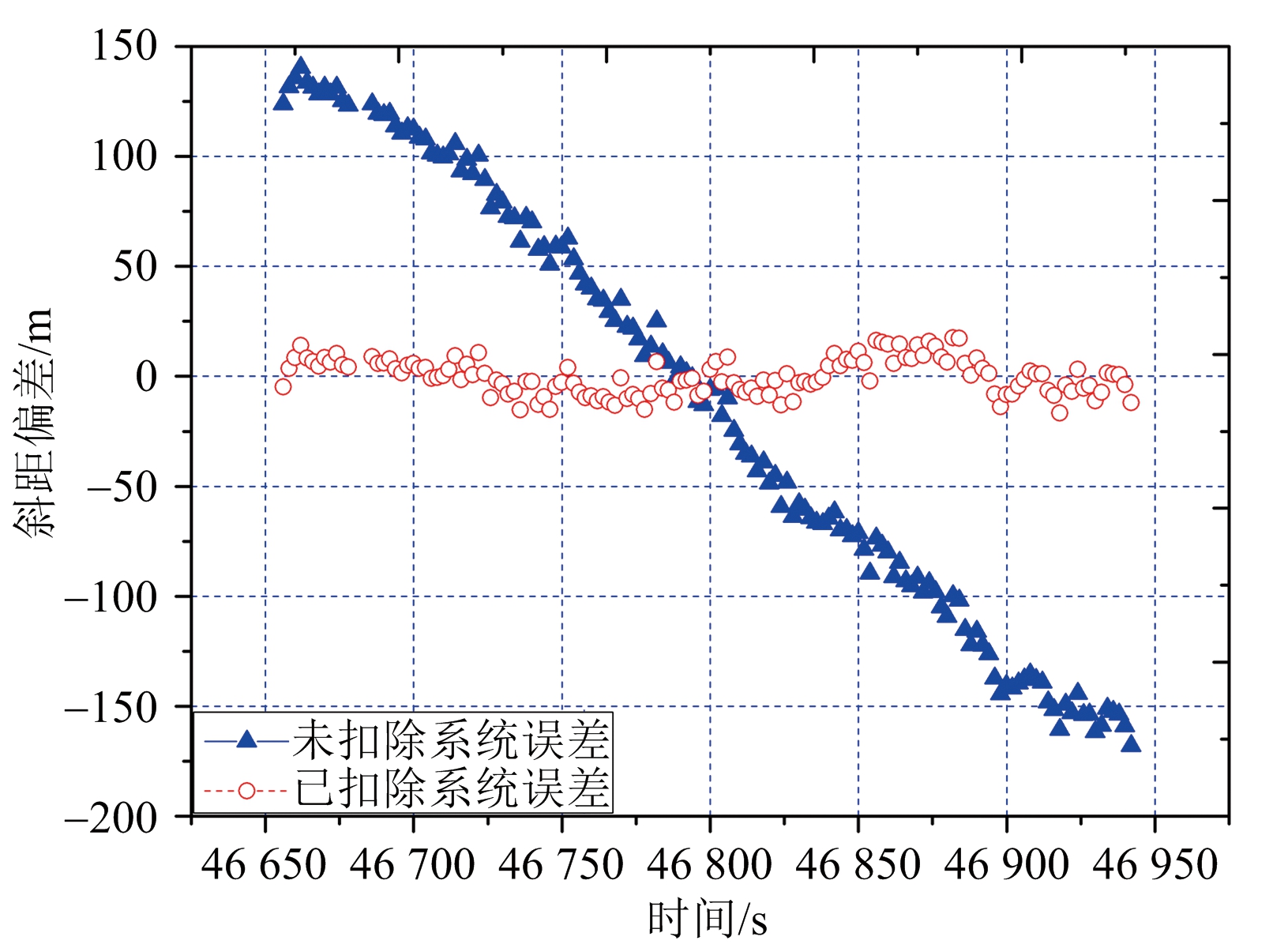
图3 某脉冲雷达跟踪卫星的测距残差曲线
同样对雷达的方位、俯仰角进行系统误差估算与分析。首先添加所有误差项,发现方位角不正交误差与动态滞后误差较大;俯仰角零值误差较大;然后忽略其他误差项分别进行重新估计,认为该设备方位角确实存在不正交误差和动态滞后误差,在与设备人员沟通后对不正交误差重新进行标校后,分别修正方位角的动态滞后误差和俯仰角的零值误差。系统修正前后的雷达方位角、俯仰角残差序列如图4所示。
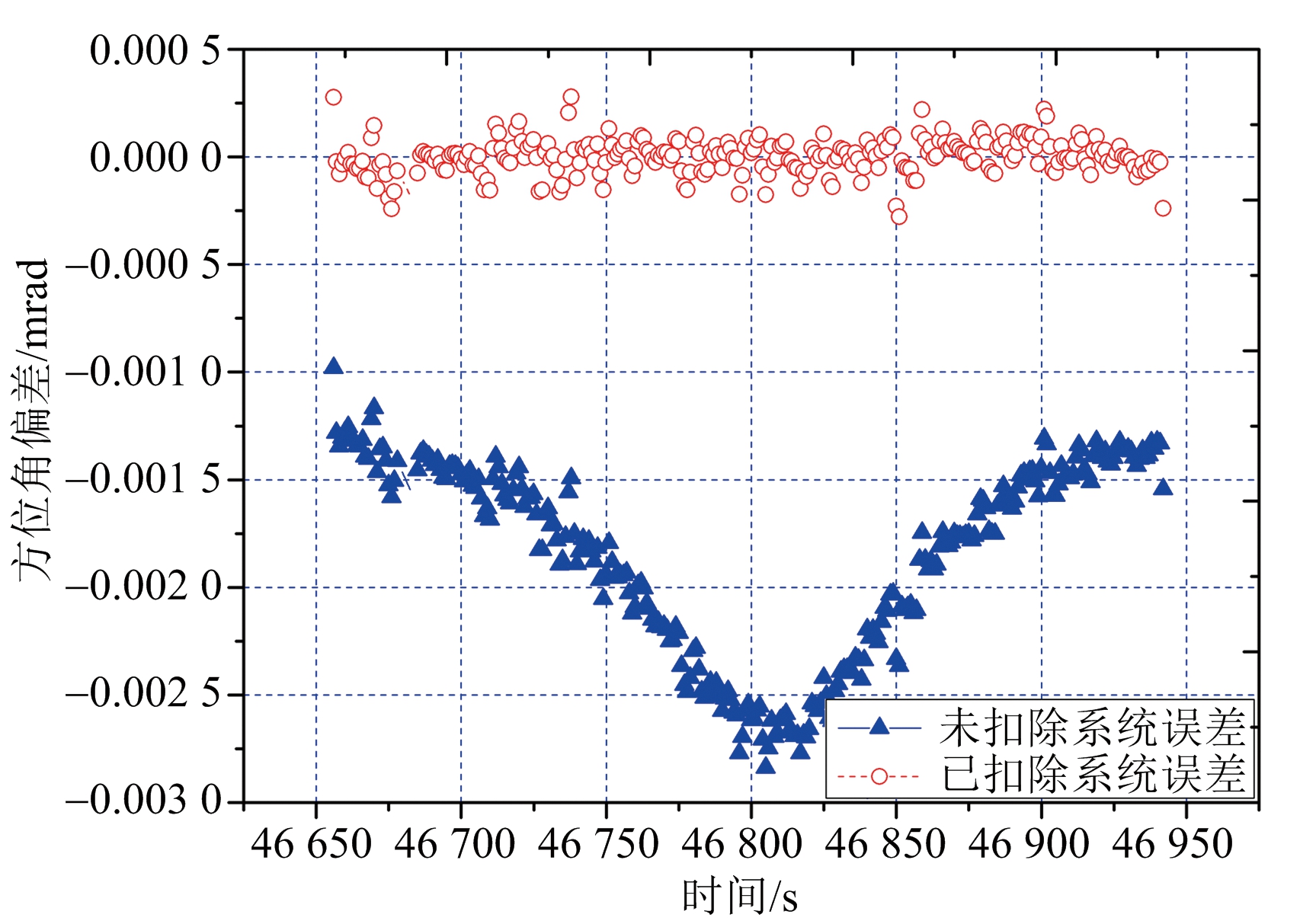
(a) 方位角残差
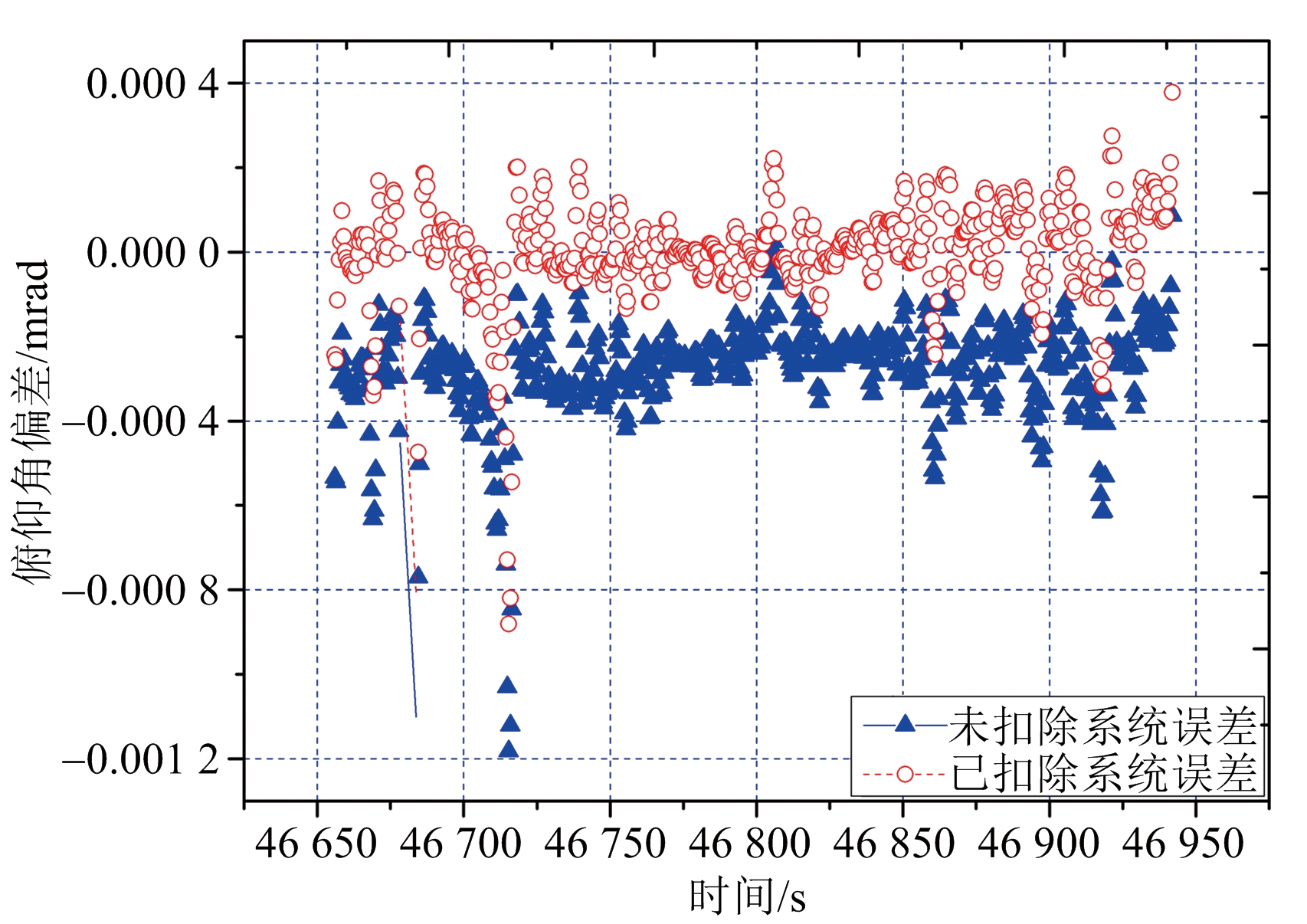
(b) 俯仰角残差
图4 某脉冲雷达精度鉴定时测角残差曲线
由图4可见,系统误差修正后,雷达方位角、俯仰角偏差基本被消除,测量精度明显提高。通过多次仿真测试表明,该方法在事后数据处理中能准确、有效分离出系统残差的主要成分。同时,误差识别结果在实时数据处理中应用可以最大限度地消除系统误差,提高实时弹道参数求解精度。
3 结束语
高密度、常态化的航天任务对发射场外测数据预处理方法提出了越来越高的要求,本文提出的小波非线性滤波和回归匹配诊断新方法,解决了传统方法难于对发射场测控设备测元误差进行准确分离与估计的难题,可有效提高参与融合求解的测元数据质量和外弹道参数精度。
[1] 邢卫国,岳素华.提高航天飞行器外测数据精度的处理方法[J].无线电通信技术,2003,29(3):1-2.
[2] 王翔.基于多弧段测量数据的低轨空间目标精确定轨方法研究[D].哈尔滨:哈尔滨工业大学,2017.
[3] 单时卓,张南,兰洪亮,等.导弹武器系统精度类数据误差统计方法研究[J].现代防御技术,2018,46(3):133-138.
[4] 王欢,张永顺.小波分析在雷达绝对精度分析中的应用[J].弹箭与制导学报,2007(4):305-306.
[5] 董长虹.Matlab小波分析工具箱原理与应用[M].北京:国防工业出版社,2004:34-35.
[6] 郭丽华,朱元昌,尹文龙.小波变换在外测数据随机误差分离中的应用[J].弹箭与制导学报,2011,31(4):249-252.
[7] 孙延奎.小波分析及其应用[M].北京:机械工业出版社,2004:233-235.
[8] 王永凯.基于阈值函数和阈值的小波去噪方法研究[D].秦皇岛:燕山大学,2017.
[9] 刘世奎.导弹外弹道测量数据处理工程方法[M].北京:国防工业出版社,2017:243-250.
[10] 郭军海,钱卫平,张艳.弹道测量数据融合技术[M].北京:国防工业出版社,2012:60-61.
[11] 胡亚男,淳静.基于事后数据分析的脉冲雷达误差分离方法研究[J].装备指挥技术学院学报,2010,21(6):97-101.
[12] 王子润.雷达组网系统误差自适应修正方法研究[D].南京:南京理工大学,2018.
[13] 胡亚男,陈大庆,甘友谊.单脉冲雷达系统误差特性与分离方法研究[J].现代雷达,2010,32(5):39-43.
