0 引言
强杂波环境下慢速运动目标的检测一直是雷达探测的重点之一[1]。由于雷达实际工作环境比较复杂,目标回波信号易受到强地杂波干扰,使得运动目标很容易被淹没在杂波中难以检测[2]。此外,由于运动目标的速度低,目标回波多普勒频率处在零频附近,与强地物固定杂波及慢速杂波存在严重交叠[3],传统的基于动目标显示(Moving Target Indication,MTI)和动目标检测(Moving Target Detection,MTD)的杂波抑制算法性能严重下降,无法完成对杂波的有效抑制[4]。因此,如何在强杂波背景下实现杂波有效抑制并提高对慢速运动目标的检测能力成为了一个急需解决的问题[5]。
传统的杂波抑制方法主要从时域或频域上滤除杂波,当它们的多普勒频谱明显重叠时,不能充分地分离目标回波和杂波。近年来,基于子空间的杂波抑制方法被广泛应用于雷达目标检测领域中,现有的子空间方法主要基于奇异值分解(Singular Value Decomposition,SVD)或特征值分解(Eigenvalue Decomposition,EVD),主要思想是基于回波信号特征,通过特征分解分离目标子空间和杂波子空间,以抑制杂波成分并突显目标信号。针对海杂波环境下微小目标检测问题,文献[6]提出了正交投影抑制海杂波的方法,通过利用参考单元观测数据构造杂波子空间,然后将待测信号投影到杂波正交子空间中抑制海杂波,能够降低计算复杂度。针对强杂波环境下微小目标的检测问题,文献[7]以奇异值分解理论为基础,利用奇异值差分谱的极值点对雷达回波进行分区,从而达到杂波抑制和目标检测的目的,文献[8]提出了一种基于相位编码及子空间投影的方法,先通过相位解码白化杂波,再依据白化杂波和目标的自相关性差异及特征值比值来分离杂波和目标子空间,最后通过子空间投影来抑制杂波。针对血流成像中杂波的抑制问题,文献[9]对比分析了基于奇异值,空间奇异向量和时间奇异向量选择阈值的方法,证明了利用空间奇异向量的相关性进行奇异值分解杂波抑制的效果最优。基于子空间杂波滤波方法具有一定的杂波抑制效果。然而,现有的基于子空间杂波抑制方法的一个主要问题是杂波子空间难以精确划分,尤其在慢动目标检测中,目标回波与杂波存在严重混叠,其杂波子空间的准确划分将会直接影响到目标检测的性能。如上述在基于子空间方法的滤波中,实现杂波基阈值选择的方法很多,但是大多数方法都是根据特定场景的经验值来选取杂波基,其并不具有普适性。
针对杂波阈值难以确定的问题,本文设计了一种基于K-均值聚类的子空间投影杂波抑制方法,主要利用奇异值幅度分布、回波信号反映在奇异向量上的空间相关性特征和平均多普勒频率特征,对相应的特征分量进行聚类。根据杂波和目标信号具有不同的空时特性,应用 K-均值聚类算法自适应地确认与杂波对应的特征分量,并构建杂波子空间,最后通过正交子空间投影,实现对回波信号中杂波成分的有效抑制,从而提高在强杂波环境下慢速运动目标的检测性能。
1 信号模型
雷达发射机发射信号为线性调频信号,雷达脉冲宽度为Tp,脉冲重复周期为Tr,调频带宽为B,调频斜率定义为μ=B/Tp,载频为fc,则雷达在第n个发射周期的发射信号为
Sn(t)=![]()
(1)
设t=0 时刻,目标相对于雷达的距离为R0,匀速运动的速度为v,则此时目标的回波延迟可以表示为τ=2(R0-vtn)/c,tn=nTr,因此,可以得到单个目标在第n个周期内的回波模型为
xnr(t)=![]()
exp[j2π(fc(t-nTr-τ)+
(2)
式中,c(t)为杂波,n(t)为高斯白噪声。
将得到的回波信号xnr(t)重排成快慢时间维回波矩阵,并对快时间维脉冲压缩可得
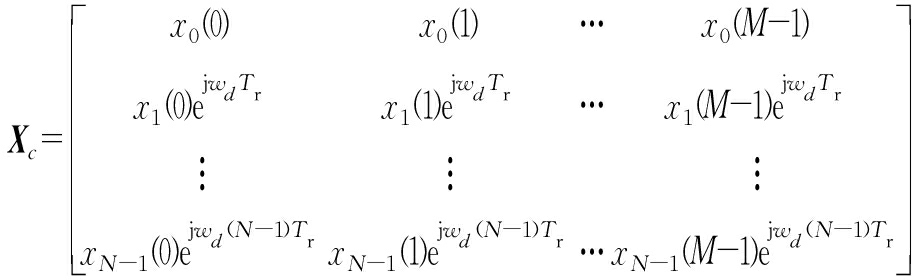
(3)
式中,Xc为N×M维的回波数据矩阵,N为脉冲积累个数,M为距离单元数。
2 基于K-均值聚类的SVD杂波抑制算法
2.1 SVD子空间投影
对经过脉冲压缩的回波数据矩阵Xc进行奇异值分解可得
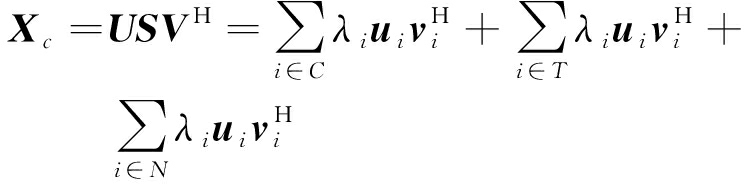
(4)
式中,C,T,N分别表示杂波、目标和噪声子空间的奇异值集合,上标H表示矩阵的共轭转置,ui和vi分别为矩阵Xc的第i个左奇异值向量和右奇异值向量,λi为第i个奇异值,按从大到小降序排列。在确定表征杂波的奇异值集合C之后,可以得到下面的奇异向量矢量积来表示杂波子空间:
(5)
基于最小二乘法构建与杂波子空间正交的子空间矩阵![]() 可以表示为
可以表示为
(6)
式中,I为单位矩阵。为了抑制强杂波的影响,将回波信号矩阵Xc投影到该正交子空间中:
(7)
2.2 杂波子空间的确定
为了充分抑制杂波,如何选取表征杂波子空间所对应的奇异谱向量是关键问题。现有奇异值分解大多数只从奇异值分布情况(如最大奇异值或奇异值差分谱)来确定杂波基,或单从奇异向量入手确定杂波基,未能充分利用杂波的特性来选取杂波基,导致杂波抑制出现较大的残余。本文分析了回波数据中主要构成成分的特性,接收端回波信号主要由杂波、目标信号以及噪声三种成分构成,其中杂波成分是由发射信号经静止物体如地面、墙体、灌木等或慢速运动的物体一次或多次反射造成,主要分布在零多普勒附近,因此在不同的距离单元具有较强的空间相关性且平均多普勒较低,同时由于墙体和地面的反射能力强,杂波的回波能量强度较高;而待检测运动目标只在某个或若干个距离单元出现且目标的RCS比较小,所以目标的空间相关性较小、回波能量弱,且平均多普勒一般高于静止或慢速杂波信号。根据杂波和信号的差异性,利用奇异值幅值分布、奇异向量的空间相关性和平均多普勒频率三个特性对特征分量进行聚类,无需人为设定阈值参数估计杂波基,能够自适应确定杂波子空间所对应的奇异向量。
2.2.1 奇异值谱及奇异向量分析
1) 奇异值谱分布。在强杂波环境下,杂波占主导地位,杂波回波能量往往比目标信号回波能量大,通过奇异值分解获得雷达回波数据矩阵的归一化奇异值幅度分布如图1(a)所示,虽然只截取了前40个奇异值,但可以看到奇异值的幅值下降得比较平缓,不存在明显的突变点,这是因为杂波成分的特征分布具有多维性,导致杂波子空间和目标子空间发生混叠。
2) 奇异向量的相关性。回波矩阵Xc的奇异值分解结果是V奇异向量提供空间信息,而U奇异向量表示Xc中的多普勒信息[10-11]。地杂波的相关性主要是指距离项的空间相关性[12],不同距离分辨单元中的地杂波具有较强的相关性,而目标只存在某一个或若干个距离分辨单元中,因此目标信号的空间相关性较差,利用目标信号分量和地杂波分量的空间相关性差异,也是子空间分解类杂波抑制算法能够有效抑制杂波的基础[13]。接收的回波信号中杂波与杂波之间的相关性较强,而杂波与目标信号回波的相关性较弱,对回波信号矩阵进行奇异值分解,得到的奇异向量表征了这种特性。其中,因为回波信号中杂波成分占主导地位,杂波能量较强,因此最大奇异值对应的奇异向量V1表征了杂波成分,计算V1与左奇异向量之间的相关系数:
ρV1,Vk=![]()
(8)
式中:Vk为第k个奇异值对应的右奇异向量,k∈[1,M],M为快时间维的采样点数;V1为第一个奇异值对应的右奇异向量;E(Vk),σk分别表示Vk的均值和标准差;ρV1,Vk为相关系数向量。相关系数向量的曲线图如图1(b)所示,从图中可知,前面二十几个奇异向量的相关性大于后面奇异向量的相关性,揭示了与杂波所对应的低阶奇异向量的高相关性,以及对应目标的高阶奇异向量的低空间相关性。
3) 平均多普勒估计。地杂波主要分布在零多普勒频率附近,相对于运动目标,平均多普勒较小。利用滞后一位的自相关估计器,计算每个左奇异向量Uk的平均多普勒频率:
![]()
(9)
(10)
式中,![]() 为第k个左奇异向量Uk的平均多普勒估计,PRT为脉冲重复周期。图1(c)给出了左奇异向量的平均多普勒频率估计曲线。从图中可知,前面二十几个奇异值向量的平均多普勒频率在零频附近上下波动,符合杂波的特性。
为第k个左奇异向量Uk的平均多普勒估计,PRT为脉冲重复周期。图1(c)给出了左奇异向量的平均多普勒频率估计曲线。从图中可知,前面二十几个奇异值向量的平均多普勒频率在零频附近上下波动,符合杂波的特性。
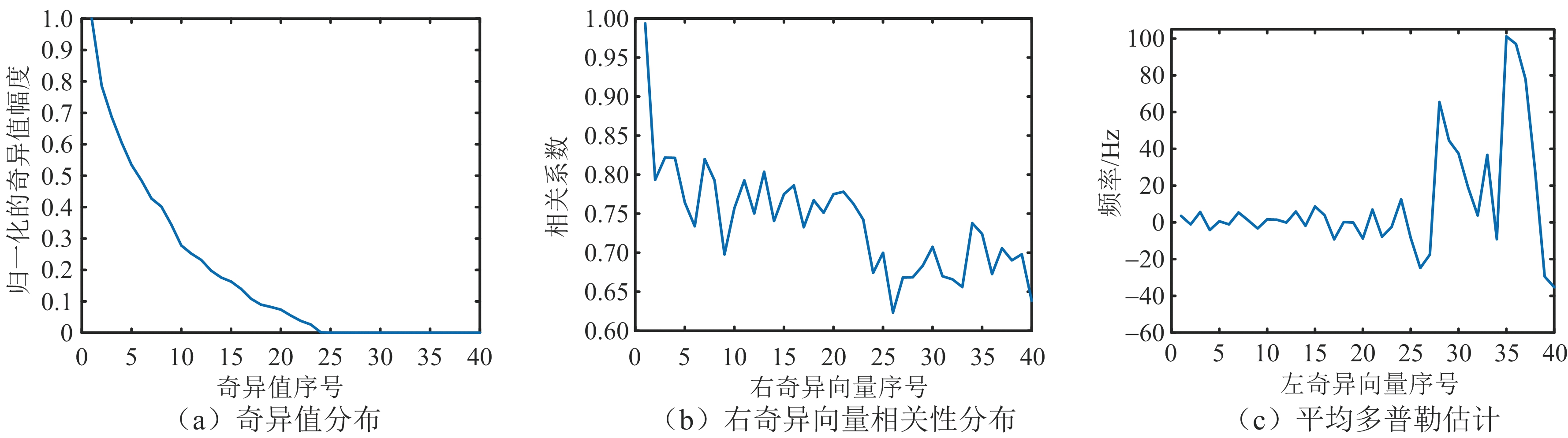
图1 奇异值及奇异向量特征分布图
2.2.2 K-均值聚类
K-均值聚类算法主要通过迭代法将一个给定的数据集划分为k个簇,具有简单高效、收敛速度快等优点,被广泛应用于科学研究等诸多领域。K-均值算法基本思想是首先确定期望被划分簇的个数k值,然后从给定的数据集中随机选取k个数据点作为质心即初始聚类中心,一般以欧式距离作为相似性度量计算数据集每一个数据点到k个质心的距离,最后根据最近邻原则将数据点划归到就近质心的簇中。接下来重新确定k个簇中的质心,计算式如式(11),假设有数据集X,将其按照上述过程划分为k个簇(C1,C2,…,Ck),则求质心μi的表达式为
(11)
将新得到的质心与上一次划分簇时的质心相比较,判定质心是否发生变化,如果没有发生变化,则迭代终止得到最终的聚类质心,否则根据上述方法重新划分簇,直到满足算法的收敛条件为止。
依据奇异值幅度分布、奇异向量的空间相关性特征和平均多普勒频率特征三个特征,本文采用K-均值聚类算法对回波信号奇异值分解后的数据进行聚类,如图2所示。从图中可知,“聚类3”数据(蓝色)分布在奇异值幅值较大,空间相关性较强,以及平均多普勒较小的区域,与杂波的特性相符,因此“聚类3”被确定为代表杂波成分的类。而“聚类1”和“聚类2”的数据分布在奇异值幅值较小、空间相关性较弱和平均多普勒较大的区域,因此分别代表了目标回波成分与噪声成分。因为噪声能量较小,且噪声的频率丰富,在整个频谱上都有成分,而弱目标的回波信号能量小,目标的多普勒信息未知,因此聚类为表征目标回波与噪声的类的类间距非常接近,不易分开。所以本文选择表征为杂波信号的聚类作为杂波子空间,如图3所示,蓝色部分奇异值对应的奇异向量作为杂波基。基于此,本文自适应地确定代表杂波成分的奇异向量作为杂波基,然后利用构建的杂波基,根据最小二乘法做子空间投影以实现抑制回波信号中的杂波成分。
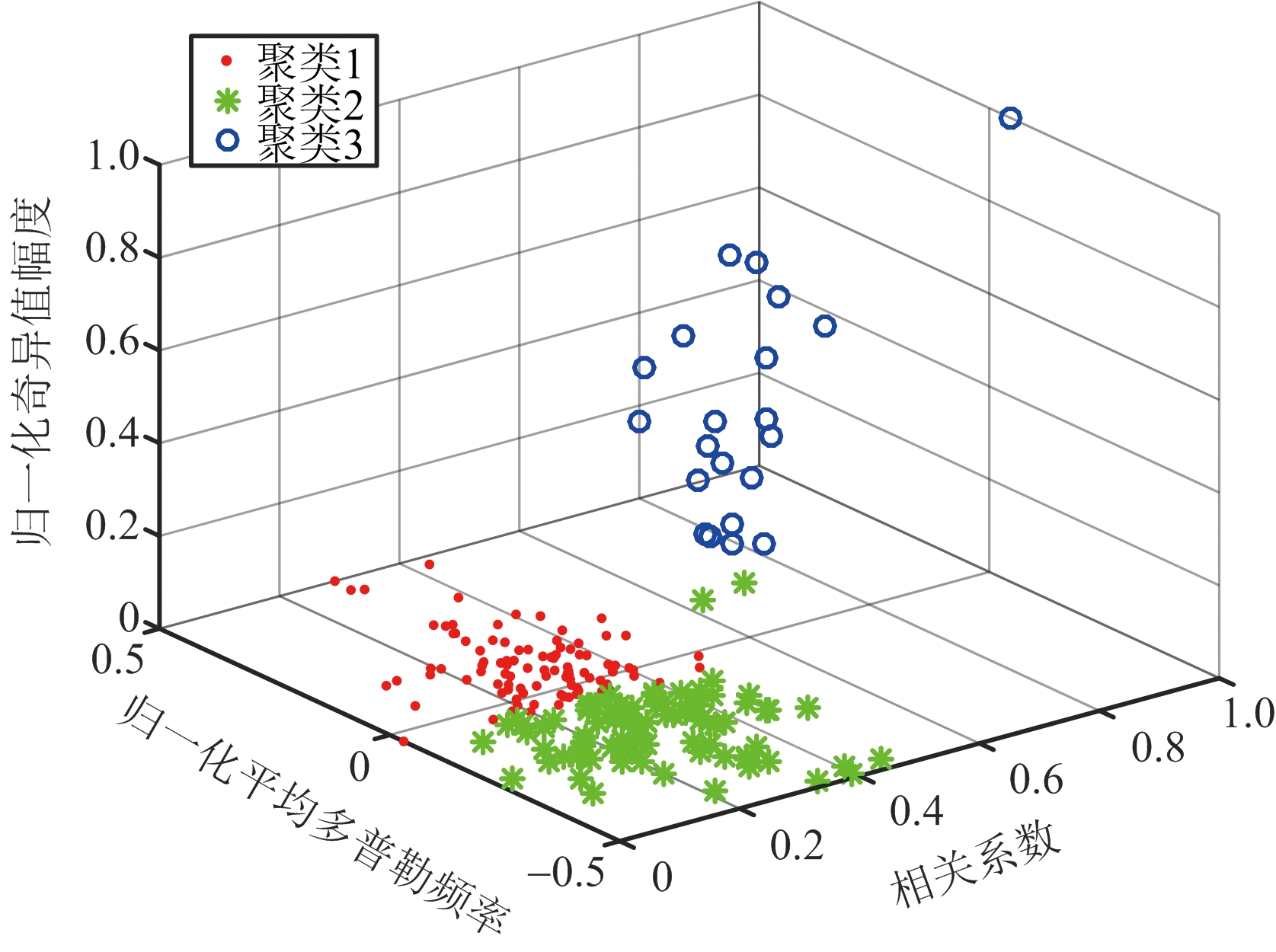
图2 K-均值聚类三维分布图
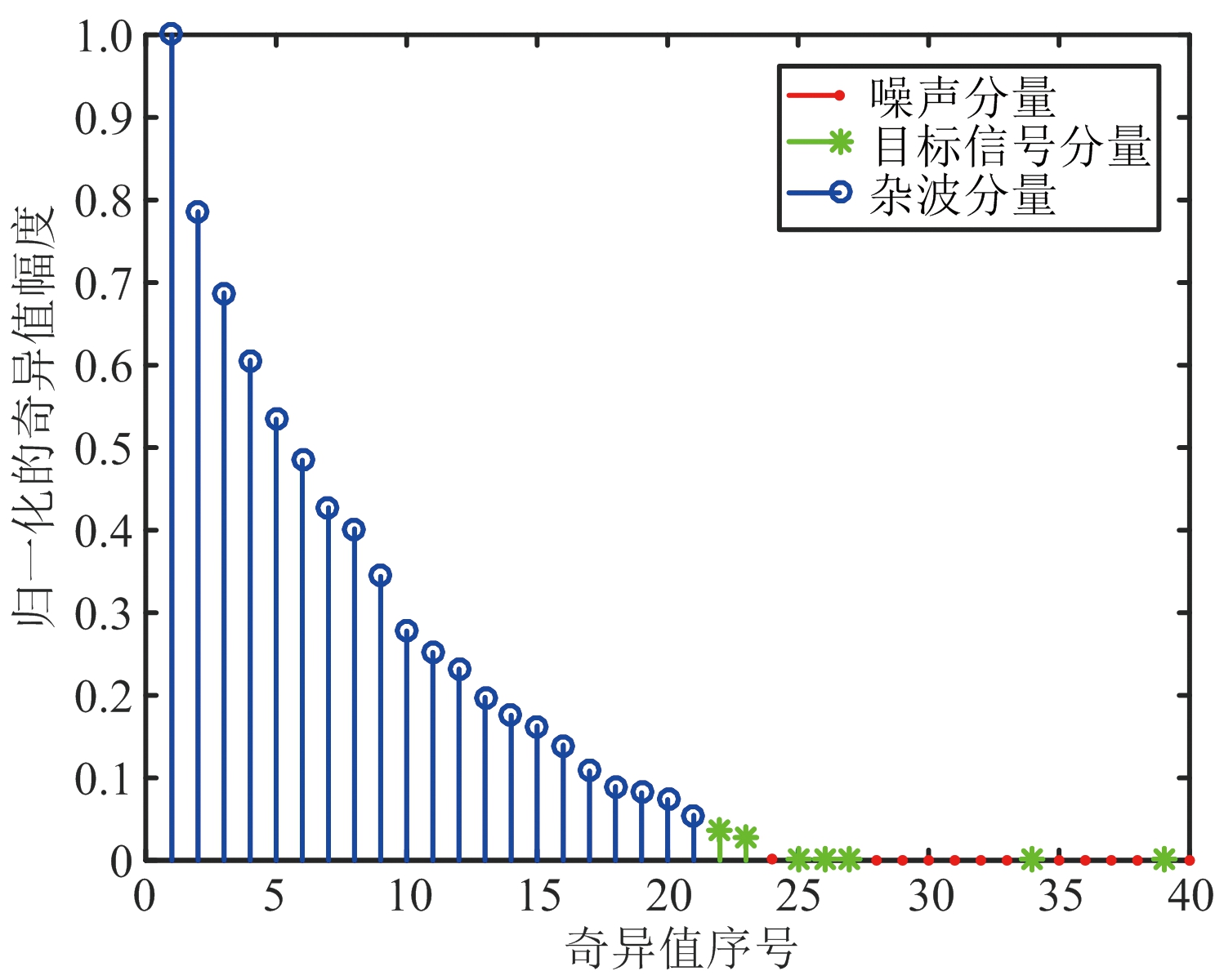
图3 奇异值分布图
3 仿真实验
为了验证算法的有效性,本文按照表1所给的雷达参数进行了仿真实验,并与现有的基于传统杂波抑制方法进行了比较分析。仿真实验的杂波信号采用符合地杂波特性的瑞利杂波模型生成,且预先在场景中设置一个径向速度为2 m/s,距离为40 m运动目标。为了体现强杂波环境,设置的信杂比为-28 dB。
表1 雷达系统仿真参数
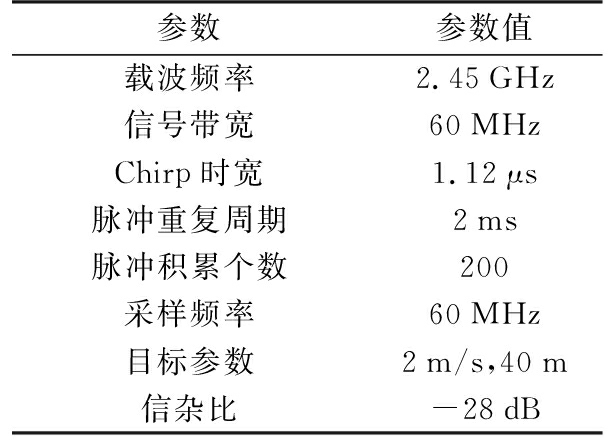
参数参数值载波频率2.45GHz信号带宽60MHzChirp时宽1.12μs脉冲重复周期2ms脉冲积累个数200采样频率60MHz目标参数2m/s,40m信杂比-28dB
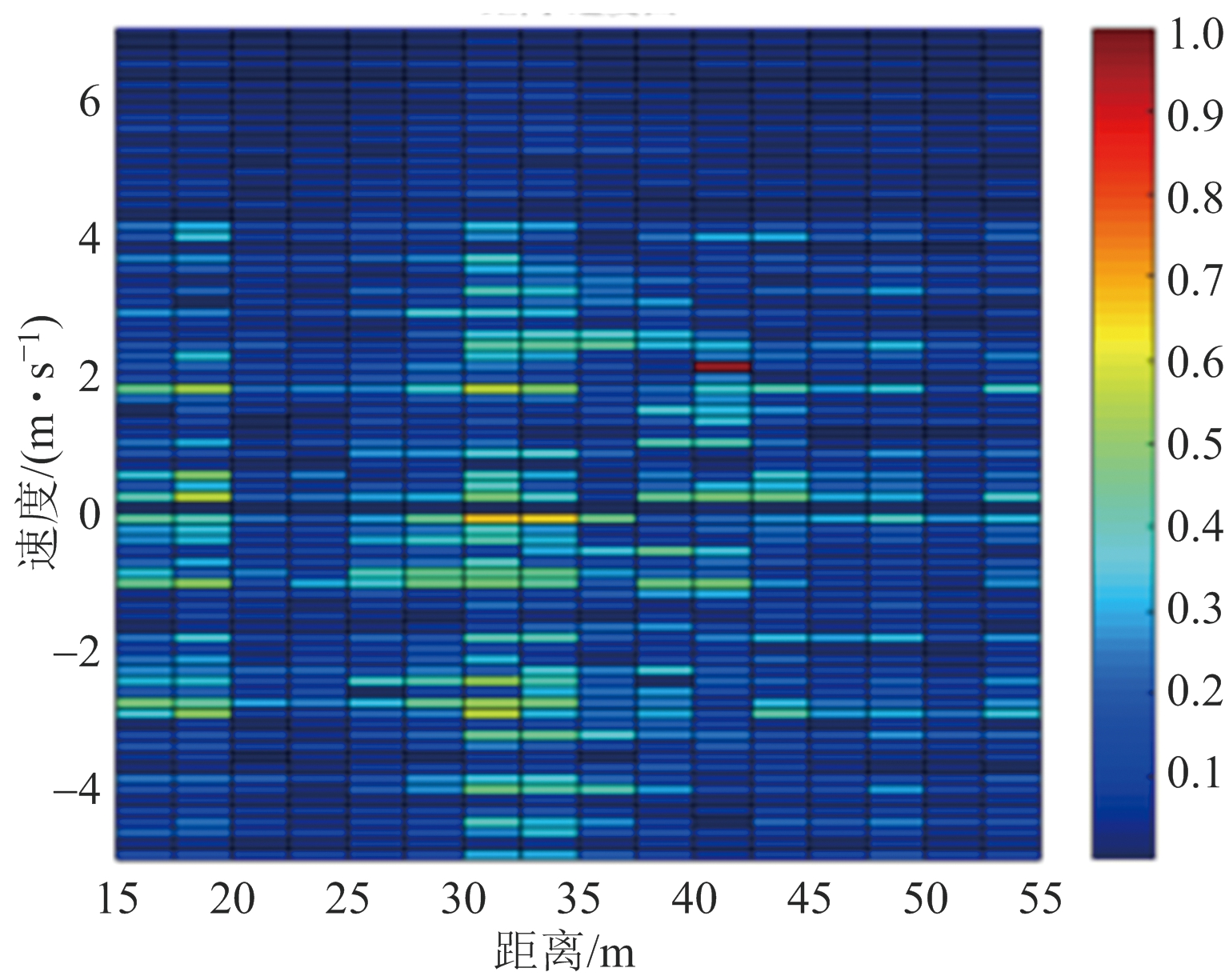
图4(a)给出了仅相参积累后的距离-速度图。从图中可以看出,由于地杂波的扩展使得目标信号在多普勒谱上被杂波成分所掩盖,目标无法被清晰地检测出来。图4(b)、(c)、(d)分别是采用二阶MTI算法、传统子空间方法和本文基于K-均值聚类的子空间杂波抑制方法处理结果图。MTI处理的基本思想是基于杂波与目标回波多普勒频率的不同,在零频附近产生一个凹陷来滤除零频杂波,但对于慢速目标来说,其回波多普勒也处在零频附近,MTI算法在抑制零频杂波的同时,对目标回波也有较大的衰减。而且在强杂波环境下目标被杂波所掩没时,MTI处理后的残余杂波对运动目标仍有较大影响,如图4(b)所示,MTI算法无法起到较好的抑制效果。传统的子空间方法一般选择最大的一个或几个特征值对应的特征向量来构建杂波子空间,但是杂波子空间往往存在交织特性,当奇异值阈值选择过小时,抑制后仍有较大杂波残留;当奇异值阈值选择过大时,部分目标信号的成分会被当作杂波成分抑制掉,导致目标能量减弱,不利于目标检测。如图4(c)所示选取前15个特征向量作为杂波基,经过子空间投影后仍残留较多的杂波,杂波抑制效果并不理想。
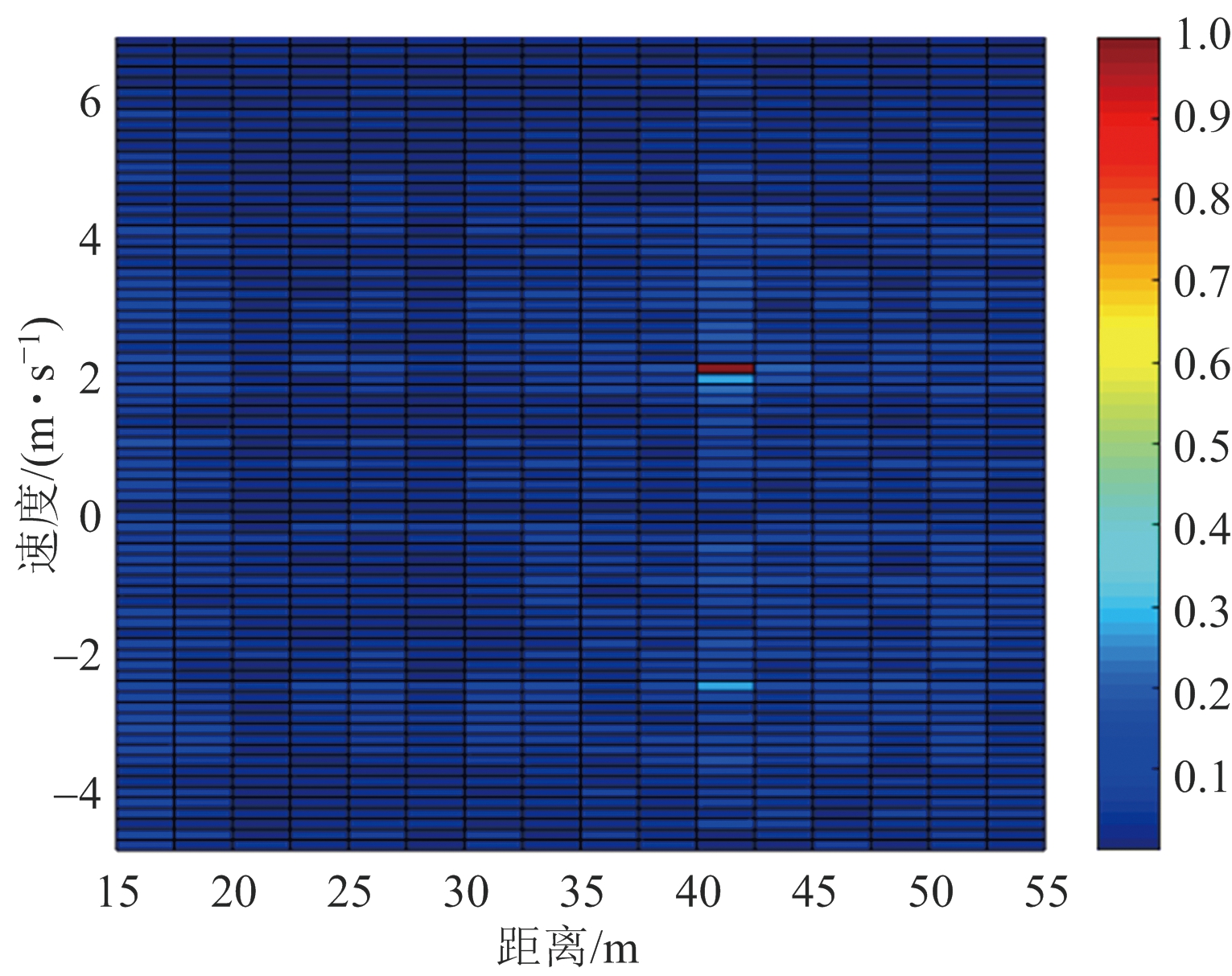
图4(d)是本文的子空间方法杂波抑制的效果,从图上可以看出目标的距离为40 m,速度为2 m/s,和预先设置的目标运动参数一致,表明杂波能够得到较好的杂波抑制效果且目标信号得到凸显。本文的子空间方法主要是从回波信号特征出发,利用奇异值分解后的奇异值和奇异向量特性,结合聚类算法自适应地选取与杂波所对应的特征成分,然后通过构建杂波子空间并进行子空间投影,实现对杂波的有效抑制。
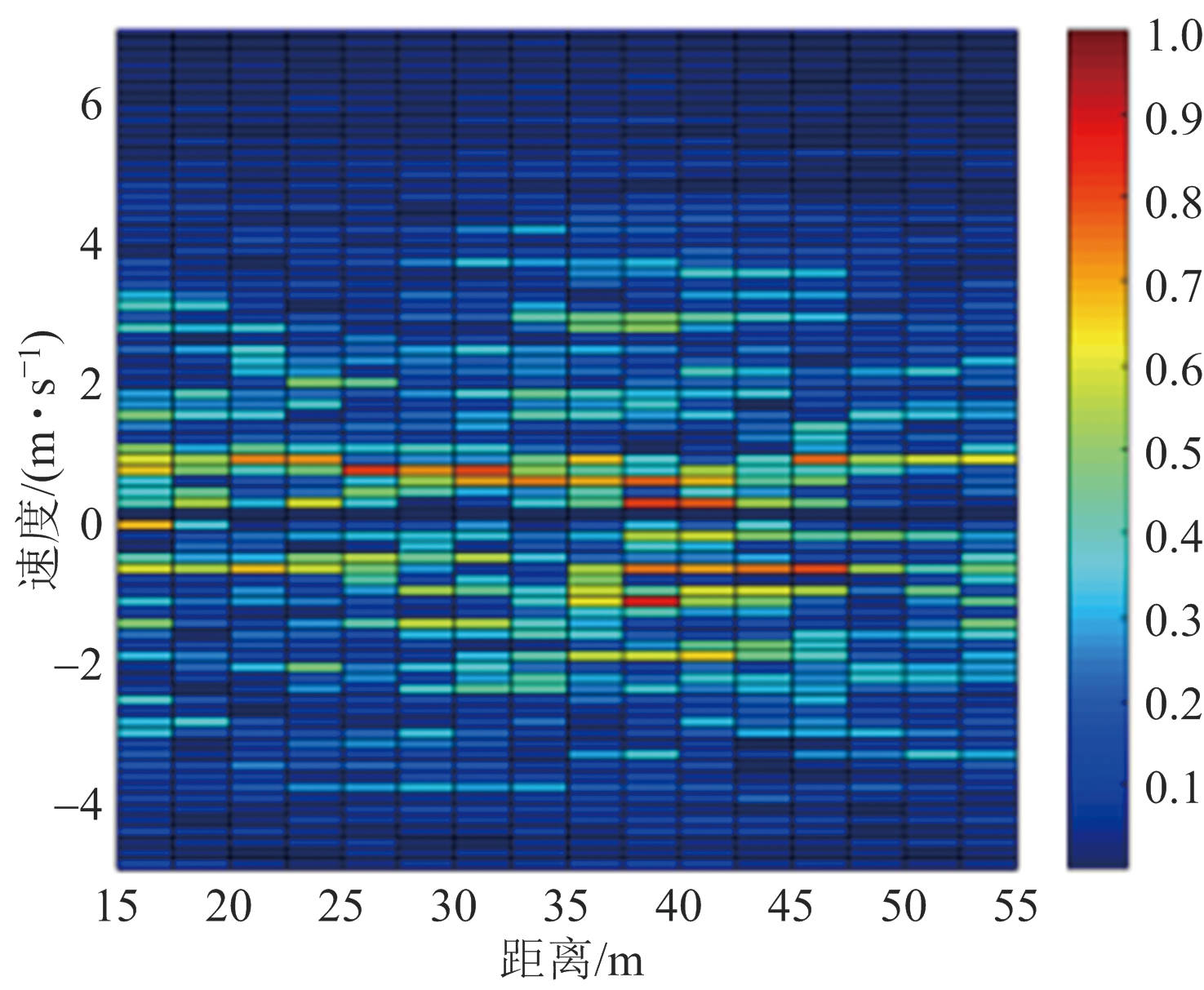
(a) 未进行杂波抑制处理
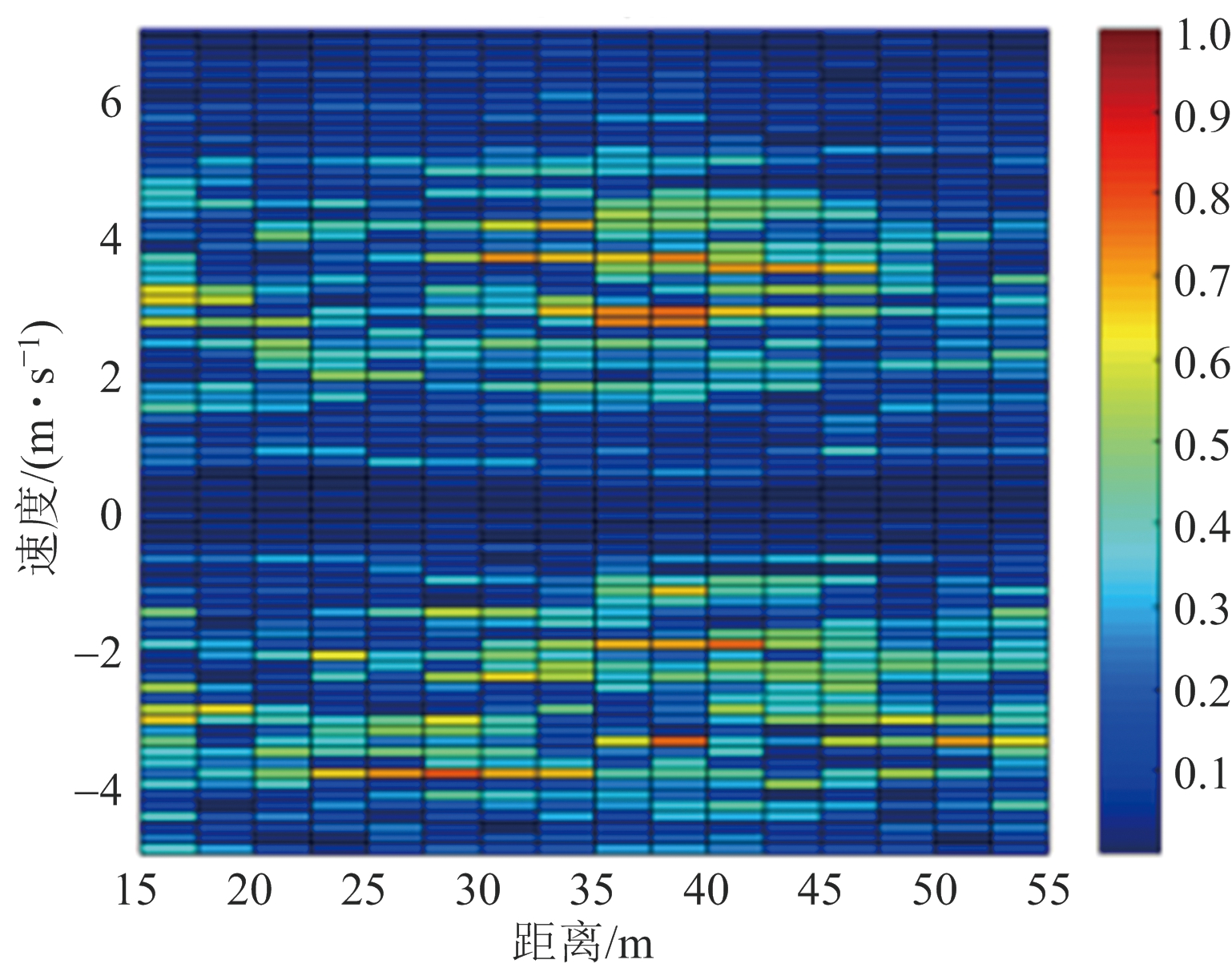
(b) MTI
(c) 传统子空间方法
(d) 本文SVD法
图4 多种目标检测算法抗杂波的性能比较
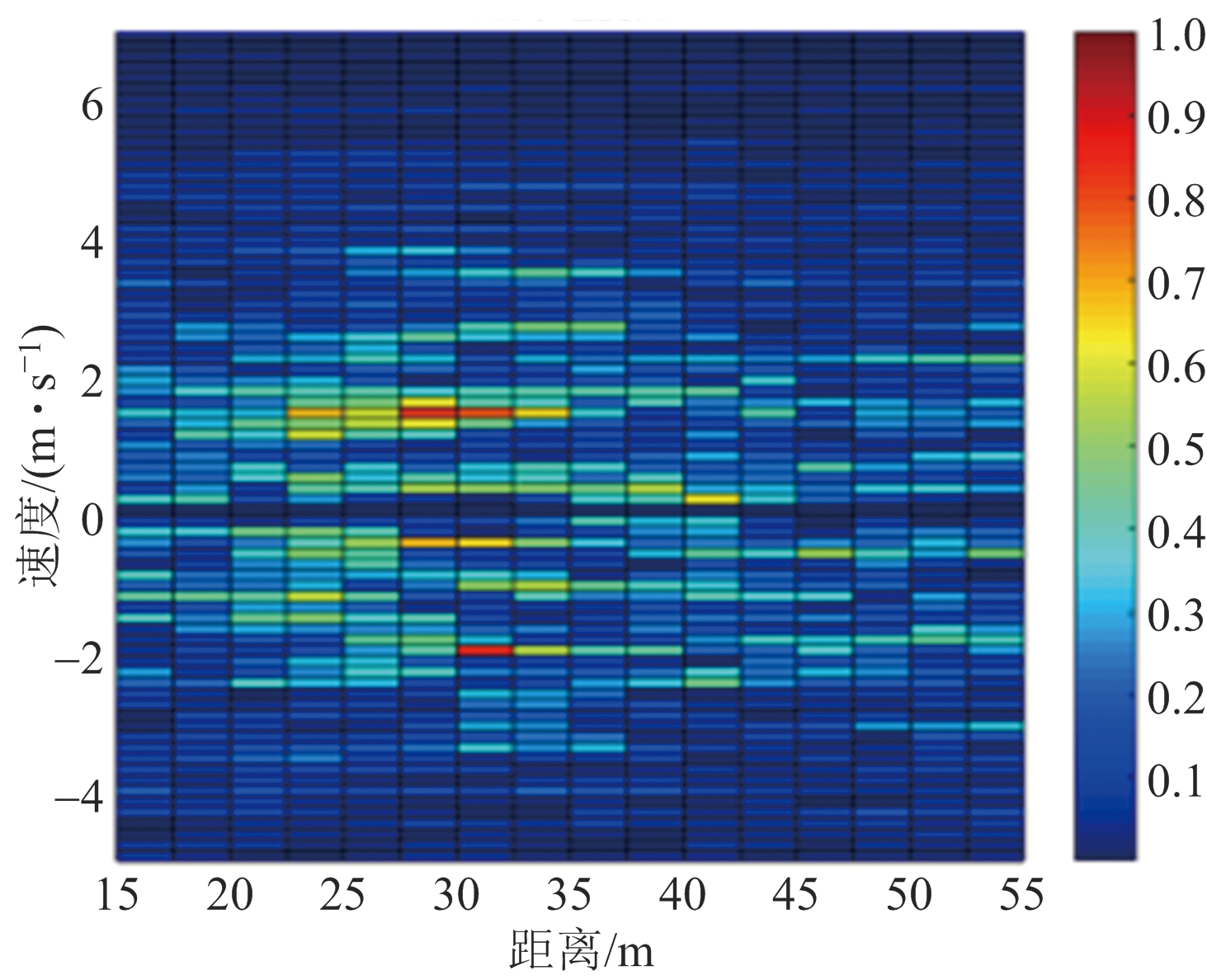
为了验证算法在多目标场景下的适用性,在实验中预先设置径向速度为-2 m/s、距离为30 m和速度为2 m/s、距离为30 m的两个运动目标。如图5(a)所示,在本文场景下运动目标均被杂波所掩盖。
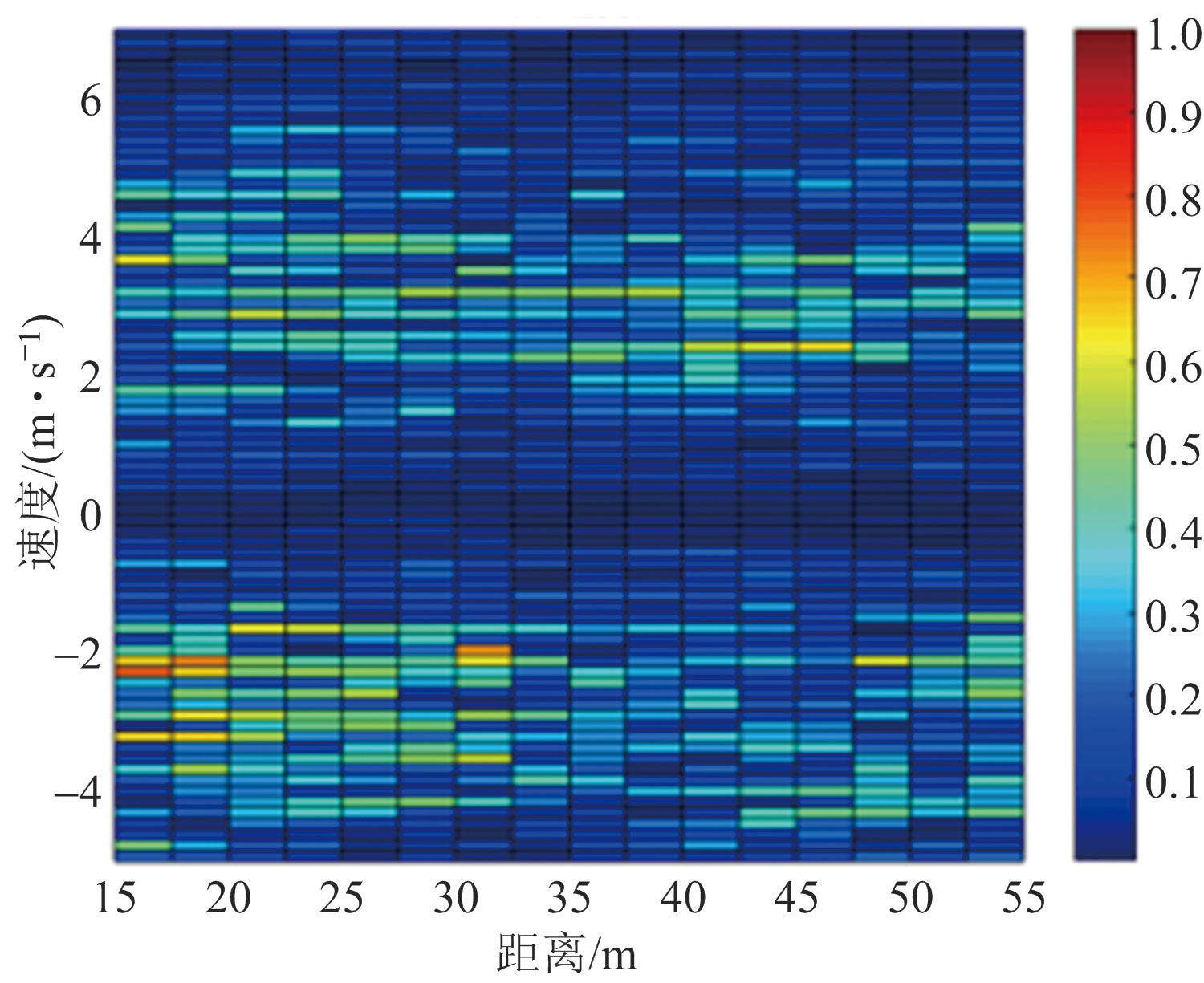
在图5(b)中,MTI方法在抑制零频杂波的同时,对运动目标回波也有较大衰减。在图5(c)中经过传统子空间方法处理后两个目标得以凸显,但是由于杂波基选取不恰当,仍存在较多的杂波残留。而图5(d)本文子空间方法可以看出,基于K-均值聚类来自适应选取奇异向量作为杂波基,能够更加充分地抑制掉杂波,使目标能更加清晰地被检测出来。
(a) 未经过杂波抑制处理
(b) MTI方法
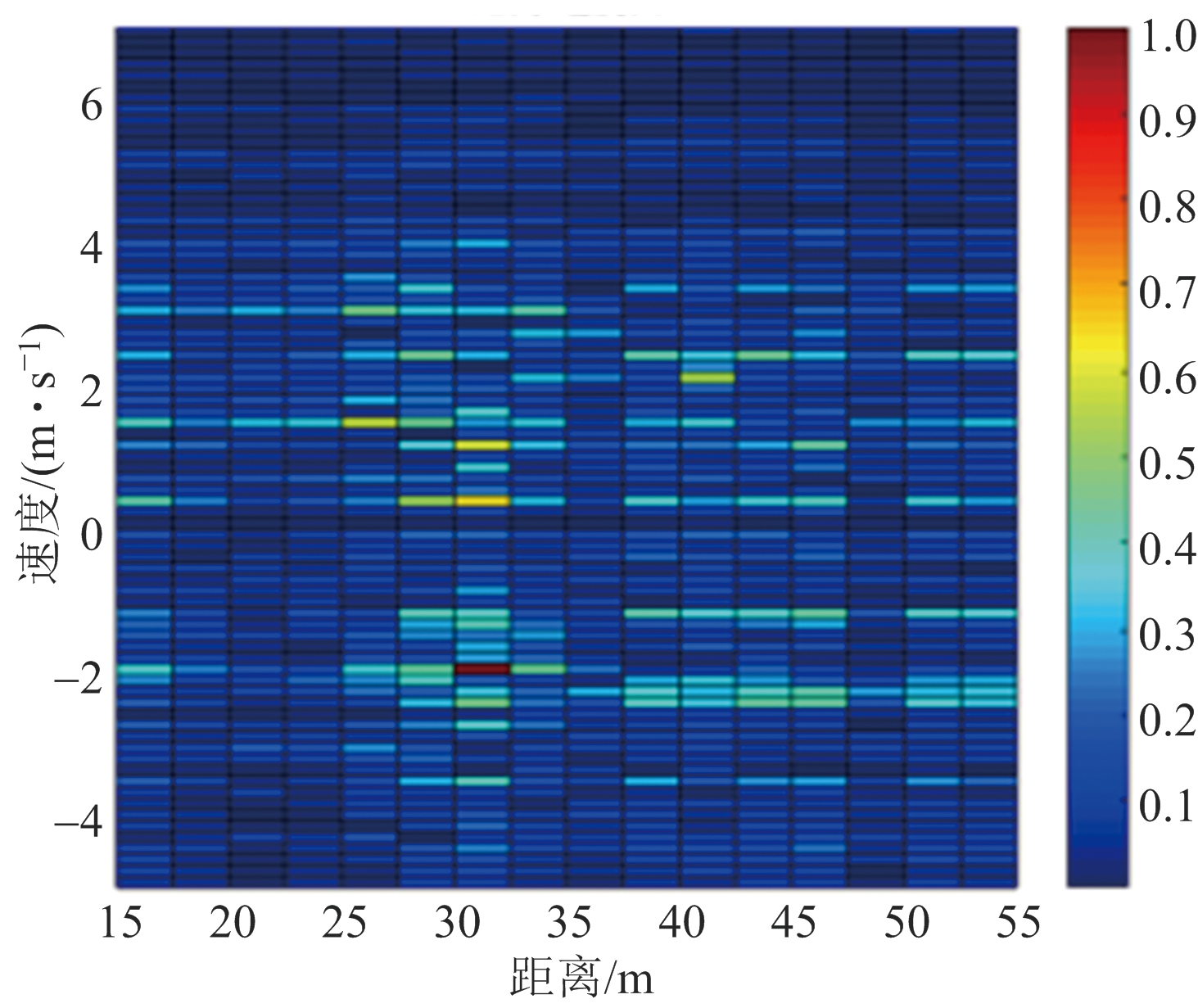
(c) 传统子空间方法
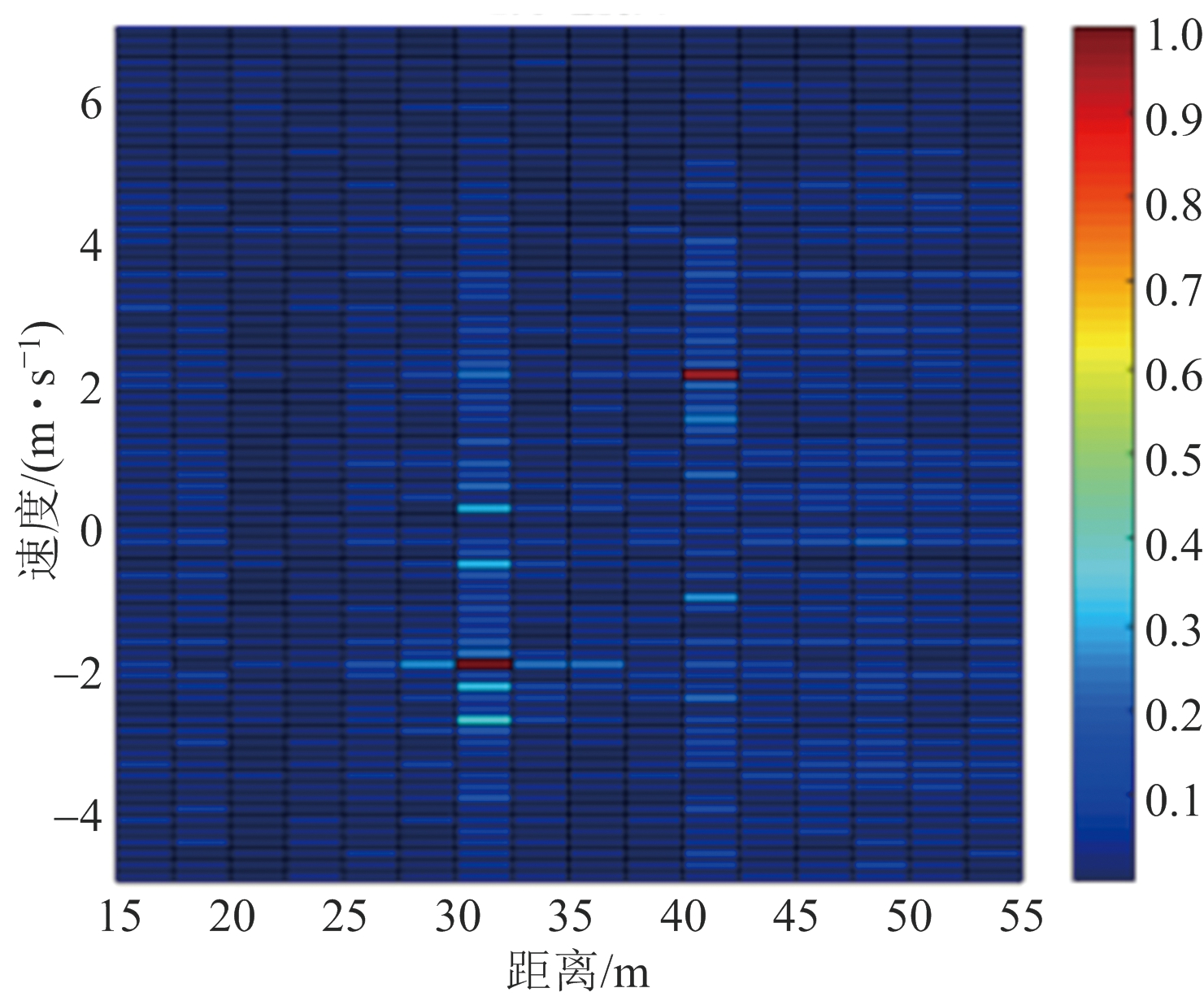
(d) 本文子空间方法
图5 多目标场景下目标检测算法抗杂波的性能比较
4 结束语
针对强杂波环境下慢速运动目标被掩盖的问题,本文设计了一种基于K-均值聚类的子空间投影杂波抑制算法。相比于传统子空间方法只选取最大一个或几个特征值所对应的特征向量构建杂波子空间,本文算法依据回波信号特性,得到相应的奇异值谱分布,以及奇异向量的空间相关性特征和平均多普勒频率特征三个特征,采用K-均值聚类算法对奇异值分解后的数据进行聚类,自适应地确定相应的奇异向量来构建杂波子空间。本文方法无需人为设定阈值参数来估计杂波基,实现了杂波的自适应抑制,也为在杂波基的选取上提供了一种新的思路。实验结果也表明了相对于传统的杂波抑制方法,本文方法提高了强杂波环境下对慢速运动目标的检测性能。
[1] 许道明,张宏伟. 雷达低慢小目标检测技术综述[J]. 现代防御技术,2018,46(1):148-155.
[2] HYUN E,JIN Y S,LEE J H. A Pedestrian Detection Scheme Using a Coherent Phase Difference Method Based on 2D Range-Doppler FMCW Radar[J]. Sensors,2016,16(1):124.
[3] GUO B,VU D,XU L Z,et al. Ground Moving Target Indication via Multichannel Airborne SAR[J]. IEEE Trans on Geoscience and Remote Sensing,2011,49(10):3753-3764.
[4] SCHLEHER D C. MTI and Pulsed Doppler Radar with MATLAB[M]. US: Artech House,1991.
[5] 于张杰. LFMCW雷达慢速弱目标检测技术研究[D].南京:南京理工大学,2017.
[6] YANG Yong,XIAO Shunping,WANG Xuesong. Radar Detection of Small Target in Sea Clutter Using Orthogonal Projection[J]. IEEE Geoscience and Remote Sensing Letters,2019,16(3):382-386.
[7] 吴琳拥,毛谨,白渭雄. 基于奇异值分解的雷达微小目标检测方法[J]. 电子科技大学学报,2019,48(3):326-330.
[8] 郑霖,姚伟伟,杨超,等. 近距离慢速目标检测杂波抑制方法[J]. 电子与信息学报,2018,40(10):2506-2512.
[9] BARANGER J,ARNAL B,PERREN F,et al. Adaptive Spatiotemporal SVD Clutter Filtering for Ultrafast Doppler Imaging Using Similarity of Spatial Singular Vectors[J]. IEEE Trans on Medical Imaging,2018,37(7):1574-1586.
[10] LEDOUX L A F,BRANDS P J,HOEKS A P G. Reduction of the Clutter Component in Doppler Ultrasound Signals Based on Singular Value Decomposition: A Simulation Study[J]. Ultrasonic Imaging,1997,19(1):1-18.
[11] DEMENE C,DEFFIEUX T,PERNOT M,et al. Spatiotemporal Clutter Filtering of Ultrafast Ultrasound Data Highly Increases Doppler and Ultrasound Sensitivity[J]. IEEE Trans on Medical Imaging,2015,34(11):2271-2285.
[12] 严韬,陈建文,鲍拯. 基于WLS的OTHR短时自适应海杂波抑制方法[J]. 华中科技大学学报(自然科学版),2017,45(8):20-25.
[13] 关泽文,陈建文,鲍拯. 一种改进的基于峰值信噪比-高阶奇异值分解的天波超视距雷达自适应海杂波抑制算法[J]. 电子与信息学报,2019,41(7):1743-1750.
[14] LI Hai,SONG Wenyu,LIU Weijian,et al. Moving Target Detection with Limited Training Data Based on the Subspace Orthogonal Projection[J]. IET Radar,Sonar & Navigation,2018,12(7):679-684.
[15] 朱建宇. K均值算法研究及其应用[D].大连:大连理工大学,2013.
[16] LI Changzhi,PENG Zhengyu,HUANG Tienyu,et al. A Review on Recent Progress of Portable Short-Range Noncontact Microwave Radar Systems[J]. IEEE Trans on Microwave Theory and Techniques,2017,65(5):1692-1706.
[17] TANG Hui,WAN Xianrong,KE Hengyu. Signal Detection in Clutter and Noise Using Well-Characte rized Subspace[J]. IEEE Signal Processing Letters,2017,24(9):1343-1347.
[18] BI Wenda,ZHAO Yonghui,AN Cong,et al. Clutter Elimination and Random-Noise Denoising of GPR Signals Using an SVD Method Based on the Hankel Matrix in the Local Frequency Domain[J]. Sensors,2018,18(10):3422.





