0 引言
机载气象雷达目标检测过程中,反射回波中包含的强地杂波分量容易将气象目标信息湮没。如何利用气象目标检测技术从强地杂波背景中获取气象目标信息受到了广泛关注。基于多通道数据处理的地杂波抑制方法虽然可以有效缓解强地杂波对气象观测的影响[1-3],但抑制性能受限于通道幅相误差、系统热噪声等不确定性因素,导致抑制后的回波中仍会残留部分地杂波分量。气象目标检测技术可以有效滤除气象目标周围的残余杂波,提高雷达观测效果。目前已有文献大多针对地基气象雷达设计地杂波检测方法[4],但关于机载气象雷达目标检测的研究尚少,此类问题亟待解决。
地杂波和气象目标在谱矩信息方面存在明显差异[5-7]。气象目标具有非零多普勒频率特性且谱宽大于1 m/s,而地杂波谱宽一般小于0.3 m/s[8]。此特性差异将影响回波慢时间域的相位变化。在相位起伏方面,地杂波比气象目标更稳定。文献[9]利用杂波相位对准(Clutter Phase Alignment,CPA)技术实现地杂波和气象的区分。文献[10]利用相位起伏指标(Phase Fluctuation Index,PFI)来反映时间序列样本的相位偏离拟合曲线的程度。文献[11]引入与PFI类似的相位结构函数(Phase Structure Function,PSF)来描述慢时间域相位变化快慢程度,以实现气象目标检测。此外,文献[8]提出了一种基于时域和频域处理的频谱杂波判别(Spectrum Clutter Identification,SCI)方法,利用四种参数实现对气象目标的联合检测。
综上所述,已有检测方法主要涉及时域和频域,且检测性能均依赖于谱矩信息。然而,多普勒频谱展宽在机载气象雷达系统中不可避免,严重影响数据相位结构的稳定性[12]。此外,为避免产生距离模糊,雷达的脉冲重复频率通常较低,但较低的方位向采样频率会产生多普勒模糊[13-14]。因此,利用谱矩信息实现气象目标检测所受的制约因素较多。
为避免多普勒频谱展宽和多普勒模糊对检测性能的影响,本文利用气象目标的高度信息,提出了一种基于干涉相位的空域气象目标检测算法。首先,利用俯仰双通道系统获取回波数据,经过多视处理和干涉相位补偿后生成待检测的干涉相位图。由于地杂波和气象目标的高度差异,二者对应的干涉相位值会有所不同。因此,该方法将干涉相位作为检验统计量,解析二者的干涉相位统计特性,设计恒虚警率(Constant False Alarm Rate,CFAR)检测器,将待检测数据与检测门限进行逐像素点比较,从而实现气象目标的鲁棒检测。
1 基于干涉相位的气象目标检测原理
为获取气象目标的高度信息,该方法利用俯仰双通道系统采集回波数据,对应的三维空间几何接收模型如图1所示。雷达工作于前视模式并以恒定速度沿X轴方向运动,扫描波束下视角为θ0。后向散射的回波经距离向脉冲压缩后可表示为[15]
s(t,τ)=η·sinc{B(τ-rs(t)/c)}·
exp{-j2πfc·(rs(t)/c)}
(1)
式中,sinc{x}=sin(πx)/(πx),τ和t分别代表快时间和慢时间,η,B,fc分别为脉冲压缩后回波信号的幅度、信号带宽和载波频率,rs(t)/c代表回波信号时延量。由上式可知,对于接收机A1和A2,双通道回波信号的幅度基本相同,但相位信息会存在差异。以地面C点(地杂波)为例,两通道信号的相位差(即干涉相位)可以表示为
(2)
式中,rA1C和rA2C分别代表点C到两接收机的距离,λ和θc分别为工作波长和点C对应的下视角。处于同一距离门的气象目标W点对应的干涉相位可表示为φW=(2π/λ)dsinθw,其中θw为气象目标对应的下视角。气象目标和地杂波二者混合信号的干涉相位取决于信杂比(Signal to Clutter Ratio,SCR),当SCR→-∞时,干涉相位值φW+C趋向于φC;反之,该值与φW保持一致。根据图1可知,|θw|<|θc|,因此,混合信号干涉相位值的范围可表示为
(3)
结合式(2)和式(3)可知,俯仰双通道接收系统中干涉相位与方位角无关。在扫描过程中,处于同一距离门的地杂波的干涉相位值随方位角的变化基本保持不变。但当此距离门存在气象目标分量时,计算所得干涉相位值将会偏离地杂波的干涉相位分布。因此,本文将干涉相位作为检验统计量,通过设定适当的干涉相位阈值对含有气象目标分量的像素点进行筛选,从而实现气象目标检测。
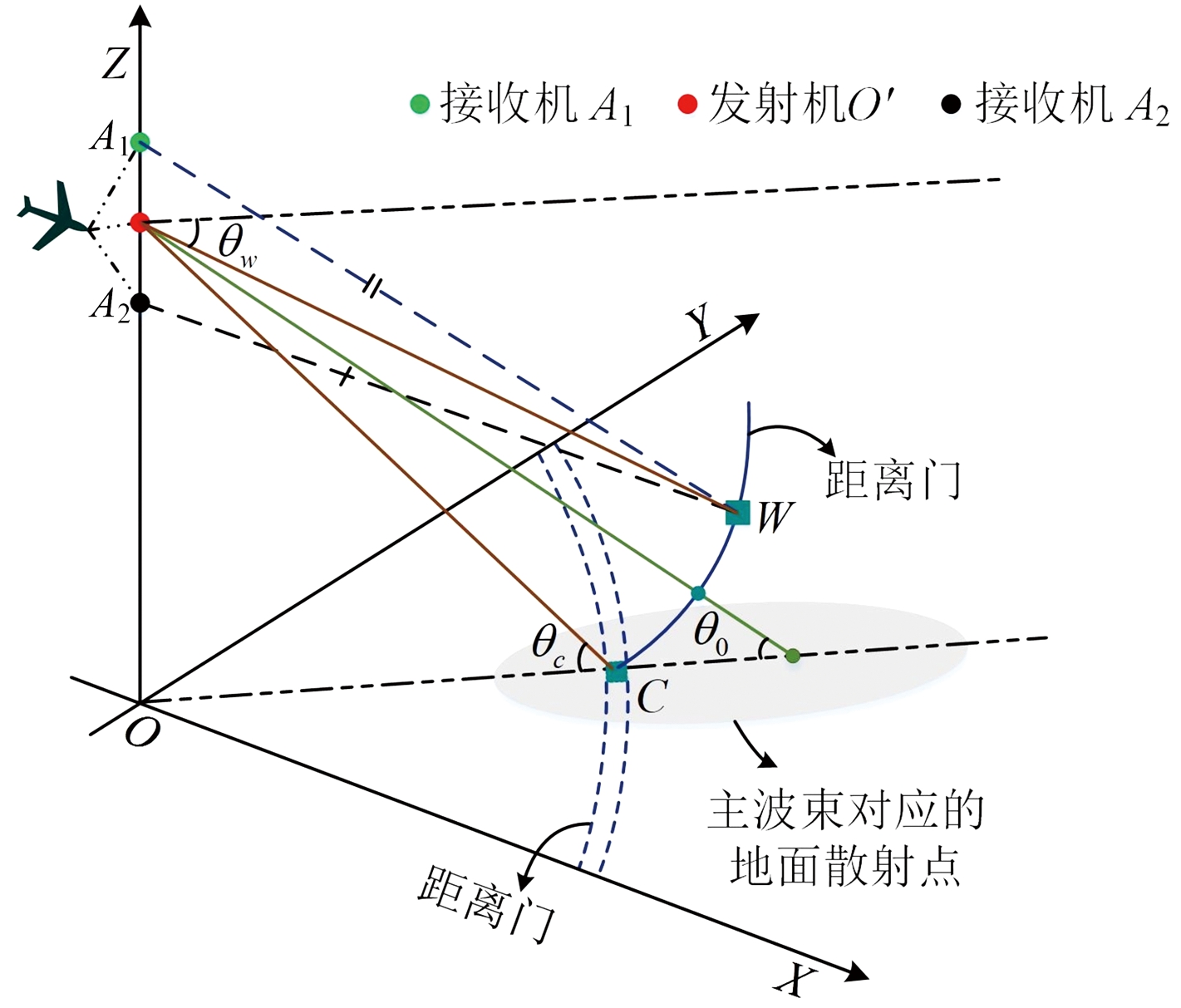
图1 三维空间几何接收模型
2 干涉相位统计特性分析
统计特性分析对于CFAR检测器的设计尤为重要[16-18]。本文的重点在于获得气象目标湮没于地杂波时混合信号的概率密度函数(Probability Density Function,PDF)。由于实测数据中不可避免地存在着多种干扰[19],为了减小各种干扰对干涉相位概率密度分布的影响,一般先对雷达原始回波数据进行多视处理。通过多视处理得到的干涉相位图可表示为
(4)
式中,arg(·)为取相位运算,上标*代表共轭运算,n为多视数,ai和bi分别代表双通道数据经过多视处理后得到的单视图像。基于多视处理的干涉相位PDF可由样本协方差矩阵的PDF导出,地杂波的样本协方差矩阵为
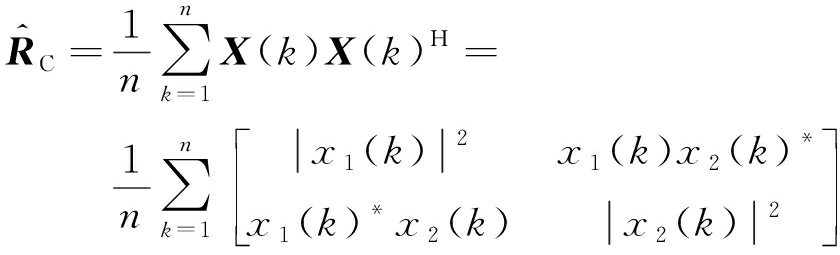
(5)
式中,H代表共轭转置运算,X(k)=![]() 为服从复高斯分布的空域快拍信号,其中T代表转置运算。样本协方差矩阵
为服从复高斯分布的空域快拍信号,其中T代表转置运算。样本协方差矩阵![]() 携带有信号的重要空间信息,而且矩阵
携带有信号的重要空间信息,而且矩阵![]() 服从复Wishart分布,即
服从复Wishart分布,即![]() 其PDF可以表示为
其PDF可以表示为
f(A)=![]() ·
·
(6)
式中,Γ(·)为gamma函数。式(5)对应的期望协方差矩阵形式为
RC=E{XXH}=
(7)
式中,E{·}代表统计期望,ρcexp(jφc)为双通道信号的复相关系数,![]() 和
和![]() 分别表示两通道信号的方差。由式(7)可知,干涉相位是样本协方差矩阵中次对角线元素的参数,即式(7)中的φc。通过对样本协方差矩阵中的相关参数进行积分,便可以得到关于干涉相位的边缘概率密度函数,即
分别表示两通道信号的方差。由式(7)可知,干涉相位是样本协方差矩阵中次对角线元素的参数,即式(7)中的φc。通过对样本协方差矩阵中的相关参数进行积分,便可以得到关于干涉相位的边缘概率密度函数,即
fφ(φ)=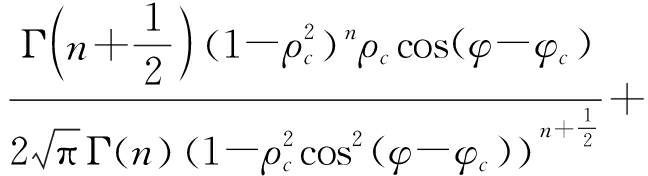
(8)
式中,2F1(a,b;c;y)代表高斯超几何函数。可以看出,干涉相位的PDF与n,ρc和φc有关。需要注意的是,在某一下视角下采集到的雷达回波中,地杂波范围内每一距离门对应的具体下视角会存在差异,这将导致地杂波干涉相位会随着距离门的变化而发生改变,不利于实现气象目标检测。因此,需要对地杂波回波进行干涉相位补偿。不同距离门对应的具体干涉相位补偿量可表示为
(9)
式中,H和r分别表示载机高度和探测距离。利用干涉相位补偿量φInPCV对地杂波干涉相位进行修正后(φc=|φrc|-φInPCV),式(8)中的φc=0,其中φrc表示由双通道回波数据计算得到的此距离门对应的干涉相位值。因此,当只含有地杂波分量时,干涉相位的PDF可表示为
p0(φ)=fφ(φ),φc=0
(10)
而且,经过干涉相位补偿后,式(3)中的关系将会发生变化,即
φc<|φw+c|≤|φs|
(11)
当SCR→+∞(-∞)时,|φw+c|≈|φs|(φc)。式(11)中,φw+c和φs分别代表干涉相位补偿后混合信号和纯净气象信号对应的干涉相位值。
此处考虑某一距离-脉冲单元同时存在地杂波分量和气象目标分量。分布式气象目标可以看作是由许多单一反射率因子的低慢速动目标组成,且强度具有时变特性。此时,样本协方差矩阵可表示为
![]()
![]()
(12)
式中,S(k)=[s1(k),s2(k)]T代表来自气象目标的空域快拍。假设快拍信号S(k)和X(k)独立同分布,均服从复高斯分布,即S~CN(0,RS),对应的样本协方差矩阵RS可以表示为
(13)
式中,ρs代表气象目标分量的相关系数。双通道数据经过通道均衡处理后信号功率相同,即![]() 同样地,式(7)中
同样地,式(7)中![]() 由于S(k)和X(k)具有独立同分布特性,则式(10)对应的理论协方差矩阵可以计算为
由于S(k)和X(k)具有独立同分布特性,则式(10)对应的理论协方差矩阵可以计算为
RW+C=E{ZZH}=RC+RS
(14)
在通道均衡的情况下,将式(7)和式(13)代入式(14)中,便可得到包含地杂波分量和气象目标分量信息的样本协方差矩阵,即
RW+C=(σ2+ζ2)·
(15)
式中,
(16)
θw+c=arctan{(δρssinφs)/(ρc+δρscosφs)}
(17)
其中,δ表示气象目标功率ζ2与地杂波功率σ2的比值,即SCR。
分析式(5)、式(7)、式(12)和式(15)可知,混合信号干涉相位的PDF与式(8)具有相同的形式,但由于气象目标分量的存在,所涉及的参数会存在一些变化。根据式(15),混合信号的干涉相位的PDF可以表示为
p1(φ)=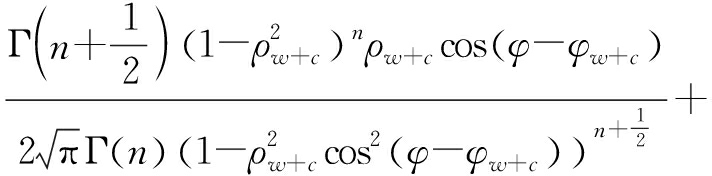
(18)
图2给出了有无气象目标时干涉相位的概率密度分布图像。其中,n=6,ρc=0.995,ρs=0.965,纯气象信号的干涉相位值φs=-15°,SCR=5 dB。从图2可以观察出,混合信号的干涉相位值主要分布在φw+c=-11.5°附近,其分布情况符合式(11)中的分析。此外,有无气象目标两种情况下干涉相位的PDF具有相同的形式,只是两者的均值和方差存在差异。
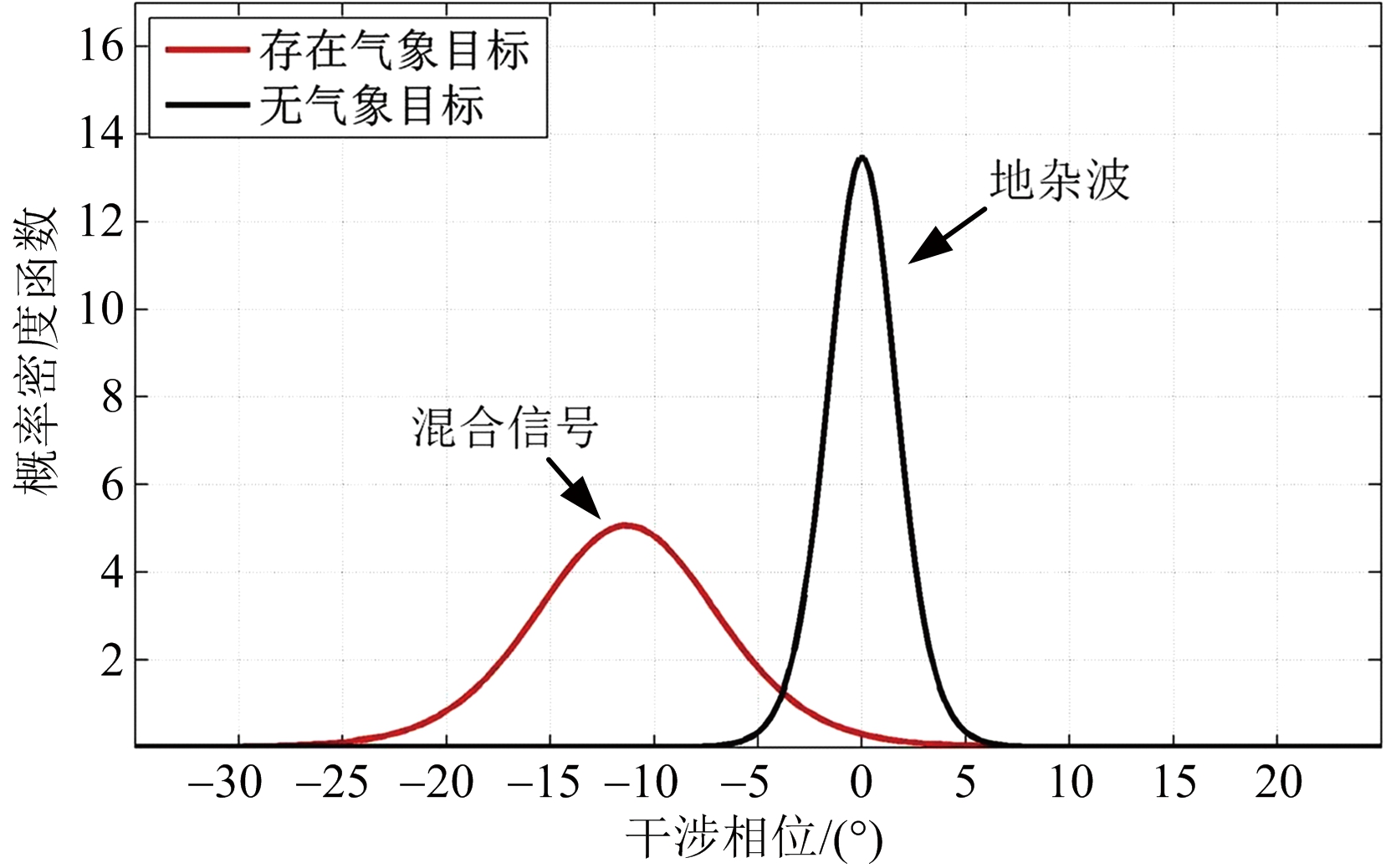
图2 有无气象目标时干涉相位概率密度分布示例图
结合式(11)和式(18)可知,干涉相位PDF的获取需要对双通道数据的相关性进行估计。双通道信号中地杂波分量的相关性可估计为
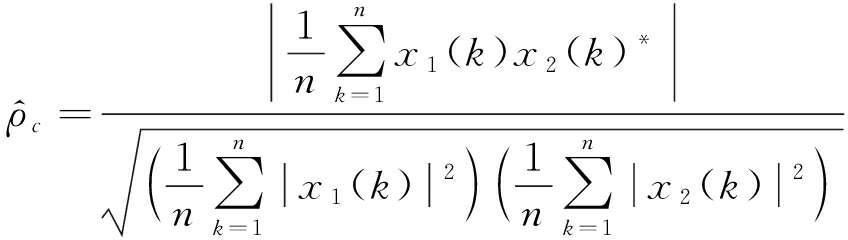
(19)
多视处理虽然可以提高相关系数的估计精度,但相关系数的估计值与理论值仍会存在偏差,在双通道信号相关性较差的情况下此现象尤为显著。估计的相关系数![]() 的概率密度分布可表示为
的概率密度分布可表示为
(20)
如图3(a)所示,相关系数的估计均值与理论值之间的偏差会随着相关系数和多视数的增加而减小。而且,图3(b)中方差的变化趋势也出现类似于图3(a)中的情况。结合图3(a)与图3(b)可知,理论相关系数值越高,多视数越多,则![]() 的方差越小(相关系数估计值越稳定),且估计值与理论值的偏差也会越小。一般而言,双通道地杂波回波的相关性与地杂波类型有关,来自固定平面的地杂波回波的相关性在0.95~0.99之间。可见,地杂波回波的相关性较强,因此当选用样本数量适当时由式(19)造成的估计误差基本上可以忽略。
的方差越小(相关系数估计值越稳定),且估计值与理论值的偏差也会越小。一般而言,双通道地杂波回波的相关性与地杂波类型有关,来自固定平面的地杂波回波的相关性在0.95~0.99之间。可见,地杂波回波的相关性较强,因此当选用样本数量适当时由式(19)造成的估计误差基本上可以忽略。
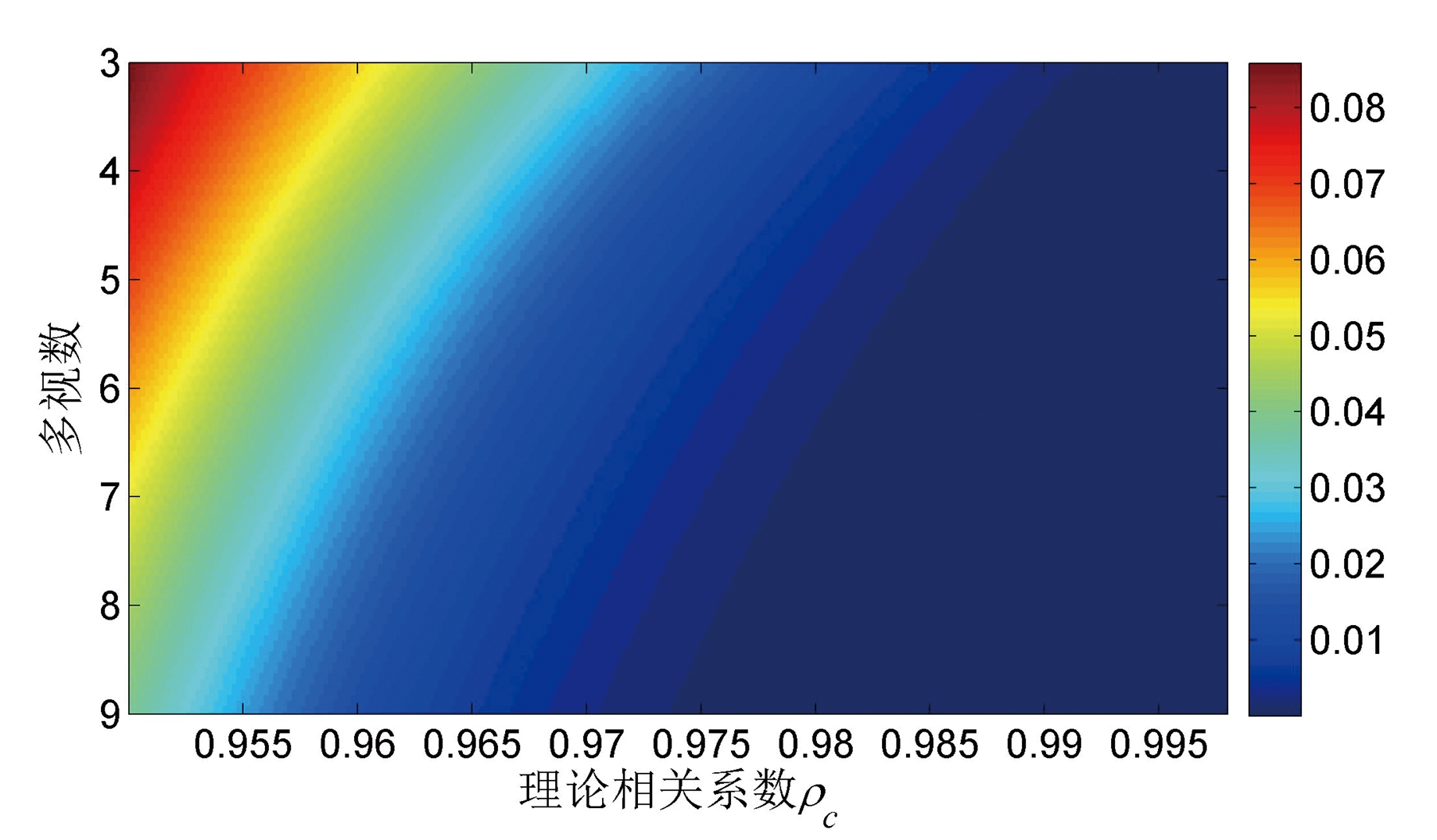
(a) 估计的![]() 均值与理论值ρc之间的误差
均值与理论值ρc之间的误差
随多视数和理论值ρc的变化趋势
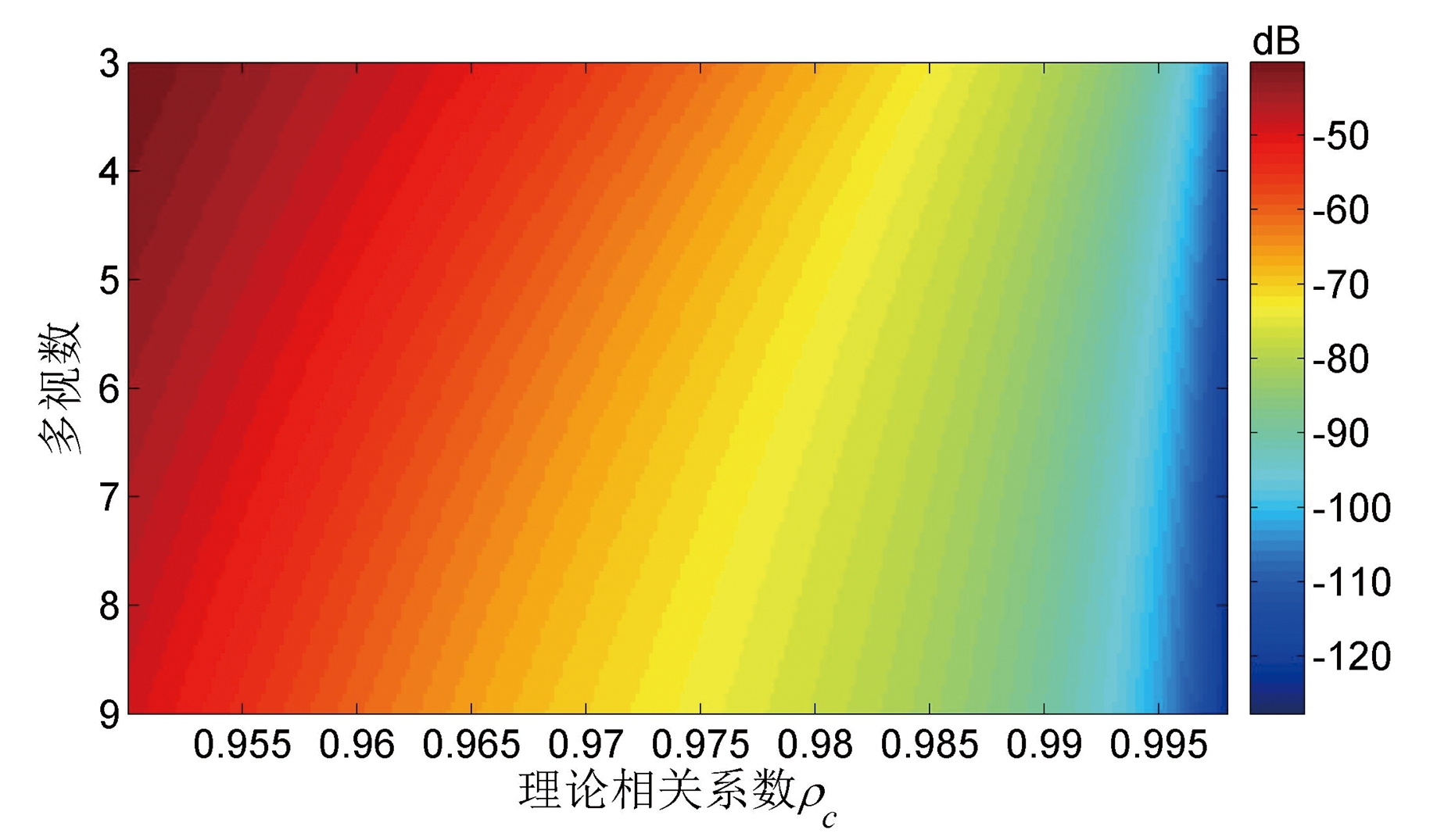
(b) 估计的![]() 方差随多视数和理论值ρc的变化趋势
方差随多视数和理论值ρc的变化趋势
图![]() 的概率密度分布特性分析
的概率密度分布特性分析
此外,式(11)和式(18)中的n代表独立样本数量,即有效多视数。通常情况下,用于估计协方差矩阵的样本并不总是统计独立的。为此,需要对有效多视数进行估计,即
(21)
式中:Δx,δx分别为方位分辨率和方位像素分辨率;L,v0,BDop和fa分别代表选取的样本数量、载机速度、多普勒带宽和方位向采样频率。
3 CFAR检测器的设计
根据双通道信号的相关系数![]() 和有效多视数
和有效多视数![]() 可生成地杂波干涉相位的具体分布,然后利用给定的虚警概率(Probability of False Alarm,PFA)确定检测门限,从而实现对气象目标的检测。对应的检测概率(Probability of Detection,POD)和PFA可表示为
可生成地杂波干涉相位的具体分布,然后利用给定的虚警概率(Probability of False Alarm,PFA)确定检测门限,从而实现对气象目标的检测。对应的检测概率(Probability of Detection,POD)和PFA可表示为
(22)
(23)
式中,φT代表检测门限。TP和TN分别表示正确检测为气象目标和地杂波,FP和FN则表示检测过程中产生的虚警和漏检。此CFAR检测器对应的判决规则可以描述为

(24)
式中,H1代表待检测单元中含有气象目标分量,H0则表示该单元只含有地杂波分量。图4给出了气象目标检测的整体流程,其主要包含两部分,第一部分是对双通道数据进行多视处理和地杂波干涉相位补偿后获得待检测的干涉相位图;第二部分是根据参数估计获得关于干涉相位的具体PDF,确定检测门限。将干涉相位图中每一像素点的干涉相位值代入式(24)中,实现对气象目标的CFAR检测。
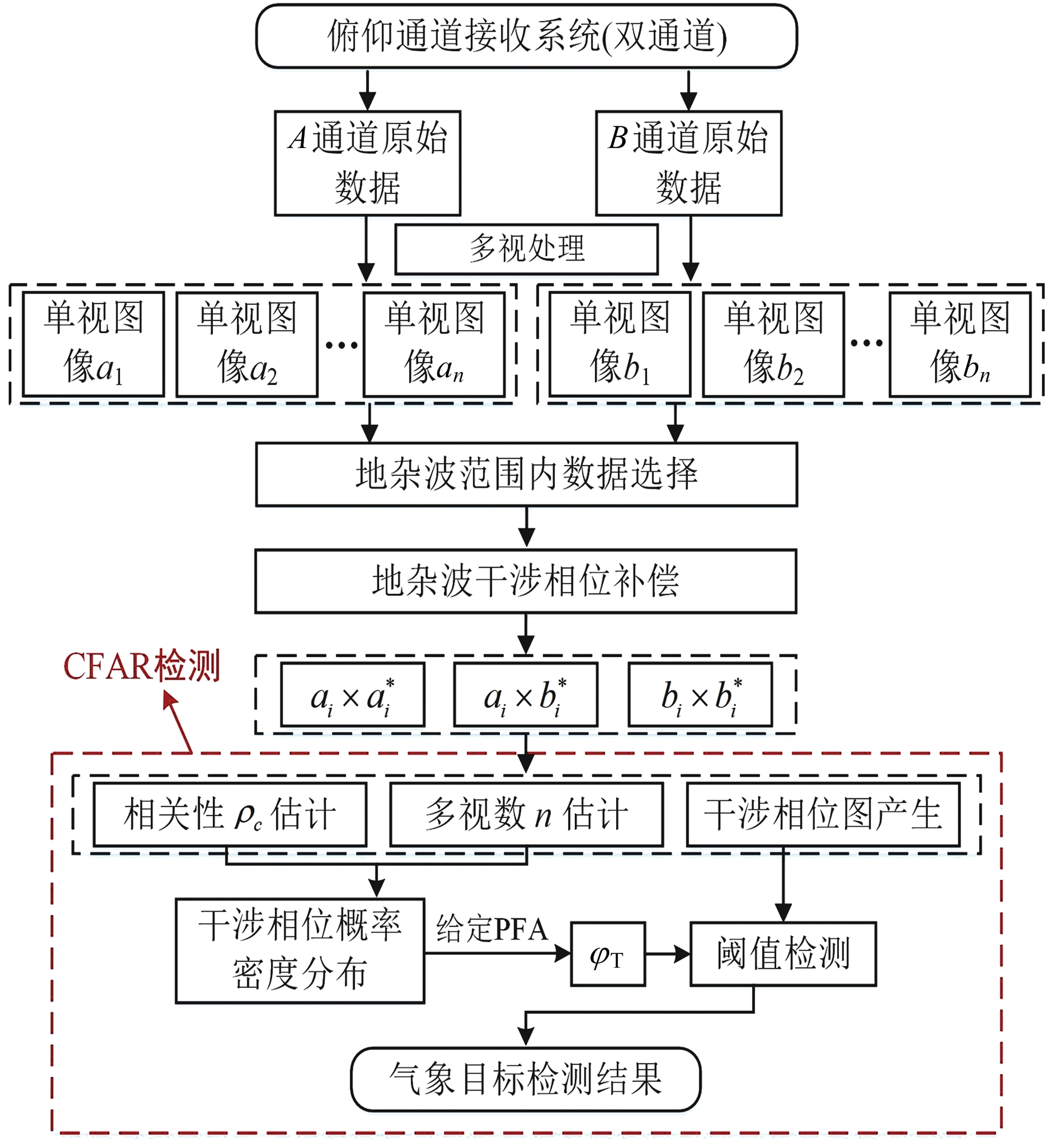
图4 基于干涉相位的空域气象目标检测算法流程图
4 实验结果与分析
4.1 统计特性验证与方法性能分析
本小节利用仿真数据对上述理论分析进行验证,对应的仿真参数如表1所示。此外,为了更全面地评价本文方法的性能,绘制仿真数据检测结果的POD曲线以反映各参数对本文方法检测性能的影响。
表1 仿真数据和实测数据涉及的主要参数
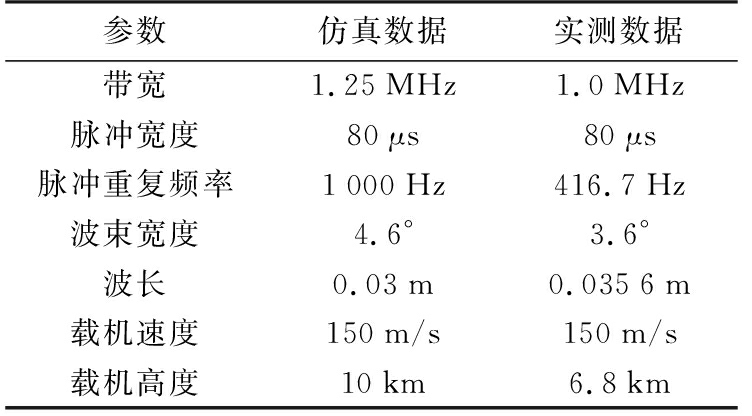
参数仿真数据实测数据带宽1.25MHz1.0MHz脉冲宽度80μs80μs脉冲重复频率1000Hz416.7Hz波束宽度4.6°3.6°波长0.03m0.0356m载机速度150m/s150m/s载机高度10km6.8km
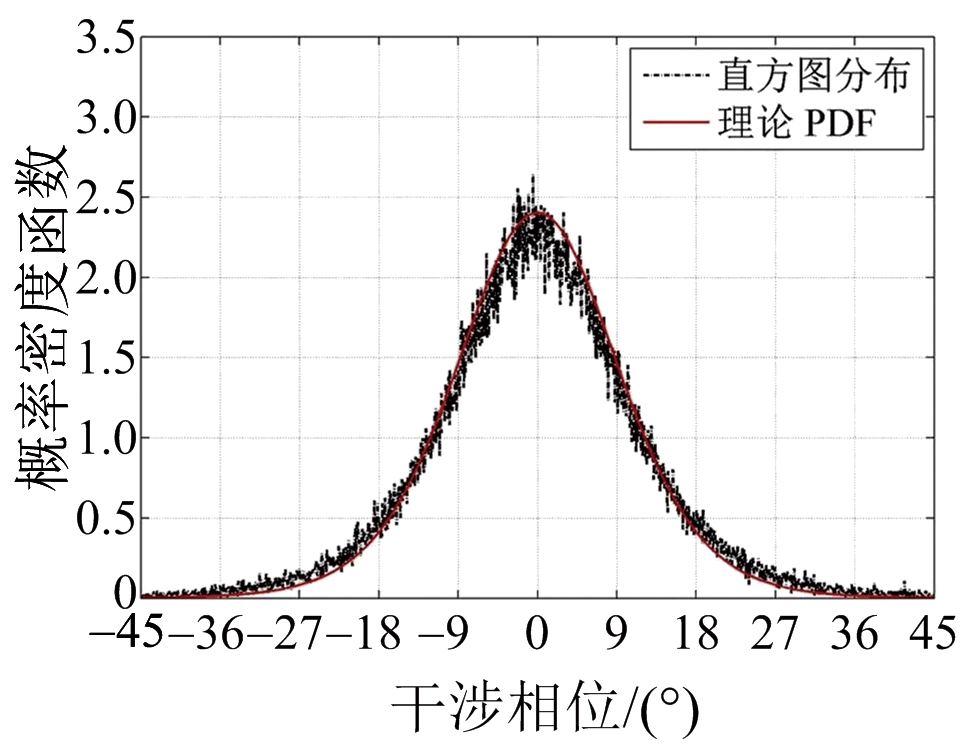
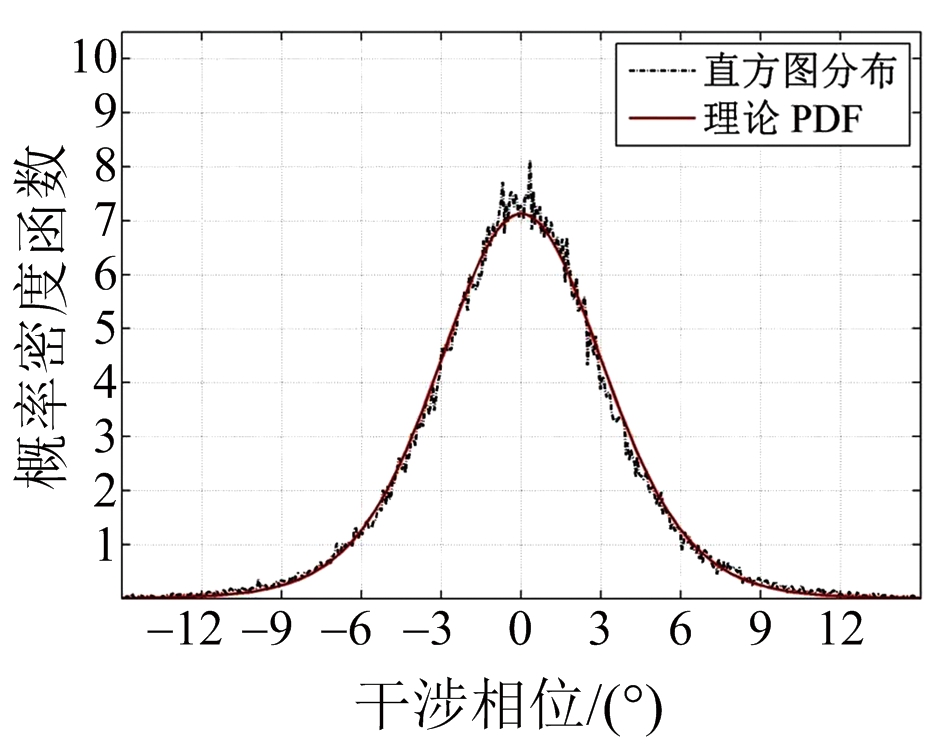
图5给出了不同杂噪比(Clutter to Noise Ratio,CNR)下地杂波干涉相位的分布直方图和理论的PDF。结合图5(a)和图5(b)可知,CNR对双通道信号的相关性有较大影响,且干涉相位的分布直方图能够很好地拟合理论的PDF。此外,图6展示了在![]() 和
和![]() 时,不同SCR下混合信号干涉相位的拟合结果。从图6可以看出,干涉相位分布直方图与理论的PDF拟合效果较好。随着SCR的增加,分布直方图的峰值逐渐靠近
时,不同SCR下混合信号干涉相位的拟合结果。从图6可以看出,干涉相位分布直方图与理论的PDF拟合效果较好。随着SCR的增加,分布直方图的峰值逐渐靠近![]() 方向,这与式(11)中的理论分析相一致。与图5相比,图6中混合信号的分布直方图与理论PDF的偏差显著增加。造成这种现象的主要原因是进行干涉相位拟合时两幅图像选用的样本数量不同,图5由约1.2×105个样本生成,而图6中大约只有6×103个样本。
方向,这与式(11)中的理论分析相一致。与图5相比,图6中混合信号的分布直方图与理论PDF的偏差显著增加。造成这种现象的主要原因是进行干涉相位拟合时两幅图像选用的样本数量不同,图5由约1.2×105个样本生成,而图6中大约只有6×103个样本。
![]()
![]()
图5 多视处理下![]() 干涉相位分布直方图与理论PDF
干涉相位分布直方图与理论PDF
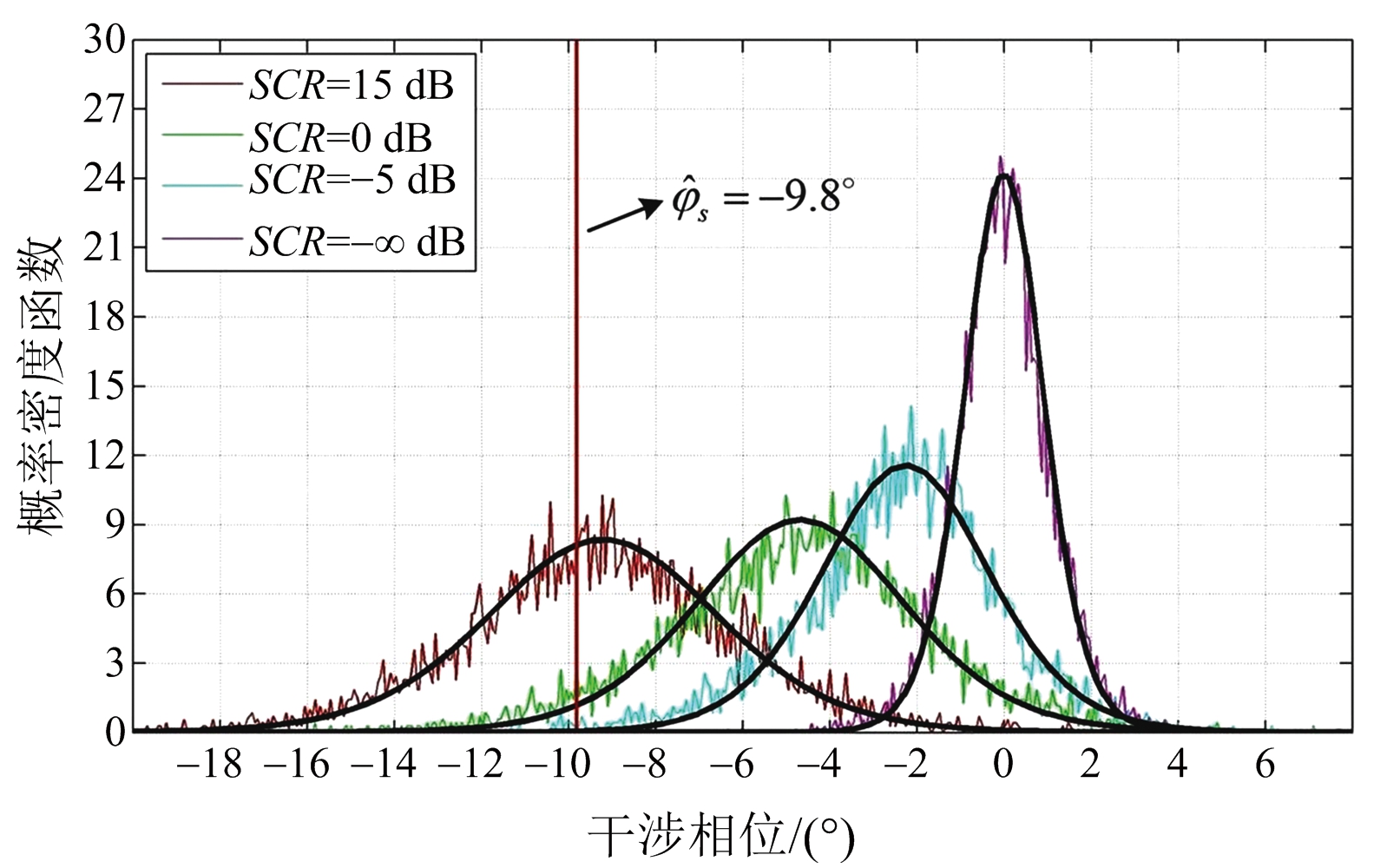
图6 不同SCR下混合信号干涉相位对应的分布直方图和理论的PDF
图7为双通道数据经过干涉相位补偿后得到的干涉相位图。由图7(a)可知,混合信号的干涉相位值(白色区域)与地杂波干涉相位值(蓝色区域)明显不同,而且二者的干涉相位值分别集中在-10°和0°左右,补偿后的干涉相位图便于通过CFAR检测器实现对气象目标的检测。以方位角为-18.5°时为例,图7(b)给出了对应的干涉相位随距离的变化曲线,其中红线代表地杂波干涉相位的理论值0。当不存在气象目标分量时,计算得到的干涉相位值在理论值0附近上下浮动,而当距离-脉冲单元存在气象目标分量时,得到的干涉相位值(椭圆内部)便会偏离地杂波干涉相位的理论值。
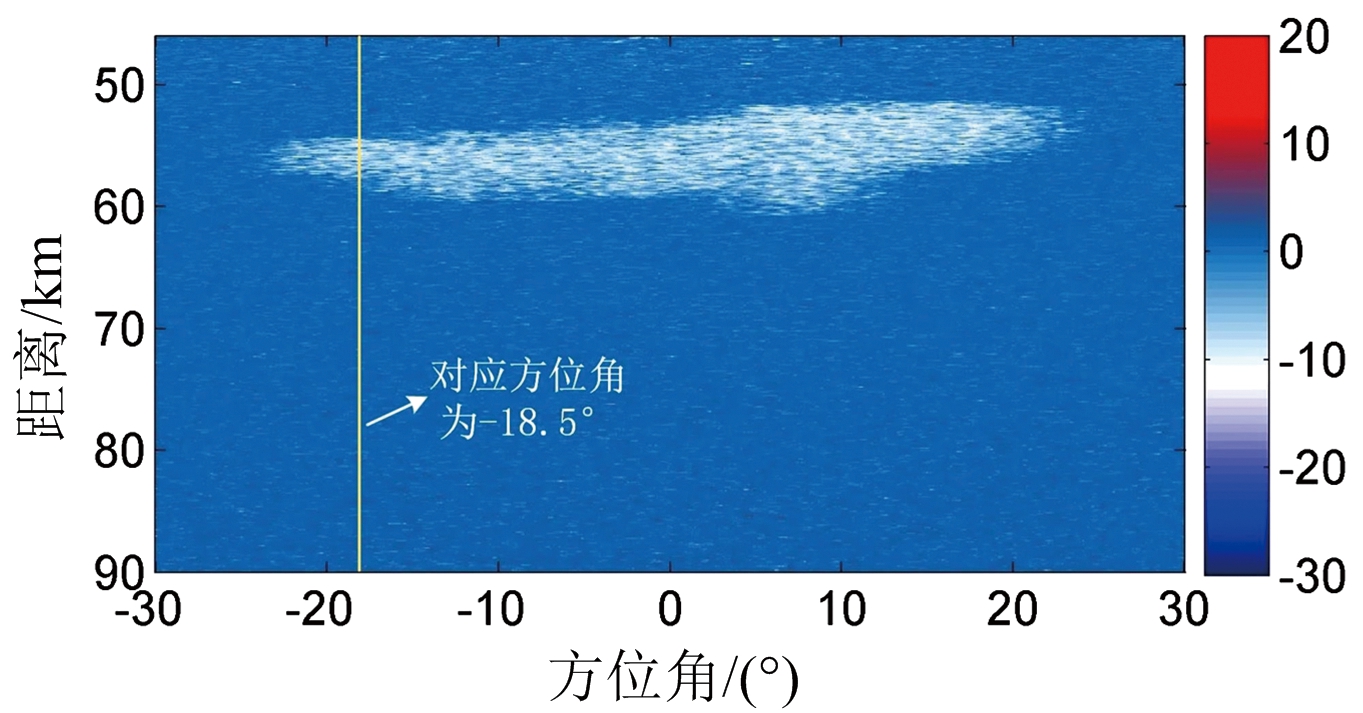
(a) 干涉相位图
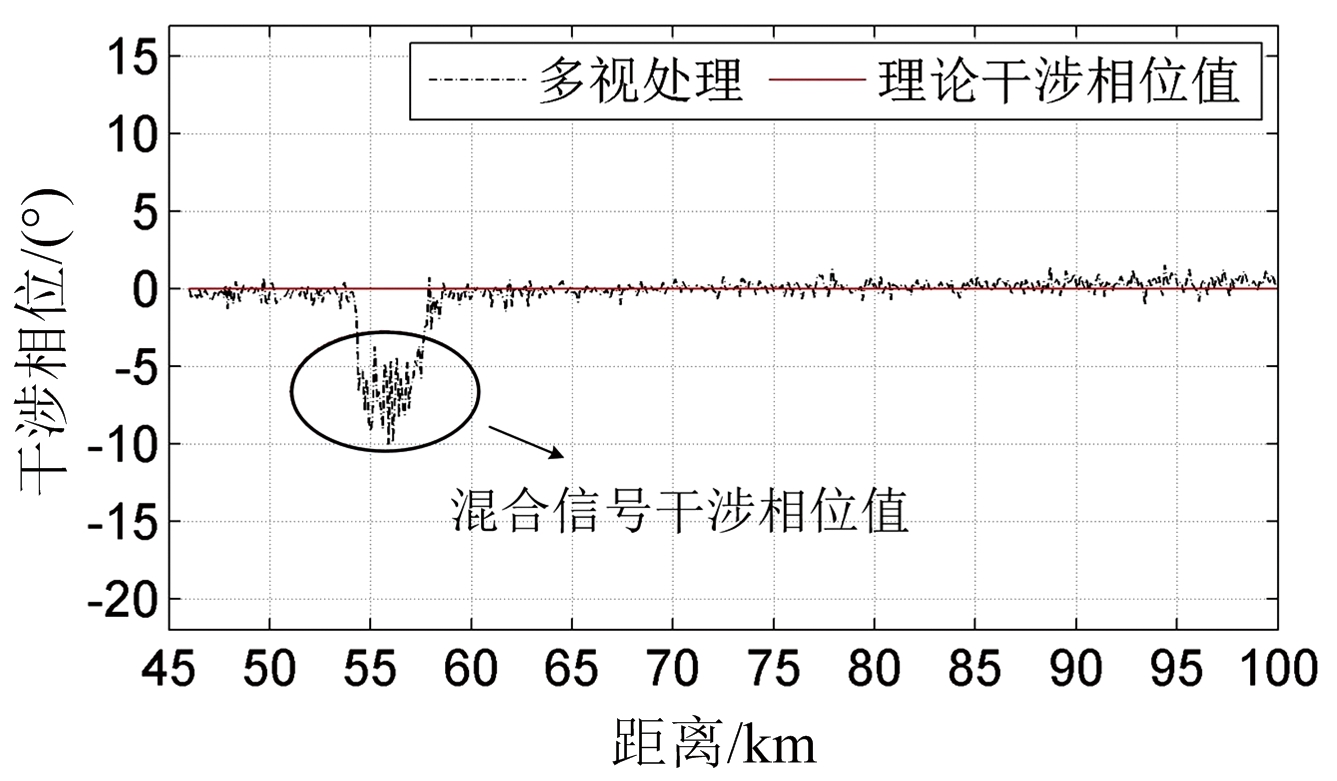
(b) 干涉相位随距离的变化曲线
图7 仿真数据处理结果
本文利用多组仿真实验详细地评估了相关参数对最终检测结果的影响,并利用定量评价指标来全面地分析本文所提方法的检测性能。图8(a)和图8(b)给出了![]() 时不同PFA情况下POD随CNR和SCR的变化曲线。图8(c)揭示了CNR的变化主要影响p0(φ)的方差
时不同PFA情况下POD随CNR和SCR的变化曲线。图8(c)揭示了CNR的变化主要影响p0(φ)的方差![]() 而p1(φ)的均值E1和方差
而p1(φ)的均值E1和方差![]() 变化较小。较高CNR值使得式(18)中的FN区域减小,从而提高了图8(a)的检测概率。同时,图8(b)中检测概率增加的主要原因是|E1|的增加,但在此过程中,方差也会发生变化,导致后续检测概率增加缓慢,最终保持不变。
变化较小。较高CNR值使得式(18)中的FN区域减小,从而提高了图8(a)的检测概率。同时,图8(b)中检测概率增加的主要原因是|E1|的增加,但在此过程中,方差也会发生变化,导致后续检测概率增加缓慢,最终保持不变。
进一步地,本文还分析了参数φs对检测性能的影响。在给定经验参数的情况下,φs只与阵元间隔和气象目标高度有关,其中目标高度信息通过Δθ(气象目标与波束中心夹角)表示。图8中所涉及的![]() 对应于Δθ=-2°。图9给出了不同PFA情况下POD随Δθ的变化曲线,由于Δθ的增加,气象目标的高度降低,使得气象目标和地杂波的干涉相位值差别不大,从而造成检测概率的下降。此外,本文还考虑了系统参数(阵元间隔d)对气象目标检测的影响。图10给出了不同阵元间隔下PFA和POD的变化趋势。可见,改变阵元间隔虽然能够提高气象目标的检测概率,但对虚警概率并不会产生预期的效果。随着阵元间隔的增大,信号间的相关性变差,导致相同检测门限下虚警概率增加。当阵元间隔较小时(d/λ介于0.5~2.0),POD显著增加;但当阵元间隔较大时(d/λ≥2.5),信号间的弱相关性限制了POD的持续增加。
对应于Δθ=-2°。图9给出了不同PFA情况下POD随Δθ的变化曲线,由于Δθ的增加,气象目标的高度降低,使得气象目标和地杂波的干涉相位值差别不大,从而造成检测概率的下降。此外,本文还考虑了系统参数(阵元间隔d)对气象目标检测的影响。图10给出了不同阵元间隔下PFA和POD的变化趋势。可见,改变阵元间隔虽然能够提高气象目标的检测概率,但对虚警概率并不会产生预期的效果。随着阵元间隔的增大,信号间的相关性变差,导致相同检测门限下虚警概率增加。当阵元间隔较小时(d/λ介于0.5~2.0),POD显著增加;但当阵元间隔较大时(d/λ≥2.5),信号间的弱相关性限制了POD的持续增加。
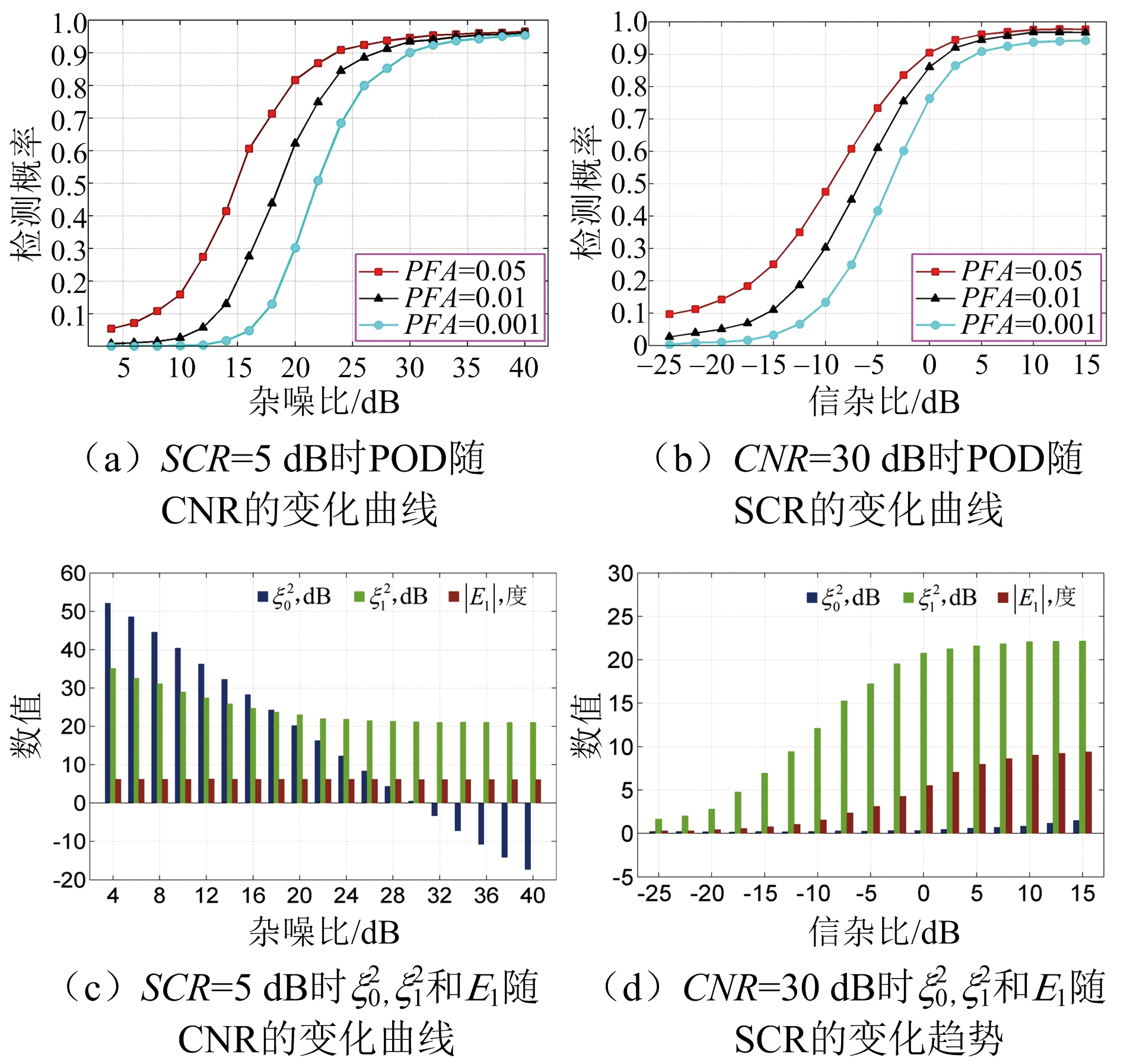
图![]() 时CNR和SCR对检测性能的影响
时CNR和SCR对检测性能的影响
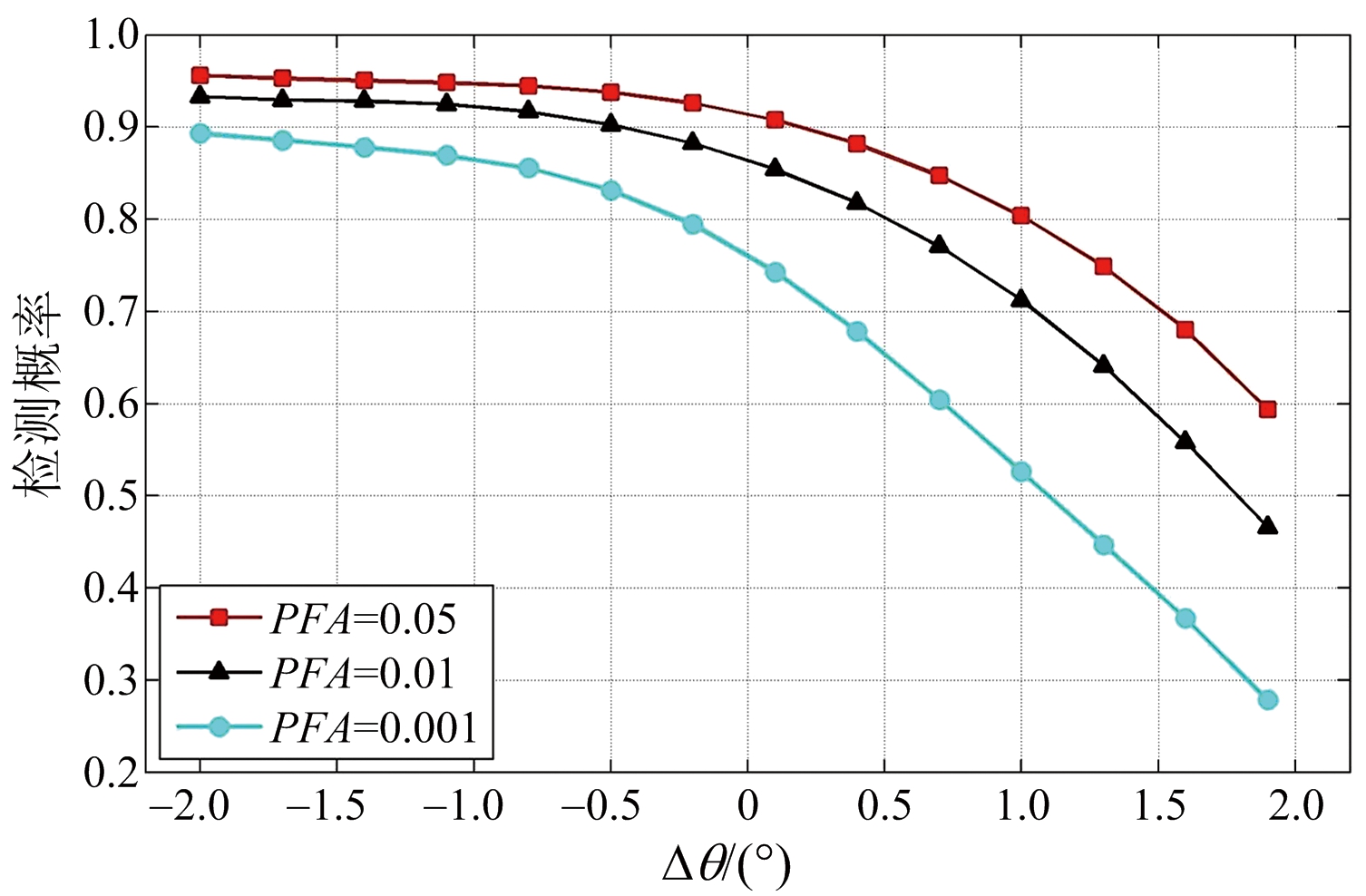
图![]() d/λ=0.5时POD随Δθ的变化趋势
d/λ=0.5时POD随Δθ的变化趋势
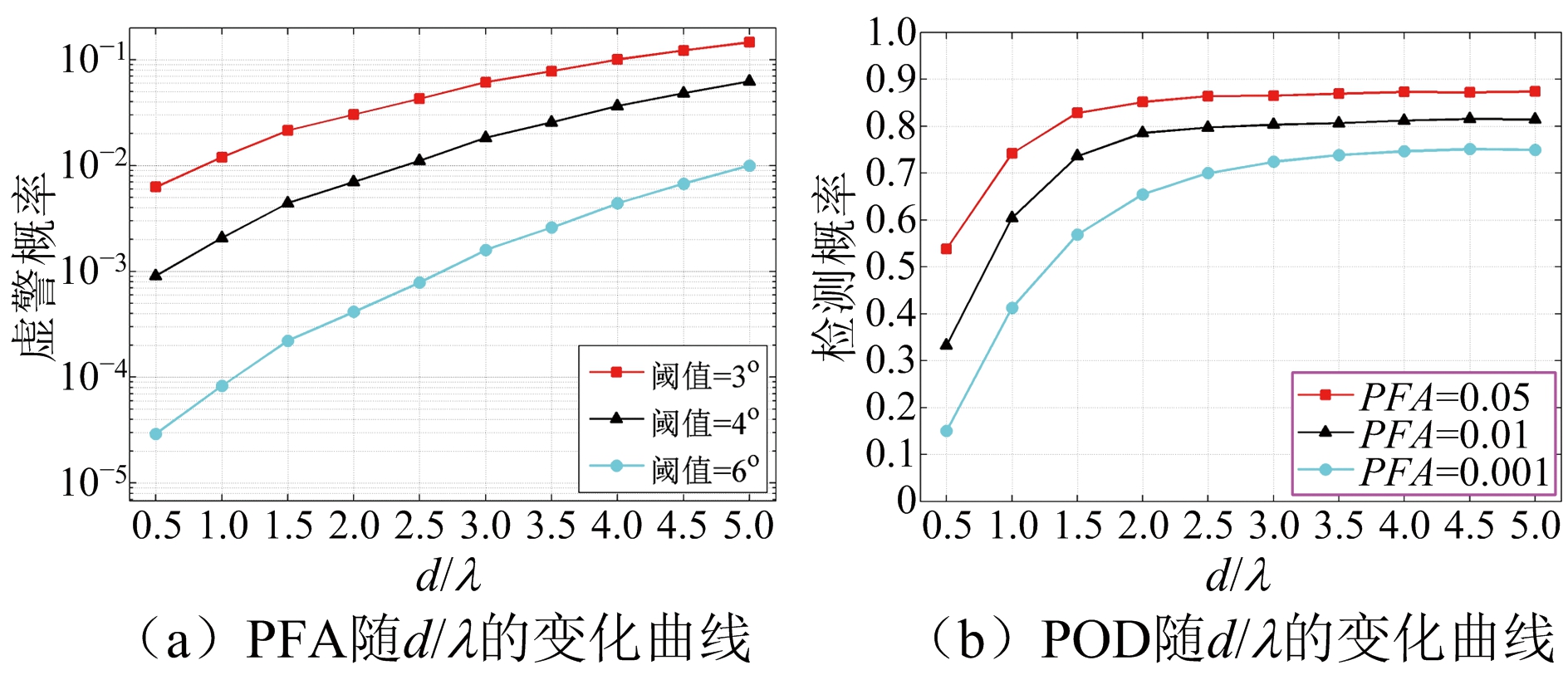
图10 ![]() 时阵元间隔对检测性能的影响
时阵元间隔对检测性能的影响
4.2 不同方法性能对比
本文所提方法与Golbon-haghhii等人提出的PFI和PSF检测方法(2019年),Hubbert等人提出的CPA检测方法(2009年),以及Li等人提出的SCI检测方法(2013年)进行了性能对比。实验所用仿真数据的谱矩信息如表2所示。PFI、PSF和CPA判别函数均表征了慢时间域相位的起伏程度,且起伏程度取决于表2中的谱矩信息。从表3中可以看出,同一待检测单元对应的PFI和PSF值与SCR成正比,而CPA则相反。此外,SCI利用谱功率分布(Spectral Power Distribution,SPD)、谱相位起伏(Spectrum Phase Fluctuation,SPF)、功率纹理(Power Texture,PT) 和谱宽纹理(Spectrum Width Texture,SWT)四种指标实现对地杂波和气象目标的检测,这些指标涉及回波数据的多普勒频移、谱宽、频谱相位和功率等信息,在不同SCR下的具体值如表3所示。图11给出在SCR=5 dB、CNR=30 dB和PFA=10-3的情况下,各种气象目标检测方法对同一组数据的检测结果。图11中,红色点表示正确检测出含有气象目标分量的像素点(TP),而黄色点则表示错误检测为地杂波的像素点(FN)。结合图11(a)和图11(b)可知,通过本文所提方法得到的检测结果与真值图最接近,只有边缘SCR较低的区域存在漏检情况。对比其他方法的检测结果,本文所提方法的检测性能更优。
表2 地杂波和气象目标对应的谱矩信息

参数参数值地杂波谱宽20Hz地杂波多普勒频移0Hz气象目标谱宽150Hz气象目标多普勒频移100Hz
表3 不同SCR(δ)下PFI、PSF、CPA和SCI对应的指标值
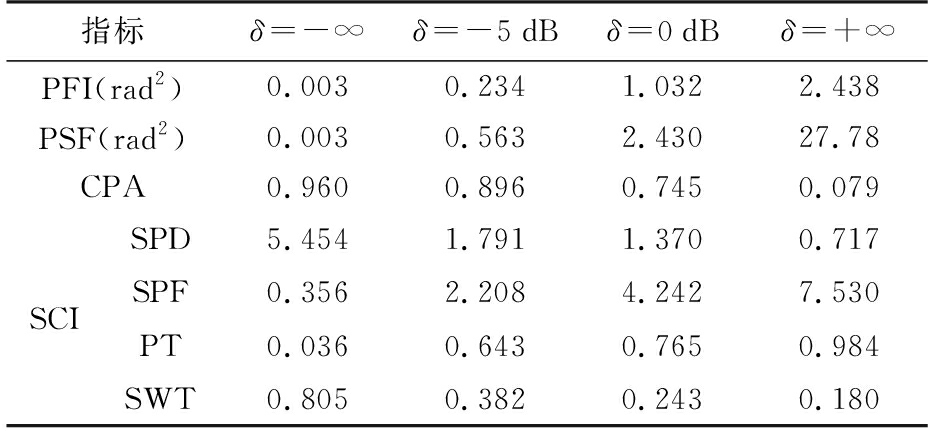
指标δ=-∞δ=-5dBδ=0dBδ=+∞PFI(rad2)0.0030.2341.0322.438PSF(rad2)0.0030.5632.43027.78CPA0.9600.8960.7450.079SCISPD5.4541.7911.3700.717SPF0.3562.2084.2427.530PT0.0360.6430.7650.984SWT0.8050.3820.2430.180
图12为通过不同方法得到的POD随SCR的变化曲线。当SCR=5 dB时,图12(a)各种方法对应的检测概率即为图11中检测结果对应的检测概率。此外,为了验证谱矩特性对PFI、PSF、CPA和SCI检测性能的影响,在合理情况下,此处以地杂波谱宽50 Hz为例,得到图12(b)对应的检测概率曲线。可见,由于谱宽的增加,基于时域和频域的气象目标检测方法性能有所下降,而基于俯仰维信息的空域气象目标检测方法的性能基本不受此变化的影响,突出了本文方法的优越性。
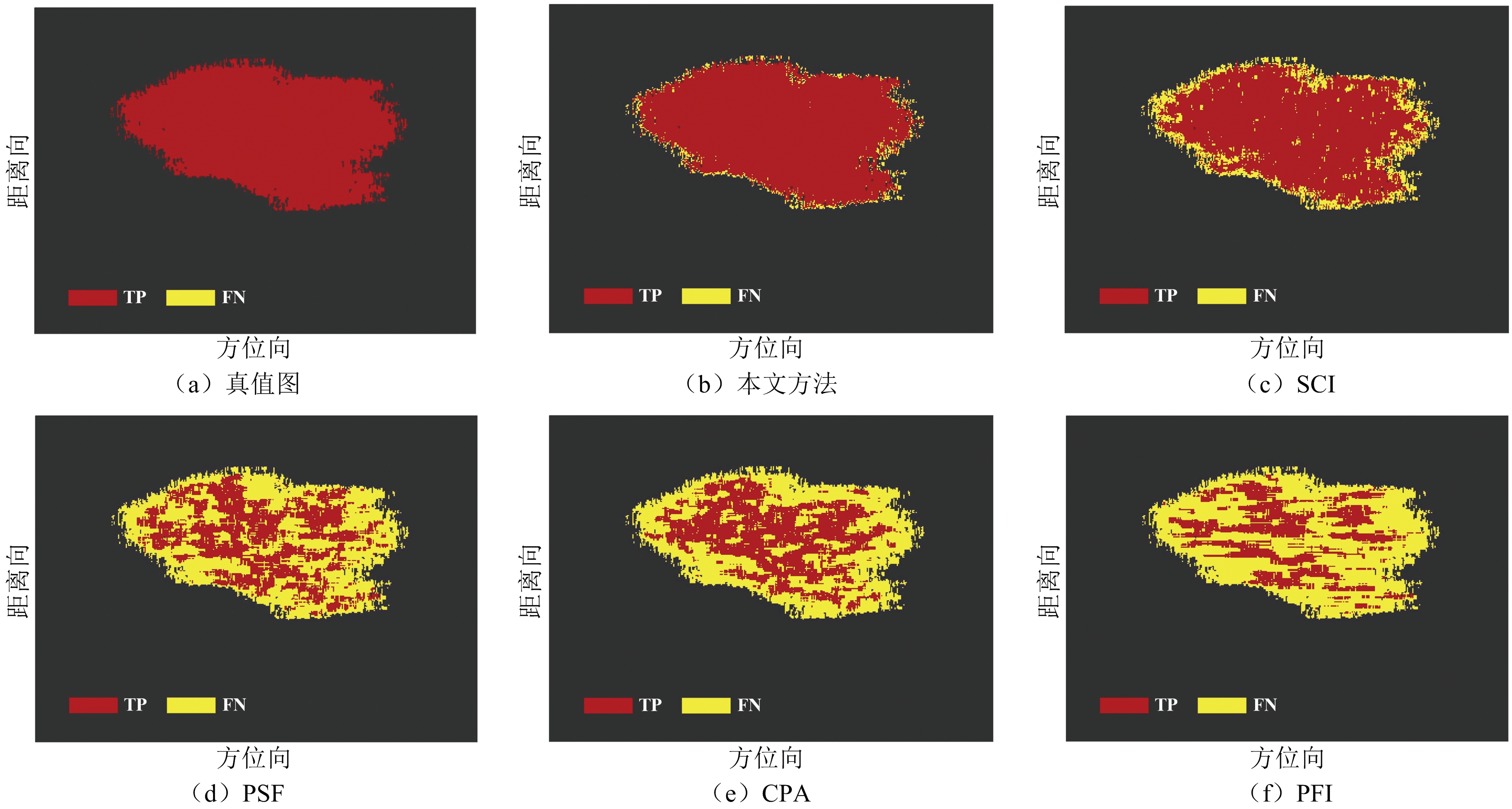
图11 利用不同方法得到的气象目标检测结果
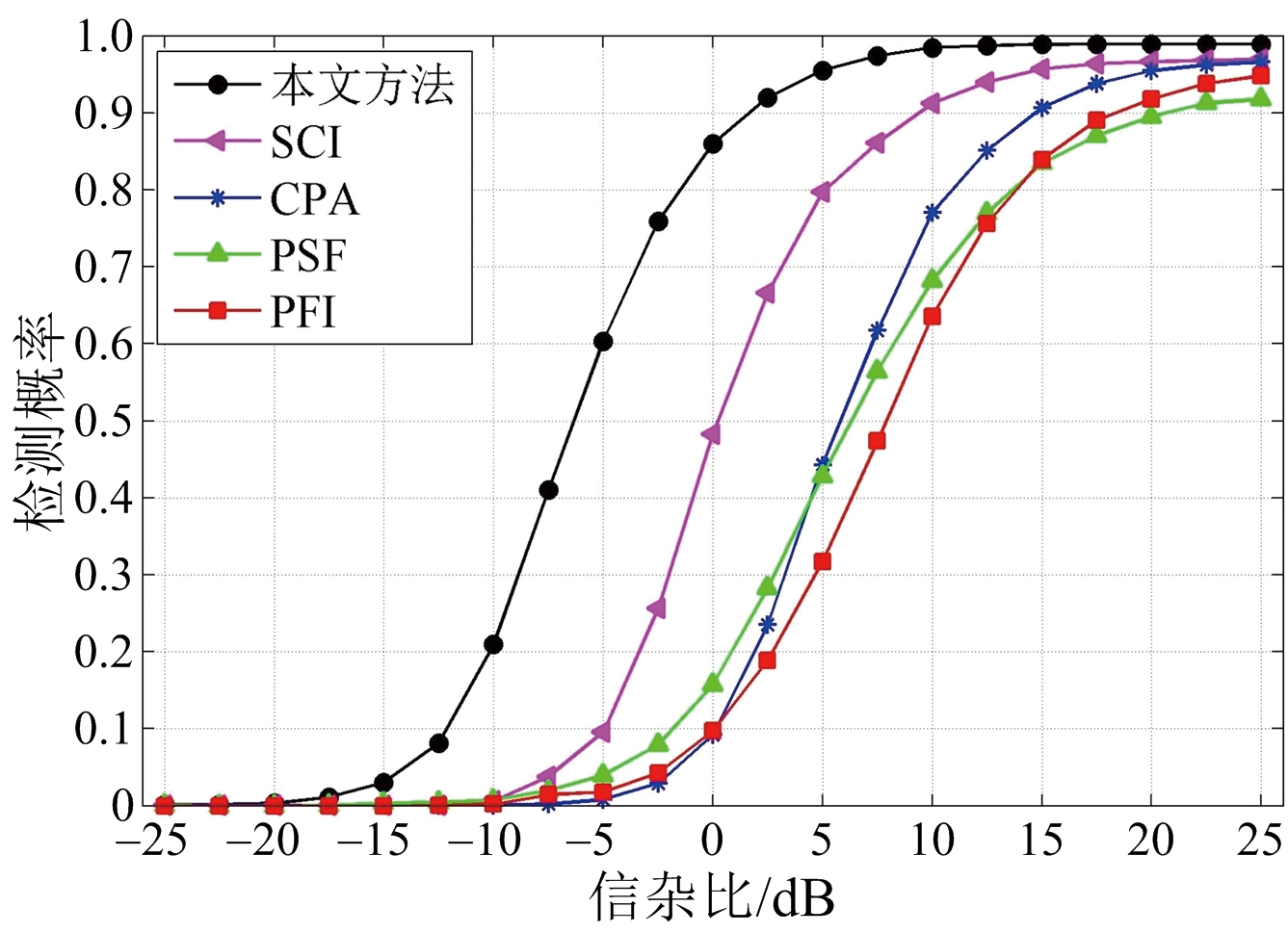
(a) 谱宽为20 Hz
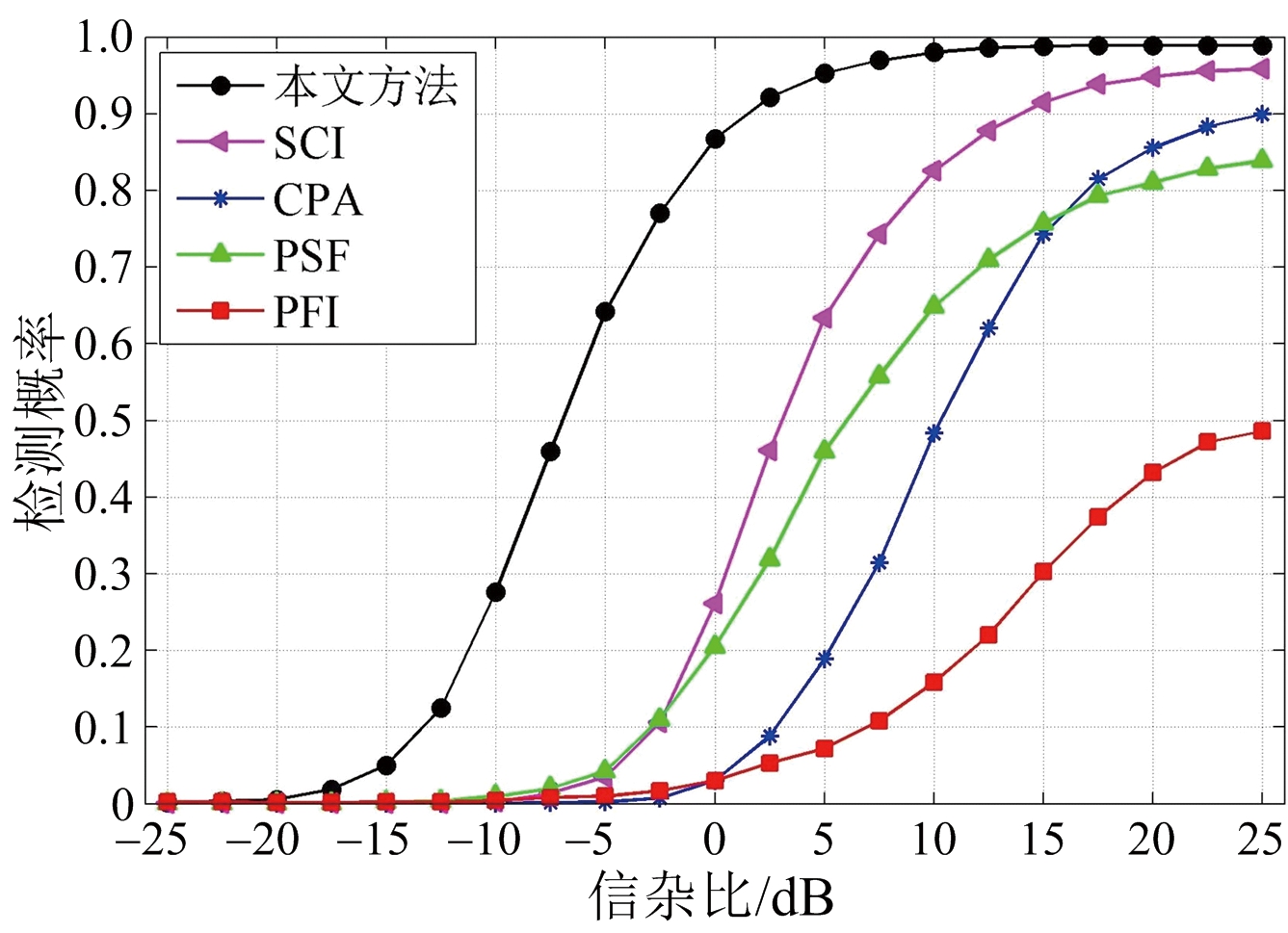
(b) 谱宽为50 Hz
图12 不同谱宽下各种检测方法对应的检测性能曲线
考虑到实际情况下雷达数据质量会受到二次后向散射、相干斑噪声和旁瓣扩展等因素的影响,本节利用雷达实测数据验证该方法的鲁棒性,实测数据的主要参数如表1所示。图13给出了针对实测数据的处理结果。本文主要对地杂波范围内的气象目标进行检测,图13(a)白线上方区域(不存在地杂波)中的信号均视为气象目标。计算可得,实测数据地杂波的覆盖范围为46~90 km。由图13(c)可知干涉相位分布直方图与理论PDF基本吻合。图13(d)和图13(e)代表干涉相位补偿前后得到的干涉相位图,区域1和区域2存在气象分量像素点的干涉相位值明显小于地杂波的干涉相位值。因此,将图13(e)中每一像素点的干涉相位值与检测门限进行比较,便可以得到最终检测结果,如图13(f)所示。最终的检测结果是对每个像素点进行二值化得到的,即‘1’代表检测为气象目标(白色区域),‘0’代表检测为地杂波(黑色区域),图13(f)中的稀疏点代表虚警像素点。由于实测数据存在多普勒模糊,导致基于时域和频域的检测方法失效。因此,相较于其他方法,本文所提方法具有良好的实测数据处理性能。

图13 实测数据处理结果
5 结束语
本文提出一种基于俯仰维信息的空域气象目标检测方法,该方法能够很好地实现气象目标和地杂波的判别。所提方法将干涉相位的统计特性用于CFAR检测器的设计,并用于最终的气象目标检测。该方法能够较好地解决气象目标湮没于强地杂波中导致目标信息缺失和检测虚警的问题。与目前的PFI、PSF、CPA和SCI等气象目标检测方法相比,该方法不受多普勒频谱展宽和多普勒模糊等现象的影响,具备良好的实际应用性能。
[1] ZHANG Wei,AN Ruixue,HE Ningyu,et al. Reduced Dimension STAP Based on Sparse Recovery in Heterogeneous Clutter Environments[J]. IEEE Trans on Aerospace and Electronic Systems,2020,56(1):785-795.
[2] 田明明,廖桂生,李云鹏,等. 超高速平台载雷达杂波特性与抑制方法[J]. 系统工程与电子技术,2020,42(2):301-308.
[3] 杨璟茂,吕晓德,岳琦,等. 机载双基雷达杂波分类及抑制方法[J]. 雷达科学与技术,2018,16(6):608-614.
[4] YIN Jiapeng,UNAL C,SCHLEISS M,et al. Radar Target and Moving Clutter Separation Based on the Low-Rank Matrix Optimization[J]. IEEE Trans on Geoscience and Remote Sensing,2018,56(8):4765-4780.
[5] 卢晓光,范源丹,李海,等. 利用RR-MWF的低信噪比下机载气象雷达回波谱矩估计方法[J]. 信号处理,2019,35(7):1125-1132.
[6] 李海,宋迪,呼延泽,等. LFMCW体制下基于TDPC-JDL的低空风切变风速估计方法[J]. 系统工程与电子技术,2020,42(7):1504-1509.
[7] 余磊,卢晓光,黄敬雄,等. 机载气象雷达湍流定标问题的研究[J]. 雷达科学与技术,2011,9(5):401-404.
[8] LI Yinguang,ZHANG Guifu,DOVIAK R J,et al. A New Approach to Detect Ground Clutter Mixed with Weather Signals[J]. IEEE Trans on Geoscience and Remote Sensing,2013,51(4):2373-2387.
[9] HUBBERT J C,DIXON M,ELLIS S M,et al. Weather Radar Ground Clutter. Part I: Identification,Modeling,and Simulation[J]. Journal of Atmospheric & Oceanic Technology,2009,26(7):1165-1180.
[10] GOLBON-HAGHIGHI M H,ZHANG Guifu,DOVIAK R J. Ground Clutter Detection for Weather Radar Using Phase Fluctuation Index[J]. IEEE Trans on Geoscience and Remote Sensing,2019,57(5):2889-2895.
[11] GOLBON-HAGHIGHI M H,ZHANG Guifu. Detection of Ground Clutter for Dual-Polarization Weather Radar Using A Novel 3D Discriminant Function[J]. Journal of Atmospheric & Oceanic Techno-logy,2019,36(7):1285-1296.
[12] NEPAL R,ZHANG Y R,ZHANG Guifu,et al. Data Quality Analysis and Enhancement of An Airborne Weather Radar for Scientific and Multi-Mission Operations[J]. SPIE,2018 (8):1-22.
[13] 刘丰恺,冯存前,黄大荣,等.高速机动目标多普勒解模糊高分辨成像方法[J/OL].北京航空航天大学学报:1-10[2020-10-21].https://doi.org/10.13700/j.bh.1001-5965.2019.0648.
[14] NEEMAT S,KRASNOV O,ZWAN F,et al. Decoupling the Doppler Ambiguity Interval from the Maximum Operational Range and Range-Resolution in FMCW Radars[J]. IEEE Sensors Journal,2020,20(11):5992-6003.
[15] MAO Xinhua,DING Lan,ZHANG Yudong,et al. Knowledge-Aided 2-D Autofocus for Spotlight SAR Filtered Backprojection Imagery[J]. IEEE Trans on Geoscience and Remote Sensing,2019,57(11):9041-9058.
[16] TIAN Min,YANG Zhiwei,DUAN Chongdi,et al. A Method for Active Marine Target Detection Based on Complex Interferometric Dissimilarity in Dual-Channel ATI-SAR Systems[J]. IEEE Trans on Geoscience and Remote Sensing,2020,58(1):251-267.
[17] DING Chibiao,JIN Tiantian,QIU Xiaolan,et al. Velocity Estimation of Moving Targets for Spaceborne Multichannel Synthetic Aperture Radar Systems Based on Equivalent Along-Track Interfe-rometry Technique[J]. IET Radar,Sonar & Navigation,2018,12(9):964-972.
[18] 夏勇,田西兰,常沛,等. 基于深度学习的复杂沙漠背景SAR目标检测[J]. 雷达科学与技术,2019,17(3):305-309.
[19] 张振仟,胡明宝,孟鑫,等. 门限设置对雷达数据质量的影响研究[J]. 雷达科学与技术,2015,13(5):490-495.
[20] 袁上策,何子述. 改进的多通道系统频域信道均衡算法[J]. 雷达科学与技术,2014,12(5):517-521.
[21] 刘良琦,张良,孟祥东. 宽带阵列通道均衡的工程实现方法研究[J]. 现代雷达,2019,41(6):50-54.


