0 引言
目标检测是雷达系统的基本功能之一。传统的目标检测通常采用固定门限法,该方法思路简单,但是需要获得检测区域内杂波的先验知识才能获得合理的检测门限。在非均匀杂波背景中,由于杂波环境的时变特性和非平稳特性,固定门限法会产生大量的虚警,在实际外场环境中往往应用受限。恒虚警(Constant False Alarm Rate,CFAR)检测能够根据杂波和干扰环境自适应调整检测门限,在雷达自动检测系统中具有广泛的应用。CFAR检测器通常采用滑窗技术,通过对参考窗中的样本进行统计分析获得待检测单元(Cell Under Test,CUT)对应的平均噪底估计值,并乘上一个与虚警率有关的乘积因子获得相应的检测门限,能够克服杂波起伏带来的诸多影响。在近几十年内,CFAR检测算法一直作为雷达信号处理领域中的热门课题,得到了广泛的研究和深入的发展[1-11]。
多目标环境中的CFAR检测一直是雷达实际工作中需要着重考虑的问题。随着现代雷达分辨率的逐渐提高,这类问题在工程应用中进一步凸显。文献[2-3]提出了一种基于Grubbs法则的CAG-CFAR检测算法。该方法通过对正交数字机中的I、Q两路信号分别进行处理,获得了参考窗中的干扰目标判决结果,在进行平均杂波功率估计时将这类干扰目标剔除,获得更加准确的平均杂波功率估计值。该方法理论可行,性能优秀,但在实际应用中由于需要处理两路数据,后续信号处理流程稍显复杂,不利于工程实现。本文基于文献[2-3]的基本思路,提出了一种利于工程实现的简化CAG-CFAR算法,即CAGp-CFAR检测器,并通过仿真处理结果验证了该方法的有效性。
1 经典CFAR检测器
本节主要介绍几种经典的CFAR算法用以后续性能分析与评估,包括CA-CFAR[7]、GO-CFAR[8]、OS-CFAR[9]、TM-CFAR[11]和CMLD[10]。几乎所有的CFAR检测器都期望尽可能去除参考窗中干扰目标对自适应检测门限估计的影响,常用的CFAR检测器皆采用如图1所示的滑窗处理技术。
在平方律检波条件下,通常假设参考窗P中的样本X1,X2,…,XN的概率密度函数服从指数分布,即
(1)
式中,x为杂波样本功率值,σ为指数分布参数。
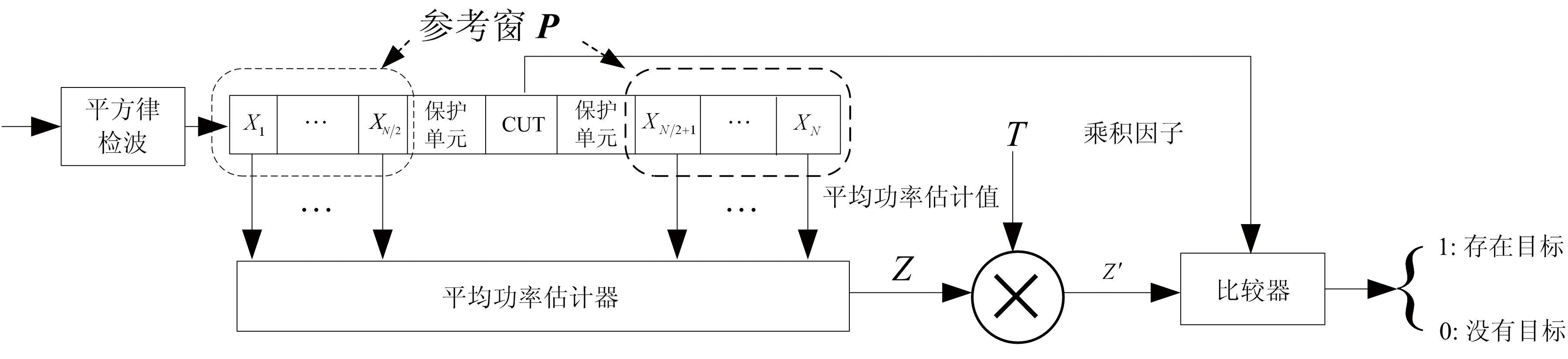
图1 CFAR检测器基本框图
上述几类经典CFAR检测器的基本检测思路总结如下。
2.1 CA-CFAR
CA-CFAR检测器通过计算参考窗中样本的算术平均值估计获得杂波平均功率,即
(2)
当杂波样本服从指数分布时,CA-CFAR的虚警率可以表示为
(3)
式中,T为归一化乘积因子。
2.2 GO-CFAR
GO-CFAR检测器分别计算待检测单元前、后两个局部参考窗中样本的算术平均值,选择其中较大值作为杂波平均功率,即有
(4)
相应地,其虚警率表示为
Pfa,GO=![]()
(5)
2.3 OS-CFAR
OS-CFAR检测器首先对参考窗中的样本按照强度大小进行排序,选择其中第k个作为杂波平均功率。假设经过排序后的参考样本为
X(1)≤X(2)≤…X(N)
(6)
式中,X(1)和X(N)分别为参考窗中强度最小、最大的样本。选择经过排序后样本中的第k个,则杂波平均功率可以表示为
ZOS=X(k),k∈{1,2,…,N}
(7)
通常将k称为噪底样本次序指数,该参数的取值与参考窗长度和所需的虚警率有关,在实际应用中通常选择k=3/4N。此时,OS-CFAR的虚警率可以表示为
(8)
2.4 CMLD
CMLD检测器首先对参考窗中的样本按照如式(6)所示的升序排列,随后剔除掉其中强度最大的n个样本,计算剩下N-n个参考样本的算术平均值并将其作为杂波平均功率,即有
(9)
显然,当干扰目标数目不大于n时CMLD具有良好的抗干扰能力。当n=1时,其虚警率可以表示为
Pfa,CMLD(1)=![]()
(10)
2.5 TM-CFAR
TM-CFAR可以认为是一种广义化的CMLD或OS-CFAR。该检测器通过对如式(6)所示的排序后的参考样本进行线性组合获得杂波平均功率的估计值。其中,式(6)中强度最小的T1个样本和强度最大的T2个样本在进行杂波平均功率估计时被剔除,等效为这类样本的权系数等于0;这种处理有利于剔除参考窗中的强干扰目标或者奇异值。需要注意的是,该方法存在与CMLD方法类似的局限性,即需要事先获知干扰目标的数目,否则检测性能会出现一定下降。TM-CFAR检测器估计获得的杂波平均功率值可以表示为
(11)
对应的虚警率可以表示为
(12)
式中,
MV1(T)=![]() ×
×
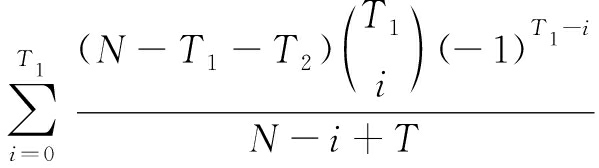
(13)
且有
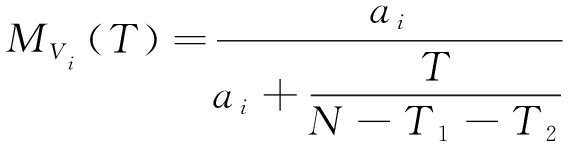
(14)
其中ai=(N-T1-i+1)/(N-T1-T2-i+1),i=2,…,N-T1-T2。从上式可以明显看出OS-CFAR和CMLD都是TM-CFAR的特例。
2 改进的CAGp-CFAR算法
本节主要介绍本文所提出的CAGp-CFAR基本原理。该方法主要包含两个步骤:基于Grubbs法则的野值剔除和自适应检测门限估计。
2.1 基于Grubbs法则的野值剔除方法
在实际应用中,CFAR检测器的参考窗中可能存在奇异值或干扰目标,此时若不加以剔除会严重影响杂波平均功率的估计,从而导致检测性能下降。因此,在进行自适应检测门限估计之前有必要进行野值剔除。常规的野值剔除方法包括Lomnaofski准则、Grubbs准则、Dixon准则和3σ准则。本文选用Grubbs法则进行野值剔除,主要原因如下:
1) Grubbs法则适用于样本数目较小的情况;
2) 临界值的选取仅取决于样本数目和显著性水平。
考虑到实际情况中背景杂波通常未知且参考单元数目往往有限,此时Grubbs法则更具有实际应用优势。
假设一簇样本X1,X2,…,XN服从正态分布,则可以设计统计量
(15)
式中,Xi为参考样本,N为参考窗长度,![]() 为方便起见,若根据式(15)有
为方便起见,若根据式(15)有
(16)
其中
且意味着Xj被判定为野值,需要被剔除;g(N,a/2)为格拉布斯法则的临界值,其取值大小与样本总数目N和显著性水平α有关。常用的临界值取值可见表1。
表1 Grubbs法则的临界值
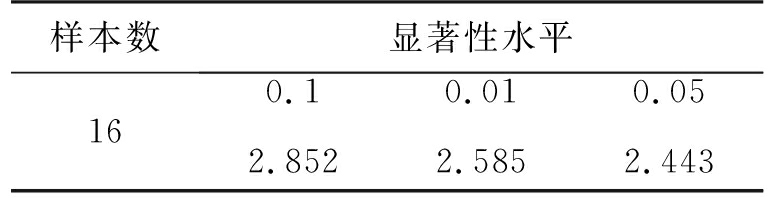
样本数显著性水平160.010.050.12.8522.5852.443
2.2 CAG-CFAR检测器
在CAG-CFAR检测器[2-3]中,首先需要基于Grubbs法则对参考窗中的样本进行野值剔除。经过平方律检波后,如图1所示的参考窗P中的样本为I、Q通道样本的平方和,其概率密度函数服从指数分布;其中,I、Q通道样本的概率密度函数皆服从高斯分布。因此,可预先采用格拉布斯(Grubbs)法则分别对I、Q两个通路的参考单元进行野值剔除,再利用处理之后的参考样本进行杂波平均功率估计,从而在计算自适应检测门限时尽可能地减少干扰目标带来的影响,降低均值类恒虚警检测器可能产生的“遮盖效应”。
CAG-CFAR检测器的基本框图如图2所示。需要注意的是该框图中包含一个额外的参考窗C,其他省略的部分与图1的基本CFAR检测器完全一致。参考窗C中包含了雷达回波的I、Q两路数字信号,分别位于子参考窗CI和CQ中,其次序与图1中参考窗P中经过平方律检波后的样本X完全一致,易知有![]() 其基本处理流程如下:
其基本处理流程如下:
1) 利用Grubbs法则对CI、CQ中的I、Q信号分别进行处理,存储判定出的野值对应的下标pCI和pCQ;
2) 利用获得的pCI和pCQ剔除图1参考窗P中的平方律检波后的野值样本,对应的野值样本序号集p为pCI和pCQ的并集,即有
p={pCI}∪{pCQ}
(17)
上式表明,参考窗CI和CQ中判定出的野值在参考窗P中皆需剔除。例如,若参考窗CI中的第3、6、9个样本和参考窗CQ中第4、6个样本被判定为野值,则参考窗P中的第3、4、6、9个样本需要在进行杂波平均功率估计时剔除。
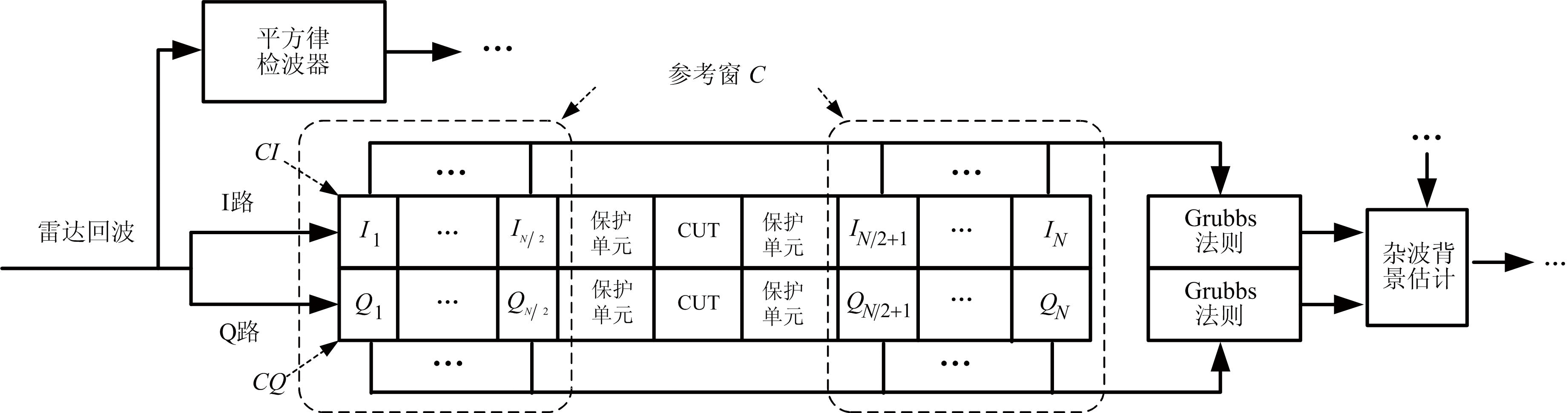
图2 CAG-CFAR处理框图
2.3 改进的CAGp-CFAR
虽然CAG-CFAR检测器在理论上具备良好的干扰目标剔除能力,但由于该方法需要在平方律检波之前对雷达回波复信号的I、Q两路分别进行处理,且处理结果需要同步反馈至平方律检波之后的平均功率估计器,在实际应用中需要较为复杂的检测器形式,对雷达软件的配置要求较高,在工程应用中存在一定限制。
基于此,本文提出了一种改进的CAGp-CFAR检测算法。该方法与CAG-CFAR检测器[2-3]的基本思路一致,但在应用Grubbs法则时对检测器的形式进行了简化。本方案中,不再对I、Q两路分别进行基于Grubbs法则的野值剔除,而是直接对如图1所示检测器参考窗P中的样本进行处理。此时,图2对应的检测器形式可以简化为图3。
需要注意的是,由于Grubbs法则仅在样本的概率密度函数服从正态分布时具有明确的物理意义,考虑到经过平方律检波之后的参考样本服从指数分布,则此时难以从物理层面理论评估Grubbs法则的野值剔除,但作为一种次优的工程应用方案,该方法依旧具备良好的应用价值。为区分Grubbs法则在正态分布中的临界值g,CAGp-CFAR在指数分布杂波中利用Grubbs法则进行野值剔除时采用的临界值用gα表示,工程上可取gα=2或者3。
3 性能分析
3.1 恒虚警特性分析
由于CAGp-CFAR检测器中利用Grubbs进行野值剔除,其计算过程是非线性的,难以获得虚警率与乘积因子之间关系的解析表达式,因此本文利用蒙特卡洛方法对CAGp-CFAR在指数分布杂波中的虚警率进行仿真分析。图4给出了CAGp-CFAR检测器在均匀背景下不同杂波功率时的虚警率,对应的gα分别为2和3,检测器参考窗长度为16,蒙特卡洛试验次数为108。由图中结
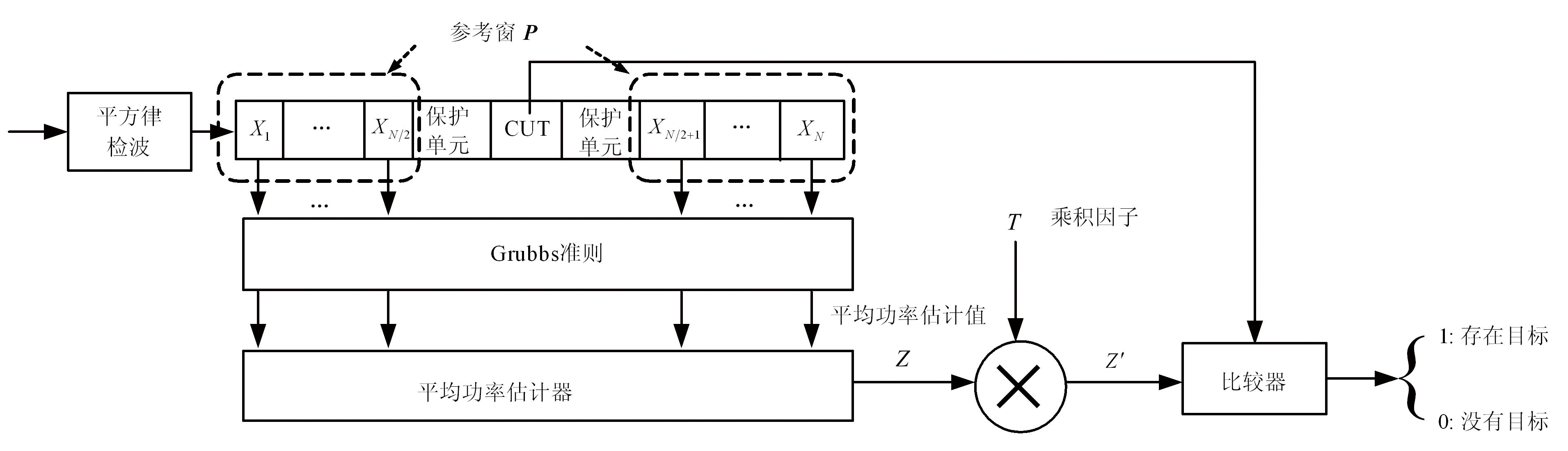
图3 CAGp-CFAR处理框图
果可知,CAGp-CFAR的虚警率-乘积因子曲线在不同指数分布参数μ下基本重合,表明该方法对指数分布杂波具备恒虚警特性;同时,当gα取不同值时对应的虚警率曲线略有不同,这意味着在实际应用中需要考虑gα对检测器的影响。
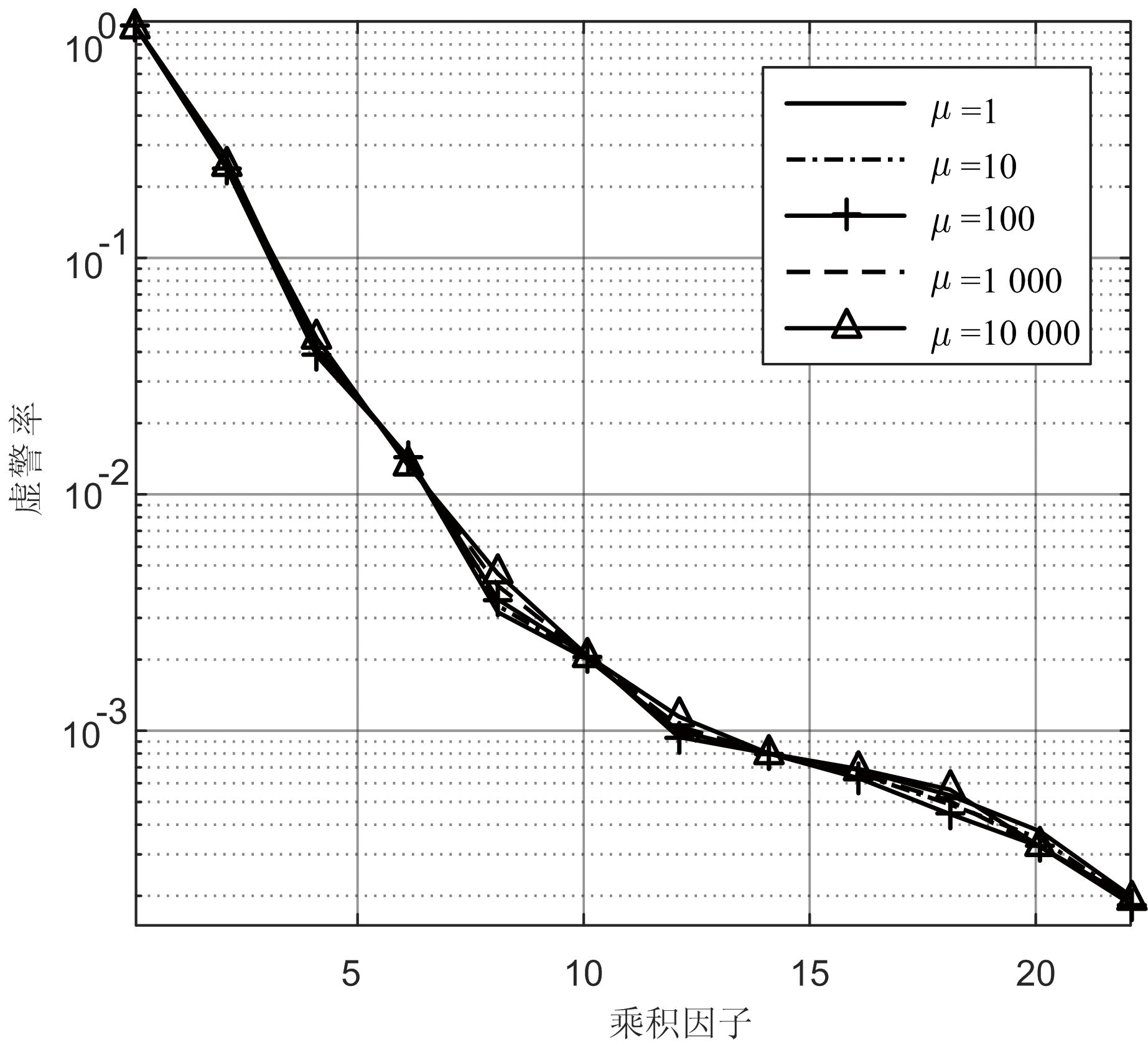
(a) gα=2

(b) gα=3
图4 CAGp-CFAR的虚警率结果
3.2 均匀背景下的检测性能
图5给出了CAGp-CFAR与几类经典CFAR检测器在目标信杂比为12 dB时的接收机工作曲线。这几类检测器分别为GO-CFAR[8]、OS-CFAR[9]、CMLD[10]、CA-CFAR[7]和TM-CFAR[11]。仿真试验中各类检测器参考窗长度皆为16,保护单元数为3,乘积因子对应的虚警率Pfa=10-5,OS-CFAR的噪底样本次序指数为12,CMLD的目标剔除数为1,TM-CFAR的极大、极小值剔除数皆为2。由结果可知,CAGp-CFAR检测器在均匀背景下的检测性能与已被证明具备最优性能的CA-CFAR检测器相当。这意味着CAGp-CFAR在均匀背景下对杂波平均功率具备良好的估计性能。
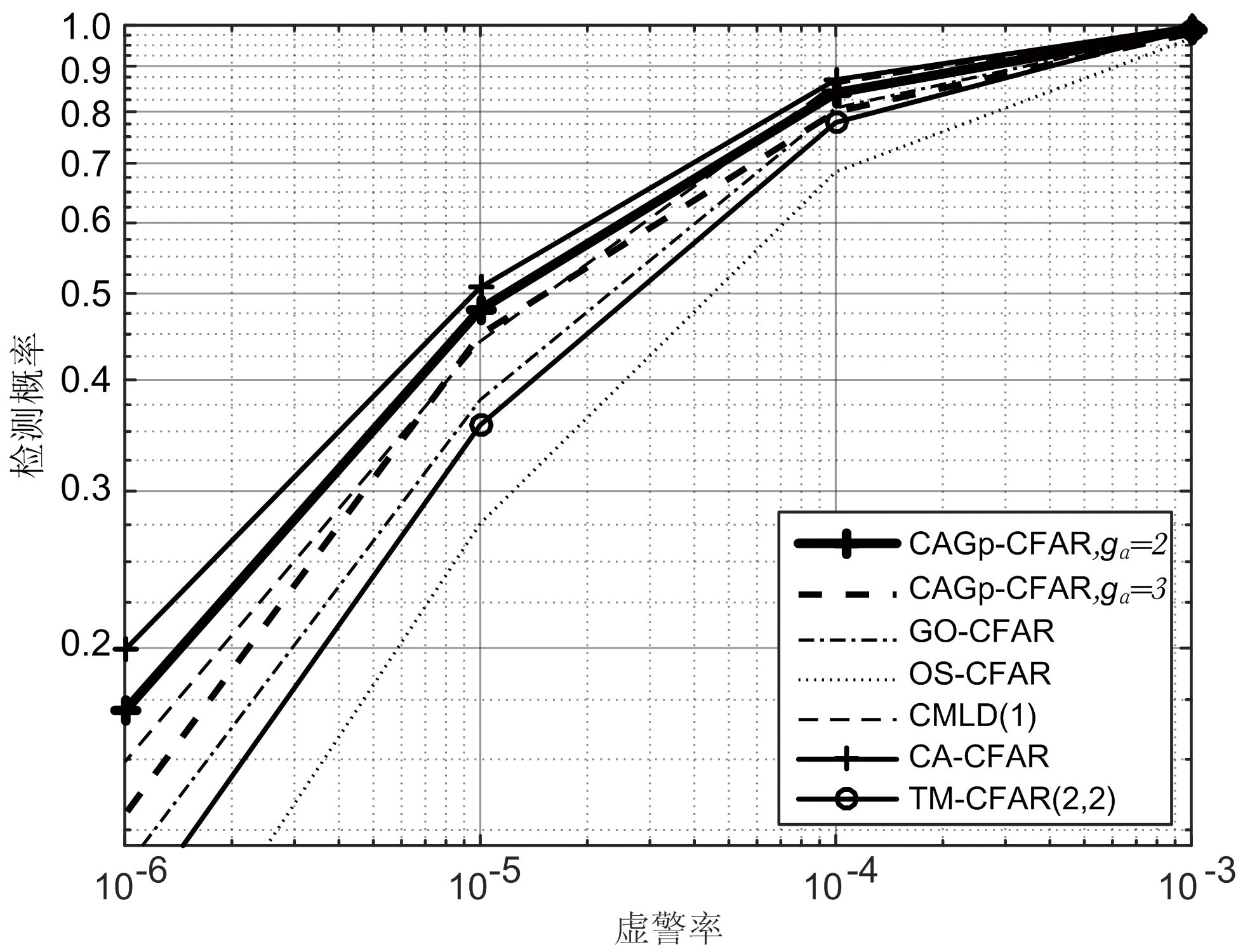
图5 CAGp-CFAR与几类经典CFAR检测器的接收机工作曲线(目标信杂比12 dB,工作虚警率Pfa=10-5)
3.3 多目标背景下的检测性能
图6给出了CAGp-CFAR在同时存在2个干杂比(INR)为10 dB的干扰目标时的检测性能。仿真试验中各类检测器参考窗长度皆为16,保护单元数为3,乘积因子对应的虚警率Pfa=10-5,OS-CFAR的噪底样本次序指数为12,CMLD的目标剔除数为1,TM-CFAR的极大、极小值剔除数皆为2。由结果可知,当干扰目标INR为10 dB时,由于CA-CFAR和GO-CFAR利用参考窗中所有样本进行杂波功率估计,干扰目标会引起检测门限太高而降低检测性能;CMLD由于只能剔除1个干扰目标,因此会出现一定程度的性能下降;OS-CFAR虽然具备多目标检测能力,但由于该方法估计杂波功率时只用了一个样本,因此会出现较大的损失;TM-CFAR能够剔除2个目标,因此具备相对较好的性能;此时,CAGp-CFAR具有相对最优的检测性能。当干扰目标INR上升为20 dB时,CAGp-CFAR在gα为3时出现明显的性能下降,而在gα取2时仍具备鲁棒的最优检测性能。
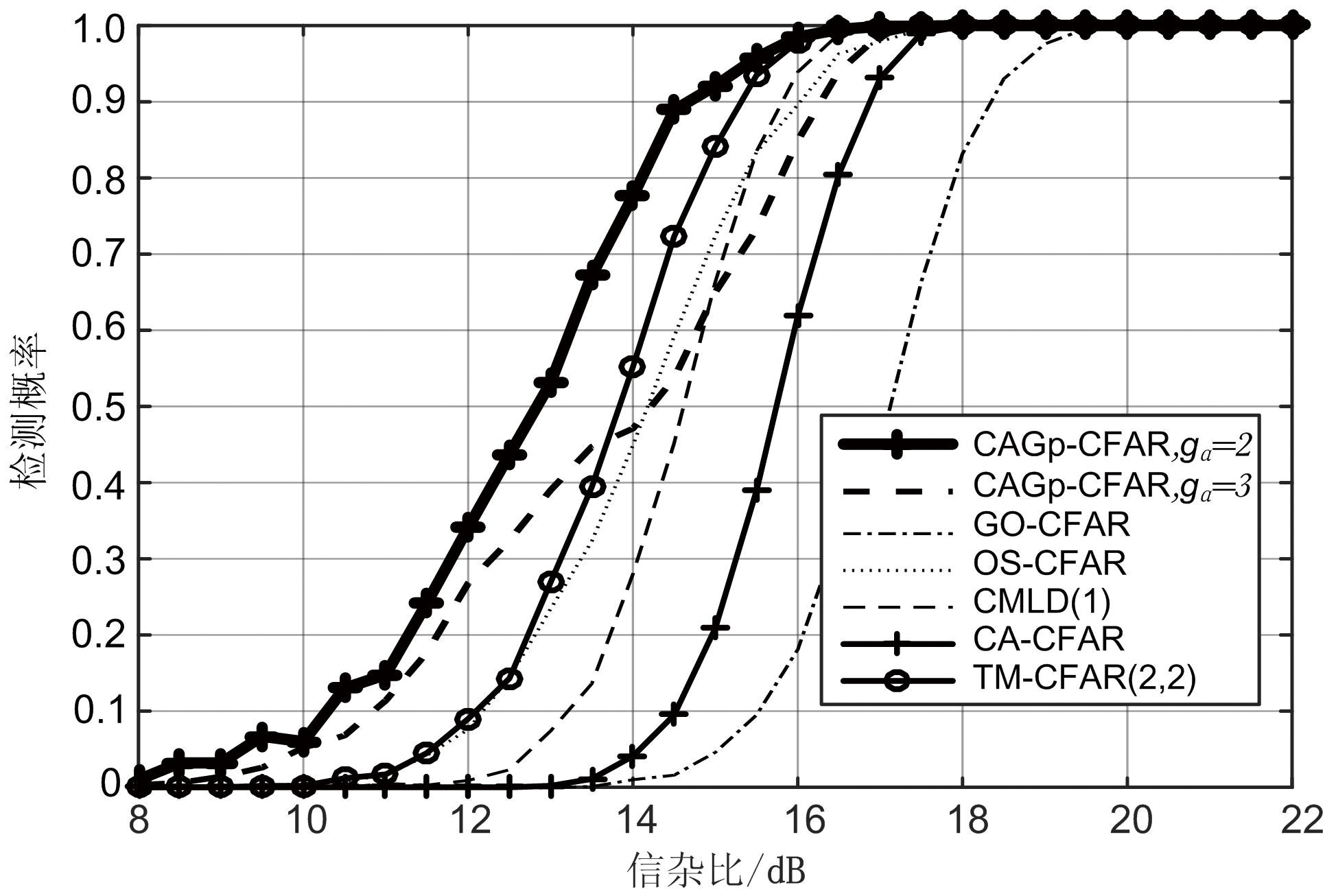
(a) INR=10 dB
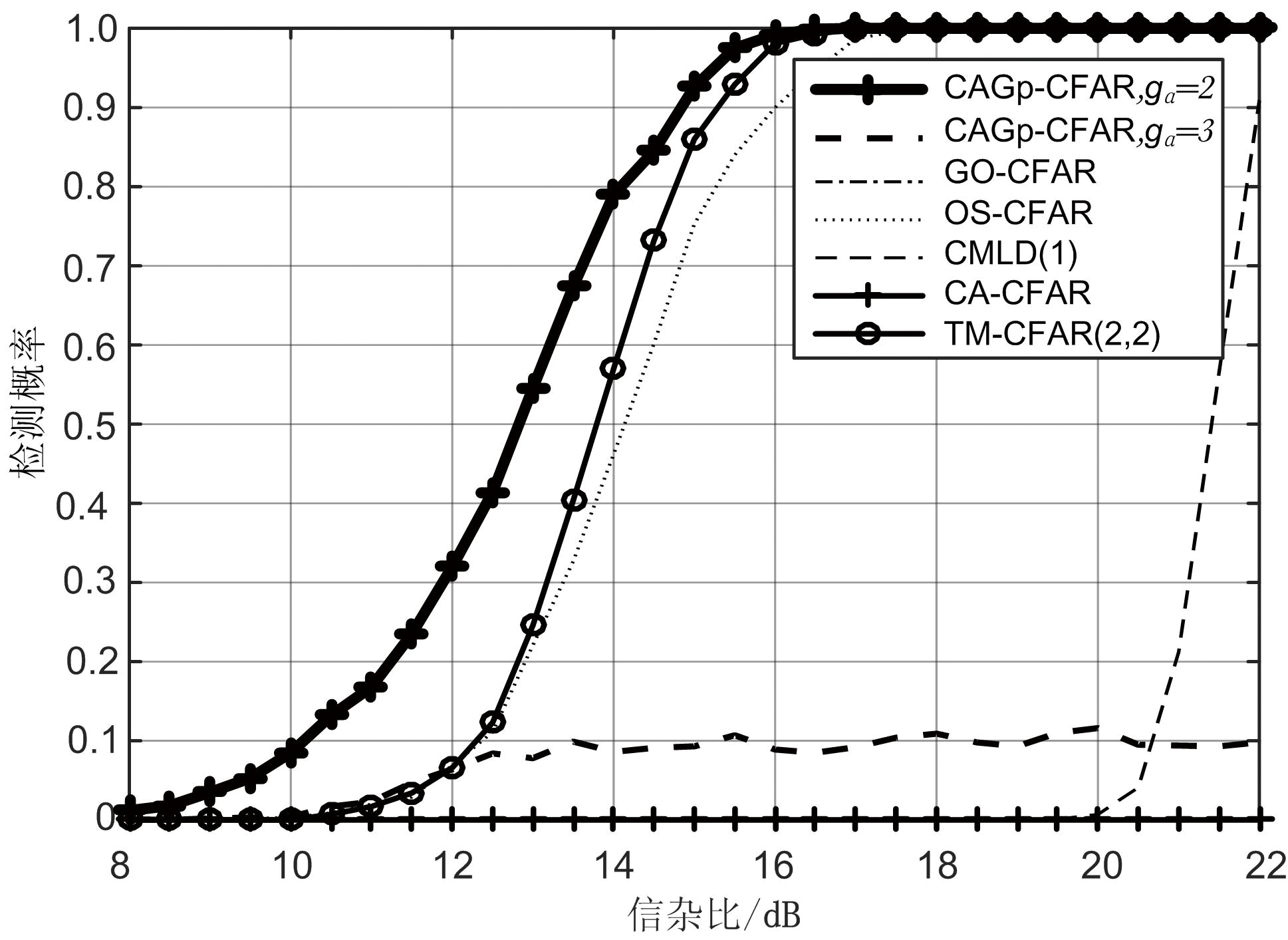
(b) INR=20 dB
图6 CAGp-CFAR与几类经典CFAR检测器在2个干扰目标、不同INR条件下的检测性能
图7给出了CAGp-CFAR在干扰目标干杂比与主目标信杂比相同时的检测性能,干扰目标数目分别为1和2。这类情况对应了最恶劣的多目标情形,此时由于干扰目标干杂比与主目标信杂比始终一致,如果不进行野值剔除,则传统的均值类检测器会出现不可容忍的性能下降。仿真试验中各类检测器参考窗长度皆为16,保护单元数为3,乘积因子对应的虚警率Pfa=10-5,OS-CFAR的噪底样本次序指数为12,CMLD的目标剔除数为1,TM-CFAR的极值剔除数皆为2。
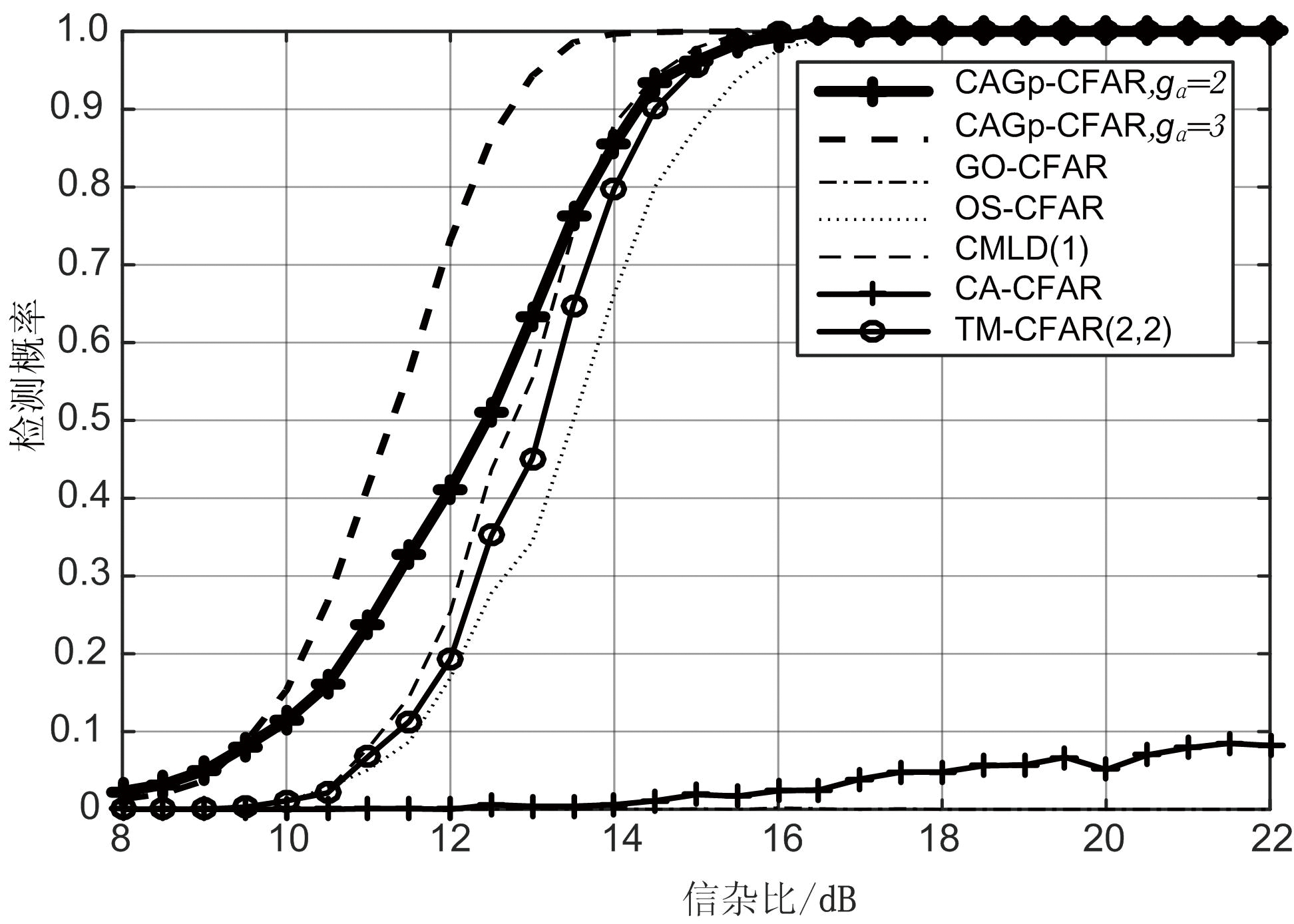
(a) 1个干扰目标
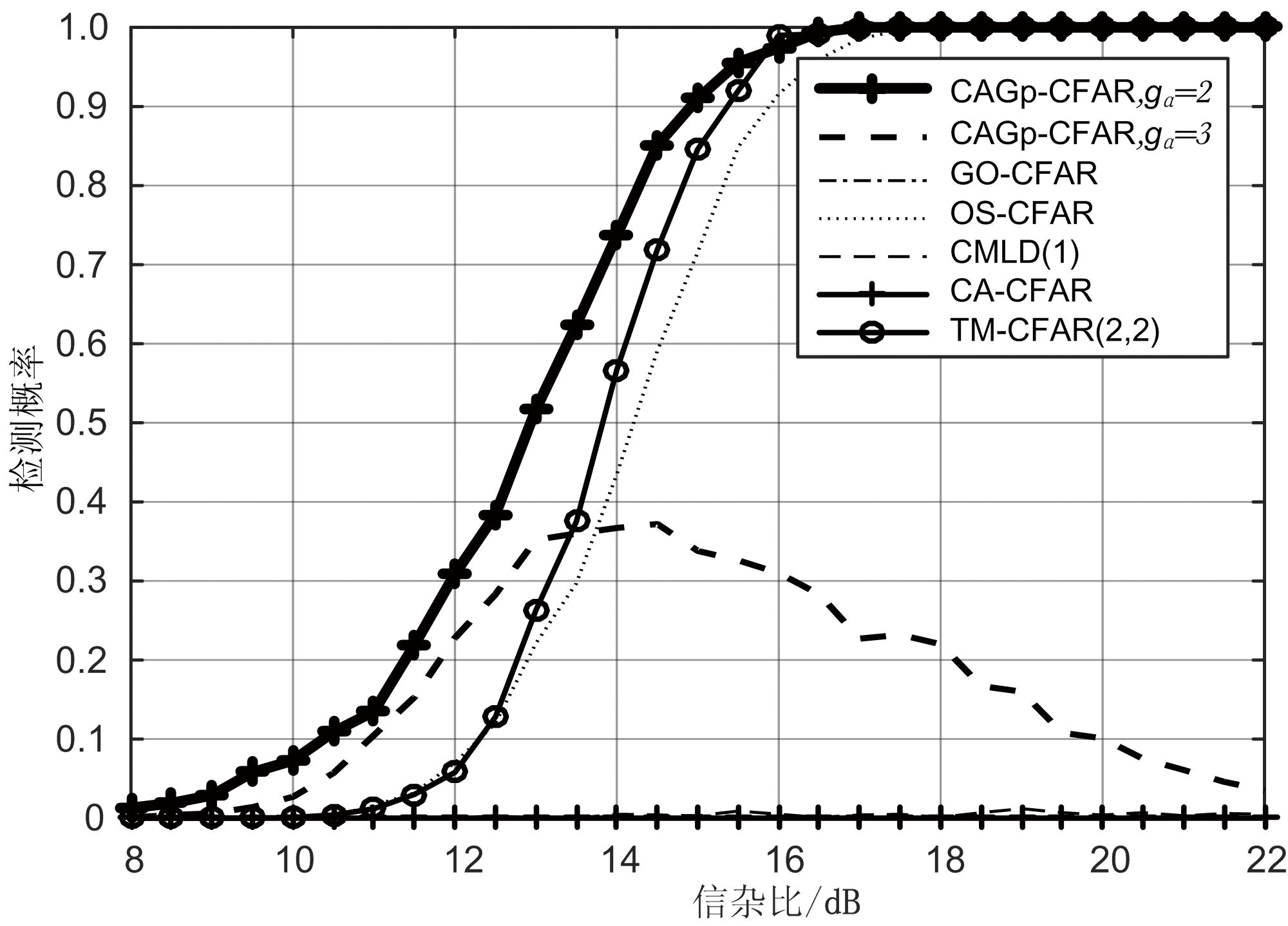
(b) 2个干扰目标
图7 CAGp-CFAR与几类经典CFAR检测器在INR与目标信杂比相同条件下的检测性能
图7(a)给出了干扰目标数目为1的情况。由结果可知,CA-CFAR和GO-CFAR由于不具备野值剔除的能力,出现检测饱和现象即主目标几乎不能被正常检测;由于只存在1个干扰目标,因此CMLD和TM-CFAR具备可用的剔除能力,检测性能相对较好;OS-CFAR仍存在由其检测机理决定的恒虚警损失;此时,CAGp-CFAR具有相对最优的检测性能。图7(b)给出了干扰目标数目为2的情况。此时,CA-CFAR和GO-CFAR的性能依旧令人难以接受;由于干扰目标数目超过了CMLD的容忍程度,因此CMLD也出现检测饱和现象,而TM-CFAR和OS-CFAR具备相对稳定的性能;此时,CAGp-CFAR在gα取2时具备相对最优的检测性能,而当gα取3时出现明显的性能下降。因此,结合上文的分析,在实际应用中建议采用gα=2的CAGp-CFAR检测器。
4 结束语
本文提出了一种利于工程实现的CAGp-CFAR检测器,该方法基于Grubbs法则剔除参考窗中的干扰目标,实现杂波平均功率的准确估计。仿真结果表明,该方法在均匀背景下的检测性能与已被证明性能最优的CA-CFAR检测器相当,在多目标背景下与几类经典CFAR检测器相比具备更优的检测性能。考虑到本文的分析结果主要针对参考单元为16,可根据理论分析合理预估本方法在参考单元数目提高时亦具备更优的检测性能、更低的恒虚警损失。本文方法可应用于各类预警雷达,适用于海面小目标和地面目标自动检测,具备广阔的应用前景。
[1] ZHOU Wei,XIE Junhao,LI Gaopeng,et al. Robust CFAR Detector with Weighted Amplitude Iteration in Nonhomogeneous Sea Clutter[J]. IEEE Trans on Aerospace and Electronic Systems,2017,53(3):1520-1535.
[2] ZHOU Wei,XIE Junhao,XI Kun,et al. Modified Cell Averaging CFAR Detector Based on Grubbs Criterion in Multiple-Target Scenario[C]∥ 2018 International Conference on Radar,Brisbane,QLD,Australia:IEEE,2018:1-6.
[3] ZHOU Wei,XIE Junhao,XI Kun,et al. Modified Cell Averaging CFAR Detector Based on Grubbs Criterion in Non-Homogeneous Background[J]. IET Radar,Sonar & Navigation,2019,13(1):104-112.
[4] ZHOU Wei,XIE Junhao,ZHANG Baiqiang,et al. Maximum Likelihood Detector in Gamma-Distributed Sea Clutter[J]. IEEE Geoscience and Remote Sensing Letters,2018,15(11):1705-1709.
[5] GAO Gui,SHI Gongtao. CFAR Ship Detection in Nonhomogeneous Sea Clutter Using Polarimetric SAR Data Based on the Notch Filter[J]. IEEE Trans on Geoscience and Remote Sensing,2017,55(8):4811-4824.
[6] WANG Yikai,XIA Wei,HE Zishu. CFAR Knowledge-Aided Radar Detection with Heterogeneous Samples[J]. IEEE Signal Processing Letters,2017,24(5):693-697.
[7] FINN H M,JOHNSON R S. Adaptive Detection Mode with Threshold Control as a Function of Spatially Sampled Clutter-Level Estimates[J].RCA Review,1968:414.
[8] HANSEN V G. Constant False Alarm Rate Processing in Search Radars[J].Computer Science,1973:325-332.
[9] ROHLING H. Radar CFAR Thresholding in Clutter and Multiple Target Situations[J]. IEEE Trans on Aerospace and Electronic Systems,1983,19(4):608-621.
[10] RITCEY J A. Performance Analysis of the Censored Mean-Level Detector[J]. IEEE Trans on Aerospace and Electronic Systems,1986,22(4):443-454.
[11] GANDHI P P,KASSAM S A. Analysis of CFAR Processors in Nonhomogeneous Background[J]. IEEE Trans on Aerospace and Electronic Systems,1988,24(4):427-445.


