0 引言
为了提高目标参数的精确测量，特别是空间目标、导弹、火控系统、靶场测量的需求，近几十年来，雷达测量技术有了很大发展。美国导弹防御局2002 年开展了“基于相位导出测距的分辨技术”研究，其中的关键技术是在宽带雷达上利用相位信息精确测距，对目标的精细运动进行分辨，实现瞬时成像、获取微动特征。
国内相关高校院所也先后开展相推测距研究。其中，南京电子技术研究所 [1]研究了窄带游标测距应用于精密测量雷达；南京理工大学[2-3]研究了窄带游标测距在窄带线性调频脉冲雷达中的应用，对解模糊纠错问题进行分析，提出了解模糊出错判决准则和纠错方法。中国航天科工集团公司第二研究院23 所[4]研究了基于游标法的空间目标距离精确测量技术。此外，中国电子科技集团公司第三十八研究所、北京理工大学、国防科技大学[5]、西安电子科技大学等单位也在基于相推测距方面开展研究，方法或方向有所差别，有窄带相推测距技术、宽带相推测距技术、步进频合成宽带相推测距技术、基于高精度相推测距技术的微动特征提取等多方面内容。
多年来，在反隐身技术研究中，特别是20世纪末科索沃战争，F-117A隐身飞机被萨姆导弹击落，米波雷达再次得到关注和发展。过去认为的米波雷达缺陷，如空域覆盖、测量精度、抗干扰、目标识别等问题，随着现代阵列雷达技术，特别是先进信号处理技术的发展，在先进米波雷达[6]中逐步得到解决。
相推测距技术由于利用相位信息获得更高的距离精度，可以达到波长级，通过消除运动目标的进动可以获得目标微动特征，为目标识别提供有力的手段。本文探讨一种高精度窄带相推测距方法，可解决米波雷达因工作频率低和绝对频带窄带来的测速测距精度低等问题，在一定的信噪比下可达到分米级，使得先进米波雷达不仅在防空警戒雷达使用，也可以在火控系统中担负搜索制导作用。
1 相推测距原理
1.1 窄带回波信号解析
当雷达发射信号为f(t)，则经过距离R的点目标反射，接收信号延时[7]为
(1)
式中，c为光速。
接收信号g(t)为
(2)
式中，s为时间拉伸因子。
当信号相干处理时间Tc满足窄带条件：
(3)
式中，v为目标速度，B为信号带宽。
则接收可近似为
g(t)=f(t-τ)ejωdt
(4)
对宽带雷达而言，目标不能假设为点目标，而是多个散射点组成的面目标，除了目标平动外，还要考虑目标自旋等微动特性。当相干时间较长时还要考虑目标运动带来的时间拉伸和距离跨越等问题。对窄带雷达，目标可认为是点目标，信号为调制信号的延迟以及发射载频的多普勒效应，其处理模型可以简化。
在脉冲体制雷达中，通常为了增加探测威力，发射一定带宽的调制信号，如线性调频信号。具体而言，若雷达发射信号[8]为
s(t)=p(t)exp(jπμt2)
(5)
式中：p(t)为矩形信号，即当
时，p(t)为0；T为脉冲持续时间；μ为调频斜率。
在信号经过空间传输后，接收端接收到的信号的相位会随着每次脉冲对应的雷达与目标之间的距离变化而不同，输出的信号为
xr(t)=z·s(t-τ(t))·
exp(j2πfc(t-τ(t)))+u(t)
(6)
式中，u(t)为高斯加性白噪声，fc为载波频率，z为目标复反射系数。
经过带阻滤波器后，得到基带信号：
xrb(t)=z·s(t-τ(t))·
exp(-j2πfcτ(t))+u(t)
(7)
这样，第m个脉冲的基带信号可近似地表示为
xm(t)=z·s(t-τm)·
exp(-j2πfcτm)+u(t)
(8)
一般，在有限时间内对目标运动采用三阶运动模型即可，则
(9)
式中，R0，v0和a0分别为t=0基准时刻(即第 m=0个脉冲的发送时刻)雷达与目标的距离、目标的径向速度和加速度，Tr为脉冲重复周期。
也就是说，回波信号中相位信息包含目标距离以及径向速度和加速度等高阶运动信息。只要估计出径向速度和加速度等高阶运动参数，则可以对多普勒相位进行补偿，并获得距离以及距离增量等。
对目标径向速度与加速度估计可采用相关处理，从高阶差分开始，依次向低阶进行。文献[9]进行分析，本质上是对时间量微分降阶处理，提取相位差获得对应参数估计值，这里不展开讨论。目标速度估计原则上只要2个脉冲，加速度估计只要3个脉冲即可。根据需要，在系统时序设计中根据雷达参数确定，只要满足速度解模糊要求就可以获得很高的速度估计精度。
对窄带信号，简单说，多普勒相位θ(t)(雷达发射波与回波的瞬时载波相位差)为
θ(t)=ω0τ(t)
(10)
这样
(11)
相推测距就是通过测量多普勒相位来得到目标径向距离。由于相位以2π为模糊，一般得到的是模糊相位值。在脉冲体制的相推测距中需要一定的方法解相位模糊获得相位增量(速度等带来的目标距离增量)，这个问题后面讨论。同样，初始距离对应的相位也是模糊的，而窄带雷达距离估计精度不足以实现距离解模糊(宽带信号满足一定条件就可以实现绝对距离精确测量)。由于是两个时刻的距离相对变化，因此可采用游标测距的办法实现距离连续测量。
其测距方程为
游标距离=基准距离+相对距离
其中基准距离可由脉冲雷达的包络测距或其他方式得到，相对距离用相推测距方法得到。
1.2 模糊相位的估计
根据电磁波传播与距离的关系得到相位测距的基本关系。一个波长的距离，雷达波来回有两个波长，即有4π，这样式(11)变为相位测距方程：
(12)
显然，由于测尺长度为半个波长，因此实际上距离高度模糊。
上式也可以写为
(13)
式中，L为相位2π模糊数，φ为模糊后的相位，由 I/Q数据即可获得。
经研究，对于线性调频信号脉冲压缩积累后，从脉压后峰值对应的时刻提取其多普勒相位是可行的[2]。
脉冲压缩后信号可表示为
y(t)=exp(jπfd(t-τ)-j2πfcτ)(T-|t-τ|)·
(14)
式中，|t-τ|≤T。
其峰值对应时刻相位为
(15)
脉压后的峰值相位中包含多普勒相位θi，也包括噪声εi。为了提取多普勒相位，需要进行相位补偿，去掉噪声εi。通常测速误差对εi影响很小，可以忽略。
由I/Q提取的相位信息是以2π为模的模糊相位，包含了目标距离、径向速度、加速度，以及雷达系统等带来的相位信息。
1.3 相位解模糊
若雷达波束始终指向目标，令第i个发射脉冲内的某点在ti时刻由目标反射，此时目标径向距离为R(ti)。用相推测距方法得到相邻脉冲的距离增量ΔRi：
(16)
式中，Di=θi+1-θi称为多普勒相位增量。
因此，若已知起始时刻的目标径向距离为R0(基准距离)，则任意时刻的径向距离为
Ri=R0+ΔRi-1,0
(17)
式中相对距离
ΔRi-1,0=ΔR0+ΔR1+…+ΔRi-1
(18)
由此可知，窄带相推测距的核心问题就是获得多普勒相位增量Di。同时基准距离只是反映起始时刻目标的距离，其误差可以理解为这时间序列中目标轨迹的距离系统误差，其误差大小并不影响目标运动轨迹的特征。
由式(9)、式(15)、式(16)可知，对于匀速运动目标，其相位差体现为径向速度带来的距离变化，初始距离R0对相位差没有影响。
一般地，目标运动，其相位增量Di也涉及相位模糊的问题，通常获得的测量值是模糊值，显然，就需要相位解模糊。文献[3]对此进行分析，这里简单讨论。
设
为Di的测量值，有
(19)
式中，
为
的误差。显然，可以表示为以2π为模的小数部分
和整数
之和。
(20)
式中，
为θi的模糊测量值，可由I/Q获得，即
(21)
式中:Ki为θi的整周数，
为
的误差，令
获得可通过测量
和
并求解
即解模糊。
当引入多普勒相位增量的估计值
有
(22)
式中,
为
的误差。
若误差满足式(23)时
(23)
则利用
和
和
可通过不等式(24)解模糊，即
估计模糊数。
(24)
如前所述，模糊多普勒相位在全相参脉冲多普勒雷达中很容易得到。对于脉冲调制信号可以先积累并对其I/Q估计相位。在杂波环境中，可采用MTD/PD方式抑制杂波并实现目标信号相参积累也可实现I/Q相位提取。
对脉冲体制雷达可用近似积分的方法得到Di的估计值(要注意这里是近似，在工程中就需要考虑满足近似条件，特别是高速高机动性目标，提高雷达系统跟踪数据率，进行高阶运动带来的相位补偿是需要考虑的措施)。
(25)
式中
为平均多普勒频率。再根据t′i=ti-τi/2，则可变为
(26)
计算式(26)需要测量多普勒频率(速度)、时差(ti+1-ti)和延迟时间。当消去延迟时间项，同时利用多普勒频率远小于载频的性质，得到只须测量多普勒频率和时差的多普勒相位增量的估计方法。
(27)
若测量时刻在脉冲边缘时产生最大误差。对于信号调制的脉冲，其取决于脉冲压缩后的脉冲宽度。提高雷达系统时标信息精度可减小多普勒相位增量估计误差。
fd误差关系到多普勒相位增量的估计误差，对于跟踪测量雷达，可以获得较高精度的无模糊多普勒频率fd。由于fd是基于梯形估计中值逼近多普勒相位增量，因此脉冲周期的选择要考虑目标的机动性影响，即目标的加速度和加加速度因素。对于跟踪雷达而言，其跟踪数据率通常较高，这个影响基本可以忽略。在跟踪数据率不高的情况下，可考虑增加波位驻留时间，提高脉冲重复频率等设计，提高测速精度和速度不模糊范围。
对相位增量求和，有
(28)
目标质心在ti时刻径向距离用Ri表示，将多普勒相位增量和
转化为距离，得到第i个脉冲发射时刻目标相对于第0个脉冲发射时刻的距离变化。
(29)
可见，基于相推测距测得的距离增量误差很小，其精度达到波长级，通常优于λ/4。对米波雷达而言，其精度也远高于窄带包络测距精度。若已知起始时刻距离
(即常规包络测距获得的距离)，则可得到其他脉冲发射时刻目标质心距离。
(30)
也就是目标质心平动轨迹。
1.4 提高基准距离精度
相推测距的实质就是将多普勒相位增量和转化为距离，获得目标相对于初始时刻t0的精确距离增量，从而获得精确的运动轨迹。对于初始位置距离误差较大，并不影响运动规律估计。这个过程中关键是正确解相位增量模糊。
对于窄带相推测距，由于基准距离的精度影响，因此其测量的绝对距离精度受其影响变成系统误差。
要提高窄带雷达测量绝对距离精度，则需要提高基准距离精度。可考虑的方法有：
通过宽窄带结合的方式，实现跟踪目标距离高精度测量。窄带方式进行常规搜索发现目标，捕获跟踪后可以发射宽带信号进行测量，获得高精度的初始距离，并作为基准距离。
在窄带雷达中采用步进频合成宽带[10]提高测距精度，同样提高基准距离精度。
还有一种方式是在目标跟踪过程中通过历史样本提高基准距离估计精度[11]，消除或减小单次测量中的随机距离误差。这种方式不需额外措施，在跟踪过程中即可完成。简单说明如下：
在常规距离测量值中，根据误差和真值构成，第i次常规距离测量Ri表示为
Ri=ri+Rs+Rδi=
(31)
假定真实距离为ri，其中距离量测误差中既包含常规包络测量的随机误差Rδi，又包括其系统误差Rs。由于相推测距计算得到的距离增量ΔRi的距离随机误差小，可达到λ/2以下，远远小于Rδi。相对常规窄带包络测距，窄带相推测距精度高约两个数量级。
R′i=Ri-ΔRi=ri+Rs+Rδi-ΔRi≈
r0+Rs+Rδi
(32)
为R(t)序列的均值。因此基准距离估计：
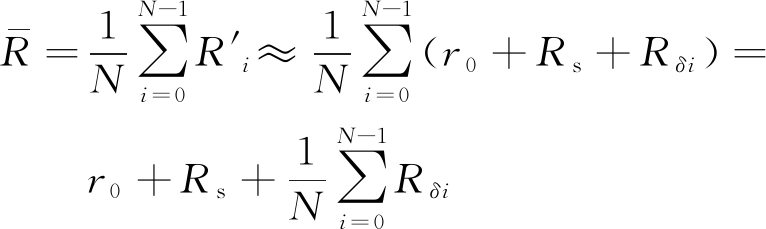
(33)
距离系统误差Rs可以通过标校补偿。这样基准距离可以通过常规距离跟踪测量与窄带相推测距相结合提高窄带雷达的距离探测精度。
2 处理流程及试验结果
综合前面分析，窄带相推测距处理流程有几个要点：
1) 常规包络测距，并进行跟踪滤波处理，获得目标距离以及速度粗估计，若需要可进行加速度粗估计；
2) 脉冲压缩处理，获得模糊相位；
3) 进行速度或加速度精估计，并结合粗估计进行速度解模糊，获得高精度速度估计值；
4) 根据雷达系统选择合适方法对基准距离估计；
5) 通过多普勒速度估计相位增量，形成高精度距离变化量；
6) 采用游标测距形成窄带相推测距值。
其处理流程如图1所示。
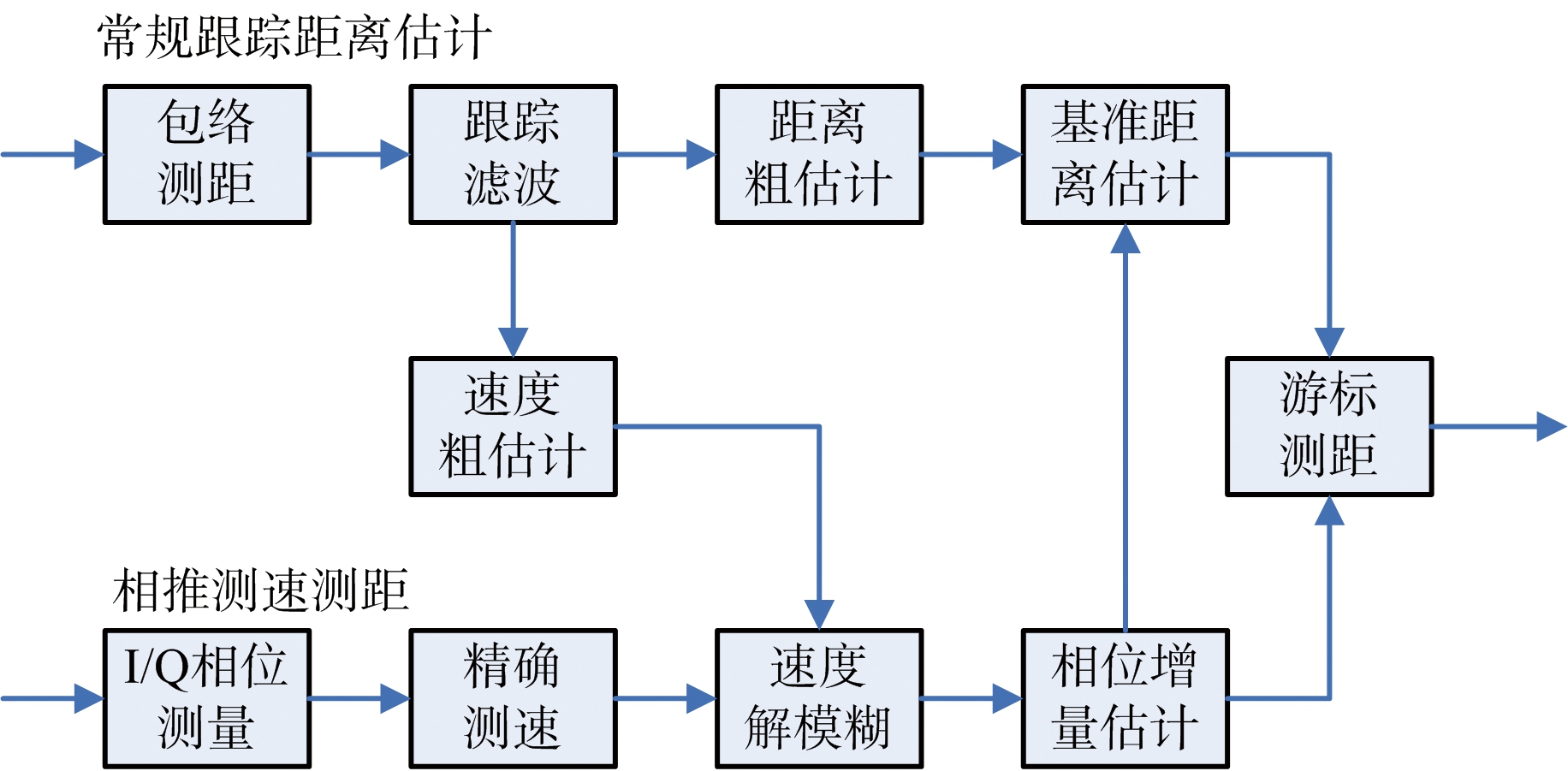
图1 窄带相推测速测距流程图
为探索提高米波雷达距离测量精度，针对该方法结合某米波雷达开展探测试验，并对其数据进行分析拟合对比。试验环境为目标类型：飞机；信噪比：约30 dB；信号带宽： 0.8 MHz；采样率：1 MHz；每波位16个脉冲，脉冲周期：4.6 ms；跟踪数据率：2 Hz。其处理结果(以拟合值作为真实值估计相推测距误差)如图2～图5所示。
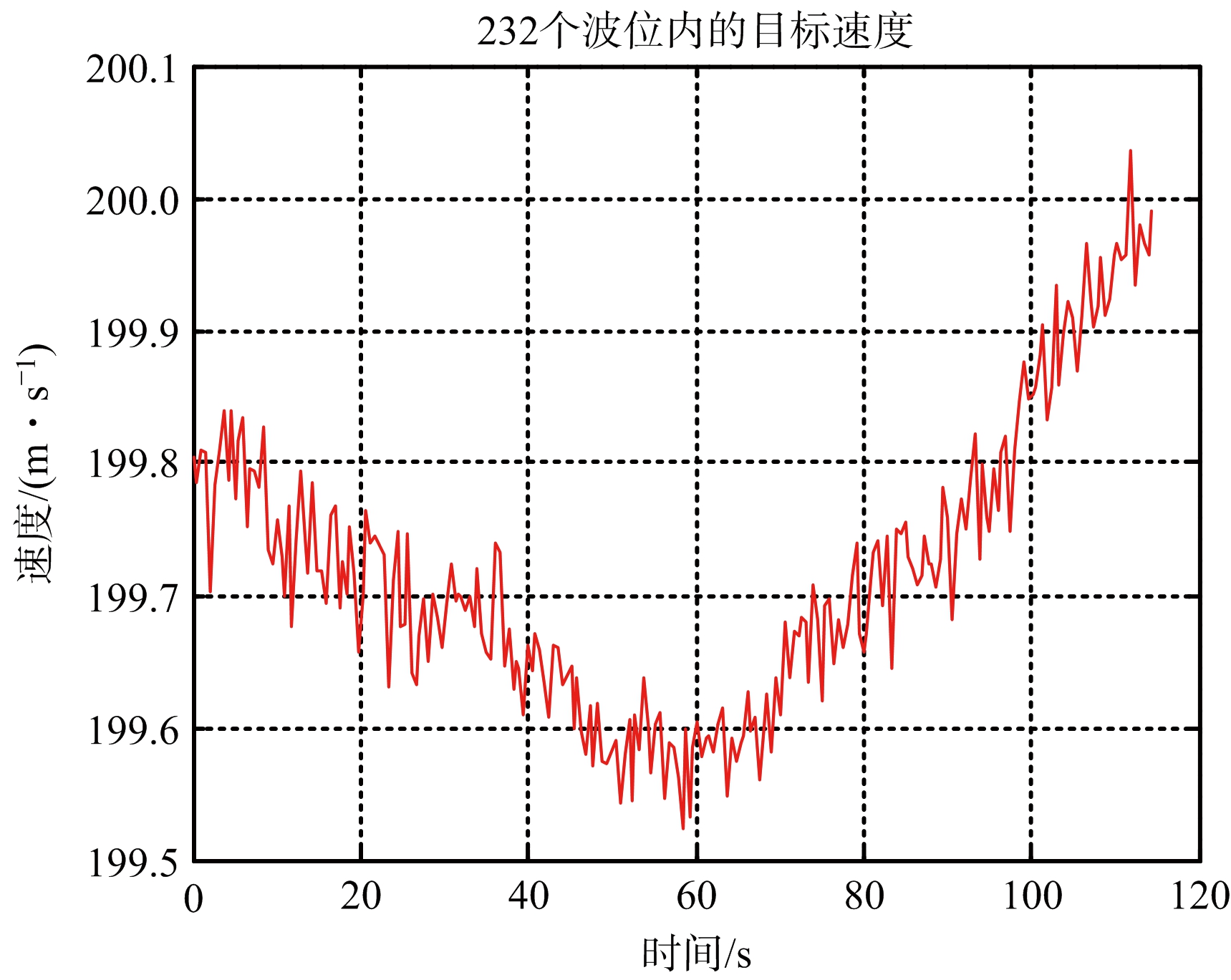
图2 窄带相推测距高精度速度估计
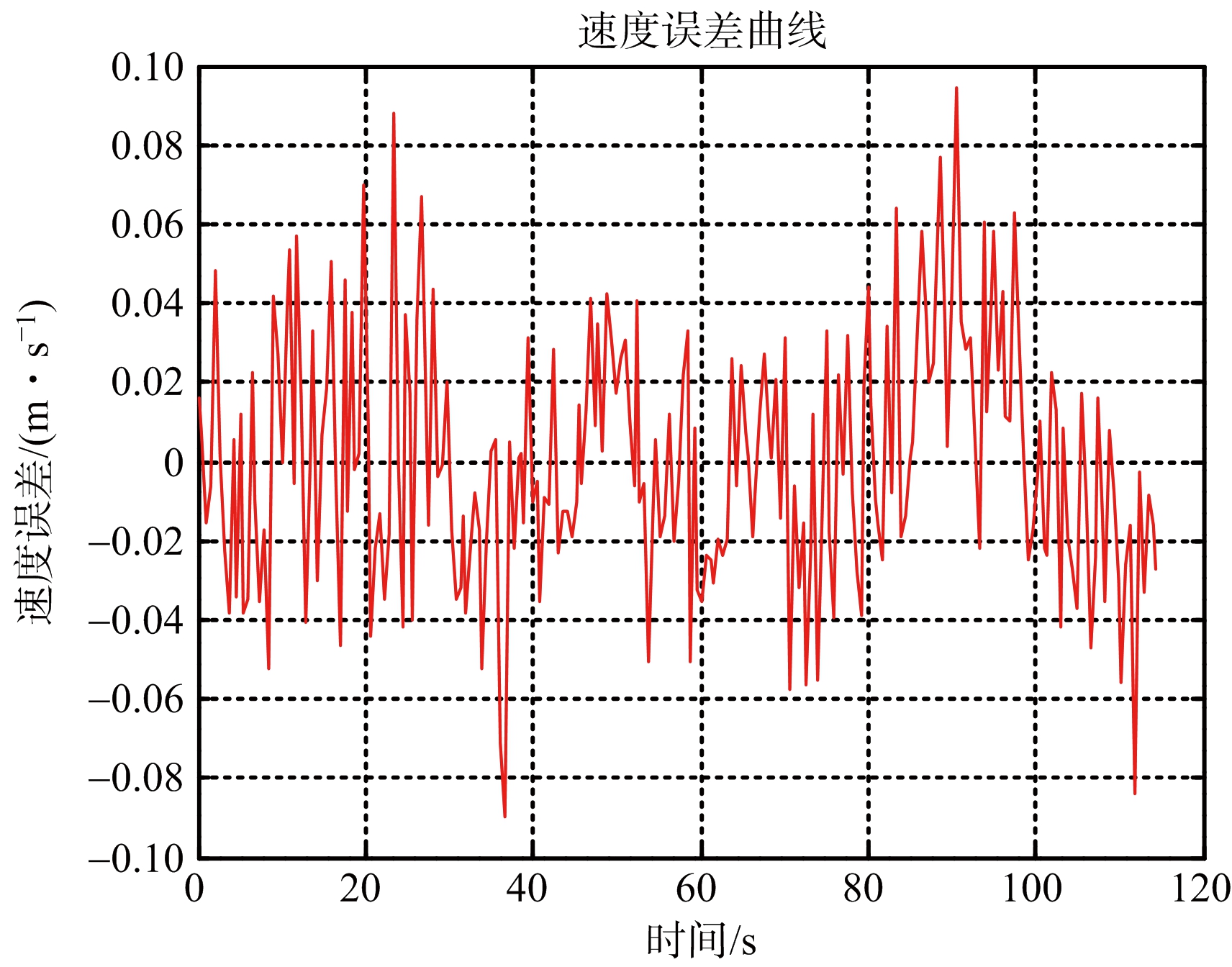
图3 目标速度估计误差曲线
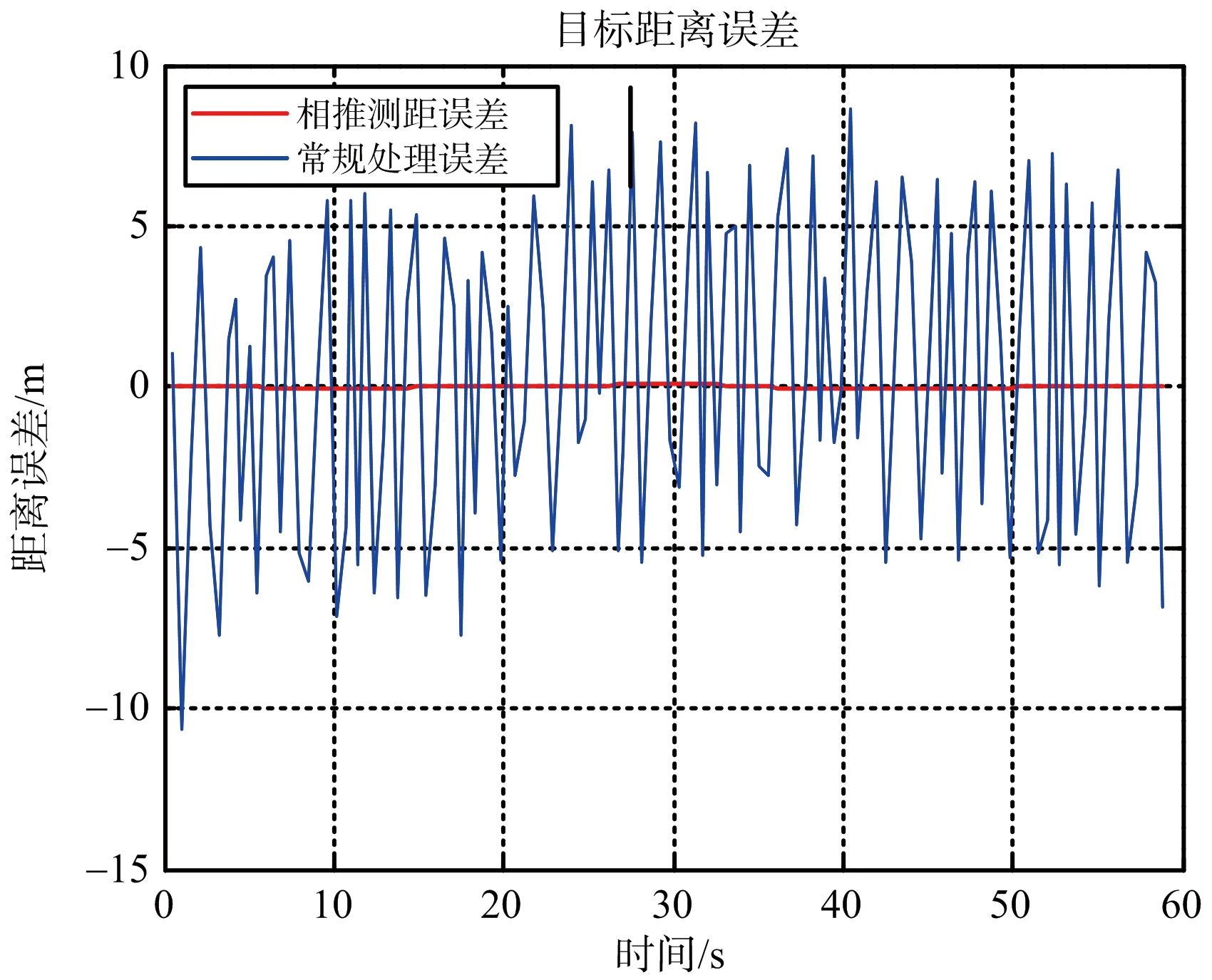
图4 相推测距与常规处理误差曲线对比
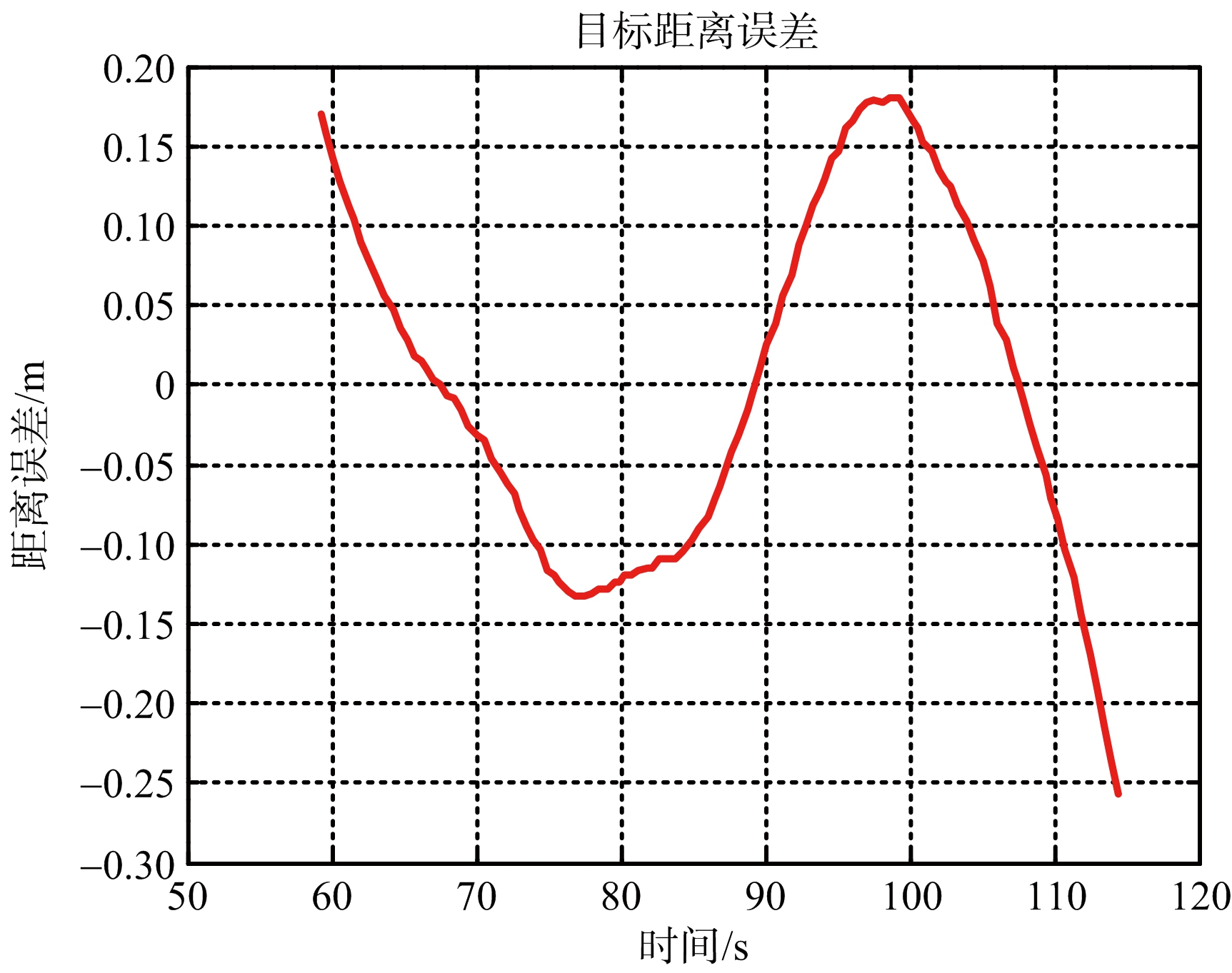
图5 窄带相推测距目标距离误差曲线
3 结束语
窄带相推测距可以获取较高的速度和距离精度，并适用于常规雷达测量装备，其技术措施简便可行。对于反隐身突出的米波等低频段雷达，该技术突破传统思维，把米波雷达高精度距离测量提升一个新高度，使得米波雷达不仅作警戒引导雷达，而且可作精密跟踪或制导雷达使用。
[1] 郭利强. 距离游标应用于精密测量雷达[D].南京:南京电子技术研究所，2005.
[2] 陆锦辉，刘一峰. 游标测距在LFM全相参脉冲雷达中的应用[J].现代雷达，2006,28(7)：59-61.
[3] 陆锦辉，刘一峰. 游标测距在全相参脉冲多普勒雷达中的应用[J].南京理工大学学报(自然科学版)，2006，30(6)：767-769.
[4] 文树梁, 鲁耀兵. 基于游标法的空间目标距离精确测量技术[J]. 航天电子对抗，2007，23(6)：1-3.
[5] 朱得糠，刘永祥，李康乐，等. 基于雷达相位测距的微动特征获取[J]. 宇航学报，2013，34(4):574-582.
[6] 吴剑旗.反隐身与发展先进米波雷达[J].雷达科学与技术，2015，13(1)：1-4.
WU Jianqi.Anti-Stealth and Development of Advanced Metric-Wave Radar[J]. Radar Science and Technology, 2015，13(1)：1-4.(in Chinese)
[7] WEISS L G. Wavelets and Wideband Correlation Processing[J].IEEE Signal Processing Magazine，1994,11(1):13-32.
[8] ABATZOGLOU T J，GHEEN G O. Range, Radial Velocity, and Acceleration MLE Using Radar LFM Pulse Train[J]. IEEE Trans on Aerospace and Electronic Systems，1998，34(4):1070-1083.
[9] PELEG S，FRIEDLANDER B. The Discrete Polynomial-Phase Transform[J].IEEE Trans on Signal Processing，1995，43(8):1901-1914.
[10] 毛二可，范花玉. 合成宽带脉冲多普勒雷达[J].系统工程与电子技术，2016，38(12)：2717-2724.
[11] 王大军，郭永强，毛茅. 一种提高脉冲雷达游标测距起始距离精度方法[J]. 现代雷达，2012，34(11)：31-33.
