0 引言
2020年12月6日凌晨，我国实现了首次月球轨道交会对接，也是人类首次在月球轨道进行无人交会对接[1]。由中国航天科工集团二院25所研制的交会对接微波雷达，作为主要的测量敏感器之一，成功引导完成了嫦娥五号的交会对接任务。测角功能是交会对接微波雷达主要测量功能之一，需要在(±60°)×(±60°)宽视场范围内，从100 km作用至20 m，且测角精度要求在0.05°以内。鉴于该需求，本文提出一种兼具远近距离和宽视场测角需求的十形干涉仪几何对消测角算法，并在远距离采用基于当前模型的自适应Kalman滤波算法，提高测角精度。
1 干涉仪几何对消测角算法[2]
交会对接微波雷达采用十形正交天线[3]，如图1所示，A1～A4、B1～B4分别表示水平基线和垂直基线的4个测角天线阵元，且水平基线和垂直基线的4个测角天线阵元分别相对于天线中心O对称，即B1B2=B3B4=A1A2=A3A4 =2.5λ，B2O=B3O=A2O=A3O=2.75λ，其中λ为载波波长。P点表示目标位置，ρ为目标P点到天线中心O点的距离，Pxy为P点在XOY平面的α为俯仰角，β为方位角，θ为水平入射角。α定义为OP在XOY平面的投影与OP的夹角，β定义为OP在XOY平面的投影与X轴正向的夹角，θ定义为OP在XOZ平面的投影与OP的夹角，图中所示α>0、β>0、θ>0。
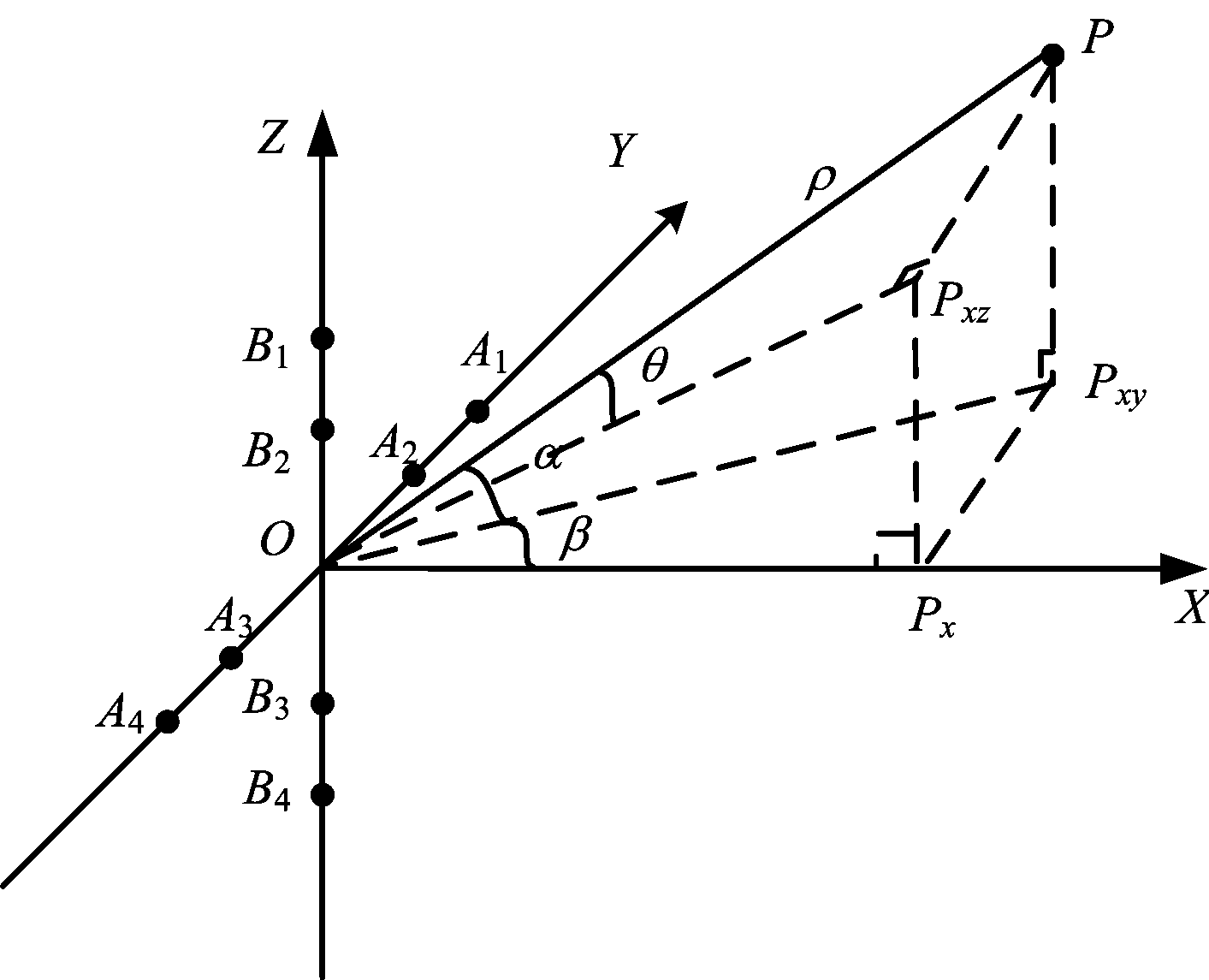
图1 近距离时的测角原理图
下文以垂直基线的入射角解算为例，根据余弦定理，可得PB1的距离：
ρB1=
(1)
当
时，那么
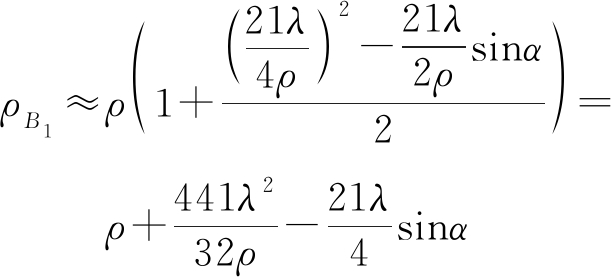
(2)
同理可得
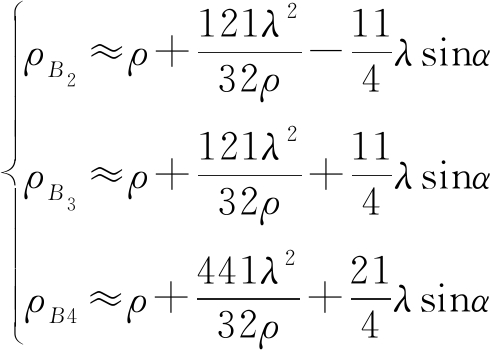
(3)
由此可得到垂直基线各测角天线阵元间的载波相位差为
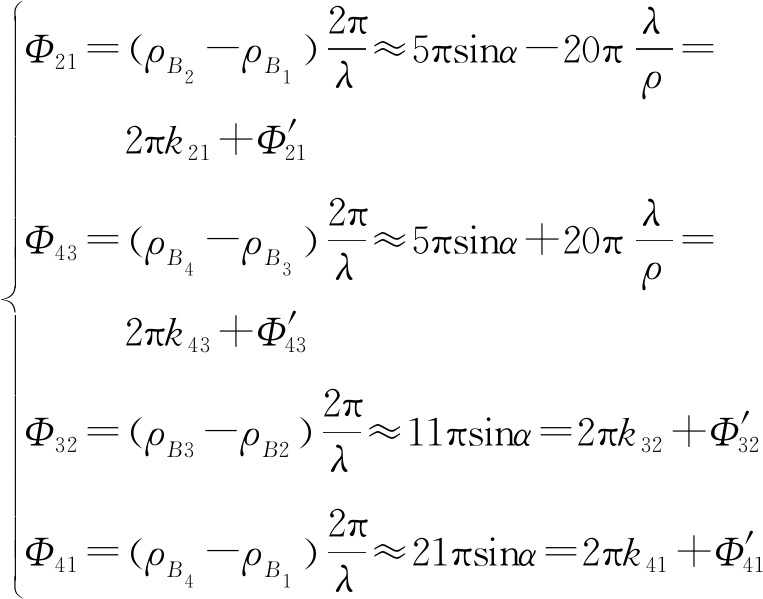
(4)
式中：Φ′ij为i,j测角天线阵元间的载波相位差，Φ′ij∈[-π,π)；kij为整周模糊数，i,j=1,2,3,4且 i≠j。
由式(4)可得虚拟短基线相位差Ψ1：
Ψ1=Φ32-Φ21-Φ43≈πsinα=
mod(Φ′32-Φ′21-Φ′43,2π)∈[-π,π)
(5)
其中mod(·,2π)为模2π操作。
由式(4)可得逐次解算基线相位差Ψ5、Ψ11和Ψ21：
(6)
式中，Ψ′5，Ψ′11，Ψ′21为位于区间[-π,π)的相位差。虚拟短基线相位差Ψ1是无模糊的，逐次法解模糊算法步骤如下：
第一步：解算整周模糊值kM
(7)
其中，M=5，N=1，Round( )为四舍五入取整操作。
第二步：解算基线相位差ΨM
ΨM=2π×kM+Ψ′M
(8)
其中，M=5，N=1。
第三步：重复第一步和第二步逐次解算基线相位差Ψ11(M=11，N=5)和Ψ21(M=21，N=11)。
第四步：解算得到垂直基线的入射角α
(9)
同理可得水平基线的入射角θ。
根据俯仰角与方位角的定义，俯仰角为垂直基线的入射角α，方位角β则根据图1的几何关系可得
(10)
2 测角误差分析
由式(9)微分可得俯仰角随机误差dα：
(11)
式中，dΦ′41为垂直基线1、4测角天线阵元间载波相位差的随机误差。
由于测角天线阵元的载波相位是通过锁相环进行测量的，而锁相环随机误差的估算公式[4]为
(12)
式中，BL为锁相环带宽，C/N0为载噪比，Tcoh为相干积分时间。
由于垂直基线1、4测角天线的载波相位随机误差相同，则俯仰角的随机误差为
(13)
同理可得方位角的随机误差dβ：
(14)
当距离为100 km时，C/N0约为38 dBHz，假设锁相环带宽BL=10 Hz，Tcoh=0.01 s，则俯仰角的随机误差见图2(a)，方位角的随机误差见图2(b)。
(a) 俯仰角随机误差
(b) 方位角随机误差
图2 角度随机误差
任务要求角度指标不大于0.05°，但从图2可知，远距离的角度误差不能满足任务要求，需对角度Kalman滤波进行降噪来提升测量性能。
3 Kalman滤波算法
采用当前统计模型的自适应Kalman滤波算法对角度进行降噪处理，离散化的状态方程和观测方程[5]为
(15)
式中：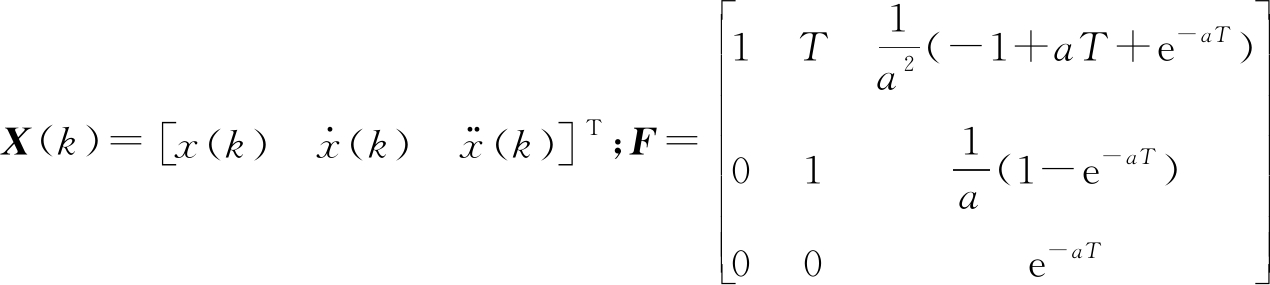
为状态转移矩阵，
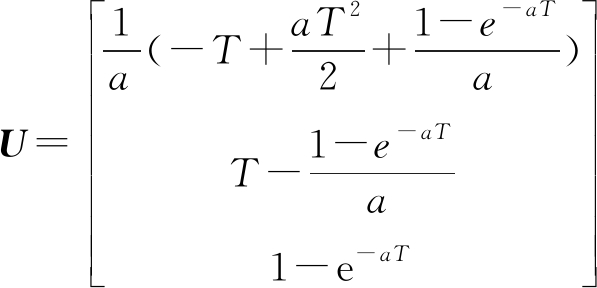为状态输入矩阵，T为采样周期，a为自相关机动频率；
为当前加速度均值；观测量Z(k)为俯仰角α或方位角β；观测矩阵
和v(k)为均值为0、方差分别为Q(k)和R(k)相互独立的高斯白噪声过程。
Kalman递推算法步骤如下：
第一步：状态预测
X(k,k-1)=F×X(k-1,k-1)+
(16)
式中，
第二步：误差协方差预测
P(k,k-1)=
λ(k)F×P(k-1,k-1)FT+Q(k)
(17)
其中，状态噪声方差[6]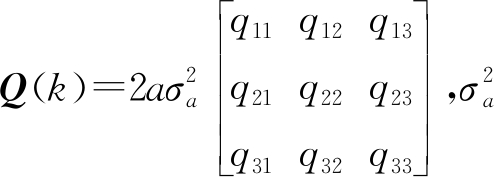
为当前加速度方差，
为最大加速度，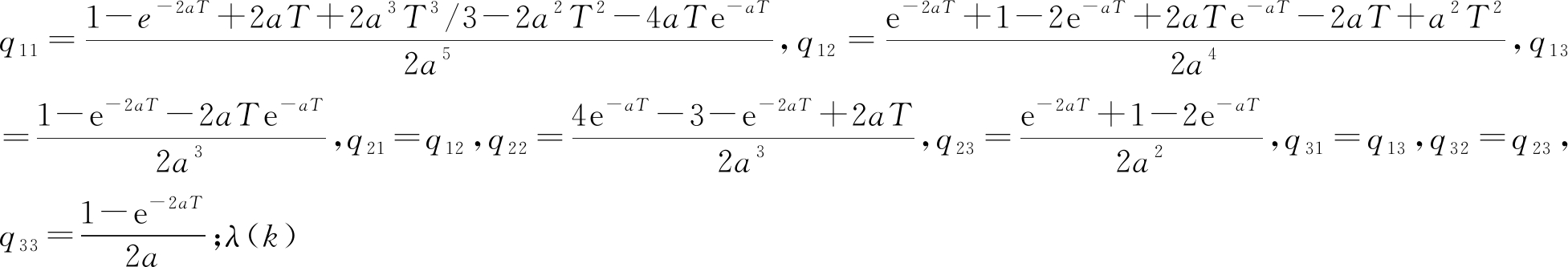
是渐消因子[7]，为了加快滤波收敛，滤波初始化后λ(k)= 1.02，滤波收敛后考虑滤波性能，λ(k)=1。
第三步：增益计算
K(k)=P(k,k-1)HT·
(H×P(k,k-1)HT+R(k))-1
(18)
式中，R(k)为观测噪声方差，通过对观测量z(k)的差值Δz(k)=z(k)-z(k-N)进行计算，
第四步：误差协方差更新
P(k,k)=(I-K(k)H)P(k,k-1)
(19)
第五步：状态更新
X(k,k)=X(k,k-1)+
K(k)(Z(k)-H×X(k,k-1))
(20)
4 试验结果与分析
下面通过4个试验分别验证十形干涉仪几何对消测角算法和Kalman滤波算法的性能。
试验1： 通过桌面联调模拟试验测试近距离1.5 m的十形干涉仪几何对消测角算法性能，测量结果如图3所示。
由图3可知，俯仰角的测量精度为0.007°，方位角的测量精度为0.007°，由于测量结果输出的最小分辨率为0.01°，所以两者的角度测量精度相似，与理论计算稍有差异。
(a) 俯仰角测量结果
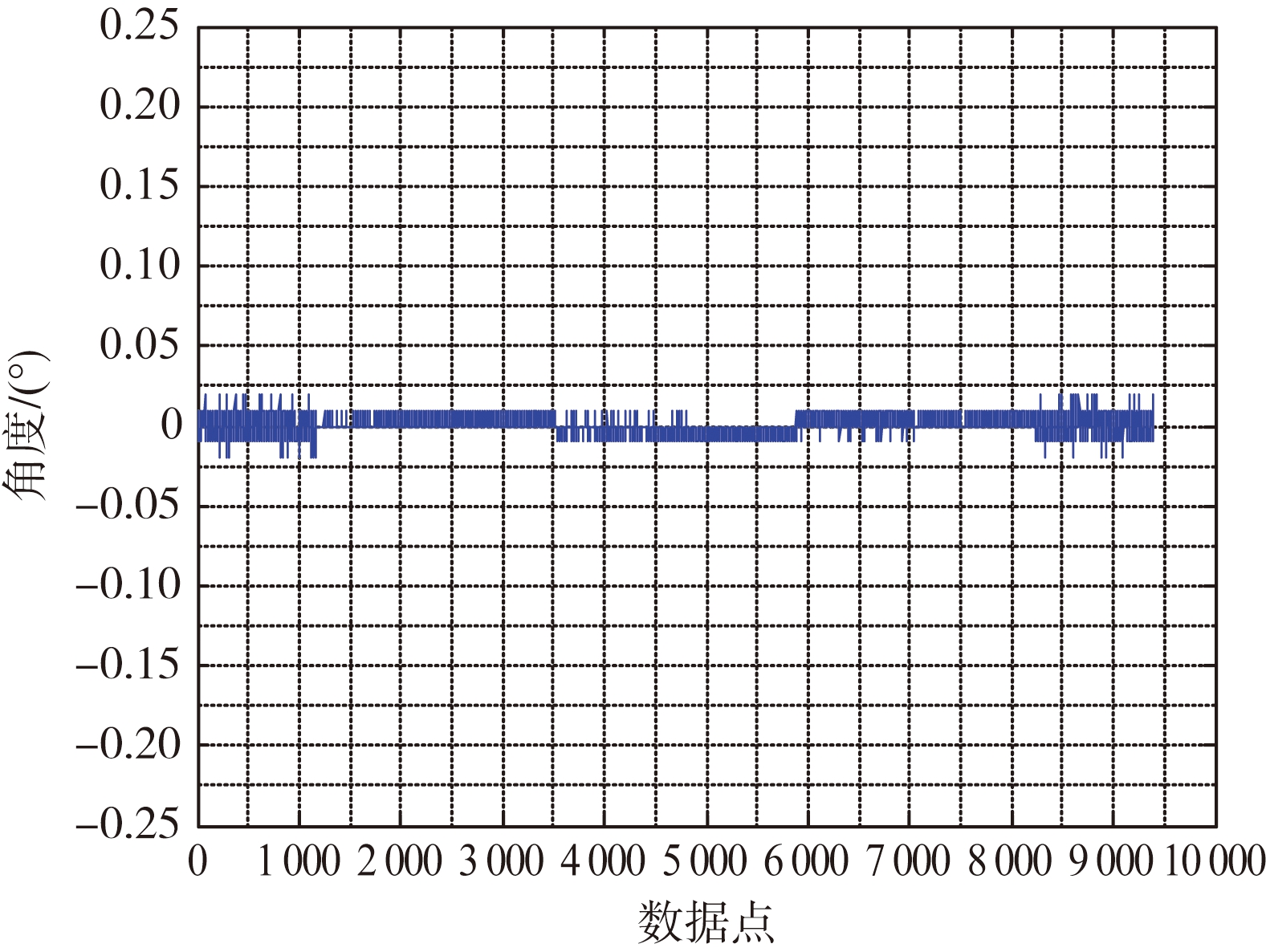
(b) 俯仰角误差
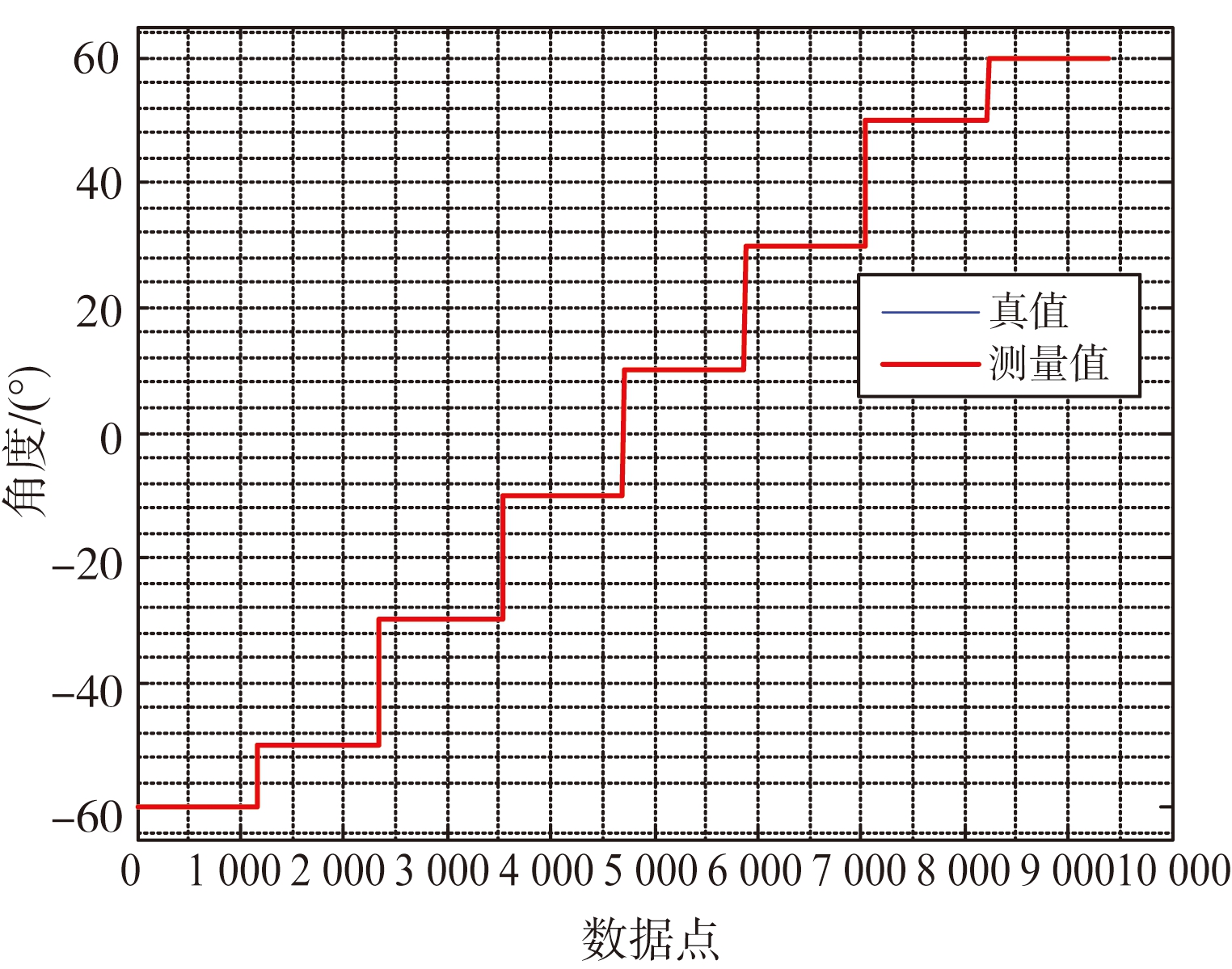
(c) 方位角测量结果
(d) 方位角误差
图3 模拟1.5 m处的角度测量结果
试验2： 通过暗室试验测试近距离8 m的十形干涉仪几何对消测角算法性能，由于受暗室条件限制，无法测试距离小于8 m的角度测量。真值由经过标校的暗室高精度转台得到，测量结果如图4所示。
由图4可知，俯仰角的测量精度为0.02°，方位角的测量精度为0.03°。测量精度大于理论计算是因为在暗室中为了方便测试，微波应答机端的收发射频电缆增加了20 m，C/N0约减小20 dBHz。
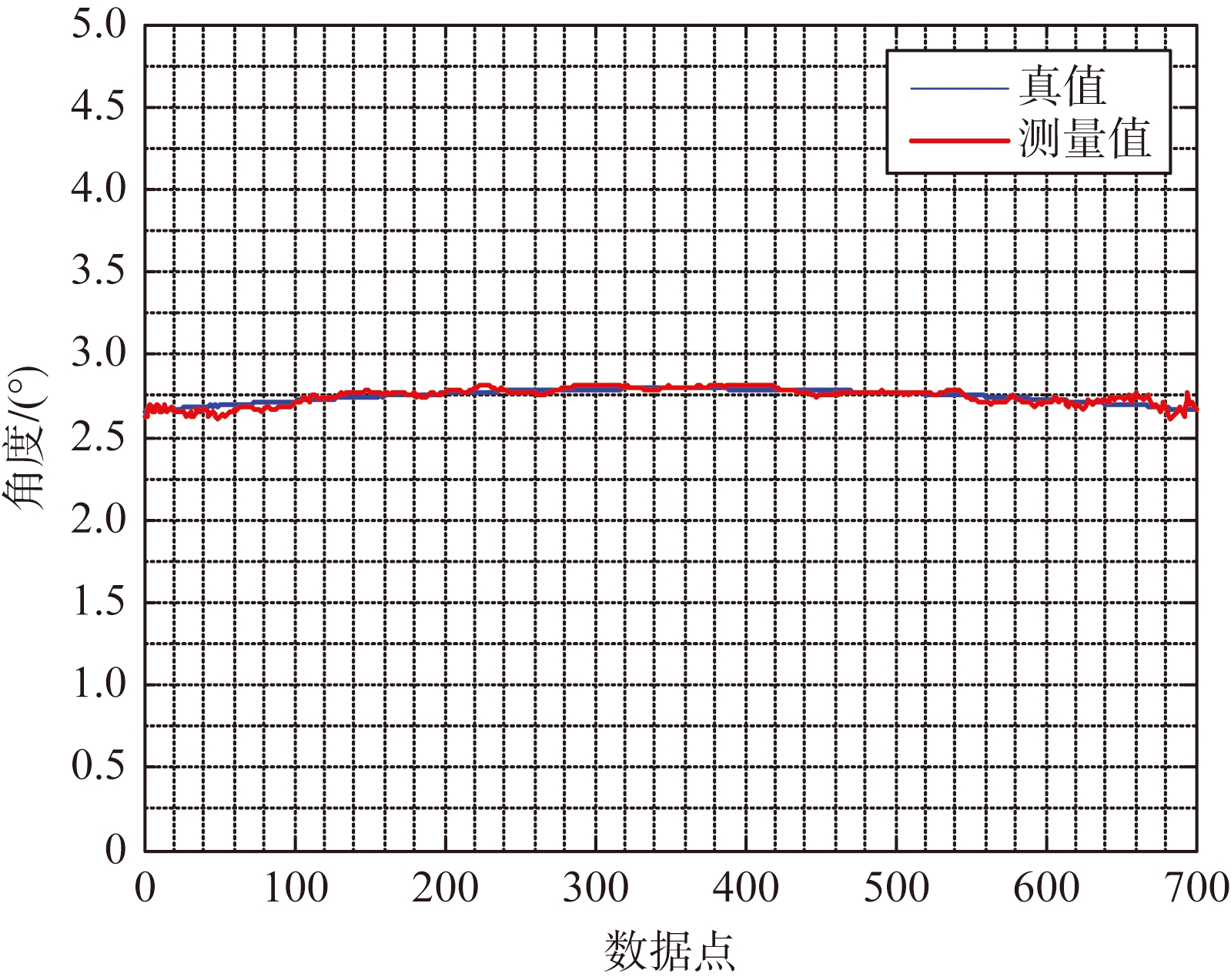
(a) 俯仰角测量结果
(b) 俯仰角误差
(c) 方位角测量结果
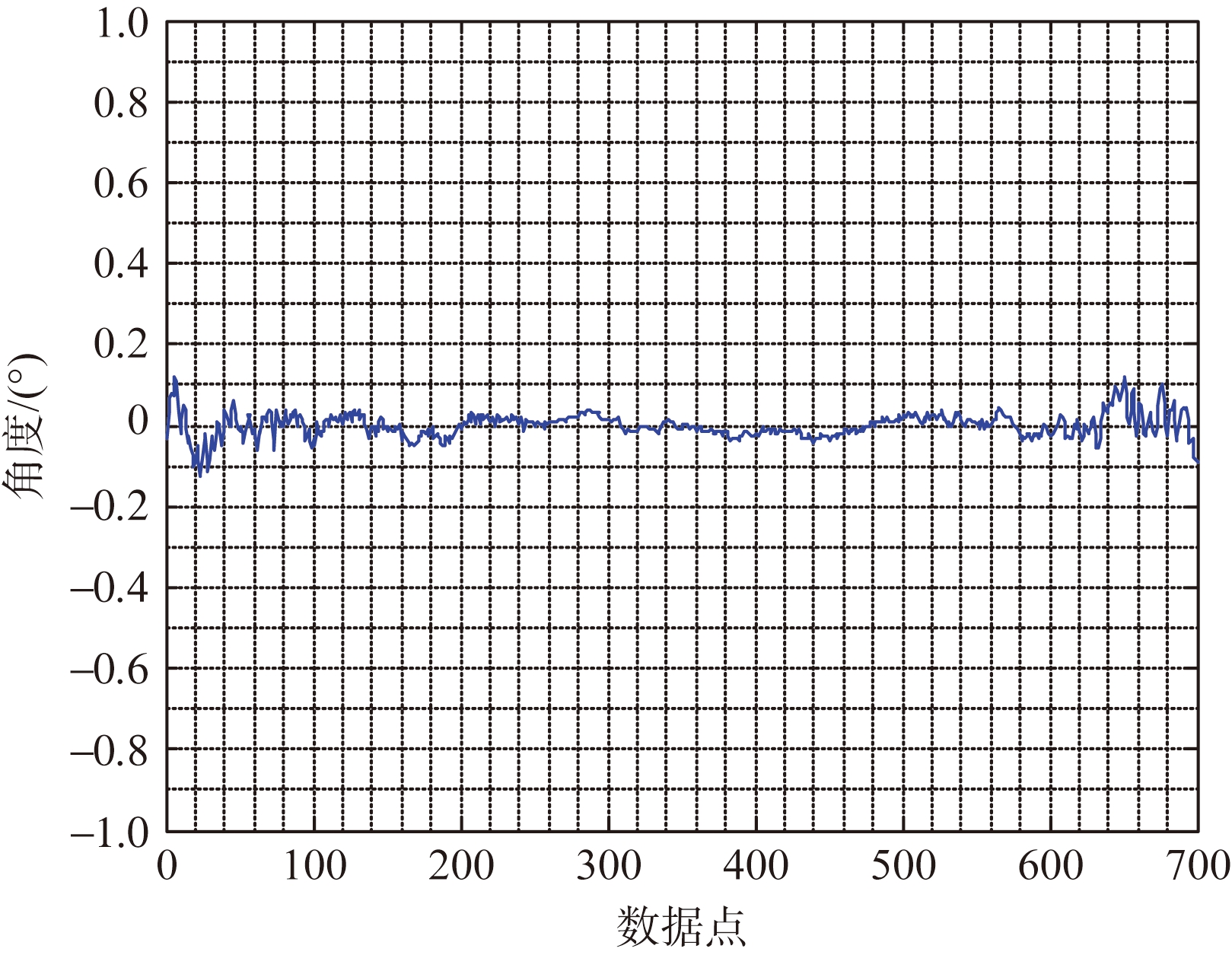
(d) 方位角误差
图4 暗室试验8 m处的角度测量结果
试验3： 通过桌面联调模拟试验测试距离50 km大角度的十形干涉仪几何对消测角算法和Kalman滤波算法性能，测量结果如图5所示。
(a) 俯仰角测量结果
(b) 方位角测量结果
图5 模拟50 km处的角度测量结果
由图5可知，俯仰角-60°的测量精度为0.028 8°，Kalman滤波后的测量精度为0.005°；方位角60°的测量精度为0.100°，Kalman滤波后的测量精度为0.012°。
试验4： 通过外场直升机挂飞试验测试十形干涉仪几何对消测角算法和Kalman滤波算法性能，测量结果如图6所示，真值由GPS差分数据和惯导数据联合解算得到。
(a) 距离测量结果
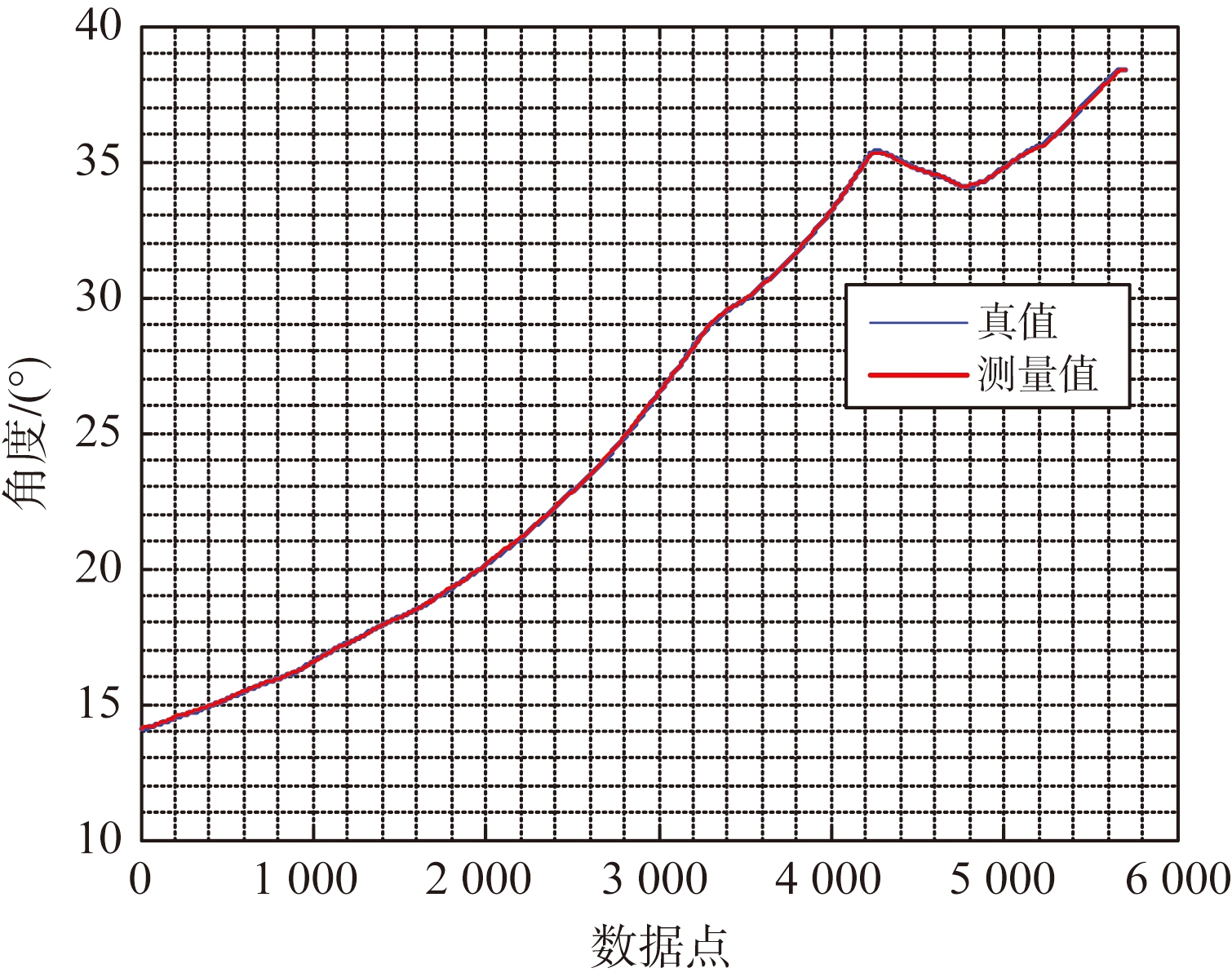
(b) 俯仰角测量结果
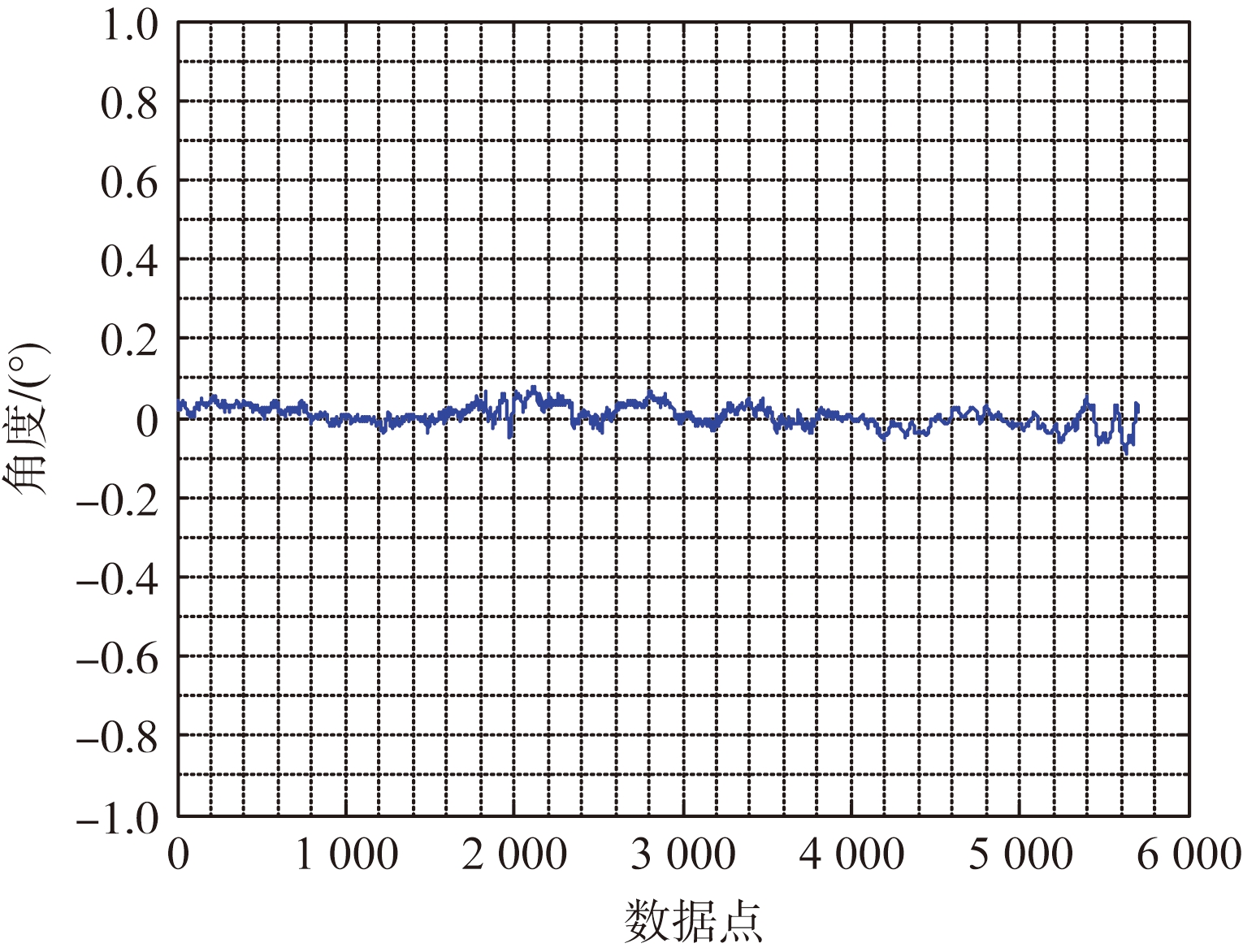
(c) 俯仰角测量误差
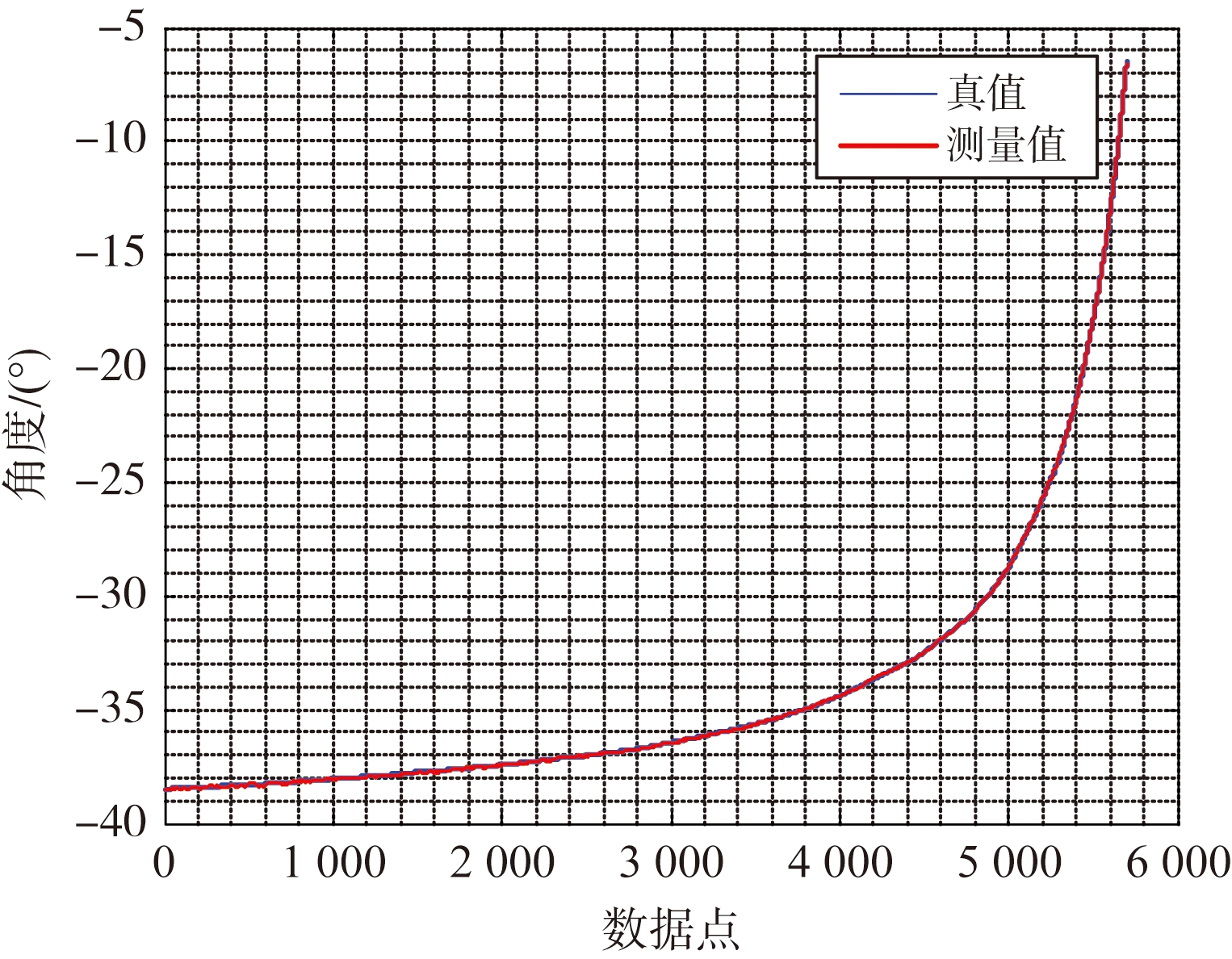
(d) 方位角测量结果
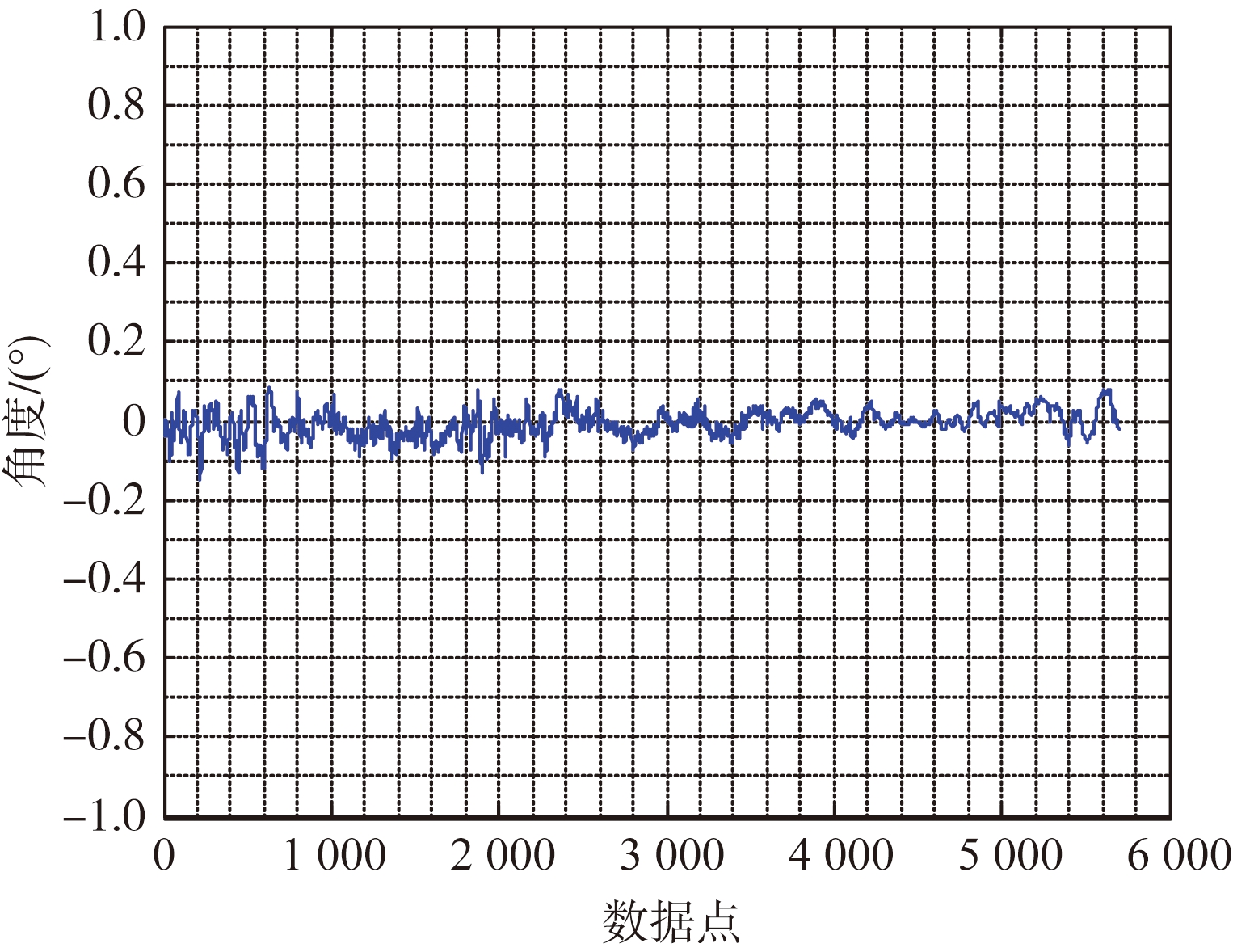
(e) 方位角测量误差
图6 直升机挂飞试验测量结果
由图6可知，俯仰角的测量精度为0.03°，方位角的测量精度为0.04°。
通过分析模拟试验、暗室试验和外场挂飞试验的测量结果可知：交会对接微波雷达测角范围能够覆盖远近距离和大宽视场，且测角性能优于高精度的交会对接任务需求。
5 结束语
本文针对交会对接微波雷达需要在(±60°)×(±60°)宽视场范围内、从100 km作用至20 m、且测角精度要求在0.05°以内的需求，提出一种兼具远近距离和宽视场测角需求的十形干涉仪几何对消测角算法，并且针对远距离测角精度无法满足精度要求的问题，采用基于当前统计模型的自适应Kalman滤波算法来提高测角精度。模拟试验、暗室试验和外场挂飞试验验证了干涉仪几何对消测角算法的有效、可行，经过Kalman滤波后角度测量结果优于高精度的交会对接任务需求,已成功应用于月球轨道交会对接。
[1] 庞之浩. 嫦娥五号月球“挖土”归来[J]. 科学,2021, 73(1):34-38.
[2] 孙武,蒋清富,徐秋锋,等. 一种交会对接微波雷达几何误差对消干涉测角方法:中国, ZL201218003913.0[P]. 2015.
[3] 耿生群,吴嗣亮. 伪码连续波交会对接雷达信号处理机设计[J]. 现代雷达, 2006, 28(9):37-41.
GENG Shengqun,WU Siliang.Pseudo-Code CW RVD Radar Signal Processor Design[J].Modern Radar,2006,28(9):37-41.(in Chinese)
[4] 高亢,侯孝民,赵强,等. 采用锁频环和锁相环联合捕获的载波跟踪[J]. 电讯技术, 2018, 58(4):402-406.
GAO Kang,HOU Xiaomin,ZHAO Qiang,et al.Carrier Tracking Based on Joint Acquisition of Frequency Locked Loop and Phase Locked Loop[J]. Telecommu-nication Engineering,2018,58(4):402-406.(in Chinese)
[5] 张晴月,蒋志迪. 基于ICS-IMMUKF-3D的水下目标自适应跟踪算法[J]. 无线通信技术, 2018, 27(1):1-6.
ZHANG Qingyue,JIANG Zhidi.An Adaptive Tracking Argorithm of Underwater Target Based on ICS-IMMUKF-3D[J]. Wireless Communication Technology,2018,27(1):1-6.(in Chinese)
[6] 周宏仁. 机动目标“当前”统计模型与自适应跟踪算法[J]. 航空学报, 1983, 4(1):73-86.
[7] 叶晨,崔双喜. 一种强跟踪UKF及其在GPS/SINS深组合导航中的应用[J]. 导弹与航天运载技术, 2018 (2):61-64.
YE Chen,CUI Shuangxi. Strong Tracking UKF and Its Application in GPS/SINS Deeply Integrated Navigation[J].Missiles and Space Vehicles,2018(2):61-64.(in Chinese)
