0 引言
PD雷达常用于机载预警和火控雷达领域，利用目标与雷达之间的相对运动产生的多普勒效应进行目标信息提取和处理。机载PD雷达具有良好的下视和上视探测能力、精确的多普勒速度量测能力和同时探测数十批甚至上千批目标的能力。雷达数据处理系统对量测数据进行关联和滤波，形成可靠的雷达情报 [1-2]。航迹跟踪中滤波算法的性能直接影响雷达情报质量。
机载雷达在以载机为中心的运动平台上获得量测数据，量测数据直接描述的是雷达和目标的相对位置变化[3]，一般情况下雷达和目标的相对运动状态方程是非线性方程，很难直接进行滤波和预测。机载PD雷达滤波时一般将量测数据转换到以地面测量站为中心的惯性坐标系(简称地面惯性坐标系)下，再采用与地面雷达相同的处理方法进行滤波。该方法存在以下缺点：目标在某一时刻只能有一种假设的运动模型，如果目标运动状态与运动模型不匹配，会导致滤波器严重发散；量测数据转换到地面惯性坐标系下进行滤波，用经过非线性变换后的数据滤波，数据的噪声特性失真，导致滤波器精度下降；作为PD雷达特色的目标多普勒速度在滤波过程中没有得到利用，损失了一维重要的信息。
目前机动目标跟踪的主流算法是交互多模型(Interactive Multi-Model，IMM)滤波算法[4-6]。本文方法采用IMM滤波器，模型集由匀速直线运动(CV)模型、当前统计(CS)模型和估计角速度的匀速转弯运动(CT)模型组成。其中，CV模型和CS模型采用线性卡尔曼滤波实现，CT模型采用容积卡尔曼滤波实现[7]。滤波器量测误差协方差矩阵由天线坐标系下的量测误差和天线坐标系下的量测值进行无偏转换近似计算。利用机载PD雷达多普勒速度量测精度高的特性，将其应用到模型概率初始估计和模型参数初始估计中，提高模型初始参数的精度。
1 基于CV模型、CS模型和CT模型的交互多模型滤波器
基于CV模型、CS模型和CT模型的交互多模型滤波器周期运行，由数据驱动，每一次关联成功后，滤波器的工作步骤如下：
1) 量测数据预处理
接收到每一个周期的探测数据后进行量测数据的预处理，包括量测误差协方差矩阵计算和滤波器输入量测数据计算。
2) 模型初始化
滤波器第一次调用时，初始化模型概率、模型参数和Markova转移矩阵。
3) 状态向量和协方差初始化
滤波器第一次调用时，根据先验信息和已获得的量测数据初始化各模型的状态向量和协方差 (j=1,2,3分别对应CS、CV、CT模型，下同)。
4) 相互作用
计算与每一个模型匹配的滤波器的混合初始条件。模型j在k时刻的初始状态向量为
(1)
相应的协方差为
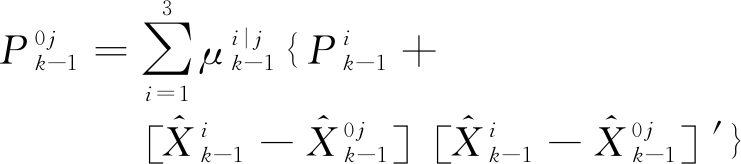
(2)
式中，
为k-1周期滤波器i的状态向量的估计值，
为相应的状态协方差阵，
为k-1周期模型i的概率。
5) 卡尔曼滤波
以新的量测值Zk为输入，基于混合初始状态估计
及其协方差
计算第k个周期基于模型j的状态估计
协方差
新息
和新息协方差
模型和CV模型采用线性卡尔曼滤波(KF)实现，CT模型采用容积卡尔曼滤波(CKF)实现。
6) 计算模型的可能性
(3)
式中，
为模型j第k帧滤波的新息，
为模型j第k帧滤波的新息协方差，计算时假定服从高斯分布。
7) 模型概率更新
(4)
(5)
8) 组合估计
状态向量和协方差的最终组合结果为
(6)
(7)
2 量测数据预处理
滤波器启动前需要先进行量测数据的预处理，包括量测误差协方差矩阵计算和滤波器输入量测数据计算。计算量测误差协方差矩阵时，先由直接测量得到的目标在天线坐标系下的距离、方位和载机姿态角信息获取对应的距离量测误差、方位量测误差和载机惯性坐标系下的极坐标量测值，再采用无偏转换方法计算量测误差协方差矩阵。载机惯性极坐标系下的量测值和对应时刻的载机大地坐标位置进行坐标变换获得地面惯性坐标系下的位置作为滤波器输入量测数据[8]。
由式(8)计算目标在天线坐标系下的直角坐标位置P1=[x1,y1,z1]T。其中r1，a1，e1为根据第k个周期雷达探测的目标原始回波解算出的位置坐标，分别表示目标距离(单位：m)、目标方位角(以机头为中心，单位：rad)和目标俯仰角(单位：rad)。
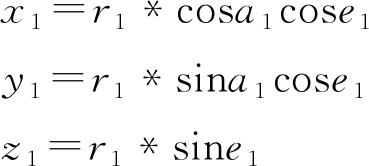
(8)
根据探测点迹距离r1和方位角a1，由雷达特性和统计分布等先验信息，获得距离量测误差dr和方位量测误差da。计算量测误差协方差矩阵为
(9)
其中，
r11=
(cosh(2·da2)-cosh(da2))+
(sin(a1))2·(sinh(2·da2)-sinh(da2)))+
dr2·exp(-2·da2)·((cos(a1))2·
(2·cosh(2·da2)-cosh(da2))+
(sin(a1))2·(2·sinh(2·da2)-sinh(da2)))
r22=
(cosh(2·da2)-cosh(da2))+
(cos(a1))2·(sinh(2·da2)-sinh(da2)))+
dr2·exp(-2·da2)·((sin(a1))2·
(2·cosh(2·da2)-cosh(da2))+
(cos(a1))2·(2·sinh(2·da2)-sinh(da2)))
r12=sin(a1)·cos(a1)·exp(-4·da2)·
r21=r12
由式(10)计算旋转变换公式T1，其中，α、β、γ分别为载机的偏航角、俯仰角和横滚角(单位：rad)。
T1=
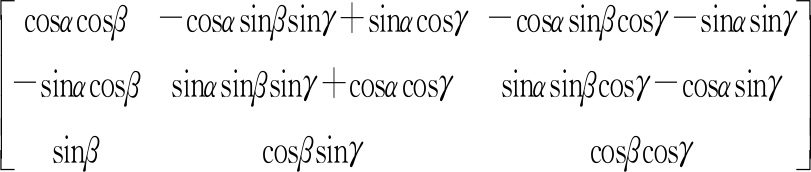
(10)
由式(11)计算目标在载机惯性坐标系下的直角坐标值P2=[x2,y2,z2]T。
P2=T1*P1
(11)
再由式(12)计算目标在载机惯性坐标系下的极坐标值。
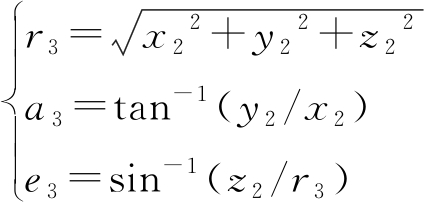
(12)
已知P2、载机位置和地面测量站的位置，利用大地坐标变换公式计算目标在测站坐标系下的直角坐标位置Zk=[x,y,z]T，Zk即是第k个周期滤波器的输入量测值。
3 滤波器实现
3.1 模型的初始概率和参数初始化
交互多模型滤波器中各模型的初始概率和模型参数根据速度、加速度和径向速度估计，加速度和径向速度的变化对应目标的机动情况，对一批目标第一次滤波时，根据径向速度、加速度和目标机动的先验分布，获得模型初始概率和初始机动参数。
1) 模型概率初始化
根据初始机动状态估计每个模型的初始概率
计算起始航迹的点迹之间的航速v0和径向距离变化率与量测径向速度的误差dλ，由v0、dλ和已知的各模型条件概率分布计算模型的概率
对模型概率归一化获得各模型的初始概率。
(13)
2) 初始化模型预置参数
由dλ和CS模型机动因子的先验分布获得机动因子α的最大后验估计。CT模型的转弯角速度w初始化为0。
α=argmaxp(α|dλ)
(14)
3) 初始化Markova转移矩阵
滤波器第一次调用时，初始化模型组的Mar-kova转移矩阵P，其中pij(i=1,2,3;j=1,2,3)表示模型i到模型j的转移概率。转移矩阵中CV模型与CS模型可相互转换，CV模型与CT模型可相互转换，CS模型与CT模型之间不能相互转换。
(15)
3.2 容积卡尔曼滤波器
容积卡尔曼滤波根据非线性高斯滤波器处理状态估计的方法，利用求三维球体容积的办法去近似非线性函数的高斯积分值。状态维数n取7，状态向量定义为
其中w为转弯角速度。
已知k-1时刻的状态估计
和状态估计的协方差
一个处理周期可分为时间更新和测量更新两部分实现。
时间更新的计算步骤如下：
1) 将k-1时刻的状态协方差矩阵
进行乔列斯基分解，分解得到矩阵Lk-1
(16)
2) 计算2n个cubature点
(17)
3) 计算经过CT模型状态方程转移传递过的2n个cubature点的状态
(18)
4) 通过经CT模型状态方程传递后的2n个cubature点的状态来估计k时刻的状态
(19)
5) 计算k时刻2n个cubature点的状态对应的协方差的一步预测
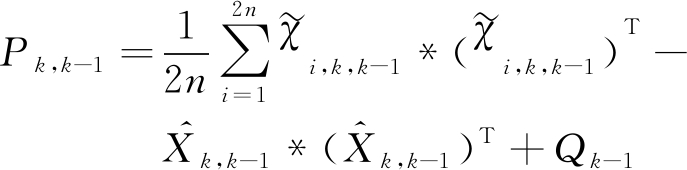
(20)
式中，Qk-1为过程噪声协方差矩阵。
观测更新的计算步骤如下：
1) 对协方差的一步预测Pk,k-1进行乔列斯基分解：
Pk,k-1=Lk,k-1*(Lk,k-1)T
(21)
用上式得到的Lk-1计算cubature点：
(22)
2) 计算cubature点经过量测方程
传递后的量测的预测值：
(23)
取量测的预测值
的均值作为整体的量测预测：
(24)
3) 求k时刻的新息协方差：
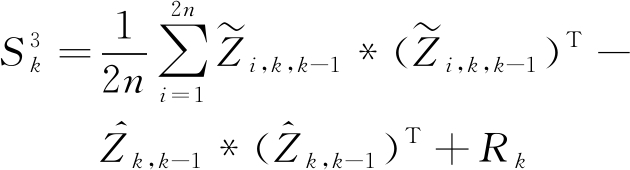
(25)
求k时刻状态预测误差与量测预测误差的互协方差矩阵：
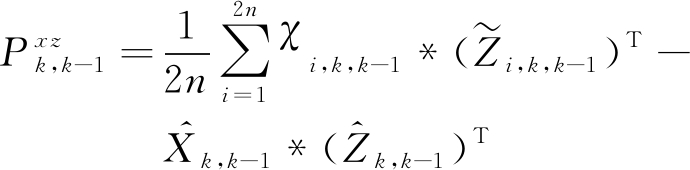
(26)
计算容积卡尔曼滤波的滤波器增益:
(27)
计算k时刻的新息：
(28)
进行k时刻的状态更新：
(29)
进行k时刻的协方差更新：
(30)
4 仿真实验
为了验证算法的有效性，结合目标仿真系统进行了仿真实验，实验结果显示本文方法明显提高了滤波精度，对机动和非机动状态的目标均有稳定的滤波效果。
4.1 实验一
实验一采用MATLAB仿真，仿真参数如下：
载机运动轨迹：载机与目标初始距离100 km，载机以100 m/s的速度向正北方向进行匀速直线运动。
目标运动轨迹：目标以200 m/s的速度进行40 s的匀速直线运动，之后以0.1 rad/s的角速度进行60 s的匀速转弯运动，之后匀速运动30 s，再以-0.1 rad/s的角速度进行60 s匀速转弯运动，最后匀速运动30 s。
滤波器参数设置：距离量测误差150 m；方位角量测误差0.1°；帧周期10 s；蒙特卡洛仿真次数100。
图1所示为目标真实运动轨迹的采样值，图2为观测值和滤波值的绝对距离误差的均方根。由图可见，在目标机动或非机动状态下，滤波结果都优于观测结果，滤波器具有良好的自适应性能。
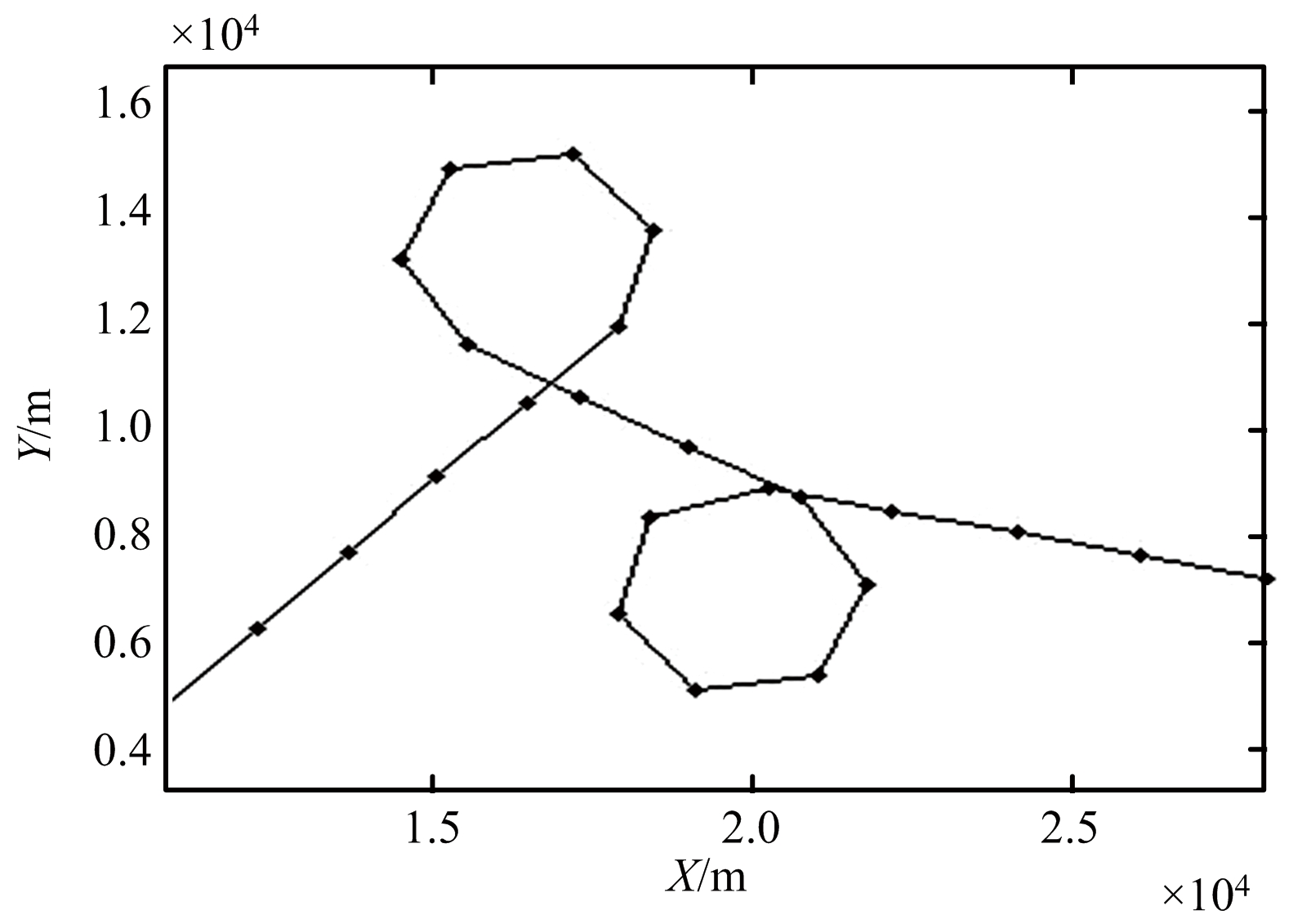
图1 实验一目标轨迹
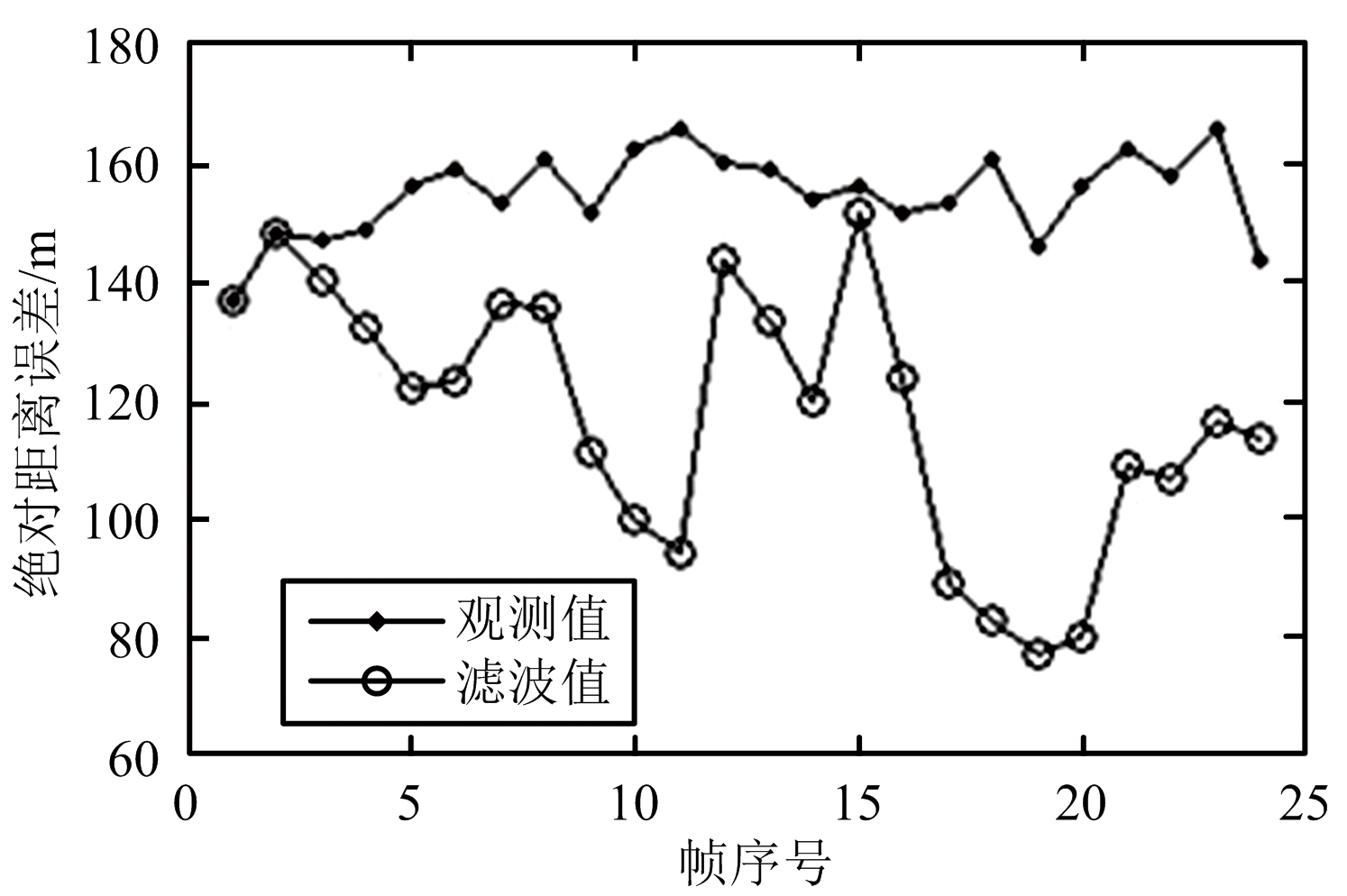
图2 实验一目标滤波前后误差
4.2 实验二
实验数据来源于某机载雷达仿真系统，目标进行随机机动，目标轨迹如图3所示，滤波前后目标位置的绝对距离均方根误差如图4所示。滤波后精度明显优于测量精度。
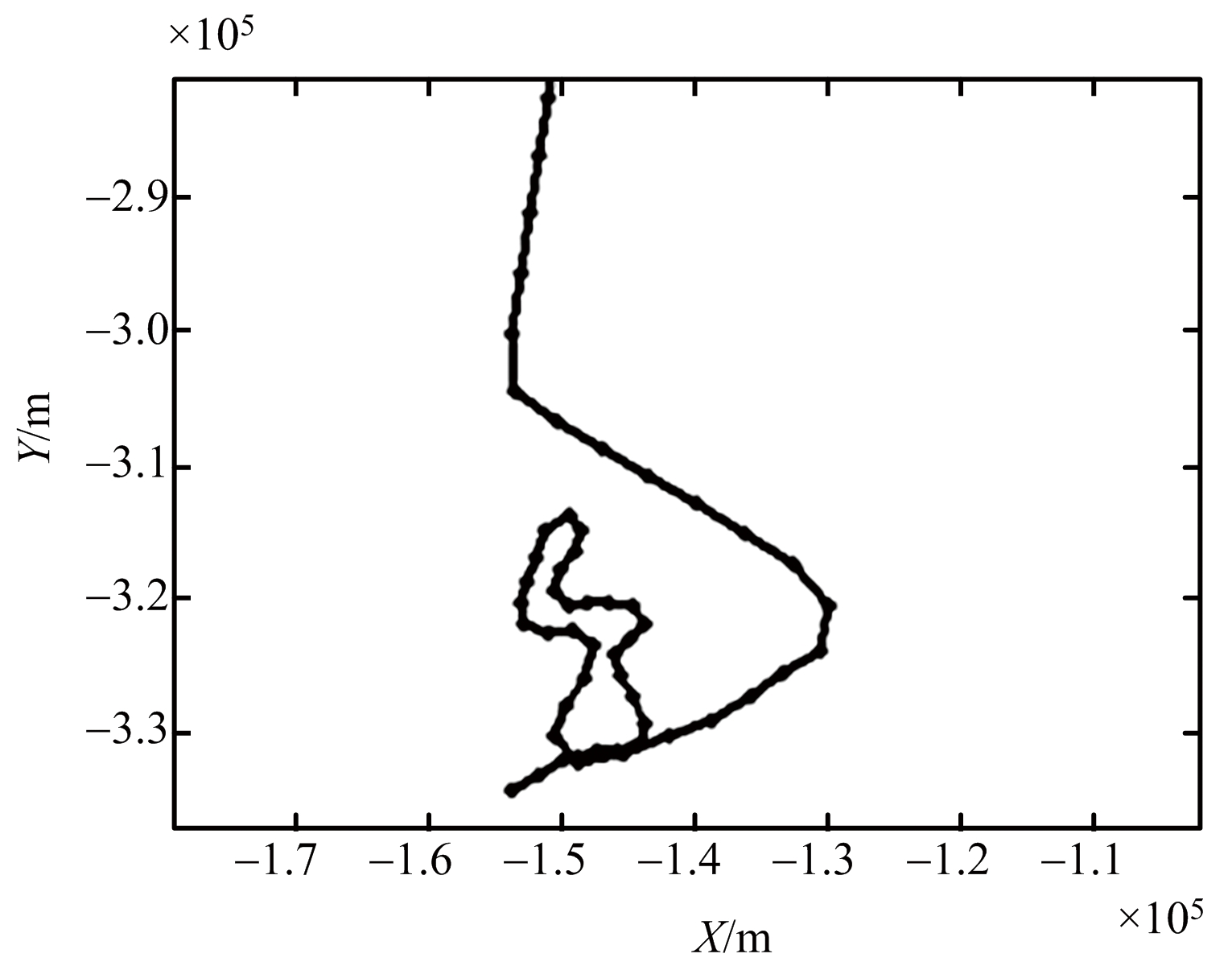
图3 实验二目标轨迹
图4 实验二目标滤波前后误差
5 结束语
本方法避免了模型与滤波器不匹配导致的滤波器精度严重下降，减少了平台运动和坐标变换对量测误差的影响。将多普勒速度应用到模型概率初始化和模型参数初始化中，进一步提高了滤波器的初始精度和可靠性。线性滤波采用线性卡尔曼滤波，非线性滤波采用容积卡尔曼滤波，既保证了滤波器的精度和数值稳定性，又使运算量最小。仿真实验表明该算法提高了机载PD雷达的航迹情报质量，尤其是提高了航迹滤波的精度和稳定性。
[1] 何友,修建娟,张晶炜,等.雷达数据处理及应用[M]. 北京: 电子工业出版社,2006.
[2] 朱自谦. 机载雷达多目标跟踪技术研究[D].南京：南京航空航天大学，2010:1-4.
[3] 贲德, 韦传安, 林幼权.机载雷达技术[M].北京：电子工业出版社, 2006:235-236.
[4] JEON W, ZEMOUCHE A, RAJAMANI R. Tracking of Vehicle Motion on Highways and Urban Roads Using a Nonlinear Observer[J]. IEEE Trans on Mechatronics, 2019,24(2):644-655.
[5] YU Miao,GONG Liyun,OH H,et al. Multiple Model Ballistic Missile Tracking with State-Dependent Transitions and Gaussian Particle Filtering[J]. IEEE Trans on Aerospace and Electronic Systems，2018，54(3):1066-1081.
[6] 夏小虎, 刘明. 联合约束级联交互式多模型滤波器及其在机动目标跟踪中的应用[J]. 电子与信息学报,2017,39(1):117-123.
[7] LI Wenling, JIA Yingmin. Location of Mobile Station with Maneuvers Using an IMM-Based Cubature Kalman Filter[J]. IEEE Trans on Industrial Electronics，2012，59(11):4338-4348.
[8] 张雅声.弹道与轨道基础[M]. 北京: 国防工业出版社, 2019:20-54.
