0 引言
对远距离目标进行空中防御时，为捕获目标，雷达需要长时间处于开机状态，这样无异于会增加雷达暴露的几率。为了避免该情况发生，在实际作战时，一般都是由预警机协同作战，对空域进行预搜索。在目标达到地面雷达搜索范围时打开雷达，并根据预警机所提供的引导信息进行小范围的搜索，以实现目标的快速捕获[1]。因此，如何有效地利用引导信息来提高相控阵雷达的搜索效率成为了研究的关键。
就目前而言，关于相控阵雷达搜索这一研究方向已经有许多研究成果。文献[2]基于近空高超音速目标防御的背景，根据目标运动状态确定最短的跨屏距离和最少的雷达扫描次数。对于有预警信息的小范围引导搜索，文献[3]分别在单目标和多目标情况下建立目标平均发现时间模型，通过合理地分配波束的照射时间来优化搜索性能。以上研究皆没有考虑搜索过程中波位照射顺序对雷达搜索性能的影响。对此，文献[4]通过将全局信息增益最大的波位作为下一时刻雷达需要搜索的波位来确定搜索顺序，降低虚警概率对雷达搜索效率的影响的同时提高雷达搜索检测性能，但因其计算量较大导致耗时过多且每个波位驻留时间是均匀分配的。
本文结合以上研究工作，同时对波位的搜索顺序以及各波位上雷达的波束驻留时间进行优化，使得雷达搜索效率最大化。将目标平均发现时间作为评判雷达搜索性能的标准，以各个波位的驻留时间为连续变量，结合整数规划的思想，将搜索顺序表示为离散变量，建立搜索资源最优分配模型，并采用拉格朗日乘子法对该混合规划模型求解。仿真结果表明，本文方法不仅能保证高搜索效率，还能同时得到各波位的最优搜索数据率以及搜索顺序。
1 引导信息下的搜索模型
1.1 搜索区域模型
对于协同作战来说，预警机先进行大空域搜索，发现目标后向雷达提供目标的位置信息，此时相控阵雷达可根据预警机提供的引导信息在小范围内进行搜索，从而较快地检测出目标。但是预警机所提供的信息一般都会伴随着随机误差和系统误差。在此假定引导信息的误差统计特性已知，假设预警机所提供的目标方位及俯仰向的位置信息为(θEp,θAp)，目标的真实位置信息为(θE0,θA0)，则可得到
(θE0,θA0)=(θEp,θAp)+(εE,εA)
(1)
式中，(εE,εA)表示引导信息的误差，假设其满足 f(εE,εA)二维联合分布。通常情况下，引导信息下的搜索区域的确定要遵守一定的原则，即该区域不可过小，搜索区域太小会导致该区域中并无目标，亦不可过大，太大会浪费雷达资源在无目标的区域，导致引导信息失去意义。因此引入目标出现置信度ι，其定义为目标出现在搜索区域Ω中的概率，即[4]
(2)
需要注意的是，搜索区域确定时需要使得方位向与俯仰向的范围相当，以避免出现其中一个方向范围过大而另一个方向过小的情况。考虑到置信度法求解搜索区域时计算过于复杂，在此选用置信度法的一个特例，3倍均方差法来简化求解搜索空域。根据概率论内容，假设变量x以及均方差σ服从高斯分布，则有
P(|x|<3σ)=99.7%
(3)
因此，根据预警信息所给的位置，对方位以及俯仰向前后各取3倍均方差的距离构成一个正方形区域，取该正方形的外接圆作为搜索区域即可保证目标落入此区域的概率足够大。
1.2 目标出现概率模型
在通过3倍均方差法确定最佳的搜索区域之后，需要根据雷达的波束宽度，在搜索区域内进行合理的编排。由于雷达波束在球面坐标系中存在波束展宽效应[5]，而这一现象在正弦坐标系下不复存在，因此需要进行坐标系转换，将搜索区域以及雷达波束由雷达球面坐标系转换成正弦坐标系来进行波位编排。对于雷达球面坐标系中一点(E,A)转换到正弦坐标系下坐标(α,β)，其转换公式为
(4)
式中,T为雷达阵面倾角。
为了使波位可以尽可能地覆盖搜索区域且不会造成因波位重叠而导致的资源浪费。本文选择交错波束编排方式来对搜索空域进行编排[6]。假设编排后的总波位数为N，Ωk表示为第k号波位。想要获得波位的出现概率pk就需要在每个波位范围内对引导误差概率密度分布函数f(εE,εA)进行积分，同时忽略波束内部的差别。这样一来会对目标出现概率的计算带来一定的误差，并且计算过程相对复杂。因此本文采取统计方法来计算各波位中目标出现的概率。计算过程如下：
步骤1： 在雷达球面坐标系下，随机产生Q个服从二维误差分布f(εE,εA)的目标。
步骤2： 将Q个目标的坐标转换到正弦坐标系中，对于编排好的波位，记Qk(k=1,2,…,N)为落在第k号波位内的目标数。
步骤3： 第k号波位的目标出现概率为
步骤4： 由于目标可能会落在搜索区域内波位无法覆盖到的位置，因此对其进行归一化处理，得到各波位的先验目标出现概率
当Q的取值越大，通过上述过程所得到的目标出现概率越接近于真实值。至此即可得到引导信息下的搜索空域确定以及各波位的目标出现概率。波位编排具体流程如图1所示。
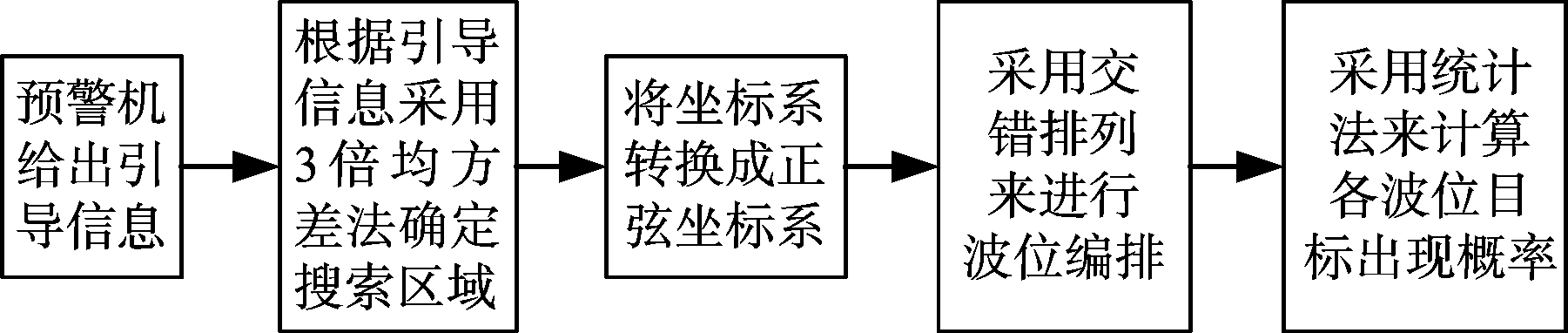
图1 波位编排流程图
2 引导信息下雷达最优所搜算法
2.1 目标平均发现时间模型
对于传统的搜索方式，雷达一般将资源平均分配给每个波位进行照射，这样就会导致部分资源会浪费在目标出现可能性低的波位中，以至于发现目标所用的时间较长。对此，就需要将资源合理地分配给每一个波位，从而缩短目标被发现的时间。
假设目标出现在第k号波位上，此时可得雷达对目标的平均发现时间[7]为
Tk=
+
(5)
式中，tk为雷达在第k号波位上的驻留时间，Tpri为脉冲重复周期，Tr表示搜索帧周期。此时总的平均搜索时间可以表示为
(6)
Pdk表示第k号波位上的检测概率。假设目标为Swerling Ι型且虚警概率为Pfa，此时Pdk可由下式计算得到：
(7)
式中,SNRk为第k号波位上的回波信噪比。假设雷达发射功率为Pt，根据雷达方程，雷达接收的回波功率可表示为
(8)
式中，Gt,Gr分别为雷达发射与接收天线增益，λ为波长，σ为目标的RCS，R为目标与雷达间的距离。根据波位k上的驻留时间tk可得到相参积累的脉冲数为
进而得到脉冲积累后的SNRk的表达式：
(9)
式中，k0为玻耳兹曼常数，B为发射信号的带宽，FN为雷达接收机噪声系数，T0为标准室温。实际情况下，目标一般都会自身携带干扰机或者借助支援式干扰机，向雷达施加干扰信号(本文以压制干扰为例)，严重降低雷达接收端SNR，从而干扰雷达对目标的检测，达到自卫的目的。本文以雷达接收SNR降低程度表示压制干扰的强度，则可得到对应压制干扰条件下脉冲积累后的信噪比为
(10)
式中,Jk表示第k号波位受到的干扰强度。
2.2 基于混合变量规划的雷达最优搜索算法
通过上节所提模型可以求得各个波位的最优驻留时间。但无法确定搜索空域下最优的波位搜索顺序。针对该问题，本文借用整数规划的思想，引入搜索顺序变量δk,j=1/0，分别表示第k号波位的搜索次序是否为j，其中k=1,2,…,N,j=1,2,…,N。为了更好地理解，我们随机定义了一组搜索顺序，以N=6为例，如表1所示。
表1 搜索顺序变量分配
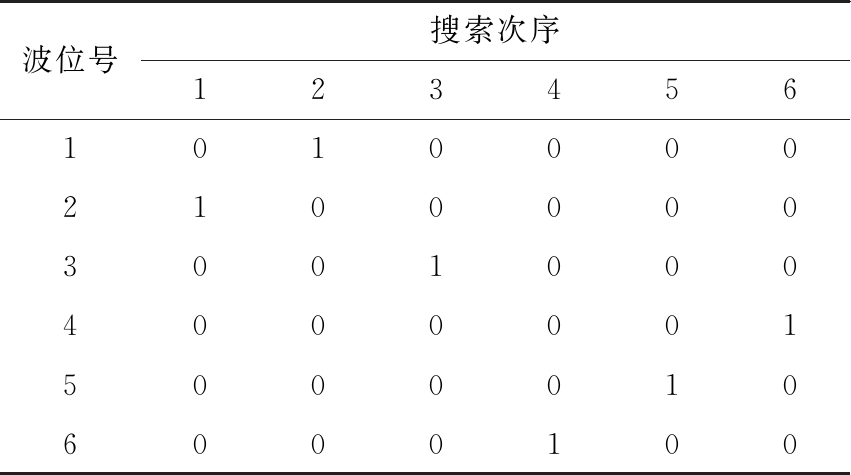
波位号搜索次序123456101000021000003001000400000150000106000100
由表1可知，δ2,1=1可表示雷达对第2号波位第一个进行照射，以此类推可得到其他波位照射顺序的表示。并且可以发现表中的每一行有且仅有一个顺序变量为1，每一列也有且仅有一个顺序变量为1，这就可以分析得到顺序变量δk,j的约束条件，即
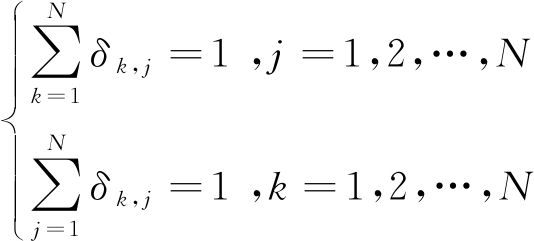
(11)
将每一个波位行中的1替换成对应波位的驻留时间tk，即可得到同时具有驻留时间变量和搜索顺序变量的联合变量
其表示为雷达在第k号波位上照射次数为j时驻留时间为tk。将tsk代入式(5)以替换tk，可得到带有搜索顺序变量的平均发现时间Tsk：
Tsk=
+
(12)
将式(12)代入式(6)来替换其中的Tk，可得到总的包含搜索顺序变量的目标平均发现时间：
(13)
根据上述可知，雷达波束照射顺序问题可以看作为一个指派问题[8]，即雷达波束在同一时刻只能照射一个波位，且每个波位在搜索帧周期内只能被照射一次。为了获得最佳的指派方案，需要定义一个矩阵C(N×N矩阵)作为该指派问题的效率矩阵。通过最小化
来优化搜索顺序。矩阵中的行表示波位序号，列表示搜索顺序，其中的元素为各波位对应搜索顺序的目标的发现时间。
综上所述，雷达搜索顺序可由效率矩阵和式(13)共同决定，可得到相控阵雷达最优搜索模型如下：
(14)
式中，δk,j为离散的整数变量,tk为连续变量，η为搜索过程占用总的雷达时间的比例，T_resourse为雷达总的时间资源。对于这种混合变量模型，本文引入NCP函数方法，将0-1离散变量经过转换变为等价的非光滑方程，进一步使用凝聚函数法对其进行光滑化[9]。再使用连续变量的优化方法对模型进行求解。离散变量δk,j的转化过程如下：
(15)
式中,
对式(14)中的变量约束条件进行转化后得到新的约束为
s.t.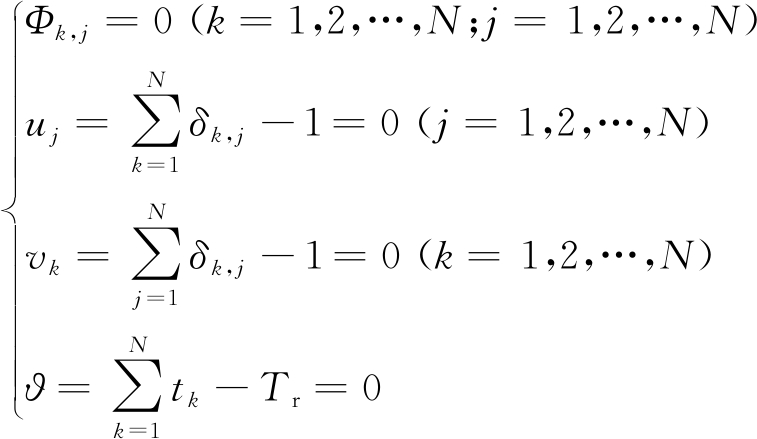
(16)
该优化模型共有N2+2N+1个等式约束，在此令C1=Φ1,1，C2=Φ1,2,…,CN2=ΦN,N ，CN2+1=u1, …，CN2+N=uN，CN2+N+1=v1，…，CN2+2N=vN，CN2+2N+1=ϑ。即可把约束问题转化为无约束的增广拉格朗日乘子法来求解问题，得到增广拉格朗日函数:
(17)
式中,
算法流程如表2所示。
表2 拉格朗日乘子法求解流程
步骤1 选定初始值(δ0,t0),初始化λl=0.1×ones(1,N2+2N+1),σl=2,令l=1,ε=10-5,η=2,θ=0.8;步骤2 以(δl-1,tl-1)为起点,使用BFGS算法求解子问题minL(δ,t,σ,λ),得到:(δl,tl)=argmin(δ,t)La(δ,t,σ,λ)=f(δ,t)-λlCT+σl2C2;步骤3 检验终止判决条件,若Γl=C(δl,tl)<ε,则(δl,tl)为雷达最优搜索顺序以及各波位最优驻留时间结果,终止运算,否则转为步骤4;步骤4 若Γl/Γl-1>θ,罚因子更新为:σl+1=ησl,否则σl+1=σl;步骤5 更新乘子参数:λl+1=λl-σlC;步骤6 令l=l+1,返回步骤2
3 计算机仿真试验
为了体现本文算法的有效性，本节设计了两种场景：其一为目标的干扰落在搜索区域内，这种情况下可将区域内各波位受到的干扰强度等效为相等；其二为目标的干扰落在搜索区域外，此时区域内各波位受到的干扰强度由波位与干扰的相对位置决定。在不同的雷达时间资源下针对两种场景比较本文所提算法与均匀顺序搜索方法所得到的平均发现时间。
3.1 仿真参数
本次仿真以某一相控阵雷达为例，雷达的系统参数如表3所示，雷达的阵面倾角T=15°，阵面法线指向的方位角为80°，雷达搜索波束的宽度为3°×3°，雷达的总的时间资源T_resourse=4 s，Tpri=0.001 s，搜索资源比例η=0.5，即总时间资源的一半用来搜索。目标向雷达施加的干扰强度J=16 dB，在此假设两个场景，场景一为目标施加的干扰处于搜索区域内部，场景二为目标施加的干扰处于搜索区域外部，靠近搜索区域最左侧。其分布如图2所示。两种场景下预警机向雷达提供的引导信息均为：目标在雷达球坐标系下的位置为(16°,24°)，目标与雷达距离为50 km。引导信息的位置误差为(εE,εA)，分别为方位向与俯仰向上相互独立的零均值高斯白噪声，误差标准差均为2°。
表3 雷达系统仿真参数
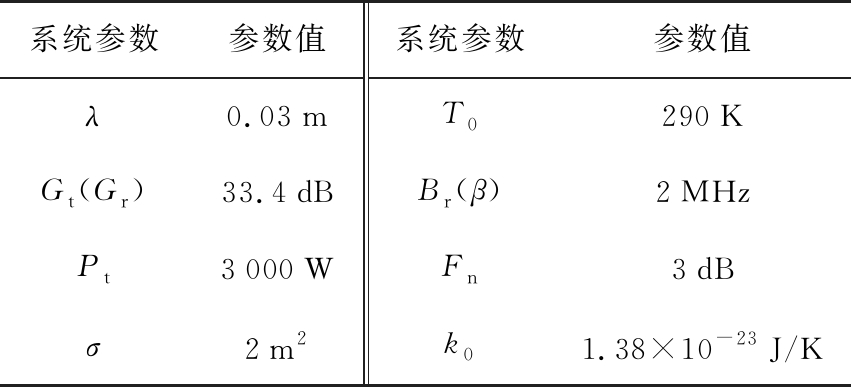
系统参数参数值系统参数参数值λ0.03mT0290KGt(Gr)33.4dBBr(β)2MHzPt3000WFn3dBσ2m2k01.38×10-23J/K
3.2 仿真结果分析
基于以上参数，首先要对搜索区域进行确定，根据3倍均方差法可以确定出目标落入置信度为99.7%的搜索区域，再将该区域转换到正弦坐标系中，采用常用的交错编排方式在该区域中进行波位编排并对波位进行编号，结果如图2所示。随机产生1 000个服从二维误差分布f(εE,εA)的目标并将其转化到正弦坐标系如图3所示，通过前文提到的统计法可以求得目标在各个波位上的出现概率,如表4所示。
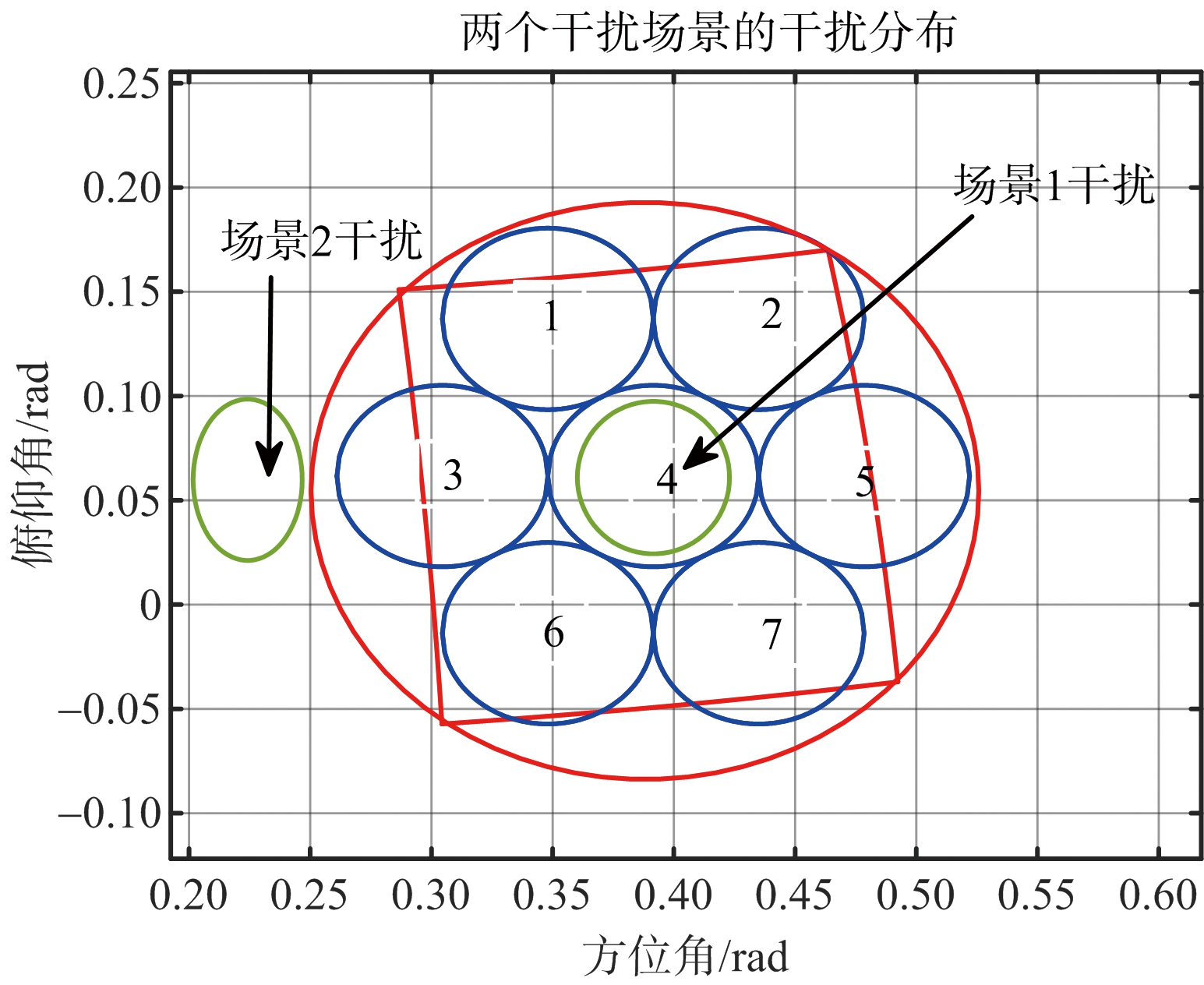
图2 搜索区域与波位编排
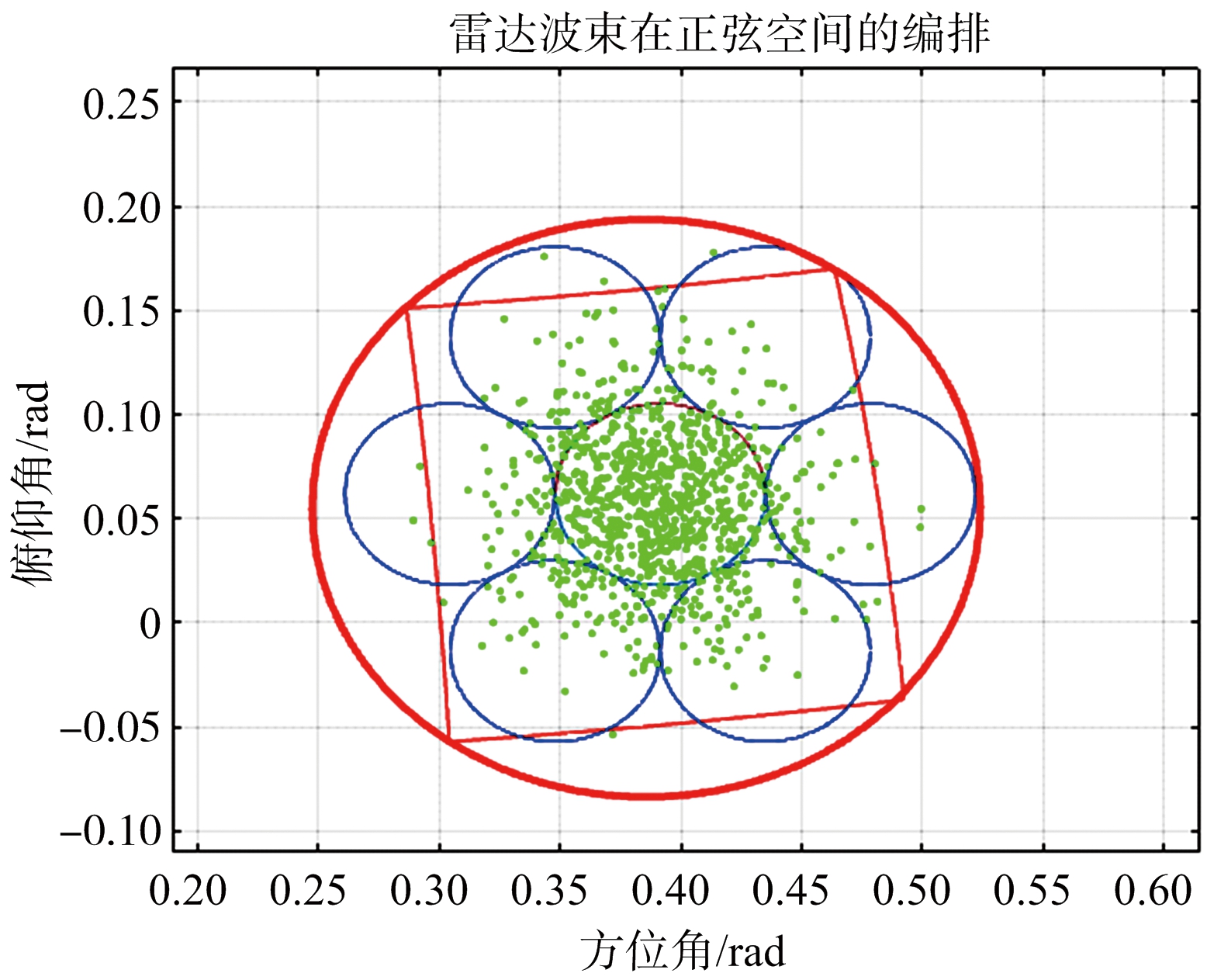
图3 随机目标在各波位的分布
表4 各波位的目标出现概率
波位号目标出现概率10.055120.048230.040340.60450.051660.10270.074
根据前面假设的两种干扰场景，可以通过计算分别得到两种场景下各个波位所受到的干扰强度，结果如图4所示。在得到各波位的目标出现概率之后，采用本文所提算法进行优化，分别在两个场景下计算得到每个波位上的回波信噪比和最佳波束驻留时间以及最优的波束照射顺序如图5、图6和图7所示。
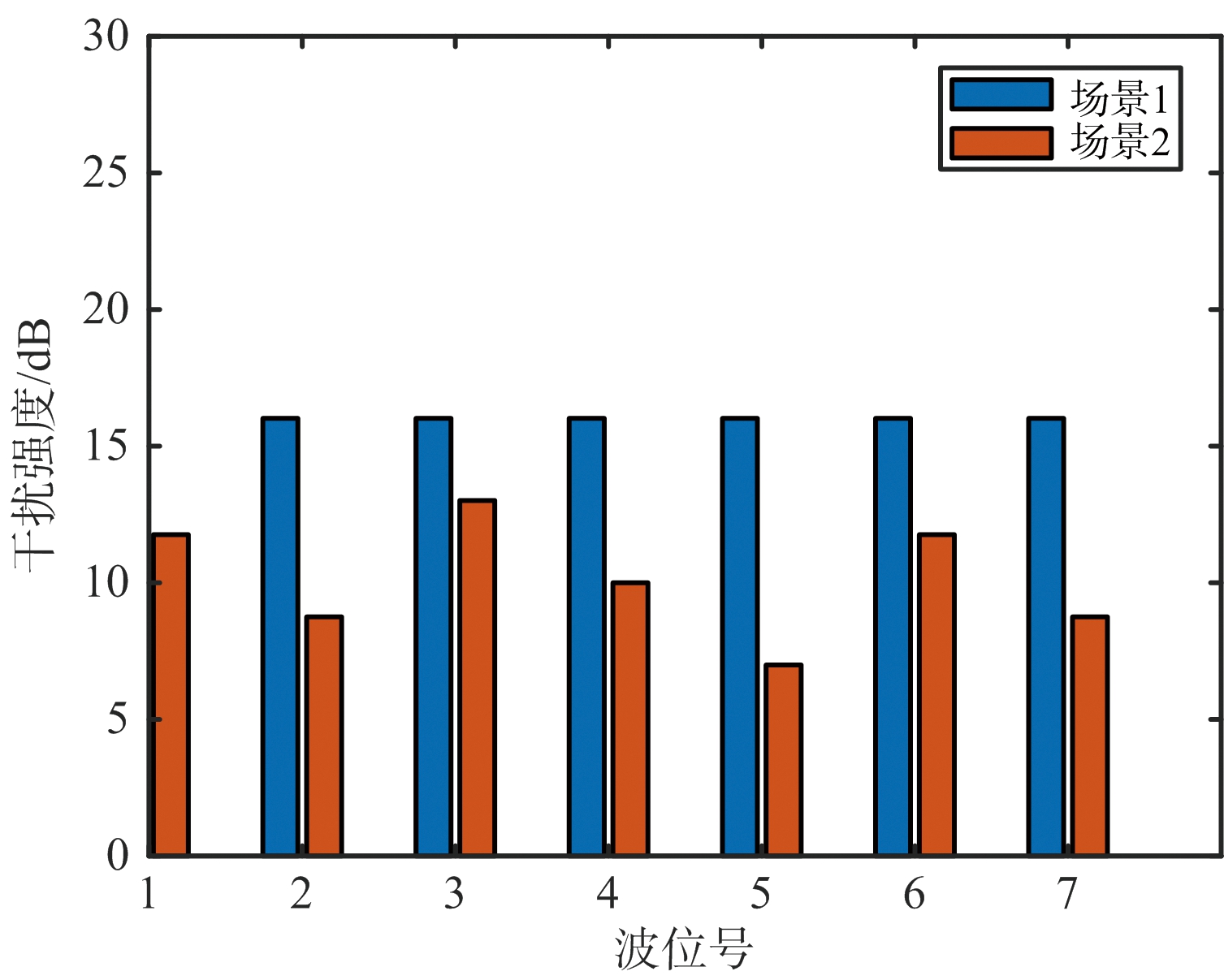
图4 两种场景下各波位的干扰强度
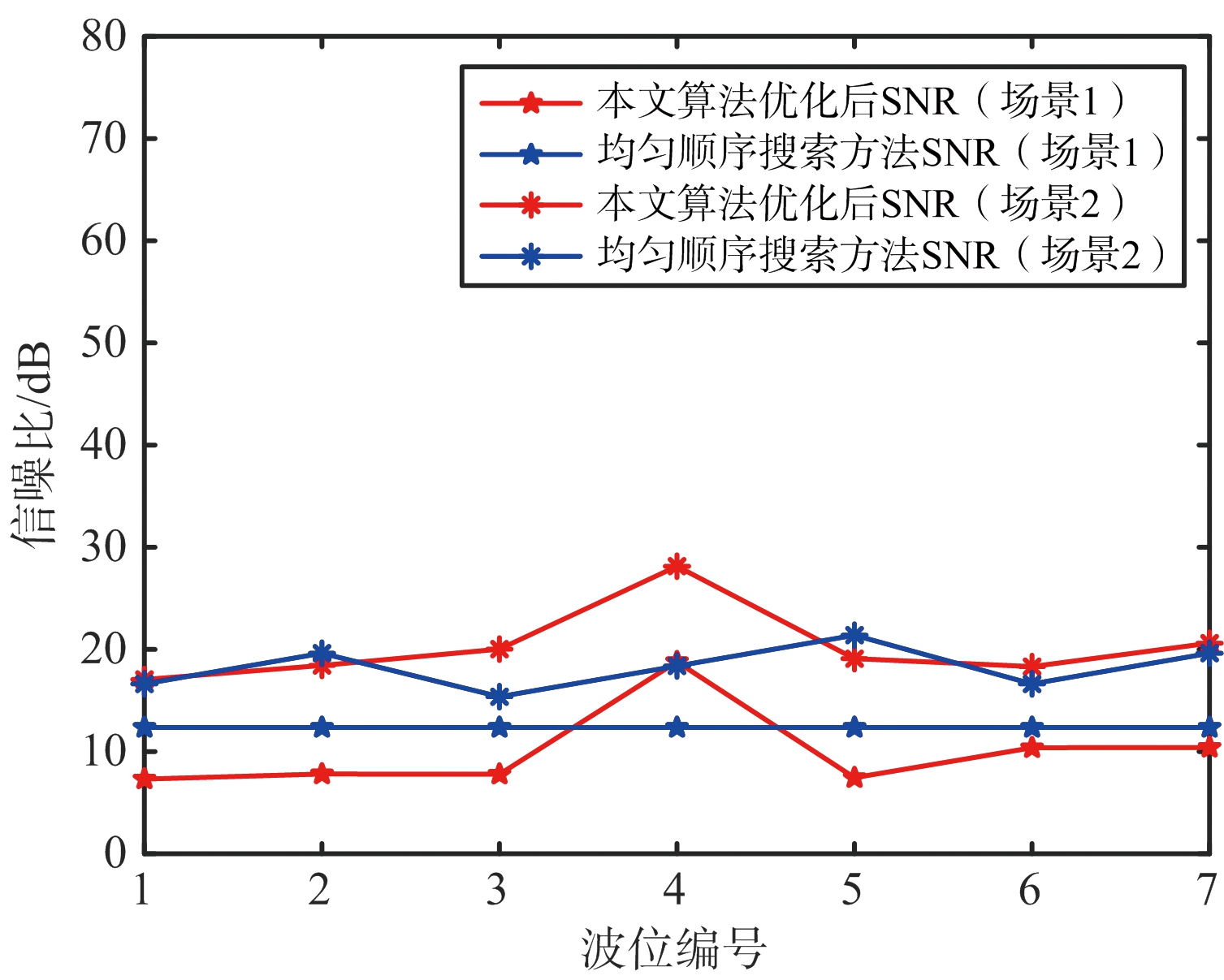
图5 两种场景下两种方法优化后的SNR
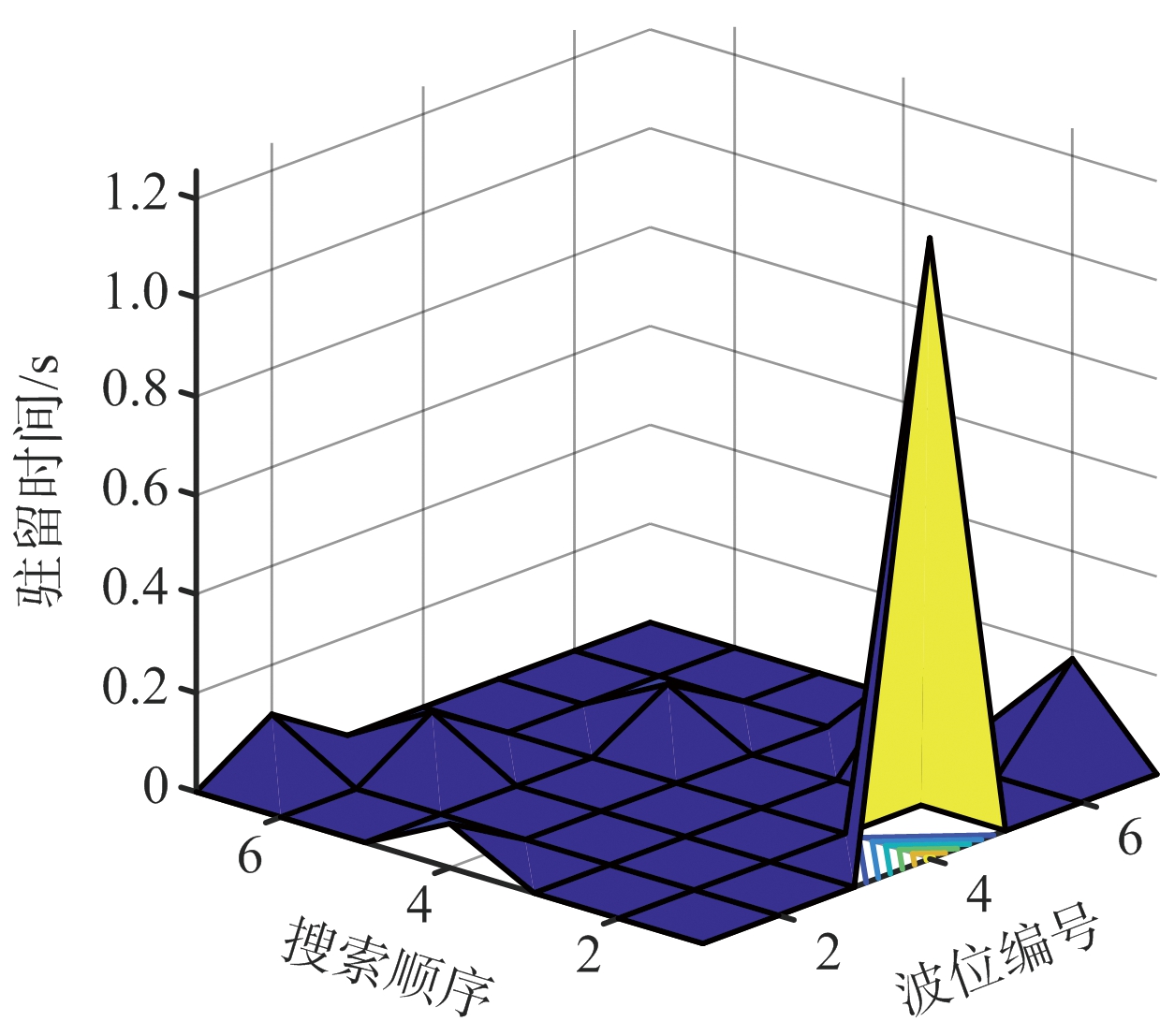
图6 场景1下的搜索资源分配与搜索顺序
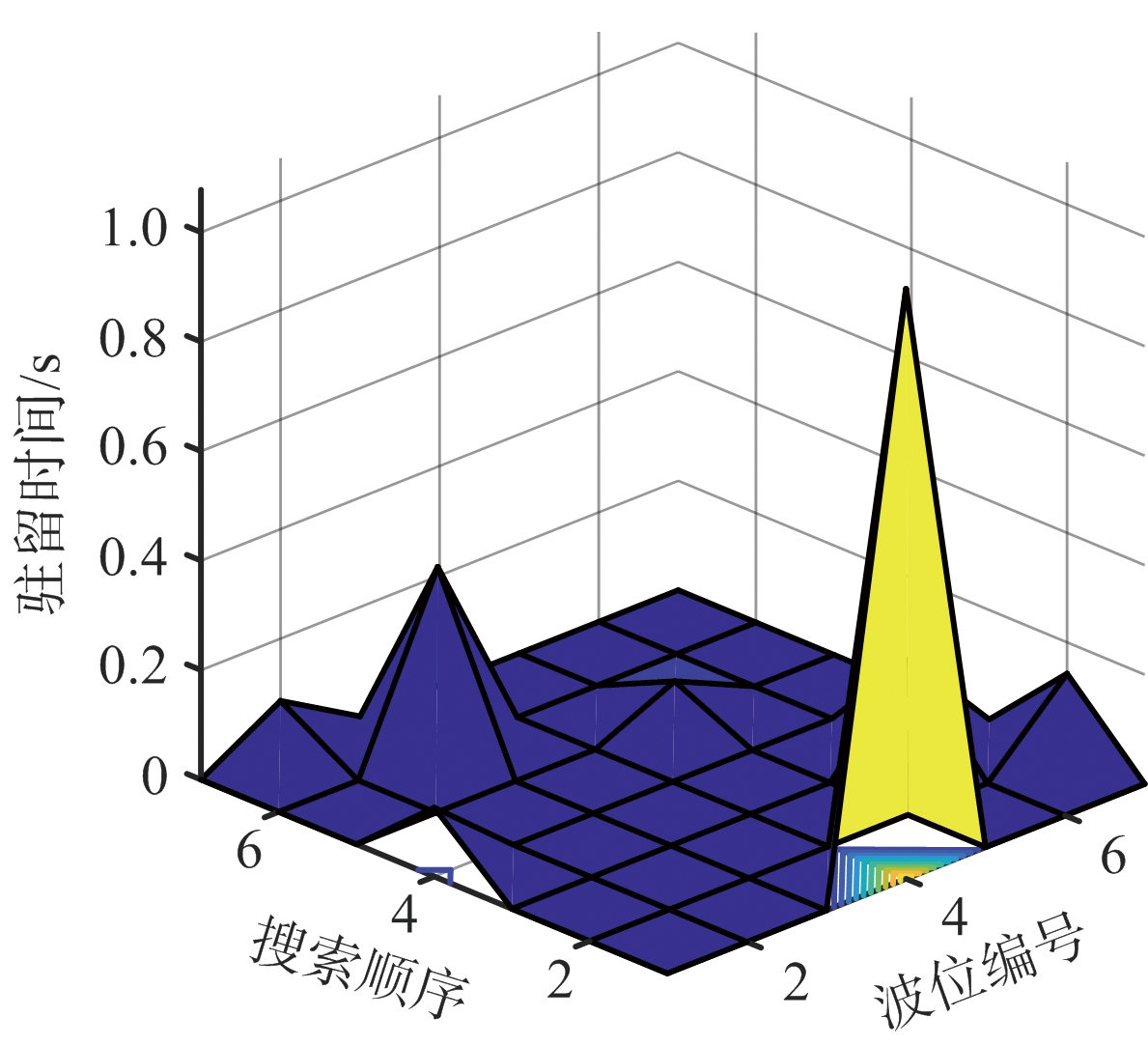
图7 场景2下的搜索资源分配与搜索顺序
对上述过程进行500次蒙特卡洛仿真实验，计算得到场景1下目标的平均发现时间为Topt_1=0.788 2 s，相对而言，通过顺序搜索算法计算得到的平均发现时间Tave_1=1.088 5 s，场景2下两种算法计算得到的平均发现时间结果分别为Tave_2=1.011 5 s，Topt_2=0.701 s，两种场景下均匀搜索方法均大于最优搜索算法优化所得结果，体现了本文算法的有效性。
由图5可知，由于场景1中各波位所受干扰强度相同，影响时间资源分配的因素主要为目标出现概率，因此该场景下优化后只有4号波位的SNR大于均匀顺序搜索方法得到的SNR。而场景2中由于各波位受到干扰强度不同，各波位分配的时间资源由检测概率和出现概率共同决定，因此场景2下本文算法优化后大部分波位的SNR都大于均匀搜索方法。
通过对比图6和图7可知，场景2下3号波位所分配的时间资源占比相对于场景1有明显提高，这是由于场景2中干扰位于3号波位左侧导致搜索区域内各波位受到干扰强度不均匀，结合图4可知 3号波位受到的干扰强度相比于其他波位要大，为了对抗干扰，雷达对其所分配的时间资源也相对较多，体现了本文算法可针对不同场景对时间进行动态分配。
为了更好地验证本文算法所提供的高搜索效率，将针对两种场景在不同的搜索资源比例下与传统的顺序搜索算法进行对比试验，结果如图8和图9所示。
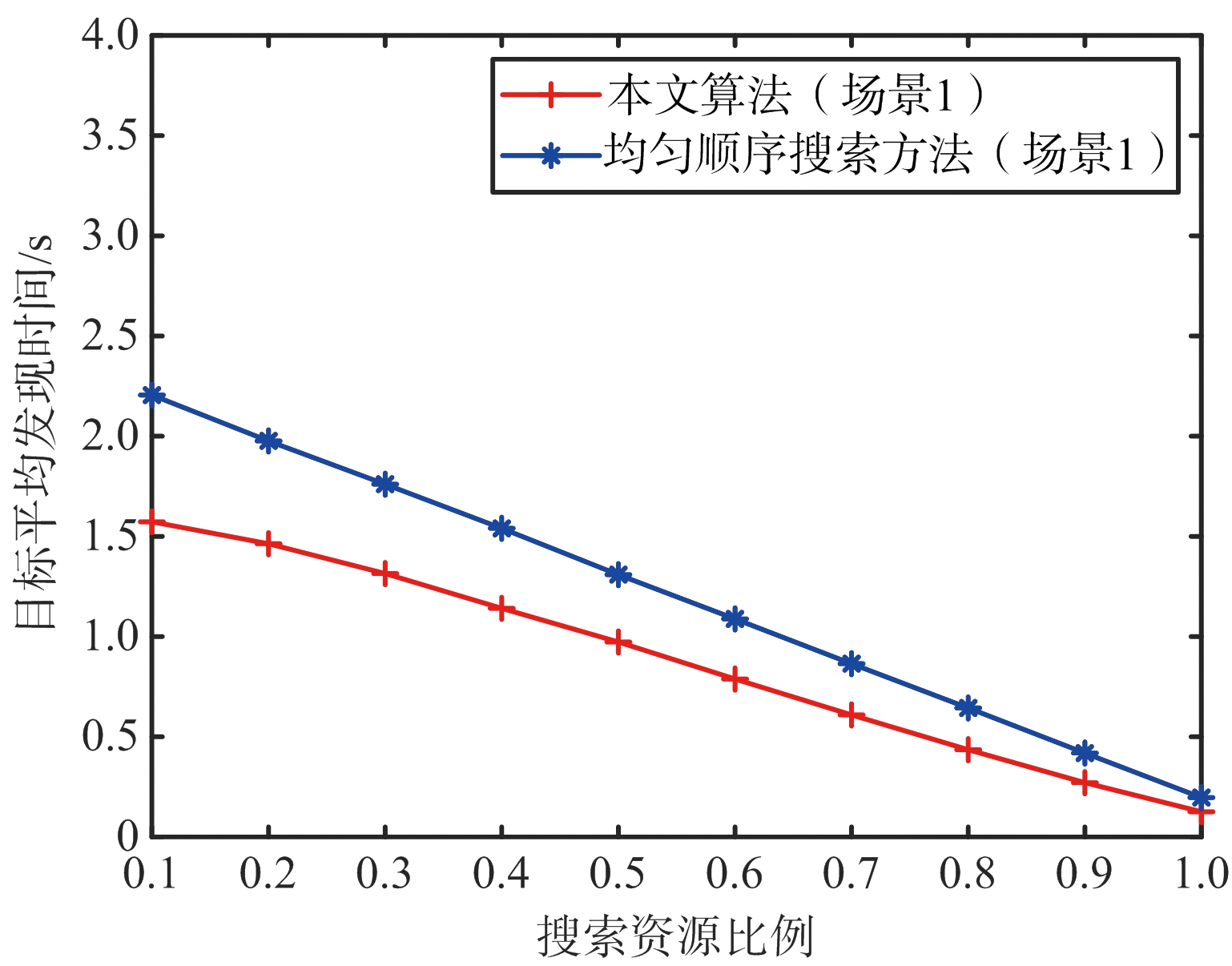
图8 场景1下两种算法平均发现时间比较
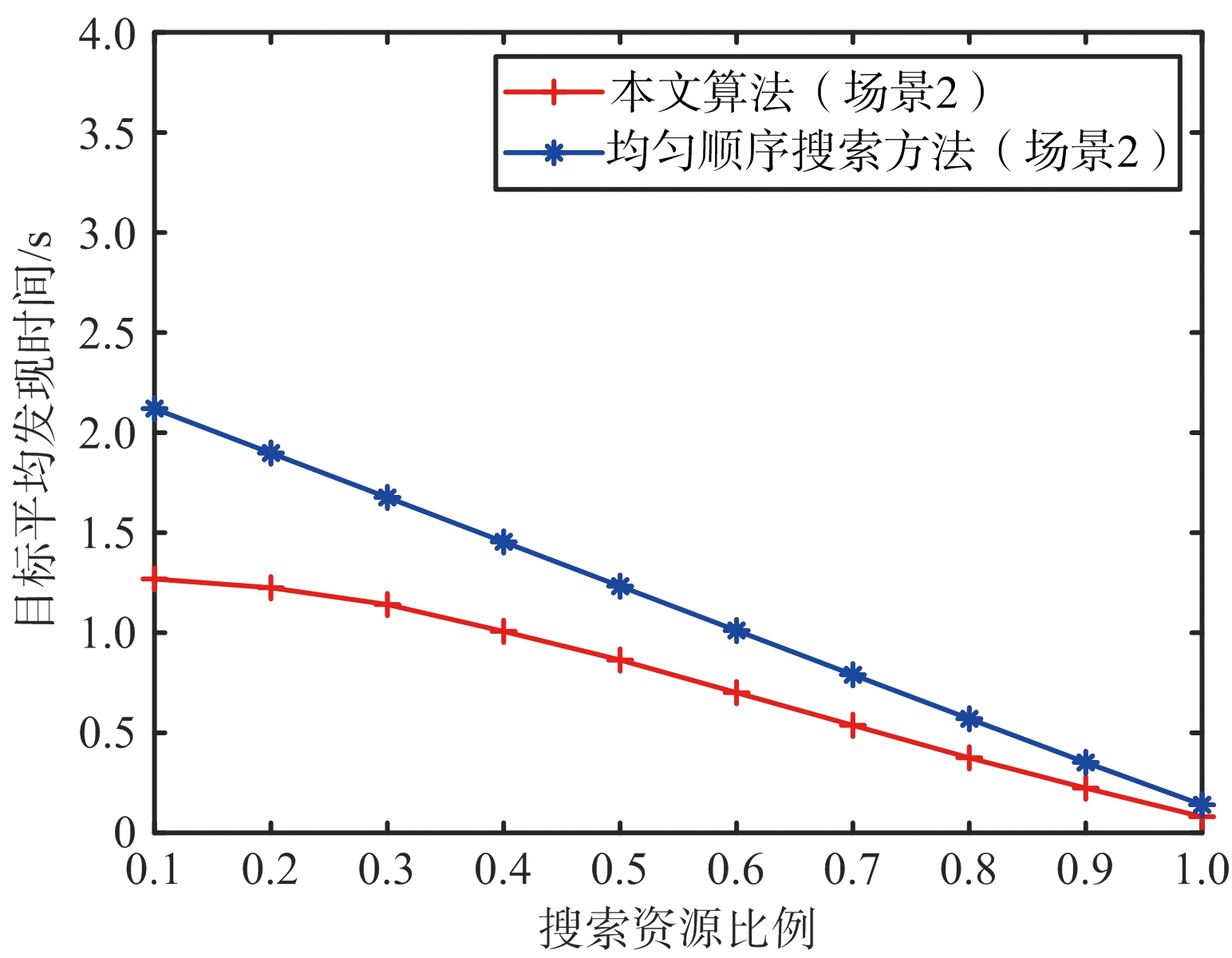
图9 场景2下两种算法平均发现时间比较
由图8和图9可知，相比于传统顺序搜索方法，本文方法在两个场景中的各个搜索资源比例下所得到的目标平均发现时间更小。此外，随着搜索资源比例的提高，两种方法计算得到的目标平均发现时间不断减小，并且本文算法相对于传统方法的优化程度也随之缩小。这也从侧面说明在资源受限的情况下，本文所提算法的有效性更高。对比图8和图9可知，场景2下两种方法所得到的平均发现时间要小于场景1，这是因为干扰位于搜索区域外，导致各波位的干扰强度要小于场景1中的情况。且在搜索资源比例较低的情况下，场景2中本文算法相较于均匀顺序搜索算法，优化效果比场景1要好。证明了本文算法对场景的变化具有较好的适应性。
4 结束语
本文针对预警机引导信息下相控阵雷达快速搜索问题，首先根据引导信息确定搜索区域以及波位编排，其次计算各个波位的目标出现概率，最后以目标平均发现时间为标准，提出了基于混合变量规划的雷达最优搜索方法，该方法同时对各波位的波束驻留时间以及照射顺序进行优化。仿真结果表明，本文方法可以快速地搜索到目标并且可得到各波位最佳驻留时间以及最优搜索顺序。证明了该方案具有有效性的同时，还体现出其对场景变化具有一定的适应性。
[1] 黄佳沁,贺丰收,缪礼锋.基于预警机引导信息的雷达最优搜索算法[J].雷达科学与技术,2019,17(4):379-388.
[2] YU Chenlong, TAN Xiansi, LI Fan. Study on Search Performance of Long Range Early-Warning Phased Array Radar[C]∥2016 CIE International Conference on Radar, Guangzhou:IEEE, 2016:1-5.
[3] WU Qihua, LIU Jin, ZHAO Feng,et al. A Novel Method of Optimal Multi-Area Search for Phased Array Radar[C]∥IET International Radar Conference, Hangzhou, China:IET,2015:1-6.
[4] 唐书娟,许蕴山,毕笃彦,等.信息引导条件下雷达搜索空域及策略[J].西安电子科技大学学报,2016,43(1):173-179.
[5] 刘一鸣,盛文.相控阵雷达资源受限时搜索参数调整策略[J].现代雷达,2020,42(1):8-12.
[6] 陈建平,刘志中,尤立志.相控阵雷达最优波位编排策略仿真算法[J].科学技术与工程,2019,19(33):244-250.
[7] 李晓东.相控阵雷达调度与TAS协同控制算法研究[D]. 哈尔滨：哈尔滨工业大学,2016.
[8] JAIN E, DAHIYA K, VERMA V. A Priority Based Unbalanced Time Minimization Assignment Problem [J]. OPSEARCH, 2020, 57(1):13-45.
[9] 李兴斯,谭涛.离散变量结构优化设计的连续化方法[J].应用力学学报,2007(1):26-30.
