0 引言
雷达作为空间探测的电子设备，利用经过空间目标的电磁波回波对其进行定位，同时获得空间参数信息，如相对距离、径向速度、角度等。当前，隐身技术、复杂的电磁环境以及先进的反雷达手段已成为现代雷达蓬勃发展的掣肘。MIMO(Multiple Input Multiple Output)雷达就是在此背景下，以应用需求为牵引提出的一种新型雷达[1-3]。
相干MIMO雷达最早雏形是由法国ONERA和汤姆逊-CSF公司在20世纪80年代联合研制的综合脉冲与孔径雷达(SIAR)，20世纪90年代初华东电子工程研究所开始相关理论研究[4]，随后完成实验研究[5]，并于2011年完成世界上首个大型实用MIMO雷达。非相关MIMO雷达在2003年由美国林肯实验室提出[2]，它通过借鉴通信领域的多输入多输出概念，让收发阵列协同工作，从而能够在空间中形成多个并行观测通道，提高雷达的生存和探测性能[4-5]，现已成为国内外雷达领域中的前沿技术。根据收发天线的位置和空间目标参数之间的关系，MIMO雷达可以分为集中式和分布式。集中式MIMO雷达的收发阵列与传统阵列类似，阵元间距一般小于目标信号的半波长且雷达视角近似相同；同时，发射端采用波形分集的思想，各天线单元发射彼此正交的信号，接收端采用相干处理，可以扩大阵列的虚拟孔径，以及提高雷达的测角精度和信号的截获能力等[6-7]。针对收发天线是否共置的问题，集中式MIMO雷达又分为单基地和双基地雷达。分布式MIMO雷达中收发阵列各阵元彼此之间有较大间隔，具有不同的雷达视角；由于接收阵列通过空间分集在观测空间中形成多个通道，因此，具有克服目标的雷达散射截面积(Radar Cross Section，RCS)在空间中的起伏能力[8]。虽然分布式比集中式MIMO雷达拥有更优良的信号检测和参数估计性能，但是分布式MIMO雷达的工程实现存在诸多困难，且现阶段只停留在理论研究阶段，而集中式MIMO雷达具有更加广泛的实际应用价值。
经过多年发展，国内外已有一些关于MIMO雷达的研究文献[9-20]。但关于MIMO雷达角度估计的综述文献尚未见报道。作为空间目标的重要参数之一，角度估计在雷达对目标进行定位时起着重要作用。考虑到系统实现成本，一味增大阵列孔径以提高角度估计性能是不现实的。同时，由于MIMO雷达具有新体制的雷达结构，传统的阵列测角理论无法直接应用。基于此目的，本文以集中式MIMO雷达信号模型入手，将目前广泛使用的MIMO雷达角度估计算法划分为搜索类、免搜索类、求根类以及子空间快速估计类四大类别，全面总结了各类角度估计算法的原理，同时深入对比分析它们的优缺点。最后，以理论研究的工程化推进为目的，指出MIMO雷达角度估计算法的未来发展趋势。
1 MIMO雷达模型
1.1 单基地MIMO雷达信号模型
单基地MIMO雷达的阵列结构和传统的阵列结构类似，阵元间距很近，考虑收发均为均匀线阵，如图1所示，因此收发阵列具有相同的波离角(Direction of Departure，DOD)
和波达角(Direction of Arrival，DOA)θ。假设阵元间距为d=λ/2,λ是信号波长，发射信号sm(t)为M路编码长度为J的基带信号且彼此正交。对空间第p,p=1,2,…,P个远场目标的回波信号x(t)在接收端进行匹配滤波后的输出为
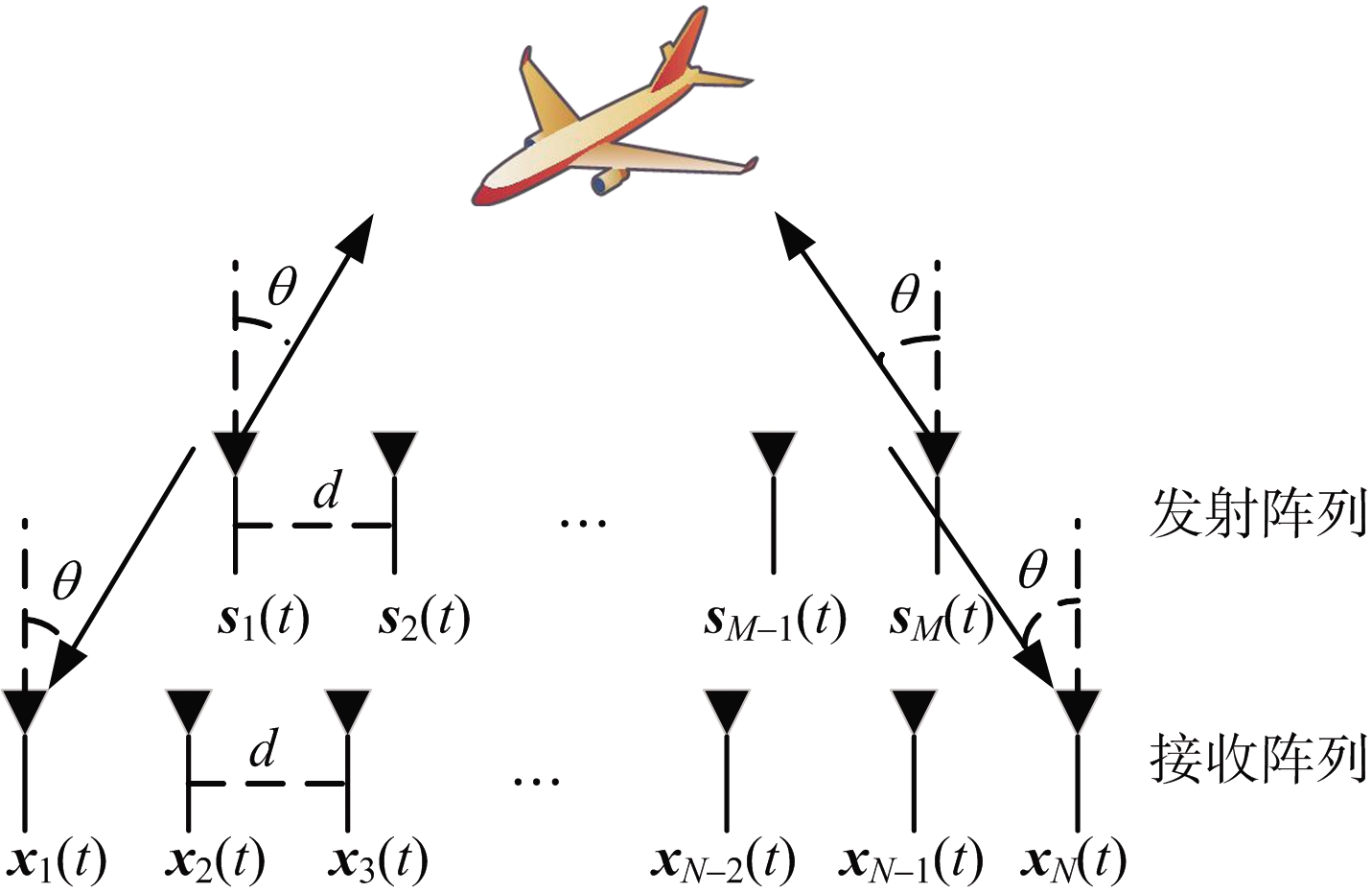
图1 单基地MIMO雷达示意图
(1)
式中：βp和fp分别为反射系数和多普勒频率，nm,n(t)为第m路匹配滤波后的噪声矢量，图2给出了信号在匹配滤波中的处理过程；
和
分别为发射端和接收端的导向矢量，atm(θp)和arn(θp)分别为 at(θp)和ar(θp)中第m个和第n个元素；同时，定义发射端和接收端的导向矢量矩阵分别为AT=[at(θ1) … at(θP)]和AR=[ar(θ1)… ar(θP)]。将N路匹配滤波后的T次快拍信号写成矩阵形式为
图2 回波信号匹配滤波示意图
y(t)=As(t)+n(t), t=1,2,…,T
(2)
式中：
a(θ)=at(θ)⊗ar(θ)；⊙和⊗分别代表Khatri-Rao积和Kronecker积。
1.2 双基地MIMO雷达信号模型
对于双基地雷达而言，收发阵列间距较远，因此波离角φ和波达角θ不同，如图3所示。不失一般性，对单基地MIMO雷达信号接收过程的推导可推广到双基地MIMO雷达中，经过匹配滤波后的接收信号矩阵同样为
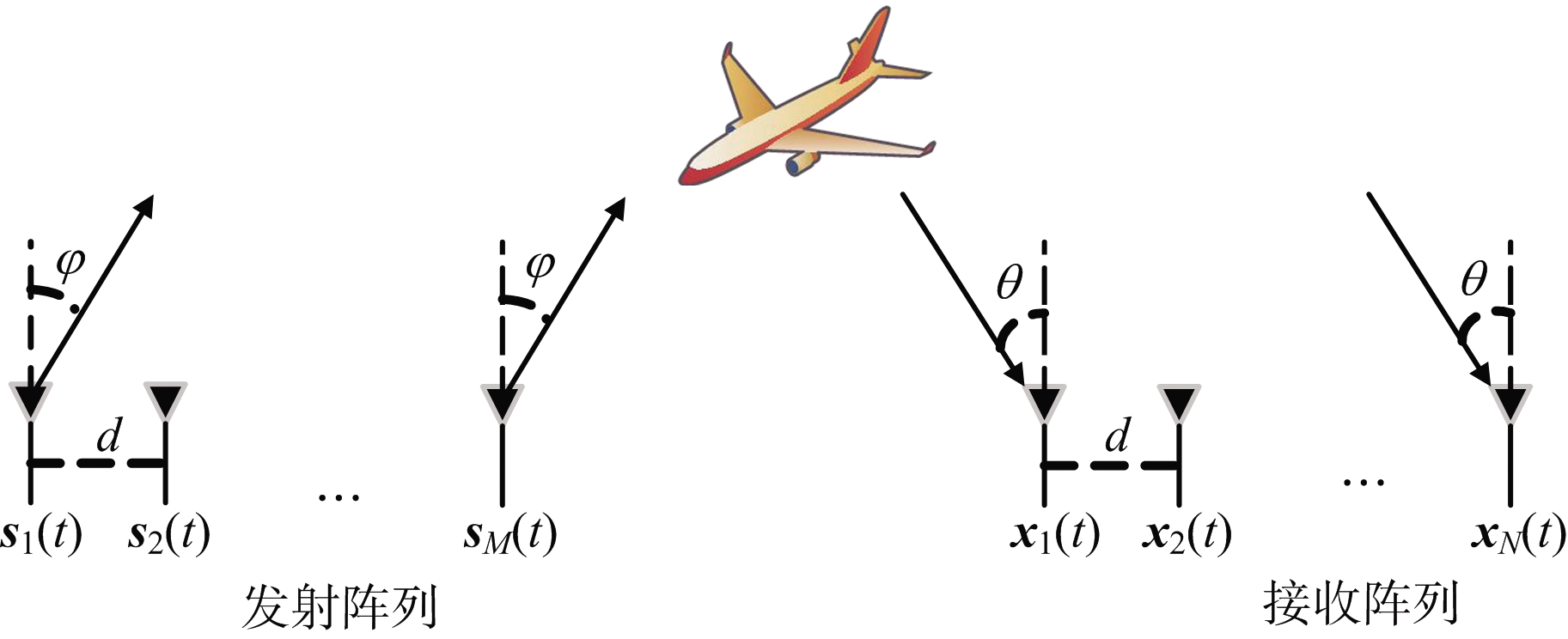
图3 双基地MIMO雷达示意图
y(t)=(AT⊙AR)s(t)+n(t), t=1,2,…,T
(3)
式中：发射端导向矢量矩阵为AT=[at(φ1),…,at(φP)]，接收端导向矢量矩阵为AR=[ar(θ1),…,ar(θP)]。可见，单基地MIMO雷达是双基地MIMO雷达的一种特殊形式。另一方面，从单/双基地MIMO雷达的接收信号模型可以看出，MIMO雷达通过发射端的波形分集技术可以产生彼此相互正交的波形，同样也可以产生完全相同的波形，此时MIMO雷达则转换为相控阵雷达；因此，MIMO雷达是相控阵雷达的一种拓展，并且可以完全兼容相控阵雷达。
2 搜索类角度估计算法
在传统阵列测角的各类方法中，MUSIC算法的提出是一个重要里程碑。由于单基地雷达和传统阵列具有相似的天线布置结构，首先进行对单基地MIMO雷达MUSIC算法的研究将会为其他各类角度估计算法打下铺垫。
2.1 单基地MIMO雷达1D-MUSIC算法
在第2节给出的信号模型下，对匹配滤波后的接收信号y(t)构造协方差矩阵
并进行特征值分解，可得到相应的特征值和特征向量。假设λi和λj分别为协方差矩阵R的P个大特征值和MN-P个小特征值；ei和ej分别对应为λi和λj的特征向量。定义矩阵Us
[e1e2 … eP]，Un[eP+1 … eMN]，Us和Un的列向量张成信号子空间span(Us)和噪声子空间span(Un)；同时根据子空间的正交原理 span(Us)⊥span(Un)以及span(Us)=span(A)可知，在信号的入射方向θ处，有aH(θ)Un=0。由此，可以得到单基地MIMO雷达MUSIC算法的谱峰搜索函数[10]：
(4)
对式(4)进行遍历搜索，当f1D-MUSIC (θ)出现最大峰值时所对应的角度θ即为目标的角度估计值。此外，在1D-MUSIC算法中，计算量主要由协方差矩阵的获取、特征值分解以及谱峰搜索产生，这三部分的计算量分别为O((MN)2T)、O((MN)3)和O(J(MN)2)，其中J是搜索步长。
2.2 双基地MIMO雷达2D-MUSIC算法
双基地MIMO雷达2D-MUSIC算法具有和单基地MIMO雷达1D-MUSIC算法相似的处理方式，唯一不同在于，收发阵列分置的双基地MIMO雷达具有不同的波离角φ和波达角θ，即导向矢量应为a(φ,θ)；因此，双基地MIMO雷达的谱峰搜索函数f2D-MUSIC (φ,θ)是一个二维函数[11]，P个最大峰值对应为DOD-DOA二维角度联合估计，如图4所示。
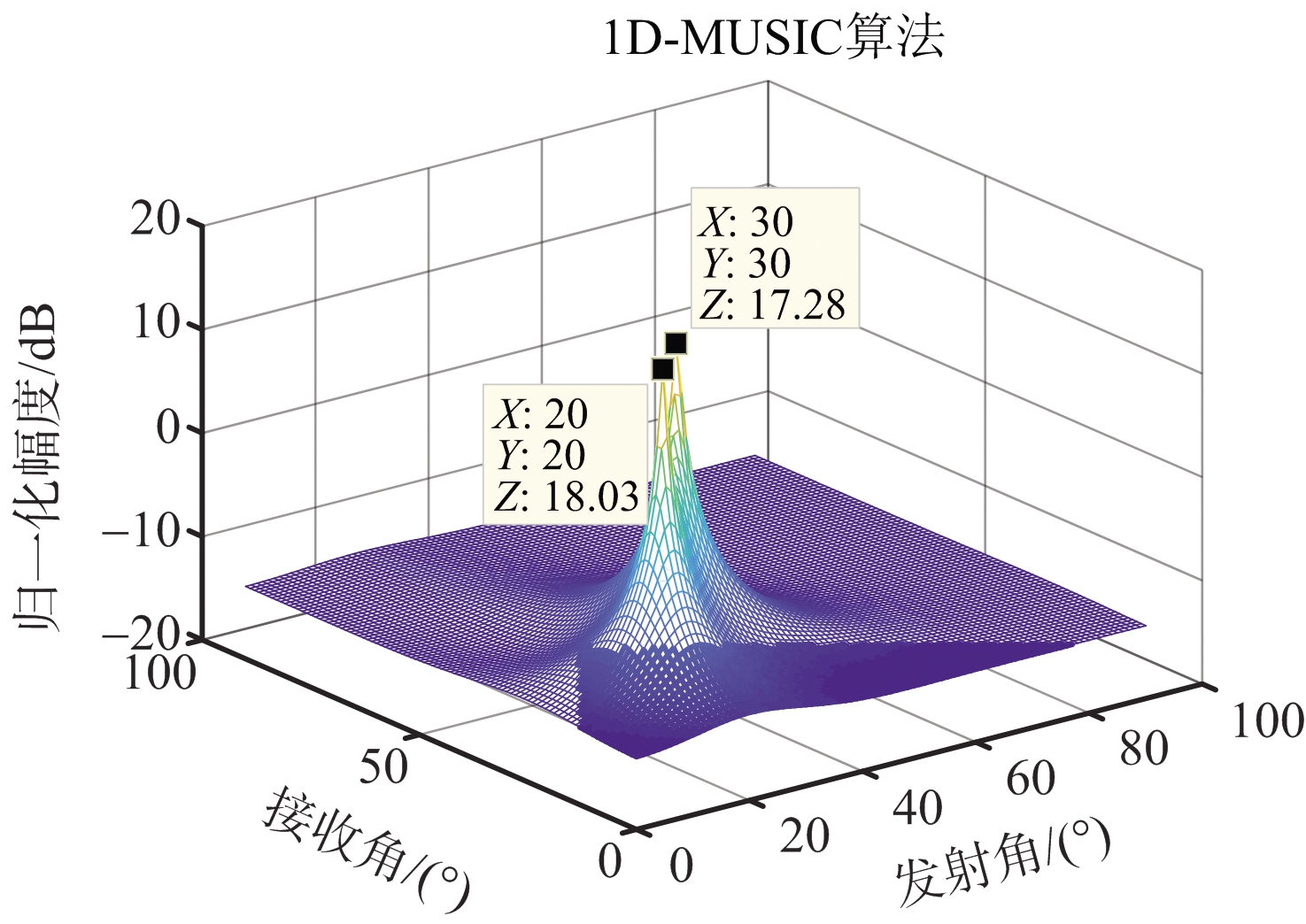
(a) 单基地MIMO雷达1D-MUSIC算法示意图
(b) 双基地MIMO雷达2D-MUSIC算法示意图
图4 4发5收单/双基地MIMO雷达关于P=2个空间目标的谱峰搜索示意图
2.3 双基地MIMO雷达2D-Capon算法
双基地MIMO雷达的2D-Capon算法[12]具有和传统的阵列测角Capon算法相同的原理，两者均利用协方差矩阵R的逆来代替噪声子空间投影矩阵
且估计精度略高于2D-MUSIC算法。相比于2D-MUSIC算法，2D-Capon算法的计算量仅缺少特征值分解这一项。
3 免搜索类角度估计算法
搜索类算法作为传统阵列测角到MIMO雷达角度估计的过渡算法，虽然被广泛采用，但是由于需要进行二维角度遍历搜索，计算量很高，因此研究免搜索的MIMO雷达角度估计算法非常必要。
3.1 双基地MIMO雷达降维2D-MUSIC算法
在2D-MUSIC算法基础上，介绍一种谱峰搜索的改进措施。首先，将式(4)中含有两个角度信息的谱峰搜索函数分解为分别只含有一个角度信息的准则函数乘积的形式，即
(5)
式中：
为N×1维向量，加入约束条件的原因在于消除无用解，如ar(θ)=0。可以看出，式(5)将式(4)的搜索问题转化为最小优化问题。降维2D-MUSIC算法为了通过拉格朗日乘子法将优化问题进一步地转化为无约束问题，后续再利用求导操作和最小二乘方法分别可以求出φ和θ。此方法的思想不仅可以对搜索类算法进行降维，也可以拓展到其他阵型。该算法通过线性优化将获取目标角度信息的计算量降低为O(JM2(N+1))，同时保证了具有和2D-MUSIC算法相似的估计精度。
3.2 双基地MIMO雷达PARAFAC算法
平行因子(Parallel Factor，PARAFAC)分解法作为张量理论的代表，可以无模糊地辨识模型参数。在MIMO雷达中，PARAFAC算法将匹配滤波后的接收信号y(t)用三阶张量表示为[13]
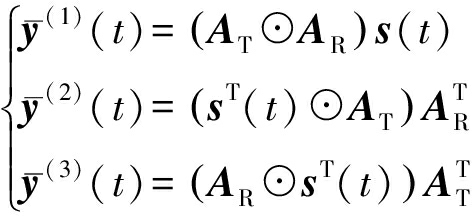
(6)
式中,
和
分别表示y(t)的三阶张量沿接收、发射和快拍数方向的切片集合。一般来说，收发导向矢量矩阵AT和AR均为列满秩矩阵，因此，只要rank(s)≥2即可满足模型分解的唯一性，从而AT，AR和S可唯一确定。最终，通过各类迭代算法可以实现角度估计。该算法的计算为O(3P3+2(MN+MQ+NQ)P2+6MNQP)，其中Q为相干处理间隔内的脉冲个数，那么，PARAFAC算法的计算量虽然上升，但是其估计精度要高于2D-MUSIC算法和2D-Capon算法。
3.3 双基地MIMO雷达2D-ESPRIT算法
通过收发阵列间的旋转不变性关系对空间目标进行角度估计的ESPRIT 算法，可避免2D-MUSIC 算法中繁杂的谱峰搜索过程[14]。在双基地MIMO雷达中，收发阵列的导向矢量满足式(7)的线性关系:
AT2=AT1ΦT, AR2=AR1ΦR
(7)
式中：AT1，AT2，AR1和AR2分别是ΑT和ΑR的子矩阵，ΦT和ΦR是只包含波离角φ和波达角θ旋转因子。2D-ESPRIT算法分别对旋转因子进行特征值分解，可直接得到目标信号角度估计的闭式解，此部分计算量仅为O(P3)；同时，2D-ESPRIT算法的估计精度要明显高于2D-MUSIC算法。
3.4 双基地MIMO雷达2D-ESPRIT自动配对算法
由于2D-ESPRIT算法将波离角φ和波达角θ的求解看作两个独立的过程，因此仍需要额外的配对算法对φ和θ进行适配，这将给算法带来多余的计算负担。2D-ESPRIT自动配对算法的提出成功地解决了这个问题，如图5所示。该算法在2D-ESPRIT算法的基础上，深刻地剖析了目标角度φ和θ在收发阵列的内在联系[15]，巧妙地对空间目标进行DOD-DOA联合估计，不仅保证了估计精度，还提高了角度估计算法的计算效率。
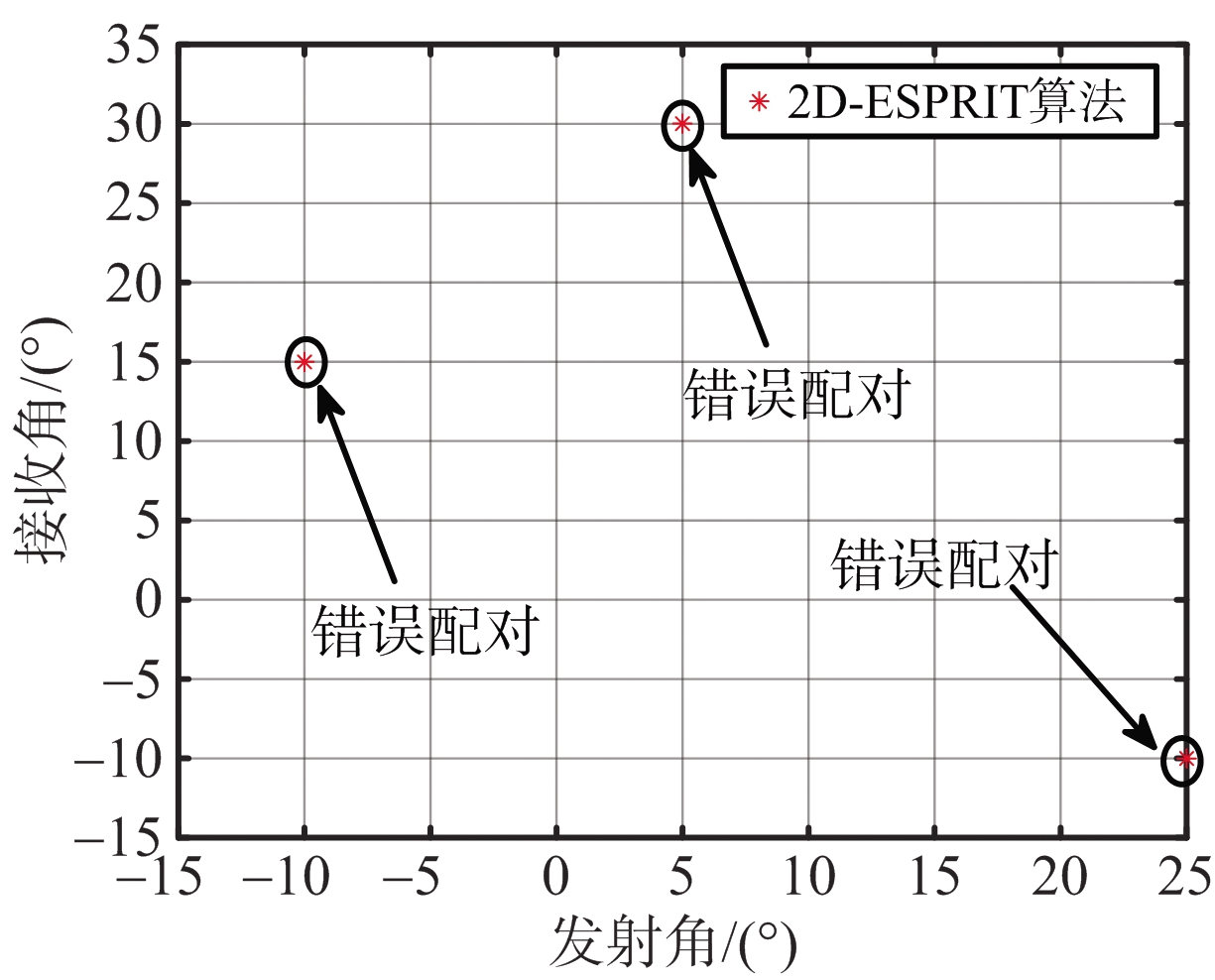
(a) 2D-ESPRIT错误配对示意图
(b) 2D-ESPRIT自动配对示意图
图5 6发8收双基地MIMO雷达关于P=3个空间目标且方向角度分别为(-10°,30°)、(25°,15°)和(5°,-10°)的2D-ESPRIT算法
4 求根类角度估计算法
求根(root)类角度估计算法通过构造含有目标角度信息的多项式并对其进行求根运算，从而获得正确的角度估计值。该类算法是除2D-ESPRIT算法外，另一种低复杂度角度估计算法的典型代表。
4.1 单基地MIMO雷达1D-root算法
在单基地MIMO雷达中，1D-root算法[16-17]为了降低特征值分解的计算量，首先需要在离线计算参数矩阵，然后对经过匹配滤波后的接收信号y(t)进行降维处理；此时，接收信号的数据维度从M2×1维降低到(2M-1)×1维。和2D-Capon算法相似，1D-root算法也通过R-1构造4M-2阶求根多项式，且具有比搜索类更高的角度估计精度[17]。由于求根运算的计算量仅与多项式的阶数成正比，即O((4M-2)3)；因此，相比于1D-MUSIC算法，计算量大幅度降低。
4.2 双基地MIMO雷达2D-root算法
通过求根运算获取目标角度信息的方法仅适用于包含一个角度信息的多项式，然而，由于双基地MIMO雷达具有不同的波离角φ和波达角θ，因此，双基地的求根角度估计算法无法仿照单基地的1D-root算法对二维角度多项式直接进行求根运算。双基地MIMO雷达的2D-root算法在1D-root算法基础之上，进一步研究收发导向矢量的内在关系，将二维求根多项式转换为两个一维多项式[18-19]，即
(8)
式中：
是噪声子空间投影矩阵
中的N×N维分块矩阵。当rank(Πn)=MN-P≥N时，可以通过求解行列式
来获得目标的波离角φ；再将波离角φ的估计值代入式(8)，可获得波达角θ。注意到，φ和θ在求解过程中一一对应，不需要额外配对过程就能实现DOD-DOA联合估计。但2D-root算法需进行两次求根运算，计算量提升为O((4M-2)3)+O((2N-2)3)。
4.3 双基地MIMO雷达波束空间2D-root算法
在波束空间对接收信号进行处理是提高角度估计的稳健性、降低计算量的一种重要方式，其作用原理如图6所示。将双基地MIMO雷达阵元空间的接收信号y(t)转换到波束空间后的输出数据表示为[20]
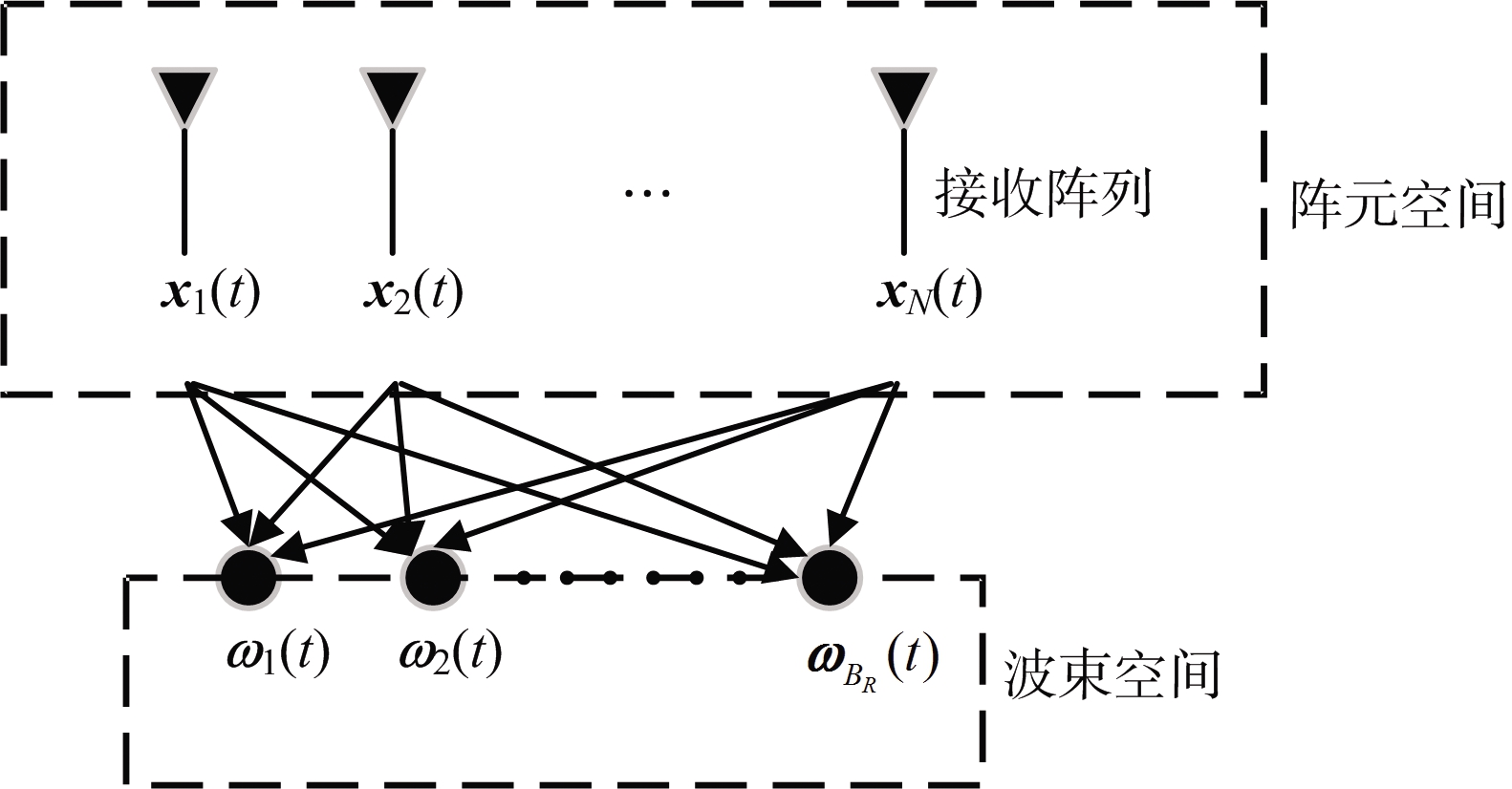
图6 接收阵列波束空间原理图
ω(t)=THy(t)
(9)
式中，T=TT⊗TR为MN×B维波束变换矩阵，数据维度从MN×1维降低到B×1维，其优势在于以收发阵列天线个数为维度的角度估计问题转换为以波束个数为维度的角度估计问题。这种维度的降低，是波束空间具有低复杂度角度估计的基础。波束空间2D-root算法利用阵元空间2D-root算法的思想，同样将二维角度求根多项式中的φ和θ进行分离，分别求解后依旧可以实现角度的自动配对。波束空间2D-root算法通过空间转换，将计算量降为O((2(BT-1)BR)3)+ O((2(BR-1))3)；但也使得收发阵列的观测空间区域变小，因此，角度估计的精度受到了一定的损失。
5 子空间快速估计类角度估计算法
前文中所介绍的各种算法，除2D-Capon算法和PARAFAC算法外，其余均需要对协方差矩阵进行特征值分解，从而获得信号以及噪声子空间，这些算法均可称为子空间类角度估计算法。但当双基地MIMO雷达的收发天线数量以及快拍数增大时，虚拟阵元的数量和协方差矩阵维度也随之增大，此时若进行子空间类算法，特征值分解所带来庞大的计算量会导致运算速度降低。
为了避免双基地MIMO雷达中特征值分解的步骤，需要寻找一种子空间快速估计方法。其中，线性算子(Propagator Method，PM)算法的效果最为明显。2D-PM算法通过对接收信号y(t)进行最小二乘，可获得连接导向矢量内部线性关系PHA1=A2的线性算子P。2D-PM算法和2D-ESPRIT算法相似，均通过线性关系获得角度估计的高精度闭式解，但计算量可降至O(MNPT+P3)。
6 MIMO雷达角度估计算法应用对比
本节在双基地MIMO雷达模型下，对前文四类算法的典型代表进行归纳，并以2D-MUSIC算法的精度分析和计算量分析作为对比对象，系统地分析了其他各种算法的优缺点，如表1所示。
由表1可见，MIMO雷达在对空间目标进行测角时，其计算量和估计精度是一对难以调和的对立面。表1中各算法的优缺点具体分析如下：
表1 MIMO雷达角度估计算法对比
算法名称精度分析计算量分析优点缺点2D-MUSICO((MN)2T)+O((MN)3)+O(J(MN)2)阵列结构可扩展谱峰搜索计算量庞大,且当收发阵列均为小型天线阵列、空间存在多目标时,谱峰分辨率降低PARAFAC高于2D-MUSICO(3P3+2(MN+MQ+NQ)P2+6MNQP)精度高需要迭代,计算量大2D-ESPRIT高于2D-MUSICO((MN)2T)+O((MN)3)+O(P3)精度高、计算量低收发阵列的结构要具有旋转不变性2D-root高于2D-MUSIC,且略高于2D-ESPRITO((MN)2T)+O((MN)3)+O((4M-2)3)+O((2N-2)3)精度高、计算量较低收发阵列均为均匀线阵波束空间2D-root略低于2D-rootO((MN)2T)+O((MN)3)+O((2(BT-1)BR)3)+O((2(BR-1))3)计算量低观测空间缩小导致精度降低2D-PM高于2D-MUSIC和2D-ESPRITO(MNPT+P3)精度高、计算量低收发阵列均为均匀线阵
1)搜索类角度估计算法：1D-MUSIC和2D-MUSIC算法虽然被广泛地使用，但是其计算量与全角度范围内的搜索步长J密切相关，这也是该算法计算量高居不下的关键原因。另外，为了追求1D-MUSIC和2D-MUSIC算法良好角度分辨率的优势，通常假定空间目标位于某个角度分片区域之内；因此，需要了解波离角和波达角的先验信息。
2)免搜索类和求根类角度估计算法：2D-ESPRIT和2D-root算法作为低复杂度角度估计算法的典型代表，虽然提高了计算效率，但是要求收发阵列均为均匀线阵。这种对阵列结构的强依赖性，严重限制了算法的使用场合。换言之，如果要使估计精度和计算效率达到平衡，那么通常需要以特定的阵列结构作为代价。另一方面，当收发阵列均为大型天线阵列的时候，求根类算法中求根多项式的阶数非常高，其计算量和搜索类算法的计算量十分接近，计算优势也将不复存在。
3)子空间快速估计算法：2D-PM算法虽然通过线性运算来获得子空间的近似值，降低了特征值分解的计算量。但是当收发阵列的天线单元个数较小时，或低信噪比小快拍数的情况下，2D-PM算法的性能有较大幅度的下降。
7 MIMO雷达角度估计算法发展趋势
目前，虽然国内外众多算法的提出逐渐丰富了MIMO雷达角度估计的理论体系，但MIMO雷达的优势和劣势并存，本节以MIMO雷达角度估计算法的工程应用需求为向导，讨论未来发展趋势：
1)提高在实际工程中对数据的实时处理能力和角度估计精度。当收发阵列均为大型天线阵列MIMO雷达时，比如：超视距雷达。首先，其收发阵列所构成的虚拟阵元个数十分接近快拍数，庞大的计算量无法满足雷达系统对数据计算要有实时处理能力的要求；因此，对低复杂度角度估计算法的研究有待进一步深入。其次，超视距雷达具有长波长、宽波束的缺陷，在有限的天线物理孔径范围内，角度估计的精度较差；因此，如果通过MIMO雷达体制中虚拟孔径扩展的能力，可以提高角度估计的精度。
2)提高算法在实际工程中对阵列结构的普适性。现有算法大多基于均匀线阵、均匀圆阵、L阵等，对阵列结构具有强依赖性。然而，实际的雷达系统中，天线阵列通常是非均匀阵。因此，降低算法对阵列结构的依赖性、研究任意收发阵列情况下的角度估计算法是一个重点方向。
3)提高算法在实际复杂的电磁环境下对目标多维参数的准确获取能力。在雷达系统中，对空间目标进行参数估计时，获得的参数越多越能够提高雷达对目标的分辨能力。然而，仅利用电磁波在空-时域获得的角度参数已经远远无法满足现实复杂的电磁环境了。极化作为电磁波自有的性质，可以反映目标的众多特征，比如形状、结构、姿态、材料等；同时，对极化参数进行适当的提取，可以准确地将目标进行分类和识别。因此，关于空间目标极化参数与其特征之间内在联系的研究值得关注。
4)提高动目标跟踪能力。MIMO雷达对空间目标进行探测时，目标大部分处于运动状态，角度实时变化。然而，2D-MUSIC算法、2D-root算法以及2D-ESPRIT算法等均是假设目标为静止状态，且通过离线的方式对接收信号进行处理。此时，这些方法已不再适用于动目标探测。因此，研究高效的MIMO雷达角度实时跟踪算法是一个亟待解决的问题。此外，当目标进行低空或者贴近海平面运动时，会存在严重的多径效应；对于多径效应情况下的MIMO雷达目标角度实时跟踪算法也应该得到重视。
5)提高目标定位的效率。MIMO雷达对空间目标进行定位时，除了需要对角度进行估计，还需要对距离进行计算；显然，这一过程需要额外的距离估计算法。频控阵(Frequency Diverse Array，FDA)雷达概念的提出，可有效解决这一问题。FDA雷达通过在发射天线间引入一个远小于载频的频率增量，形成与距离-角度双重有关的波束方向图，这与MIMO雷达中仅与角度有关的方向图完全不同，FDA雷达为角度-距离联合估计奠定了基础。所以，在MIMO雷达的体制下，开展FDA-MIMO雷达角度-距离联合估计也是一个重要的研究方向。
8 结束语
MIMO雷达通过分集技术提高了测角精度，作为新体制雷达的代表，给雷达领域带来了一次颠覆性的变化。空间目标角度估计在军民融合领域有着极大应用价值，其发展虽日益成熟但依旧停留在理论研究的层面。目前，为了推动MIMO 雷达逐步走向装备研发阶段，在将测角精度维持在合理范围内的同时，应针对减少测角系统的研发成本、提高测角的计算效率开展深入研究并形成可行方案，加快MIMO雷达角度估计理论工程化推进。
[1]吴剑旗.先进米波雷达[M].北京:国防工业出版社, 2015.
[2]BLISS D W, FORSYTHE K W.Multiple-Input Multiple-Output(MIMO)Radar and Imaging: Degrees of Freedom and Resolution[C]∥37th Asilomar Conference on Signals, Systems and Computers, Pacific Grove, USA:IEEE,2003:54-59.
[3]CHEN Peng, CAO Zhenxin, CHEN Zhimin, et al.Off-Grid DOA Estimation Using Sparse Bayesian Learning in MIMO Radar with Unknown Mutual Coupling[J].IEEE Trans on Signal Processing,2019,67(1):208-220.
[4]吴剑旗, 阮信畅.稀布阵综合脉冲孔径雷达主要性能分析[J].现代电子,1994(3):1-6.
[5]吴剑旗, 贺瑞龙, 江凯, 等.稀布阵综合脉冲孔径雷达的研究与实验[J].现代电子,1998(3):1-5.
[6]MISHRA K V, ELDAR Y C, SHOSHAN E, et al.A Cognitive Sub-Nyquist MIMO Radar Prototype[J].IEEE Trans on Aerospace and Electronic Systems,2020,56(2):937-955.
[7]WU Linlong, BABU P, PALOMAR D P.Transmit Waveform/Receive Filter Design for MIMO Radar with Multiple Waveform Constraints[J].IEEE Trans on Signal Processing,2018,66(6):1526-1540.
[8]AMIRI R, BEHNIA F, SADR M.Exact Solution for Elliptic Localization in Distributed MIMO Radar Systems[J].IEEE Trans on Vehicular Technology,2018,67(2):1075-1086.
[9]孙龙, 江凯, 邬伯才, 等.一种新的MIMO SAR/GMTI时空等效重构方法[J].雷达科学与技术,2011,9(2):120-124.
[10]WEN Fangqing.Computationally Efficient DOA Estimation Algorithm for MIMO Radar with Imperfect Waveforms[J].IEEE Communications Letters,2019,23(6):1037-1040.
[11]LI Jiangfeng, HE Lang, HE Yi, et al.Joint Direction of Arrival Estimation and Array Calibration for Coprime MIMO Radar[J].Digital Signal Processing,2019,94:67-74.
[12]ZHAO Anqi, JIANG Hong, LI Song.Improved Capon Estimators for DOD and DOA Estimation in Large Array MIMO Radar: A Random Matrix Method[C]∥2018 IEEE Radar Conference, Oklahoma City, USA: IEEE,2018:1140-1145.
[13]WEN Fangqing, SHI Junpeng, ZHANG Zijing.Joint 2D-DOD, 2D-DOA and Polarization Angles Estimation for Bistatic EMVS-MIMO Radar via PARAFAC Analysis[J].IEEE Trans on Vehicular Technology,2020,69(2):1626-1638.
[14]XU Baoqing, ZHAO Yongbo.Transmit Beamspace-Based DOD and DOA Estimation Method for Bistatic MIMO Radar[J].Signal Processing,2019,157:88-96.
[15]CHEN Jinli, GU Hong, SU Weimin.A New Method for Joint DOD and DOA Estimation in Bistatic MIMO Radar[J].Signal Processing,2010,90:714-718.
[16]马红星, 陈思佳.水面杂波背景的统计MIMO 雷达检测方法研究[J].雷达科学与技术,2015,13(5):479-484.
MA Hongxing, CHEN Sijia.Statistical MIMO Radar Detection Approaches Against Water Clutter[J].Radar Science and Technology,2015,13(5):479-484.(in Chinese)
[17]XIE Rong, LIU Zheng, ZHANG Zijing.DOA Estimation for Monostatic MIMO Radar Using Polynomial Rooting[J].Signal Processing,2010,90:3284-3288.
[18]LEE J H, PARK J Y, CHUN J W.Weighted Two-Dimensional Root MUSIC for Joint Angle-Doppler Estimation with MIMO Radar[J].IEEE Trans on Aerospace and Electronic Systems,2018,55(11):1474-1482.
[19]陆鹏程, 吴剑旗.米波雷达系统设计的几个问题[J].雷达科学与技术,2017,15(3):236-240.
LU Pengcheng, WU Jianqi.Some Issues on VHF MIMO Radar System Design[J].Radar Science and Technology,2017,15(3):236-240.(in Chinese)
[20]ZHENG Guimei.Beamspace Root-MUSIC Algorithm for Joint DOD DOA Estimation in Bistatic MIMO Radar[J].Wireless Personal Communications,2014,75(4):1879-1889.
