0 引言
雷达导引头[1-2]是远程精确制导武器常采用的中末段制导方式,具有全天时、全天候工作能力,作用距离远,抗干扰能力强,相对于光学、红外等制导方式,具有明显的优越性。该制导方式通过装载在导弹上的合成孔径雷达(Synthetic Aperture Radar, SAR)获取目标或目标附近典型地物地貌特征信息形成实时图,并根据实时图的目标识别结果或景象匹配信息返回精确的弹目相对位置关系从而参与制导。SAR成像过程中,雷达平台与成像区域的相对高度是影响斜地几何校正精度的重要参数,高度误差会引起明显的几何形变并影响目标识别或景象匹配过程从而降低制导精度[3]。因此雷达导引头相对目标精确高度的获取对于导弹中末段精确制导有着重要意义。
雷达导引头的高度信息一般通过全球定位系统(Globe Positioning System, GPS)或惯性导航系统(Inertial Navigation System, INS)获取,目标高度信息通过数字高程模型(Digital Elevation Model, DEM)提供保障。然而,GPS系统在军事应用中存在易受干扰、动态环境中可靠性差等不足,INS系统存在误差随时间迅速积累导致导航精度随时间发散的问题。因此需要通过雷达测高获得准确的相对高度。目前广泛使用的雷达高度计为延时/多普勒高度计(Delay/Doppler radar Altimeter, DDA)[4-6],在星载雷达地形测绘和海面监测中具有很高的测高精度。然而,DDA获取数据时要求天线指向平台正下方,而在雷达导引头系统中,天线通常以一定安装倾角安装于弹体正前方,且由于波束扫描角的限制,平飞条件下导引头天线不能指向平台正下方。雷达测高还可以通过干涉技术[7]实现,该技术采用两个或多个天线同时对同一目标区域内同一个地面单元进行观测,然后对多个天线接收到的地面单元的回波信号进行一系列相关的处理,通过地面单元的干涉角度以及斜距信息估计出该单元的高度信息。干涉技术需要至少两个以上天线以及一定的基线,在弹载雷达导引头系统中的应用也受到一定限制。
基于上述现状,本文围绕适用于弹载前视几何构型的雷达非干涉测高方法展开研究。DDA测高算法将合成孔径技术引入到高度计,主要应用于匀速运动星载平台的星下点测高过程。由于测高几何差异及平台运动差异,将DDA算法应用到弹载平台前视测高,需进行一定的修正且信噪比有所下降[8]。本文提出一种基于回波斜距多普勒分析的弹载雷达前视测高方法,利用弹目相对高度、速度与斜距/多普勒之间的几何关系实现高度测量,称为斜距-多普勒高度估计法(Range-Doppler based Altitude Estimation method, RDAE)。RDAE中,通过距离匹配滤波和方位去斜处理实现回波二维聚焦,采用方位谱相关法提高非均匀谱分布下的多普勒中心频率估计精度,并通过距离分段与平均提高高度测量精度与稳定性。
1 测高几何模型与原理
RDAE前视测高几何关系如图1所示。导弹沿AC方向飞行,天线波束中心指向AB方向,速度矢量与波束指向矢量在同一垂直面内,即在xoz平面的投影均在x轴上,两者夹角为α。垂直速度分量vv与合速度夹角为γ,波束指向与y轴负方向夹角为β。
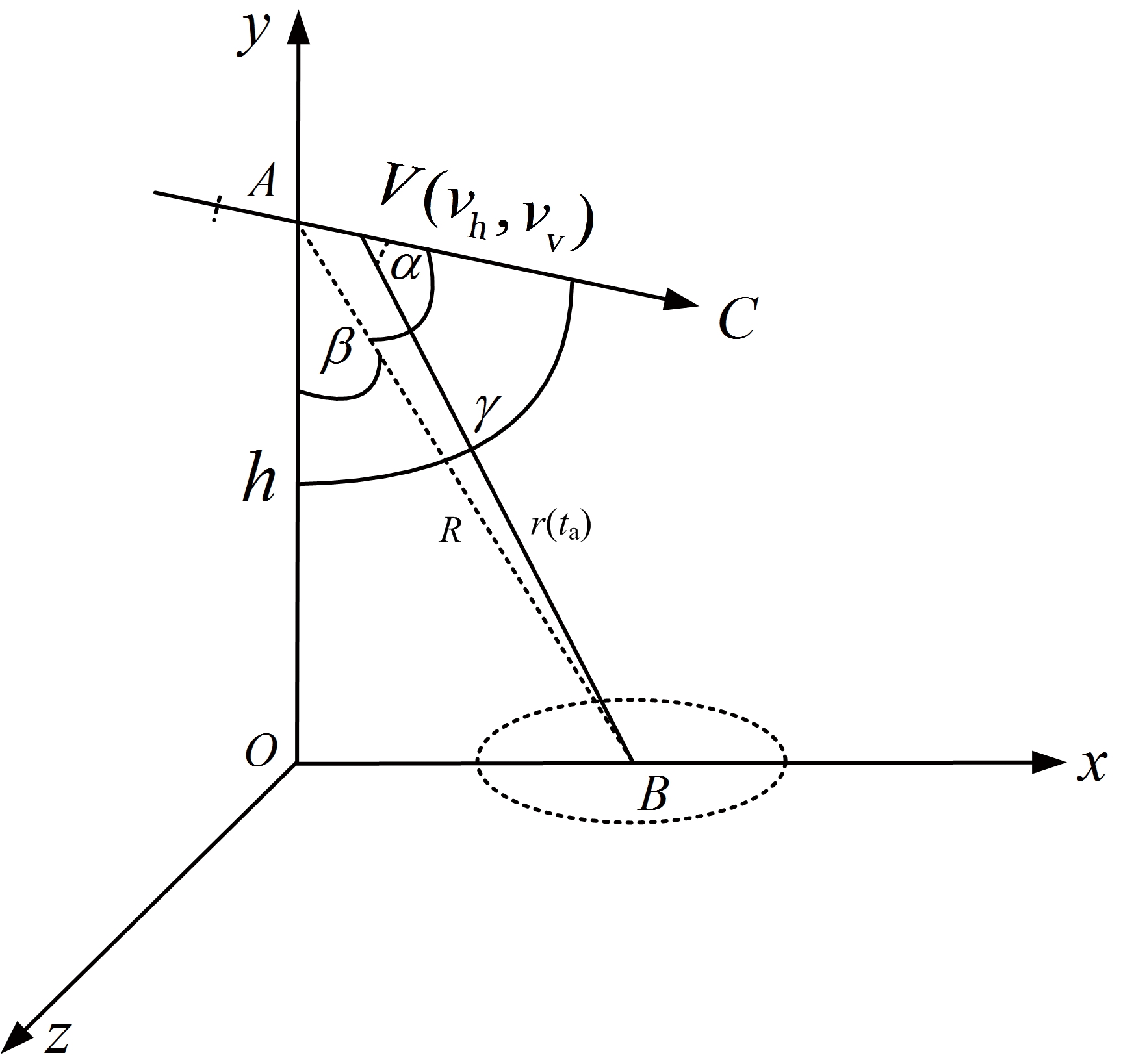
图1 RDAE测高几何模型示意图
雷达接收若干条回波,在距离对齐后对某一距离单元(斜距为R)作方位傅里叶变换,并进一步估计该距离单元对应的多普勒中心频率,由多普勒中心频率和多普勒公式可求得速度方向与该距离单元视线夹角。多普勒公式[9]为
(1)
式中,f为多普勒中心频率,λ为波长,α为速度矢量与该距离单元视线夹角,v为合速度,可由水平速度分量vh和垂直速度分量vv合成:
(2)
由于AB,AO和AC在同一平面内,故有
(3)
式中,β为该距离单元视线与y轴负方向夹角,γ为垂直速度分量vv与合速度夹角:
γ=arccos(-vv/v)
(4)
根据几何关系,弹目相对高度h可估计如下:
(5)
式中,λ为已知参数,vv和v可以从惯导系统得到,斜距R和多普勒f需要从回波中进行估计。
前视几何构型下,测高回波经聚焦处理后典型斜距多普勒分布如图2所示,相应的雷达参数如表1所示。在给定高度下,回波斜距多普勒呈窄条状分布,斜距随多普勒变化灵敏,反之亦然,因此通过回波斜距多普勒分析估计斜距R和多普勒f,并根据公式(5)计算高度值,有很强的理论可实现性。
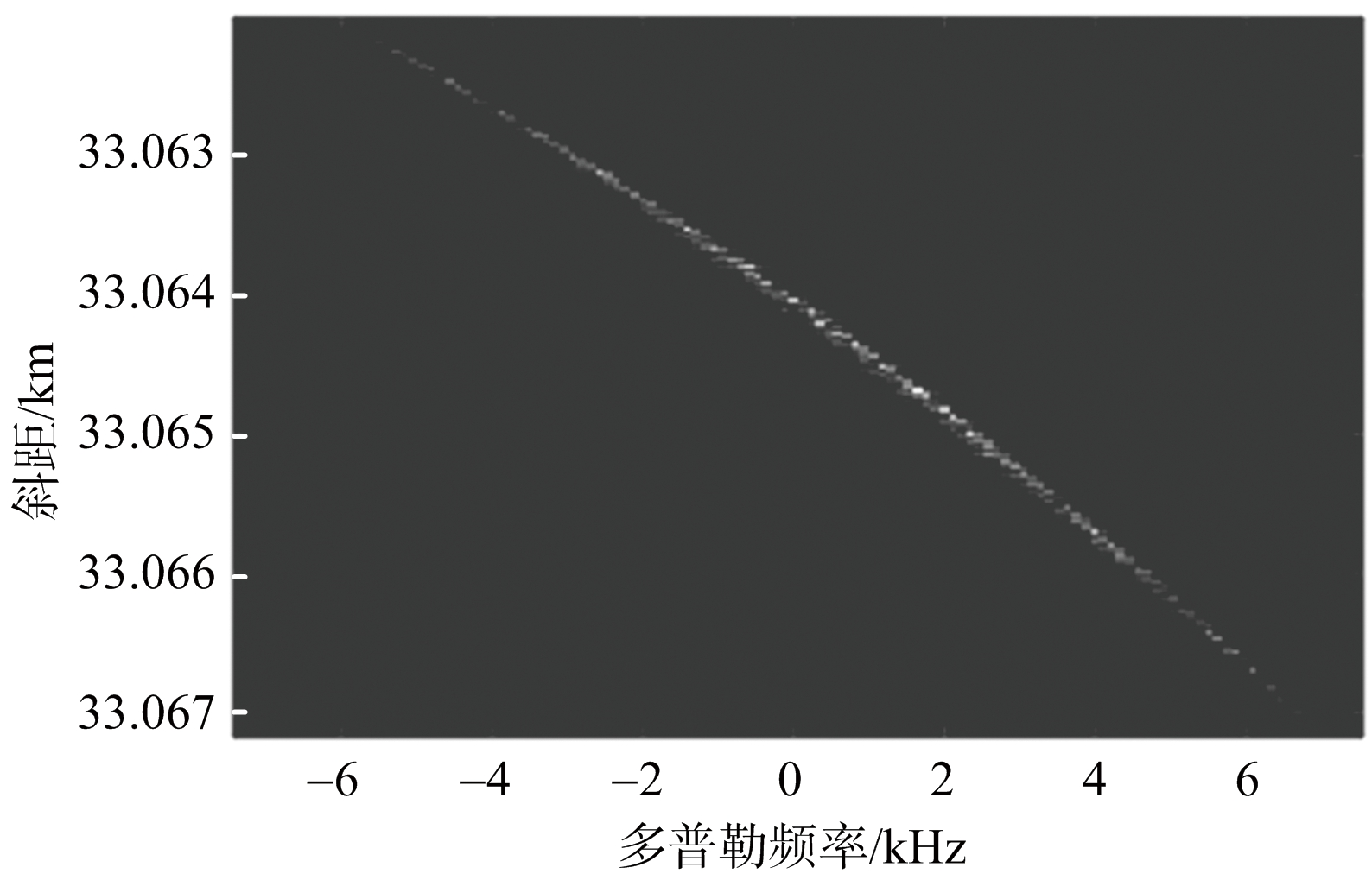
图2 前视测高几何下典型斜距多普勒分布
表1 仿真雷达参数
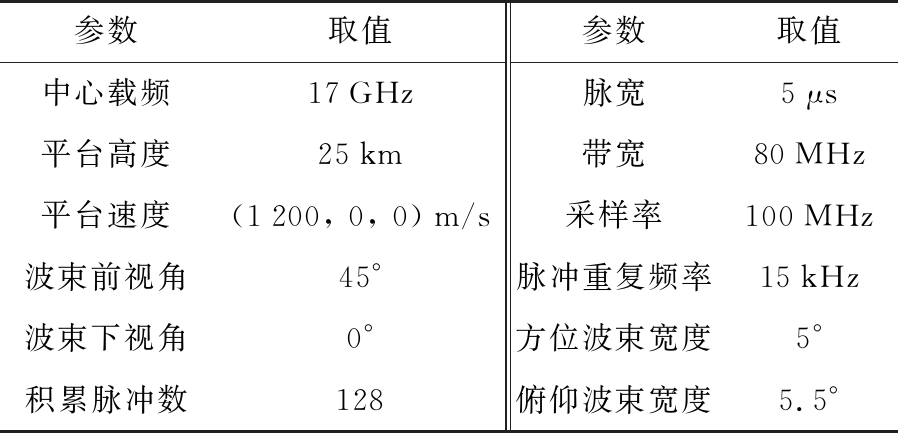
参数取值参数取值中心载频17GHz脉宽5μs平台高度25km带宽80MHz平台速度(1200, 0, 0)m/s采样率100MHz波束前视角45°脉冲重复频率15kHz波束下视角0°方位波束宽度5°积累脉冲数128俯仰波束宽度5.5°
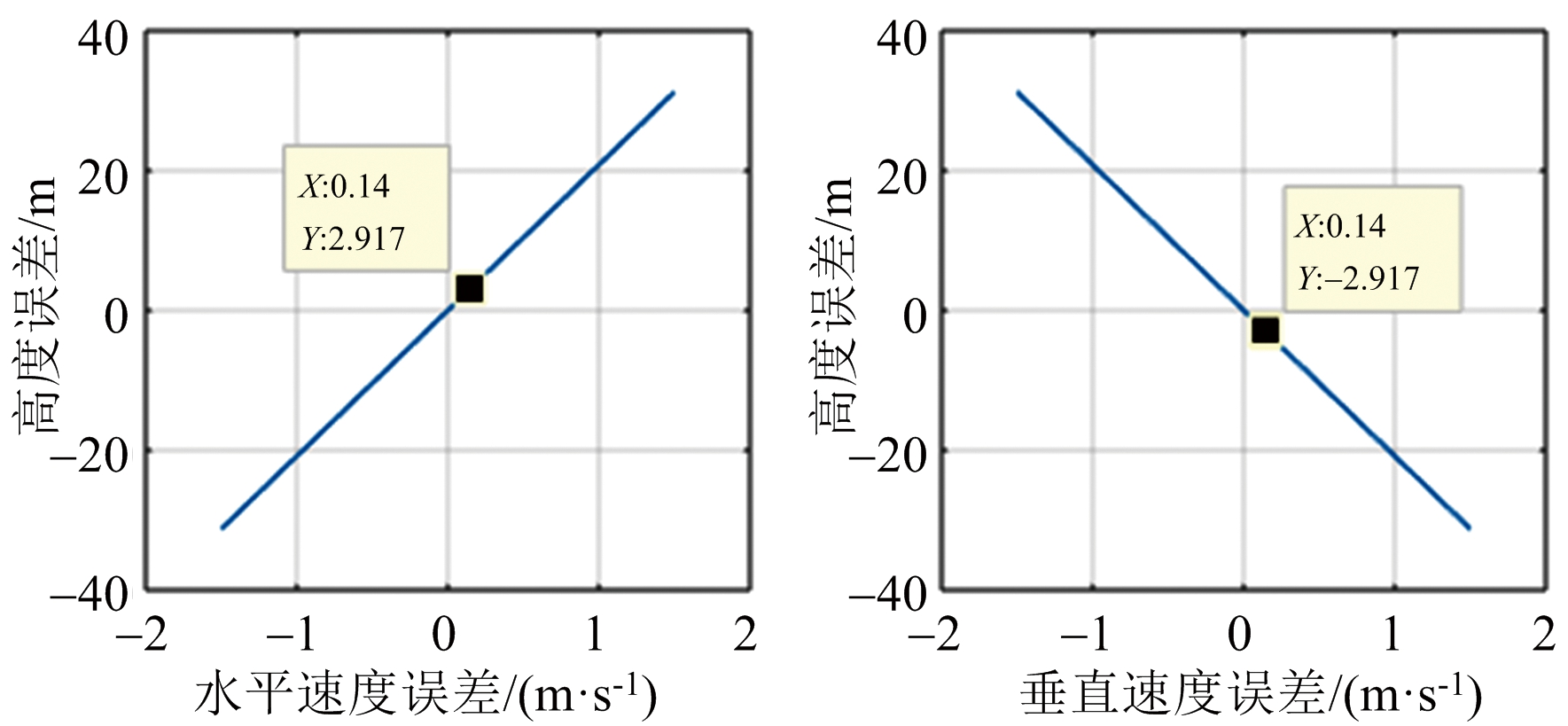
一般对于平坦地形,测高误差指标要求优于 3 m,以下从理论上对测高误差因素进行分析。将公式(5)分别对斜距R、多普勒频率f、水平速度vh和垂直速度vv进行求导,并在表1所示参数下进行理论误差分析,结果如图3所示。
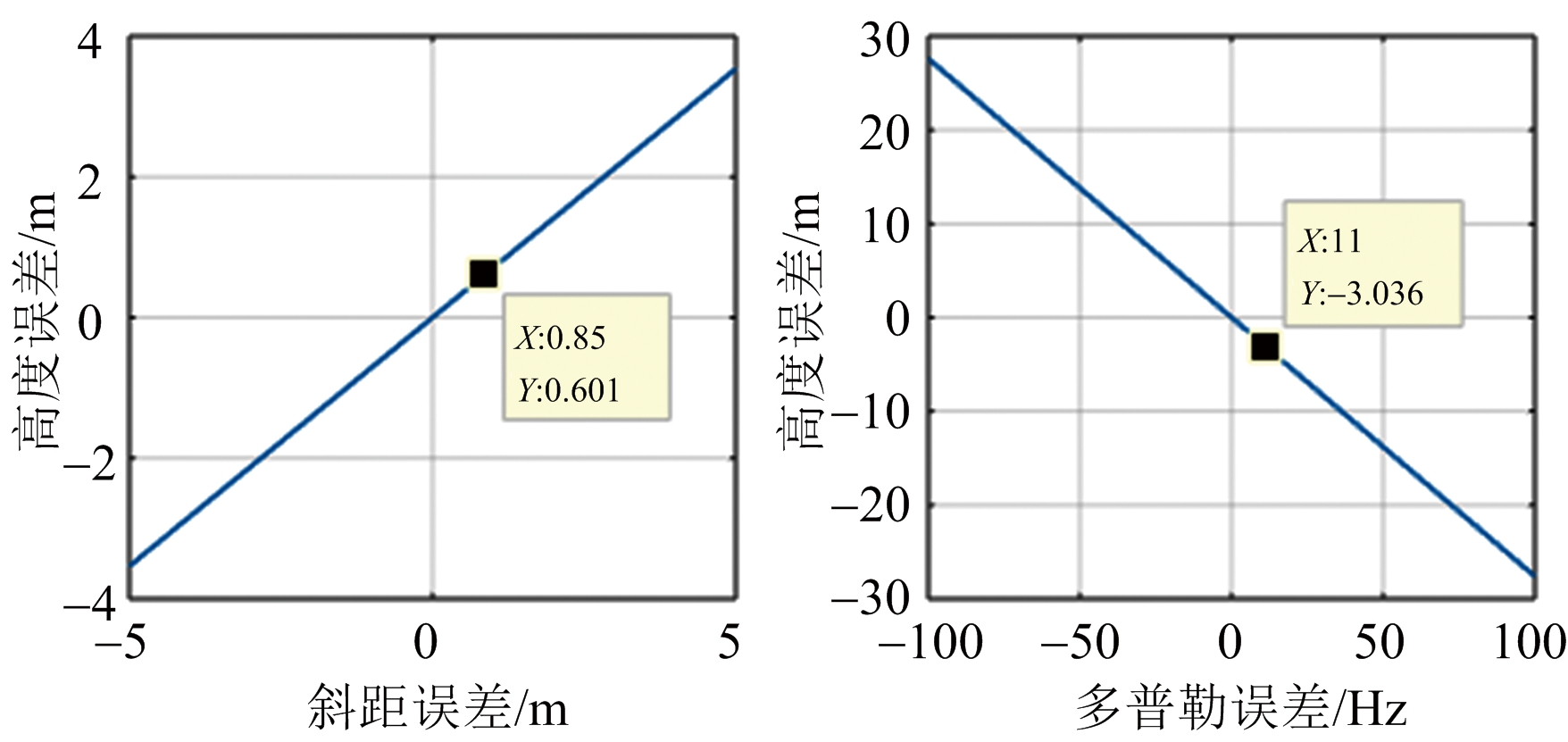
(a) 斜距误差分析 (b) 多普勒误差分析
(c) 水平速度误差分析 (d) 垂直速度误差分析
图3 理论误差因素分析
RDAE中,斜距通过波门和采样点进行推算,因此斜距误差主要由系统延时和信号采样量化引起,系统延时通过时延校正精度可达0.1 m,信号采样量化主要由采样率决定,100 MHz采样率对应量化误差约为0.75 m,结合图3(a)结果可知由斜距误差引起的测高精度优于1 m。多普勒误差与多普勒中心估计方法密切相关,由图3(b)可知,如要满足优于3 m的测高误差,多普勒估计精度要优于10 Hz。同时,不考虑其他因素影响,为满足优于3 m的测高误差,惯导速度误差需小于0.14 m/s,如图3(c)和图3(d)所示。
RDAE测高要求波束指向矢量与速度矢量在同一垂直面内,实际工作过程中,由于弹体姿态角误差、安装角误差以及波控误差等影响,波束指向角存在一定的偏差,该偏差也是影响测高精度的误差因素。理论上,波束俯仰角偏差影响沿飞行方向波束地面覆盖范围内回波能量强度,对测高精度影响相对较小;波束方位角偏差会使得速度矢量与波束指向矢量不在同一垂直面内,表现为方位多普勒谱展宽并导致多普勒中心估计误差增大,对测高精度影响相对较大。波束指向角偏差对测高精度影响的定量分析详见本文仿真结果。
2 测高回波模型与实现方法
2.1 测高回波模型
RADE采用线性调频信号(Linear Frequency Modulation, LFM)提高测高精度同时保证作用距离。发射信号模型为
St(tr)=![]()
(6)
式中,tr为快时间,Tp为发射脉冲宽度,fc为载频,Kr为LFM调频率,Am为幅度信息。
波束照射区域某一点目标的回波信号经解调后的复信号模型为
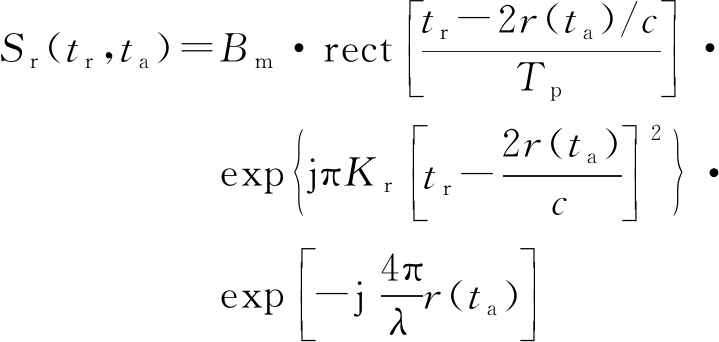
(7)
式中,ta为慢时间,r(ta)为ta时刻平台到该点目标的斜距,c为电磁波速度,Bm为幅度信息。根据图1几何模型,r(ta)及其二阶泰勒近似可表示如下:

2.2 测高实现方法
根据以上测高回波模型,测高信号处理流程如图4所示,主要包括距离匹配滤波、方位去斜处理、距离分段、子段多普勒中心估计、子段高度解算与高度平滑。
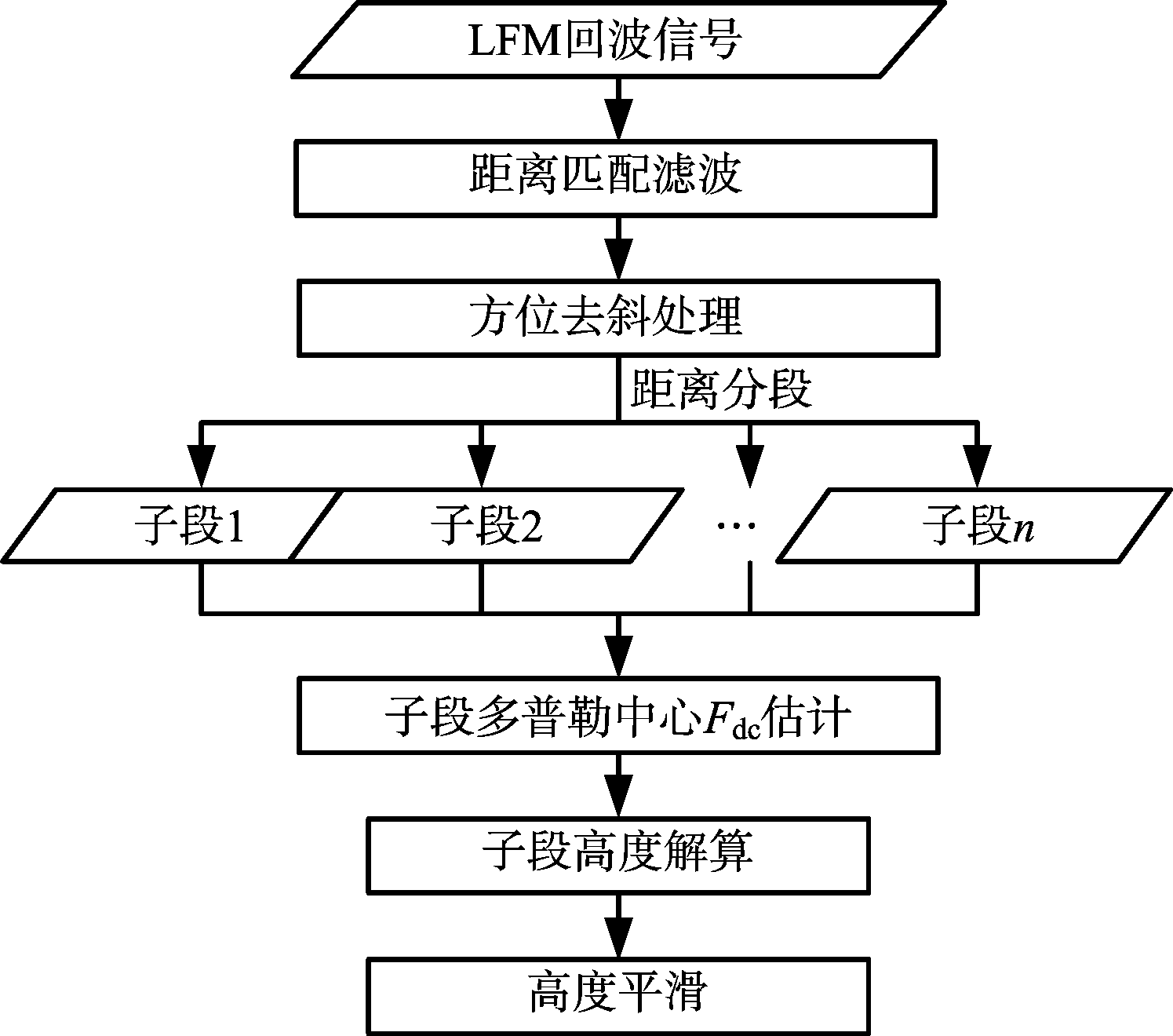
图4 RDAE测高流程
1) 距离匹配滤波
距离匹配滤波过程在距离频域、方位时域实现,包括距离脉压和距离走动校正。距离匹配函数在距离频域可表示如下:
(9)
式中,ΔR(ta)=vtacosα0,α0为速度矢量与波束中心视线夹角。经计算,波束边缘距离空变约为1/4采样单元,可忽略。
2) 方位去斜处理
方位去斜处理过程在距离时域、方位时域实现,包括方位脉压和逐距离单元的多普勒中心频率补偿,其中后者将各距离单元的多普勒中心线性搬移到零频附近,以利于后续方位谱能量叠加从而提高多普勒估计精度。方位去斜函数在方位时域可表示如下:
![]()
(10)
式中,Ka(r)=-2v2sin2α/(λr)为多普勒调频率,r为距离单元,fdc(r)=2vcosα/λ为该距离单元对应的粗多普勒中心频率,Ka(r)和fdc(r)均从初始惯导参数与几何关系计算得到。在去斜处理后信号变换到方位频域完成方位聚焦,此时回波所在信号域为距离时域、方位频域,即斜距多普勒域。
3) 多普勒中心估计
高度估计在斜距多普勒域进行,为提高测高精度与测高稳定性,在距离向将回波信号分为若干子段,在每一子段分别对斜距和多普勒中心进行提取。其中,子段斜距通过波门和采样中心进行推算,相应的多普勒中心通过回波估计获得。为提高多普勒估计精度,首先沿距离向对子段内方位谱进行能量叠加,然后对叠加后方位谱进行插值处理,最后采用方位谱相关法实现多普勒中心估计。
在图1所示测高几何模型下,航线左右两侧对称波束覆盖区域具有相同的多普勒值,等多普勒能量叠加会导致多普勒中心不在方位谱峰值处,且方位谱具有非均匀分布。传统基于方位谱峰值以及基于方位谱重心的多普勒中心估计法都会存在较大误差[9]。因此,本文提出一种方位谱相关法实现非均匀谱分布下的高精度多普勒中心频率估计,信号互相关在频域实现,公式表示如下:
(11)
式中,R(f)为互相关函数,Sref为子段中心参考方位谱的傅里叶变换,S为采集回波子段方位谱的傅里叶变换,F-1{·}表示逆傅里叶变换,*表示共轭,下标i表示不同距离子段号。子段中心参考方位谱通过雷达参数与测高几何构型进行理论建模仿真得到。互相关函数峰值频率fi加上各距离子段的粗多普勒中心频率fdc(rci)即为相应距离子段(子段中心斜距为rci)的高精度多普勒中心频率fi_est:
fi_est=fi+fdc(rci)
fi∈[Ri(fi)=max(Ri(f))]
f∈[-PRF/2, PRF/2]
(12)
4) 高度解算与平滑
在得到各距离子段斜距与相应多普勒中心后,根据公式(5)解算各子段高度测量值,并根据子段方位谱能量值对测高结果进行筛选,将近天线波束主瓣宽度范围内的测高值进行平均后输出最终测高结果,公式如下:
Hest=Mean(hj), j∈[Ej>0.7max(Ei)]
(13)
式中,Hest为最终测高输出结果,h为距离子段测高值,E为距离子段方位谱能量,下标i表示不同距离子段号,下标j表示近波束主瓣范围内距离子段号。
3 仿真及实测数据处理结果
3.1 仿真分析结果
本文首先通过仿真对RDAE的测高性能进行分析,仿真基于Ku频段,地形为均匀平坦地形,使用的雷达参数如表1所示。采用基于距离时域脉冲相干法[10]进行雷达测高回波仿真,原始回波如图5所示。经匹配滤波与去斜处理后,回波在距离向和方位向均实现了聚焦,同时所有距离单元的多普勒中心均搬移到零频附近,此时斜距多普勒分布如图6所示,方位谱分布具有非均匀性。
图5 原始IQ波形
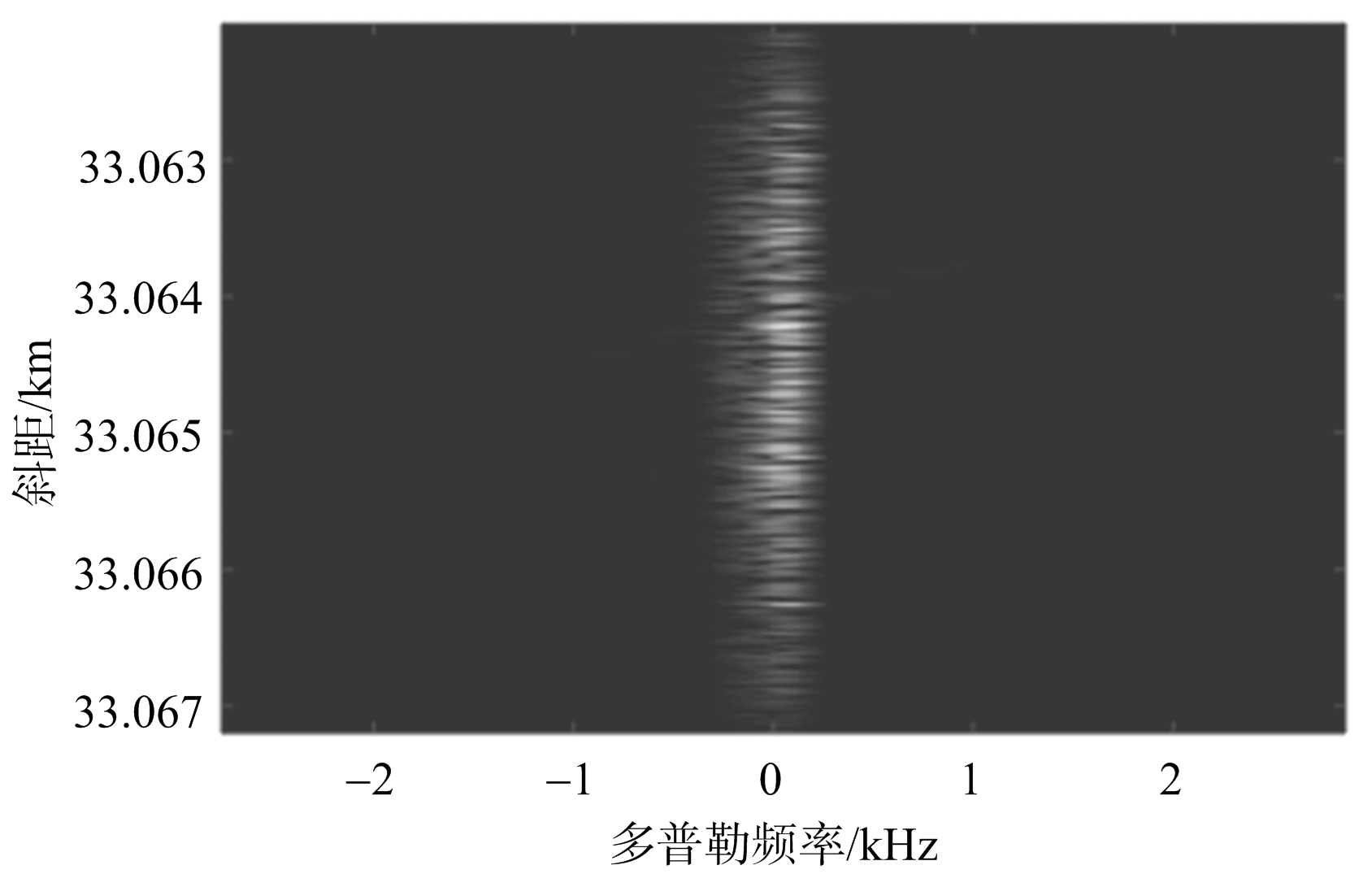
图6 匹配滤波与去斜处理后斜距多普勒分布
在每一距离子段内,采用方位谱相关法实现多普勒中心估计,典型的方位谱相关法结果如图7所示。图中,蓝色实线为回波方位谱,蓝色点划线为参考方位谱,红色实线为两者的互相关,回波方位谱与参考方位谱有相似的形状但峰值点位置有一定偏移。当估计所用的初始高度与实际高度相同,峰值点位置偏移较小,如图7(a)所示,这一偏移主要由地速(速度在地面投影)左右两侧波束照射区域内等多普勒能量叠加导致多普勒中心频率偏离方位谱峰值位置引起。当估计所用的初始高度与实际高度有差异,峰值点位置偏移较大,如图7(b)所示,该偏移除了方位谱分布因素外还与初始高度误差有关。通过对互相关函数峰值位置的提取可以同时兼顾以上两个因素引起的多普勒中心偏移,从而实现高精度多普勒中心估计。图7对应回波获取的实际高度均为25 km,RDAE方位谱估计过程采用初始高度与实际高度误差分别为0 m(图7(a))和100 m(图7(b))情况对应的测高误差分别为-0.625 m和-0.748 m,表明初始高度误差对RDAE测高结果的影响基本可以忽略。
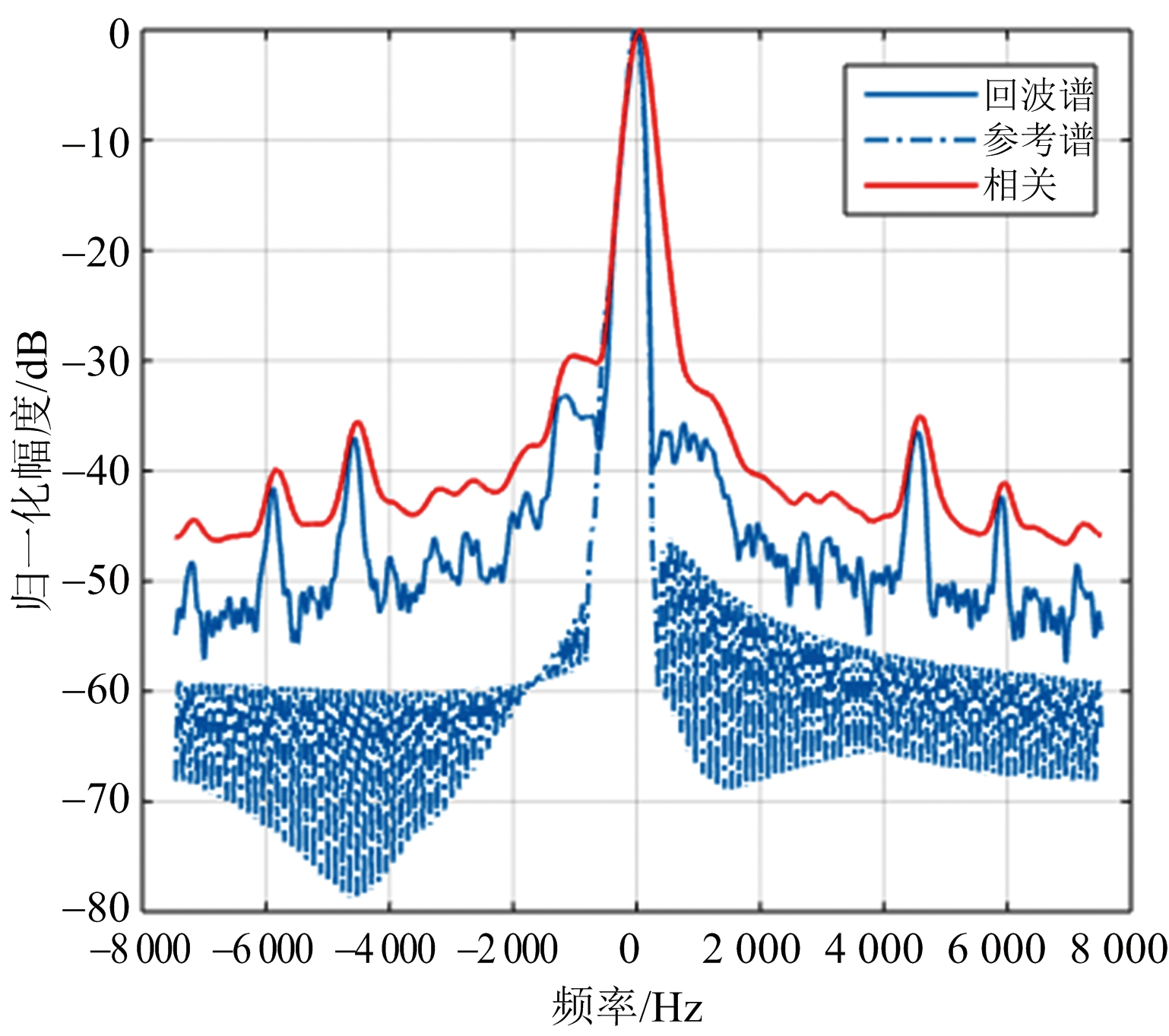
(a) 初始高度25 km
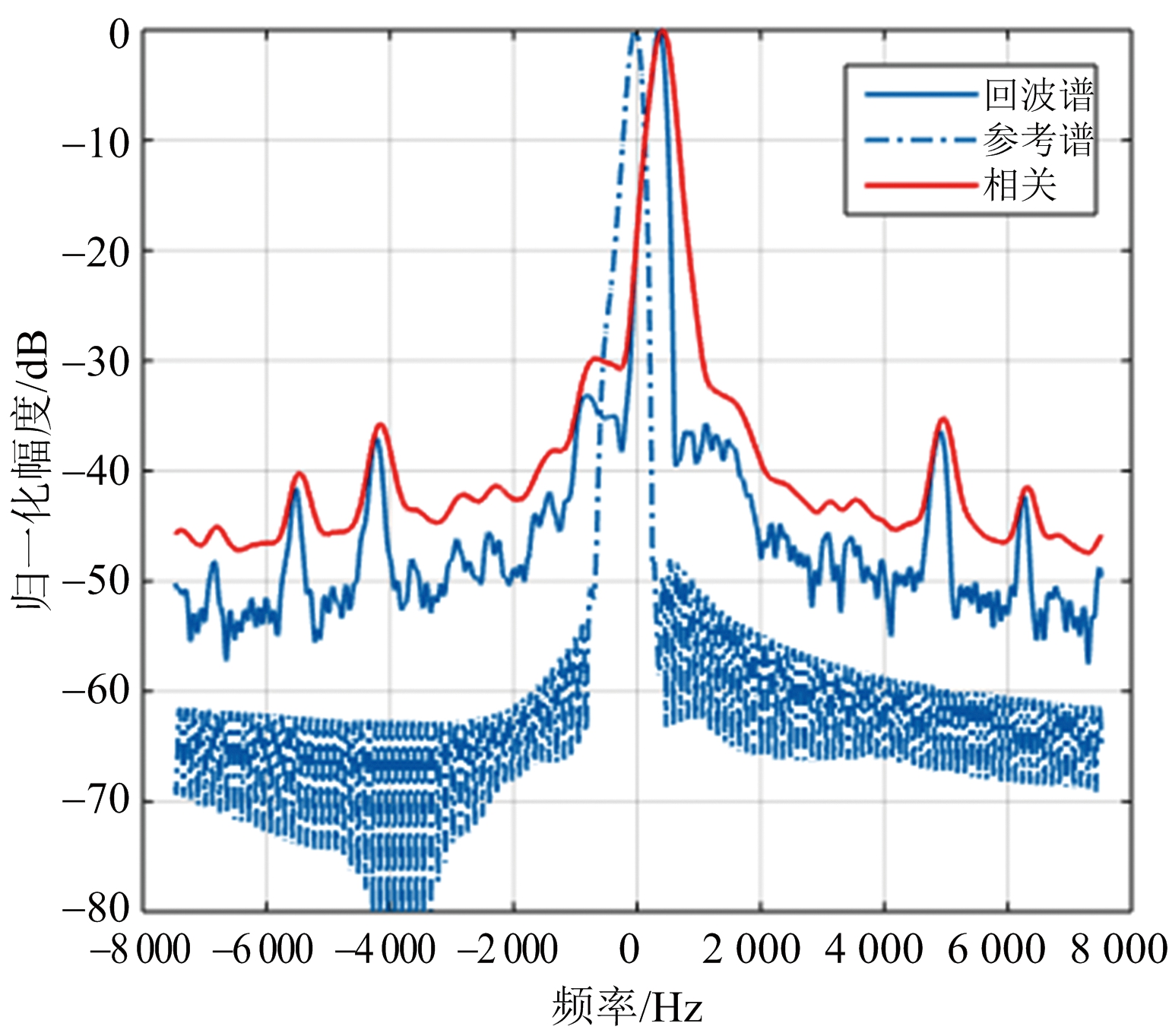
(b) 初始高度25.1 km
图7 典型方位谱相关结果
本文进行了连续100次的测高仿真,测高结果如图8所示。为证实本文所用的基于方位谱相关的多普勒中心估计方法相比于传统方位谱峰值估计法的优越性,在均匀场景分布前提下将采用方位谱峰值估计[9]的测高结果作为对比组。从结果可知,RDAE法测高误差均值-1.08 m,均方根误差1.29 m。对比组测高误差均值10.42 m,均方根误差10.44 m。传统方位谱峰值估计所得多普勒中心频率存在一定误差(约40 Hz),导致对比组的测高精度远低于本文提出的基于方位谱相关方法的RDAE的测高结果。
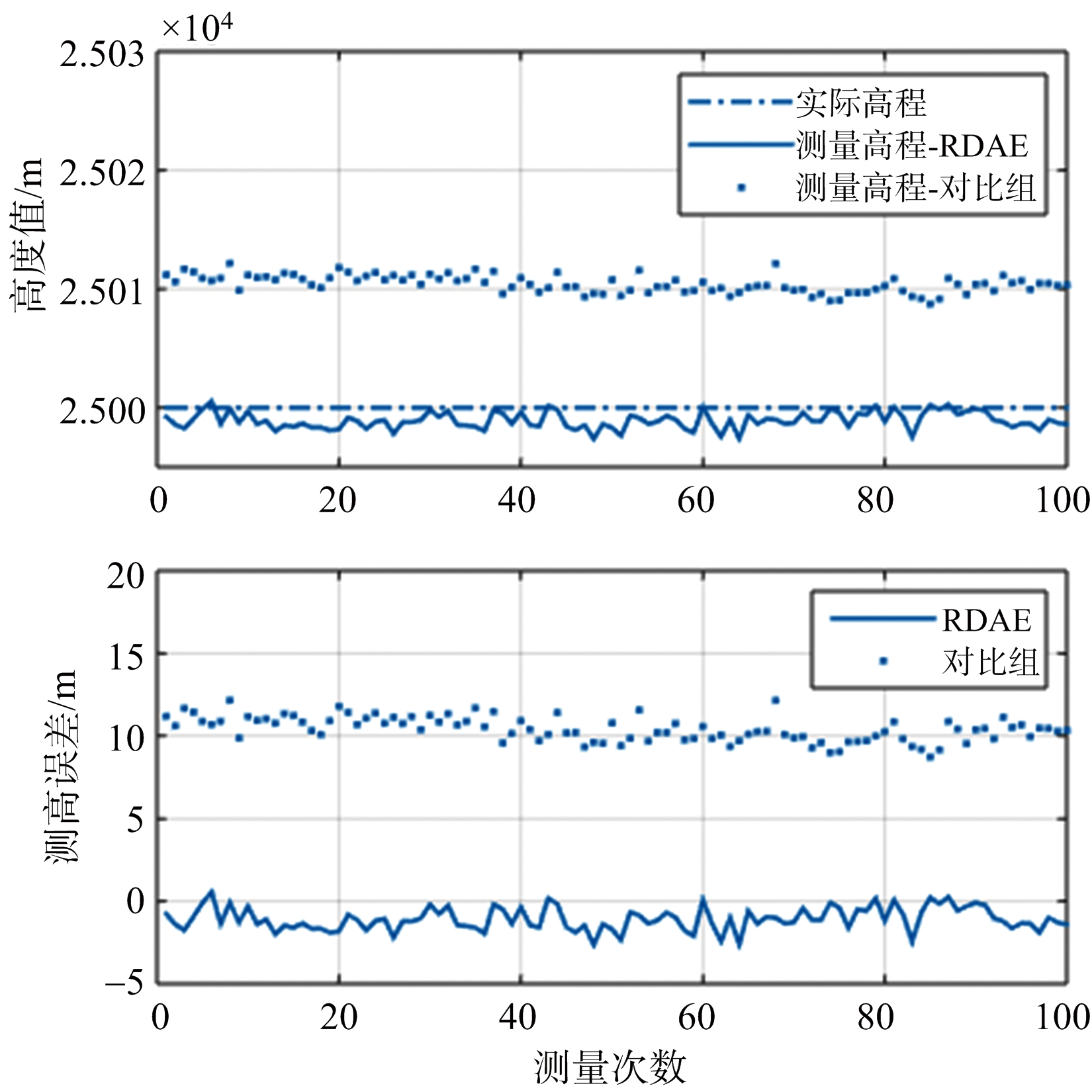
图8 仿真测高结果
在RDAE测高性能分析基础上,本文进一步针对波束指向角偏差对RDAE测高精度的影响进行仿真与定量分析。设置波束俯仰角偏差和方位角偏差分别从-1.5°以0.05°间隔变化到1.5°,采用表1参数进行波束指向角偏差下的测高误差仿真分析,结果如图9所示。
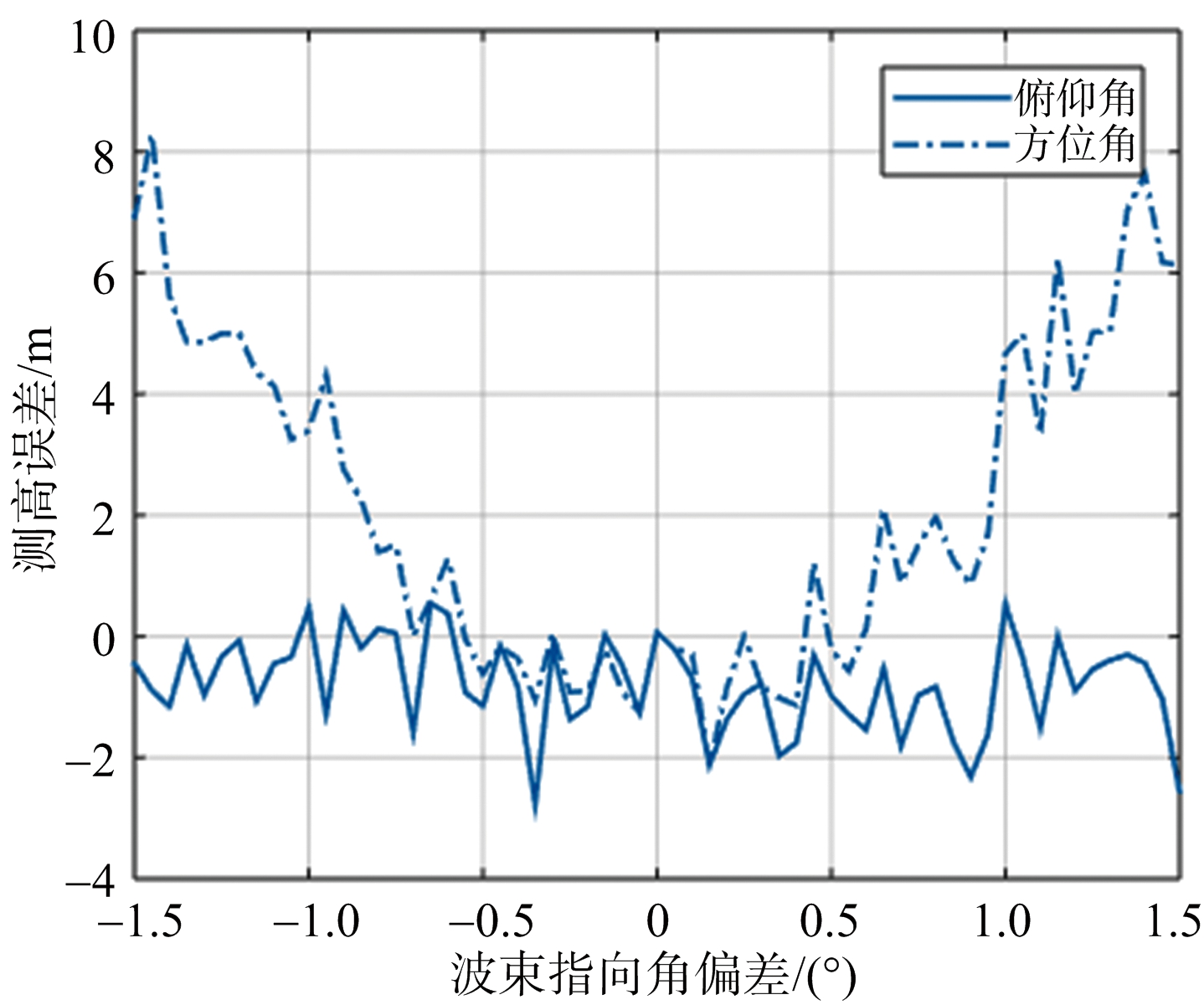
图9 测高误差随波束指向角偏差变化曲线
从结果可知,波束俯仰角偏差对测高精度的影响很小,可以忽略;波束方位角偏差对测高精度的影响相对较大,1.5°方位角偏差引起的测高误差约8 m,0.5°以内的方位角偏差对测高结果的影响也可忽略不计。实际飞行过程中,弹体姿态角偏差小于0.1°,同时考虑安装角误差以及波控误差,波束指向角偏差一般不超过0.2°,因此实际工作中波束指向偏差对RDAE测高的影响基本可以忽略。
3.2 实测数据处理结果
在仿真分析的基础上,本文将RDAE方法用于实测数据处理,某机载挂飞测高结果如图10所示。
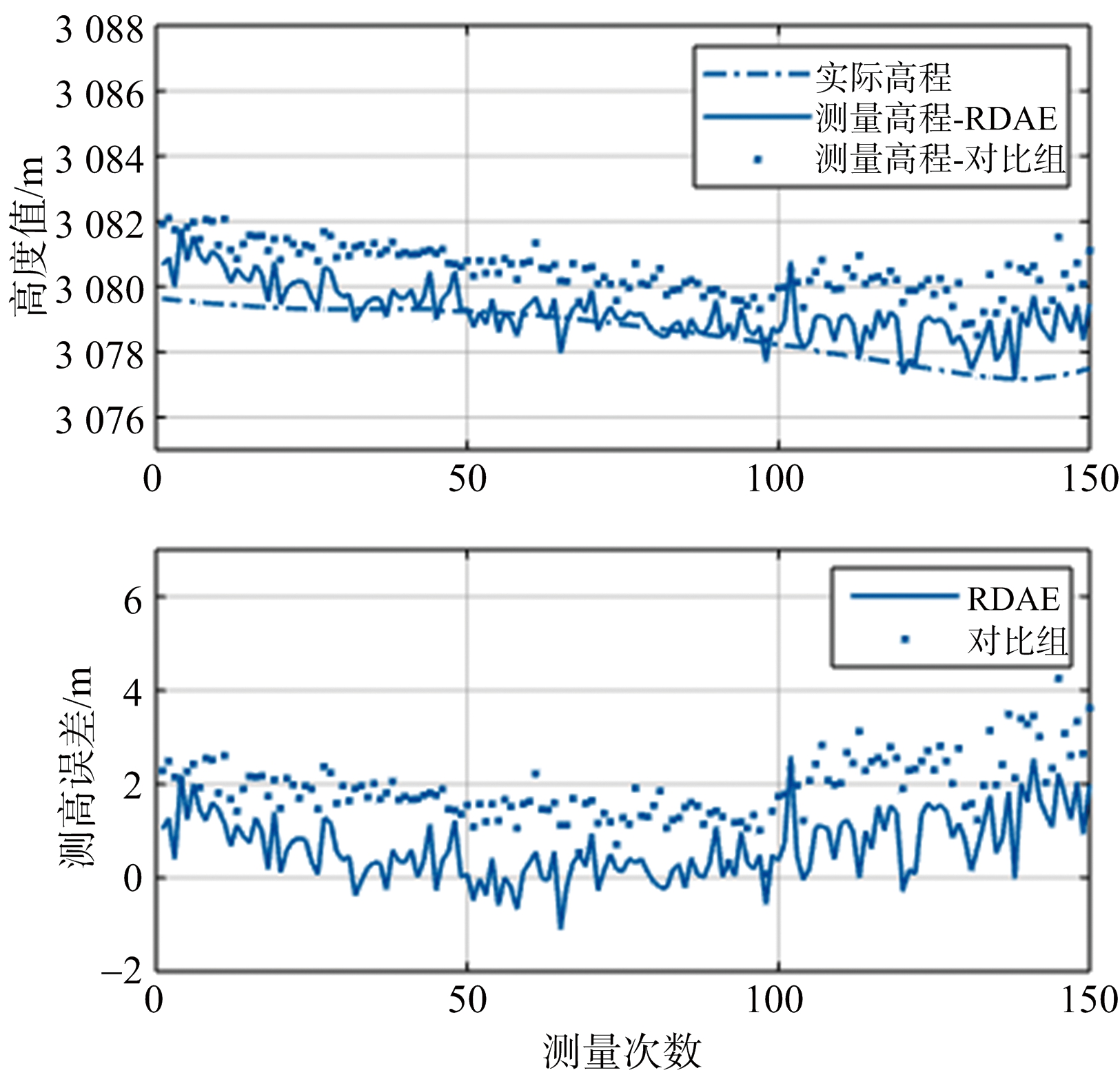
图10 挂飞测高结果
RDAE测高误差均值0.65 m,均方根误差0.95 m;对比组测高误差均值1.91 m,均方根误差2.02 m。挂飞结果进一步证实了RDAE测高方法的有效性。由于机载挂飞高度约3 km,速度约70 m/s,方位谱非均匀引起的谱能量偏移远小于弹载平台,因此对照组测高误差较小,但是本文RDAE方法仍有更高的测高精度。
4 结束语
本文提出一种基于斜距多普勒分析的适用于弹载前下视几何构型的RDAE测高方法。首先根据前视测高几何构型推导了高度计算公式,然后介绍了RDAE具体实现方法,最后通过仿真和实测数据处理对该方法的测高性能进行了评估。仿真和实测结果均表明RDAE法用于雷达导引头前下视测高有很好的测高精度及稳定性,采用本文提出的方位谱相关法估计多普勒中心用于高度解算比传统方位谱峰值法估计多普勒中心用于高度解算有更好的测高精度。
[1] 邵慧, 刘建业, 熊智. 惯性/SAR图像组合导航技术的发展[J]. 航空科学技术,2013(5):71-75.
[2] 秦玉亮, 李宏, 王宏强,等. 基于SAR导引头的弹体定位技术[J]. 系统工程与电子技术,2009,31(1):121-124.
[3] 俞根苗, 邓海涛, 吴顺君. 弹载SAR图像几何失真校正误差分析[J]. 电子与信息学报, 2007,29(2):383-386.
[4] 谌华, 郭伟, 杨双宝, 等. 一种合成孔径雷达高度计定标方法[J]. 电子与信息学报,2017,39(9):2232-2237.
[5] EGIDO A, SMITH W H F. Fully Focused SAR Altimetry: Theory and Applications[J]. IEEE Trans on Geoscience and Remote Sensing,2017,55(1):392-405.
[6] 杨双宝, 翟振和, 许可,等. 合成孔径雷达高度计数据处理方法[J]. 遥感技术与应用,2017(6):1083-1092.
[7] 汪洋, 江凯, 湛金童, 等. 干涉SAR系统测高精度仿真分析[J]. 雷达科学与技术,2010,8(4):312-316.
[8] 徐宗强, 江舸, 李中云. 延时多普勒高度表波形分析[J].科技展望,2016,26(17):177.
[9] CUMMING I G,WONG F H. Digital Signal Processing of Synthetic Aperture Radar Data[M]. USA: Artech House,2004.
[10] 杨路江, 王开志, 刘兴钊. SAR回波数据仿真软件设计[J]. 信息技术,2016(10):141-144.
