0 引言
传统的单脉冲技术通过和差波束在波束指向附近的比值接近线性的原理实现对目标角度(Direction of Arrival，DOA)的精确估计，但当波束内存在干扰时，单脉冲技术无法实现对干扰的抑制，从而导致了干扰环境下无法正确地估计目标角度。现代阵列信号处理中通过数字加权的方式实现单脉冲技术并且能更加灵活地对波束进行控制。数字单脉冲技术利用自适应波束形成技术，在干扰从旁瓣进入时，可以在和差波束上同时对干扰进行抑制，保持稳定的单脉冲比，从而实现干扰环境下的准确测角[1-2]。但是，当干扰位于主瓣内时，自适应算法会在干扰处形成零陷，这将使波束在主瓣内的方向图产生畸变，从而引起单脉冲比曲线严重失真，导致对目标测角错误[3]。
针对主瓣干扰引起的单脉冲比失真问题，基于极大似然估计的自适应单脉冲算法[4]、基于线性约束的自适应单脉冲算法[5]、基于主旁瓣分别抑制的两级自适应单脉冲算法[6]和基于阻塞矩阵预处理的旁瓣对消算法[7]相继被提出，这些算法通过增加约束或对主瓣内的干扰信号进行预处理[8]，在抑制干扰的前提下保证了单脉冲比不失真，从而实现主瓣干扰下的高精度测角。然而，两级自适应单脉冲算法需要优先抑制旁瓣干扰和主瓣保形，目前主瓣保形算法效果并不理想[9-11]，并且两个或多个干扰从主瓣进入时，两级自适应单脉冲算法缺少同时抑制多个干扰的自由度。阻塞矩阵算法无法完成对主瓣干扰完全抑制的同时保证阵列结构不发生变化。线性约束算法能较好的保持单脉冲比，但主瓣干扰附近单脉冲比仍然存在失真，而且当主瓣存在多个干扰时，会导致单脉冲比不失真的范围会大大减少，影响了测角精度。
为了解决在主、旁瓣干扰下的自适应单脉冲测角问题，并且能在多主瓣干扰下保持更高的测角精度，本文在文献[5]的基础上，提出了一种结合线性约束和干扰调零约束的差波束合成方式，可以同时抑制主瓣和旁瓣干扰并保证单脉冲比不失真，而且在多主瓣干扰下相比只利用线性约束的自适应方法拥有更高的脉冲比无失真范围和测角精度。
1 数字自适应单脉冲模型
考虑一个由N个阵元组成的均匀线性阵列，远场存在P个窄带干扰信号，且P<N，入射角度依次为θ1,θ2,…,θP，则接收信号可以用下式表示：
(1)
式中，s(t)和a(θj)分别表示第j个信号的波形和对应的导向向量，θj为第j个信号的来波方向， n(t)表示噪声信号。假设各个信号互不相关，噪声信号是均值为零、方差为
的高斯白噪声，噪声和干扰信号的协方差矩阵为R，则利用线性约束最小方差(Linearly Constrained Minimum Variance，LCMV)准则，最优权矢量为
w=μR-1a(θ)
(2)
实际中协方差矩阵R并不知道，因此采用采样协方差矩阵
来代替R:
(3)
式中，L代表采样快拍个数，
表示矩阵的共轭转置。
假设阵列波束指向为θ0，和波束静态权矢量wΣ=a(θ0)，设J为和差波束转化矩阵，则差波束静态权矢量为
wΔ=JwΣ
(4)
对于线性阵列
(5)
则自适应后的和差波束权矢量为
(6)
自适应后的和差单脉冲比为
(7)
式中，ζ{·}为单脉冲比转换函数，一般为取复数的虚部或实部函数。图1为存在3个旁瓣干扰时自适应和差波束方向图，自适应处理后的和差方向图均对干扰方向进行抑制，且主瓣内的方向图保持不变。图2是线性区域内的静态单脉冲比曲线与抑制干扰后的单脉冲比曲线，可以看到旁瓣干扰下的自适应单脉冲比基本不变。
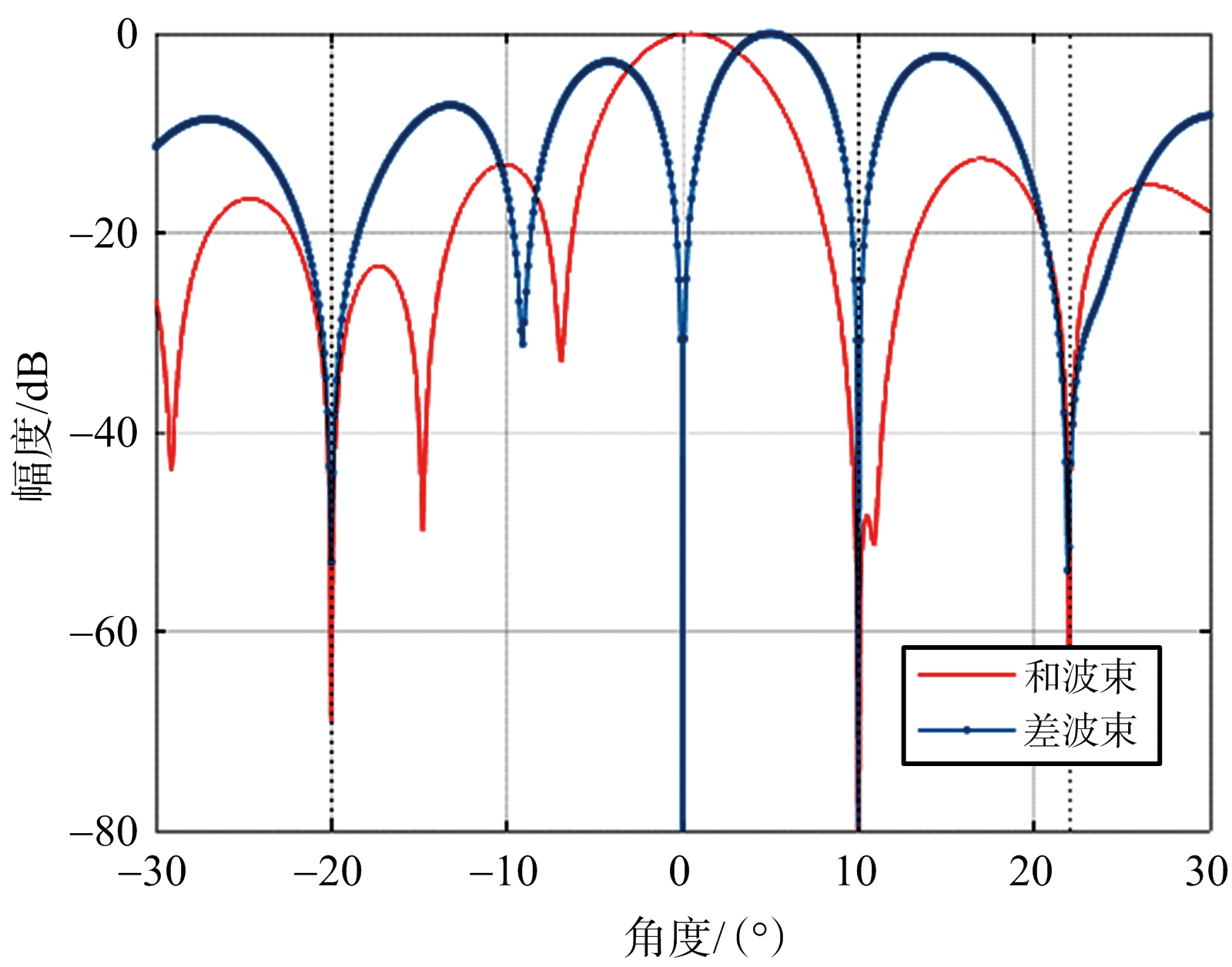
图1 自适应和差方向图
图2 旁瓣干扰下的自适应单脉冲比
将自适应后的差比和结果与静态的单脉冲比对照即可确定目标角度，即旁瓣干扰下的自适应单脉冲维持了测角精度，可以准确地估计目标方向。然而当主瓣内存在干扰时，自适应算法会在主瓣干扰方向形成零陷，导致主瓣方向图发生畸变，引起单脉冲比失真，从而影响到测角精度。
2 调零线性约束下的自适应单脉冲
根据上述分析，保持单脉冲比不失真是单脉冲能否精确测角的关键所在。当存在主瓣干扰时，必须对自适应单脉冲算法增加约束以修正由主瓣干扰引起的单脉冲比失真问题。单脉冲法测角通常首先由和通道检测目标，再由目标位置的差和比值与静态单脉冲比斜率的乘积得到目标偏离波束角度，因此为了能在干扰环境下正确地检测出目标，和波束需要由LCMV准则得到自适应权值来保证输出最大信干噪比(SINR)，然后在自适应差波束合成中对单脉冲比进行约束，保证单脉冲比最大无失真并抑制干扰，这样在抑制干扰的同时保持了自适应单脉冲的测角精度。
假设波束指向为θ0，在线性区域的单脉冲测角范围为[θ0-Δθ,θ0+Δθ]，对自适应差波束权值
增加约束，确定首先由线性约束保证在线性区域斜率不变：
(8)
式中，ks表示静态单脉冲比，是由静态单脉冲曲线在线性区域的近似斜率估算出的常数。式中和差波束输出为
(9)
其次，自适应后的差波束需要在波束指向处增益为零，保持自适应单脉冲比过零点，由下式进行约束：
(10)
最后，由于和差方向图均在主瓣干扰方向形成零陷，为了让主瓣干扰附近范围的单脉冲比满足线性关系，需要差方向图上主瓣干扰位置满足单脉冲比不变，保持在其他方向上的方向图增益，由下式调零约束保证:
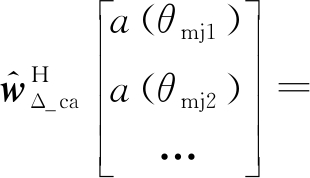
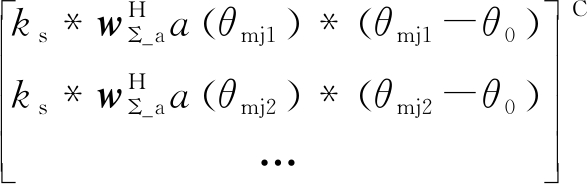
(11)
式中，(·)C表示矩阵的共轭，θmj为主瓣干扰方向由DOA估计算法得到，如MUSIC算法，构造如下空间谱：
(12)
通过搜索Pmusic(θ)的谱峰值可得到信号的角度估计。由于干扰信号一般认为很强，即干噪比足够大，所以可以保证干扰信号的DOA估计精度，其次将谱峰搜索范围限制在主瓣范围内可以保证搜索时间以及搜索算法的精度。
综上所述，自适应差波束可由线性约束最小方差法确定:
(13)
式中，C为约束方向矩阵，F为约束响应矩阵，选取如下：
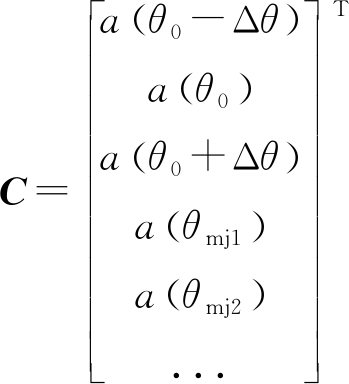
(14)
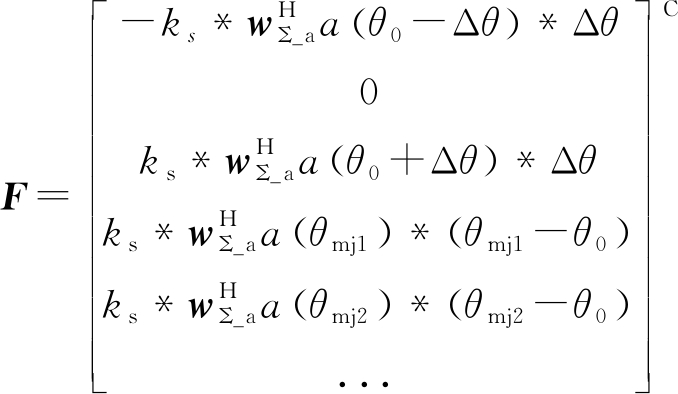
(15)
式中，(·)T表示矩阵的转置，(·)C表示矩阵的共轭。最后由LCMV准则得到的约束自适应差波束权矢量为
(16)
而通过约束后的自适应单脉冲比为
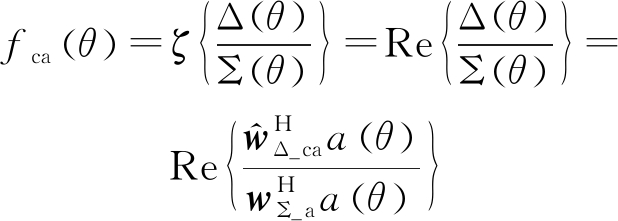
(17)
式中，Re{·}表示取复数的实部。
图3表示了稳健自适应单脉冲测角流程，和波束通过自适应算法处理抑制干扰，用于目标的检测与测角，差波束通过调零线性约束在抑制干扰的同时保持单脉冲比不变，用于目标的测角。这种方法在线性约束的基础上增加干扰调零约束，作进一步限制，减少由主瓣干扰零陷而导致的单脉冲比失真范围，从而进一步提高了单脉冲测角精度。通过式(14)、式(15)约束条件和线性约束条件对比，可以知道添加干扰调零约束并未因为自由度的减少而减少最大干扰抑制数目，即调零线性约束与三点线性约束的最大干扰抑制个数相同。此外，自适应方向图在主瓣干扰处出现零陷也会导致信号方向的增益降低，为了提高检测性能和测角精度，应该在自适应处理后，通过匹配滤波、相参积累等技术进一步提高信噪比，然后再对目标进行测角。
图3 自适应单脉冲测角流程图
3 仿真
下面利用计算机仿真实验对算法性能进行分析。考虑阵元个数为16的均匀线阵，阵元间隔为半个波长，静态波束半功率波束宽度约为6.4°，零点波束宽度约为14.4°，单脉冲线性区域测角范围为±3°。假设存在两个主瓣干扰分别位于2.2°和-2°处，干扰类型为噪声压制，干噪比均为35 dB并且存在一个旁瓣干扰，位于10°，干噪比为50 dB，噪声为高斯白噪声。
3.1 自适应方向图合成
采用式(6)的自适应算法与本文提出的调零线性约束自适应算法对干扰环境下的自适应方向图进行仿真。
图4、图5是一般自适应方法和调零线性约束自适应方法得到的和差方向图，自适应处理后的和方向图在干扰方向形成零陷，即抑制了干扰，提高了信干比，但主瓣形状发生畸变。差方向自适应后的方向图则因为在主瓣干扰处形成零陷，而并未在波束指向方向形成零陷，这导致自适应后的单脉冲比与静态单脉冲比差别很大，无法准确测角，而线性约束后的方向图则在波束指向处幅度为零，保持了静态差方向图的特性，并且使线性区域的单脉冲比维持不变，因此能在主瓣干扰下准确地测角。
图4 和波束方向图
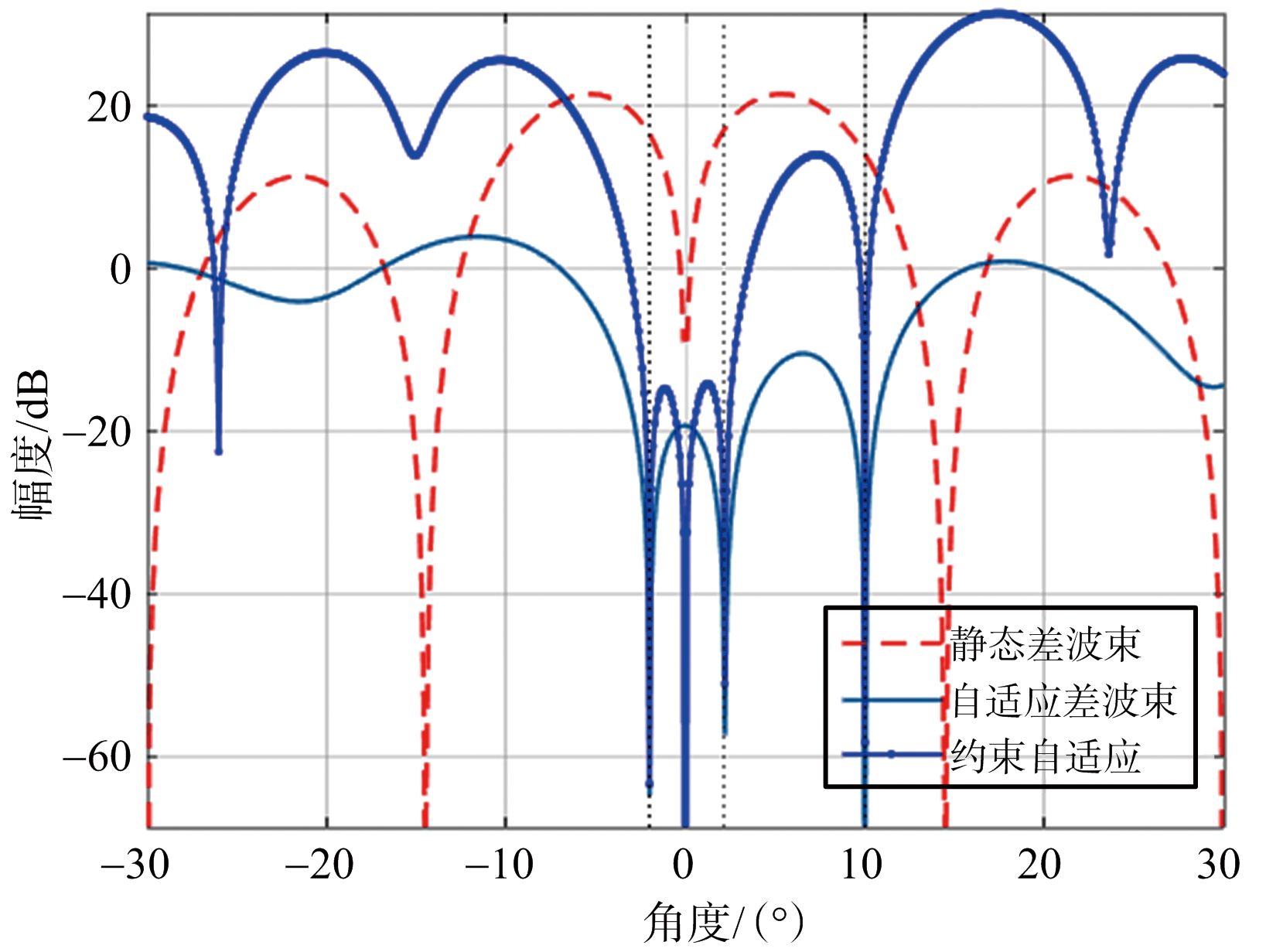
图5 差波束方向图
3.2 测角精度与算法性能分析
下面比较文献[6]中线性约束法与本文提出的调零线性约束法在性能上的差异。定义理论均方根误差表达式如下:
(18)
式中，fca(θ)为根据自适应后的方向图计算的单脉冲比，ks为静态单脉冲比拟合斜率，θ为角度的真实值。
图6给出了线性区域内线性约束自适应算法和调零线性约束自适应算法抑制主瓣干扰后得到的单脉冲比曲线，并与静态单脉冲比曲线进行比较，图中可以看出，线性约束算法得到的单脉冲比受到干扰的影响严重，在主瓣干扰附近的角度区域发生畸变，无失真范围缩减到波束中间附近，而经过调零约束后，将干扰处的单脉冲比调节到与静态单脉冲比一致，纠正了主瓣干扰附近的畸变。
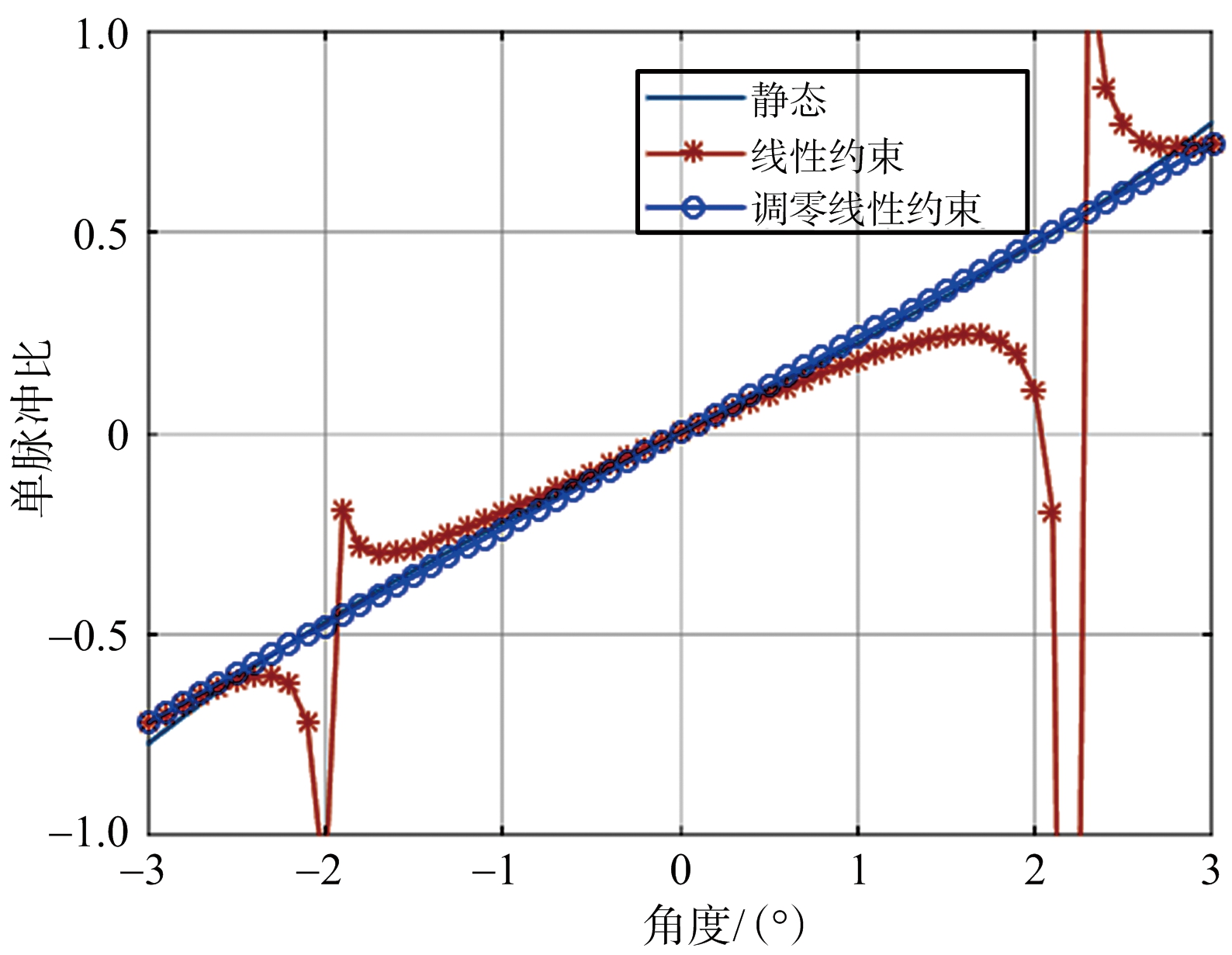
图6 单脉冲比曲线
图7是利用式(18)计算的自适应单脉冲比曲线测角后的均方根误差，常规自适应算法得到的误差基本无法满足测角精度，线性约束下的测角精度在远离主瓣干扰处较好，但多主瓣干扰下缩小了线性约束下的单脉冲比无失真范围，而本文提出的调零线性约束算法则在主瓣干扰附近也保持了单脉冲比无失真。
图7 单脉冲比RMSE
按上述干扰条件设置实验场景，实验仿真中对目标在各个角度下进行角度测量，假设目标信噪比为10 dB，脉冲压缩和相参积累增益为40 dB，每个仿真为100次蒙特卡洛实验的平均结果。定义实验均方根误差表达式如下:
(19)
式中，K为实验次数，
和θ分别为角度测量值和真实值。
图8为3种自适应算法实际角度估计的均方根误差随目标角度的变化曲线。可以看出均方根误差与理论计算结果基本一致，调零线性约束在靠近主瓣处测角误差增大的原因是在干扰附近的目标方向图增益过小，导致差通道目标被噪声信号淹没，从而无法反映真实的差比和的结果。
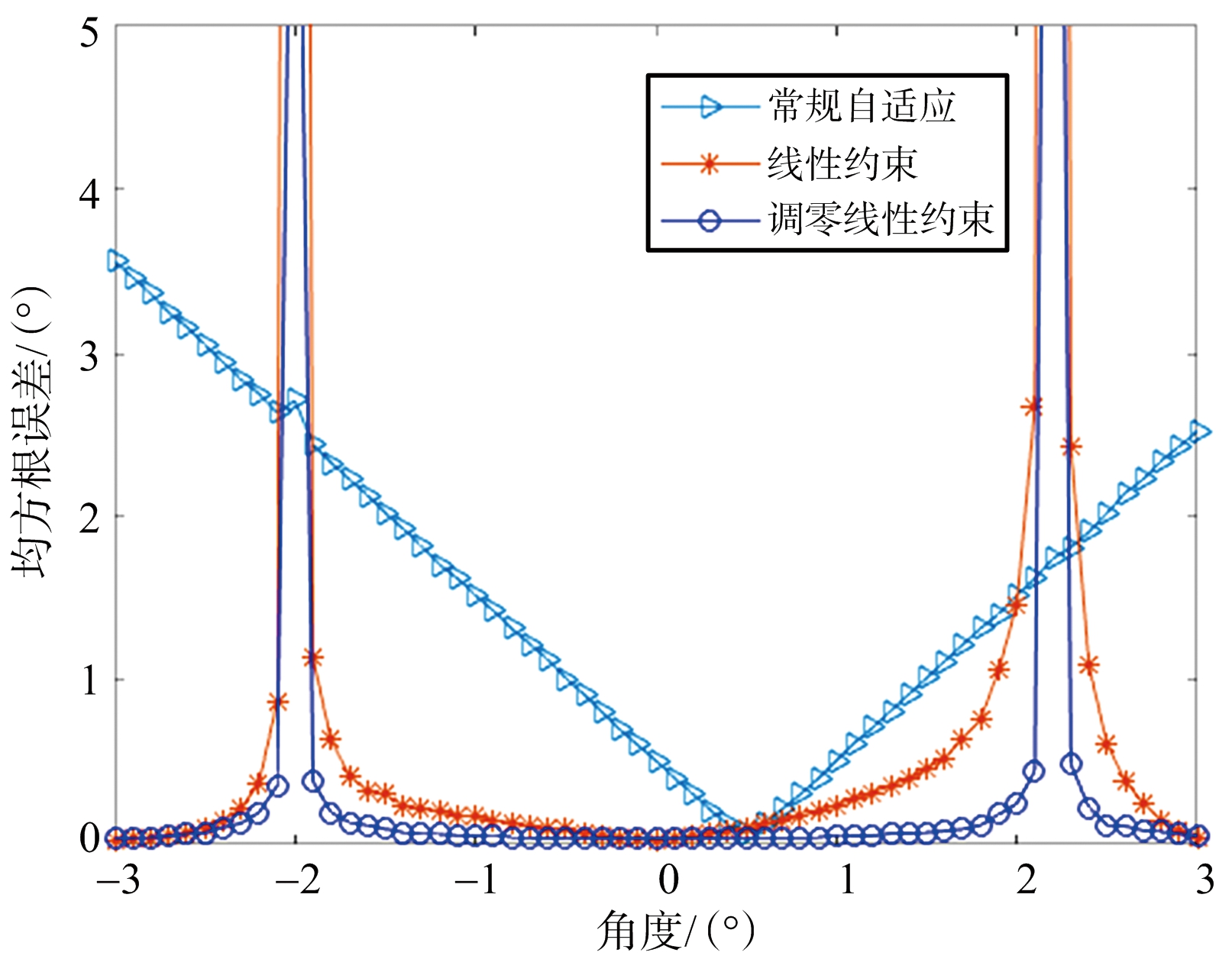
图8 目标测量RMSE
图9显示目标信噪比对测角性能的影响，常规自适应算法角度估计误差随信噪比增加基本无变化，约束自适应算法的均方根误差均随信噪比的提升而减小，再趋于稳定，可以看出线性约束算法在信噪比约为10 dB后测角误差趋于稳定并不在减小，达到了最佳性能，而调零线性约束的测角性能则可以随信噪比的增加而进一步提升，理论上信噪比足够大的情况下，调零线性约束算法可以保持较高的测角精度。
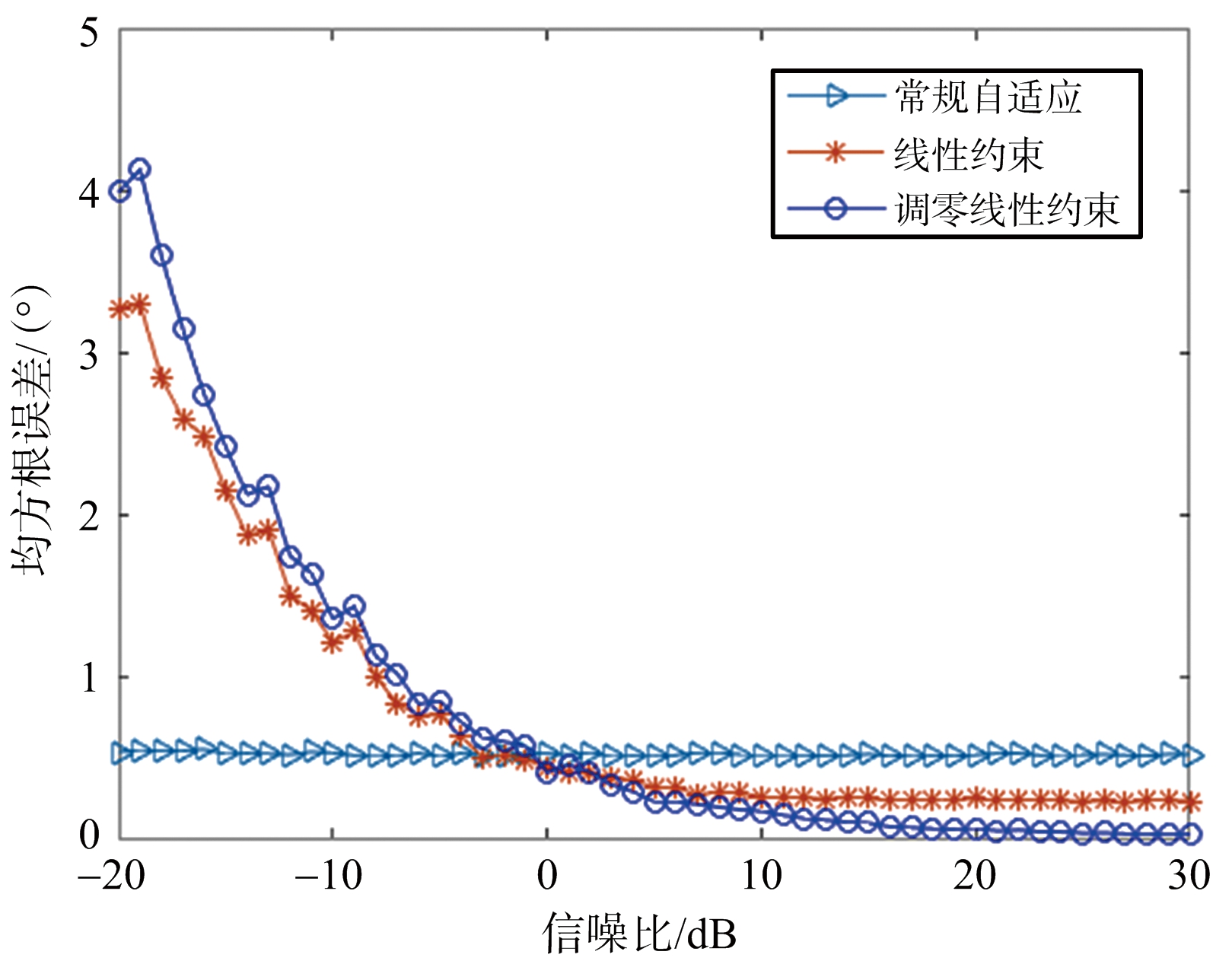
图9 测角RMSE随SNR的变化
3.3 干扰角度估计误差的影响
实际中对干扰的DOA估计会存在误差，因此需要考虑DOA估计误差对本文算法的影响。定义测角无偏范围函数如下:
P(σ)=p{θRMSE<σ}
(20)
式中，σ为测角精确评价门限，P(σ)即为测角均方根误差小于门限的范围占总的测角范围的比例，越接近于1，则表示测角误差在门限内的角度范围越大。
图10是无偏测角范围占总的线性范围的比率与无偏测角门限的曲线图，随门限提高，无偏测角范围比率增大，图中可以看出调零线性约束在门限很小的情况下无偏测角范围就已经覆盖整个线性测角区域了。
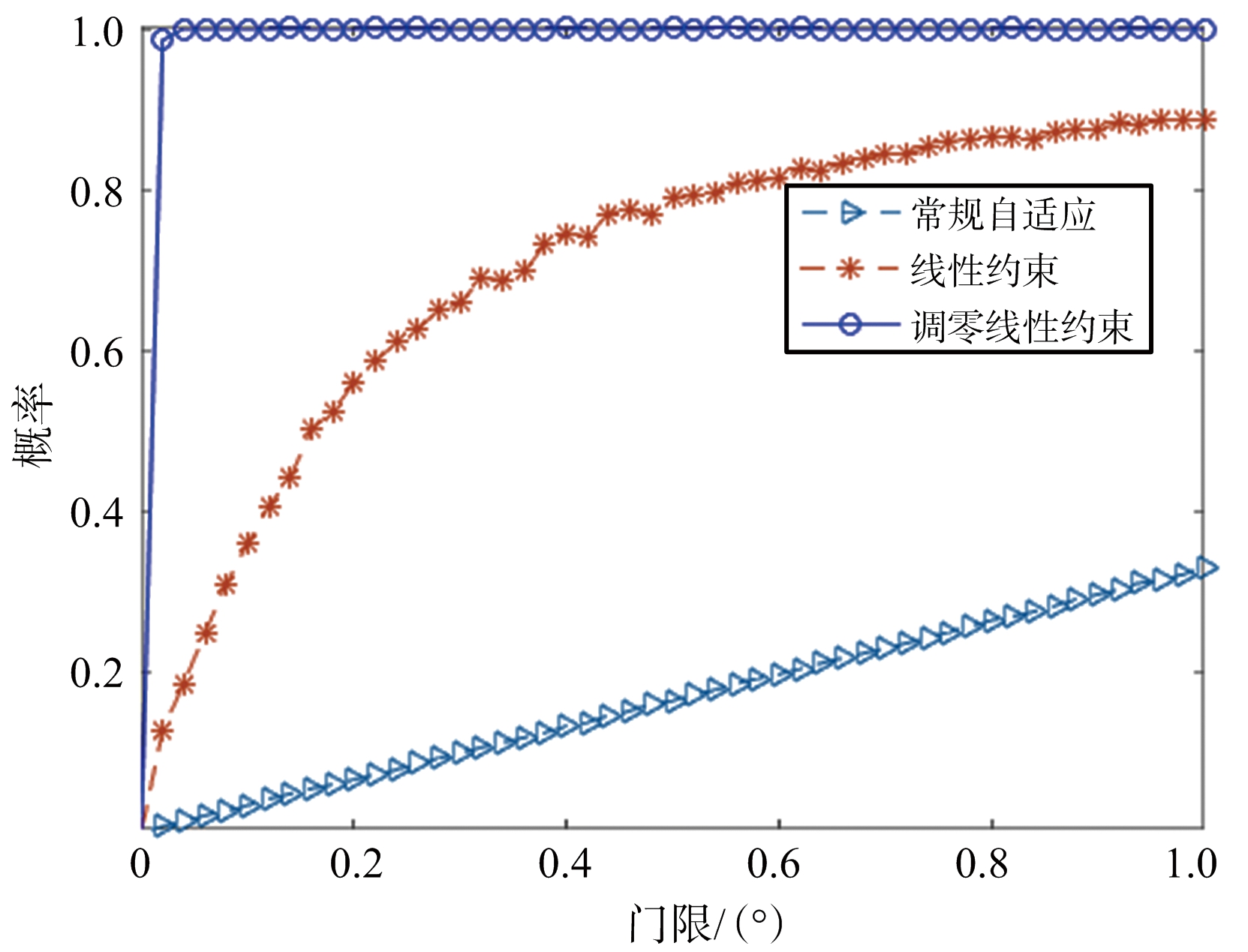
图10 测角无偏范围
将门限设置为0.2°，图11表示干扰角度估计误差对角度测量无偏比率的影响结果，可以看出干扰估计误差对结果影响较小，这是因为即使存在角度估计误差，调零线性约束可以看作在线性约束的基础上再增加多个点约束，所以仿真结果优于线性约束。
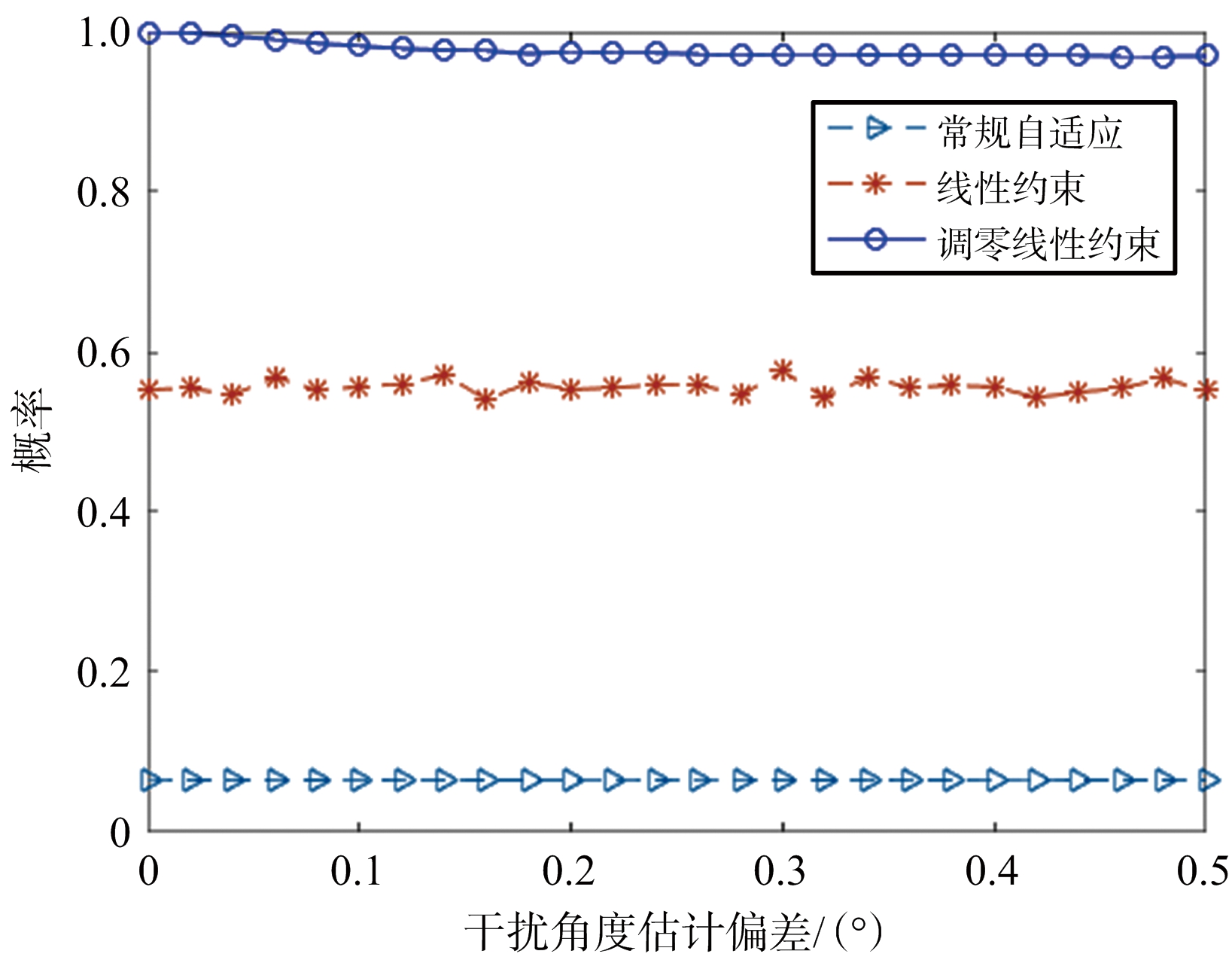
图11 DOA估计误差对测角的影响
4 结束语
本文提出了一种基于调零线性约束的自适应差波束合成方式，通过对主瓣干扰的DOA估计与和波束的自适应权值构造差波束的约束条件，在抑制干扰的同时保持单脉冲比不变，实现了主瓣干扰环境下的稳健测角。通过计算机仿真，验证了本文方法改善了线性约束算法的性能，并且在多主瓣干扰环境下表现优异，并且拥有良好的鲁棒性，是一种稳健的单脉冲测角技术。
[1] NICKEL U. Monopulse Estimation with Adaptive Arrays[J]. IEE Proceedings F (Radar and Signal Processing),1993,140(5):303-308.
[2] TALISA S, O’HAVER K W, COMBERIATE T, et al. Benefits of Digital Phased Array Radars[J]. Processings of the IEEE,2016,104(3):530-543.
[3] 向巍,葛志强,崔剑,等. 多通道相控阵自适应数字单脉冲合成方法[J]. 系统工程与电子技术,2019,41(4):765-771.
[4] NICKEL U. Monopulse Estimation with Subarray Adaptive Arrays and Arbitrary Sum and Difference Beams[J] .IEE Proceedings-Radar, Sonar & Navigation,1996,143(4):232-238.
[5] FANTE R L. Synthesis of Adaptive Monopulse Patterns[J]. IEEE Trans on Antennas and Propagation,1999,47(5):773-774.
[6] YU K, MURROW D J. Adaptive Digital Beamform-ing for Angle Estimation in Jamming[J]. IEEE Trans on Aerospace and Electronic Systems,2001,37(2):508-523.
[7] 陈华才,王永明,王世练,等. 基于信号预处理的数字单脉冲技术[J]. 信息化研究,2015,41(3):63-67.
[8] 陈亮,盛卫星,马晓峰,等. 一种主瓣干扰下的快速自适应单脉冲算法[J]. 南京理工大学学报,2013,37(4):471-478.
[9] YANG Xiaopeng, ZHANG Zongao, ZENG Tao, et al. Mainlobe Interference Suppression Based on Eigen-Projection Processing and Covariance Matrix Reconstruction[J].IEEE Antennas and Wireless Propagation Letters,2014,13:1369-1372.
[10] LUO Zhangkai, WANG Huali, LV Wanghan, et al. Mainlobe Anti-Jamming via Eigen-Projection Processing and Covariance Matrix Reconstruction[J]. IEICE Trans on Fundamentals of Electronics Communications and Computer Sciences,2017,E100-A(4):1055-1059.
[11] LI Xin, YU Baoguo, HUANG Ping, et al. Mainlobe Interference Suppression via Eigen-Projection Processing and Covariance Matrix Sparse Reconstruction[J]. IEICE Electronics Express,2018,15(17):1-9.
