0 引言
合成孔径雷达(Synthetic Aperture Radar,SAR)是一种主动微波成像遥感设备,在工作过程中容易受到射频干扰[1-2](Radio Frequency Interference,RFI)的影响,使得接收回波的信干噪比(Signal to Interference plus Noise Ratio,SINR)降低,严重时会影响SAR成像质量及后续图像解译,因此在回波中对RFI信号进行有效抑制具有重要意义[3-4]。
SAR射频干扰抑制方法的研究是一项重要的课题。在缺乏先验信息和参数模型的情况下,非参数化方法可在时域或频域实现回波数据中干扰的自适应抑制,与参数化方法相比有较大优势。频域陷波法[5]和子空间滤波法[6]是两种经典的非参数化方法,它们处理流程简单,不足是忽视了干扰的非平稳局部特性,而且频域陷波法会完全损失与干扰信号处于同频带内的有用信号,从而造成后续成像质量的下降。
本文提出一种基于GST时频滤波的SAR射频干扰抑制算法,有效利用了时频分布关注干扰的非平稳局部特性,在有效抑制干扰的同时避免有用信号的损失。该方法首先利用配对样本T检验[7]进行干扰的方位检测,接着分别处理包含干扰数据的实部和虚部:进行GST[8],得到其时频分布,在此基础上,利用子空间滤波法去除每一个时间窗内数据中的干扰分量,逆GST后得到干扰抑制后的数据。最后,实验结果验证了所提方法的有效性。
1 SAR射频干扰的特性及模型
SAR系统受到射频信号干扰的接收回波 x(t)有如下形式:
x(t)=s(t)+rfi(t)+noi(t)
(1)
式中,s(t)为目标回波,rfi(t)为射频干扰,noi(t)为加性噪声,近似为高斯白噪声。
实测大场景SAR回波数据的统计分析表明:
1) 不含干扰的SAR目标回波信号近似服从于复高斯分布[9];
2) RFI具有比较复杂的时频特性:有窄带性和非平稳性;
3) RFI从源到SAR接收通道主要是单程传播,干扰功率一般大于SAR接收回波功率。
基于上述特点,目标回波和噪声信号可以被统一视作宽带高斯白噪声信号,所以SAR射频干扰抑制问题就转化为在高斯白噪声背景下的窄带干扰抑制问题。因此,式(1)可表示为
x(t)=sn(t)+rfi(t)
(2)
式中,sn(t)=s(t)+n(t)。与x(t)相对应的离散表达式为
x(n)=s(n)+rfi(n)+noi(n)=
sn(n)+rfi(n)
(3)
式中,n=1,2,…,Nr,Nr为距离向采样点数,上式中的元素均是式(1)和式(2)的离散形式。
对于窄带RFI信号,具有类似线性调频(LFM)信号的形式:
![]()
(4)
式中,Bk,fk和γk分别表示第k个干扰分量的幅度、中心频率及调频率。
2 GST时频滤波干扰抑制原理
2.1 配对样本T检验原理
目前合成孔径雷达RFI抑制算法的处理对象多是快时间距离向回波数据。然而对全部接收回波进行干扰抑制,在理论上可以极大地使算法发挥作用,但会增加无意义运算,降低信号处理效率,所以有必要进行RFI检测,标记出不存在干扰的方位。文献[10]指出快时间回波数据之间具有相关性,并提出基于相关系数检测的方法,然而实际纯净回波的相关程度较难判断,无法按照常规设置门限进行检测。实际上,这种相关性也体现在纯净回波信号期望值μ小的起伏程度;同时,纯净SAR回波的实部与虚部均近似服从高斯分布。通过以上分析,本文提出了一种基于配对样本T检验的方位向干扰检测方法。其步骤为:
1) 计算所有距离向快时间数据的功率并进行比较,考虑受RFI影响的回波具有相对大的功率,进一步地选取功率值较小的快时间信号xk(n)作为不含干扰的参考信号,其中k为方位向标号。
2) 将参考信号xk(n)分别与其他所有距离快时间信号xs(n)进行配对样本T检验,其中s= 1,…,Na,且s≠k,Na为最大方位向标号。第一步,建立原假设和备择假设,分别记为H0:μk=μs和H1:μk≠μs,确定显著性水平参数α,为了防止包含弱干扰方位的漏检,实际中取α=0.1可以满足要求。第二步,按照以下公式计算统计量t′值:
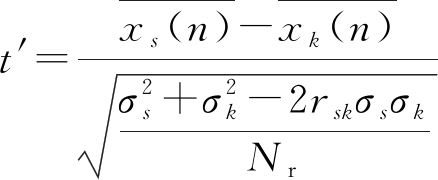
(5)
式中:![]() 为两个信号的期望值;σs,σk为两个信号的标准差;rsk为相关系数。第三步,采用双侧检验形式并根据显著性结果进行决断:接受或拒绝原假设。若是拒绝原假设,则记录该方位向标号。
为两个信号的期望值;σs,σk为两个信号的标准差;rsk为相关系数。第三步,采用双侧检验形式并根据显著性结果进行决断:接受或拒绝原假设。若是拒绝原假设,则记录该方位向标号。
该算法利用了SAR一维距离向时域回波的相关性及起伏不大的特性,通过计算统计量t′,并比较其显著性以判断干扰的存在,计算量小,实用性强。
2.2 RFI抑制流程
假设RFI检测后被标记的某条距离向复信号为xi(n),它由实部和虚部组成:
xi(n)=ai(n)ejφi(n)=pi(n)+jqi(n)
(6)
![]()
(7)
φi(n)=arctg(qi(n)/pi(n))
(8)
式中,n=0,1,…,Nr-1,ai(n)为幅度,φi(n)为相位,pi(n)为实部,qi(n)为虚部,且pi(n)和 qi(n)均为实数。
由于RFI信号具有比SAR回波高的功率及具有未知的相位,会同时影响接收回波的幅度与相位,使得接收回波信号的实部和虚部电平被抬高;同时为有效减少处理后可能存在的残余相位与相位畸变,分别处理实部和虚部可作为一种选择。
GST是一种用于分析非平稳信号的有效工具,高频处有高的时间分辨率,通过改变调节因子可以获得高的频率分辨率,高的时频分辨率可令基于该变换域的干扰抑制处理精细化,即更大程度地保留与干扰信号谱图不重叠的有用信号;同时,子空间滤波能有效地分离混合信号,降低与干扰信号谱图重叠的有用信号损失。
2.2.1 GST及窗函数调节因子
广义S变换是S变换的推广,通过引入窗函数调节因子缓解了窗口函数宽度减小而导致的频率分辨率降低问题,从而可以获得理想的二维分辨率。
由小波变换可以推出如式(9)的一维连续信号x(t)的S变换表达式,选用的小波变换基函数为式(10)的高斯窗函数,满足积分为1。其中,ψ为小波基函数,τ为时移因子,f为频率。
(9)
(10)
对于式(9),引入窗函数调节因子λ,p,得到GST:
GST(f,τ)=![]()
e-j2πftdt
(11)
通过调节两个因子可以调节二维时频分辨率。当且仅当λ=1,p=1时,GST退化为S变换;当调节λ<1或p<1时,可以使得频率分辨率提高而时间分辨率下降;当调节λ>1或p>1时,可以使得时间分辨率提高而频率分辨率下降。一般来说,两个因子取值不宜过大或过小,应取在1的附近。文献[11]指出p值的改变对窗函数窗宽、幅值、窗脊的变化具有决定性作用,而λ对窗的形态改变远不及p值,在实际应用过程中可以起到对窗口微调的作用。
为了对(λ,p)有效取值,利用反映信号在二维域聚集特性(二维分辨率)两种度量[12]χ1和χ2对不同(λ,p)组合的GST时频分辨率进行评估。假设待处理的SAR一维距离向数据实部为pi(n),其经GST得到的时频域分布为GSi(该符号代表GST的离散形式),GSi(m,v)为矩阵中的元素,m和v分别为频率和时间标号,则两个度量可以表示为
(12)
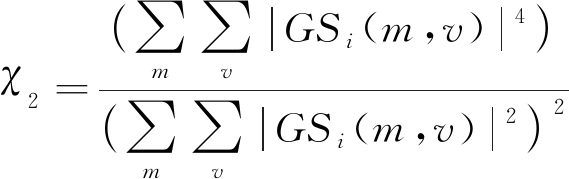
(13)
χ1和χ2越大表示能量越集中。
为选取合适的因子,一般需要进行二维寻优,并根据两个度量来评价因子选取的合适性,这需要利用每一组(λ,p)进行GST,这必然会降低处理效率。实际过程中,提出利用以下步骤选取(λ,p):
1) λ取1,在p的选择区间0.5~1.5中,计算度量χ1和χ2,选择使得两个度量最大时对应的p值(一般取p<1,以达到良好的频率分辨率);
2) 确定p后,微调λ,补偿时间分辨率(一般如果p<1,λ选择略大于1)。
2.2.2 GST时频滤波干扰抑制算法
针对被标记的一维距离向信号的实部pi(n),调节(λ,p)(也可以统一预设),将pi(n)进行GST得到GSi,列向量为各时间窗内的数据谱。GSi按列作IFFT,记gsv为其第v个时间窗内的数据向量,即gsv=[gsv(1),gsv(2),…,gsv(L)]Τ,L为数据向量长度,(·)Τ表示转置。接下来,利用子空间滤波对每个时间窗内数据进行干扰抑制处理:
1) gsv延迟嵌套构造Hankel矩阵Gv:
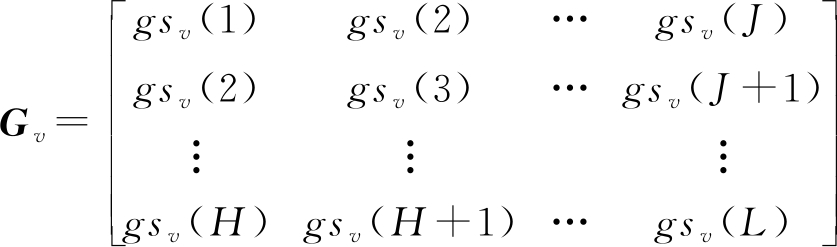
(14)
H和J为矩阵的行数与列数,且满足:J=L- H+1和(L-H+1)≥2H。
2) 构造Rv并特征分解:
Rv=GvGvΗ=UΛUΗ
(15)
式中,Λ=diag[λ1,λ2,…,λH]是H维对角阵,λ表示特征值且λ1≥λ2≥…≥λH,对应特征向量排成矩阵为U=[u1,u2,…,uH]。此时的干扰子空间由代表干扰信号的前r个大特征值对应的特征向量Ur张成,进一步地,Gr=UrUrΗGv表示 Gv向干扰子空间投影后得到的干扰信号矩阵。大特征值个数r利用AIC准则估计:
(16)
式中,LLF(r)和PAIC(H,r)分别为
LLF(r)=(H-r)·
(17)
PAIC(H,r)=r(2H-r)
(18)
3) 从Gr中重建一维干扰信号序列gsjv(l):

(19)
4) 依据式(20)将gsjv(l)从gsv(l)中减去,完成对一个时间窗内数据的干扰抑制处理:
gssv(l)=gsv(l)-gsjv(l), l=1,2,…,L
(20)
对所有时间窗内的数据进行以上四步操作,即可完成对GSi的干扰抑制。最后,按列作FFT得到干扰抑制后时频分布,再通过逆GST得到干扰抑制后的一维时域数据![]()
虚部![]() 的求法与
的求法与![]() 相同,故干扰抑制后的SAR一维距离向信号
相同,故干扰抑制后的SAR一维距离向信号![]() 为
为
(21)
对所有被标记受干扰影响的SAR回波信号进行上述操作,即可完成SAR回波的干扰抑制。图1是整个干扰抑制流程的框图。
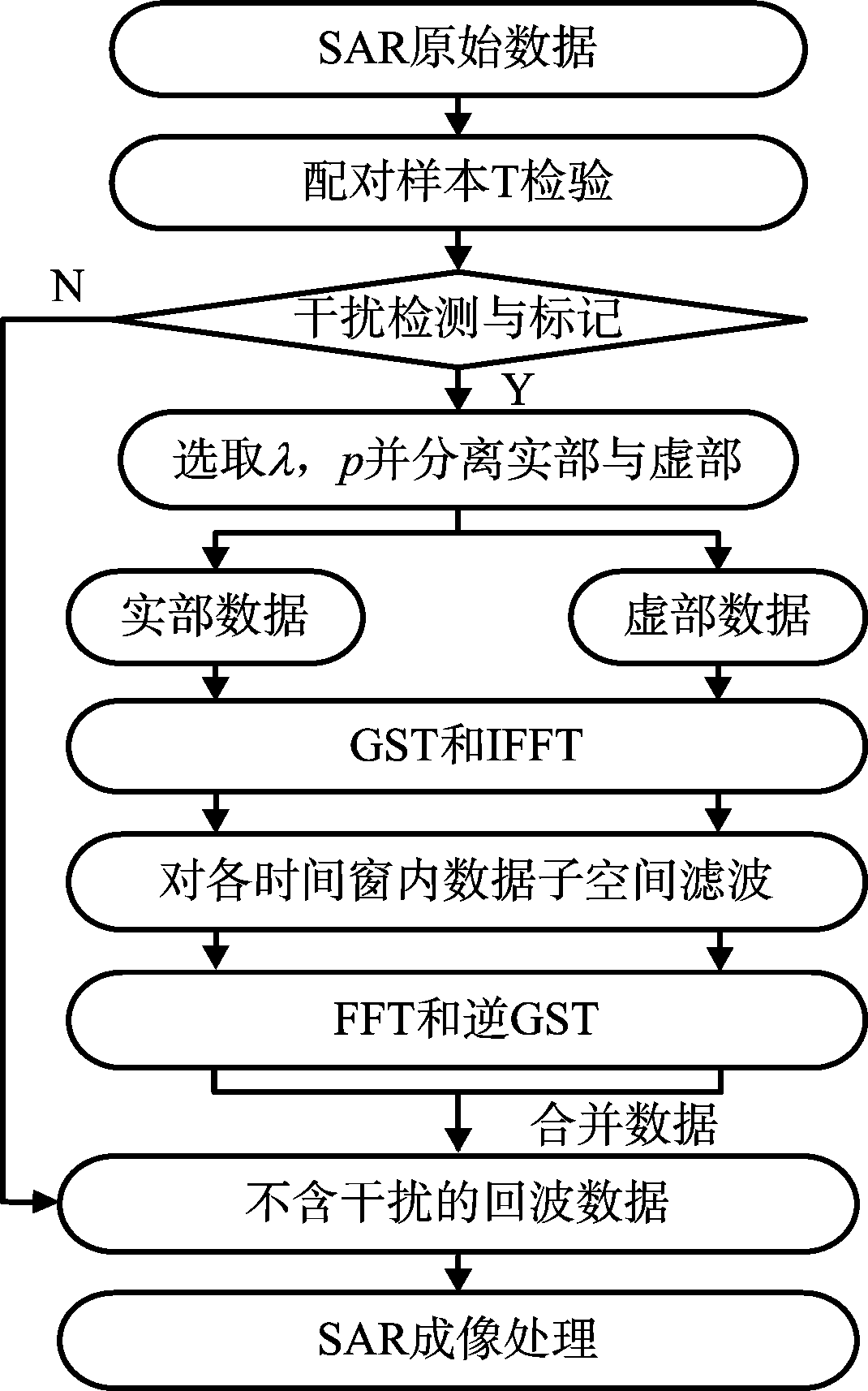
图1 GST时频滤波干扰抑制流程
3 实验结果与分析
3.1 基于SAR一维距离向回波的实验
本实验中,引入两个指标来定量评估干扰抑制方法:干扰抑制比(ISR)和信号失真度(SDR)[13]。ISR表示干扰抑制的程度。SDR表示干扰抑制后对有用信号的损失程度。实验数据来自Radarsat-1,干扰为人为添加,部分参数如表1所示。
表1 实验的参数设置

参数数值调频率/(Hz·s-1)0.72135×1012带宽/MHz30.116采样率/MHz32.317添加干扰与信号功率比值/dB15
图2(a)和2(b)分别为原始距离向回波频谱和时频谱。在数据中加入干扰后,两种谱图如图2(c)和2(d)所示,图中的干扰具有窄带及非平稳的特性,其中的非平稳性体现在:其一,干扰信号的持续时间可能小于回波的持续时间;其二,干扰的频率随时间的变化。采用频域陷波法后的结果如图2(e)和2(f)所示,从频谱图可见存在干扰的频带被置零,在抑制干扰的同时严重损失了该频带的有用回波信号,在时频谱图中,损失了所有时间窗内干扰频点处的信号。图2(g)和2(h)是采用本文方法处理后的结果,选取(p,λ)=(0.5,1.2),与频域陷波法相比,该方法有效利用了干扰的窄带及非平稳特性,即对混合信号GST瞬时谱滤波,所以在抑制干扰的同时,对不含干扰的瞬时谱和与干扰重叠的有用信号谱的损失很小。同时,表2中干扰抑制性能指标的比较表明,本文方法的ISR与频域陷波法相当,但具有比频域陷波法更低的SDR,从而表明其性能优于频域陷波法。
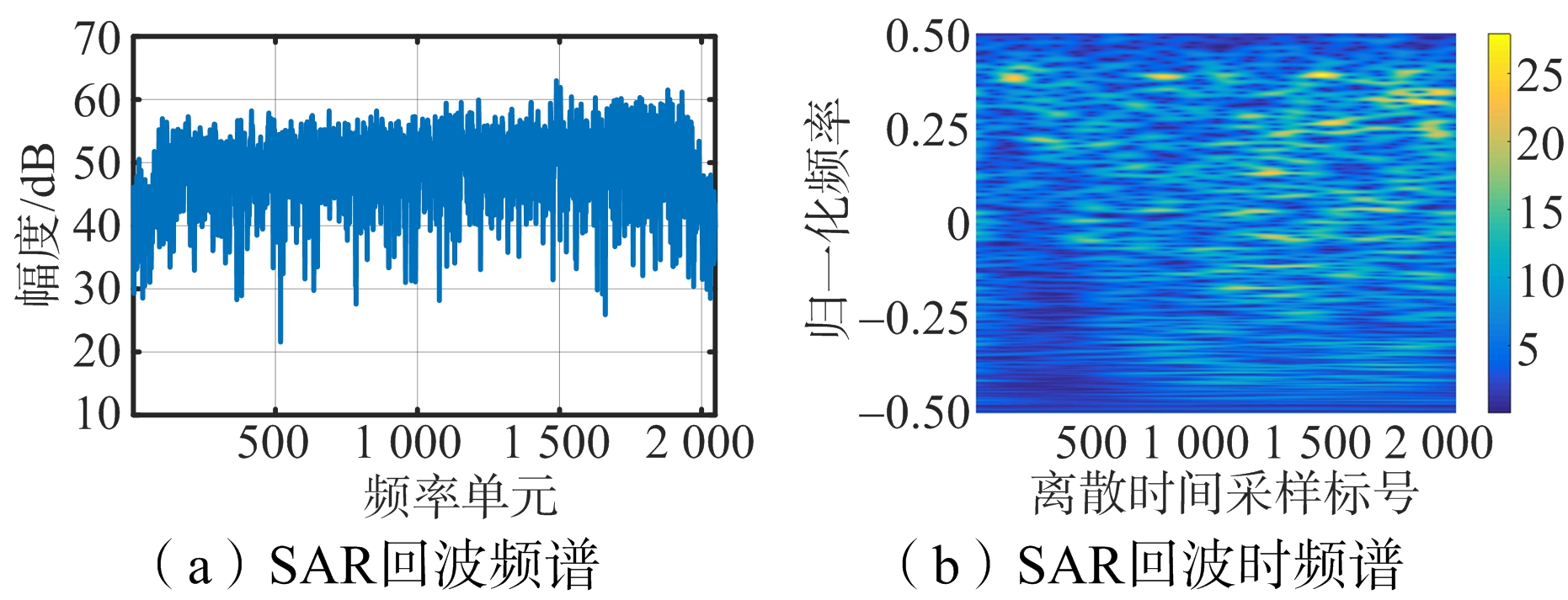
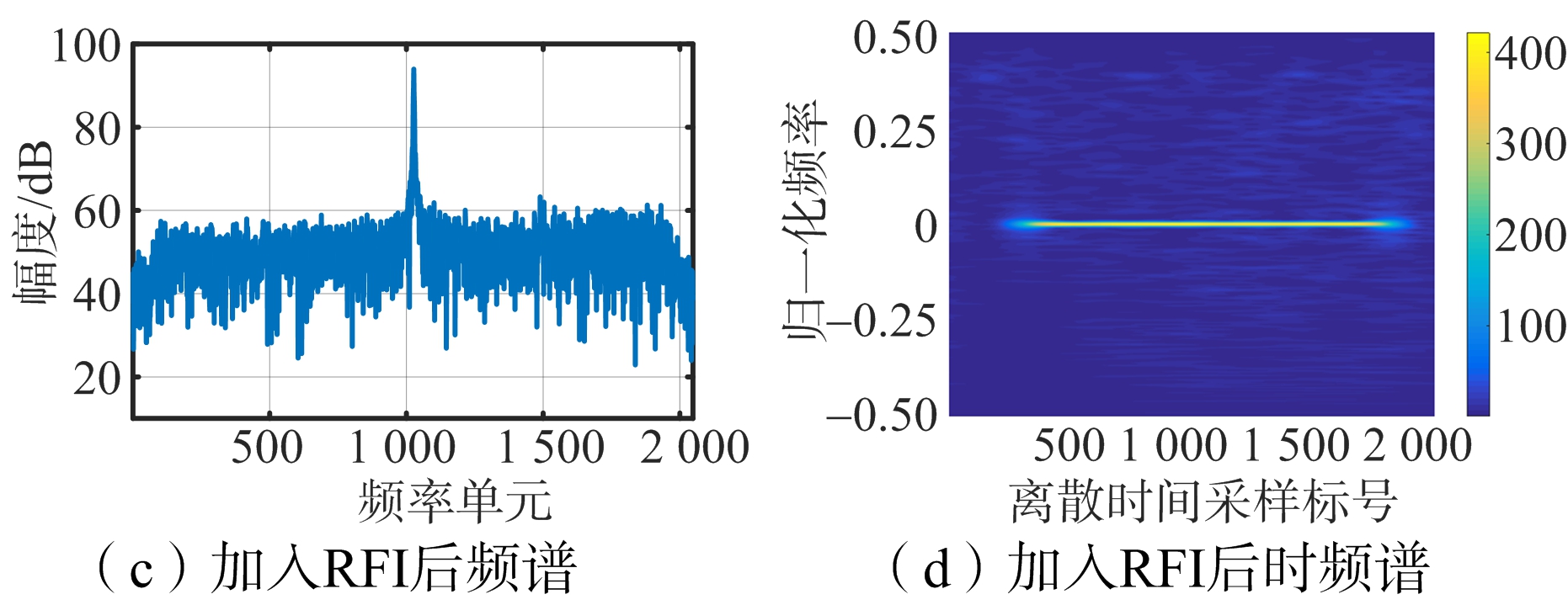
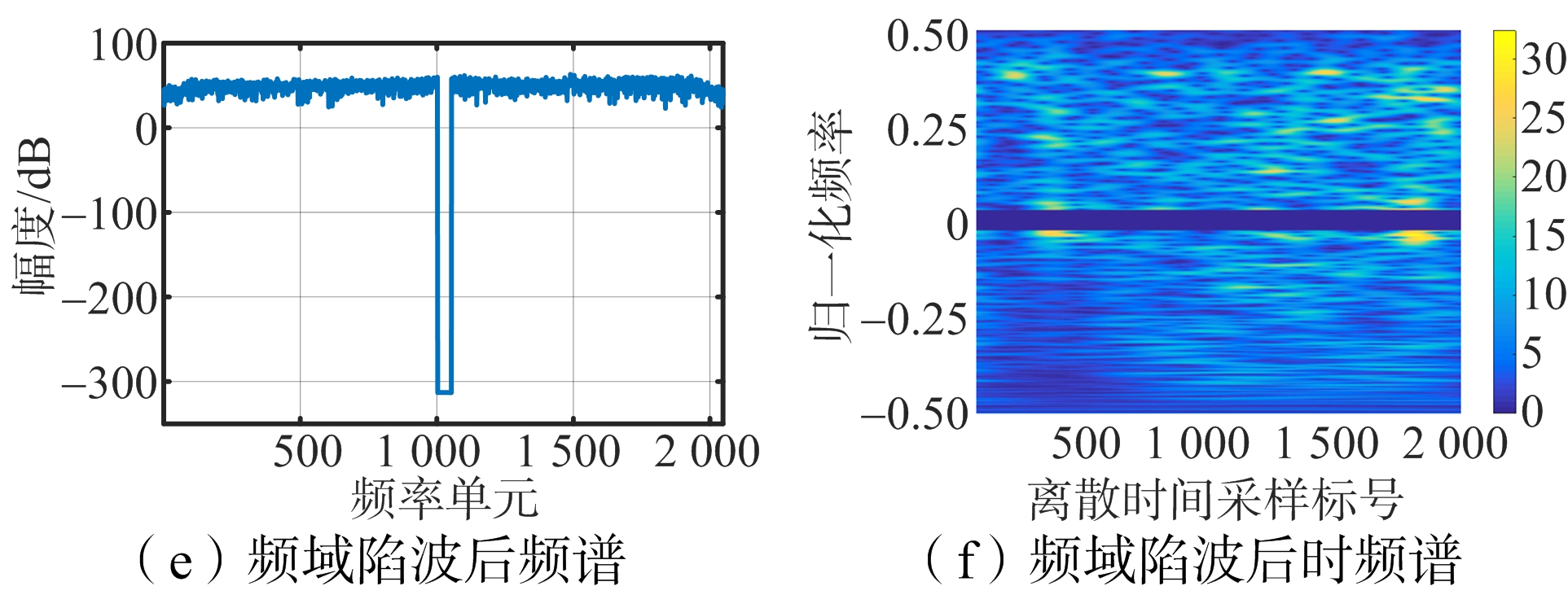
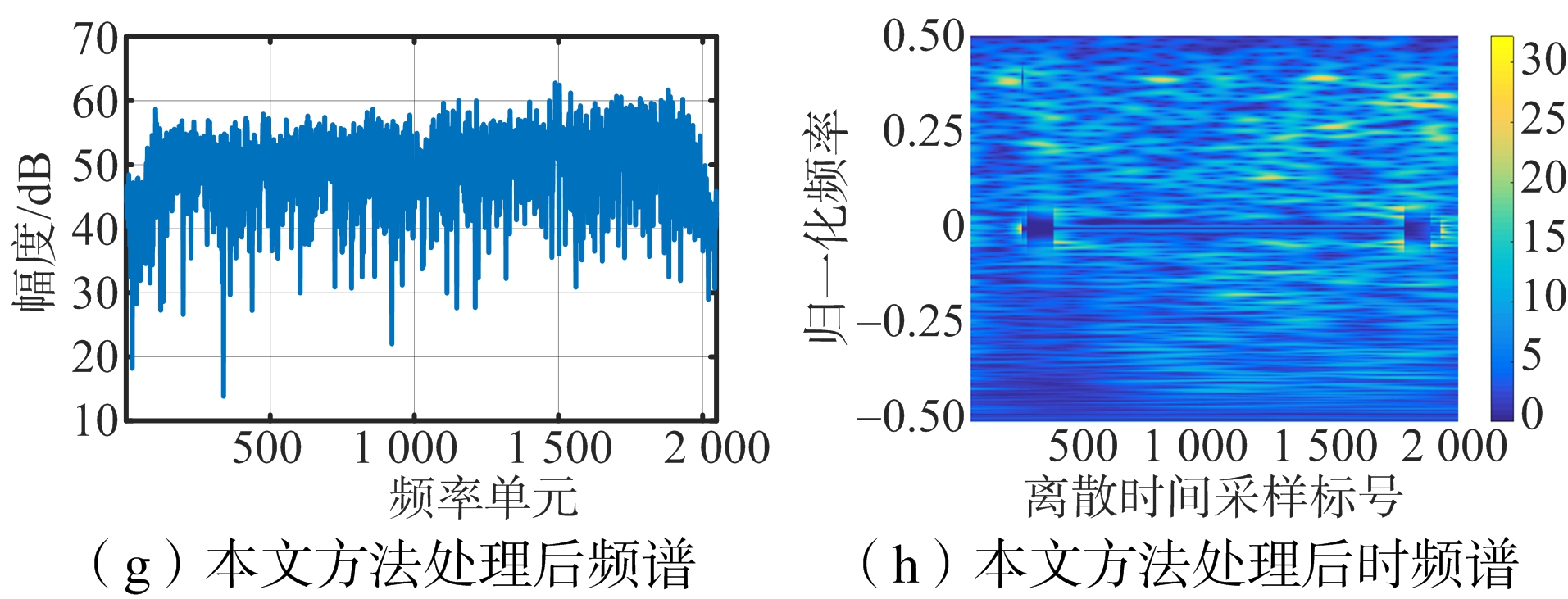
图2 距离向回波的干扰抑制分析
表2 距离向回波干扰抑制后的结果

干扰抑制方法ISR/dBSDR/dB频域陷波法13.05693.7389GST时频滤波法14.5807-19.1844
3.2 基于SAR回波的成像实验
为有效定量评估利用干扰抑制处理后的数据成像的结果,同样利用文献[13]中所采取的两个指标:对比度D和信噪比γ。两个指标值的大小与干扰抑制方法的有效性高低呈正相关。
如图3(a)为受到干扰影响的SAR回波数据成像结果(横向为距离向,纵向为方位向),可见RFI在SAR图像中的表现形式是沿着距离向密集的亮纹,该亮纹遮盖了图中的目标继而影响了图像的判读,使得后续基于SAR图像的各种应用变得困难。图3(b)为采用频域陷波法后的成像结果,RFI对成像的影响有所降低,干扰覆盖场景的轮廓可以分辨,但是仍然丢失了图像细节信息,原因是部分干扰的残留和处理造成的有用信号损失。图3(c)为利用本文所提方法得到的结果,场景轮廓很清晰,而且更多的细节信息被保留,成像质量明显优于图3(b)。同时表3中的图像对比度和信噪比指标的定量对比也证明了本文方法的有效性。


(c) 本文所提方法处理的图像
图3 干扰抑制成像结果
表3 干扰抑制后的成像结果
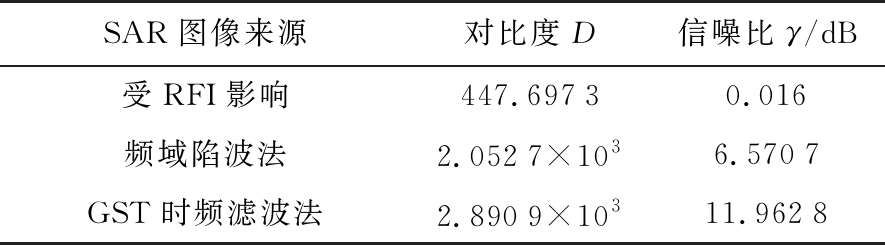
SAR图像来源对比度D信噪比γ/dB受RFI影响447.69730.016 频域陷波法2.0527×1036.5707 GST时频滤波法2.8909×10311.9628
4 结束语
针对SAR射频干扰抑制,本文提出一种基于GST时频滤波的方法。该方法在处理前首先进行RFI方位检测,提高了处理效率;同时在GST时频域进行子空间滤波处理,与频域陷波法相比,在抑制干扰的同时,尽可能地保留了有用回波信号,进而提高了SAR图像质量。实验的干扰抑制结果均表明所提方法优于频域陷波法。
[1] BOLLIAN T, OSMANOGLU B, RINCON R F, et al. Detection and Geolocation of P-Band Radio Frequency Interference Using EcoSAR[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing,2018,11(10):3608-3616.
[2] 李永祯, 黄大通, 邢世其,等. 合成孔径雷达干扰技术研究综述[J]. 雷达学报,2020,9(5):753-764.
[3] 黄岩, 赵博, 陶明亮,等. 合成孔径雷达抗干扰技术综述[J]. 雷达学报,2020,9(1):87-106.
[4] 王雅甜, 岳显昌, 张兰,等. 分布式地波雷达系统射频干扰抑制的研究[J]. 雷达科学与技术, 2017,15(5):537-543.
WANG Yatian, YUE Xianchang, ZHANG Lan, et al. Radio Frequency Interference Suppression for Distributed HF Surface Wave Radar System[J]. Radar Science and Technology, 2017,15(5):537-542.(in Chinese)
[5] BUCKREUSS S. Filtering Interferences from P-Band SAR Data[C]∥EUSAR’98 Conference, Friedrichshafen,Germany:IEEE,1998,98(5):25-27.
[6] ZHOU F, WU R, XING M, et al. Eigensubspace-Based Filtering with Application in Narrow-Band Inter-ference Suppression for SAR [J]. IEEE Geoscience & Remote Sensing Letters,2007,4(1):75-79.
[7] STRUNK K K, MWAVITA M. Paired Samples T-Test Case Studies, Design and Analysis in Educational Research [M]. London: Routledge,2020:205-210.
[8] 李燕,何怡刚, 于文新,等.广义S变换多分量LFM信号检测及参数估计[J]. 电子测量与仪器学报,2017,31(12):2056-2062.
[9] 吴鹏, 杨淋, 张永胜,等. 基于联合滤波的SAR射频干扰抑制方法[J]. 雷达科学与技术,2016,14(3):225-230.
WU Peng,YANG Lin,ZHANG Yongsheng,et al.A Combined Filtering Method for Radio Frequency Interference in SAR Data[J]. Radar Science and Technology,2016,14(3):225-230.(in Chinese)
[10] 李东, 占木杨, 方志平,等. 基于HAF的参数化SAR宽带干扰抑制[J]. 系统工程与电子技术,2017,39(3):514-521.
[11] 黄斌, 张宏兵, 王强,等. 广义S变换与短时傅里叶变换在地震时频分析中的对比研究[J]. 中国煤炭地质,2017,29(1):60-63.
[12] OUYANG X, AMIN M G. Short-Time Fourier Transform Receiver for Non-Stationary Interference Excision in Direct Sequence Spread Spectrum Communications [J]. IEEE Trans on Signal Processing,2001,49(4):851-863.
[13] 张双喜. 高分辨宽测绘带多通道SAR和动目标成像理论与方法[D]. 西安:西安电子科技大学,2014:166-170.
