0 引言
极化作为电磁波的基本物理参量,描述了电磁波的矢量特征。极化雷达可以测量目标形状、结构等丰富物理属性信息。利用目标极化信息可以有效改善和提高雷达目标探测、分类和识别以及抗干扰等性能,而目标极化信息的精确获取是极化信息利用的前提和基础[1]。随着极化雷达的发展,雷达技术实现了从“标量感知时代”到“矢量感知时代”的跨越发展,目标极化信息获取经历了由不完整极化信息向全极化信息获取的发展历程[2]。极化雷达具有其他雷达无法替代的突出优势,已成为导弹防御、空间监视、精确制导等领域的“尖兵利器”。随着相控阵雷达技术逐步发展成熟,将极化与相控阵雷达技术相结合,研究具有极化测量能力的极化相控阵雷达(Polarimetric Phased Array Radar,PPAR)是极化雷达发展的重要方向之一[3-4]。
1 极化相控阵雷达的发展
极化相控阵雷达已成功用于防空反导、空间监视和精确制导等尖端领域,是世界军事雷达技术竞争的战略制高点。上世纪80年代末,美国斥巨资研制了以GBR反导雷达[5](见图1(a))为代表的多部极化相控阵雷达,其基本性能和技术手段属于美国的国家机密,鲜有公开报道。

(a) GBR反导雷达

(b) LRDR远程鉴别雷达
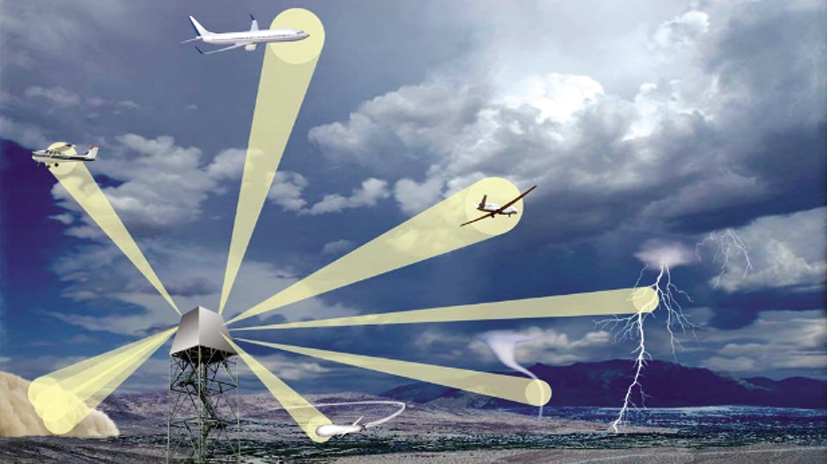
(c) MPAR示意图
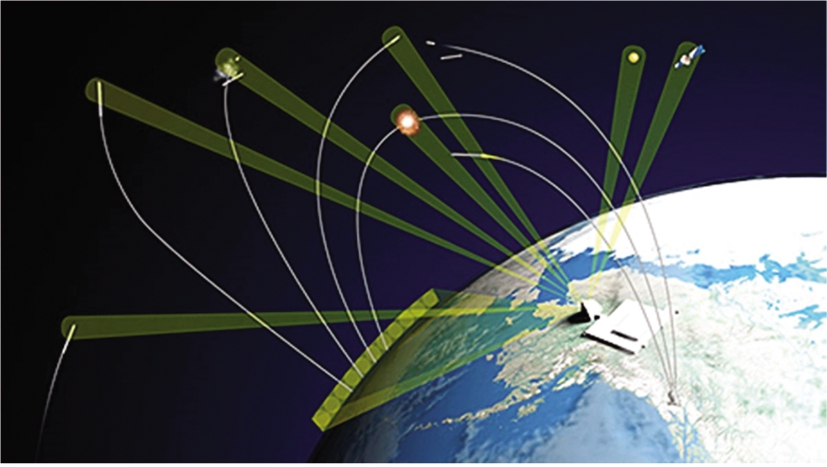
(d) LRDR示意图
图1 典型的极化相控阵雷达系统
近年来,美国等军事强国一直在开展极化相控阵雷达核心关键技术的研究,也从未停止极化相控阵雷达的建造升级步伐。比较有代表性的有美国的多功能相控阵雷达(Multi-function Phased Array Radar,MPAR)计划和远程鉴别雷达(Long Range Discrimination Radar,LRDR),如图1所示。MPAR是一部具有全极化测量能力的相控阵雷达(图1(c)),于2006年在美国运输部联邦航空局(FAA)、商业部国家海洋与大气局(NOAA)和国防部海军研究局三家单位联合资助下启动研制[6]。MPAR具备多功能能力,能够同时执行飞机跟踪、风廓线和天气监视、国土防御等任务。计划于2025年利用约365部多功能雷达替换350部飞机跟踪雷达和200部气象雷达。除此之外,MPAR的核心技术已在军事应用中得到验证。2020年,美国陆基中段弹道导弹防御系统的LRDR远程鉴别雷达(见图1(b)、(d))在阿拉斯加Clear空军基地即将投入使用。LRDR是一部双极化相控阵体制的远程鉴别雷达,利用了极化技术获取目标形状方面的信息,据称可以实现真假弹头识别,为陆基中段导弹防御提供关键技术支撑[7]。美国导弹防御局局长乔恩·希尔(Jon Hill)透露,LRDR将于2021年首次参加导弹防御系统作战试验。基于研制成本的考虑,LRDR选用了S波段,而非更有利于目标识别的X波段。尽管如此,得益于极化分集能力的LRDR仍具有真假弹头识别能力,这标志着美国极化相控阵雷达的极化测量与利用能力已经相当成熟。
近年来,我国在极化相控阵雷达基础理论、关键技术和系统研制等方面取得了长足进步,已有多部极化相控阵雷达相继问世。例如,航天科工23所研制的某大型相控阵雷达、中国电科14所研制的多型相控阵雷达和航天科工集团二院、三院研制的相控阵雷达导引头等已具备全极化测量能力。尽管现有极化相控阵雷达具备目标极化信息测量的基本物理条件,但就雷达目标极化信息利用而言,极化信息测量精度与实际应用需求之间仍存在突出矛盾。作为极化滤波和极化特征提取与识别的前提,极化信息测量的精度长期困扰着极化相控阵雷达的效能发挥,直接决定着极化信息能否“用得上、用得好”,是“卡脖子”关键问题。
从技术体制出发,深入剖析具体原因。相控阵雷达技术体制具有宽角扫描的特有优势,然而,波束扫描通常会带来增益下降、波束展宽和方向图对称性下降等问题。而对极化相控阵雷达而言,波束扫描还会使电场极化正交性下降,从而引起交叉极化耦合,进而导致极化测量误差。另外,为追求更高的目标分辨率,目前的防空反导、空间监视和精确制导等领域通常采用宽带雷达。鉴于极化的频率敏感性,实现对极化的精确控制则更为困难。上述问题严重限制了极化相控阵雷达的有效波束扫描范围,因此,“宽带”、“宽角扫描”、“极化”和“相控阵”的结合给极化精密测量带来了严峻挑战。
近年来,极化相控阵雷达技术迎来了快速发展期,有力推动了极化相控阵雷达在气象观测、防空反导、精确制导、空中管制等领域的广泛研究和应用[8-9]。当前,以美国、日本、中国等为主的世界大国均在极化相控阵雷达理论和系统研制上投入大量的力量和资源。下面对世界范围内的极化相控阵雷达系统进行介绍。
1.1 气象观测领域
2006年,美国启动了全极化多功能相控阵雷达(MPAR)研制计划[6],服务于飞机跟踪、风廓线和天气监视、空中交通管制、国土防御等任务。在MPAR计划的支持以及应用需求的牵引下,美国多所科研机构和工业部门开展了一系列研究,在相控阵雷达的双极化能力研究和系统研制方面取得了丰硕的成果。其中,有麻省理工学院林肯实验室(Massachusetts Institute of Technology Lincoln Laboratory,MIT LL)牵头的多平面阵方案,以先进技术演示样机(Advanced Technology Demonstrator,ATD)为代表;以及美国俄克拉荷马大学先进雷达研究中心(The University of Oklahoma Advanced Radar Research Center,OU ARRC)牵头的圆柱形相控阵方案,也称CPPAR(Cylindrical Polarimetric Phased Array Radar)。MPAR计划不仅应用于气象观测领域,还将应用于空中监视领域。
早在2007年,MIT LL就在FAA、NOAA和美国空军的资助下开发了8×8共64个发射/接收单元的双极化面阵(dual pol panel)[10]。经过几代的设计和改进,降低了成本并提高了性能和可制造性。如今,该面阵已发展到第5代,其中,第3代后较为成熟。第3代面阵的分解图如图2(a)所示,图2 (b)中的演示系统由两个面阵组成,用于演示验证重叠子阵波束形成技术。第4代面阵组成的十面阵演示机(Ten-Panel Demonstrator,TPD)如图3所示,主要目的是研究和验证收集双极化气象数据的能力。2017年,由76个第5代面阵组成的先进技术演示样机(ATD)(如图4所示)安装在NOAA的国家强风暴实验室(National Severe Storms Laboratory,NSSL),以演示验证MPAR的初步运行能力和探测性能,为下一步逐步替代现有多型雷达网作准备[11-12]。值得一提的是,MIT LL的面阵中每个阵元采用了平衡馈电多层双极化微带天线,以实现低交叉极化性能。同时,每个8×8面阵采用了一种独特的极化可重构发射/接收(Transmit/Receive,T/R)组件,并在ATD中采用了单芯片的重叠子阵波束形成网络。
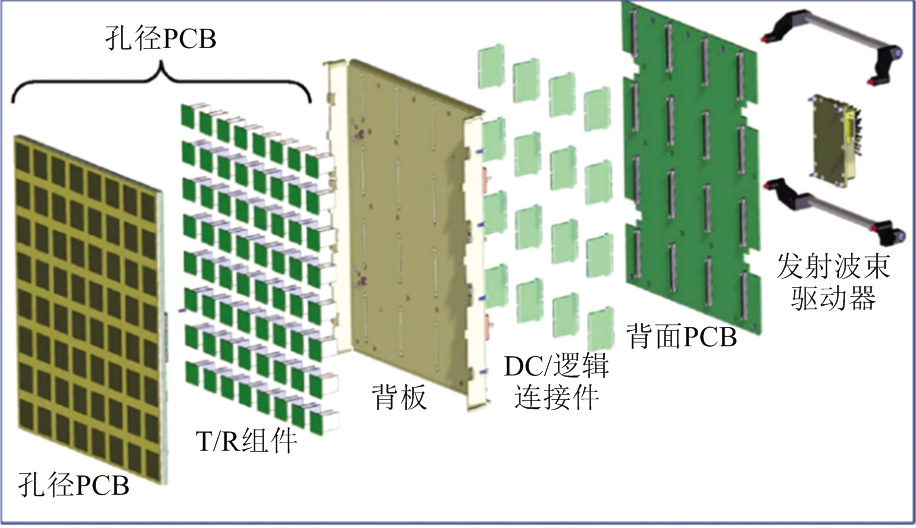
(a) 第3代面阵分解图

(b) 由两个第3代面阵组成的阵列
图2 MIT LL第3代双极化面阵

(a) TPD示意图
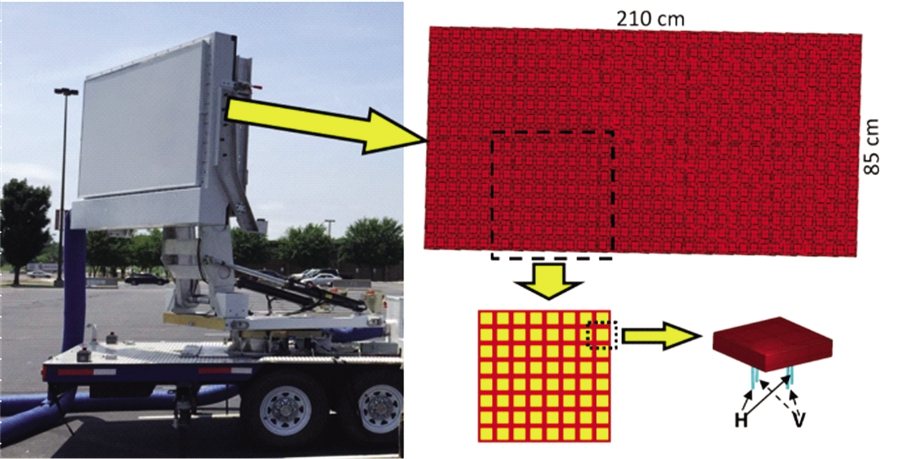
(b) TPD车载雷达系统
图3 MIT LL第4代面阵构成的TPD

图4 MIT LL第5代面阵构成的ATD
与此同时,OU ARRC研制了一种圆柱形极化相控阵雷达系统,即CPPAR系统[13]。CPPAR的共形天线设计方式不仅可以简化对每个波束的校准过程,使其具有匹配的主极化方向图,而且扫描时阵元分布的对称性会降低交叉极化水平。该系统的柱面共形天线具有96列一维频率扫描线阵,每一列包括19个双极化多层贴片阵元天线,如图5所示。在俯仰方向采用频率扫描方式,扫描范围为0°~20°,分别对应着2.7~3.1 GHz的频率范围。ATD和CPPAR两套系统各有优缺点,其参数和性能对比如表1所示。

图5 OU ARRC的CPPAR系统
表1 ATD和CPPAR性能参数对比
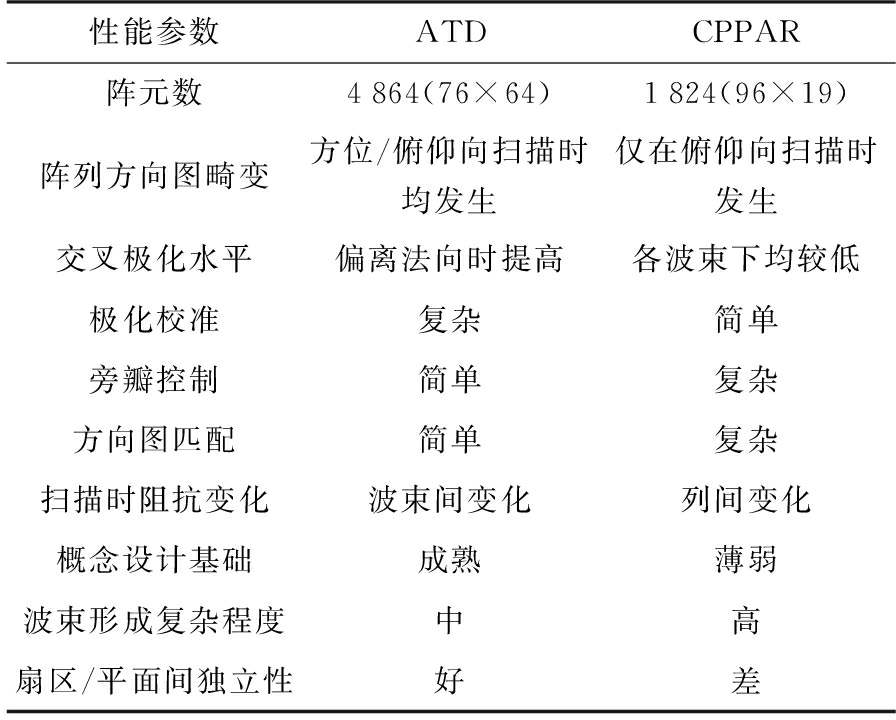
性能参数ATDCPPAR阵元数4864(76×64)1824(96×19)阵列方向图畸变方位/俯仰向扫描时均发生仅在俯仰向扫描时发生交叉极化水平偏离法向时提高各波束下均较低极化校准复杂简单旁瓣控制简单复杂方向图匹配简单复杂扫描时阻抗变化波束间变化列间变化概念设计基础成熟薄弱波束形成复杂程度中高扇区/平面间独立性好差
事实上,俄克拉荷马大学已经在极化相控阵雷达技术方面有着十多年的积累,目前也是全美唯一一所研制全数字极化相控阵雷达的大学。OU ARRC在近几年开发了移动式S波段的“阵元级”全数字化极化相控阵雷达原型样机,代号为Horus[14],如图6(b)所示。Horus的相控阵天线共有1 024个阵元,分为16个8×8的面阵,有着“阵元级”数字波束形成架构(见图6(a))。该系统可实现极化控制,可以发射单水平(Horizontal,H)极化、单垂直(Vertical,V)极化、斜45°极化、左旋圆极化(Left-Hand Circular,LHC)、右旋圆极化(Right-Hand Circular,RHC)或任意极化状态。同时,还具有灵活的波形,能够同时执行多种任务。基于与Horus同样的灵活阵列结构和数据网络,OU ARRC还开发了C波段极化大气成像雷达(Polarimetric Atmospheric Imaging Radar,PAIR)(见图6(c)),也为极化相控阵体制[15]。扫描方式为方位向机扫,俯仰向电扫。

图6 OU ARRC的全数字极化相控阵系统
值得一提的是,ATD和CPPAR的研发得益于多所科研机构多年的技术积累,更在于机构间的密切交流合作。在关键技术攻关上,除了MIT LL和OU ARRC,还有马萨诸塞大学、普渡大学、科罗拉多州立大学以及美国国家大气研究中心等科研机构。下面对其他科研机构的工作分别展开介绍。
马萨诸塞大学(University of Massachusetts)微波遥感实验室开发了一部X波段双极化相控阵雷达[16],也称PTWR(Phase-Tilt Weather Radar),如图7所示。PTWR为一维电扫有源相控阵雷达,在方位向上电扫,波束扫描范围为±45°,在俯仰向上机扫。相控阵天线为具有72列微带贴片天线的平面结构,其中,中间的64列分别由专用的发射/接收模块馈电,其余列不工作,这样设计的目的是为了降低阵列边缘的衍射和非均匀互耦的影响[17]。每列子阵由32个串联馈电的双极化口径耦合微带天线组成。与此同时,马萨诸塞大学对雷神(Raytheon)公司开发的低功率雷达(Low Power Radar,LPR)进行对比测试和极化校准,以期达到或接近当前双极化反射面雷达(如WSR-88DP)的极化测量精度[18],LPR如图8所示。

图7 马萨诸塞大学研制的PTWR原型系统

图8 雷神公司的LPR原型系统
LPR是X波段双极化相控阵雷达,包括20个瓦片结构,每个瓦片含128个微带贴片天线阵元,共计2 560个双极化阵元[19]。上述的PTWR和LPR的极化测量体制为“分时发射、分时接收”(Alternate Transmit/Alternate Receive,ATAR)模式。
俄克拉荷马大学和普渡大学(Purdue University)联合设计和研制了一种高度集成的双极化数字阵列雷达(Digitial Array Radar,DAR)原型系统[20],如图9所示。该系统受到美国陆军项目支持,阵列包含4×4个双极化天线阵元,每个双极化天线的两个极化端口分别连接独立的数字化T/R组件。

图9 DAR 原型系统
美国国家大气研究中心(NCAR)联合科罗拉多州立大学(Colorado State University,CSU)共同研制了一种机载双极化相控阵气象雷达[21],也称APAR(Airborne Phased Array Radar)。APAR有56个面阵,每个面阵有64(8×8)个辐射单元。该雷达作为美国下一代机载气象雷达,包含4个C波段的双极化二维电扫有源相控阵天线,如图10所示。该雷达计划安装在NCAR的C-130飞机后部机身两侧、机身顶部和尾部,并有三种工作模式:监视、多普勒和双极化反射率测量。
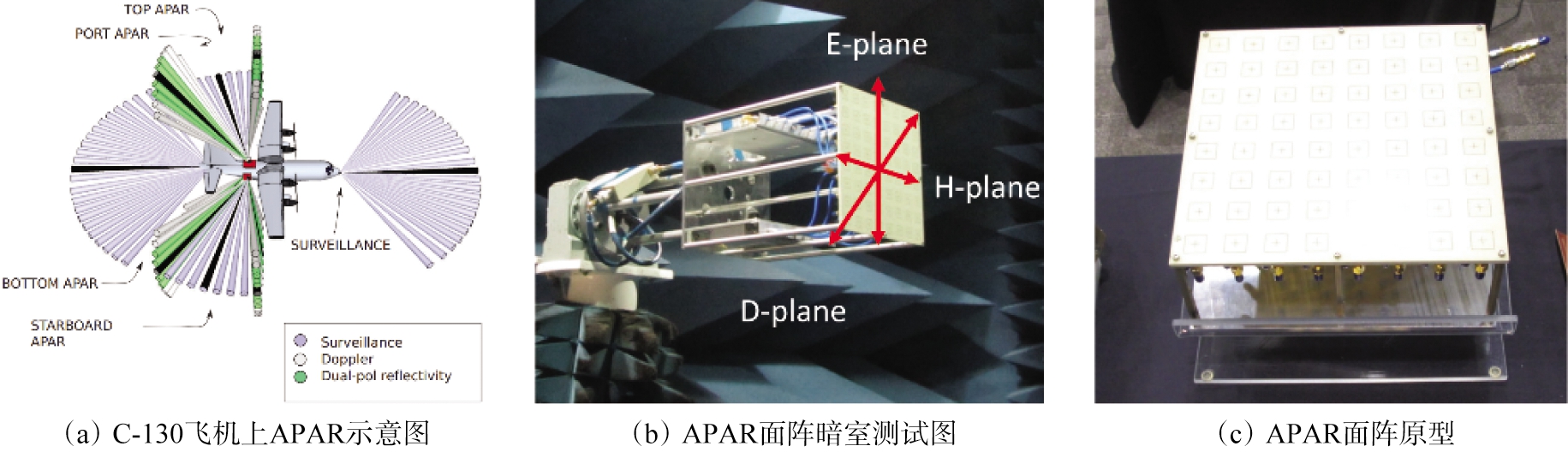
图10 NCAR和CSU研制的APAR原型系统
2012年,日本东芝(Toshiba)公司、大阪大学(Osaka University)和日本国家信息与通信技术研究所(NICT)联合研制了X波段相控阵气象雷达(Phased-Array Weather Radar,PAWR)[22],该雷达为单极化体制,如图11(a)所示。在此基础上,2014年上述机构联合日本气象厅开始开发双极化相控阵雷达(图11(b)),阵元为双极化口径缝隙耦合贴片天线。2018年,研制完成了双极化相控阵(多普勒)气象雷达(Multi-Parameter Phased-Array Weather Radar,MP-PAWR)[23],如图11(c)所示。MP-PAWR具有先进的数字波束形成技术,能够实现同时多波束。MP-PAWR的极化测量体制为“同时发射,同时接收”(Simultaneous Transmission and Simultaneous Reception,STSR)模式。该雷达能够获取高空时分辨率双极化信息,将是日本下一代气象雷达,计划服务于2021年东京奥运会。
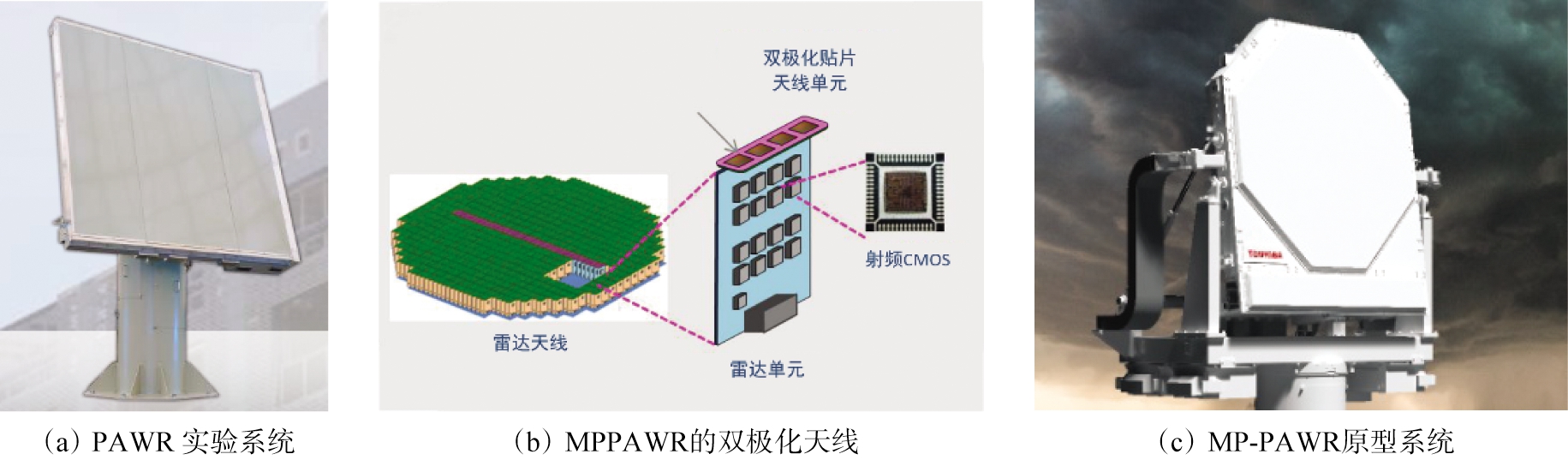
图11 日本的MPPAWR原型系统
近年来,我国在极化相控阵气象雷达研制方面也取得了重要进展,双极化相控阵雷达已经开始应用于我国的气象监测,它可以有效地提高雷达扫描的时间分辨率。利用相控阵雷达,可以在几十秒内得到天气系统的三维高精度信息。2010年,中国气象科学研究院与中国电科14所联合研制了我国首部S波段相控阵气象雷达[24],如图12(a)所示。该雷达采用了单极化工作模式,且为一维电扫体制,方位向机扫,俯仰向电扫。2016年,中国电科14所成功中标相控阵气象雷达,图12(b)为其C波段一维有源数字相控阵气象雷达,2019年9月投入运行并服务于北京大兴机场。2019年,中国航天科工二院23所研发的我国首部C波段相控阵气象雷达落成,如图12(c)所示,主要用于降水观测,可实现对龙卷风、冰雹、雷暴等灾害性天气实时监测。该型气象雷达采用全数字阵列和同时多波束接收技术,对天气的演变过程进行精细化探测。随着微波技术、微电子技术以及数字信号处理技术的迅速发展,极化相控阵天线逐渐成为相控阵雷达系统实现极化分集的主要途径,实现了由单极化相控阵雷达向双极化相控阵雷达的快速演进。中国电科14所旗下国睿科技股份有限公司(国睿科技)的X波段双极化一维相控阵雷达(见图13(a)),具有超低副瓣天线、高集成度收发数字化等技术。湖南宜通华盛科技有限公司(宜通华盛)的X波段双极化一维相控阵雷达(见图13 (b)),方位向机扫,俯仰向电扫,为双极化测量体制雷达。广东纳睿雷达科技股份有限公司(纳睿达)也有多款X波段双极化一维相控阵气象雷达,如图13(c)所示,其阵元采用微带贴片天线,可实现高交叉极化隔离度。

图12 我国的单极化相控阵气象雷达系统

图13 我国的X波段双极化相控阵气象雷达系统
1.2 射电天文领域
在射电天文学领域,极化相控阵同样受到重视和发展。2008年,首部双极化相控阵馈源(Phased Array Feed,PAF)样机部署在澳大利亚的帕克斯天文台(Parkes Observatory)[25],如图14(a)所示。2011年,荷兰射电天文研究所和瑞典查尔姆斯理工大学(Chalmers University of Technology)联合设计并研制了基于双极化PAF的射电天文望远镜[26]。图14(b)为荷兰射电天文研究所安装在荷兰北部Westerbork小镇的射电天文望远镜系统。PAF可以同时提供紧密重叠波束,大大提高天文望远镜视场。同时,PAF还具有极化分集能力,包括正交波束和本征交叉极化比。2017年,在德国普朗克射电天文学研究所的100 m口径埃弗斯堡(Effelsberg)望远镜上安装了PAF系统(图14(c)),用于脉冲星和快速无线电脉冲群搜索以及宽视场成像。

图14 基于PAF的射电天文望远镜
1.3 微波遥感领域
尽管极化相控阵雷达在气象领域发展迅速并已逐渐成熟,然而,极化相控阵雷达的最早应用却是在微波遥感领域。1994 年,美国宇航局(NASA)、德国航天局(DARA)和意大利航天局(ASI)合作开发的SIR-C/X-SAR在航天飞机上发射成功(见图15(a))。SIR-C/X-SAR是首个能够同时获得多频段雷达图像的星载合成孔径雷达(SAR)系统[27]。SIR-C也是首个能够同时进行4个极化分量测量(VV、VH、HV和HH)的星载SAR。SIR-C的天线由L波段和C波段的两个有源相控阵天线组成,每个阵列的阵元为双极化微带天线,每个极化端口由单独的馈电网络馈电。在当时,人们不仅意识到了宽带在描述目标特性上的潜力,也认识到极化在表征目标散射机理上的先天理论优势。由于受限于波束扫描角度,极化相控阵雷达在微波遥感领域相对缓慢。
21世纪初以来,随着雷达极化测量技术发展进入繁荣期,极化信息理论在微波遥感领域也得到了极大发展和广泛应用。极化相控阵雷达技术与SAR/InSAR的结合成为更具前景的研究和应用方向。各国研制了多个星载极化SAR系统:2007年德国宇航中心发射了TerraSAR-X星载极化SAR[28](见图15(b))、2007年加拿大发射了RADARSAT-2星载极化SAR[29](见图15(c)),可用于危害监测、土壤湿度估算、积雪和水含量估算、森林传感、城市规划、洋流和波浪动力学传感以及地球物理应力变化评估等。

图15 典型的星载极化SAR系统
近年来,我国极化相控阵雷达系统的关键器件和工艺水平提升很快,成功研制了多套相控阵体制极化SAR系统。具有代表性的有:2009年中国电科38所研制的机载极化SAR——POLINSAR[30]、2016年发射的首颗全极化星载极化SAR——高分三号卫星[31]等。高分三号卫星搭载的C波段多极化SAR具有条带、聚束、扫描等12种成像模式,空间分辨率可达1 m,是目前国际上较为先进的星载SAR之一[32]。另外,中科院电子所也研制了极化相控阵体制的机载极化SAR系统[1]。
1.4 防空反导领域
根据美国导弹防御局(MDA)的合同要求,自2015年起,洛克希德·马丁(Lockheed Martin,以下简称洛马)公司开始开发、测试和建造远程鉴别雷达LRDR,主要用于精确跟踪和识别,原计划于2020年在阿拉斯加Clear空军基地服役,如图16所示。LRDR是一部S波段双极化相控阵体制的远程鉴别雷达。基于成本的考虑,LRDR并未选择更具目标识别能力优势的X波段,而是选用S波段。LRDR采用了双极化测量体制,能够获取目标形状方面的信息,据称可以实现真假弹头识别,为陆基中段导弹防御提供关键技术支撑[7]。另外,LRDR系统具有两个天线阵面,每个阵面具备120°的方位覆盖范围,因此雷达具有约240°的方位角视场。图16(c)所示为洛马公司在其位于新泽西州摩尔斯敦(Moorestown)厂区建立的一个缩小版LRDR原型系统,能够测试LRDR系统90%的指标需求。除了具有双极化测量能力,该雷达系统还在T/R组件中使用先进的氮化镓(GaN)技术,以更低成本实现了更高功率和效率。

图16 远程鉴别雷达(LRDR)系统
1.5 精确制导领域
国外在相控阵雷达导引头方面的发展已经较为成熟,目前主要为单极化体制。例如,日本三菱于2001年启动的AAM-4改进型AAM-4B空空导弹,已于2012年列装。该导弹的雷达导引头为J/APG-2型有源相控阵雷达导引头,Ka波段,这也是空空导弹首次采用有源相控阵末制导导引头。俄罗斯于2013年首次对外披露了R-77的升级型K-77M空空导弹,该导弹采用64单元有源相控阵雷达,如图17所示。同年,美国雷神公司就开始研发被动/主动导引头,并准备将其集成到“战斧”Block IV巡航导弹上。2014年,洛马公司推出一款新式空空导弹,该导弹采用了先进的多波段多模有源相控阵雷达导引头,融合了宽频带被动高精度射频接收器和双波段(C 波段和Ka波段)有源相控阵主动导引头[33]。2015年,美军开始秘密研制新型远程交战武器(LREW),采用有源相控阵雷达导引头,计划搭载到F-22和F-35战机上。2017年,日本与英国合作开发搭载于F-35战机的联合新型空空导弹(JNAAM)的初步研制工作,同样采用了有源相控阵雷达导引头。俄罗斯和印度于2019年联合研制完成下一代“布拉莫斯”(BrahMos-NG)“轻量化”巡航导弹,拥有陆基、机载、舰载和潜艇发射型号。其中,相控阵雷达导引头是其中的关键技术之一。可见,美、俄、日、英、印、意等国的相控阵雷达导引头技术正在快速发展。无论是对现有型号升级改装或者新研制,基本上采用了有源相控阵体制。从用途上看,有反辐射、空空、反导、巡航、反舰、弹道等导弹种类;从相控阵天线类型上看,有平面阵和共形阵。

图17 国外相控阵雷达导引头
由于涉密等原因,目前公开的关于极化相控阵雷达导引头的文献报道较少。不过,在极化雷达导引头方面,相关的系统并不少见。1995年,美国研制的“长弓海尔法”(Long-bow Hellfire)AGM-114L空地导弹(见图18(a)),采用了8 mm波长双极化雷达导引头,能够实现轮式车、履带车、地面防空单元等目标的分类。同年,由英国MBDA公司研制的“硫磺石”(Brimstone)空地导弹配备3 mm波长雷达导引头。借助于高距离分辨和双极化测量技术,可以对装甲车、地面防空单元和武装运兵车进行分类[34](见图18(b))。另外,美国休斯(Hughes)公司研制的AIM-4“猎鹰”X波段半主动雷达寻的导引头也为双极化体制,水平极化天线为微带馈电缝隙波导阵列,垂直极化天线为微带偶极子阵列(见图18(c))。

图18 国外双极化雷达导引头
近年来,我国相控阵雷达导引头技术发展迅速,且逐步占据了雷达导引头的主导地位。随着极化雷达系统的关键器件和工艺水平的不断提升,中国航天科工二院25所、三院、八院802所和航天科技九院704所等均研制了具备极化测量能力的多种类型极化相控阵雷达导引头,中国电科38所研制了主/被动复合制导双极化相控阵导引头。当前,我国在相关技术上已经接近和达到实用要求。部分高校也在极化相控阵雷达导引头实验平台方面进行了积极探索。哈尔滨工业大学乔晓林教授团队研制了一种反舰导弹极化雷达导引头,对箔条和舷外有源诱饵等干扰样式具有良好的抗干扰性能。南京理工大学设计了一种8.75 GHz频段的四源端馈双极化方形微带相控阵天线,天线带宽为150 MHz,天线增益为12.4 dB,天线端口隔离度在-25 dB以下,通过外围幅度控制(放大器)和相位控制电路(移相器)可组成有源变极化发射系统[35]。电子科技大学徐军教授开展了毫米波相控阵雷达导引头研制,完成了相控阵阵面、波束控制以及T/R组件等多项关键技术,研制出对海弹载雷达导引头原理样机,并完成了海面环境性能试验验证,如图19(a)所示。国防科技大学柴舜连教授研制了S波段全极化微带共形相控阵实验样机系统(图19(b)),并开展了全极化数字波束形成实验。该团队研制的全极化共形相控阵天线可实现多个发射通道的精确幅相控制与通道校准,并且能够实现信号幅度的大范围动态调整[36]。

(a) 电子科技大学毫米波雷达导引头

(b) 国防科技大学全极化共形相控阵天线
图19 相控阵雷达导引头实验平台
此外,我国还有多个在研的相控阵雷达系统具备全极化测量能力,如在远程预警领域,航天科工二院23所在研的某大型相控阵雷达;在反导和(临近)空间目标监视领域,中国电科14所在研的某型相控阵雷达。总体而言,我国在极化相控阵雷达技术方面取得了长足进步,其硬件平台的性能指标已趋于国际先进水平。
综上所述,随着微波器件与工艺水平、数字信号处理技术的进步,极化相控阵雷达迎来了发展高潮。纵观国内外极化相控阵雷达技术的研究现状及发展趋势,具有以下特点:
① 研究的重点集中在,低成本高可靠T/R组件研制、极化测量对雷达系统性能提升作用,以及极化带来的多通道信号处理问题。
② 涉及的关键技术有,极化测量误差校正、极化信息的精确获取以及极化分类与识别应用。
③ 未来的发展方向,由气象探测、天文观测、微波遥感等民用领域与防空反导、精确制导、远程预警、空间目标监视等军事领域并行发展,相互促进,呈现出蓬勃发展态势。
随着相控阵雷达技术和系统建设更加成熟,极化相控阵雷达的关键技术重点在于因引入极化而带来的一系列问题。可以预见,极化相控阵雷达将成为相控阵雷达甚或是雷达的重要发展方向之一,并推动相关技术在各个领域发挥积极作用。
2 相控阵雷达的极化测量关键技术
随着极化相控阵雷达技术在气象观测、防空反导和精确制导等领域中的应用日益深化,极化信息测量精度与极化相控阵雷达应用需求之间的矛盾愈加凸显,促使雷达极化测量向精密测量时代迈进。极化测量精度已经成为制约极化相控阵雷达效能发挥的核心关键,困扰着极化相控阵雷达的推广应用,亟待发展能够提升极化信息精确获取能力的关键技术和手段[37-39]。
2.1 极化测量误差校正技术
对于极化相控阵雷达而言,具有两个正交极化通道的天线阵元可以构成极化相控阵天线,用于发射与接收空间中两个正交的电磁波,即极化相控阵天线具有两个独立的极化分集波束。为产生具有正交的电场极化,双极化天线阵元的两个极化端口一般采用相同的结构和馈电方式。然而,在偏离天线平面法向时,双极化天线阵元的电场极化通常不再正交[40],如图20所示。图20描述了正交无限小电偶极子天线的辐射场,红色箭头表示沿X轴放置的电偶极子的辐射电场,蓝色箭头表示沿Y轴放置的电偶极子的辐射电场。在天线平面的法线上,两个电偶极子的辐射电场幅度相同且方向完全正交;在偏离平面法线后,在水平和垂直两个主平面上,两个辐射电场幅度不同但方向不完全正交;在其他主平面,特别是斜对角平面上,两个辐射电场不仅幅度不同而且方向正交性恶化十分严重。这种非正交性会给接收通道带来交叉极化耦合,从而导致极化测量结果存在严重的系统性误差,这对极化精密测量而言是不可忽视的[37]。测得的目标极化散射矩阵不能客观反映目标的实际散射特性,从而给相控阵雷达极化精密测量带来了新挑战。
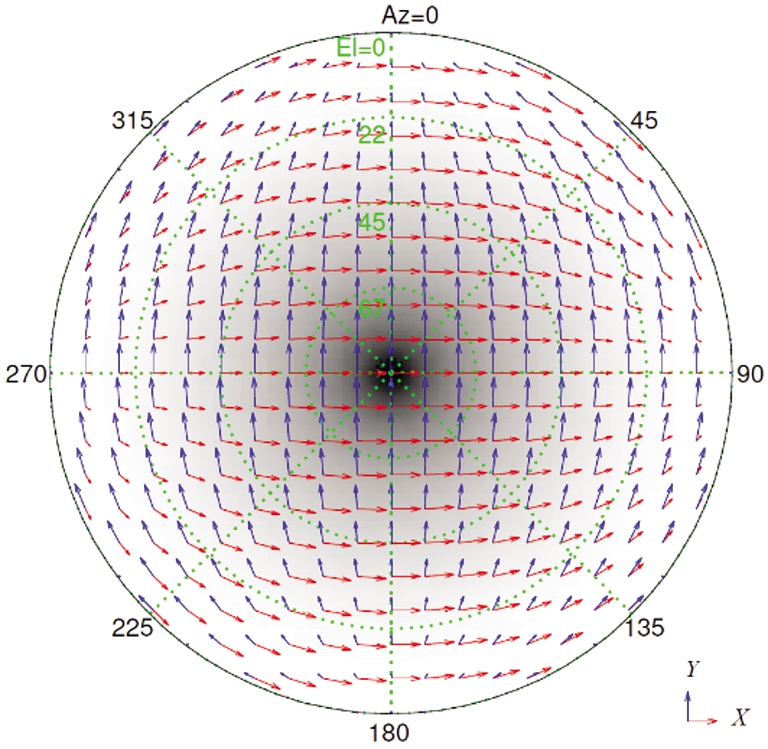
图20 正交无限小电偶极子辐射场
同时,在宽带情况下,电磁波各个频率分量所对应的极化状态有所不同。对此,国防科技大学的王雪松教授团队对宽带极化信息处理展开深入研究[41],在其博士论文中详细论述了电磁波极化随频率的演化、分布特性。对于极化相控阵雷达而言,极化状态与频率的耦合关系则表现为辐射电场极化非正交性随频率而变化。从系统层面上,宽带雷达系统的幅频特性和相频特性改变了信号波形,从而导致不同频点下极化状态的起伏特性。综上所述,极化非正交性和宽带条件下的极化状态起伏特性,已成为制约宽带相控阵极化测量精度的关键因素。要实现目标极化散射特性的精密测量,需要在理论模型和补偿技术上寻求降低测量误差的新途径、新手段,这也正是极化测量误差校正面临的新挑战。
有关相控阵雷达系统内部非理想性和外部环境给极化测量带来的误差已经有较多研究,并提出了一系列校准/校正方法。在极化测量中,“校准”更加侧重于对雷达系统非理想性的修正,如对H和V通道的幅相失衡进行修正;“校正”则更加侧重于对极化信息测量结果的偏差进行修正,如对测量得到的极化散射矩阵的修正[4]。我们这里重点梳理因波束扫描而带来的极化测量误差。与反射面天线不同,相控阵天线在偏离法向扫描时引起的极化波束形状失配和交叉极化耦合会产生极化偏差[37,42],这是相控阵雷达的显著特点[10]。虽然这些偏差在偏离角度不大时很小,但在进行差分反射率(ZDR)或主极化相关系数(ρHV)等极化变量的测量时,波束扫描则会产生显著的测量偏差[43]。下面从减少误差来源和测量误差校正两个方面阐述。
(1) 减少误差源方面
NOAA的Stailey等人在关于MPAR的综述中指出[10],当波束指向不偏离天线的水平或者垂直主平面时,天然具有较高的交叉极化隔离度,并在理论上能够满足极化精密测量需求。可见,一维电扫可以降低误差源,这一观点在两类系统中得以验证。① 一维电扫的平面相控阵。例如,马萨诸塞大学研制的一维电扫的PTWR系统[16,44]。在方位向上采用电扫方式,扫描范围为±45°,在俯仰向上采用机扫方式。另外,该天线阵(共72列子阵)在天线结构设计上也能够降低误差源。阵列中间的64列由专用T/R模块馈电,两侧的其余8列用作端接虚拟单元,以尽量减小阵列边缘衍射效应。PTWR系统的这种扫描方式和天线结构减少了所需的T/R模块的数量,从而显著地降低了总体系统成本和复杂性,更重要的是从源头上减小波束扫描引起的误差。国内的双极化相控阵气象雷达基本上采用了一维电扫方式,如图13所示的系统。因此,结合电扫和机扫两种方式,使相控阵天线仅在天线主平面进行扫描,交叉极化隔离度更容易保证。但是,一维扫描方式的缺点在于没有充分利用阵列二维电扫的优势,机扫方式的利用在一定程度上提高了扫描时长。② 一维电扫的圆柱形相控阵。例如,俄克拉荷马大学的CPPAR系统[45](见图5)。在方位向上通过阵列工作扇区的转换进行波束扫描,也可以同时形成多个波束,每个波束由圆柱形表面的阵列扇区产生,其波束方向总是过圆柱的圆心线,即波束垂直于阵列扇区的切面。加之扇区内天线结构的对称性,因此,极化波束的正交性可以保证。在俯仰向上采用频率扫描方式,利用2.7~3.1 GHz的频率实现0°~ 20°的扫描范围。在理论上,CPPAR的天线结构和俯仰频率扫描方式将极化正交性与波束扫描完全解耦合,使得所有方向上的极化正交性都保持不变,从而减少误差源。然而,CPPAR系统的代价包括更高的复杂度和更高的成本,及其对阵列自适应扫描能力的影响[10]。
当然,除了在扫描方式和阵列天线结构设计上的探索,波形设计也是一种有效的方法。具体来讲,利用对脉冲间信号的相位编码技术可以有效消除一阶交叉极化项,降低交叉极化耦合对极化信息测量的影响。![]() 和
和![]() 提出了脉冲编码方法,可以将STSR模式下45 dB的交叉极化隔离度约束松弛到25 dB[46-47]。同时,针对多普勒数据采集中的系统编码应用,接着提出了时间复用H和V脉冲,同样可以将交叉极化隔离度约束松弛到25 dB。然而,
提出了脉冲编码方法,可以将STSR模式下45 dB的交叉极化隔离度约束松弛到25 dB[46-47]。同时,针对多普勒数据采集中的系统编码应用,接着提出了时间复用H和V脉冲,同样可以将交叉极化隔离度约束松弛到25 dB。然而,![]() 提出的脉冲编码方法在降低差分反射率误差的同时却提高了主极化相关系数估计误差。针对此问题,
提出的脉冲编码方法在降低差分反射率误差的同时却提高了主极化相关系数估计误差。针对此问题,![]() 改进了相位编码方法,使得在保持差分反射率误差抑制效果的同时,降低主极化相关系数和差分相位误差。在此基础上,接着在麻省理工学院林肯实验室(MIT LL)的ATD原型样机(见图4)上进行试验测试[48],验证了相位编码方法在抑制交叉极化方向图上的良好效果。以上文献在时域上对信号进行处理和分析,但尚未对频域上的影响进行研究。为此,文献[49]研究了相位编码下交叉极化耦合对多普勒谱估计的影响。
改进了相位编码方法,使得在保持差分反射率误差抑制效果的同时,降低主极化相关系数和差分相位误差。在此基础上,接着在麻省理工学院林肯实验室(MIT LL)的ATD原型样机(见图4)上进行试验测试[48],验证了相位编码方法在抑制交叉极化方向图上的良好效果。以上文献在时域上对信号进行处理和分析,但尚未对频域上的影响进行研究。为此,文献[49]研究了相位编码下交叉极化耦合对多普勒谱估计的影响。
然而,相位编码技术也不可避免地存在缺点和局限性。正如![]() 在文献[48]中总结到,尽管相位编码能够有效地消除一阶交叉极化项,将交叉极化要求降低到“交替发射,同时接收”(Alternate Transmission and Simultaneous Reception,ATSR)模式下的要求(-25 dB),但是该方法的局限性在于:如果交叉极化水平较高,则会导致ρHV的估计误差;任何信号设计/处理程序都不能消除二阶耦合,即使在ATSR模式下也存在二阶耦合。不过,相位编码仍然是STSR模式下显著降低交叉极化要求的最直接方法。
在文献[48]中总结到,尽管相位编码能够有效地消除一阶交叉极化项,将交叉极化要求降低到“交替发射,同时接收”(Alternate Transmission and Simultaneous Reception,ATSR)模式下的要求(-25 dB),但是该方法的局限性在于:如果交叉极化水平较高,则会导致ρHV的估计误差;任何信号设计/处理程序都不能消除二阶耦合,即使在ATSR模式下也存在二阶耦合。不过,相位编码仍然是STSR模式下显著降低交叉极化要求的最直接方法。
(2) 测量误差校正方面
对于现有的极化相控阵雷达实验平台或者原型系统,更多的还是采用二维(方位和俯仰)电扫方式进行波束扫描。如MIT LL的先进技术演示样机ATD、雷神公司的低功率雷达LPR系统,以及日本大阪大学的MP-PAWR。针对波束扫描导致的极化测量误差,俄克拉荷马大学的Zhang等人提出了基于投影矩阵(Projection Matrix)的误差校正方法,并基于无限小交叉电偶极子天线在理论上验证了方法的可行性[37],该方法通过对测量的散射矩阵进行乘积操作可以消除误差。文献[39]将文献[37]中的交叉电偶极子天线阵元扩展到其他天线类型,如理想的口径天线和贴片天线阵元,并给出了ATSR和STSR模式下的校正矩阵。Staiman将文献[37]中的交叉电偶极子天线阵元扩展到阵列天线,分析了信号幅度、发射和接收信号中的相位不平衡、阵元交叉极化特性和天线阵列倾斜对差分反射率ZDR测量精度的影响[50]。Fulton将文献[37]中的误差校正方法应用到数字相控阵雷达系统中,用S波段8阵元双极化数字阵列雷达(DAR)试验平台(见图9(b))演示了校准和补偿技术,并建立了系统模型和校准流程,接着分析了不同的校准误差对整体性能的制约。本质上讲,投影矩阵由某个波束扫描角度下的辐射方向图构成,再取投影矩阵的逆矩阵推导出误差校正矩阵。然而,所采用的辐射方向图通常根据阵列方向图乘积定理得到[10,51],即通过阵元方向图乘以阵因子。严格来讲,由此得到的校正矩阵并不一定能满足要求,这是因为由各种非理想因素带来的阵元方向图各异性会引入新的误差。针对天线方向图测量误差问题,国防科技大学庞晨博士定义了分别针对发射方向图和接收方向图的两个校正矩阵,提出了轴向校正法,将文献[37]中的校正方法由“阵元级”扩展到“阵列级”[52]。该方法可以校正由极化相控阵天线波束中心指向上辐射电场极化非正交性所引起的极化测量误差,并分析了ATSR和STSR两种极化测量模式下的极化误差校正性能。在此基础上,针对宽波束和分布式目标条件下,整个波束内辐射场极化非正交性对极化测量产生的影响,庞晨又接着提出了全方向图校正法[53]。同时,针对宽带宽角扫描相控阵雷达极化测量误差校正难题,国防科技大学王雪松教授团队提出了迭代频带划分方法,在降低误差校正复杂度的同时显著提高了极化测量精度。
然而,上述的极化测量误差校正方法仅是从理论或者仿真层面上验证了可行性,其中,天线是理想或者仿真的天线阵元,校正矩阵由理论或仿真方向图组成。在实际的极化相控阵雷达系统中,特别是小规模阵列,不可避免地会受到阵元间互耦[54]、边缘衍射效应[55]和阵元缝隙间隔[56]等影响,这些因素将导致辐射方向图的畸变,从而改变校正矩阵。针对小规模阵列中的互耦效应,马萨诸塞大学的Orzel等人开发了现场校准技术,并在其研制的PTWR系统上进行了测试。幸运的是,对于较大阵列,波束中心处的极化基本不受互耦效应、边缘衍射效应和阵元缝隙间隔的影响。因此,需要基于实际情况和测量数据实现校正过程。对方向图进行测量分为近场测量和远场测量,两种方式各有优缺点,且各自的影响因素各不相同[57]。MIT LL的Kowalski等人在暗室内对ATD进行了近场测量和校准[11-12]。近场测量通常用于初始校准,原则上也可以提供极化校正[58]。为了避免近场测量中阵列的多轴旋转问题,OU ARRC正在探索利用安装在无人机(Unmanned Aerial Vehicle,UAV)上的探头对雷达进行远场测量,分析了无人机位置、外部误差导致的天线测量误差,提出无人机远场测量是未来实现天线特性描述和天线极化测量误差校正的一种可行手段[59]。
2.2 天线方向图重构技术
由2.1节中所述,电磁波极化的非正交性在不同波束指向上各不相同,即图20所示的极化非正交性具有空变性,究其原因在于,极化相控阵天线的工作原理是利用各极化阵元的空域极化特性。进一步地,从正交无限小电偶极子的空域极化特性来描述角度偏离天线法线带来的交叉极化耦合,仿真结果如图21所示,其中,已经对主极化方向图进行归一化,并基于主极化归一化了交叉极化方向图。可见,水平和垂直电偶极子的主极化随着偏离角度的增大而降低,水平电偶极子的交叉极化随着偏离角度的增大而增加。交叉偶极子天线的主极化分量和交叉极化分量均具有空域非均匀性的特点[3,37]。对此,相关测量实验已经证实,当交叉极化与系统隔离度相当时,极化测量结果将不可接受[60]。
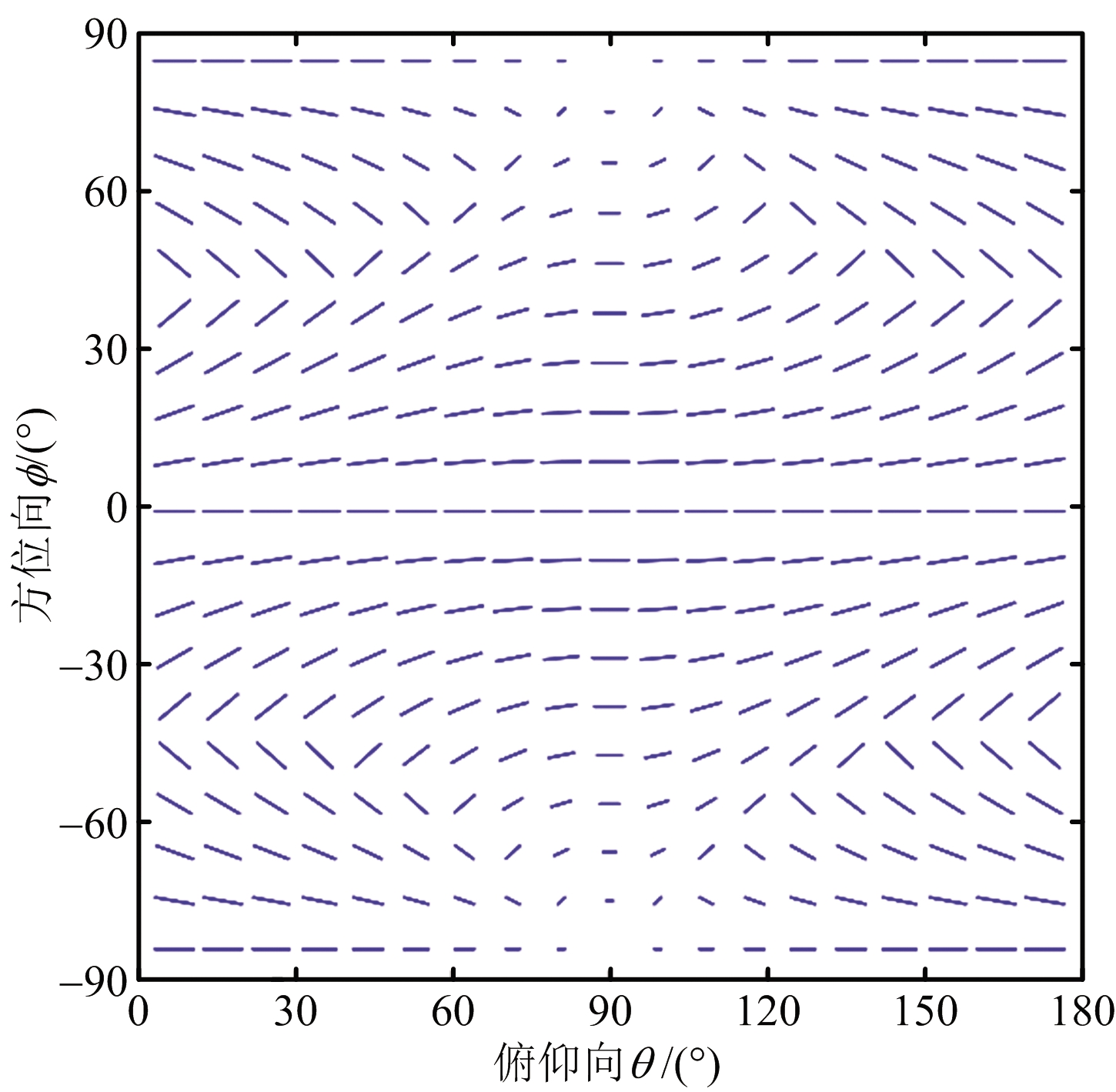
(a) 水平偶极子
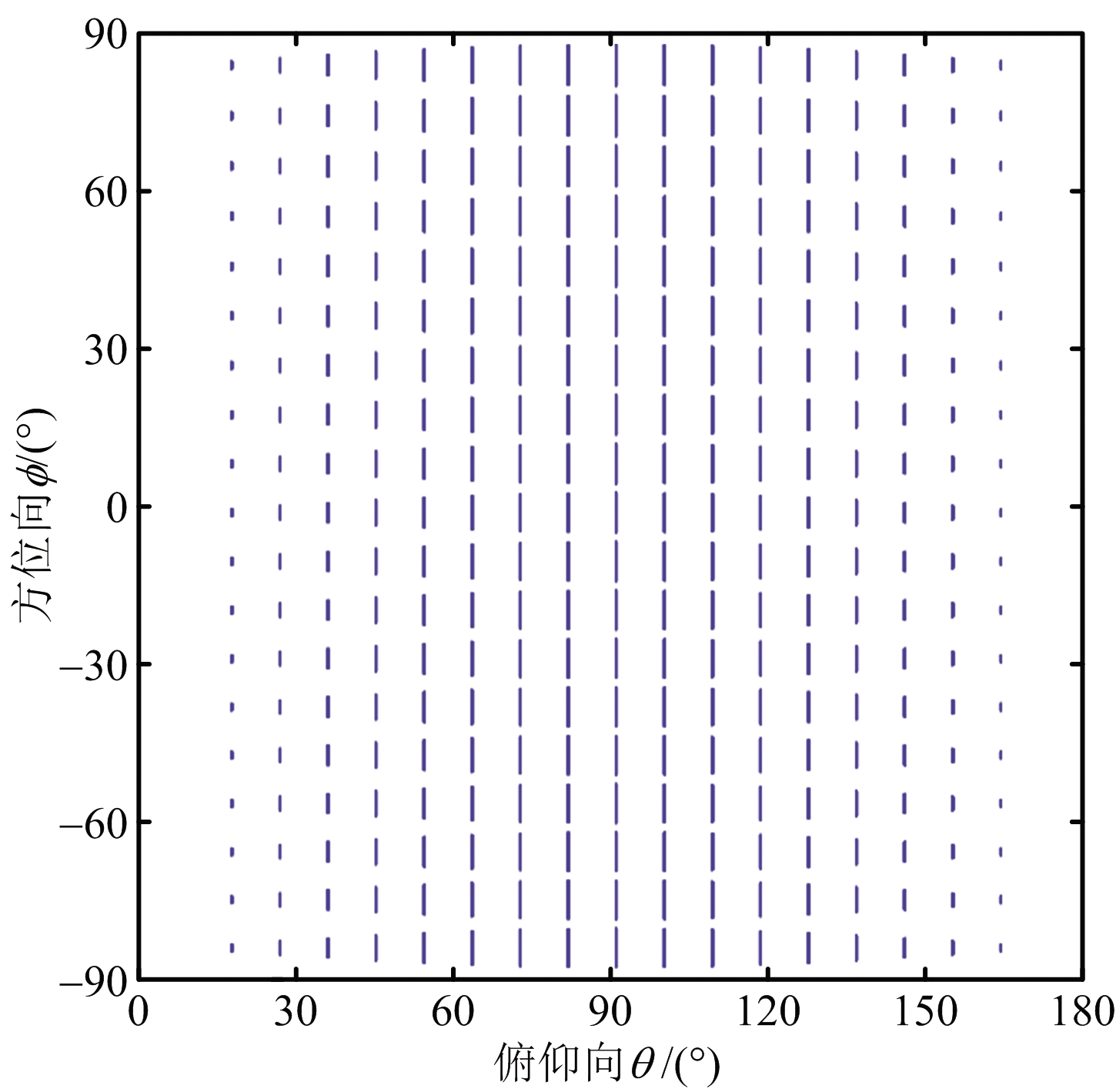
(b) 垂直偶极子
图21 正交无限小电偶极子极化方向图
上文2.1节所述的极化测量误差可通过特定的校正方法降低[37]。其中,误差校正方法的前提条件是获取天线的完整方向图特性,以构造校正矩阵实现误差校正。对于极化相控阵雷达,需要逐个波束进行极化校准[44]。然而,极化相控阵天线波束的快速电扫带来了数量巨大的波位数。理论上讲,只要极化相控阵天线在某个波束指向下工作,则需要对当前波位下的天线方向图进行测量,再利用文献[37]中的投影矩阵法进行测量误差校正。因此,极化相控阵天线方向图的测量是一个十分耗时且复杂的问题,给极化精密测量带来了新挑战。
对于气象观测或空间监视应用背景下的大规模相控阵天线,在暗室内通常难以满足天线辐射远场条件,而在外场进行测试将不可避免地引入杂波、多径效应等更为复杂的测量误差。另外,天线的波束扫描范围更宽,一般包括成百上千个波位,逐个波位进行天线方向图测量是一个十分耗时耗力的工程问题。例如,对于MIT LL研制的极化相控阵雷达(如ATD系统,如图4所示),波位数约为5 400个[61]。对于精确制导应用背景下的小规模相控阵天线,其波束扫描范围较窄,波位数相对更少,极化测量的精度有赖于天线方向图测量的精度。由此可见,如何快速、准确地获取所有可能波位下的天线方向图是极化相控阵雷达测量误差校正面临的新难题。
对于二维电扫极化相控阵雷达极化测量误差的校正更加复杂,但考虑到实际天线方向图的非理想性,因此研究二维电扫下的校正问题更具代表性。2.1节已提到,误差校正的重点和难点在于获得校正矩阵。完备的校正矩阵将通过在所有扫描角度上测量相控阵天线的极化方向图特性来确定[50]。为了快速、准确地获取极化相控阵天线各个波位下的方向图特性,可采用天线方向图重构技术。通过梳理现有文献,常见的方法可分为两类:
(1) 从主平面二维到完整二维
天线的制造商通常仅提供两个平面的天线辐射方向图,如水平方向图和垂直方向图,即二维(Two-Dimensional,2D)方向图。鉴于对三维(Three-Dimensional,3D)辐射方向图的需求,文献[62]提出通过对最接近的4个已知采样点进行加权,计算插值增益,具体取决于每个采样点的角度间隔。该方法在定向的二元偶极子阵列中显示出中等精度,但没有考察方向性较好高的基站天线的情况。这种插值方法的主要缺点在于不能精确地重构全向方向图。以半波长偶极子为例,内插方向图和理论方向图之间的最大偏差为12 dB。鉴于此,文献[63]提出了基于模型的参数估计算法,文献[64]对此作了进一步扩展,用于在空域和频域内插值辐射方向图。Araujo Lopes等人则给出了生成3D方向图的经验公式,但未采用统计方法评估其性能[64]。文献[65]利用了典型的数学插值方法(如三次样条曲线),通过有限的一组2D方向图的测量数据来近似重构3D方向图。该方法仅对比了不同插值样本数对应的重构方向图来评价算法性能,而并未与天线理论方向图进行对比。
针对以上算法的局限性,Vasiliadis等人提出了基于两个2D方向图外推出3D辐射方向图的混合算法[66]。该算法不仅可以用于全向天线,而且可以用于定向天线。在用于全向方向图重建时,近似误差为零。对于定向天线,重构的绝对误差仍然低于上述的其他重构方法。Schmitz等人提出了级数分解法[67],用截断级数逼近有多种方法(多项式、傅里叶等),使用球谐函数可获得最佳效果。如文献中所用的天线需要100多个球谐系数,但所获得的结果可能并非理想,这主要取决于截断。对此,Petrita等人提出了新的插值算法[68],利用正弦函数和余弦函数作为加权函数。该算法既不需要双线性插值方法[62]的象限检测,也不需要加权求和方法[66]的辅助函数,同时能够保持两种方法的优势,重构误差低且全向天线误差为零。为进一步提高定向天线的重构精度,文献[69]基于加权求和法提出了新的插值方法。和以往提出的方法相比,该方法降低了均方根误差,重构的3D方向图有更好的近似性。但其缺点在于,在靠近天线法向的区域内误差更大,这将不利于在高定向天线上的应用。
(2) 从稀疏三维到完整三维
梳理现有的相关文献,从稀疏3D方向图重构出完整3D方向图主要围绕以下三个问题开展研究[70]:一是采样样本数,定义为空间维数;二是计算复杂度;三是重构精度。下面进行简要介绍。文献[71]通过优化采样角度间的间隔,以便在重构精度和测量时间复杂度之间寻求折中。类似地,Flint等人基于球面分割算法来降低球面采样个数,该方法比等角度间隔进行采样具有更低的误差,且对天线与测量系统坐标系间的对准要求更低[72]。然而,独立的方向图插值方法并不能消除天线安装结构的多径反射的影响。为了解决该问题,Robinson考虑到天线设计问题并提出了更为实用的可适用于多种天线类型的算法,使用少量的测量值来估计天线的自由空间辐射方向图[73]。该算法通过求解约束逆源问题来预测辐射方向图,能够准确预测来自天线安装基座的多径分量。传统方法依赖于球面上曲面积分的近似计算,为了进一步降低精确评估所需的采样数,文献[74]考察了不同的等纬度采样方案,如等角度采样[75]、高斯-勒让德(Gauss-Legendre)采样[76]和最佳维数采样[70]等来获取天线球面辐射方向图的测量值,以便重构、分析和评估天线的性能参数。
综上所述,以上两类方法的核心在于在方向图测量时降低波束内的数据采样点数,上述的重构方法可以降低单个方向图的测量时间,但对各个不同波束而言,均需要将该测量过程重复一遍。由此可见,这两类方法并没有降低所需要的波束数量。对于极化相控阵雷达来讲,需要逐个波束进行校准[44],意味着需要获取各个扫描角度下的天线方向图特性。为了降低既定扫描范围内的波位测量个数,需要探索其他可行的方向图重构技术方案,即从稀疏波位到完整波位。为此,作者提出了相控阵雷达波位优选下的天线方向图重构方法[77]。与传统相控阵雷达天线方向图测量方法相比,该方法通过分析波位分布特点并优化波位排布,用部分波位即可达到对整个扫描空域的有效覆盖效果,不再需要逐个波位进行天线方向图测量。在保证天线方向图精度的情况下,该方法可以将所需波位数量降低35%,有效降低了所需测量天线方向图的时间和成本。
2.3 极化方向图综合技术
天线方向图综合技术是指通过对各个阵元的加权合成一定形状和指向的天线方向图,接收有用信号的同时抑制不期望的干扰信号。针对不同的应用场景,发展出了特定形状波束、同时多波束等技术[78]。作为一种空域滤波技术,在方向图综合研究中通常直接将各个阵元的辐射特性进行线性叠加,其中隐含了两条假设:一是各个阵元为点源形式的全向天线,二是各个阵元的天线方向图相同。然而,在实际应用中,阵元布局方式和阵列结构特性不可避免地引入阵列互耦和边缘效应等非理想因素,从而导致的问题主要有:一是阵列中的阵元与孤立阵元的辐射特性有所不同,二是阵列中的各个阵元之间的辐射特性各异。对于极化相控阵而言,除了通过天线方向图综合技术实现空域滤波,还期望通过对极化的控制技术实现极化域滤波。相应地,极化方向图综合面临的挑战表现在两个方面:
一方面,在实际工程应用中,极化相控阵雷达与一般意义上的相控阵雷达(单极化)在发射和接收方面并无实质区别,仅是采用了更多通道和多极化处理器。因此,阵列互耦和边缘效应引起的上述两方面问题在极化相控阵雷达中同样存在[3]。每个阵元天线的空域极化特性各异,若采用理论模型进行方向图综合,将带来波束指向偏差、阵列方向图畸变等问题,不利于实现对极化相控阵天线空域极化特性的精确控制,从而给极化方向图综合带来了挑战。
另一方面,在极化方向图综合算法上,极化相控阵天线与一般相控阵天线类似,利用优化算法优化各个阵元的激励幅度和相位,尽可能地降低合成波束的交叉极化水平,并提高交叉极化隔离度。作为极化相控阵雷达精确获取极化信息的前提和基础,可从“硬”和“软”两个层面着手提高交叉极化隔离度。当前,“硬”的层面体现在天线设计方面,经过良好设计后双极化天线在轴向上的交叉极化水平最低可达到-40 dB量级[79],考虑到实际的工程误差等因素,仅通过天线设计手段难以满足更高交叉极化隔离度要求。“软”的层面则借助智能优化算法进行极化方向图优化,但算法的复杂程度越来越高,运算实时性不能保证。针对极化相控阵雷达的极化精密测量应用背景,以及在提高交叉极化隔离度的同时满足实时性的迫切需求,亟需在极化方向图综合技术上有所突破。
极化方向图综合与传统的方向图综合既有联系又有区别。联系在于,二者均通过对各个阵元进行加权求和,以实现在不同方向上形成不同增益。区别在于,前者是矢量形式的方向图综合,同时实现空域滤波和极化域滤波,特别是交叉极化水平的抑制;后者是标量形式的方向图综合,仅实现了空域滤波。对于极化相控阵雷达,极化方向图综合技术是实现极化控制,进而达到极化精密测量的关键技术之一。下面分窄带和宽带两个方面进行阐述。
(1) 窄带情况
在主波束(main beam)的极化状态控制上,Vaskelainen[80]首先采用迭代最小二乘法基于共形阵优化合成了圆极化主波束。基于此,文献[81]提出在进行波束形成优化之前,通过对双极化天线端口进行加权,实现具有期望极化的主波束。文献[82]研究了利用电磁矢量天线阵列(EMVA)实现具有全极化控制能力的方向图优化综合。Fuchs等人将阵元权系数求解看作是一个凸优化问题,提出了可用于任意阵列的功率方向图与极化的联合综合方法[83]。在主极化和交叉极化的联合极化控制上,对主极化方向图综合的同时实现对交叉极化的抑制。文献[84]研究了同时实现窄带共形阵波束赋形以及交叉极化抑制的综合方法,该方法将非凸的方向图函数线性化为凸子问题,并利用二阶锥规划(Second Order Cone Programming,SOCP)进行优化求解。该方法可以解决任意几何形状阵列、任意极化特性和互耦效应的一般非凸方向图综合问题。国防科技大学的李棉全博士提出了基于凸优化的方向图综合与极化联合控制方法,能够在保证功率方向图主瓣和旁瓣特性的同时,将交叉极化控制在较低水平[85]。在此基础上,国防科技大学的孙彬博士提出了一种基于半正定松弛法[86]的全极化共形阵方向图综合与极化控制方法,能够灵活地控制波束扫描角度和波束内极化状态[87]。电子科技大学的刘颜回教授团队提出了一种基于凸优化的高效数值综合方法,在旁瓣约束、零深约束和交叉极化水平约束等多约束条件下实现主极化方向图优化,并在平面阵列、柱面共形阵和锥形阵上进行验证[88]。接着,文献[89]和[90]也提出了一种半定松弛方法用于线极化方向图赋形,从而降低了交叉极化和旁瓣电平。由于相控阵雷达的波束作用方式是进行空域电扫描,固定的极化状态难以在整个扫描空域内满足交叉极化隔离度需求。针对宽角扫描相控阵雷达波束扫描时带来的交叉极化隔离度严重恶化及其随波位各异性问题,作者提出了极化状态配置方法[91-92]。与传统的固定极化状态相比,在要求更为严苛的STSR极化测量体制下,交叉极化隔离度可提高2~3个数量级,将能够满足极化精密测量的有效波束扫描范围从近0°提高到约±60°;同时,交叉极化隔离度在不同波位下较为稳定,不会随着波束扫描而出现恶化现象。由此可见,无论是主波束极化状态的控制,还是主极化和交叉极化的联合控制,均体现出极化方向图综合与传统的方向图综合的本质区别和关联。
(2) 宽带情况
上述方法是基于窄带信号提出的,如何扩展到宽带情况还需要联合考虑宽带阵列方向图综合问题。目前,关于宽带阵列方向图综合方法已有较多研究。2005年,美国海军研究实验室的Coleman等人提出基于二阶锥规划(SOCP)方法优化复数FIR滤波器系数,实现了宽带平面阵列方向图综合[93]。在此基础上,2007年空军研究实验室资助的项目基于贝塞尔函数提出了频率重聚焦技术[94]。而文献[95]通过波形设计而不仅仅是通过优化权值,来实现宽带多通道雷达系统的恒定波束方向图综合,相对带宽可达50%。在此基础上,通过设计一个用于宽带阵列方向图综合的多通道波形集,不仅可以实现频率不变的方向图,而且可以降低方向图的旁瓣电平[96]。为了利用尽可能少的阵元实现较为复杂的宽带方向图综合,在多个二阶锥约束下提出了一种稀疏宽带频率不变方向图综合方法[97]。然而,以上提到的宽带阵列方向图综合方法对交叉极化考虑较少、关注较少。文献[98]提出了一种空-时-极化域联合滤波方法实现了共形阵方向图综合的频不变特性,利用交错投影法降低了交叉极化水平。同时,凸优化方法在宽带极化方向图综合中发挥了重要作用,特别是在有效降低交叉极化水平和旁瓣电平方面[99]。以上两个优化方法[98-99]需要对每个波束指向下每个阵元的加权系数进行计算,计算量大且难以满足实时性要求。目前常见的宽带极化方向图综合通常基于线极化这类固定的极化状态的实现,极化控制效果将更加依赖于优化算法的计算性能,且优化结果取决于目标函数的收敛性。为解决该问题,本文研究了基于极化状态配置技术的宽带极化方向图综合问题。
3 未来展望
经过多年的技术发展,极化相控阵雷达系统和核心技术已经取得长足进步。然而,就极化相控阵雷达的性能发挥而言,还有多项关键技术值得研究和创新发展。具体而言,主要有以下几个方面。
3.1 低成本极化相控阵技术
一般而言,极化相控阵雷达与单极化相控阵雷达在原理上并无实质差异,而是成倍地增加了极化通道,内部的射频馈电网络和后端信号处理更为复杂,工程实现和成本上都更为困难和昂贵,这将不利于极化相控阵雷达的广泛应用。为了降低成本,常用的方式有采用划分子阵、稀疏布阵、超材料天线以及提高制造工艺等。
考虑到极化相控阵具有更多的极化通道,进一步降低成本更具实际意义。如何在保证极化测量性能的同时,将极化相控阵的成本降低至与单极化相控阵成本相当,甚或是低于单极化相控阵,是未来极化相控阵雷达技术的重要发展趋势,也是极化相控阵雷达推广应用的重要前提。
3.2 氮化镓半导体技术
氮化镓(GaN)是一种在功率放大器中逐渐取代砷化镓(GaAs)的半导体材料,体积更小但可提供更高功率,GaN的使用正在使电子设备变得更加轻型和小型化。
美国雷神公司和洛马公司在这一领域处于领先地位。在相同封装的情况下,雷神公司的GaN功放芯片可提供5倍于GaAs功放芯片的功率。洛马公司在LRDR极化相控阵雷达中已采用先进的大功率、高效GaN天线技术。另外,在AN/TPS-80地/空多任务雷达(G/ATOR)、“太空篱笆”(Space Fence),TPY-X陆基远程多任务雷达系统、SPY-7等单极化相控阵雷达中也逐步使用GaN技术。
3.3 极化信息挖掘新技术
不同的测量体制对应着不同的应用背景,不同应用中有着特定的极化信息获取需求。为了更好地利用极化信息,近年来国内外学者提出了多种校准/校正方法来提高目标极化散射特性的测量精度。然而,有关极化相控阵多通道极化信息的挖掘和利用,尚未形成系统性的研究。
为了更加深入地研究极化信息获取能力的得益,需要进一步挖掘极化相控阵雷达在目标特征提取、轮廓识别、抗典型干扰等应用场景下的潜力,对比分析单极化、双极化和全极化测量体制下对应的极化信息处理算法需求,在雷达极化方式选择、极化波形设计、极化测量体制和极化信号处理算法等方面继续瞄准需求、创新发展。
除此之外,极化相控阵雷达在架构上也在不断创新。全数字化可使相控阵雷达更具灵活性和可靠性;可扩展化体系架构,使未来任务的升级成为可能;模块化则可以加速相控阵雷达的部署和运维。
4 结束语
极化相控阵雷达技术已在气象观测、微波遥感、防空反导和精确制导等诸多领域得到初步应用。在气象观测领域,极化相控阵体制可以实现快速、自适应的体扫,能够提高恶劣天气预报性能;在微波遥感领域,极化技术在表征地物散射机理上具有理论优势;在防空反导领域,挖掘极化测量能力将有效提升真假弹头识别能力,进一步强化导弹防御能力;在精确制导领域,充分利用极化信息有利于精确打击高价值目标,遂行作战任务。面对目标和环境特性的精确获取、目标分类和识别、抗干扰等各种应用需求,具有极化精密测量能力的相控阵雷达体制已经成为相控阵雷达重要发展趋势。
近年来,我国陆续研制成功多部具有极化测量能力的相控阵雷达系统,极化雷达系统硬件建设水平整体上已接近甚至达到国际先进水平。相比之下,雷达极化信息开发利用的“软能力”发展则相对不足,包括目标极化信息测量精度、目标极化特征提取、极化目标分类识别等在内的诸多基础科学问题成为制约应用的瓶颈。随着各种新的应用需求的强劲增长,以及雷达系统关键器件和工艺水平的提升,极化相控阵雷达技术将进入发展的快车道,从而推动极化相控阵雷达在上述各应用领域的极大发展和广泛应用。
[1] 王雪松. 雷达极化技术研究现状与展望[J]. 雷达学报,2016,5(2):119-131.
[2] 李永祯, 李棉全, 程旭, 等.雷达极化测量体制研究综述[J].系统工程与电子技术,2013,35(9):1873-1877.
[3] 李棉全.全极化相控阵雷达精密测量技术[D].长沙:国防科学技术大学,2013.
[4] 庞晨.相控阵雷达精密极化测量理论与技术研究[D].长沙:国防科学技术大学,2015.
[5] 李永祯, 王雪松, 肖顺平, 等. GBR防御系统有源假目标极化鉴别能力分析[C]∥第九届全国雷达学术年会论文集, 烟台:中国电子学会, 2004:900-904.
[6] WEADON M, HEINSELMAN P, FORSYTH D, et al. Multifunction Phased Array Radar[J]. Bulletin of the American Meteorological Society,2009, 90 (3):385-389.
[7] KELLER J. Lockheed Martin to Build Long Range Discrimination Radar[EB/OL].[2015-11-03]. Military & Aerospace Electronics. https:∥digital. military-aerospace. com/militaryaerospace/201511? pg=5# pg5.
[8] FULTON C, YEARY M, THOMPSON D, et al. Digital Phased Arrays: Challenges and Opportunities[J]. Proceedings of the IEEE,2016,104(3):487-503.
[9] ZHANG G, MAHALE V, J PUTNAM B, et al. Current Status and Future Challenges of Weather Radar Polarimetry: Bridging the Gap Between Radar Meteorology/Hydrology/Engineering and Numerical Weather Prediction[J]. Advances in Atmospheric Sciences,2019,36(6):571-588.
[10] STAILEY J E, HONDL K D. Multifunction Phased Array Radar for Aircraft and Weather Surveillance[J]. Proceedings of the IEEE,2016,104(3):649-659.
[11] CONMAY M D, RUSSEL D D, MORRIS A, et al. Multifunction Phased Array Radar Advanced Technology Demonstrator Nearfield Test Results[C]∥2018 IEEE Radar Conference, Oklahoma City, OK, USA:IEEE,2018:1412-1415.
[12] KOWALSKI E, CONWAY D, MORRIS A, et al. Multifunction Phased Array Radar Advanced Technology Demonstrator (MPAR ATD) Nearfield Testing and Fielding[C]∥2019 IEEE Radar Conference, Boston, MA, USA:IEEE,2019:1-4.
[13] FULTON C, SALAZAR J L, ZHANG Y, et al. Cylindrical Polarimetric Phased Array Radar: Beamforming and Calibration for Weather Applications[J]. IEEE Trans on Geoscience and Remote Sensing,2017,55(5):2827-2841.
[14] YEARY M, PALMER R, FULTON C, et al. Recent Advances on an S-Band All-Digital Mobile Phased Array Radar[C]∥ 2019 IEEE International Symposium on Phased Array System Technology (PAST),Waltham, MA, USA:IEEE,2019:1-5.
[15] SALAZAR J L, YU T Y, MCCORD M, et al. An Ultra-Fast Scan C-Band Polarimetric Atmospheric Imaging Radar (PAIR)[C]∥ 2019 IEEE International Symposium on Phased Array System &Technology (PAST), Waltham, MA, USA:IEEE,2019:1-5.
[16] ORZEL K, VENKATEH V, HARTLEY T, et al. Development and Calibration of a X-Band Dual Polarization Phased Array Radar[C]∥ 2013 IEEE Radar Conference, Ottawa, ON, Canada: IEEE,2013:1-4.
[17] KNAPP E J, SALAZAR J, MEDINA R H, et al. Phase-Tilt Radar Antenna Array[C]∥ 2011 41st European Microwave Conference, Manchester, UK:IEEE,2011:1055-1058.
[18] HEBERLING W, FRASIER S, WOLSIEFFER C, et al. Comparison of Phased Array and Parabolic Antenna Polarimetric Weather Radar Variables at X-Band[C]∥ 2019 IEEE International Geoscience and Remote Sensing Symposium, Yokohama, Japan: IEEE, 2019:7579-7582.
[19] PUZELLA A, ALM R. Air-Cooled, Active Transmit/Receive Panel Array[C]∥ 2008 IEEE Radar Conference, Rome, Italy: IEEE, 2008:1-6.
[20] FULTON C, CHAPPELL W. A Dual-Polarized Patch Antenna for Weather Radar Applications[C]∥ 2011 IEEE International Conference on Microwaves, Communications, Antennas and Electronic Systems (COMCAS 2011), Tel Aviv, Israel:IEEE,2011:1-5.
[21] SALAZAR J L, LOEW E, TSAI P S, et al. Design Tradeoffs for Airborne Phased Array Radar for Atmospheric Research[C]∥ 2013 IEEE International Symposium on Phased Array Systems and Technology, Waltham, MA, USA: IEEE, 2013:371-378.
[22] YOSHIKAWA E, USHIO T, KAWASAKI Z, et al. MMSE Beam Forming on Fast-Scanning Phased Array Weather Radar[J]. IEEE Trans on Geoscience and Remote Sensing, 2013, 51(5):3077-3088.
[23] MIZUTANI F, USHIO T, YOSHIKAWA E, et al. Fast-Scanning Phased-Array Weather Radar with Angular Imaging Technique[J]. IEEE Trans on Geoscience and Remote Sensing,2018,56(5):2664-2673.
[24] 张志强, 刘黎平. 相控阵技术在天气雷达中的初步应用[J]. 高原气象,2011,30(4):1102-1107.
[25] DEBOER D R, GOUGH R G, BUNTON J D, et al. Australian SKA Pathfinder: A High-Dynamic Range Wide-Field of View Survey Telescope[J]. Proceedings of the IEEE, 2009,97 (8):1507-1521.
[26] IVASHINA M V, IUPIKOV O, MAASKANT R, et al. An Optimal Beamforming Strategy for Wide-Field Surveys with Phased-Array-Fed Reflector Antennas[J]. IEEE Trans on Antennas and Propagation, 2011,59(6):1864-1875.
[27] LEE J S, POTTIER E. Polarimetric Radar Imaging: Basics to Applications(Second Edition)[M]. US: Crc Press, 2016.
[28] STANGL M, WERNINGHAUS R, ZAHN R. The TERRASAR-X Active Phased Array Antenna[C]∥ IEEE International Symposium on Phased Array Systems and Technology, Boston, MA, USA: IEEE, 2003:70-75.
[29] LUSCOMBE A P, CHOTOO K, HUXTABLE B D. Polarimetric Calibration for RADARSAT-2[C]∥ IEEE 2000 International Geoscience and Remote Sensing Symposium. Taking the Pulse of the Planet: The Role of Remote Sensing in Managing the Environment. Proceedings (Cat. No.00CH37120), Honolulu, HI, USA:IEEE, 2000:2197-2199.
[30] WANG Yang, CHEN Xi, GE Jialong, et al. Internal and External Calibration of POLINSAR[C]∥ Proceedings of 2011 IEEE CIE International Conference on Radar, Chengdu, China: IEEE, 2011:879-882.
[31] 李亮, 洪峻, 陈琦, 等. 基于极化有源定标器的高分三号SAR 在轨测试分析[J]. 电子学报, 2018,46(9):2157-2164.
[32]丁赤飚, 刘佳音, 雷斌, 等. 高分三号SAR 卫星系统级几何定位精度初探[J]. 雷达学报,2017,6(1):11-16.
[33] 赵鸿燕. 国外相控阵雷达导引头技术发展研究[J]. 航空兵器,2018 (3):11-17.
[34] 何晓晴. “硫磺石” 导弹的发展及其作战应用[J]. 现代军事,2016 (1):58-62.
[35] 晁淑媛, 邓磊, 马亮,等. 全极化雷达导引头抗干扰技术[J]. 制导与引信,2016,37(3):1-7.
[36] 赵菲.共形相控阵天线分析综合技术与实验研究[D].长沙:国防科学技术大学,2012.
[37] ZHANG G, DOVIAK R J, ![]() D S, et al. Phased Array Radar Polarimetry for Weather Sensing: A Theoretical Formulation for Bias Corrections[J]. IEEE Trans on Geoscience and Remote Sensing, 2009, 47(11):3679-3689.
D S, et al. Phased Array Radar Polarimetry for Weather Sensing: A Theoretical Formulation for Bias Corrections[J]. IEEE Trans on Geoscience and Remote Sensing, 2009, 47(11):3679-3689.
[38] FULTON C, SALAZAR J, ![]() D, et al. Polarimetric Phased Array Calibration for Largescale Multi-Mission Radar Applications[C]∥ 2018 IEEE Radar Conference, Oklahoma City, OK, USA:IEEE, 2018:1272-1277.
D, et al. Polarimetric Phased Array Calibration for Largescale Multi-Mission Radar Applications[C]∥ 2018 IEEE Radar Conference, Oklahoma City, OK, USA:IEEE, 2018:1272-1277.
[39] LEI L, ZHANG G, DOVIAK R J. Bias Correction for Polarimetric Phased Array Radar with Idealized Aperture and Patch Antenna Elements[J]. IEEE Trans on Geoscience and Remote Sensing,2013,51(1):473-486.
[40] CAROZZI T, WOAN G, MAASKANT R. Polarization Diversity for SKA Wide-field Polarimetry[C]∥ In SKADS Conference 2009, Belgium:[s.n.], 2009:125-130.
[41] 王雪松.宽带极化信息处理的研究[D].长沙:国防科学技术大学,1999.
[42] ZHANG G F, DOVIAK R, ![]() D, et al. Phased Array Radar Polarimetry for Weather Sensing: Challenges and Opportunities[C]∥ 2008 IEEE International Geoscience and Remote Sensing Symposium, Boston, MA, USA:IEEE, 2008:449-452.
D, et al. Phased Array Radar Polarimetry for Weather Sensing: Challenges and Opportunities[C]∥ 2008 IEEE International Geoscience and Remote Sensing Symposium, Boston, MA, USA:IEEE, 2008:449-452.
![]() D S, ZHANG G, DOVIAK R J. Bias Correction and Doppler Measurement for Polarimetric Phased-Array Radar[J]. IEEE Trans on Geoscience and Remote Sensing, 2011,49(2):843-853.
D S, ZHANG G, DOVIAK R J. Bias Correction and Doppler Measurement for Polarimetric Phased-Array Radar[J]. IEEE Trans on Geoscience and Remote Sensing, 2011,49(2):843-853.
[44] ORZEL K A, FRASIER S J. Weather Observation by an Electronically Scanned Dual-Polarization Phase-Tilt Radar[J]. IEEE Trans on Geoscience and Remote Sensing, 2018,56(5):2722-2734.
[45] ZHANG G, DOVIAK R, ![]() D, et al. Polarimetric Phased-Array Radar for Weather Measurement: A Planar or Cylindrical Configuration?[J]. Journal of Atmospheric and Oceanic Technology, 2011,28(1):63-73.
D, et al. Polarimetric Phased-Array Radar for Weather Measurement: A Planar or Cylindrical Configuration?[J]. Journal of Atmospheric and Oceanic Technology, 2011,28(1):63-73.
![]() D S. Statistical Evaluation of Pulse Phase Coding to Suppress Coupling in the Polarimetric Radar[C]∥ 36th Conference on Radar Meteoro-logy, Breckenridge, CO, USA:IEEE, 2013:1-18.
D S. Statistical Evaluation of Pulse Phase Coding to Suppress Coupling in the Polarimetric Radar[C]∥ 36th Conference on Radar Meteoro-logy, Breckenridge, CO, USA:IEEE, 2013:1-18.
![]() D S, DOVIAK R, MELNIKOV V, et al. Signal Design to Suppress Coupling in the Polarimetric Phased Array Radar[J]. Journal of Atmospheric and Oceanic Technology, 2014,31(5):1063-1077.
D S, DOVIAK R, MELNIKOV V, et al. Signal Design to Suppress Coupling in the Polarimetric Phased Array Radar[J]. Journal of Atmospheric and Oceanic Technology, 2014,31(5):1063-1077.
[48] ![]() I R. Options for Polarimetric Variable Mea-surements on the MPAR Advanced Technology De-monstrator[C]∥2018 IEEE Radar Conference, Oklahoma City, OK, USA:IEEE, 2018:129-134.
I R. Options for Polarimetric Variable Mea-surements on the MPAR Advanced Technology De-monstrator[C]∥2018 IEEE Radar Conference, Oklahoma City, OK, USA:IEEE, 2018:129-134.
![]() I R. Effects of Phase Coding on Doppler Spectra in PPAR Weather Radar[J]. IEEE Trans on Geoscience and Remote Sensing, 2018,56(4):2043-2065.
I R. Effects of Phase Coding on Doppler Spectra in PPAR Weather Radar[J]. IEEE Trans on Geoscience and Remote Sensing, 2018,56(4):2043-2065.
[50] STAIMAN D. Calibration of Polarimetric Phased Array Radar for Improved Measurement Accuracy[C]∥ 25th Conference on International Interactive Information and Processing Systems (IIPS) for Meteorology, Oceanography, and Hydrology,[S.l.]:[s.n.], 2009:1-9.
[51] DIAZ J D, SALAZAR J L, ORTIZ J A, et al. A Dual-Polarized Cross-Stacked Patch Antenna with Wide-Angle and Low Cross-Polarization for Fully Digital Multifunction Phased Array Radars[C]∥ 2016 IEEE International Symposium on Phased Array Systems and Technology, Waltham, MA, USA:IEEE, 2016: 1-4.
[52] PANG C, DONG J, WANG T, et al. A Polarimetric Calibration Error Model for Dual-Polarized Antenna Element Patterns[J]. IEEE Antennas and Wireless Propagation Letters, 2016,15:782-785.
[53] PANG C, HOOGEBOOM P, CHEVALIER F L, et al. Polarimetric Bias Correction of Practical Planar Scanned Antennas for Meteorological Applications[J]. IEEE Trans on Geoscience and Remote Sensing, 2016, 54(3):1488-1504.
[54] HUANG Q L, ZHOU H X, BAO J H, et al. Mutual Coupling Calibration for Microstrip Antenna Arrays via Element Pattern Reconstruction Method[J]. IEEE Antennas and Wireless Propagation Letters, 2014, 13:51-54.
[55] SALAZAR J L, ABOSERWAL N, DIAZ J D, et al. Edge Diffractions Impact on the Cross-Polarization Performance of Active Phased Array Antennas[C]∥2016 IEEE International Symposium on Phased Array Systems and Technology, Waltham, MA, USA:IEEE, 2016:1-5.
[56] BHOWMIK L M, FULTON C J. Analysis and Measurement of Grating Lobe Effects in Infinite Planar Arrays of Finite-Sized Subarrays[C] ∥2016 IEEE International Symposium on Phased Array Systems and Technology, Waltham, MA, USA:IEEE, 2016:1-6.
[57] SALAZAR J L, SIQUIERA P, TRABAL J, et al. Performance of the Wet Radomes for Phased-Array Weather Radars: Evaluation and Applications[C]∥2012 9th European Radar Conference, Amsterdam, Netherlands:IEEE, 2012:341-344.
[58] BREINBJERG O, PIVNENKO S N, KIM O S, et al. Recent Advances in Antenna Measurement Techniques at the DTUESA Spherical Nearfield Antenna Test Facility[C]∥ 2014 URSI General Assembly and Scientific Symposium (URSI GASS), Beijing, China:IEEE,2014:1-4.
[59] UMEYAMA A Y, SALAZAR-CERRENO J L, FULTON C. UAV-Based Antenna Measurements for Polarimetric Weather Radars: Probe Analysis[J]. IEEE Access, 2020, 8:191862-191874.
[60] 翟计全, 马林, 杨文军. 全极化雷达极化标校技术研究[J]. 电波科学学报, 2019, 34(6):806-813.
[61] WEBER M E. Meteorological Phased Array Radar Research at NOAA’s National Severe Storms Laboratory[C]∥ 2019 IEEE International Conference on Microwaves, Antennas, Communications and Electronic Systems (COMCAS), Tel-Aviv, Israel:IEEE,2019:1-6.
[62] GIL F, CLARO A R, FERREIRA J M, et al. A 3D Interpolation Method for Basestation-Antenna Radiation Patterns[J]. IEEE Antennas and Propagation Magazine, 2001, 43(2):132-137.
[63] WERNER D H, ALLARD R J. The Simultaneous Interpolation of Antenna Radiation Patterns in both the Spatial and Frequency Domains Using Model-Based Parameter Estimation[J]. IEEE Trans on Antennas and Propagation, 2000, 48(3):383-392.
[64] ALLARD R J, WERNER D H. The Model-Based Parameter Estimation of Antenna Radiation Patterns Using Windowed Interpolation and Spherical Harmonics[J]. IEEE Trans on Antennas and Propagation, 2003, 51(8):1891-1906.
[65] MIKAS F, PECHAC P. The 3D Approximation of Antenna Radiation Patterns[C]∥ Twelfth International Conference on Antennas and Propagation, Exeter, UK:IET, 2003:751-754.
[66] VASILIADIS T G, DIMITRIOU A G, SERGIADIS G D. A Novel Technique for the Approximation of 3D Antenna Radiation Patterns[J]. IEEE Trans on Antennas and Propagation, 2005,53(7):2212-2219.
[67] SCHMITZ A, KAROLSKI T, KOBBELT L. Using Spherical Harmonics for Modeling Antenna Patterns[C]∥2012 IEEE Radio and Wireless Symposium,Santa Clara, CA, USA: IEEE,2012:155-158.
[68] PETRITA T, IGNEA A. A New Method for Interpolation of 3D Antenna Pattern from 2D Plane Patterns[C]∥2012 10th International Symposium on Electronics and Telecommunications, Timisoara, Romania:IEEE, 2012:393-396.
[69] LEONOR N R, CALDEIRINHA R F S, SANCHEZ M G, et al. A Three-Dimensional Directive Antenna Pattern Interpolation Method[J]. IEEE Antennas and Wireless Propagation Letters,2016,15:881-884.
[70] KHALID Z, KENNEDY R A, MCEWEN J D. An Optimal Dimensionality Sampling Scheme on the Sphere with Fast Spherical Harmonic Transforms[J]. IEEE Trans on Signal Processing, 2014, 62 (17):4597-4610.
[71] NIELSEN J O, PEDERSEN G F. Mobile Handset Performance Evaluation Using Radiation Pattern Measurements[J]. IEEE Trans on Antennas and Propagation, 2006, 54(7):2154-2165.
[72] FLINT J A, ULLAH S, SEAGER R D, et al. Low Resolution Radiation Pattern Sampling for a Thin Dipole[C]∥ 2010 Loughborough Antennas Propagation Conference, Loughborough, UK: IEEE, 2010: 601-604.
[73] ROBINSON M. Knowledge-Based Antenna Pattern Interpolation[J]. IEEE Trans on Antennas and Propagation, 2014, 62(1):72-79.
[74] AHMED U, KHALID Z. Sampling Schemes for Accurate Reconstruction and Computation of Performance Parameters of Antenna Radiation Pattern[C]∥ 2019 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Brighton,UK:IEEE, 2019:4639-4643.
[75] MCEWEN J D, WIAUX Y. A Novel Sampling Theorem on the Sphere[J]. IEEE Trans on Signal Processing, 2011, 59(12):5876-5887.
[76] DOROSHKEVICH A G, NASELSKY P D, VERKHODANOV O V, et al. Gauss-Legendre Sky Pixe-lization (GLESP) for CMB Maps[J]. International Journal of Modern Physics D,2005,4(2):275-290.
[77] WANG Z, PANG C, LI Y, et al. A Method for Radiation Pattern Reconstruction of Phased-Array Antenna[J]. IEEE Antennas and Wireless Propagation Letters, 2020, 19(1):168-172.
[78] 张光义.相控阵雷达原理[M].北京:国防工业出版社,2009.
[79] MIRMOZAFARI M, ZHANG G, FULTON C, et al. Dual-Polarization Antennas with High Isolation and Polarization Purity: A Review and Comparison of Cross-Coupling Mechanisms[J]. IEEE Antennas and Propagation Magazine, 2019, 61(1):50-63.
[80] VASKELAINEN L I. Iterative Least-Squares Synthesis Methods for Conformal Array Antennas with Optimized Polarization and Frequency Properties[J]. IEEE Trans on Antennas and Propagation, 1997, 45 (7):1179-1185.
[81] DOHMEN C, ODENDAAL J W, JOUBERT J. Synthesis of Conformal Arrays with Optimized Pola-rization[J]. IEEE Trans on Antennas and Propagation, 2007, 55(10):2922-2925.
[82] XIAO J, NEHORAI A. Optimal Polarized Beampattern Synthesis Using a Vector Antenna Array[J]. IEEE Trans on Signal Processing, 2009, 57 (2):576-587.
[83] FUCHS B, FUCHS J J. Optimal Polarization Synthesis of Arbitrary Arrays with Focused Power Pattern[J]. IEEE Trans on Antennas and Propagation, 2011,59(12):4512-4519.
[84] TSUI K M, CHAN S C. Pattern Synthesis of Narrowband Conformal Arrays Using Iterative Second-Order Cone Programming[J]. IEEE Trans on Antennas and Propagation, 2010, 58 (6):1959-1970.
[85] LI M, WANG X, DONG J, et al. Optimal Difference Pattern Synthesis with Polarization Control for Arbitrary Arrays[J]. IEEE Antennas and Wireless Propagation Letters, 2012, 11:1358-1361.
[86] FUCHS B. Application of Convex Relaxation to Array Synthesis Problems[J]. IEEE Trans on Antennas and Propagation, 2014, 62(2):634-640.
[87] SUN B, REN B, LIU C, et al. Experimental Investigation on the Synthesis of Scanning Beam Pattern with Antenna Selection for Conformal Array[J]. IET Microwaves Antennas & Propagation, 2016, 10 (9):969-975.
[88] 杨晶, 刘颜回, 白晶晶, 等. 交叉极化及副瓣约束的任意阵列最优方向性综合[J]. 电子学报,2017, 45 (3):712-718.
[89] LIU Y H, BAI J J, XU K D, et al. Linearly Pola-rized Shaped Power Pattern Synthesis with Sidelobe and Cross-Polarization Control by Using Semidefinite Relaxation[J]. IEEE Trans on Antennas and Propagation, 2018, 66(6):3207-3212.
[90] XU Z Y, LIU Y H, LI M, et al. Linearly Polarized Shaped Power Pattern Synthesis with Dynamic Range Ratio Control for Arbitrary Antenna Arrays[J]. IEEE Access,2019, 7:53621-53628.
[91] 王占领, 殷加鹏, 庞晨, 等. 一种提高全极化相控阵雷达极化测量精度的方法[J]. 中国科学: 信息科学,2021, 51(7):1183-1198.
[92] WANG Z, YIN J, PANG C, et al. An Adaptive Direction-Dependent Polarization State Configuration Method for High Isolation in Polarimetric Phased Array Radar[J]. IEEE Trans on Antennas and Propagation,2021,69(6):3257-3272.
[93] COLEMAN J O, SCHOLNIK D P, CAHILL P E. Synthesis of a Polarization-Controlled Pattern for a Wideband Array by Solving a Second-Order Cone Program[C]∥ 2005 IEEE Antennas and Propagation Society International Symposium, Washington, DC, USA: IEEE,2005:437-440.
[94] PILLAI S U, LI K Y, GUERCI J R. Efficient Wideband Processing Without Sub-Banding[C]∥ 2008 IEEE Radar Conference, Rome, Italy: IEEE,2008: 1-5.
[95] UYSAL F, YEARY M, GOODMAN N, et al. Waveform Design for Wideband Beampattern and Beamforming[C]∥ 2015 IEEE Radar Conference, Arlington, VA, USA:IEEE, 2015:1062-1066.
[96] UYSAL F, DUNN Z. Application of Waveform Weighting for a Frequency-Invariant Transmit Beampattern[J]. IEEE Aerospace and Electronic Systems Magazine, 2016, 31(12):4-12.
[97] LIU Y, ZHANG L, YE L, et al. Synthesis of Sparse Arrays with Frequency-Invariant-Focused Beam Patterns Under Accurate Sidelobe Control by Iterative Second-Order Cone Programming[J]. IEEE Trans on Antennas and Propagation, 2015, 63 (12):5826-5832.
[98] WANG B, GUO Y, WANG Y, et al. Frequency-Invariant Pattern Synthesis of Conformal Array Antenna with Low Cross-Polarisation[J]. IET Microwaves, Antennas Propagation, 2008,2(5):442-450.
[99] LI M, CHANG Y, LI Y, et al. Optimal Polarised Pattern Synthesis of Wideband Arrays via Convex Optimisation[J]. IET Microwaves, Antennas & Propagation,2013,7(15):1228-1237.



