0 引言
近些年来，MIMO雷达目标定位一直是学者们研究的热点[1-3]。但对于MIMO雷达近场目标定位的研究却很少，目前大部分的近场源目标定位文献只局限于阵列信号处理，不适用于收发阵列并存的场景[4]。而近场源目标定位越来越受到重视，其中地面穿透雷达和室内定位是近场源目标定位的典型应用。
传统的目标定位方法都是基于远场假设的，尽管经典算法很多，但不能直接用于近场信号模型。而在有源阵列信号处理领域内，有关MIMO雷达近场目标定位算法的文献较少。文献[5]提出基于平行因子的双基地MIMO雷达目标定位算法，该算法信号模型中收发阵列距离较近，但阵元间隔可以拓展到λ/2；文献[6]提出一种双基地MIMO雷达近场目标四维参数估计算法，但阵元间隔局限在λ/4内；文献[7]提出的算法利用MIMO雷达接收信号的互协方差矩阵来构造二阶统计量矩阵，再通过特征值分解估计近场目标的三维参数，但此算法在加性复高斯噪声环境下角度模糊现象严重，且阵元间隔局限在λ/4内。
联合对角化算法在阵列信号处理领域和MIMO雷达远场源定位方面都有应用，而且性能较好[8-9] 。本文利用联合对角化算法解决单基地MIMO雷达近场目标定位问题，并通过仿真实验证明了算法的有效性。和文献[7]所提算法相比，本文算法参数估计精度高，无角度模糊现象，而且接收阵元间隔可以拓展到λ/2。
1 MIMO雷达近场信号模型
假设这样一个场景，如图1所示：单基地雷达系统由Mt=2M+1个发射阵元和Mr=2N+1个接收阵元组成，发射阵列和接收阵列都是均匀线阵，阵元间隔分别是dt和dr，中间阵元为参考阵元；假设空间有P个目标，第l(l=1，…，L)个快拍内接收信号可以表示为：
第l个快拍(l∈[1,2,3,…,L])内接收信号可以表示为
(1)
式中，
A(θr,r)=[a1(θr1,r1),a2(θr2,r2),…,
aP(θrP,rP)]
(2)
B(θt,r)=[b1(θt1,r1),b2(θt2,r2),…,
bP(θtP,rP)]
(3)
ε(tl)=[ε1(tl),ε2(tl),…,εP(tl)]T
(4)
(5)
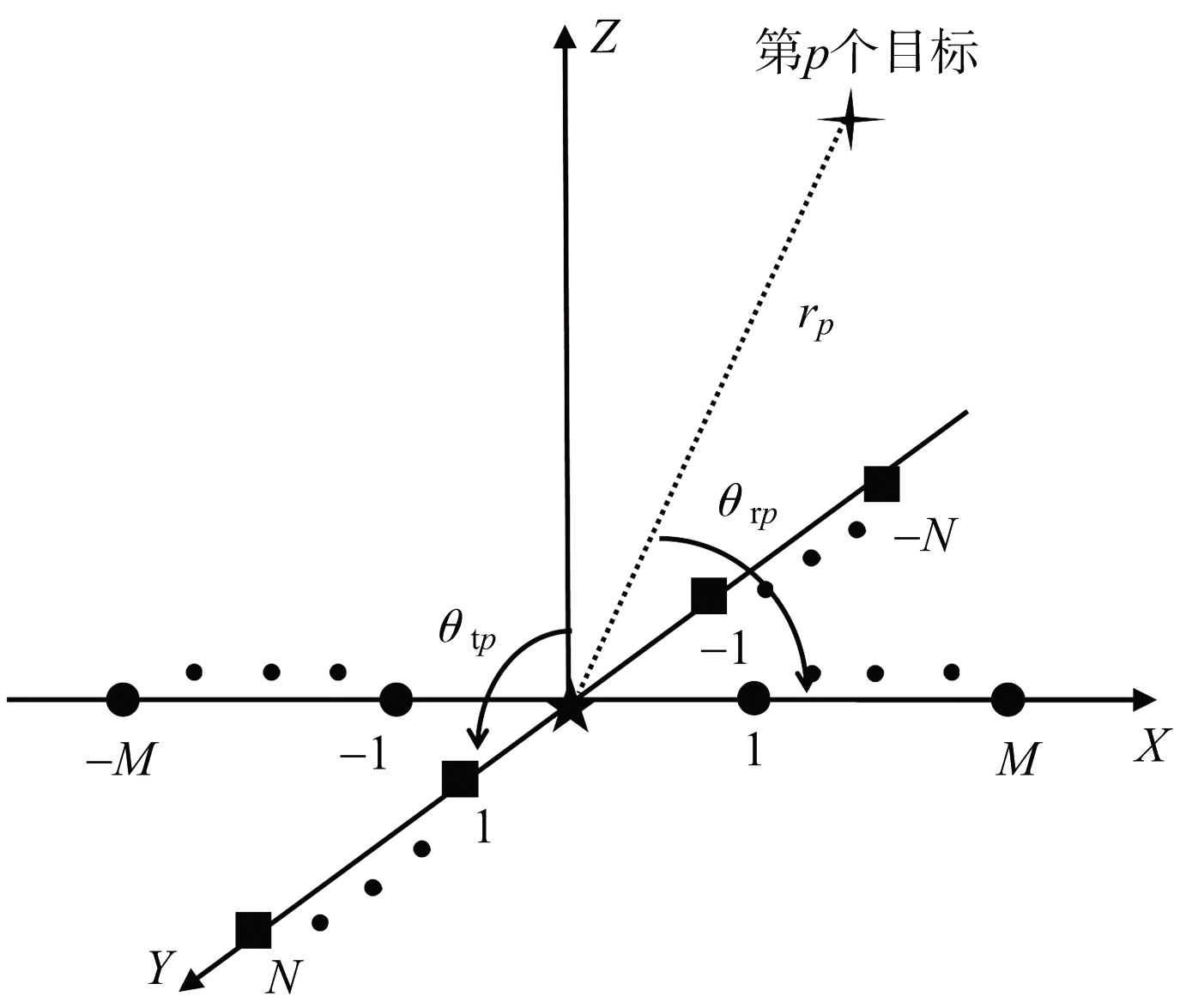
图1 单基地MIMO雷达信号模型
第p个目标的接收导向矢量和发射导向矢量分别为
ap(θrp,rp)=[ej(Nωrp+(-N)2φrp),…,
ej(ωrp+φrp),1,ej(-ωrp+φrp),…,
ej(-Nωrp+(N)2φrp)]T
bp(θtp,rp)=[ej(Mωtp+(-M)2φtp),…,
ej(ωtp+φtp),1,ej(-ωtp+φtp),…,
ej(-Mωtp+(M)2φtp)]T
式中，
为信号波长，θrp，θtp和rp分别为第p个目标的接收角、发射角和距离。第p个目标的反射系数可以表示成εp(tl)=upej2πfdptl，其中up是第p个目标的反射面积，fdp是多普勒频移，tl是慢时间。S是发射信号，可以表示成
(6)
假设不同的阵元发射信号相互正交且码长为K，即
表示加性复噪声。
接收信号经过发射信号sm(m=-M,…, -1,0,1,…,M)滤波后得到
Xm=A(θr,r)diag(ε(tl))dm+Nm
(7)
式中，dm=[ej(-mωt1+(-m)2φt1),ej(-mωt2+(-m)2φt2),…, ej(-mωtP+(-m)2φtP)]T。
将式(7)矢量化得到
[a1⊗ej(-mωt1+(-m)2φt1),…,
(8)
式中，“⊗”表示求Kronecker积。在L个快拍后，式(8)变成
Ym=Amε+Zm
(9)
式中,
2 算法描述
所提出的算法主要包括3个部分：首先，根据接收信号构造相关矩阵；其次，构造选择矩阵，利用相关矩阵和选择矩阵，通过联合对角化算法得到自动配对的发射角和距离估计值；最后，通过谱峰搜索得到接收角估计值。
求Ym和Y0之间的互协方差矩阵，即
Rm,0=
(10)
式中，Rε=E⎣εεH」。取m=-1,0,1，则
(11)
(12)
(13)
利用互协方差矩阵R-1,0，R0,0和R1,0构造矩阵R:
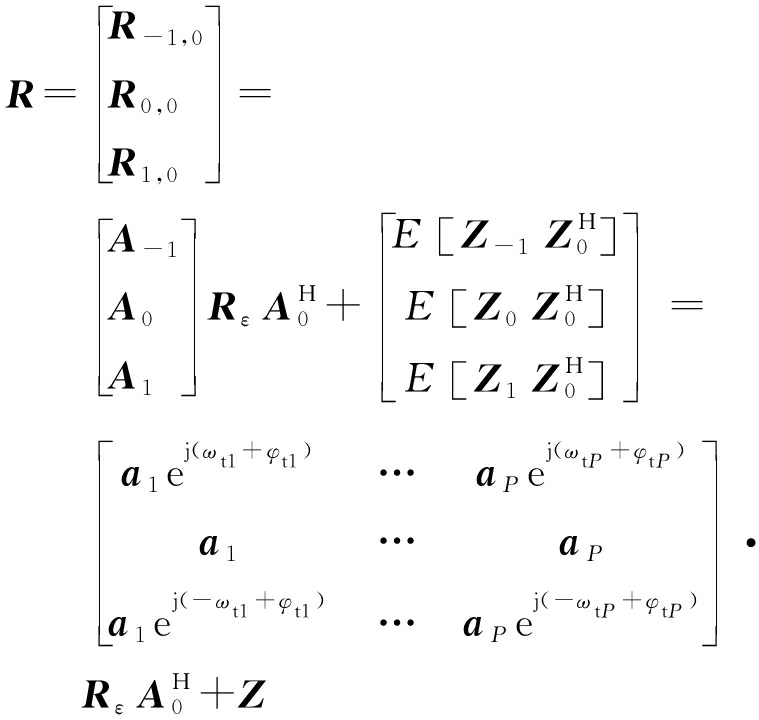
(14)
式中，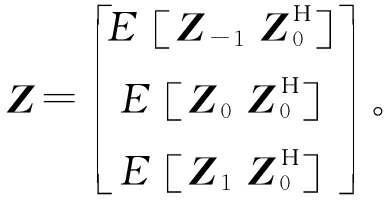
对R进行奇异值分解可得
R=USVH
(15)
式中，S为R的奇异值矩阵，U和V为相应的奇异向量矩阵，则信号子空间Up=UsSs包含方向信息，其中Ss是P个最大奇异值组成的对角阵，Us是相应的奇异向量矩阵。
定义3个矩阵：
则发射角θt和距离r的选择矩阵可以表示成
K1=J1⊗I
(16)
K2=J2⊗I
(17)
K3=J3⊗I
(18)
式中：I为Mr×Mr的单位阵；K1，K2，K3分别用来选取Up中和R-1,0，R0,0，R1,0对应的子块。
根据联合对角化方法[8]，定义两个矩阵：
G1=(K1Up)-1K2Up=TD1T-1
(19)
G2=(K3Up)-1K2Up=TD2T-1
(20)
式中，
D1=diag[ej(-ωt1-φt1),…,ej(-ωtP-φtP)]
(21)
D2=diag[ej(ωt1-φt1),…,ej(ωtP-φtP)]
(22)
则对角矩阵D1和D2中包含发射角和距离信息，且G1和G2具有相同的特征向量矩阵。分别对G1和R0,0进行特征值分解:
(23)
(24)
式中，
为G1的特征值，
为对应的特征向量矩阵，S0为R0,0最大P个特征值组成的对角阵，U0为对应的特征向量矩阵，Sz为最小的Mr-P个特征值组成的对角阵，Uz为对应的特征向量矩阵。由式(19)、式(20)和式(23)可得
(25)
定义
式中“*”表示求共轭，由式(21)和式(22)可知
D=diag[ej(2ωt1),…,ej(2ωtP)]
(26)
令ρtp=ej(2ωtp)，p=1,2,…,P为D的对角线元素，则第p个目标的发射角可以用下式计算:
(27)
式中“∠”表示求相位角。
构造矩阵
则由式(21)和式(22)可知
(28)
令
为
的对角线元素，则第p个目标的距离rp的估计值为
(29)
定义矩阵
则对接收角
的估计可通过一维谱峰搜索实现，即
(30)
3 算法仿真
为验证所提算法的有效性进行如下仿真实验，仿真条件：令
快拍数L=1 000，噪声是复高斯白噪声；假设空间存在P=2个近场目标，其三维参数(θrp,θtp,rp)分别是(40°,80°,0.5λ)，(70°,60°,0.7λ)。
仿真实验一： 假设两个目标的信噪比为SNR=10 dB，进行20次重复实验，得到两个近场目标的参数估计值和配对结果，实验结果如图2所示。由图2可以看出,该算法可以实现单基地MIMO雷达近场目标三维参数联合估计，三维参数可以实现自动配对，而且精度较高。
仿真实验二： 假设两个目标的信噪比(SNR)从0 dB到30 dB变化，进行100次重复实验，得到3个参数估计值的均方根误差(RMSE)随信噪比的变化曲线，实验结果如图3～图5所示。其中RMSE的定义如下：
式中,
为i次实验估计值，αi为实际值，T为实验次数。
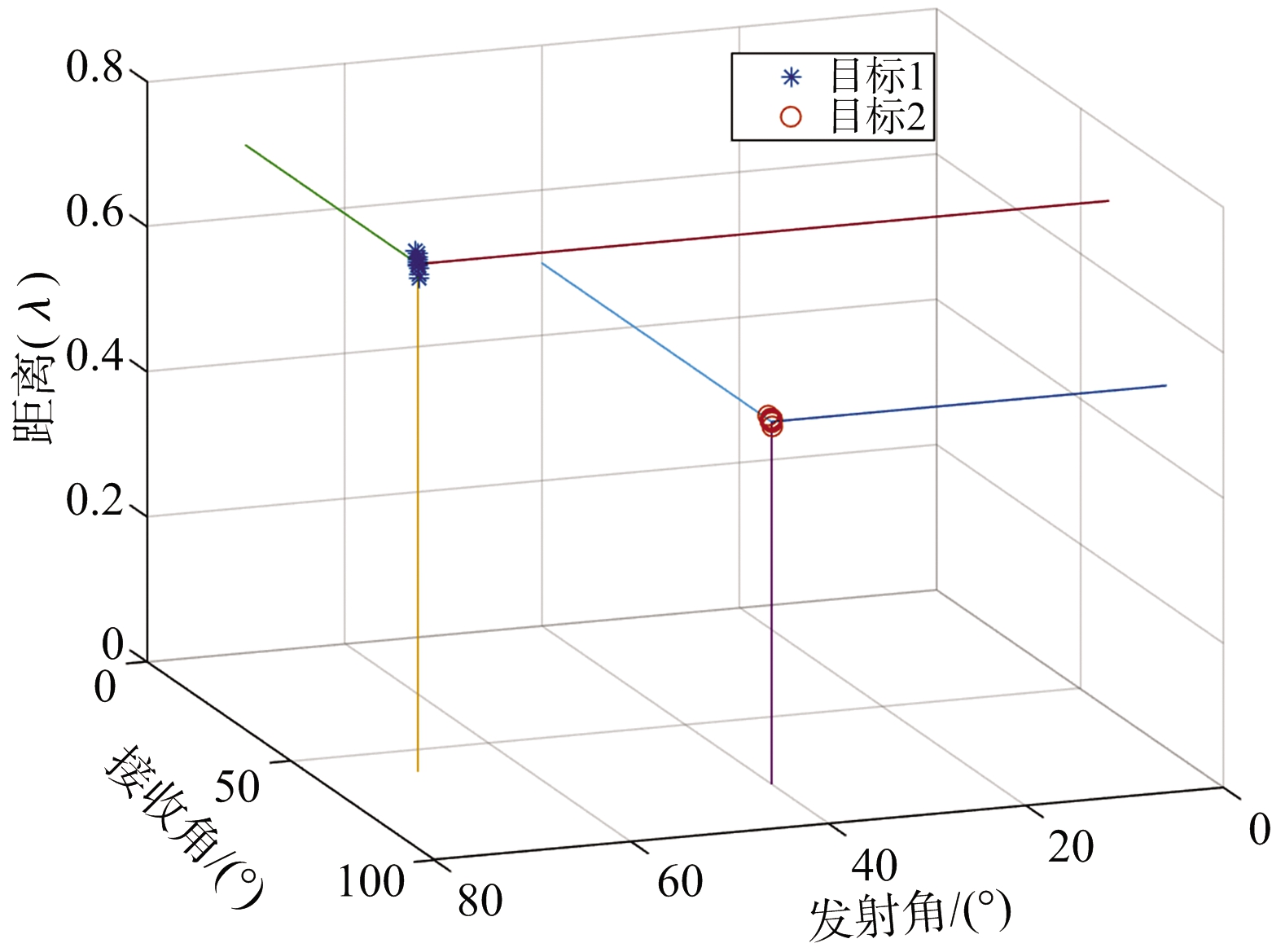
图2 两个近场目标的参数估计和配对结果
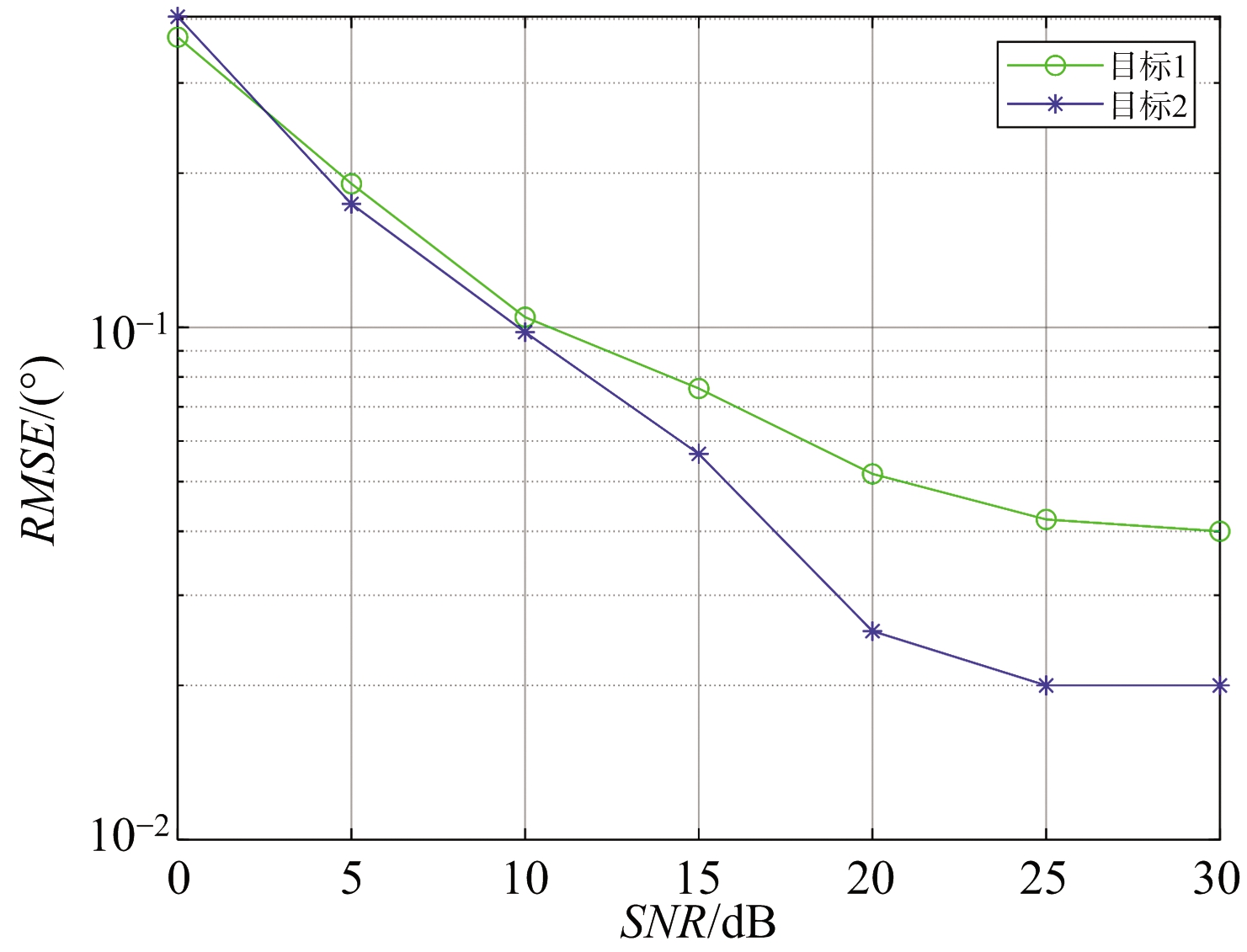
图3 接收角估计RMAE
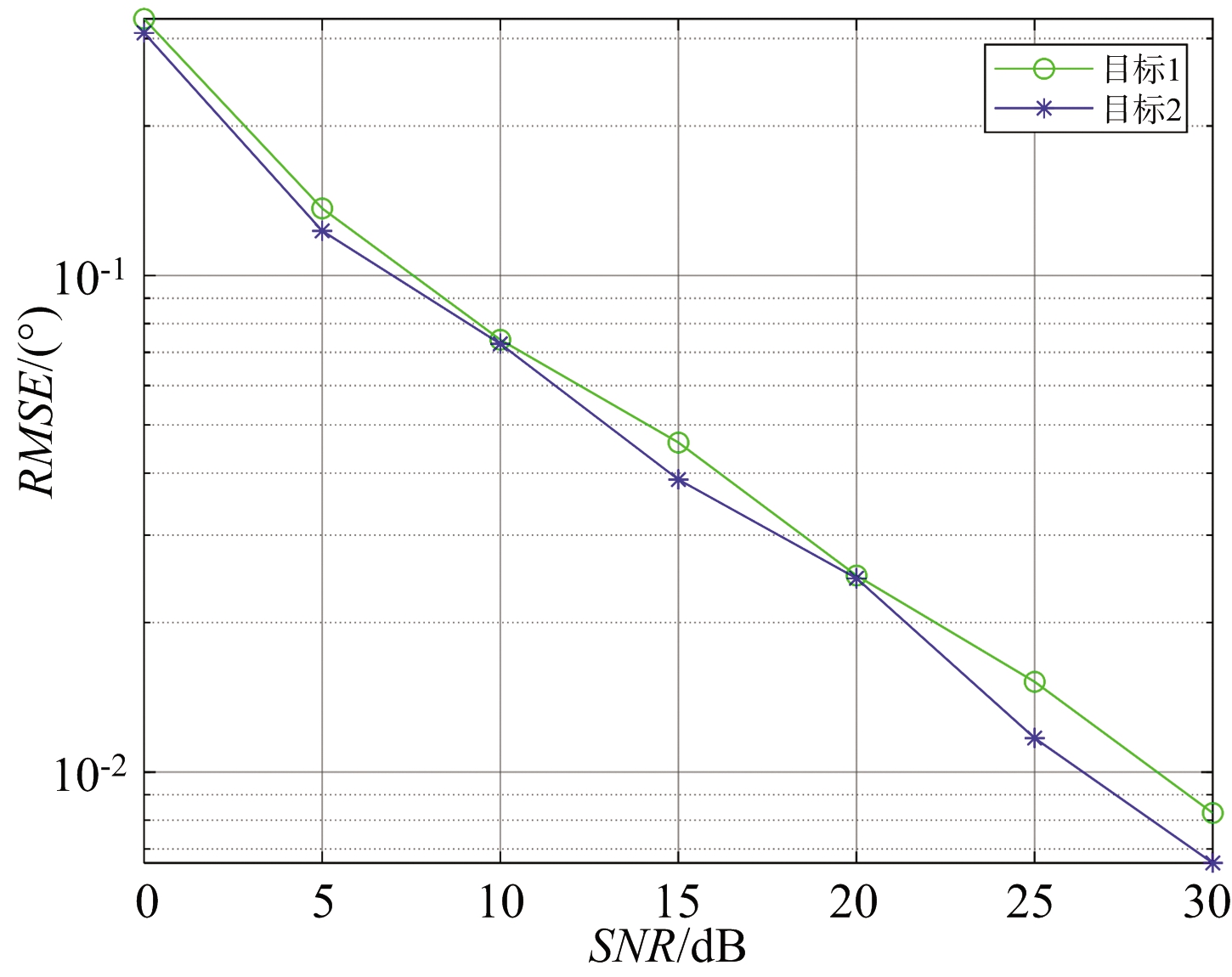
图4 发射角估计RMSE
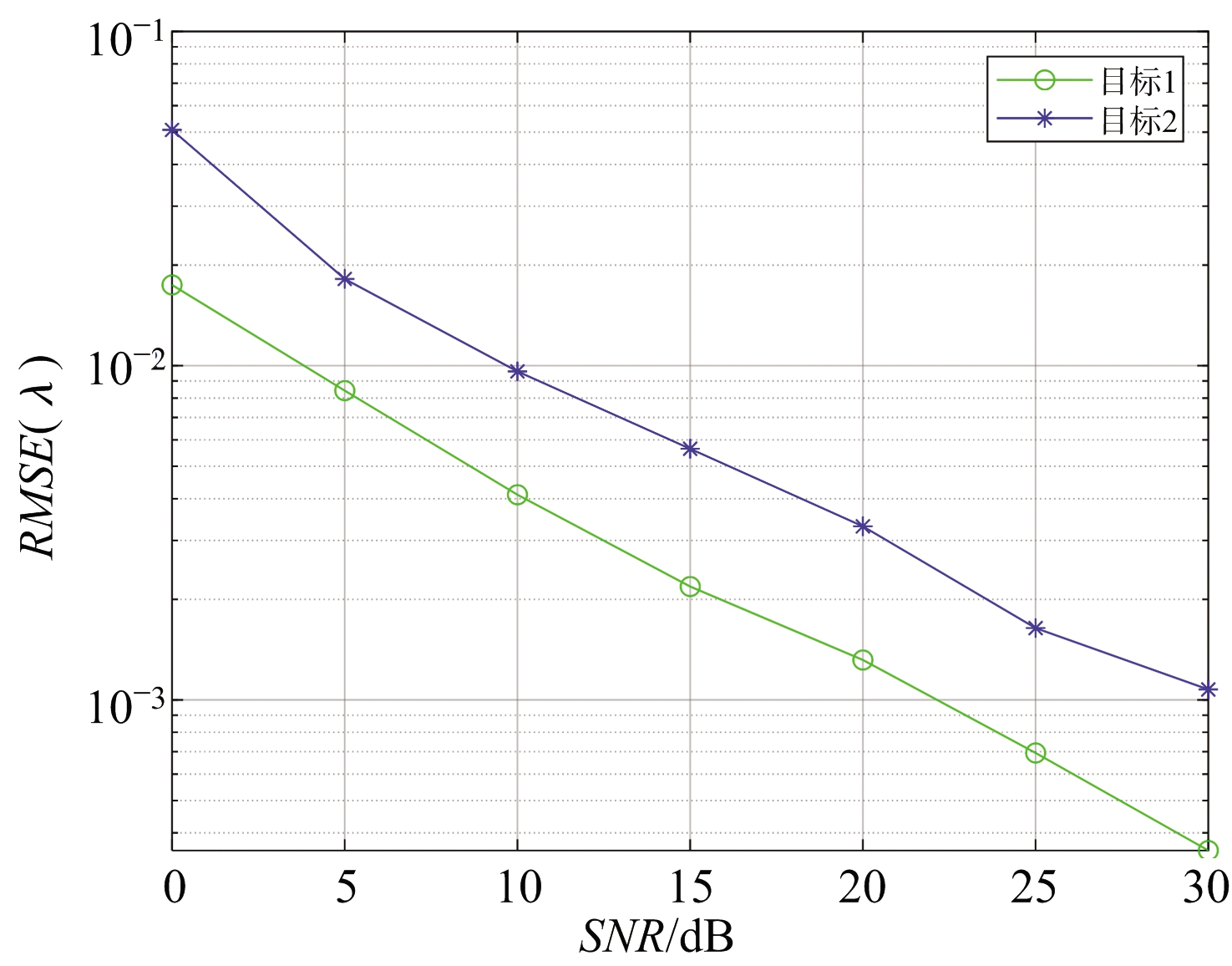
图5 距离估计RMSE
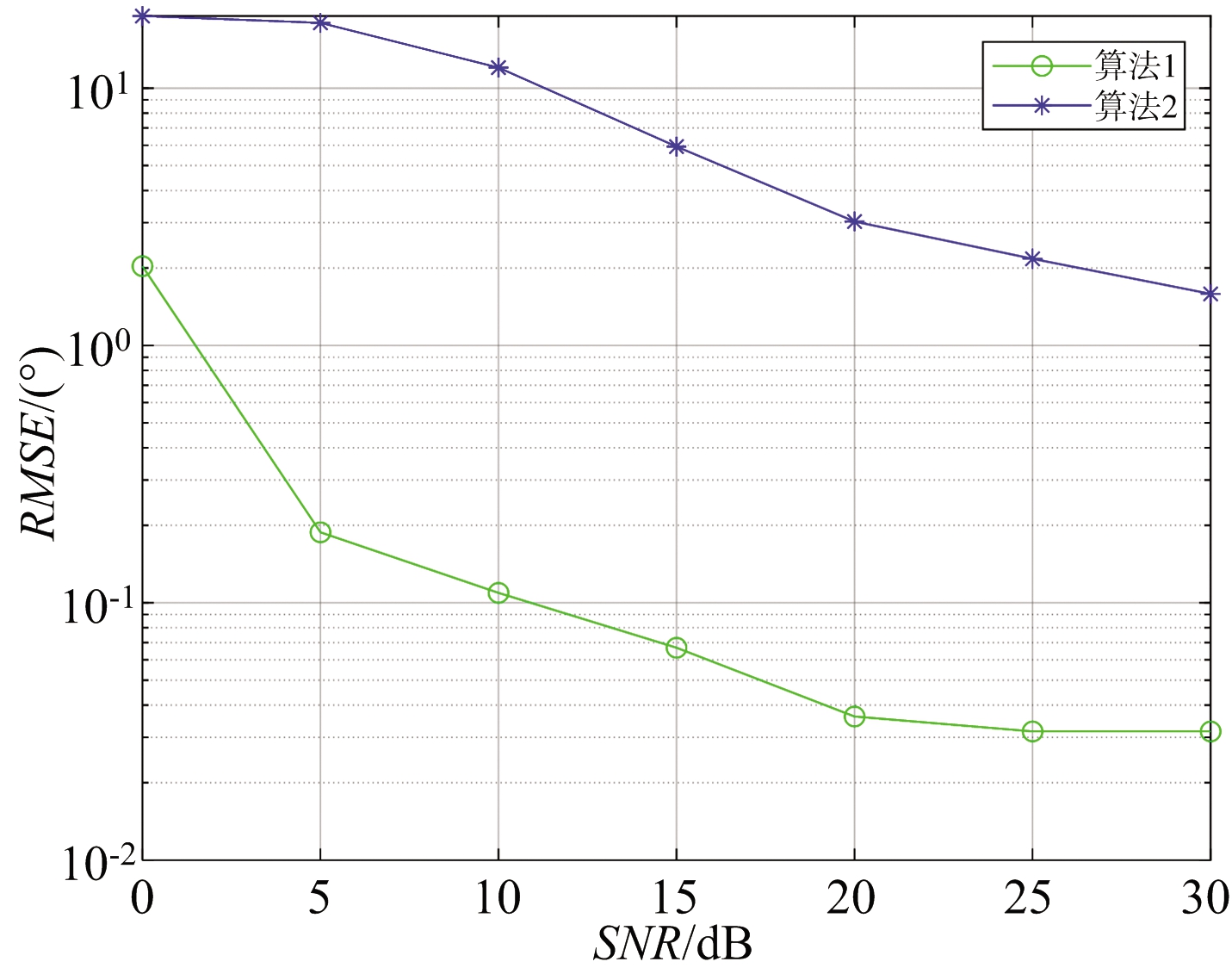
(a) 接收角估计值RMSE对比图
(b) 发射角估计值RMSE对比图
图6 角度估计性能对比图
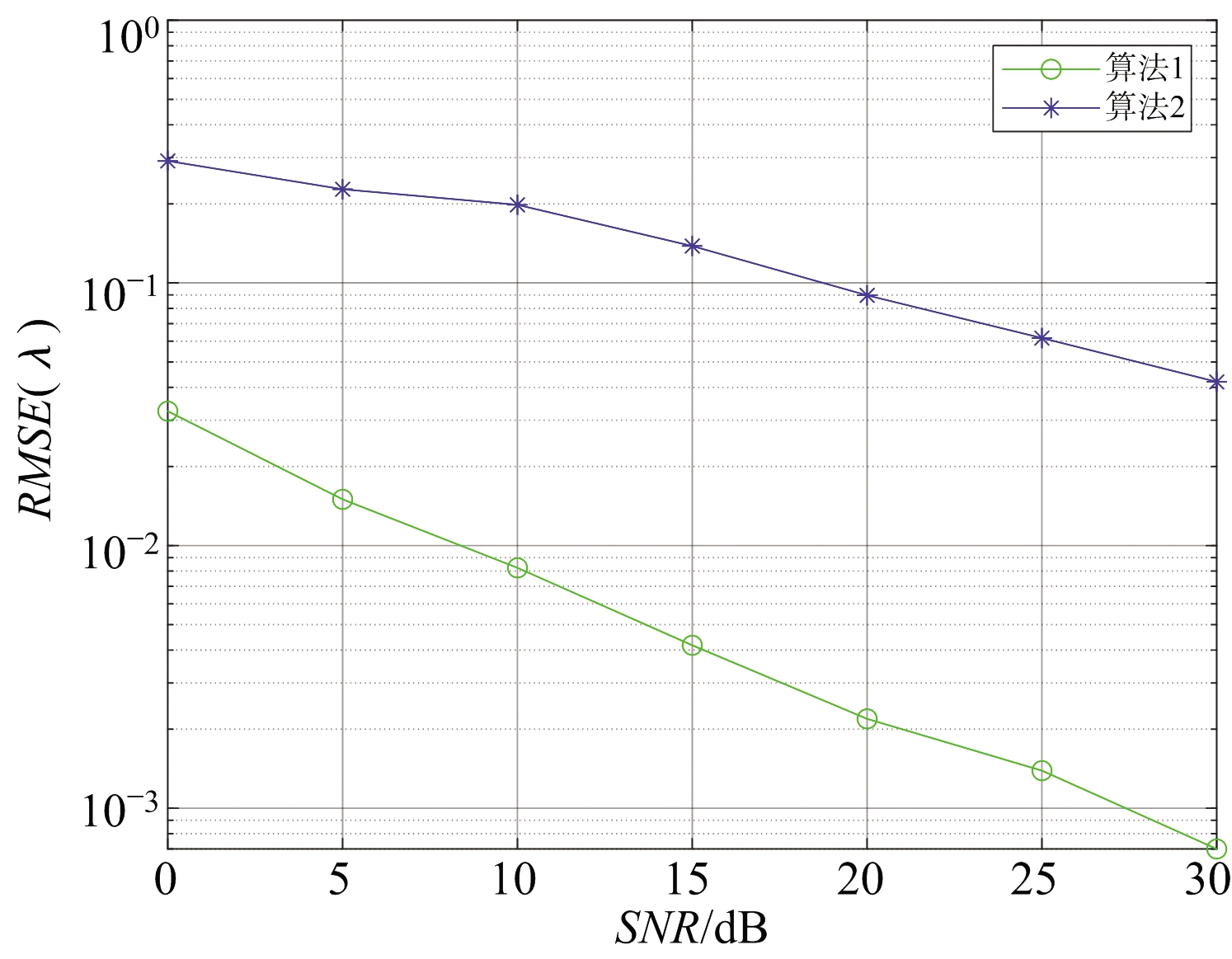
图7 距离估计性能对比图
仿真实验三：为了进一步验证算法的有效性，和已有算法进行如下对比实验。噪声为复高斯白噪声，信噪比(SNR)从0 dB到30 dB变化，进行100次重复实验，对比本文所提算法(算法1)和文献[7]所提算法(算法2)的参数估计值的RMSE随信噪比的变化曲线，结果如图6～图7所示。从图中可以看出：在高斯复噪声环境下，本文所提算法的精度明显高于文献[7]所提算法，文献[7]所提算法具有角度模糊现象，导致参数估计值的RMSE偏大，而且RMSE曲线不平滑。
4 结束语
本文提出了一种基于联合对角化的单基地MIMO雷达近场定位算法。该算法利用收发呈十字形的阵列模型，基于3个参数联合估计有效地解决了单基地MIMO雷达近场目标定位问题，参数可以自动配对，并具有较高的精度。此外，该算法对雷达系统的复杂度要求不高，只需3个发射阵列就可估计出近场目标的三维参数。另外，和文献[7]算法相比，所提算法在接收阵元间距为λ/2时依然有效，适用于任何高斯噪声环境。
[1] 王小英, 江怡帆, 赵悦. 三维移动目标无源定位算法[J]. 雷达科学与技术,2019,17(3):280-284.
WANG Xiaoying，JIANG Yifan，ZHAO Yue. An Algebraic Geometric Probabilistic Passive Location Method for Three Dimensional Moving Target[J]. Radar Science and Technology,2019,17(3):280-284.(in Chinese)
[2] 费太勇, 谭贤四, 巫勇, 等. 分布式MIMO数字阵列雷达多目标定位[J]. 火力与指挥控制,2019,44(3):55-59.
[3] 贺承杰. 天波超视距雷达海面目标定位方法研究[J]. 雷达科学与技术,2020,18(5):568-572.
HE Chengjie. Surface Target Location Method of Sky Wave Over-The-Horizon Radar[J]. Radar Science and Technology,2020,18(5):568-572.(in Chinese)
[4] 张曦文, 黄际彦, 王义圆, 等. 双频雷达运动目标近场定位算法[J]. 雷达科学与技术,2019,17(1):59-63.ZHANG Xiwen, HUANG Jiyan, WANG Yiyuan, et al. A Near Field Location Algorithm of Moving Target Based on Single Station Dual Frequency Radar[J]. Radar Science and Technology,2019,17(1):59-63.(in Chinese)
[5] SINGH P R, WANG Yide, CHARGE P. Bistatic MIMO Radar for Near Field Source Localization Using PARAFAC[J]. Electronics Letters,2015,52(12):1-2.
[6] ZHOU Erning, JIANG Hong, QI Han. 4-D Parameter Estimation in Bistatic MIMO Radar for Near-Field Target Localization[C]∥IEEE International Wireless Symposium (IWS), Shenzhen, China:IEEE,2015:1-4.
[7] 郭艺夺, 谢辉, 张永顺, 等. 基于MIMO雷达虚拟阵列的近场目标定位[J]. 雷达科学与技术,2012,10(1):82-87.
GUO Yiduo,XIE Hui,ZHANG Yongshun,et al.Localization for Near-Field Targets Based on Virtual Array of MIMO Radar [J].Radar Science and Technology,2012,10(1):82-87. (in Chinese)
[8] 项杨, 杨晋生. 非均匀L型阵列的联合对角化二维DOA估计算法[J]. 信号处理，2018，34(10):1228-1236.
[9] 龚晓峰, 毛蕾, 林秋华, 等. 基于四阶累积量联合对角化的多数据集联合盲源分离[J]. 电子与信息学报,2019,41(3):509-515.
GONG Xiaofeng, MAO Lei, LIN Qiuhua, et al. Joint Blind Source Separation Based on Ioint Diagonalization of Fourth-order Cumulant Tensors[J]. Journal of Electronics and Information Technology, 2019,41(3):509-515.(in Chinese)
