0 引言
极化合成孔径雷达(Synthetic Aperture Radar,SAR)是一种多参数、多通道的成像雷达系统,具有全天候、全天时的工作特点,具有较强的地物穿透能力,在目标识别、城市规划、地质勘探、植被生长评估、军事探测、海洋监测等众多领域有着广泛的应用。近年来,极化SAR图像地物分类已经成为雷达遥感图像领域的研究热点,且已经出现了很多较为成熟的算法。对于极化SAR农田分类,普遍存在着农田块形状不规则、区域较小、分布不均匀等问题,同时多时相图像分类[1] 也是难点之一。针对这些问题,我们对混合模型与基于马尔科夫随机场(Markov Random Field,MRF)的分类算法进行了研究,并提出了基于局部竞争思想的MAP分类器。
根据所使用的特征不同,极化SAR图像分类方法可归纳为两类:基于统计特性的分类和基于极化散射机制的分类[2-3]。极化SAR图像的统计特性是根据其数据的统计模型推导出来的,在图像分类中起到很重要的作用。其中,应用最广泛的是测量矢量的多元高斯分布和协方差(或相干)矩阵的复Wishart分布。1988年,Kong等人[4]提出了基于复高斯分布的单视极化SAR图像最大似然(Maximum Likelihood,ML)分类器。1994年,Lee等人[5]将最大似然规则推广到SAR多视情况,提出了基于复Wishart分布的ML监督分类方法,这是极化SAR数据分类研究的一座里程碑。基于复Wishart分布的Wishart距离度量也被广泛地用于监督和非监督分类中,基于该距离度量的分类技术称为Wishart分类器。1999年,Lee等人[6]提出了基于H/α分解和Wishart分类器的迭代分类算法,Ferro-famil等人[7]将该方法用于双极化数据分类。2004年,Lee等人[8]提出了基于Freeman分解和复Wishart分布的ML分类器的极化SAR图像分类算法,这种算法是一种性能十分优良的分类算法,能很好地保持各类地物的极化散射特性,是目前最为经典的极化SAR分类算法之一。
Wishart分类器和Gaussian分类器是两种经典的基于极化统计分布的Bayes最优分类算法,后来的许多算法都直接或间接用到了这两种统计模型。包括一些针对不均匀区域建模提出的乘积模型和混合模型,如K分布[9]、G分布[10]、WGΓ分布[11]、混合Gaussian模型[12-13]和混合Wishart模型[14-15]。为了充分利用图像的空间上下文信息,很多学者将MRF引入了极化SAR图像分类算法的框架中。2001年,Dong等人[16]第一次将MRF用于极化SAR图像分类。2008年,Wu等人[17]将MRF与复Wishart分布结合提出了WMRF模型,并将该模型与基于区域的分类框架相结合,得到了较好的分类结果。Li等人[18]将高斯混合模型(Gaussian Mixture Model,GMM)与MRF相结合,构造了GMM-MRF模型,Song等人[19]基于WGΓ分布构造了混合WGΓ(Mixture WGΓ,MWGΓ)模型,然后与MRF结合构造了MWGΓ-MRF模型。然而以上这些方法,均为基于全局思想的分类算法,在对像素或超像素进行分类时,需要将图像中的全部地物类型进行对比。对于基于统计分布模型的ML分类器,分类器的效果仅依赖于统计模型的准确性,这种基于全局的分类思想容易出现误分类的情况,尤其是在地物类别区域不连续、区域形状不规则的情况下。而将MRF与统计模型相结合,可以有效地利用图像的空间信息,提高了分类效果,但算法依然是基于全局的思想。该文中,我们提出一种新的基于局部竞争策略的MAP分类器,该算法的主要思想是,在对像素进行分类时,仅对比该像素附近的地物类别。该算法不仅减少了像素点需要对比的类别数目,同时也利用了图像的空间信息以及伪先验概率信息,通过局部迭代的方法提高分类的准确率。
本文中,我们主要研究基于复Wishart分布的分类模型在复杂地形区域中的分类性能,包括经典的复Wishart模型、混合复Wishart模型、基于MRF的混合复Wishart模型和基于局部竞争策略的MAP分类器。首先,分析了混合Wishart模型的优越性,然后用上述4种模型对两幅在不同时间获取的同一地区的极化SAR图像进行分类,并对比分析这4种方法对多时相极化SAR图像的分类效果。同时,我们也比较了SVM分类器的结果。文章安排如下:第2部分介绍统计模型、MRF模型和本文提出的方法;第3部分展示实验结果并进行分析;第4部分对全文进行总结。
1 基于复Wishart分布的极化SAR图像分类器
1.1 复Wishart分布及ML分类器
对于满足互易原则的媒质,极化SAR复散射矢量可以表示为![]() 其中,[·]T表示矩阵转置。一般来说,极化SAR数据有两种形式:单视数据和多视数据。多视处理是通过对若干独立的单视协方差矩阵进行平均实现的,多视处理后的协方差矩阵为
其中,[·]T表示矩阵转置。一般来说,极化SAR数据有两种形式:单视数据和多视数据。多视处理是通过对若干独立的单视协方差矩阵进行平均实现的,多视处理后的协方差矩阵为
(1)
式中,L表示视数,矢量us表示第s个单视数据样本,(·)H表示复共轭转置。
建立统计分布模型一直是极化SAR图像处理领域的研究热点,许多学者都提出了相关的统计模型。对于多视极化SAR图像,极化协方差矩阵C={C1C2 … CN}服从复Wishart分布,
(2)
式中,协方差矩阵Σ=E[uuH],tr(·)代表矩阵的迹,L代表视数,q代表通道数,K(·)为尺度函数。1994年,Lee等人[5] 提出了基于复Wishart分布的极大似然分类器。假设图像共包含M类像素,用Σm表示类ωm的类中心,则式(2)可重写为p(Ci|ωm),通过最大化p(Ci|ωm)p(ωm)可推导出n视极化SAR数据分类的距离度量方法,
d(Ci,ωm)=nln|Σm|+
(3)
式中,P(ωm)表示类ωm的先验概率。在各类先验概率都未知的情况下,可以假设P(ωm)相同,此时的距离度量与n无关,于是可以将式(3)简化为
(4)
将式(4)定义为Wishart距离度量,基于该距离度量的分类器称为复Wishart分类器,算法步骤如下:
1) 根据训练集,计算数据的类中心Σ={Σ1Σ2…ΣM},其中M表示类别数;
2) 对于图像中的每个像素Zi,若它的协方差矩阵Ci满足d(Ci,Σm)<d(Ci,Σj),j=1…M& j≠m,则将Zi归为ωm类。
1.2 基于局部竞争策略的MAP分类器
基于复Wishart的ML分类器是极化SAR图像分类的里程碑,但该方法的分类准确率完全依赖于对每种地物类型进行适当的统计建模,而没有利用图像的空间信息。基于复Wishart分布的局部MAP竞争(Local Competitive Wishart, LCW)算法利用一种简单的思想,基于初始复Wishart分类器的分类结果,在局部窗口中利用局部竞争的方式对分类结果进行迭代[20]。图1展示了该算法的核心思想,假设图像中共包含9种地物类型,在对像素i进行分类时,以图1(b)的形式对像素取一个局部窗口,首先对该窗口内部地物类别类中心进行更新,需要对比的数据类别从9个减少为4个,并且由于局部局限性,像素i必定会被分到ω1、ω2、ω5和ω6中的一个类别中,而不会被分为其他类别;当更新完局部类中心并得到窗口中每类地物的局部伪先验概率后,对i进行分类。因此可以把LCW算法看作是局部窗口内的Wishart-MAP分类器。LCW算法中使用的MAP分类器是在式(3)的基础上,将式中的先验概率P(ωm)替换为伪先验概率。由于我们无法得到地物的真值,因此只能使用伪先验概率。在LCW算法中,伪先验概率P(ωm)指的是在上一次迭代结果中该像素窗口内ωm类地物所占的像素个数比例。LCW算法的流程如图2所示,具体细节如下:
1) 获取每一类训练集X={x1x2…xM},xi表示第i类样本点的集合。计算初始类中心Σ={Σ1Σ2…ΣM},M表示图像中像素种类的个数。
2) 利用Wishart分类器对图像进行初始分类。
3) 以分类后图像中每个像素Zi为中心取w×w大小的窗口。
4) 利用窗口中的数据更新局部类中心Σl={Σ1Σ2…ΣR},R≤M,R表示窗口中像素种类的个数。
5) 计算窗口内ωr类地物的伪先验概率,利用式(3)对中心像素Zi重新分类,若满足d(Ci,Σr)<d(Ci,Σj)且j=1…R,j≠r,则将Zi重新归为ωr类。
6) 得到分类图像返回第3)步。迭代直到收敛,输出最终分类结果。
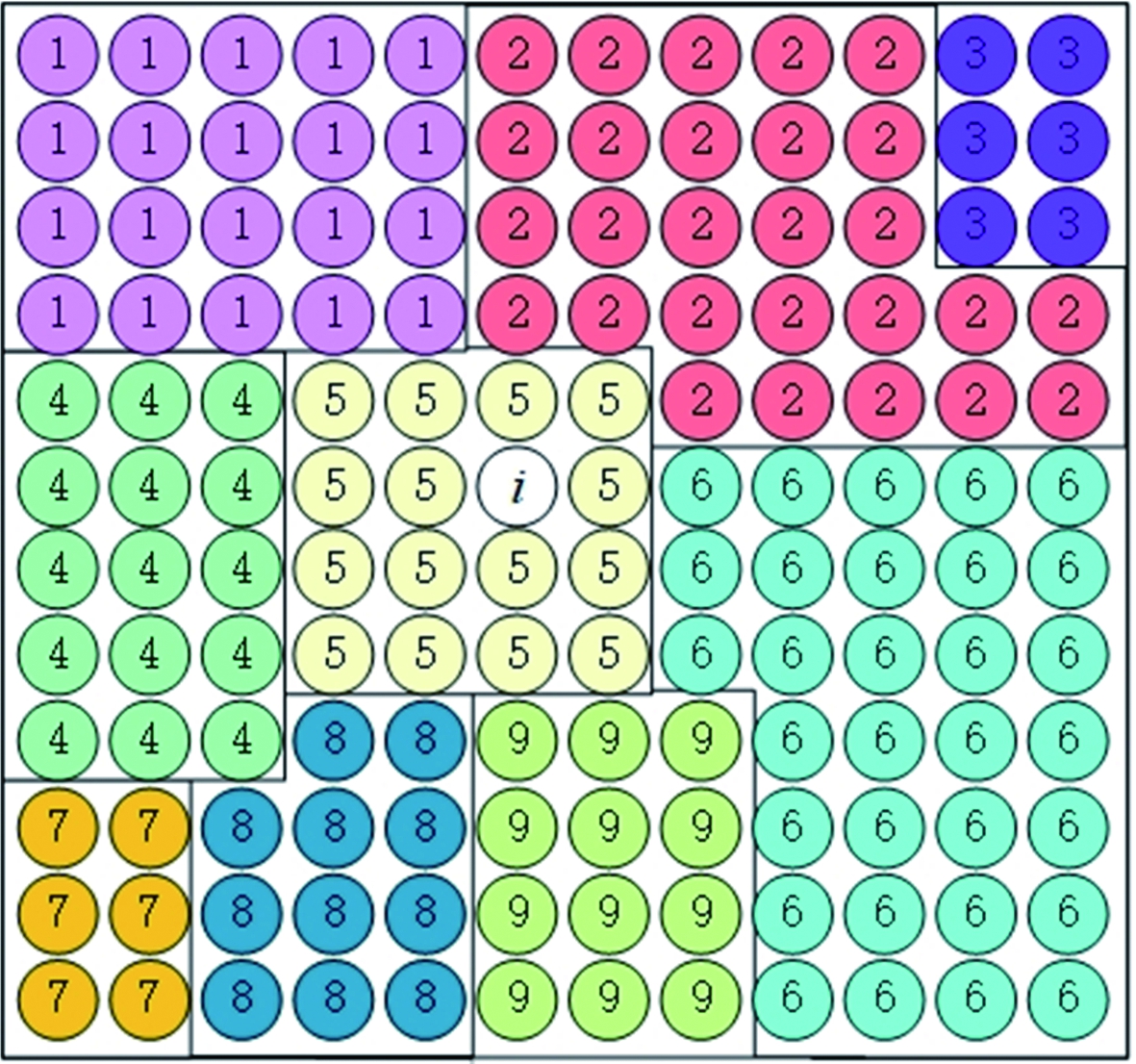
(a) 图像示意图

(b) 局部竞争算法示意图
图1 局部竞争思想

图2 LCW算法流程图
1.3 基于马尔科夫随机场(MRF)的混合Wishart分类算法
混合模型通过充分考虑区域的不均匀性来保持空间相关性,从而更好地描述极化SAR图像中的非均匀区域。对于Wishart混合模型,目前,主要有两种混合策略:一种是使用Wishart混合模型对整个图像进行建模(Mixture Wishart for a Whole Image, MWW)[14],另一种则是使用Wishart混合模型对图像中的一类数据进行建模(Mixture Wishart for a Class, MWC)[21]。根据文献[22] 可知,MWC模型对于极化SAR图像地物分类的准确率更高,因此本文主要讨论MWC模型。本小节首先介绍了MWC模型,然后将该模型与MRF结合,构造基于MRF的混合Wishart分类模型。
1.3.1 MWC混合模型
根据文献[21] 可知,MWC模型假设每个地物类型的数据都由多个Wishart分布来拟合。假设图像共包含M种地物类型,每一种类型的数据由K个Wishart分布混合建模,每一个Wishart分布的中心协方差矩阵由Σk,k=1,2,…,K表示,每一个Wishart分布的权重为πk,并且权重取值满足

(5)
则对于ωm类数据,Wishart混合模型的概率密度函数如下式所示:
![]()
![]()
(6)
由此可以看出,MWC模型共用了K×M个Wishart分布来对图像进行建模。该模型中主要的参数包括混合成分的数量K、类中心矩阵Ck和权重πk。其中参数K的值比较难以确定,从理论上来讲,K的值越大分类的准确率越高,但同时也会增加算法的时间成本。从这两个方面平衡考虑,本文将K的值设为6。类中心矩阵Ck通过随机从每一类的训练集种选取K个Zi进行初始化,![]() 的初始值为1/K,这两个参数通过EM算法迭代求出。
的初始值为1/K,这两个参数通过EM算法迭代求出。
1.3.2 MRF模型
假设图像由二维网格S={sxy,1≤x≤m,1≤y≤n}表示,则定义在S上面的随机场X如果满足以下两个条件,则X是一个马尔科夫随机场,
(7)
式中,S\i 表示图像中除去像素i之外的所有像素,ηi表示像素i的邻域。
根据Hammersley-Clifford定理[23] 可知,MRF的联合概率与Gibbs分布等价,
![]()
(8)
式中:T为形状参数,在实际应用中一般取常数![]() 为归一化系数,U(x)为能量参数,定义为
为归一化系数,U(x)为能量参数,定义为
U(xi)=-β∑j∈ηiδ(xi-xj)
(9)
式中,β>0是空间平滑参数,本文中取经验值1.4 [17,24] 。
设Y={yi,i∈S}为待观测图像,X={xi,i∈S}为Y的类别标签。根据贝叶斯准则,类别标签xi的后验概率为
![]()
(10)
P(yi)的取值与xi无关,因此,在先验概率与似然概率均已知的情况下,xi的取值可通过最大化后验概率来确定:
![]()
(11)
式中:p(yi|xi)为待观测数据的后验概率,可以根据MWC模型计算得到;P(xi)为先验概率,根据MRF模型计算得到。将式(4)与式(9)相结合,能够得到基于MRF的Wishart混合模型,下文中简称为MWC-MRF模型,该模型如下所示:
![]()
![]()
(12)
2 实验结果与分析
2.1 模型验证
为了验证混合Wishart模型的有效性,我们分别用经典Wishart模型和MWC模型来拟合真实的极化SAR数据。该实验使用的数据为Radarsat-2卫星获取的美国旧金山港湾C波段全极化数据,入射角度为28.02°~ 29.82°。该图像获取于2008年4月9日,图像大小为1 453×1 387。该数据经过多视处理,并用7×7窗口的Lee滤波进行降噪,图中有明显的海洋、森林、城市3类主要区域。图3展示了该地区的Pauli分解伪彩色图像,图像中框出的部分为实验所选择的区域。由图像可以看出,实验所选择的城市和森林地区均为不均匀区域。

图3 旧金山地区Pauli分解伪彩色图像
多视极化SAR图像数据的一般形式为3×3的极化协方差矩阵,可以看作一个9维随机向量,图4给出了对角线元素的拟合结果,分别对应HH、HV和VV三个极化通道的强度。图4中每一行对应一种地物类型,每一列对应一个极化通道。
由图4展示的数据拟合结果可以看出,相比于Wishart模型,混合Wishart模型更加贴合数据的真实分布。尤其对于城市区域,通过图4 (g) ~ (i)可以看出,Wishart模型对城市区域的建模效果并不理想,真实数据分布(蓝色圆圈)与Wishart模型(红线)的分布有较大的差异。对于海洋和森林区域,两种模型对于数据的拟合程度相差不大,但是混合Wishart模型对于真实数据的贴合程度更高。因此可以得出结论,与Wishart模型相比,混合Wishart模型能够更加准确地对均匀和不均匀的区域进行建模,误差较小。

图4 旧金山数据拟合结果
2.2 分类结果与分析
农田分类一直是极化SAR图像的重要应用之一。在本实验中,我们将对比复Wishart分类器、LCW分类器、MWC模型与MWC-MRF模型在真实极化SAR图像上的分类效果。同时,SVM分类器也是农田分类中经常使用的一种分类器[25],我们也将展示SVM的分类结果。实验所用的数据是由Radarsat-2卫星获取的位于德国Bamling 地区的农田图像,为了验证上述算法在多时相图像分类中的分类结果稳定性,我们分别采用2014年5月28日和2014年8月18日两幅此处的图像。在分类实验中,我们截取了920×500大小的子区域作为实验数据,该区域主要包含大麦、玉米、土豆、甜菜、小麦5种地物类型。图5给出了该区域的两时相Pauli分解伪彩色图和对应的地面真值图,两幅图像在实验前均用7×7窗口的Lee滤波进行了处理。在实验中,我们随机选取该区域的每类地物13%的像素为训练集。

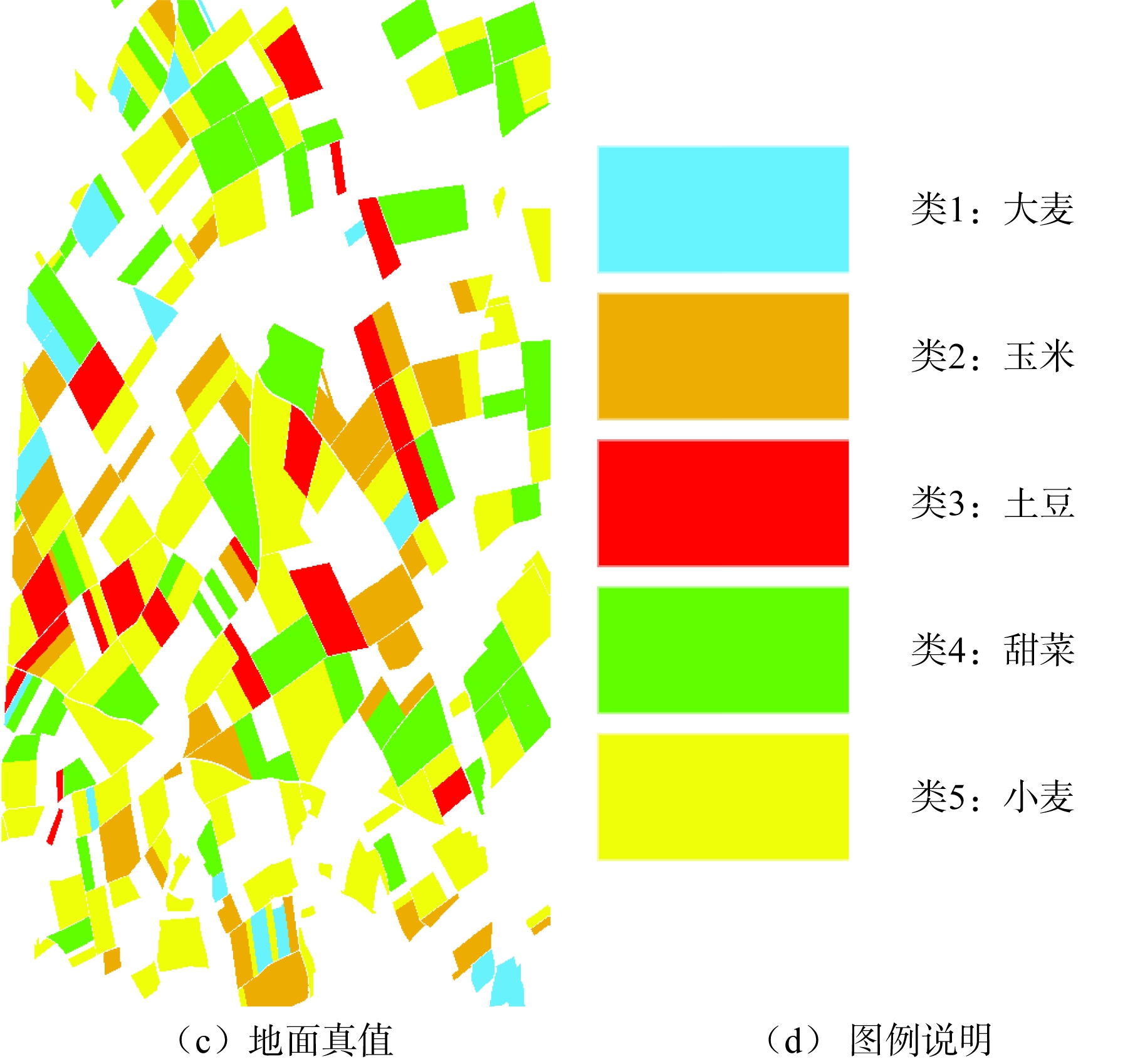
图5 德国Bamling农田数据
2.2.1 LCW参数估计
在LCW算法中,窗口大小w的取值十分重要。根据该算法的核心思想以及本实验所采用的德国农田数据(图5)可知,农田块的形状不规则而且区域较小,w值取太大会导致窗口内包含较多的地物类别,无法体现出局部竞争策略的优势。如果w取值太小,则窗口中的像素数量太少,无法计算出准确的局部类中心,会导致建模不准确,影响分类的准确性。
因此,为了使LWC算法的分类效果达到最优,我们研究了w的不同取值对分类效果的影响。实验中,我们设置迭代收敛条件为本次分类结果未变化的像素个数/总像素个数>99.5%,w的取值范围设为5~21,分别用不同w取值的LWC算法对2014年5月28日所获取的农田图像进行分类,w取值的变化对分类准确率的影响如图6所示,迭代次数或窗口大小为0表示使用复Wishart分类器得到的初始分类结果。从图6(b)可以看出,LCW算法的分类效果对w的取值十分敏感,刚开始分类准确率随着w取值的增大而提升,当w取值超过17时,分类准确率开始下降,局部竞争的策略开始失去优势。根据图6的实验结果,在后续实验中,我们将w的值设为17。
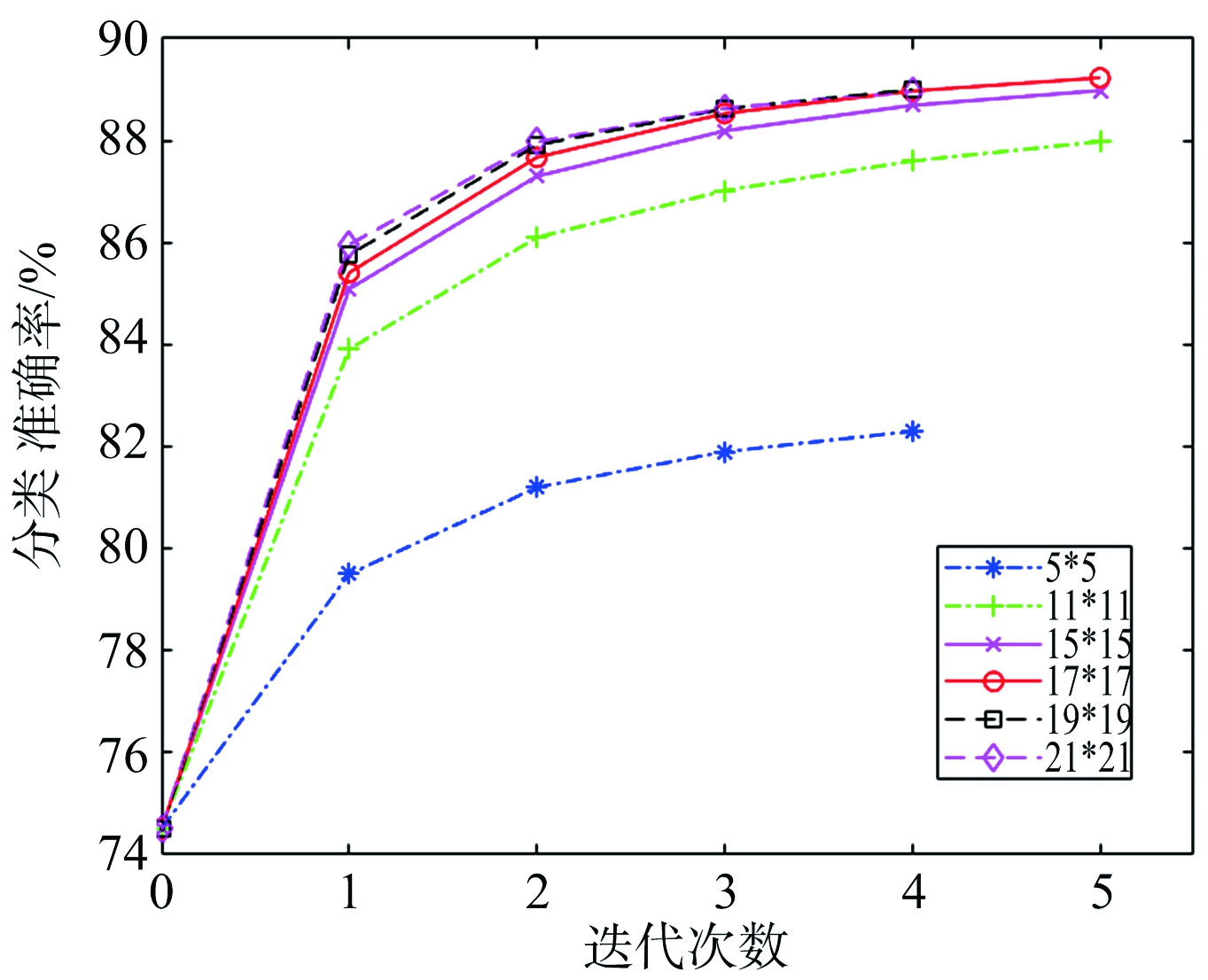
(a) 使用不同大小窗口的算法迭代次数与分类精度的折线图
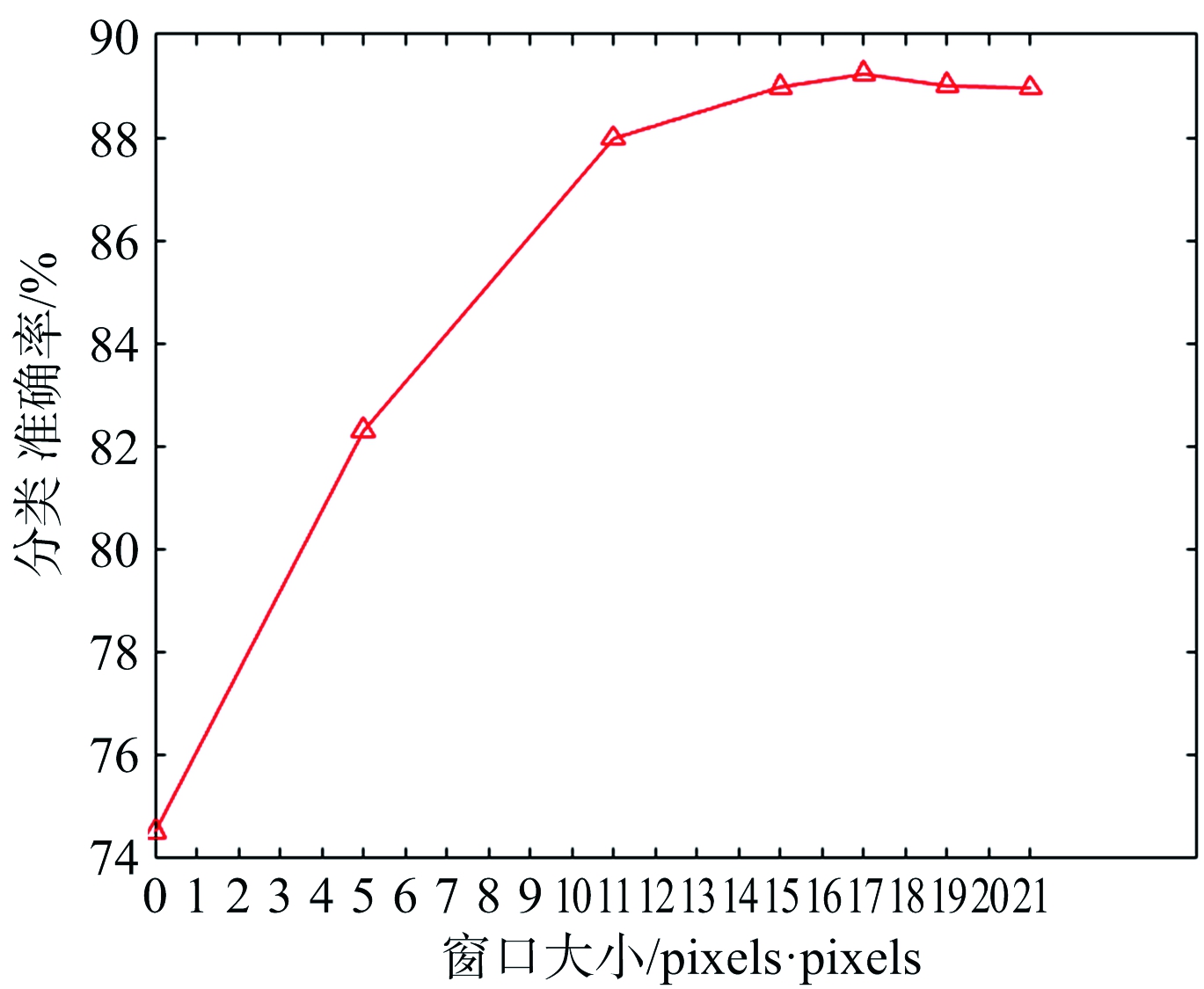
(b) 窗口大小对分类准确率的影响
图6 参数w取值与分类精度的关系
2.2.2 结果分析

图7 Wishart-ML方法2幅时相德国农田分类结果

图8 MWC-ML方法2幅时相德国农田分类结果
本小节主要分析各个算法对多时相数据的分类性能,图7~图11展示了5种分类算法的分类结果。从图7和表1可以看出,经典的复Wishart分类器得到的分类结果并不理想,两幅分类图像中的噪点较多,且分类准确率较低。同时,该方法对多时相数据的分类效果波动较大,总体的分类准确率波动于74.51%至61.98%之间,出现约13%的起伏。尤其是对于玉米和土豆这两类地物出现了大量错分,准确率分别从60.43%和56.95%降低到52.79%和48.72%。由此可见,Wishart模型虽然具有较低的计算复杂度,但是并不能准确地对该农田数据进行建模。由图8可以看出,与经典的复Wishart分类器相比,混合Wishart模型的分类效果较好,对两幅图像的分类准确率均有了提升,由此可以证明MWC模型比Wishart模型对数据的拟合更好,这与第2.1节中的分析结果一致。然而,虽然分类效果有所提升,但MWC模型的总体分类准确率依然不高, 说明混合模型也无法解决复杂区域精细分类问题。
MWC-MRF模型是对MWC模型的优化,利用了MRF去获取像素的空间信息,从而降低噪声对分类的影响。从图8和图9可以看出,与MWC相比,MWC-MRF模型的分类结果噪点较少,区域完整性更高,分类准确率和Kappa系数也更高。LCW算法同样利用了图像的空间信息,根据图10和表1的数据可以看出,LCW算法的整体分类准确率和Kappa系数值明显高于另外三种模型,但是在8月18日的分类结果里有三种地物的分类准确率低于MWC-MRF,原因是在使用Wishart分类器对8月18日数据进行初始分类后,有几类地物的分类准确率很低,在LCW算法进行局部竞争时,由于初始分类效果较差导致窗口内的正确分类地物相对较少,使得局部竞争难以得到正确的结果。由此可见,LCW算法的分类准确率很大程度上取决于初始分类结果,初始分类结果差的情况下,无法通过LCW获得较好的结果。但相对而言,LCW分类图像中的噪点较少,区域完整性也较好。从实验结果可以看出,4种模型对同一区域的分类效果均会受到时间的影响,8月份获取的农田图像分类准确率明显低于5月份获取的图像。LCW算法虽然也受到了影响,分类准确率下降约13%,但是整体的分类准确率在几个模型里还是最高的。

图9 MWC-MRF方法2幅时相德国农田分类结果
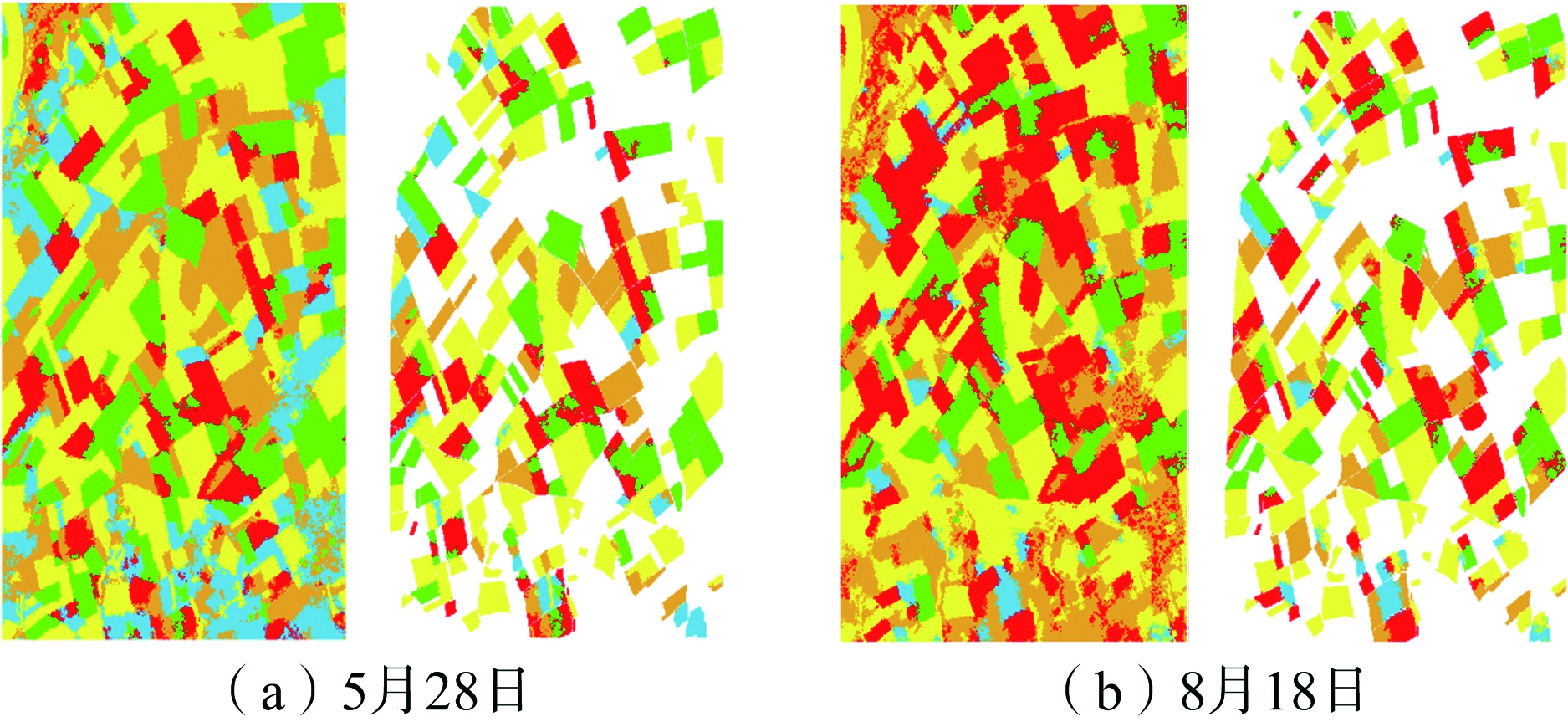
图10 LCW方法2幅时相德国农田分类结果
为了更好地评估本文所提出方法的分类性能,我们还使用目前分类效果较好的SVM分类器对德国农田的极化SAR图像进行分类,如图11所示。观察SVM分类器的分类结果与表1中的数据,并且与LCW算法的分类结果进行对比,可以发现LCW算法的分类性能有较大的优势。对多时相数据的分类结果,图10比图11的平均分类精度有10%左右的提升,这说明LCW分类器在对极化SAR图像分类时,能够有效利用上下文信息,是一种具有高鲁棒性的分类算法。

图11 SVM方法2幅时相德国农田分类结果
表1 农田分类结果对比

方法日期Class1BarleyClass 2CornClass 3PotatoesClass 4Sugar beetClass 5WheatOAKappaWishart5月28日78.58%60.43%56.95%68.07%88.09%74.51%0.72978月18日35.46%52.79%48.72%57.85%74.77%61.98%0.5980MWC5月28日80.01%61.61%56.84%75.41%88.63%77.75%0.68718月18日50.60%62.57%46.68%72.09%63.73%63.35%0.5224
续表

方法日期Class1BarleyClass 2CornClass 3PotatoesClass 4Sugar beetClass 5WheatOAKappaMWC-MRF5月28日90.47%79.15%63.30%83.79%92.72%84.40%0.78548月18日62.89%72.45%47.56%80.59%64.63%68.30%0.5853LCW5月28日93.15%79.82%82.83%86.74%95.60%89.23%0.88538月18日41.45%70.05%74.39%67.10%89.48%76.32%0.7485SVM5月28日59.56%68.37%60.04%68.68%93.44%77.52%0.69198月18日54.70%61.57%34.64%70.57%64.63%62.08%0.5053
另外,从表1可以发现每个分类器对8月18日的数据分类效果都不太好。因为在德国,夏大麦和冬大麦的收割季节都在7—8月;该地区的小麦的收割期也在7—8月,土豆和玉米在6—8月份已发育成型,不再生长。因此这些地物的散射类型和强度都较为相似,容易被误分类,造成了8月18日各类地物的分类正确率较低。
3 结束语
对于极化SAR图像区域形状不规则、区域较小、分布不均匀等带来的分类困难,以及多时相图像分类结果有时差异较大等问题,本文提出了一种基于复Wishart分布的MAP算法,该算法基于Wishart分类器的分类结果,在每个像素的局部窗口内使用MAP分类器,并进行多次迭代,直到结果收敛。实验对比研究了4种基于Wishart分布的极化SAR图像分类算法,包括复Wishart分类器、混合Wishart分类器,基于MRF的混合Wishart分类器和本文提出的局部竞争Wishart算法,并将混合Wishart模型与经典Wishart模型进行了对比。同时,为了证明所提出方法的鲁棒性,也将SVM分类器的结果进行了对比。
实验结果表明,LCW算法的分类效果优于其他算法,分类准确率和Kappa系数值远高于其他算法。此外,通过对真实数据的拟合结果和分类结果进行分析,我们可以得出结论,与Wishart模型相比,混合Wishart模型能够更加准确地对均匀和不均匀的区域进行建模,其分类的准确率也更高。而将MRF与混合Wishart模型相结合,有效地利用了图像的空间信息,能够进一步提升分类效果,但对于地形复杂的区域,优化的效果依然有限。本文所提出的LCW算法利用了空间上下文信息,得到的整体分类结果优于MWC-MRF模型;同时该算法采用的复Wishart分布模型较为简单,与MWC-MRF模型相比时间成本更低。因此,本文所提出的LCW分类器是一种高效、稳定的分类算法,在复杂场景下能够取得较为良好的效果。但该算法也有一些明显的缺点,一是需要效果较好的初始分类结果作为基础,由5月28日的实验结果可以看出,当初始分类结果较好时,使用LCW能够对分类准确率有进一步的提升,而由于局部竞争自身所具有局限性,在一些初始分类效果较差的区域,局部窗口内被误分类的像素点较多,影响了窗口内地物的伪先验概率,会导致窗口中心像素难以被正确分类,同时该中心像素的分类结果也会影响周围其他待分类像素的分类情况。从8月18日数据的大麦、玉米和甜菜的分类准确率就不如MWC-MRF的结果也可以看出,初始分类较差的情况下,LCW的分类准确率并不能提升太多。因此,可以针对局部竞争策略进行改进,例如将Wishart距离度量与其他距离度量相结合,提高局部竞争的分类准确率。
此外,通过观察可以发现实验结果中的土豆和甜菜两类地物的分类边界效果不好,原因是这两类地物计算得到的类中心数据的数值较为相似,因此在分类时容易造成误分类。因此可知LCW对特征相似地物的区域边界的保持效果并不好,这一点仍需在后续研究中改进,例如可以使用特征增强等方法,以得到更为准确的分类结果。
致谢 感谢德国宇航中心(German Aerospace Center,DLR)提供多时相RADARSAT-2 德国Bamling 地区数据以及地面真值。
[1] 陶臣嵩, 陈思伟, 李永祯, 等. 结合旋转域极化特征的极化SAR地物分类[J]. 雷达学报, 2017, 6(5):524-532.
[2] YIN J J, MOON W M, YANG J. Novel Model-Based Method for Identification of Scattering Mechanisms in Polarimetric SAR Data[J]. IEEE Trans on Geoscience and Remote Sensing,2016,54(1):520-532.
[3] LEE J S, HOPPEL K, MANGO S A. Intensity and Phase Statistics of Multi-Look Polarimetric SAR Ima-gery[J]. IEEE Trans on Geoscience and Remote Sensing,1994, 32(5):1017-1028.
[4] KONG J A, SCHWARTZ A A, YUEH H A,et al. Identification of Terrain Cover Using the Optimum Polarimetric Classifier [J]. Journal of Electromagnetic Waves and Applications,1988,2(2):171-194.
[5] LEE J S, GRUNES M R, KWOK R. Classification of Multi-Look Polarimetric SAR Imagery Based on Complex Wishart Distribution[J]. International Journal of Remote Sensing,1994,15(11):2299-2311.
[6] LEE J S, GRUNES M R, AINSWORTH T L, et al. Unsupervised Classification Using Polarimetric Decomposition and the Complex Wishart Classifier[J]. IEEE Trans on Geoscience and Remote Sensing,1999,37(5):2249-2258.
[7] FERRO-FAMIL L, POTTIER E, LEE J S. Unsupervised Classification of Multifrequency and Fully Polarimetric SAR Images Based on the H/A/Alpha-Wishart Classifier[J].IEEE Trans on Geoscience and Remote Sensing,2001,39(11):2332-2342.
[8] LEE J S, GRUNES M R, POTTIER E, et al. Unsupervised Terrain Classification Preserving Polarimetric Scattering Characteristics[J]. IEEE Trans on Geoscience and Remote Sensing,2004,42(4):722-731.
[9] LEE J S, SCHULER D L, LANG R H, et al. K-Distribution for Multi-Look Processed Polarimetric SAR Imagery[C]∥IEEE Geoscience and Remote Sensing Symposium, Pasadena, CA, USA:IEEE,1994:2179-2181.
[10] FREITAS C C, FRERY A C, CORREIA A H. The Polarimetric Distribution for SAR Data Analysis[J]. Environmetrics: The Official Journal of the International Environmetrics Society,2005,16(1):13-31.
[11] SONG W Y, LI M, ZHANG P, et al. The WGΓ Distribution for Multilook Polarimetric SAR Data and Its Application[J].IEEE Geoscience and Remote Sensing Letters,2015,12(10):2056-2060.
[12] MURTAGH F, CONTRERAS P, STARCK J L. Scale-based Gaussian Coverings: Combining Intra and Inter Mixture Models in Image Segmentation[J]. Entropy,2009,11(3):513-528.
[13] CHEN J, WANG Y,WU H. A Coded Aperture Compressive Imaging Array and Its Visual Detection and Tracking Algorithms for Surveillance Systems[J]. Sensors,2012,12(11):14397-14415.
[14] PENG Y, CHEN J, XU X, et al. SAR Images Statistical Modeling and Classification Based on the Mixture of Alpha-Stable Distributions[J]. Remote Sensing,2013,5(5):2145-2163.
[15] 钟能,杨文,杨祥立,等.基于混合Wishart模型的极化SAR图像非监督分类[J].雷达学报,2017,6(5):533-540.
[16] DONG Y, MILNE A K, FORSTER B C. Segmentation and Classification of Vegetated Areas Using Polarimetric SAR Image Data[J]. IEEE Trans on Geoscience and Remote Sensing,2001,39(2):321-329.
[17] WU Y, JI K, YU W. Region-Based Classification of Polarimetric SAR Images Using Wishart MRF[J]. IEEE Geoscience and Remote Sensing Letters, 2008, 5(4):668-672.
[18] LI W, PRASAD S, FOWLER J E. Hyperspectral Image Classification Using Gaussian Mixture Models and Markov Random Fields[J]. IEEE Geoscience and Remote Sensing Letters,2014,11(1):153-157.
[19] SONG W Y, LI M, ZHANG P, et al. Mixture WGΓ-MRF Model for PolSAR Image Classification[J]. IEEE Trans on Geoscience and Remote Sensing,2018,56(2):905-920.
[20] LIU X, YIN J, WANG T. Local Competitive Wishart Classifier for Polarimetric Sar Images[C]∥IEEE International Geoscience and Remote Sensing Symposium, Yokohama, Japan:IEEE,2019:2591-2594.
[21] GAO W, YANG J, MA W. Land Cover Classification for Polarimetric SAR Images Based on Mixture Models[J]. Remote Sensing,2014,6(5):3770-3790.
[22] YIN J, LIU X, YANG J, et al. PolSAR Image Classification Based on Statistical Distribution and MRF[J]. Remote Sensing,2020,12(6):1027.
[23] SHERMAN S. Markov Random Fields and Gibbs Random Fields[J]. Israel Journal of Mathematics,1973,14(1):92-103.
[24] RIGNOT E, CHELLAPPA R. Segmentation of Polarimetric Synthetic Aperture Radar Data[J]. IEEE Trans on Image Processing,1992,1(3):281-300.
[25] MASJEDI A, ZOEJ V, JAVAD M, et al. Classification of Polarimetric SAR Images Based on Modeling Contextual Information and Using Texture Features[J]. IEEE Trans on Geoscience and Remote Sensing,2016,54(2):932-943.



