0 引言
高速目标因其隐形、高速巡航能力、超机动能力等特点,对雷达探测能力以及雷达自身战场生存能力提出更高要求。现代高分辨双基地雷达采取宽带发射信号, 在提高生存能力、反隐身目标的同时,还可提供很高的距离分辨率[1]。由于目标的等效运动复杂与雷达信号带宽较大,信号回波将被引入脉内多普勒与尺度因子,加之观测时间段内严重的距离走动和多普勒徙动,使得雷达接收回波信号的频率发生较快的变化,从而导致积累能量分散以及检测性能恶化[2],传统动目标检测算法不再适用于宽带双基地雷达体制下高速目标的检测。如何消除脉内多普勒效应与尺度因子带来的影响,并矫正双基地雷达体制下目标等效运动产生的高阶项是实现高速目标检测所面临的关键问题。
针对目标回波包络距离走动与多普勒徙动矫正的雷达信号积累方法得到国内外学者的广泛研究,其主要分为相参积累与非相参积累[3]。这类算法的本质是利用长时间积累技术增加目标回波脉冲数量,达到提高回波信噪比的目的。Hough变换与Radon变换是非相参积累的代表算法。在20世纪90年代,有学者利用Hough变换进行雷达目标检测,实现了回波能量积累[4]。Radon变换是对图像域内二元函数的投影沿某个方向的线积分,且只能检测直线[5]。两者均是研究目标包络距离走动问题的算法,但无法解决多普勒扩散问题,且出现较大距离走动时,长时间积累效果会受到严重影响。
为实现更好的积累效果,文献[6]提出Radon-Fourier 变换(Radon-Fourier Transform, RFT)用以解决匀速运动的高速目标检测问题。该算法沿目标轨迹对回波数据进行相参积累,补偿了多普勒徙动引起的相位变化项,但该算法无法解决含有高阶徙动项的回波信号。广义Radon-Fourier变换(GRFT)则是 RFT 算法向高维的拓展,对具有任意阶运动的高速机动目标,可实现其回波能量在参数空间的聚焦[7]。然而,这些算法以单基地雷达为背景,且采用窄带发射信号,忽略了一个脉冲持续时间内目标的运动,不适用于宽带雷达体制。对于考虑宽带发射信号的相参积累算法,文献[8]提出了脉冲内多普勒补偿的Radon-Fourier变换(IPDC-RFT)。有效消除了脉冲内多普勒的影响。但是IPDC-RFT仍在单基地雷达系统下分析目标回波,忽略了比例因子带来的影响,具有一定的局限性。
针对以上这些问题,本文提出一种基于宽带高速目标回波的匹配滤波器结合改进的广义Radon傅里叶变换的多目标检测方法。该算法无近似地分析了宽带双基地雷达体制下的回波信号,及目标高速运动带来的不可忽略的尺度因子与脉内多普勒,通过构造相应的匹配滤波器积累脉内能量,然后采用改进的广义Radon傅里叶变换沿目标运动轨迹进行相参积累。所提在多目标情况下无交叉项的出现,在双基地雷达体制下具有更好的适配性,消除了脉内多普勒效应对回波能量积累的影响,仿真结果显示相参积累结果接近理论值。
1 高速目标回波信号模型
1.1 空间几何模型
本文以空-天双基地雷达模型为例,对双基地雷达与目标之间的三维相对关系进行分析,其几何模型如图1所示。
假设地球是一个半径为6 378.14 km的圆球体,采用地心旋转坐标系对双基地雷达系统与高速目标的相对关系进行分析。其中,T代表卫星发射平台,R代表空中飞行器接收平台, T′和R′分别为发射平台、接收平台的地面投影,vT和vR分别为发射平台、接收平台的速度向量,P为高速目标,P′为其地面投影,vP为目标飞行速度向量,Ω为卫星轨道、赤道平面的交线与本初子午线的夹角,θ为卫星轨道与赤道平面的交角,ω为卫星的角速度。

图1 空-天双基地雷达高速目标检测几何模型示意图
1.2 高速目标回波信号模型
假设双基地雷达系统采用线性调频信号为发射信号,发射机对外辐射M个子脉冲,其表达式为
s(t,tm)=![]()
exp[j2πf0(t-tm)]
(1)
式中,
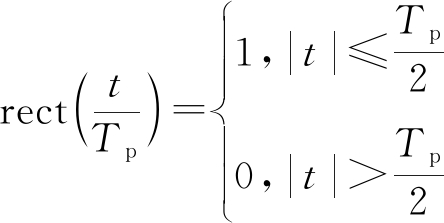
(2)
是矩形窗函数,tm=mTr, (m=0,1,…,M-1) 表示慢时间, t为快时间,f0为信号载频,Tp为脉宽, γ为调频斜率。
将目标在脉冲持续时间内的位移也考虑在内,由发射机到目标的时延可表示为
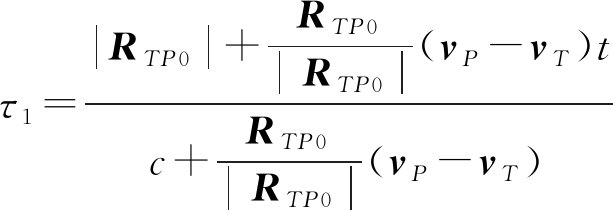
(3)
类似地,从目标到接收机的时延为

(4)
式中,RTP0表示从发射机到目标的距离向量, RRP0表示从目标到接收机的距离向量。
接收信号的总时延为
(5)
式中, vTP=(vP-vT)RTP0/|RTP0| 与 vRP=(vP-vR)RRP0/|RRP0|分别表示目标相对于发射机和接收机的速度。由于双基地雷达特殊的几何结构,目标回波的距离历程相较于单基地雷达更为复杂。具体表达式如下:
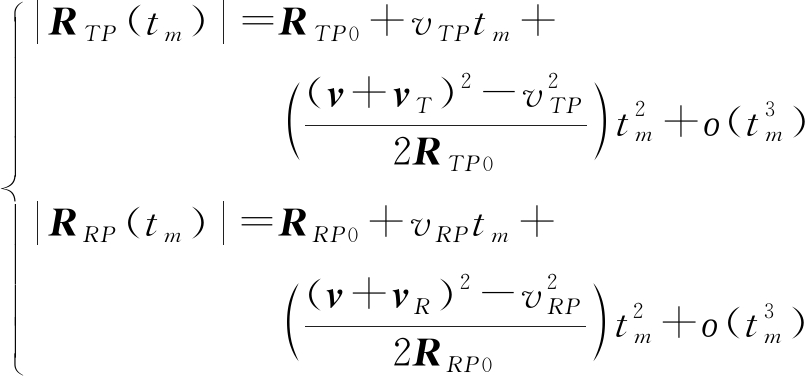
(6)
即对于匀速运动目标,会产生等效加速度项。为表达简明,我们根据等效运动参数定义如下:

(7)
将式(5)和式(6)带入回波信号,并进行下变频,基带回波信号可表示为
sb(t,tm)=ks(t-τ,tm)=
exp[-j2πf0Ψ(tm)]exp(-j2πf0ζ t)
(8)
式中,k 为目标反射系数,![]() 表示由目标距离历程产生的慢时时间时移。式(8)表明,高速目标双基地雷达的尺度因子重新定义为
表示由目标距离历程产生的慢时时间时移。式(8)表明,高速目标双基地雷达的尺度因子重新定义为
(9)
在单个脉冲内,尺度因子与快时间t耦合,导致主瓣展宽,脉内多普勒则表现为与快时间t相关的相位项exp(-j2f0ζt),使得频谱发生偏移。在多个脉冲之间,目标的高速运动引起信号包络随时间缓慢变化,无法采用传统动目标检测方法积累能量。下一节将详细讨论由尺度因子和脉冲内多普勒引起的失配效应。
2 回波脉内多普勒分析
宽带雷达系统中,目标高速运动引入的尺度因子会导致主瓣展宽,脉内多普勒会使得频谱整体发生偏移。如仍采用传统匹配滤波器,会造成匹配滤波器频谱与回波信号频谱无法对齐,进而对脉压效果产生影响,这种影响成为脉压失配现象。下面对脉压失配现象进行定量数学分析。
传统匹配滤波器的频域响应为
(10)
对式(7)沿快时间维作傅里叶变换至距离频率-慢时间信号,如下:
S(f,tm)=![]()
exp[-j2πf0Ψ(tm)]·
(11)
采用传统滤波器进行频域脉压,得到
Xpc(f,tm)=S(f,tm)·H(f)=
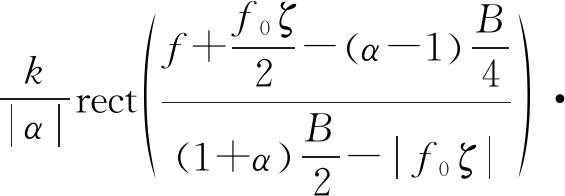

(12)
脉压结果包含4个指数项。第一个指数项是未彻底消除的距离频率二次项。第二、第三个指数项分别表示多普勒频率徙动项与距离徙动项。然而,第二项中的多普勒频率徙动项是原来的(1+ζ/α2)倍,第三个指数项中,距离频率与相位中心存在f0ζ/γ 的偏移,这表明距离中心已发生偏移。第四项是冗余的常数相位项,使得脉压信号峰值降低。距离频率维和慢时间维都存在一定程度的失真。
脉压结果按如下两种情况区分并给出结论:
情况一:当|BTpζ|≤10-3 时,采用传统匹配滤波器进行脉冲压缩,结果可以表示为
xpc(t,tm)≈![]() sinc[αB(t-Ψ(tm))]·
sinc[αB(t-Ψ(tm))]·
(13)
宽带雷达低速目标一般适用于此类情况。这表明,当脉内多普勒小至一定程度时,可认为结果是无峰值偏移的sinc函数。
情况二:当 |BTpζ|>10-3时,有|vT|≪|vp|≪c、 |vR|≪|vp|≪c,可以近似认为α≈1成立,脉压结果则可表示为
Xpc(f,tm)≈
(14)
沿距离频率维对上式进行逆傅里叶变换,可得到信号的时域表达式为
xpc(t,tm)≈


(15)
结果表明,采用传统匹配滤波器进行脉冲压缩,所得信号不再是标准的sinc函数。sinc函数中快时间t的系数减少了|f0ζ|,小于原带宽,导致主瓣展宽。 冗余的常数相位会降低信号幅度,信号峰值位置偏移了f0ζ/α2γ, 多普勒频率的中心位置也发生了同样的偏移。 随着目标速度的增加,与快时间t耦合的参数逐渐增大,脉压失配效应逐渐明显。
3 宽带双基地雷达多目标检测算法
3.1 宽带雷达高速目标匹配滤波器设计
为了避免脉压失配效应的产生,首先应该构造广义匹配滤波器。假定双基地雷达探测范围内有M个目标,回波信号表示为
sb(t,tm)=![]()
exp[-j2πf0Ψi(tm)]·
exp(-j2πf0ζit)
(16)
根据回波信号表达式及其频谱,定义考虑脉内多普勒的匹配滤波器:
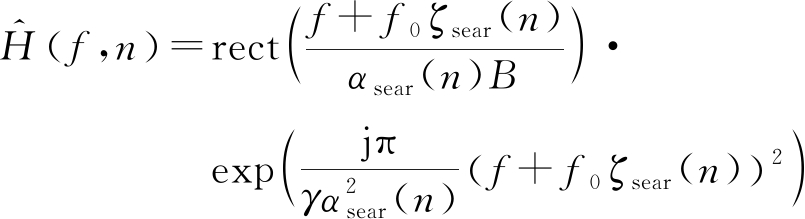
(17)
式中ζsear,αsear为搜索参数。根据第二节的分析,当补偿后的脉内多普勒参数满足|BTPζ|≤10-3时,则认为不产生脉压失配,因此,当时宽带宽积在10的4次方量级时,认为补偿后f0ζ小于300 m/s可满足要求。因此取搜索参数的范围如下:
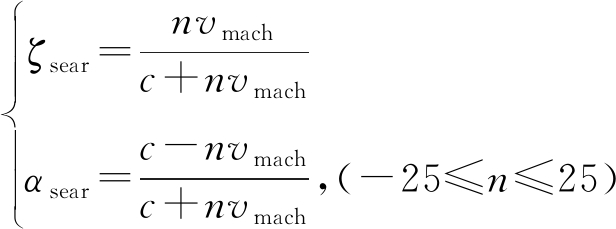
(18)
以上搜索范围对应目标等效速度搜索范围为[-25,25]马赫,即[-8 500,8 500]m/s。将基带信号变换到距离频域-慢时间域为
S(f,tm)=![]()
exp[-j2πf0Ψi(tm)]·
(19)
对于目标回波,必然存在ni使得 |ζsear(ni)-ζi|≤0.5vmach/(c+vmach)。此时,补偿后的|BTP(ζsear(ni)-ζi)|≤5×10-4,可认为无脉压失配产生。
采用脉内回波模型的匹配滤波器所得的脉压结果为
Xpc(f,tm,n)=![]()
exp[-j2πf0Ψi(tm)]·
(20)
作逆傅里叶变换变换至距离时域,得到
xpc(t,tm,n)=![]()
exp(-j2πf0ζit)·
(21)
脉压阶段至此完成。
3.2 基于GRFT的目标检测与参数估计方法
将脉内多普勒影响考虑在内,提出改进的广义Radon傅里叶变换(IGRFT),其定义为
G(ψ,ζ,ξ)=
![]() x(t,tm)HIGRFT(ψ,ζ,ξ,tm)dtm
x(t,tm)HIGRFT(ψ,ζ,ξ,tm)dtm
(22)
式中,
HIGRFT(ψ,ζ,ξ,tm)=
δ(αt-Ψ(tm))exp(j2πf0ζt)·
(23)
δ(·)为单位冲激函数。所提处的IGRFT是在考虑尺度因子与脉内多普勒的情况下,沿目标运动轨迹的积分峰值。由于仍然利用了Radon变换图像边缘检测的原理,该方法不会产生交叉项,适用于多目标聚焦。
IGRFT的具体实现的离散表达式为
G(i,p,q)=![]()
ζ(p)mTr+ξ(q)(mTr)2))·
exp(j2πf0ζ(p)m)
(24)
式中,α(p)=1-2ζ(p)。各阶参数按照一定的步长进行遍历,步长越小,则可能产生的量化误差越小,得到的参数估计结果越精确,但搜索数会越大。
将脉压后的信号采用IGRFT处理,结果为
G(ψ,ζ,ξ,α)=
![]()
exp(-j2πf0(ζ-ζi)t)·
(25)
根据算法思想,处理结果共有M个峰值点,通过峰值检测可得到运动参数估计值如下:
(26)
式中,![]() 分别为第i个回波调频率参数估计值,其与目标等效运动参数的对应关系为
分别为第i个回波调频率参数估计值,其与目标等效运动参数的对应关系为

(27)
当多个目标的反射系数差别较大时,弱目标的回波会被强目标掩盖,从而导致算法对弱目标的检测性能下降。 在这种情况下,可以采用CLEAN技术[10]来消除强目标的影响。CLEAN 技术的关键思想是将所有目标从强到弱依次检测,然后剔除最强的目标回波,再采用所提算法检测下一个目标,最终实现所有目标的检测与参数估计。
3.3 算法流程与计算量
本文所提出的宽带双基地雷达高速多目标检测算法具体实施步骤如下:
1) 对基带回波信号沿距离维进行傅里叶变换,得到距离频域-方位时域数据;
2) 采用本文设计的匹配滤波器在距离频域实现距离维脉冲压缩,即乘以匹配滤波的频域响应函数![]()
3) 确定参数ψ,ζ,ξ的搜索范围与步长,利用改进的GRFT积累目标回波能量;
4) 对相参积累结果进行恒虚警检测以获得 IGRFT 结果中所有所需的积累峰值并估计它们的运动参数;
5) 采用CLEAN运算清除散射系数较大的目标,再进行2)至5),直到所有目标均被检测到为止。
假设积累脉冲数为M,距离单元数为N,脉内多普勒补偿单元数为P,搜索等效速度单元数为K,等效加速度单元数为L,所提算法在匹配滤波阶段需要进行NMPlog2(N)/2次复数乘法和2NMlog2(N)次复数加法,在IGRFT阶段需要KLM2N2次复数乘法。传统匹配滤波器需要NMlog2(N)/2次复数乘法和NMlog2(N)次复数加法,标准二阶GRFT需要进行KLM2N2次复数乘法。相比于未考虑脉内多普勒的高速目标GRFT算法,计算量无明显增加。
4 仿真和分析
4.1 算法仿真
空-天双基地宽带雷达系统发射信号参数设置为:带宽100 MHz,采样频率200 MHz,载频1.3 GHz,脉冲重复频率500 Hz,脉冲宽度100 μs。模型参数设置如下:天基地轨卫星发射平台轨道高为500 km,天基发射平台初始轨道幅角为120°,天基发射平台轨道倾角为43°,空中飞机接收平台飞行高度为15 km,空基接收平台初始纬度为28°,空基接收平台初始经度为120°,空基接收平台飞行速度为90 m/s。目标参数设置如下:目标一,飞行高度35 km,初始经度108.025°,初始纬度30.022°,沿西北方向飞行,速度为1 800 m/s;目标二, 飞行高度35 km,初始经度108.025°,初始纬度30.022°,沿正西方向飞行,速度为1 200 m/s;目标三,飞行高度20 km,初始经度120°,初始纬度38.32°,沿正东方向飞行,速度为1 800 m/s;3个目标的反射系数分别为1,0.4,0.9。
图2为采用传统匹配滤波器与本文设计滤波器得到的脉压结果。图2(a)为采用传统匹配滤波器处理目标回波得到的脉压结果,可看到有明显的主瓣展宽、峰值降低与多余副瓣问题,另外,距离中心存在较大的偏移。这都阻碍了目标检测与参数估计。采用本文设计的匹配滤波器脉压结果峰值有明显提升,且不存在峰值偏移。
所提IGRFT算法仿真图如图3所示,由于目标一与目标二等效距离相等、速度相近且目标二为弱目标,进行一次CLEAN运算,即可全部检测出3个目标。等效距离参数与等效速度参数与仿真值吻合,证明了算法的有效性。图4为采用GRFT为对比实验所得的仿真结果。由于存在脉内多普勒,相参积累结果存在散焦,无法有效估计目标运动参数。与GRFT相比,所提算法增益提高了1 822个单位,参数估计误差降低了12.4%。仿真结果证明了算法的有效性与优越性。

(a) 传统匹配滤波器脉压结果图

(b) 本文设计滤波器脉压结果图
图2 两种脉压结果图

(a) 第一次IGRFT结果图
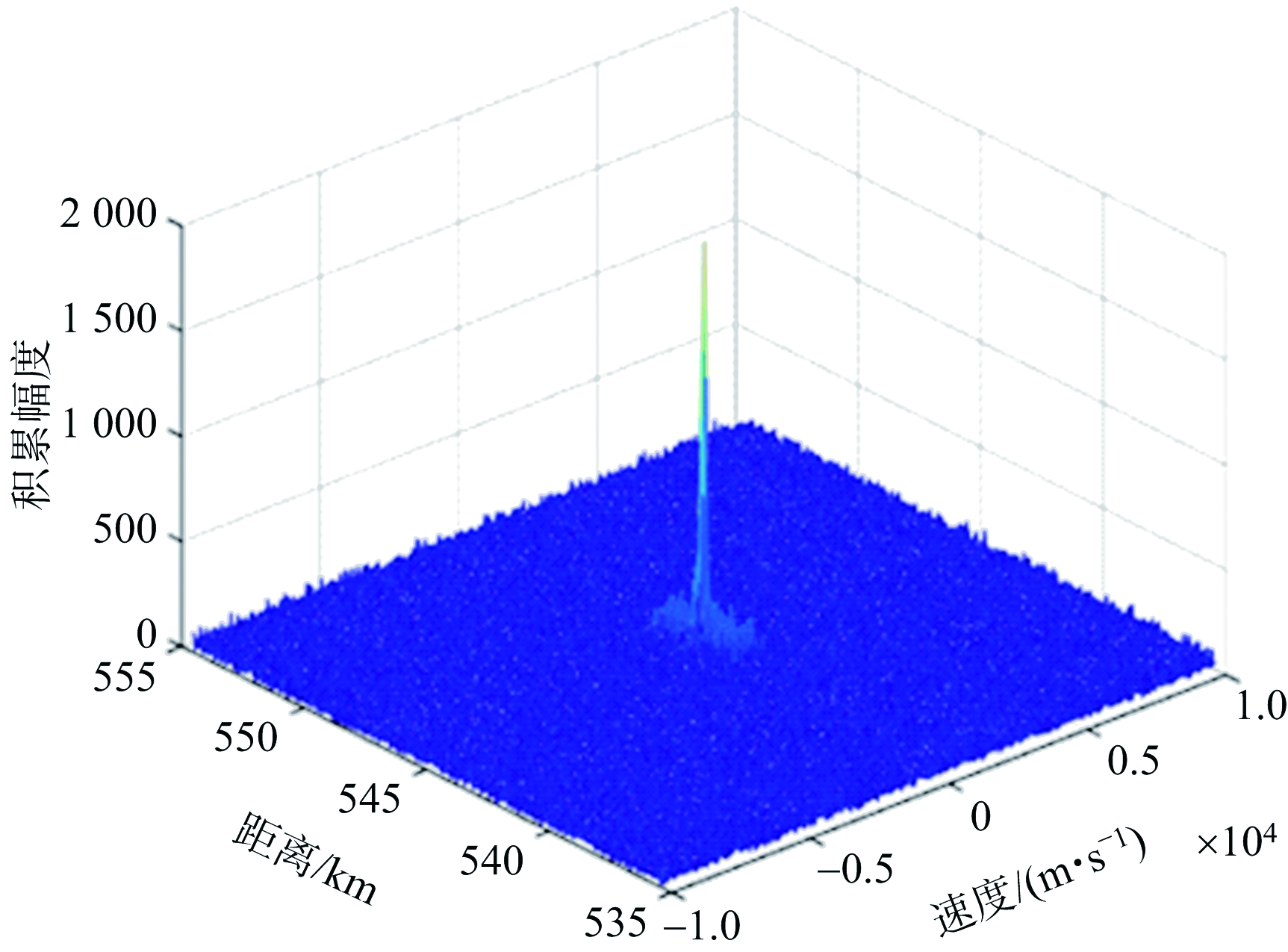
(b) CLEAN运算+第二次IGRFT结果图
图3 所提算法仿真结果图

图4 GRFT仿真结果图
4.2 检测概率分析
图5为虚警概率Pfa=10-6时以理论值、GRFT 和 IPDC-RFT 与所提方法做对比的检测概率曲线。与GRFT相比,其他两种脉冲内多普勒补偿算法的检测性能都有一定的改进。由于该方法考虑了双基地雷达系统的等效运动参数,与IPDC-RFT相比,该方法算法的检测曲线更接近理论曲线。量化误差是该算法无法接近理论值的原因。
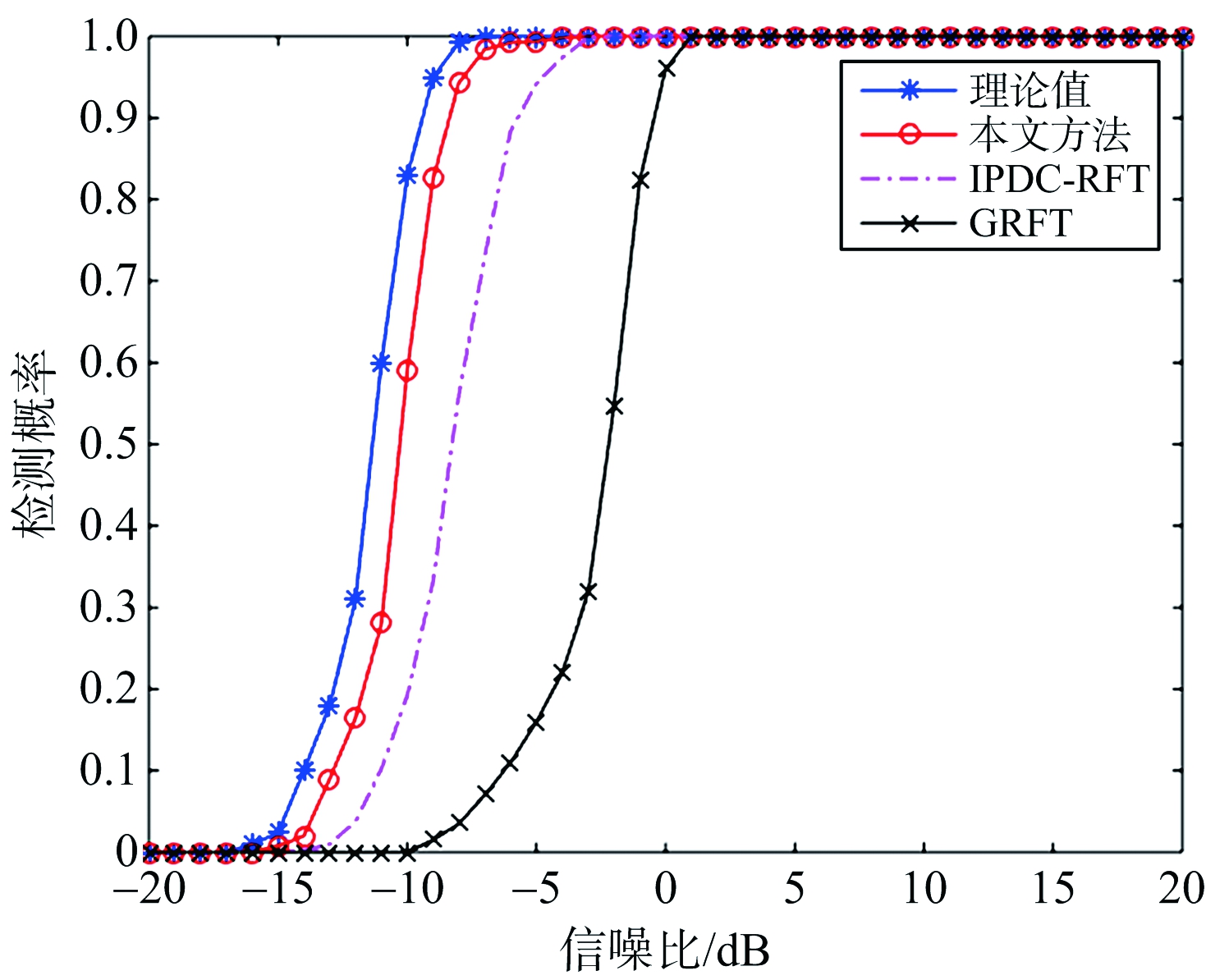
图5 检测性能曲线对比图
5 结束语
本文对于宽带双基地雷达体制下的高速多目标检测进行了研究。在建立的空-天双基地雷达空间几何模型的基础上,推导出高速目标回波信号。通过分析尺度因子与脉内多普勒现象对传统匹配滤波带来的影响,设计了一种无失配现象产生的广义匹配滤波器,并利用所提出的IGRFT算法进行多目标检测与参数估计。仿真实验表明所提方法的有效性。
[1] ELO M. High-Resolution Wideband Radar Measurement Challenges[J]. Microwave Journal, 2018, 61(6):22-30.
[2] HUANG Xiang, ZHANG Linrang, ZHANG Juan, et al. Efficient Angular Chirp-Fourier Transform and Its Application to High-Speed Target Detection[J]. Signal Processing,2019,164(11):234-248.
[3] ZHANG X L, ZHUO H, PANG C S. Analysis Method of Influencing Factors of High Speed Target Detection Performance[J]. Journal of North University of China,2018,39(2):214-219.
[4] KABAKCHIEV C, GARVANOV I, ANGELOVA D, et al. Analysis of Track-Before Detect Algorithms with Hough Transform[C]∥International Radar Symposium, Hamburg:IEEE, 2009:1-5.
[5] CHEN V C. Radar Detection of Multiple Moving Targets in Clutter Using Time-Frequency-Radon Transform[C]∥Signal and Data Processing of Small Targets, Orlando,FL,US:IEEE,2002:48-59.
[6] CULHA O, TANIK Y. Low Complexity Keystone Transform and Radon Fourier Transform Utilizing Chirp-Z Transform[J]. IEEE Access, 2020, 8(4):105535-105541.
[7] DING Zegang, ZHANG Tianyi, LI Yong, et al. A Ship ISAR Imaging Algorithm Based on Generalized Radon-Fourier Transform with Low SNR[J]. IEEE Trans on Geoscience and Remote Sensing,2019,57(9):6385-6396.
[8] ZHENG J, ZHU W, SU T. Targets Detection and Moving Parameters Estimation Based on Intra-pulse Doppler Compensation[C]∥Proceedings of the 2012 Second International Conference on Electric Information and Control Engineering, Lushan:IEEE,2012:1351-1354.
[9] ZHANG Juan, DING Tong, ZHANG Linrang. Longtime Coherent Integration Algorithm for High-Speed Maneuvering Target Detection Using Space-Based Bistatic Radar[J]. IEEE Trans on Geoscience and Remote Sensing,2020,PP(99):1-16.
[10] MISIUREWICZ J, KULPA K S, CZEKALA Z, et al. Radar Detection of Helicopters with Application of CLEAN Method[J]. IEEE Trans on Aerospace & Electronics Systems,2012,48(4):3525-3537.



