0 引言
作为一种主动式遥感手段,合成孔径雷达(Synthetic Aperture Radar, SAR)通过发射电磁波获取地物的散射信息。相较于传统光学遥感,SAR在能见度较差的区域有其独特的优势。极化SAR则通过发送与接收不同方向的电磁波,获取更为丰富的极化特征,这些极化特征对于地物分类、识别起很大作用。在极化SAR的各个模式中,全极化SAR包含了目标的全部散射信息,被广泛地应用在农业、军事等领域,但由于系统受限,全极化SAR成像幅宽小、分辨率低。为了克服全极化的缺点,简缩极化的概念得到了提出,通过发送或接收线极化波以及圆极化波,更有效地保留全极化信息,并且可以获得更大成像幅宽,有很大的应用潜力[1]。
简缩极化SAR有3种工作模式:π/4模式[2]、CTLR (Circular Transmit and Linear Receive, CTLR) 模式[3]、DCP (Dual Circular Polarization, DCP) 模式[4]。π/4模式发射±45°线极化波,接收水平(H)和垂直(V)线极化波。CTLR模式发射左旋(L)或右旋(R)圆极化波,接收H和V线极化波。DCP模式发射和接收左旋或右旋圆极化波。虽然不同的简缩极化模式获取数据的格式不同,但本质上都是全极化数据的线性组合。
在极化SAR分类方面,监督分类和无监督分类是两种主要思路[5]。监督分类需要结合真实地物信息,通过带标记样本进行分类。而无监督分类主要通过物理散射机制进行初步划分,再通过基于目标统计特性的分类器进行迭代分类,不依赖真实地物信息,从而具有一定的实际应用价值[6-8]。
对于简缩极化数据,我们常用Stokes矢量S=(S0,S1,S2,S3)T形式进行表述。通过Stokes矢量可进一步提取简缩极化特征参数,如极化度m、相对相位角δ,圆度χ,极化熵H,以及散射角α等。其中,极化度m常被用作区分完全去极化分量和完全极化分量,完全去极化分量通常被看作体散射分量。Charbonneau等人[9]提出了m- δ分解,利用相对相位角δ区分表面散射和二次散射分量。与m-δ法相似,Cloude等人[10]利用αs区分表面散射和二次散射分量,提出了适用于CTLR模式的m-αs分解。郭胜龙等人[11]将该方法引入到π/4模式的计算中,因为两种模式Stokes矢量有所区别,引入约束的方程求解方法得到了提出。以上几种分解方法都基于极化度m对体散射分量进行估计,会存在体散射分量过估计的问题。为了改善分解及分类的结果,我们采用尹嫱等人改进的简缩极化分解方法将简缩极化数据分为表面散射、二次散射和体散射三个分量,将其作为Wishart分类器的输入得到初步分类结果。然而,这种无监督分类方法基于像素点进行分类,并未考虑到空间信息,导致分类效果并不理想。因此,我们对分解后获得的伪彩色图像进行SLIC (Simple Linear Iterative Cluster) 超像素分割[10],利用超像素分割获取的空间信息对分类结果进行类别合并,以达到更好的分类效果。
1 算法原理
本文算法流程如图1所示。

图1 算法流程图
首先,通过仿真从全极化SAR数据获取两种模式(π/4模式、CTLR模式)下的简缩极化数据;其次,采用尹嫱等人改进的基于城区描述子的简缩极化分解方法进行三分量分解;随后,将分解结果作为Wishart分类器输入进行迭代分类;最后,利用SLIC超像素分割结果对Wishart分类结果进行超像素区域类别合并。
1.1 简缩极化分解
1.1.1 简缩极化数据形式
极化SAR数据信息以4种线性正交极化组合HH、HV、VV和VV的形式存储在4个通道中,每个像素的复数散射矩阵可以表示为
(1)
式中,h表示水平极化通道,v表示垂直极化通道。在单站后向散射体制下,满足互易性定理,即Shv=Svh。
简缩极化SAR目标散射矢量可表示为全极化散射矩阵S中元素的线性组合。由于散射矢量形式相比DCP模式更为简单,本文主要涉及到CTLR[3]、π/4[2]这两种模式:
![]()
(3)
其中+号表示发射波为左旋圆极化和+45°线极化,-号表示发射波为右旋圆极化和-45°线极化。
1.1.2 简缩极化分解方法
尹嫱等人通过提出简缩极化城区描述子DOOB,对Cloude提出的m-αs分解及郭胜龙的分解方法进行改进,从而降低体散射分量。
DOOB=DDP·DRD·(1-DPA)=
(γ·S0)·IRV·(1-AP)
(4)
式中,DDP为去极化分量,γ为交叉极化相关参数,S0为总功率,DRD表示随机性分量,此处用简缩极化植被参数IRV来描述,AP为简缩极化各向异性度。
根据RVoG模型,两种模式下Stokes矢量分解形式如下所示:

(5)
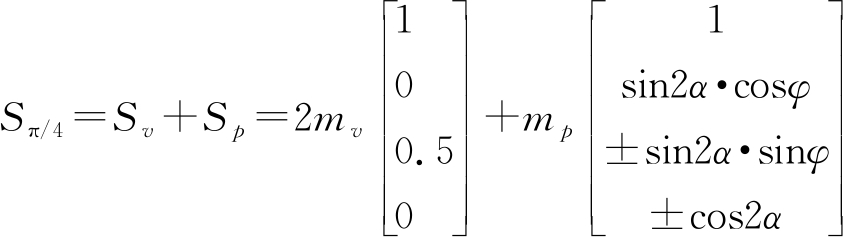
(6)
式中,Sv表示体散射机制部分,Sp 表示秩为1散射机制部分。在求解方程过程中,以下约束被引入:
a2+b2+c2=1-DOOB
(7)
式中,a为sin2α·cosφ,b为±sin2α·sinφ,c为±cos2α。方程求解过程与郭胜龙[11]等人的方法类似。通过引入城区描述子DOOB,城区部分的体散射分量在模型求解的过程中得到了降低,二次散射分量得到了提升。
1.2 Wishart分类
在极化SAR分类中,Wishart分布常被用来描述极化相干矩阵的统计分布[8]。简缩极化相干矩阵J的概率密度为
(8)
式中,n为等效视数,V为类中心极化相关矩阵,q为矢量维度,K(n,q)为归一化系数常量。由于一般情况下无法确定类的先验概率,通常假设它们相等,定义相干矩阵和第m类中心之间Vm的Wishart距离为
d(J,Vm)=ln|Vm|+tr(Vm-1J)
(9)
如图1所示,将分解结果根据主要散射机理划分为3个类别,每一大类根据散射功率再划分为30个聚类,并计算平均协方差矩阵作为类中心,利用式(9)计算像素和类中心的距离,若像素的相干矩阵J到某类的Wishart距离最小,则该像素可以被分到此类中。更新聚类中心,并进行迭代。
1.3 超像素分类
SLIC是一种对图像进行局部聚类的超像素分割算法[12]。本文采用的分类方法将超像素分割获取的空间信息与分类结果进行融合,具体步骤如下所示:
1) 初始化聚类中心。对简缩极化分解后获取的伪彩色图像均匀选取“种子点”,并设置超像素尺寸为S。
2) 对每个像素点,进行颜色距离dc和空间距离ds的度量,并计算和聚类中心的距离。
dc=![]()
(10)
(11)
(12)
式中,m和S为权重参数。
3) 根据搜索范围2S×2S,在局部区域重新进行聚类,并重新计算聚类中心。
4) 迭代至残差E达到阈值E=0.01。
通过超像素分割获取到不同的超像素区域,对于每个超像素区域,采用多数投票原则对超像素区域进行类别融合[13]。若超像素内某种类别出现的频率超过阈值H,则该超像素的标签tag(xi)可表示为
(13)
式中,xi为图像中的第i个超像素,yj为超像素内的第j个像素,m为标签,M为标签总数。本文中阈值H设置为0.6。
2 实验结果及分析
本文通过Radarsat-2全极化数据仿真合成π/4模式以及CTLR模式的简缩极化数据,验证了本文提出的分类方法的有效性。本文采用的数据是2008年4月9日获取的美国旧金山区域全极化C波段数据,全极化Pauli伪彩色图像以及所选区域光学图像如图2所示,可以看出该区域包含海洋(蓝色方框区域)、小方位角城区(红色方框区域)、大方位角城区(黄色方框区域)以及植被区域(绿色方框区域)。7×7精改Lee滤波器被用来改善相干斑噪声的问题。实验过程中,设置Wishart无监督分类迭代四次,超像素分割大小为 30×30。

图2 Radarsat-2全极化数据Pauli图
2.1 基于城区描述子的简缩极化分解
简缩极化分解结果如图3、图4所示,m-αs分解和Guo分解作为对比方法展示分解结果的优势。对于图3(a)及图4(a),海洋区域表面散射占主导地位,在伪彩色图像呈现蓝色;自然区域体散射占主导,呈现绿色;建筑区域由于体散射过估计问题,主要呈现黄绿色。经过改进后的分解方法如图3(b)及图4(b),图中建筑区域的体散射成分得到了明显的抑制,二次散射分量得到了提升,主要呈现以二次散射为主的红色。

图3 CTLR模式下简缩极化SAR分解伪彩色图

图4 π/4模式下简缩极化SAR分解伪彩色图
2.2 SLIC超像素分割
以Guo分解结果进行SLIC超像素分割为例,图5为不同超像素大小下SLIC超像素分割效果局部图。图中黑色线表示每个超像素的分界线。如图5(a)所示,当超像素尺寸为20×20大小时,对于图像中的细节保留完好,但超像素过小会导致无法很好地提取空间信息。如图5(c)所示,当超像素尺寸为40×40大小时,超像素不能很好地描述桥梁边缘等细节信息。而当超像素尺寸为30×30大小时,如图5(b)所示,可以在较好的提取空间信息的同时,保留更多细节。因此,本文选取的超像素分割大小为30×30。

图5 不同超像素大小下SLIC超像素分割效果图
2.3 分类结果


图6 CTLR模式下简缩极化分类结果图
(蓝色:表面散射;红色:二次散射;绿色:体散射)


图7 π/4模式下简缩极化分类结果图
(蓝色:表面散射;红色:二次散射;绿色:体散射)
美国旧金山区域的分类结果如图6、图7所示,像素被分为表面散射(蓝色)、二次散射(红色)、体散射(绿色),根据散射功率强弱,每个大类分为三小类,并以颜色深浅表示。对于CTLR模式,分类结果如图6所示:(a) m-αs分解+Wishart分类;(b) m-αs分解+Wishart分类+SLIC;(c)基于城区描述子分解+Wishart分类;(d)基于城区描述子分解+Wishart分类+SLIC。对于π/4模式,分类结果如图7所示:(a) Guo分解+Wishart分类;(b) Guo分解+Wishart分类+SLIC;(c)基于城区描述子分解+Wishart分类;(d)基于城区描述子分解+Wishart分类+SLIC。
经过实验发现,Wishart分类器四次迭代后基本上已经可以获得较好的结果,因此本文实验结果均为四次迭代后的分类结果。
图6、图7分别为两种模式下分类结果及城区局部放大图。如图6(a)、(c)所示,通过基于城区描述子的分解方法获取的特征,在经过Wishart分类器四次迭代后,可以获得比m-αs更好的效果。由于城区二次散射分量得到提升,更多城区像素点被正确分为红色的二次散射。如图6(a)、(b)所示,经过超像素区域类别合并后,很多城区像素被误分为绿色的体散射类别,而图6(d)却可以获得视觉上优于图6(c)的结果。这是由于图6(a)中城区的许多像素被误分为体散射类别,导致超像素中体散射类别占主导,产生误分。图7中π/4模式结果图与图6类似,基于城区描述子分解后进行Wishart分类,并采用超像素分割合并类别,可以获得较好的分解结果。
为了定量分析分类结果,我们选取了如图2所示4个方框中的4种典型区域,包括海洋、小方位角城区、大方位角城区以及植被区域,定量分析不同区域内各类别占比。分类结果如表1所示。在海洋以及植被等自然区域,m-αs、Guo分类精度略高于基于城区描述子的分类结果。这是由于改进后的分解结果一定程度提高了自然区域,尤其是植被区域的二次散射分量,导致两种模式下的分类精度略低于对比方法。对于小方位角城区,本文的方法相比较原方法分类精度提升约有20%。值得注意的是,对于m-αs分类方法以及Guo分类方法,SLIC超像素区域类别合并可能会导致一定程度上的精度下降,这是由于这两种方法的分解结果在城区附近不理想而造成的。而对于本文的方法,超像素类别合并可以提升5%左右的精度。对于大方位角城区,本文的方法相比较原方法分类精度提升约有10%。由于大方位角城区散射机制与体散射机制易混淆,该区域的分类呈现为多种类别混合的结果,所以SLIC超像素区域类别对该区域的影响较小。
表1 两种简缩极化模式下不同区域的分类结果(S:表面散射 D:二次散射 V:体散射)
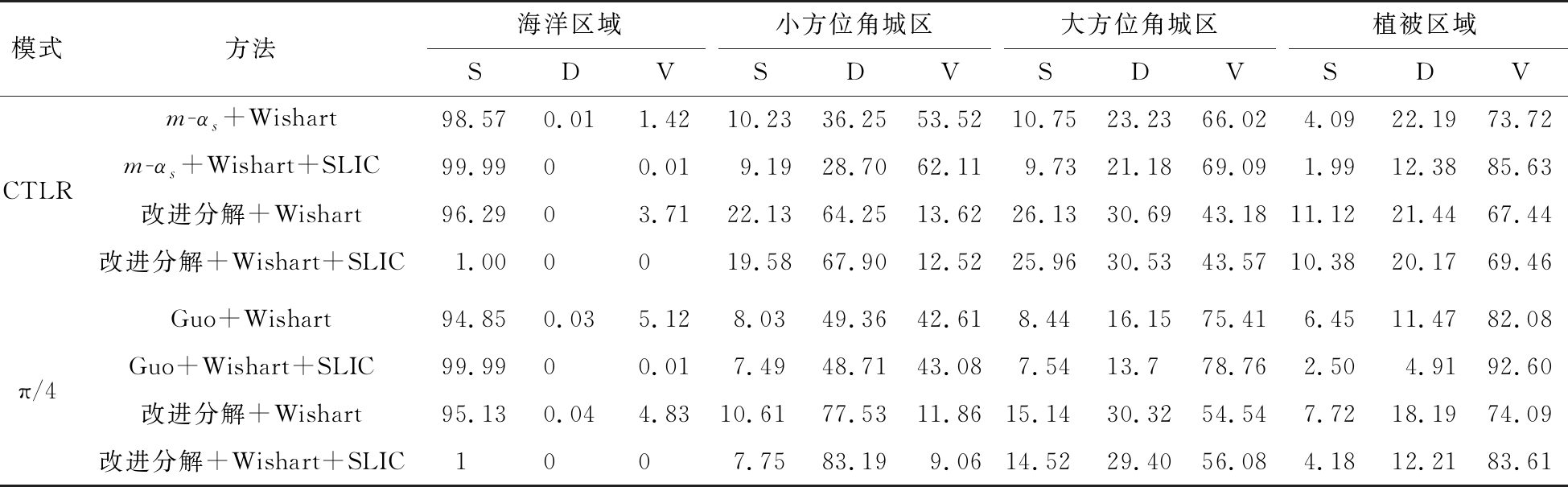
模式方法海洋区域小方位角城区大方位角城区植被区域SDVSDVSDVSDVCTLRm-αs+Wishart98.570.011.4210.2336.2553.5210.7523.2366.024.0922.1973.72m-αs+Wishart+SLIC99.9900.019.1928.7062.119.7321.1869.091.9912.3885.63改进分解+Wishart96.2903.7122.1364.2513.6226.1330.6943.1811.1221.4467.44改进分解+Wishart+SLIC1.000019.5867.9012.5225.9630.5343.5710.3820.1769.46π/4Guo+Wishart94.850.035.128.0349.3642.618.4416.1575.416.4511.4782.08Guo+Wishart+SLIC99.9900.017.4948.7143.087.5413.778.762.504.9192.60改进分解+Wishart95.130.044.8310.6177.5311.8615.1430.3254.547.7218.1974.09改进分解+Wishart+SLIC1007.7583.199.0614.5229.4056.084.1812.2183.61
3 结束语
本文提出了一种基于简缩极化SAR城区特征和超像素分割的Wishart无监督分类方法。首先通过基于城区描述子的分解方法获取表面散射、二次散射以及体散射分量,将其输入到Wishart分类器进行迭代分类。同时将分解结果进行SLIC超像素分割,在超像素区域内以多数投票原则进行类别融合,以此提高分类精度。实验表明,该算法对简缩极化SAR图像分类能够得到更好的分类效果。在小方位角城区,本文的方法相比较原方法分类精度提升约有20%;在大方位角城区,本文的方法相比较原方法分类精度提升约有10%。
[1] 许璐, 张红, 王超, 等. 简缩极化SAR数据处理与应用研究进展[J]. 雷达学报,2020,9(1):55-72.
[2] SOUYRIS J, IMBO P, FJORTOFT R, et al. Compact Polarimetry Based on Symmetry Properties of Geophysical Media: the Pi/4 Mode[J]. IEEE Trans on Geoscience and Remote Sensing,2005,43(3):634-646.
[3] RANEY R K. Hybrid-Polarity SAR Architecture[J]. IEEE Trans on Geoscience and Remote Sensing,2007,45(11):3397-3404.
[4] STACY N, PREISS M. Compact Polarimetric Analysis of X-Band SAR Data[C]∥The 6th European Conference on Synthetic Aperture Radar, Dresden, Germany:IEEE,2006:1-4.
[5] 魏丹, 李渊, 黄丹. 极化SAR图像地物分类方法综述[J]. 计算机系统应用, 2020,29(11):29-39.
[6] 韦立登, 项徳良, 张博栋, 等. 毫米波全极化SAR影像无监督分类方法[C]∥第七届高分辨率对地观测学术年会论文集, 高分辨率对地观测学术联盟: 中国科学院高分重大专项管理办公室,2020:25.
[7] 朱腾, 胡兆勇, 吴悦明, 等. 极化SAR图像Pauli-Wishart非监督分类算法[J]. 传感器与微系统,2019,38(7):135-137.
[8] 张省. 基于精细去取向角的PolSAR图像非监督分类方法[J]. 遥感信息,2019,34(5):35-40.
[9] CHARBONNEAU F J, BRISCO B, RANEY R K, et al. Compact Polarimetry Overview and Applications Assessment[J]. Canadian Journal of Remote Sensing,2010,36(2):298-315.
[10] CLOUDE S R, GOODENOUGH D G, CHEN H. Compact Decomposition Theory[J]. IEEE Geoscience and Remote Sensing Letters,2012,9(1):28-32.
[11] GUO S, LI Y, HONG W, et al. Model-Based Target Decomposition with the π/4 Mode Compact Polarimetry Data[J]. Science China, 2016,59(6):1-10.
[12] ACHANTA R, SHAJI A, SMITH K, et al. SLIC Superpixels Compared to State-of-the-Art Superpixel Methods[J]. IEEE Trans on Pattern Analysis & Machine Intelligence, 2012,34(11):2274-2282.
[13] 韩景红,王海江.基于MV与Wishart距离的极化SAR图像分类[J]. 成都信息工程大学学报,2019,34(1):31-34.

