0 引言
卫星导航是飞机飞行过程中主要的导航定位手段。虽然这一技术拥有着较高的定位精度和成熟的应用经验,然而在许多场景下这一方法失效而无法为飞机提供有效的导航信息。作为替代,机载惯性导航系统(INS)可以计算出飞机的大致位置,但由工作原理所限,其往往与真实信息之间存在较大的误差,且误差量随飞机飞行时间增加而增加[1]。
机载合成孔径雷达(SAR)因不受光照、天气等因素影响可以全天时、全天候地工作。地面基准图像中包含大范围的准确的位置信息,将实时SAR图像与之匹配,解算SAR图像中目标与基准图中相同目标的对应关系,即可以将基准图中经纬度信息对应到实时SAR图像中。由于SAR图像数据大多为军用数据,数据源稀缺并且基本没有经纬度标注,光学数据经过谷歌地图和天绘等多年的发展,精准标注的光学图像数据已经非常普及,容易获取,所以选用光学数据和SAR数据进行匹配是一种务实的工程方案。在现有的图像匹配的研究中,有基于区域的图像匹配方法[2-3],计算基于图像灰度的图像相似性往往是这类方法的关键,然而SAR图像与光学图像存在着先天差异,经典的相似度计算方法并不足以弥补这些差异。此外,基于特征的匹配方法[4-6]可以通过图像特征的匹配规避图像间成像原理不同带来的灰度差异,然而对于不同的地物目标,不同的图像分割技术难以取得一致的效果,基于特征的匹配方法也难以找到一种普遍适用的方法。综上所述,本文采取了基于区域的图像匹配方法,对不同地物目标都具有良好的适应性。针对SAR图像与光学图像的差异,本文又创新地提出了一种基于灰度映射矩阵的相似度计算准则,与传统的相似度计算方法不同,这种计算准则可以很大程度上规避异源图像差异带来的匹配误差。
获得准确的地面位置后,以此作为控制点可以实现对平台位置的反向解算。当前基于地面控制点的载机平台的解算方法的研究在近年已经有了一定的进展,曾有学者针对弹载SAR系统进行研究,提出一种基于欧拉四面体的下降轨导弹位置解算方法,通过仿真实验验证了其可行性[7]。也有学者利用了成像中间时刻平台与SAR图像中心线上物点在水平面的投影共线的特性并分析相关误差成因,给出了合理的精度计算公式解算平台位置[8]。
上述的方法都依赖于一定几何模型的选取,在此之外,本文提出了一种基于广义伪距的平台定位方法。伪距是卫星定位中的基本概念,经过几十年的发展,伪距定位技术也已经在业界有了成熟的应用[9]。也因此,本文类比这一概念并推广了这一方法。在本文研究中,地面目标与平台之间的距离即斜距可以由机载SAR发出和接收回波的时间之差测定,这一距离与两者之间的真实距离大致相等,因此可以将其引申为已精确定位的地面目标与未知的平台位置之间的广义伪距。利用这一距离及已若干确定的地面目标位置列出合适的广义伪距观测方程并求解以实现对平台位置的反向解算。
1 地理坐标
地理坐标系是为唯一表示地球上任一点位置而设置的以经纬度为单位的坐标系,也是在地理学中常用的定位方式。为方便计算距离以求解相关位置,需要将以经纬度为单位的地理坐标系Olmh转换为以距离为单位、地心为原点的三维空间坐标系Oxyz。结合相关的地理学知识,这一过程涉及地球的以下参数(见表1),其中地球扁率f=(a-b)/a。
表1 地球相关参数

参数参数值地球扁率f1∶298.257地球长半轴a6378137.0m地球短半轴b6356752.0m
首先计算地球偏心率为
当经纬度(l,m,h)以弧度制表示时,有如下转换关系:
x=(N+h)cosmcosl
y=(N+h)cosmsinl
z=[N(1-e2)+h]sinm
其中,![]()
下文所标注的位置坐标均为此坐标系下坐标。
2 SAR图像地面目标定位
2.1 绝对定位
将机载SAR所成实时图像与大范围大尺度的光学基准图像进行匹配,可以将基准图像的地理位置信息对应到SAR图像中实现对SAR图像中地面目标的准确定位。在此之前,需要对光学图像作相应裁剪,并将待匹配图像缩放至同一分辨率下进行匹配,这一过程如图1所示。在此过程中,需要结合机载INS所输出的平台大致位置信息、雷达参数与地面高程信息对地面目标位置进行初步锁定,即绝对定位过程。对于这一技术现已有广泛描述,下面作简单阐述。

图1 定位方法流程示意
根据图2,为方便计算,可以将地球假想为理想的球体,半径取其平均半径Re=6 371 004.0 m。图2中,O点为地心,飞机位置为P,目标位置为Q,飞机在地面投影点为P′。结合转换坐标系后的飞机坐标P(x,y,z)有
平台到目标距离Rs为已知参数,则可知
近似地可以求得
Rd=Resinα
(1)
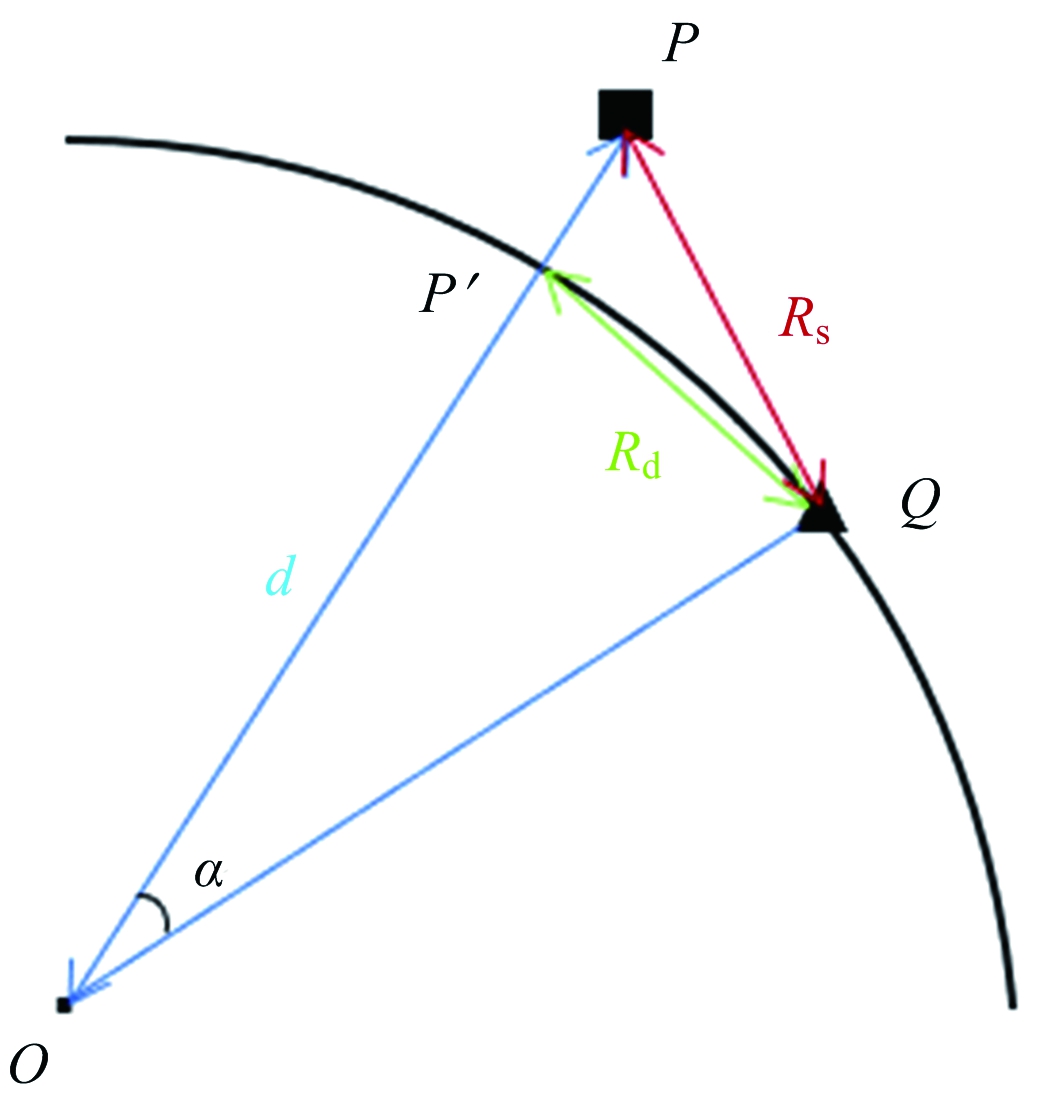
图2 飞机与目标位置示意
为求解图2中目标Q点坐标,除了需要求解目标与机下点距离Rd以外,还需要计算图2中机下点P′点的方向矢量,即求解在直角坐标系中飞机空间坐标向量与速度矢量的向量积:
S=P×V′
(2)
假设飞机在空间的运行速度矢量为V(vnorth,veast,vup),将其对应到空间直角坐标系下需要转置后点乘以下矩阵:

得到空间坐标系下的矢量V′(vx,vy,vz)。
由此,根据目标与机下点距离以及机下点的方向矢量可以求解目标点在空间坐标系下的方向矢量:
(3)
则目标点在空间坐标系下的坐标为
![]()
(4)
在上文的计算过程中,地球都是一个没有表面起伏的理想模型,这与实际是大不相符的。另一方面,虽然绝对定位的准确与否在本研究中并不绝对影响定位结果,但后续算法的稳定性、准确性与计算速度却在很大程度上依赖绝对定位的结果。因此,本文引入了高程模型以提高绝对定位精度。结合高程数据,可以计算出偏移向量Δ,则校正后的目标点坐标为
Q′=Q+Δ
(5)
将以上结果不断迭代,直到结果可以满足后续研究。
2.2 图像处理
SAR由于其自身独特的成像机制,图像存在着先天的复杂性和噪声干扰。其中1976年由Goodman提出了的完全发育的相干斑噪声概念对SAR图像存在的先天性的不足在统计规律上做出了描述[10]。为了消除这些噪声,业界已经有了许多成熟且得到工程验证的滤波方法。有学者对这些方法做出过总结[11],一般认为除了经典的空域滤波方法(均值滤波、中值滤波等)以外,基于区域统计特性的滤波方法等图像处理技术对于SAR图像的相干斑噪声都有工程级别的抑制效果。对于不同的SAR图像,由于其成像质量、图像存在的问题都存在差异,需要采取不同的图像处理手段进行操作以达到符合匹配的要求。
另一方面,可供获取的光学基准图都已经获得了良好的处理和校正,因此不存在成像质量不足的问题以及噪声干扰。然而,光学基准图是大范围大尺度的遥感图像,为避免冗余运算,提高效率,需要首先以绝对定位提供的位置信息为基准裁剪光学基准图。裁剪原则是
Rref≥max(Δr)
即基于绝对定位的物理距离绝对误差范围Δr,裁剪区域半径Rref需要大于这一误差范围的最大值,以保证真实目标点被包含在裁剪区域内。
2.3 图像匹配
金字塔分解是一种在图像匹配和分类的相关问题中较为常见的图像处理技术。其过程就是对一幅或者多幅图像进行多次的滤波和降采样,原图像为金字塔的第0层,依次压缩并依次向上堆叠。其目的是为了在不同压缩比率的图像上进行图像处理的操作并将同一操作向下传递。这一技术的优越性已经在不同的工程应用中得到印证[12]。因此,为提高计算效率和匹配精度,本文引入了图像金字塔分解技术,首先在第1层金字塔中求解图像变换参数模型即将压缩后的图像进行匹配并将匹配结果返回至金字塔第0层即未压缩的图像中,并基于这一结果再次匹配。
传统的相似度度量准则包括平均绝对差(MAD)、绝对误差(SAD)、误差平方(SSD)、平均误差平方和(MSD)和归一化积(NCC)等。这些方法在同源的图像匹配中无疑是行之有效的,然而却无法在SAR图像与光学图像匹配的过程中取得良好效果。因此,为适应SAR图像与光学图像的灰度差异,本文采用了一种灰度映射矩阵M:为适应SAR图像与光学图像的灰度差异,本文采用了一种灰度映射矩阵M。以矩阵中颜色亮度表示相似度度量大小。当图像灰度相近或相反时,可以判定图像灰度为相似。
由此,匹配步骤可以描述为:
1) 初始化灰度映射矩阵M,设置匹配窗口大小、滑动步长。
2) 对待匹配图像做出适当的预处理,并以两层图像金字塔分解图像。
3) 将图像进行翻转、缩放,保证SAR图像与光学地图在同一尺度之下进行匹配,以期获得准确的匹配结果。
4) 在第1层图像金字塔中,将待匹配图像I进行切分,以每一个分块图像ΔI作为匹配窗口。
5) 将匹配窗口以规定步长在基准图上滑动,计算匹配窗口与基准图中各区域相似度。
6) 在基准图中提取各窗口的最相似(相似度最大)区域,按各窗口与目标点在SAR图像中的距离对应关系求解目标位置。
7) 以返回结果的密集数作为最终结果。
8) 将此结果返回第0层图像金字塔中,重复过程4)~7),并由此得到最终的匹配结果。
sI1,I2=∑M(I1(i,j),I2(i,j))
来适应异源图像间的灰度差异。
3 SAR载机平台位置反向解算
图3描述了本文完整方法的大致流程。由前文所述,通过基于异源图像匹配的地面目标定位方法可以准确计算SAR图像中地面目标位置。基于此,本节对载机平台位置解算过程作详细介绍。
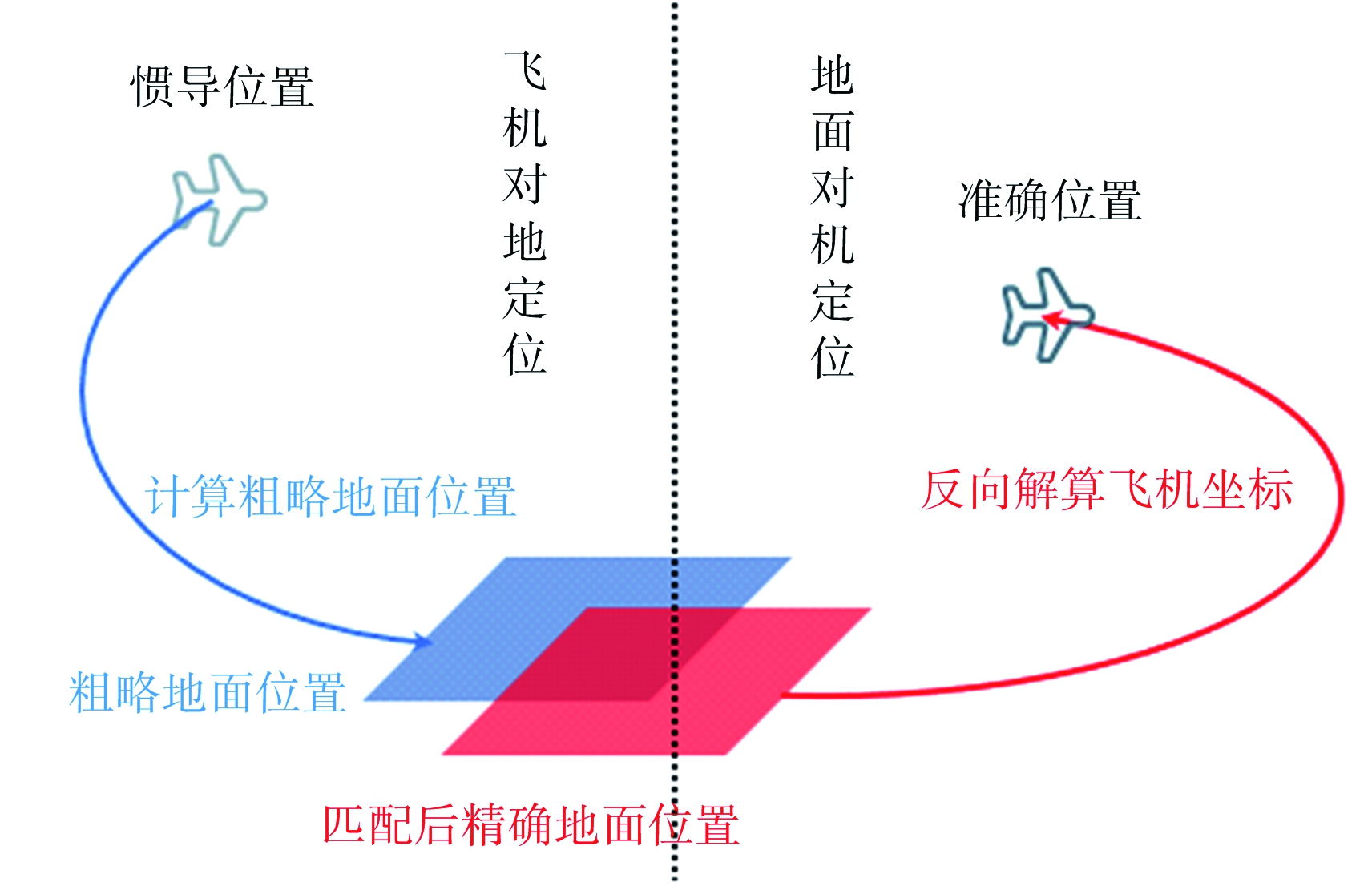
图3 SAR载机平台位置解算流程
3.1 伪距观测方程
卫星定位中常常采用伪随机噪声码测定目标与相应卫星之间的距离,这一距离并非其真实距离,故而称为伪距[13]。图4展示了这一过程的大致流程,某卫星产生一段伪随机噪声测距码并向地面发送,接收机产生与之相同的一段复制码。接收机接收到卫星信号后进行计算,当两组信号的相关系数达到最大,则可以锁定发送卫星,并根据卫星时钟与接收机时钟钟面时间之差确定接收机与该卫星之间伪距:
ρ=c·τ
式中,c为光速,τ为卫星与接收机的钟面时间之差。
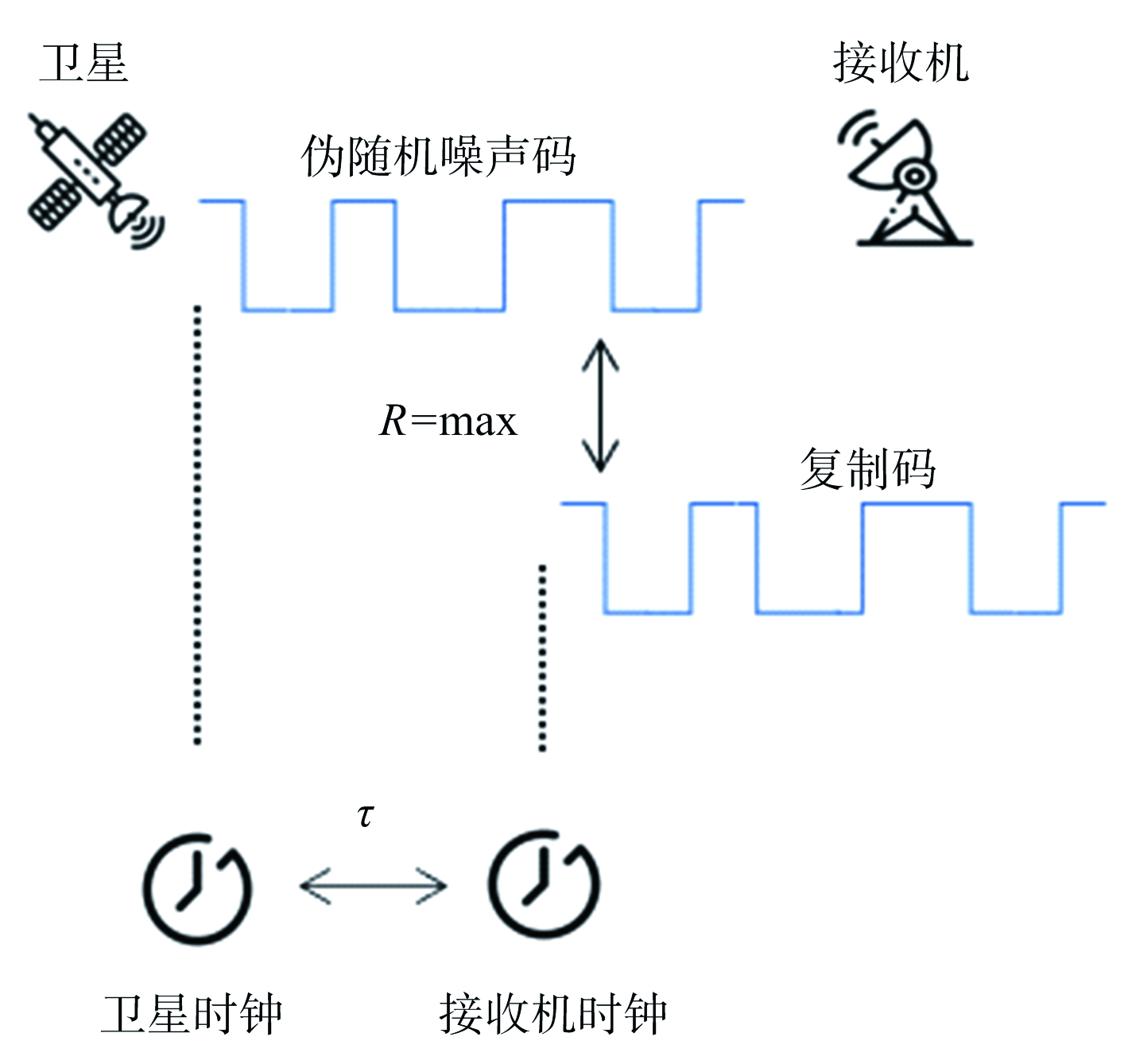
图4 伪距测定过程示意
当接收机在同一时刻锁定多颗卫星时,各卫星位置已知为(xi,yi,zi),接收机即待定位目标位置未知为(x,y,z),则其间实际距离为
![]()
(6)
忽略大气折射等其余相关因素对于伪距测定过程的影响,仅有卫星时钟和接收机时钟之间存在误差的误差造成伪距与真实距离之间的差距,考虑这一误差项则有
ρ=![]()
![]()
(7)
式(7)即为卫星定位中忽略大气折射等已知干扰项后的伪距观测方程。
3.2 广义伪距观测方程
前文所述,借鉴卫星定位中的相关理论,机载合成孔径雷达与地面目标点斜距Rs可以视作地面目标与载机之间的广义伪距。与卫星定位不同的是,这一距离可以由机载SAR从发出波束到接收回波的时间之差测定,无须考虑卫星定位中的钟差影响。由此可以将伪距与真实距离近似相等,即
![]()
(8)
式中,Rs为飞机与地面点之间斜距,(xi,yi,zi)为地面点坐标并且是已经过图像精准匹配后测定的准确值,(x,y,z)为待解算的平台位置坐标。
式(8)即为广义伪距观测方程。
3.3 INS误差传递模型
惯性导航系统是载机平台上的重要配置,为平台提供位置和飞行速度等重要信息。其原理是利用惯性原件测定载机平台航行的加速度,并由积分方法求解上述参数[14]。因此这一过程不可避免地让INS的输出参量与真实值之间出现偏差,因此需要一个数学模型来度量这一误差量,此即INS误差传递模型。
在较短的工作时间内,可以认定INS输出的速度偏移量为常值,这一模型称为6维INS误差传递模型。在这一模型下,INS输出的速度参量的各个方向分量相互独立且与平台实际速度各分量之差为常值,由此INS输出的速度参量与平台真实速度的关系表示为
vt=vIt+dv
(9)
式中,vt为t时刻平台的真实速度,vIt为这一时刻INS输出的速度参量,dv为INS的速度漂移量,在此模型下被认为是常值。
由此得到平台真实位置与INS输出的位置参量的关系为
![]()
(10)
再根据
P0= PI0+dP0
有
![]() (vI+dv)dt= PIt-PI0+dv·(t-t0)
(vI+dv)dt= PIt-PI0+dv·(t-t0)
(11)
由此,
Pt= PIt+dP0+dv·(t-t0)
(12)
式中,Pt和 PIt为t时刻平台的真实位置与INS输出位置,P0和PI0为t0时刻平台真实位置与INS输出位置,dP0为t0时刻INS输出位置参量的偏移量。
3.4 方程校正
由于载机平台的不断运动,其不同的成像时刻对应了自身的不同位置。为适应上述方程,则在解算前对平台及对应地面位置进行平移操作。
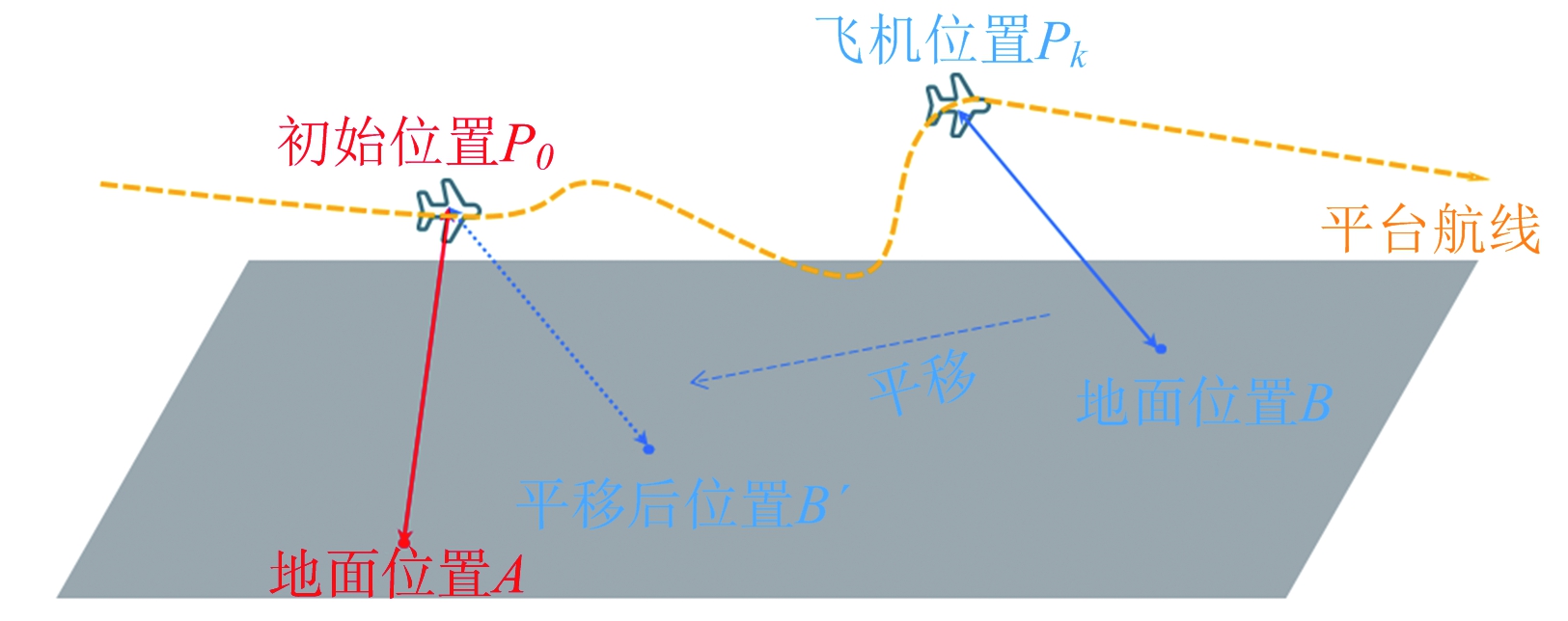
图5 平台位置平移
如图5所示,飞机在位置P0、Pk处通过机载SAR对地面成像,经过图像精准匹配后获得地面准确坐标A(x0,y0,z0),B(xk,yk,zk)。若INS输出的位置参量的漂移量恒定,则平台在P0与Pk处的真实位置之差与相应的INS输出位置之差等价。将其INS输出的位置参量分别表示为P0,Pk,则所需的平移向量,也即位置之差可以表示为
Tk=P0-Pk
平移后的地面位置为
A′=A
B′=B+Tk
由此可见,广义伪距观测方程仍可写作
![]()
(13)
但由3.3节所述,在6维INS误差传递模型下,INS输出的位置参量的漂移量并非恒定。若P0T,PkT为平台在P0、Pk处的真实坐标,dP0为INS输出的位置参量在P0处的偏移量,dv为INS输出的速度参量的漂移量,t0、tk分别为平台在位置P0、Pk记录的时刻,则由式(12)可知,
P0T=P0+dP0
PkT=Pk+dP0+dv·(tk-t0)
则平移向量,也即位置之差修正为
T′k=P0T-PkT=P0-Pk+dv·(t0-tk)=
Tk+dv·(t0-tk)
此时平移后的地面位置为
B′*=B+T′k=B+Tk+dv·(t0-tk)=
B′+dv·(t0-tk)
由此可知,计τi=t0-ti,则此时将方程修正为
Rs(i)=((x′i-x+dvx·τi)2+
(y′i-y+dvy·τi)2+
(14)
3.5 方程求解
本节讨论广义伪距观测方程的解法。观察可知,方程中斜距Rs(i)、地面目标位置(x′i,y′i,z′i)以及时差τi为已知量,平台位置X=(x,y,z)与INS输出的速度参量的漂移量dv=(dvx,dvy,dvz)为未知量。高斯-牛顿迭代法是一种经典的优化方法,也是非线性方程的常用求解方法[15]。其基本思想是用近似的线性回归模型代替非线性回归模型,多次迭代修正回归系数并获得回归参数求最小二乘解,目的是使原模型的残差平方和达到最小。
为实现对方程的迭代求解,则需要设定初值X0=(x0,y0,z0,dvx0,dvy0,dvz0),并有改正量δX=(δx,δy,δz,δvx,δvy,δvz)。将方程按麦克劳林级数展开并化简可以得到
Li=liδx+miδy+niδz+aiδvx+
biδvy+ciδvz
(15)
式中,
ai=-li·τi,bi=-mi·τi,ci=-ni·τi
ri0= (![]() +
+
![]()
Li=Rs(i)-ri0
根据最小二乘原理求得
δX=[ATA]-1[ATL]
(16)
其中,
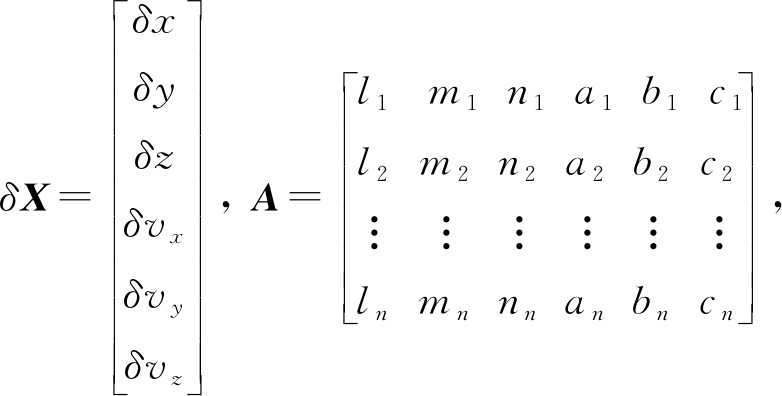

再结合
X1=X0+δX0
Xk+1=Xk+δXk
(17)
将回归系数矩阵Ak得以不断更新,得到
δXk=[(Ak)TAk]-1(Ak)T(Rs-r0k)
(18)
而在实际计算中,当初值选取不当而造成非线性模型中残差较大时,容易出现迭代过程收敛速度过慢甚至不收敛的情况,继而导致迭代无法进行。因此,本文引入阻尼高斯-牛顿方法[16]。这一方法在高斯-牛顿迭代法的基础上改进而来,原理是通过增加线性搜索策略,保证目标函数每一步下降,以此确保迭代过程的收敛性,即有
δXk=-αk·[(Ak)TAk]-1(Ak)T(Rs-r0k)
(19)
式中,αk为一维搜索因子,通常选取0到1之间的正常数。
由此,广义伪距观测方程的高斯-牛顿迭代解法步骤总结如下:
1) 设定初值X0,误差阈值ε,一维搜索因子αk以及最大迭代次数nmax;
2) 计算Ak、r0k、Nk=(Ak)TAk以及gk=![]() (Rs-r0k),由此将式化简为
(Rs-r0k),由此将式化简为
并由此计算得到
Xk+1=Xk+δXk
3) 若![]() 或k≥nmax,则得到计算结果X=Xk+1,否则继续迭代。
或k≥nmax,则得到计算结果X=Xk+1,否则继续迭代。
4 试验结果
4.1 SAR图像地面目标定位结果
论文采用sentimel-A1卫星公开SAR数据作为待定位图像及谷歌地图带有准确位置信息的卫星光学地图作为基准图像对图像匹配算法进行了测试,目的是找到SAR图像的中心点位置在光学图像中的对应位置并准确定位。结果如图6所示。
此结果表明,本文方法可以有效实现光学图像与SAR图像的匹配。基于此,光学基准图的地理位置信息可以传递给SAR图像从而实现对SAR图像中地面目标的准确定位。

(a) 光学基准图像

(b) SAR图像及其中心位置

(c) 处理后待匹配图像

(d) 匹配结果

(e) 定位结果
图6 匹配效果图
4.2 SAR载机平台位置解算结果
本文对载机平台飞行过程以及机载INS相关参数进行了仿真,在本次仿真试验模型中SAR载机平台飞行高度6 500 m,以东北天坐标系下速度(-72,-95,0)m/s飞行,对地成像的时间间隔为200±50 s。此外,在6维INS误差传递模型下,本次仿真模型中INS输出的速度参量的漂移量为恒定值。
仿真实验首先比较了几组观测方程修正前后的结果差异。如图7所示,以绝对误差δX=(δx,δy)T评估定位结果,并以![]() 比较方程校正前后的结果差异。可以看到,若忽略INS漂移误差带来的相关影响,即直接将式(13)作为广义伪距观测方进行解算,则定位结果通常会存在较大偏差。而改进方法的观测方程对这一偏差存在着显著的修正效果。不难看出,通过引入6维INS误差传递模型并修正广义伪距定位方程,定位误差可降低2~3个数量级。
比较方程校正前后的结果差异。可以看到,若忽略INS漂移误差带来的相关影响,即直接将式(13)作为广义伪距观测方进行解算,则定位结果通常会存在较大偏差。而改进方法的观测方程对这一偏差存在着显著的修正效果。不难看出,通过引入6维INS误差传递模型并修正广义伪距定位方程,定位误差可降低2~3个数量级。

(a) 忽略INS漂移量的定位结果

(b) 引入误差传递模型的定位结果
图7 校正效果图
另一方面,由于方程求解的高斯-牛顿法的线性化过程带来的误差不可避免,加上当迭代过程中非线性回归模型的回归系数矩阵的条件数偏大而导致病态时,定位结果会出现较大的难以避免的波动。基于此,本文拟增加控制点个数以求解决这一问题。
具体地,根据前文所述,求解3.5节提出的非线性广义伪距观测方程至少需要6个已知的地面位置。将这些地面位置视为控制点,实验进一步验证了控制点个数对定位精度的影响,以期在定位结果不佳时通过增加控制点改善结果以达到工程要求。如表2所示,实验选取定位一组数据并施以增加控制点的方法。结果表明,通过适当增加控制点个数可以提高定位精度。
表2 控制点个数对定位精度的影响

控制点个数x方向误差/my方向误差/m6-1.08203.16187-0.01630.52478-0.0242-0.02519-0.0118-0.044310-0.0018-0.024411-0.0019-0.0256
综上所述,在6维INS误差传递模型下,通过修正改进和广义伪距观测方程,可以有效地提高定位精度,并结合选取多个地面控制点的方法就可以获得较好的定位结果。
5 结束语
本文讨论了在机载卫星导航失效的情况下如何为飞机提供有效的导航定位信息。通过对机载SAR图像中的地面目标准确定位,获取地面准确位置信息,并以此实现对载机平台位置的反向解算。
在实现对SAR图像中地面目标准确定位的过程中,首先应用绝对定位方法粗略地计算目标点的坐标位置。为了弥补绝对定位方法自身存在的固有误差,本文创新地引入了异源图像匹配技术。将基准图像与待匹配图像进行压缩,使用图像的金字塔分解方法可以很好地提高运算效率以及提高匹配准确率。对SAR图像进行必要的滤波、反转、旋转等相应操作之后,将待匹配图像与光学基准图像压缩到统一的分辨率下,并基于实际物理距离对图像进行相应的裁剪后进行匹配。区别于传统的图像匹配方法,本文提出了一种基于灰度映射矩阵的匹配方法,既可以很好地适应SAR图像与光学图像的灰度差异,又在大部分地物目标之间都有很好的适用性。实验结果表明,这一定位办法可以极大地提高匹配精度。
在对机载SAR所成地面高清实时图像中地面目标位置准确定位的前提下,利用这一地面信息对飞机所在位置实现反向解算。本文利用了广义伪距定位方法,有效实现了这一解算过程。为解决飞行过程中INS漂移所带来的误差,本文又在6维INS误差传递模型下对上述方法中的观测方程进行了校正,有效地提高了定位的准确性。仿真实验结果表明,本文方法可以对SAR载机进行有效定位。
在日后的研究中,将这一结果与INS输出数据进行相关拟合,有望实现在卫星导航失效场景下为飞机提供有效精确的定位导航信息。
[1] CHUNG D, LEE J G, PARK C G, et al. Strapdown INS Error Model for Multiposition Alignment[J]. IEEE Trans on Aerospace and Electronic Systems,1996,32(4):1362-1366.
[2] YE Y, SHEN L, HAO M, et al. Robust Optical-to-SAR Image Matching Based on Shape Properties[J]. IEEE Geoscience and Remote Sensing Letters,2017,14(4):564-568.
[3] MERKLE N, AUER S, MULLER R, et al. Exploring the Potential of Conditional Adversarial Networks for Optical and SAR Image Matching[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing,2018,11(6):1811-1820.
[4] HUANG L, LI Z. Feature-Based Image Registration Using the Shape Context[J]. Journal of Remote Sensing,2010,31(8):2169-2177.
[5] 郑扬, 俞能海. 基于共生矩阵的 SAR 图像村庄识别方法[J]. 计算机仿真,2008,25(3):206-209.
[6] LI Q, YIN Kuiying. High-Resolution SAR Typical Targets Extraction and Heterogeneous Image Registration[J]. IETE Journal of Research,2018,67(1):1-12.
[7] 冉聃, 邓欢, 李亚超,等. 基于欧拉四面体的下降轨雷达图像定位方法[J]. 电子与信息学报,2017,39(3):677-683.
[8] 陈圣义, 刘晓春, 滕锡超,等. 基于高精度景象匹配的SAR平台定位方法[J]. 国防科技大学学报,2016,38(5):121-126.
[9] MOSAVI M R, AZARSHAHI S, EMAMGHOLIPOUR I, et al. Least Squares Techniques for GPS Receivers Positioning Filter Using Pseudo-Range and Carrier Phase Measurements[J]. Iranian Journal of Electrical and Electronic Engineering,2014,10(1):18-26.
[10] GOODMAN J W. Some Fundamental Properties of Speckle[J]. Journal of the Optical Society of America,1976,66(11):1145-1150.
[11] BO Yanchen, WANG Jinfeng, ZHU Caiying, et al. Wavelet-Based Filter for SAR Speckle Reduction and the Comparative Evaluation on Its Performance[J]. Journal of Remote Sensing,2003,4886(5):1-10.
[12] DEBELLAGILO M, KAAB A. Sub-Pixel Precision Image Matching for Measuring Surface Displacements on Mass Movements Using Normalized Cross-Correlation[J]. Remote Sensing of Environment,2011,115(1):130-142.
[13] XU G C, XU Y. GPS:Theory, Algorithms and Applications[M]. Germany:Springer,2016.
[14] TITTERTON D, WESTON J. Strapdown Inertial Navigation Technology[M]. 2nd ed.USA:American Institute of Aeronautics & Astronautics,2004.
[15] 邱明伦. 求解非线性方程组的方法研究[D]. 成都:西南石油大学,2012.
[16] PHAN A H, TICHAVSKY P, CICHOCKI A. Fast Damped Gauss-Newton Algorithm for Sparse and Nonnegative Tensor Factorization[C]∥IEEE International Conference on Acoustics, Speech, and Signal Processing, Prague, Czech Republic:IEEE,2011:1988-1991.
