0 引言
逆合成孔径雷达成像作为一种远距离目标信息获取手段,可以获得目标的二维结构用于目标识别。近年来,随着空间目标状态判别需求增加以及微波器件技术的进步,空间目标ISAR成像技术得到了迅速发展。在ISAR成像中,传统的距离-多普勒算法适用于成像时间段内目标一维距离像距离走动可以忽略情况下的中等分辨率成像。为了提高空间目标成像分辨率,当雷达系统采用大带宽时,为了实现图像二维分辨率匹配,方位向采用大转角,大带宽大转角会给ISAR高分辨率成像带来新的问题,即一维距离像在慢时间方位维的包络走动和弯曲,以及慢时间方位维的空变二次相位问题[1-3]。在空间目标ISAR成像平动补偿后,一维像中的包络一次走动可以采用Keystone[4]变换进行校正,数据中的二次空变相位可以采用调频率估计的方法对各距离单元信号中的调频率进行估计,从而完成二次相位补偿,提高图像聚焦程度。
在ISAR成像中,需要对目标进行连续时间采样,对雷达系统时间有较高的占有率,难于实现多目标同时成像。压缩感知理论的提出以及ISAR图像相对于背景具有稀疏性的特点,促进了基于压缩感知理论的ISAR成像技术发展,用于实现高分辨率成像以及稀疏采样数据高分辨成像[5-6]等。针对稀疏采样数据大带宽大转角ISAR成像,本文采用稀疏Keystone变换完成稀疏采样脉冲间的距离走动校正和缺失采样位置一维像恢复,接着利用LVD(Lv’s distribution:吕氏分布)变换对二阶转动相位进行估计并补偿,从而完成稀疏采样条件下大转角高分辨成像,最后利用仿真和暗室测量数据对算法进行了验证。
1 ISAR成像信号模型
在ISAR成像中,设发射信号为
(1)
式中,Tp为发射信号脉冲宽度,fc为中心频率,γ为线性调频信号的调频率,经过去斜接收,RVP(视频残留相位)补偿后为

(2)
进行傅里叶逆变换到时域为
(3)
令f=γt有
(4)
式中,c为光速,ΔRi=Ri(tm)-Rs(tm),经平动补偿后ΔRi=xisinθ(tm)+yicosθ(tm),对ΔRi进行泰勒展开忽略高次项,![]() 上式可写成
上式可写成

(5)
可以看出f和tm存在一次和二次耦合,一次耦合可通过Keystone变换去除,即令![]() 代入上式有
代入上式有
si(f,τm)=![]()
(6)
利用![]() 式(6)可以写成
式(6)可以写成
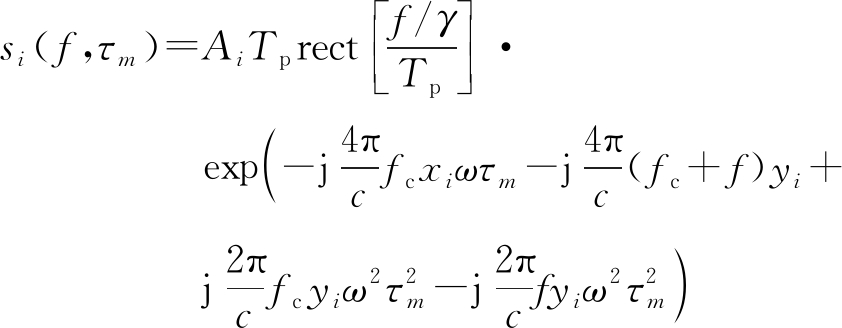
(7)
对上式进行傅里叶变换,转换到距离时域为
si(t,τm)=![]()
(8)
式中,Br为信号带宽。通过Keystone变换去除了一次耦合,但是还存在二次空变耦合,二次空变耦合会造成包络空变弯曲和二次空变相位,如果对两者同时进行补偿,则需要对转动中心和转角进行二维搜索,计算复杂程度较高,一般情况下转动分量造成的包络弯曲较小,可以忽略,可以只对空变二次相位进行补偿。
2 稀疏采样数据大转角成像
2.1 稀疏采样数据距离走动校正
当雷达发射信号具有大带宽且成像转角较大时,在成像时间内目标的转动会带来一维像一阶走动和二阶弯曲,一般情况下二阶弯曲量可以忽略,一阶走动需要进行校正。Keystone变换算法可用于方位向连续采样数据的一阶距离走动校正。对于慢时间维稀疏采样数据,将数据转换到慢时间-距离频率域,对不同的频率单元构造相应的基矩阵,在完成稀疏采样脉冲间的距离走动校正的同时实现缺失采样位置一维像的恢复重建。
根据稀疏恢复理论,对于线性测量过程,观测量可写成
Y=ΦX=ΦΨθ
(9)
式中,测量矩阵Φ是M×N维矩阵,M<N。从测量数据Y中重建长度为N的信号X,由于M<N,这个方程有无穷多个解,如果X是K阶稀疏的,只要M≥K,就可以通过基于l1范数的优化求解。
由于目标在方位多普勒域具有稀疏性,对于方位向稀疏采样数据,可通过压缩感知理论在多普勒域对信号重建。Keystone变换是通过对慢时间-距离频率域数据进行尺度变换,校正目标转动引入的距离走动的。先对式(5)表示的信号进行尺度变换,接着在慢时间维进行傅里叶变换,目标在多普勒域的系数向量和频率域数据有以下关系:
Y(i)M×1=ΦM×N0Ψ(i)N0×N0θ(i)N0×1
(10)
式中,i为距离门数,Y(i)M×1为第i个距离门频域中M个稀疏采样脉冲向量, θ(i)N0×1为从第i个距离门频率域中要恢复重建的目标多普勒系数向量,![]() 为信号中心频率,Br为信号带宽,N为需要重建的多普勒系数长度。根据Keystone变换在慢时间-距离频率域的尺度变换方式,基矩阵Ψ(i)N0×N0中的元素可以构造为[7]
为信号中心频率,Br为信号带宽,N为需要重建的多普勒系数长度。根据Keystone变换在慢时间-距离频率域的尺度变换方式,基矩阵Ψ(i)N0×N0中的元素可以构造为[7]
(11)
式中,fd(n0)为待建目标的多普勒系数, fd(n0)=([1:N0]-N0/2)/N0,n0=1,2,…,N0,m=1,2,…,N,每一距离单元对应的基矩阵各不相同。测量矩阵Φ由稀疏采样时刻决定,第i个频域距离门信号对应的基矩阵Θ(i)M×N0=ΦM×N0·Ψ(i)N0×N0中的元素可构造为
(12)
式中,fd(n0)=([1:N0]-N0/2)/N0,n0=1,2,…,N0,m=1,2,…,M。
利用稀疏恢复算法对式(10)表示的信号模型进行求解,可以获得距离走动校正后目标在方位向的多普勒分布,在分辨率不高的情况下,就可以完成方位向成像,但是在大转角情况下,需要对转动二次相位进行补偿,因此还需要对重构的多普勒域数据在方位向进行傅里叶逆变换,获得经过距离走动校正后的等效连续采样数据。在此基础上估计各距离单元中的二次相位并进行补偿,可以实现高分辨率成像。
2.2 基于LVD变换的二次相位补偿
对于方位向稀疏采样数据,在距离走动校正,缺失采样位置数据恢复后,可用式(8)表示,可以看出在慢时间维进行傅里叶变换,就可以完成方位向成像,但是慢时间二次相位会影响散射点的聚焦程度,因此需要对二次相位进行补偿。忽略包络中的距离弯曲,采用LVD变换对各距离单元二次相位系数进行估计,其中LVD变换利用信号的瞬时自相关函数作尺度变换,消除时间变量之间的耦合关系,与WVD变换相比传统避免了多分量信号间的交叉项。
定义信号的相关函数为
(13)
线性调频信号的相关函数为
R(tm,τ)=ej2π[f0(τ+a)+γtm(τ+a)]
(14)
对上述得到的相关函数作如下尺度变换[8]:
(15)
则相关函数变为
(16)
对上式作二维傅里叶变换,如下式所示:
Ls(f,γ)=![]()
(17)
由上式可以看出,变换后会在(f0,γ0/h)处出现峰值,取h=1。
在距离走动校正后,估计出距离门中信号的二次项系数,为了提高估计的稳健性,需要对估计的系数进行多项式拟合,完成向量kr的估计。数据中需要补偿的相位为
(18)
对每一个距离单元对应的慢时间序列进行相位补偿,补偿二阶转动相位。对经过转动相位补偿的数据,进行方位向FFT和自聚焦可完成成像处理。应当指出的是,在对各距离单元二次相位系数进行估计,多个距离单元进行一阶多项式拟合的过程,相当于估计出了转动分量的调频率,从而可以估计出目标转角,实现方位向定标。
稀疏采样数据大转角ISAR成像流程如图1所示。1) 对于稀疏采样数据进行包络对齐和相位补偿完成平动补偿;2) 对平动补偿后的数据,进行距离向FFT将数据变换到距离频率域;3) 对距离频率域数据的每一距离频率单元信号根据式(12)构造相应的基矩阵,然后利用稀疏恢复算法对每一距离频率单元的方位向散射点进行恢复;4) 进行两维IFFT获得距离走动校正后的方位向距离慢时间序列;5) 对经过距离走动校正后的序列,利用LVD算法估计每一距离单元信号中的二次相位系数,并对各单元估计的值进行多项式拟合,完成空变二次相位估计;6) 对各距离门信号补偿对应的二次相位,完成二次相位补偿;7) 对二次项补偿后的信号进行方位向FFT完成高分辨ISAR成像。
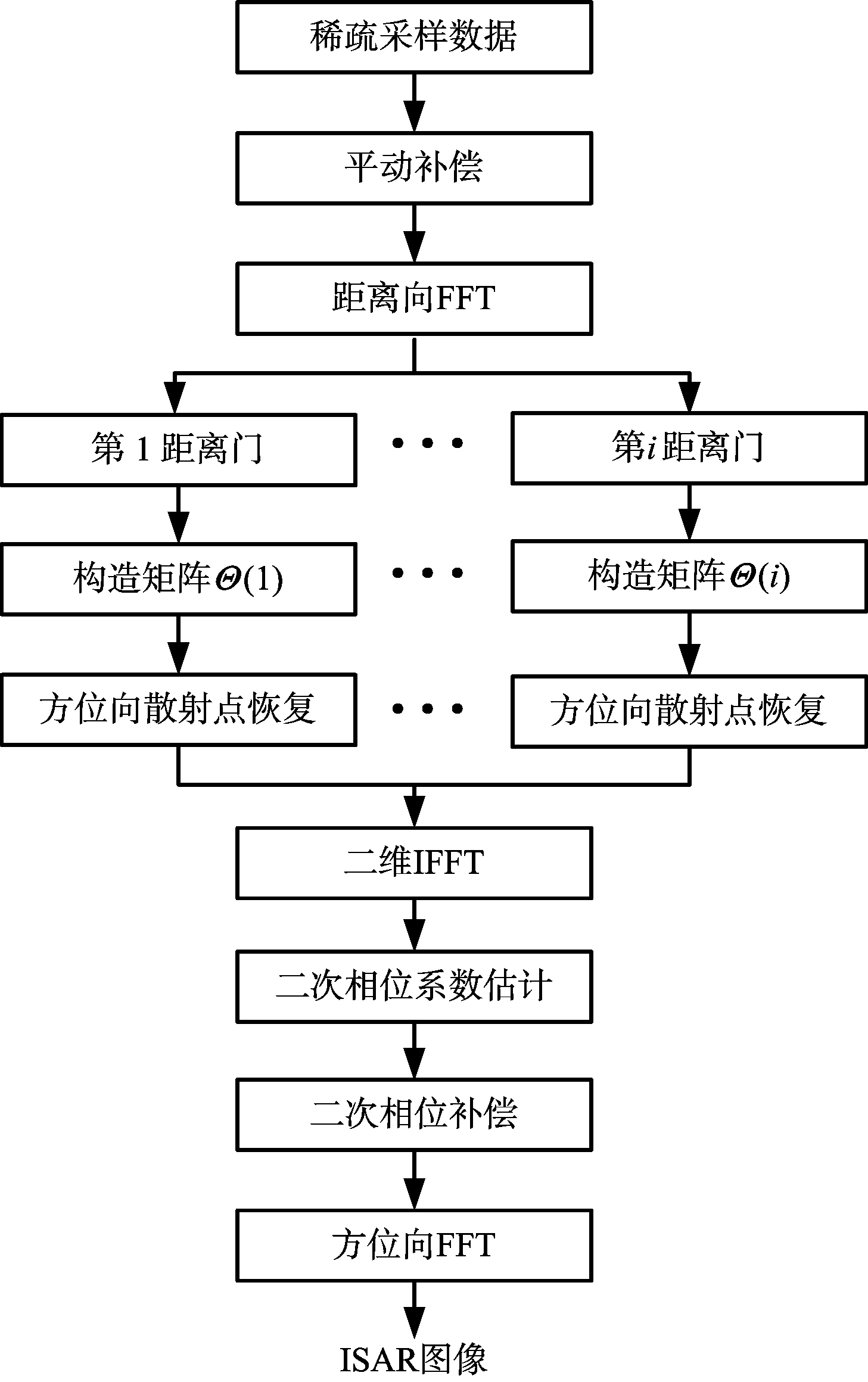
图1 信号处理流程
3 仿真及暗室数据处理

图2 点目标模型
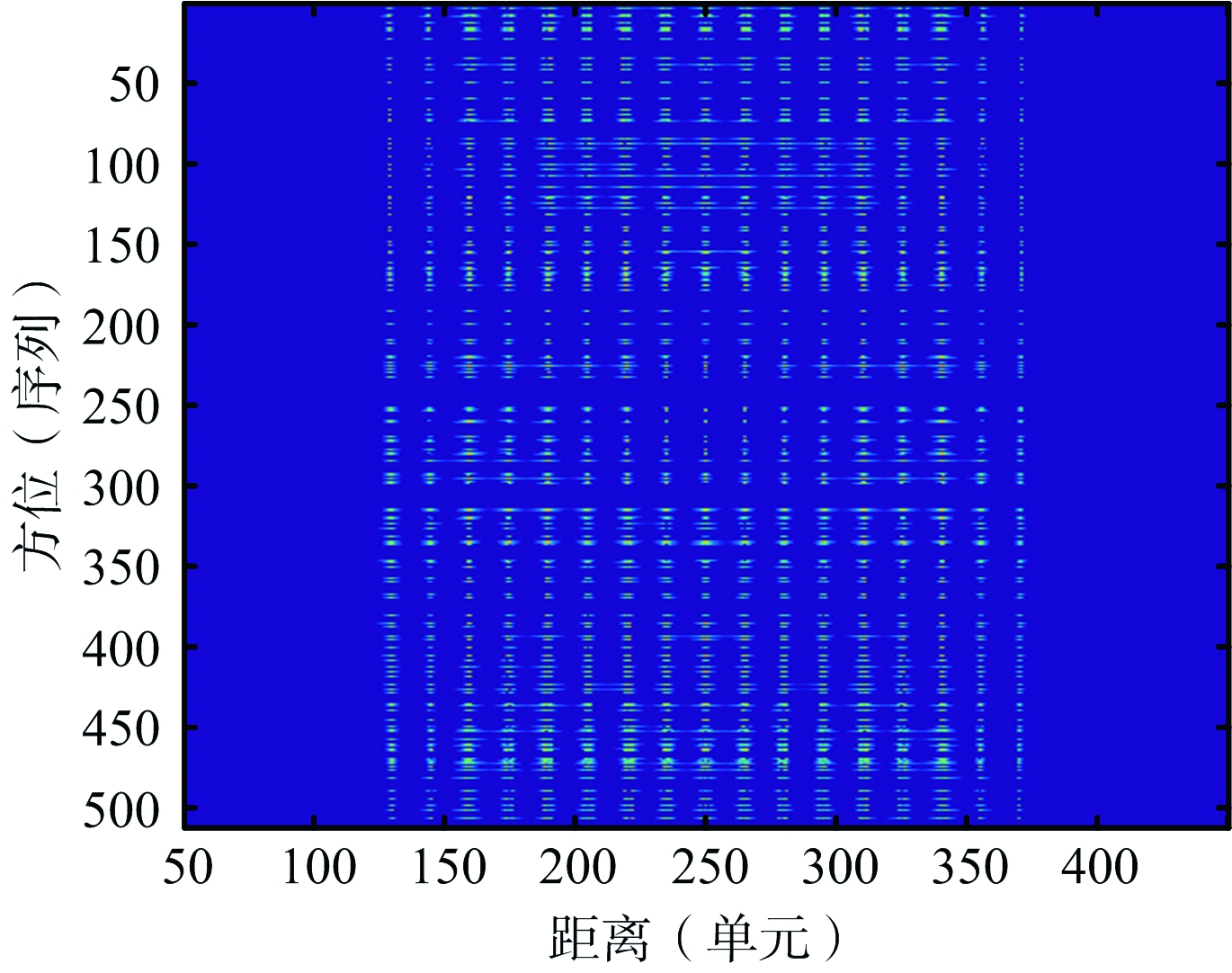
图3 稀疏采样一维距离像序列
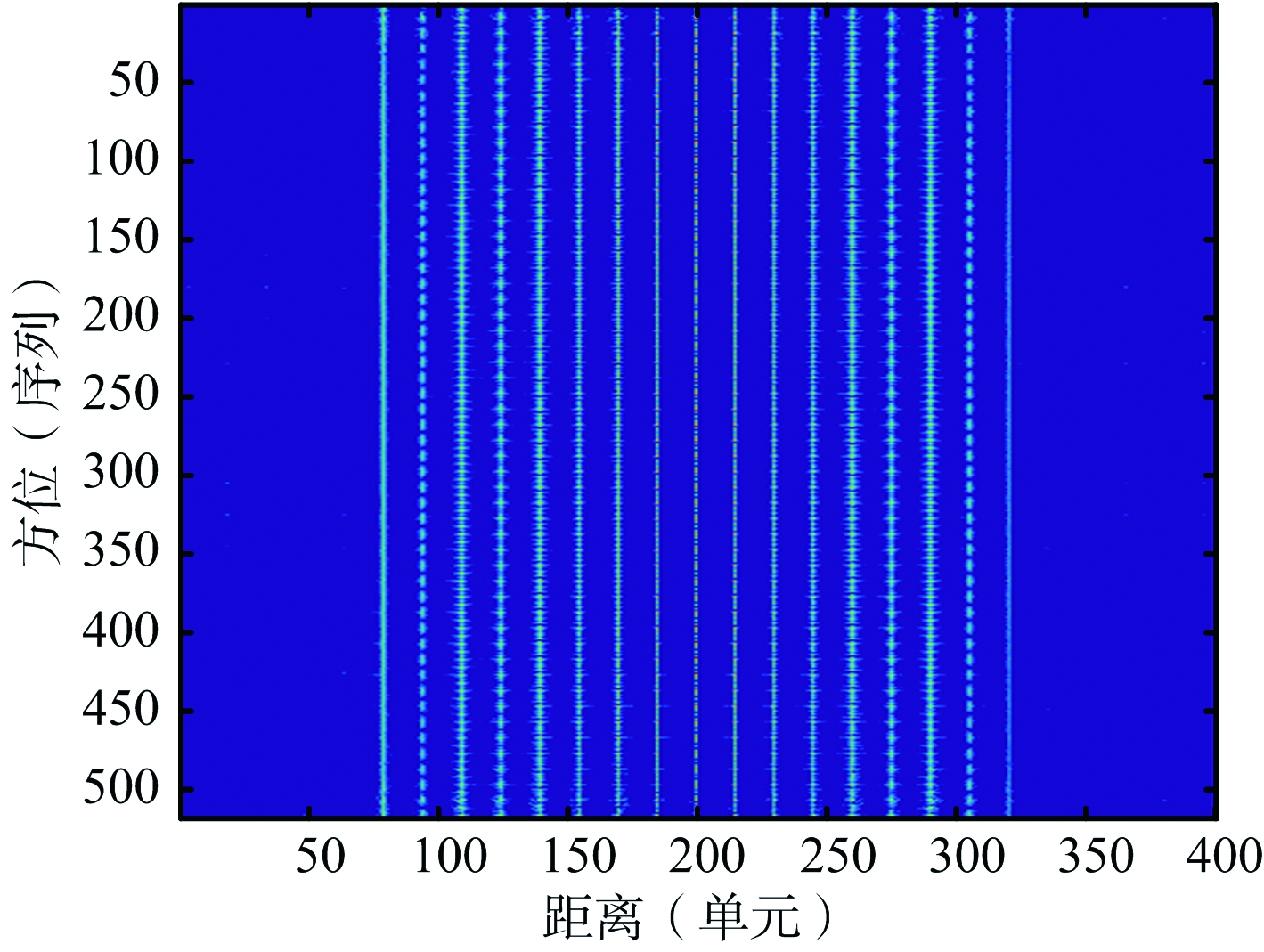
图4 距离走动校正后恢复的序列

图5 二次相位补偿前成像结果

图6 二次相位补偿前成像结果局部放大

图7 一维像序列非相参积累结果
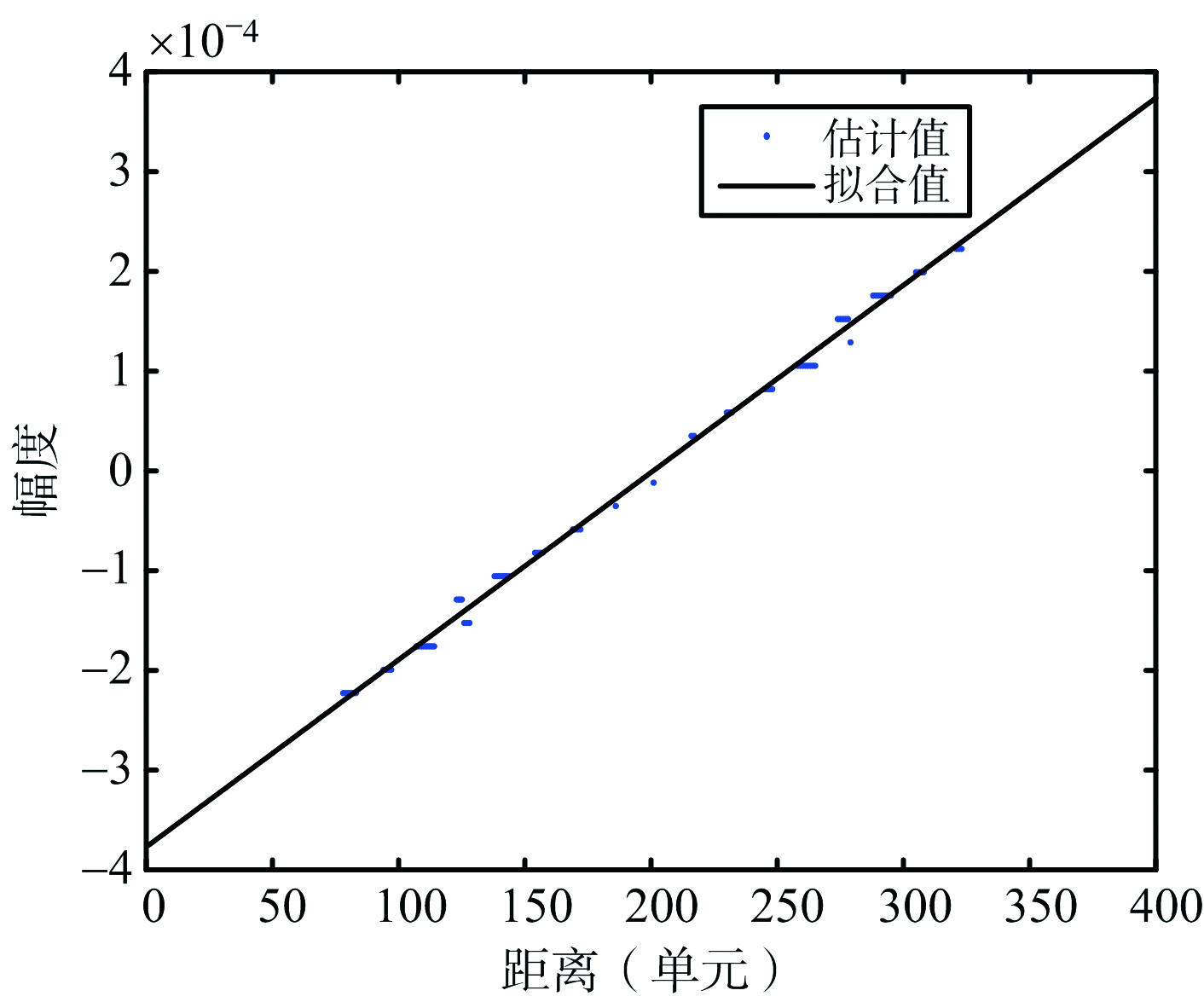
图8 二次相位系数多项式拟合结果

图9 二次相位补偿后成像结果

图10 二次相位补偿后成像结果局部放大
下面通过点目标仿真数据的处理对文中算法进行说明,假设雷达中心频率设为35 GHz,发射的线性调频信号频带宽度为2 GHz,采用去斜接收采样模式。图2为点目标模型。图3为稀疏采样一维距离像序列,采用了1/4数据,可以看出在大带宽大转角条件下,目标转动引起了散射点的距离走动。图4为方位向稀疏采样数据距离走动校正后恢复的序列,采用的稀疏恢复算法为基于内点的l1正则化算法。图5为对距离走动校正后的数据直接成像结果,图6为图5局部放大,可以看出在大带宽大转角情况下,在距离走动校正后,目标转动引入的二次相位不能够忽略,会影响成像聚焦效果。为了对二次相位进行补偿,采用LVD变换估计每一个距离单元信号中的二次相位系数,并进行多项式拟合。在二次相位系数估计中,为了降低噪声的影响,选取超过一定门限的距离单元信号,如图7中门限以上距离单元。图8为估计的二次相位系数及多项式拟合结果。图9为二次相位补偿后成像结果,图10为图9散射点局部放大,可以看出通过转动二次相位补偿,提高了图像聚焦程度。
下面通过暗室测量的毫米波频段无人机数据处理进行说明,图11为测量的无人机光学图片。图12为采用了1/2稀疏采样的一维距离像序列,可以看出由于转角较大,散射点出现了明显的距离走动。图13为采用稀疏恢复算法对距离走动校正的同时实现方位向序列恢复的结果,可以看出不仅恢复出了方位向缺失位置的采样,而且消除了散射点的距离走动。图14为直接对距离走动校正后的序列进行ISAR成像结果,可以看出在远离转动中心的位置,目标散射点出现了一定程度上的散焦。图15为在距离走动校正后的基础上,利用LVD变换估计二次相位并补偿后的成像结果,可以看出经过二次相位补偿,提高了图像聚焦效果。

图11 无人机光学图片

图12 稀疏采样一维距离像序列

图13 距离走动校正后恢复的序列
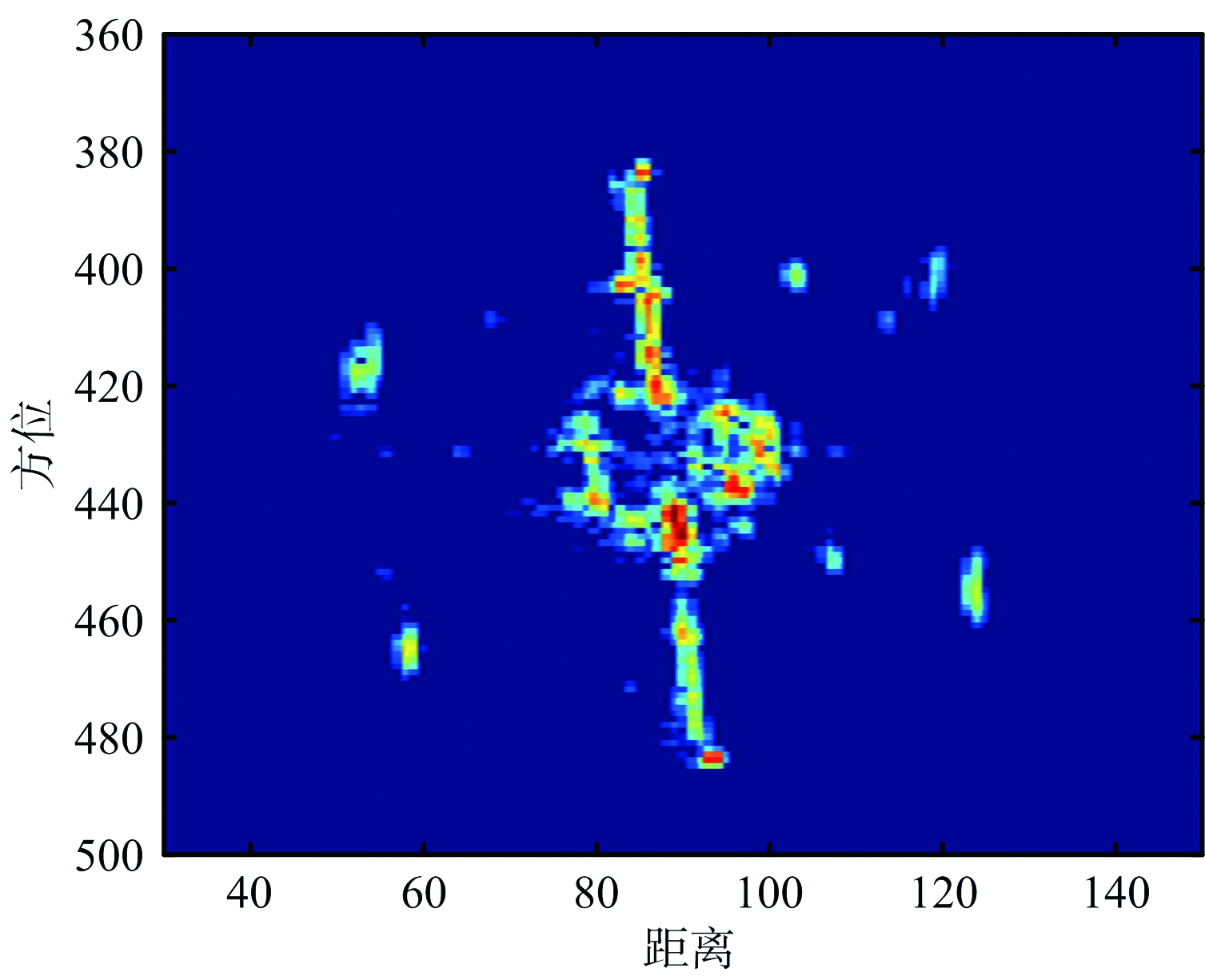
图14 二次相位补偿前成像结果
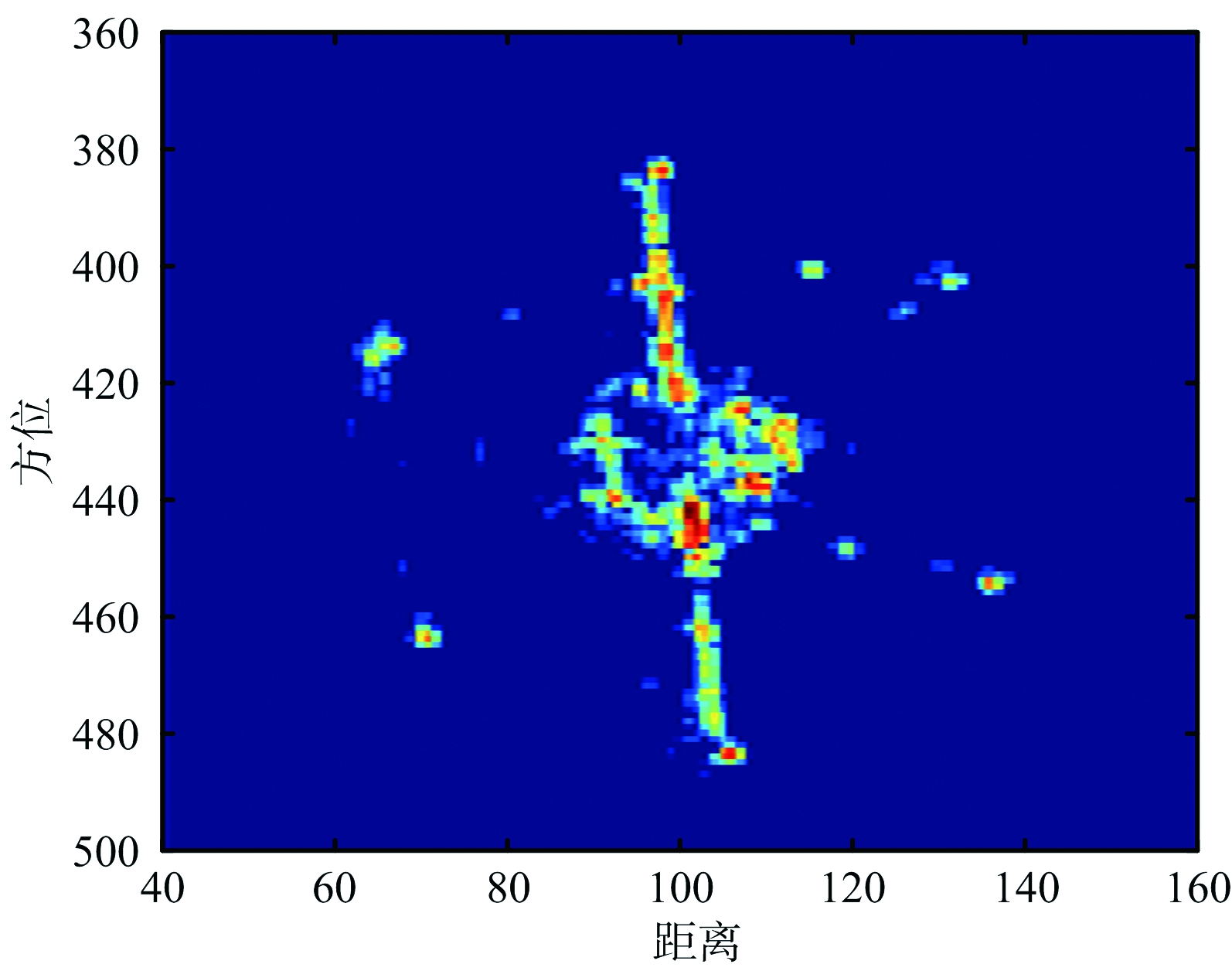
图15 二次相位补偿后成像结果
4 结束语
在雷达ISAR成像中,为了获得更高分辨率的雷达图像,需要提高信号带宽和增大成像转角。本文针对ISAR成像中方位向稀疏采样条件下大带宽大转角成像时,目标散射点产生的距离走动和二次相位问题,研究了一种稀疏采样数据高分辨ISAR成像方法。对于方位向稀疏采样数据,该方法在包络对齐和相位补偿后,将数据变换到距离频率域,对每一距离单元数据,根据方位向稀疏采样位置构造相应的Keystone基矩阵,利用稀疏恢复算法实现距离走动校正和方位向序列的恢复,最后采用基于LVD变换的二次相位估计算法对信号中的空变二次相位进行估计并补偿,完成高分辨ISAR成像。通过仿真和暗室测量数据处理验证了文中方法的有效性。
[1] ZHANG W C, CHEN Z P, YUAN B. Rotational Motion Compensation for Wide-Angle ISAR Imaging Based on Integrated Cubic Phase Function[C]∥ IET International Radar Conference, Xi’an:IET, 2013:14-16.
[2] 刘鑫阁,邢孟道,孙光才.一种高精度的ISAR转动补偿和方位定标方法[J].电子与信息学报,2018,40(9):2250-2257.
[3] 杨利超,邢孟道,孙光才,等 .一种微波光子雷达ISAR成像新方法[J].电子与信息学报,2019,41(6):1271-1279.
[4] PERRY R P, DIPIETRO R C,FANTE R L. SAR Imaging of Moving Targets [J]. IEEE Trans on Aerospace and Electronic Systems, 1999, 35(1):188-200.
[5] 刘明昊,徐久,赵付成龙,等.低空小型无人机贝叶斯学习超分辨ISAR成像[J].雷达科学与技术,2020,18(3):301-312.
LIU Minghao,XU Jiu,ZHAO Fuchenglong,et al.Low-Altitude and Small-Size UAV ISAR Imagery Based on Sparse Bayesian Learning[J].Radar Science and Technology,2020,18(3):301-312.(in Chinese)
[6] 杨磊,夏亚波,毛欣瑶,等.基于分层贝叶斯Lasso的稀疏ISAR成像算法[J].电子与信息学报,2021,43(3):623-631.
[7] 侯颖妮,杨予昊,于俊朋. 基于压缩感知的稀疏采样数据大转角ISAR成像研究[J]. 现代雷达,2018,40(12):40-45.
[8] LV Xiaolei, BI Guoan, WAN Chunru,et al. Lv’s Distribution: Principle, Implementation, Properties, and Performance [J]. IEEE Trans on Signal Processing, 2011, 59(8):3576-3591.

