0 引 言
多输入多输出(MIMO)阵列雷达系统采用电子扫描代替机械扫描，从而提高效率，具有二维(2D)天线阵列的宽带雷达系统能够获得三维(3D)成像或检测结果。因此，它们被广泛应用于自由空间监视、安检雷达、穿墙成像和医疗诊断等许多领域[1-3]。对于雷达成像，获得无旁瓣的高分辨率雷达图像，阵列需要具有宽孔径和窄阵元间距的特点。因此，雷达系统需要更多的阵元，但也增加了系统的成本、复杂度和计算负担。MIMO阵列采用M个发射单元发送正交信号，N个接收单元接收回波，其性能近似于M×N个收发单元的虚拟阵列，所需的实际天线数量，以及系统的成本和复杂性大大减少。
天线阵列的主要功能是对回波信号进行空间采样，然而，受总孔径长度和每两个天线之间的最小间距的限制，雷达的成像结果中通常会出现严重影响雷达性能的栅瓣和旁瓣。合理设计的阵列可以提高成像性能，例如锐化主瓣，抑制旁瓣和栅瓣等。在文献[4-5]中，作者提出了设计均匀线性MIMO阵列的方法，但是二维阵列设计是一个更复杂的问题，应满足低阵元阴影和基本均匀性，以避免高旁瓣水平[3, 6-7]。在文献[8-9]中，几种基于旁瓣抑制目标和迭代搜索的MIMO阵列优化方法被提出，然而这些方法牺牲了主瓣的锐度。在文献[4, 9-10]中提出了方形MIMO阵列设计方法，该方法可以产生填充均匀分布的虚拟阵元的平面阵列。文献[11-13]提出了几种周期性旋转阵列设计方法，这些阵列满足低阵元阴影和基本均匀性原则，它们的栅瓣很低，但是这些方法仅用于设计具有特定数量阵元的数组，例如3的倍数。文献[6-7]提出了一种基于“网格法”的随机阵列设计方法来设计同时满足这两个原则的稀疏阵列，但是阵元的数量仍然限制在4的倍数内。
由以上方法可知，随机的阵列提供较低的旁瓣/栅瓣，但是他们对设计的阵列中的天线数量有严格要求，不适合设计发射天线数等于接收天线数的阵列，应用范围受限。因此，本文提出了一种基于天线局部特性的MIMO阵列设计方法，以虚拟阵列的局部密度及其在方位向和垂直向上的投影局部密度作为优化函数进行计算，前一种保持了设计阵列的基本均匀性，而后一种使设计的阵列具有低阴影。采用天线阵列的最大边界和两个单元之间的最小间距作为约束，以确保设计的阵列是可实现的。与现有的阵列设计方法相比，本方法可以设计任意数量天线的MIMO阵列，且具有低旁瓣/栅瓣的特点。最后，通过实验结果和实际应用验证，证明了本文所设计的二维MIMO阵列的有效性。
1 MIMO阵列设计
1.1 MIMO阵列
MIMO雷达使用M个发射天线发送正交信号，并使用N个接收天线接收回波信号，可以等效为M×N个虚拟阵元的结果。其中每个虚拟阵元的位置可等效位于发射天线和接收天线的连线的中点，三者之间的几何关系如图1(a)所示。图1(b)给出了具有4个发射天线和4个接收天线的MIMO阵列等效示例。
图1 虚拟阵元图解
由图1可知，发射天线Tx、接收天线Rx和虚拟阵元VTRx之间的几何位置可以表示为
(XVTRx,YVTRx,ZVTRx)=
0.5(XTx+XRx,YTx+YRx,ZTx+ZRx)
(1)
MIMO阵列的探测性能很大程度上取决于其虚拟阵元的分布，两个设计原则可以提高所设计的虚拟阵列的性能。第一个是低阴影性，在每个角度的等效线阵中，其投影的单元重叠应尽可能少，以保持等效阵列具有单位加权孔径[6-7,15]。第二个是基本均匀性，即所有虚拟阵元应均匀覆盖孔径平面，几乎没有冗余，以确保每个角度切割的等效线孔径尽可能接近均匀和周期[6-7, 14]。
基于以上两个设计准则，我们提出了一种基于局部特征的MIMO阵列设计方法。通过虚拟阵元在二维投影上的局部密度和虚拟阵元的二维局部密度两个优化对象提高设计阵列的性能。其中虚拟阵元在水平和垂直方向上的投影的局部密度的优化，确保虚拟阵列的低阴影特性；虚拟阵元的二维局部密度的优化，保证了设计的虚拟阵列的基本统一。除了这两个优化对象外，本方法还评估了两个约束条件，以确保所设计的阵列可以加工制作成实物，分别是最大边界约束和两个阵元之间的最小间距约束。
1.2 优化对象
在阵列设计过程中，以方形MIMO阵列作为初始阵列，然后根据优化对象将虚拟阵元及其对应的发射天线和接收天线迭代推到所需的位置。在每次迭代中，首先计算两个优化对象，然后将阵元推向两个优化对象的下降方向。
1.2.1 虚拟阵元在两个方向上投影的局部密度
已知虚拟阵元的较低阴影会削弱旁瓣和栅瓣的影响。文献[6-7,15]在设计雷达阵列期间，虚拟阵元被反复推到其所需位置。在每个迭代周期内，首先计算虚拟阵元在水平方向及竖直方向上的投影位置。然后按照式(2)计算方位向及高度向上投影的局部密度:
(2)
其中,
(3)
为标准权重函数，xl为虚拟阵元的投影位置，h为权重函数的宽度。K(·)是决定权重函数形状的核函数，如常用的三角核、方形核和高斯核等。
在每个迭代周期内，各虚拟阵元按照式(4)移动向局部密度更低的方向，以优化阵列。
(4)
式中，V1_VTRxx(x)和V1_VTRxy(y)表示在(x,y)处虚拟阵元应被赋予的优化向量，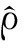
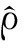x(x)和y(y)分别表示虚拟阵元在水平方向和竖直方向上投影的局部密度，α为优化系数。计算完各个虚拟阵元的优化向量后，按照式(5)计算它们所对应发射阵元及接收阵元的优化向量，对应为单次迭代中，各实际阵元以降低局部投影密度为目标应进行的移动。
(5)
1.2.2 虚拟阵元的二维局部密度
在设计二维MIMO阵列时，重要的是让所有虚拟阵元均匀覆盖孔径平面，几乎没有冗余，以确保每个角度切割的等效线孔径尽可能接近均匀和周期性。文献[6-7,14]通过逐渐将虚拟阵元推到虚拟阵元较少的区域，可以保持二维虚拟阵列的基本均匀性。
在单次迭代中，虚拟阵元的二维局部密度可以通过式(6)来计算，式中(xl,yl)表示各虚拟阵元的位置。
(6)
式中，xl为虚拟阵元位置，L为虚拟阵元总数，
(7)
为标准二维权重函数，K(x,y)为核函数。形如式(8)所示的高斯核函数即为常用核函数的一种。
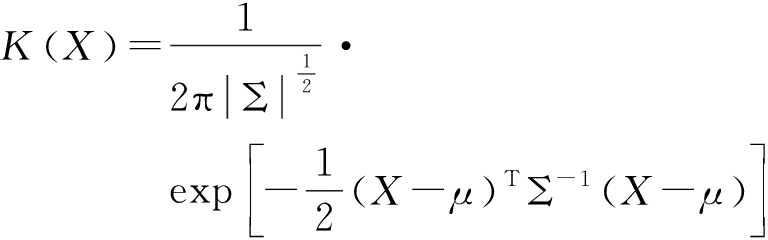
(8)
式中，μ为X的均值，Σ为协方差矩阵。在MIMO阵列的过程中，通常要求阵列具有近似对称性，因此，式中均值通常为0，而协方差矩阵则为对角阵。
虚拟阵元二维局部密度目标的梯度下降方向可以表示为
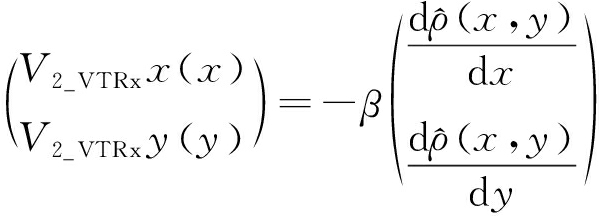
(9)
式中，V2_VTRxx(x)和V2_VTRxy(y)分别表示在单个迭代周期内(x,y)位置处虚拟阵元被赋予的优化向量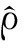，(x,y)表示虚拟阵元的二维局部密度，β为优化系数。各虚拟阵元所对应实际阵元所被赋予的优化向量同样可以按照形如式(10)的形式进行计算。
(10)
1.3 约束条件
为实际雷达系统设计MIMO阵列，总孔径长度应限制为便携式。此外，每两个天线之间的间距不应太近，以避免重叠和干扰，且可实现。因此，在优化的每次迭代中，在两个优化程序之后评估两个约束条件。
边界约束：在天线阵所在平面上，假设边界约束上指向阵列外侧的法向量为Bl(x,y)，当阵元由于优化目标作用并要移向边界外时，利用如式(11)所示的约束变量保证阵元移动后仍然留在边界内。
VB=-〈Bl(x0,y0),V0〉Bl(x0,y0)
(11)
式中，(x0,y0)为边界上距离阵元最近的点，V0是优化向量和，可表示为
(12)
最小间距约束：当两阵元不断靠近时，两阵元中心距离需保持大于单个阵元实际尺寸并满足低耦合要求。因此当两单元移动得过近时，利用形如式(13)的约束向量保持阵元间距。
VS=-〈(x0-xl,y0-yl),V0〉·
(x0-xl,y0-yl)
(13)
式中，(xl,yl)为正在移动单元的位置，而(x0,y0)为移动单元即将碰撞的单元的位置。
1.4 MIMO阵列优化方法
本节中，以10发10收低重叠方形MIMO阵列设计为例，介绍迭代优化设计算法流程。整个迭代过程可以分为如下五步进行介绍，过程流程图如图2所示。
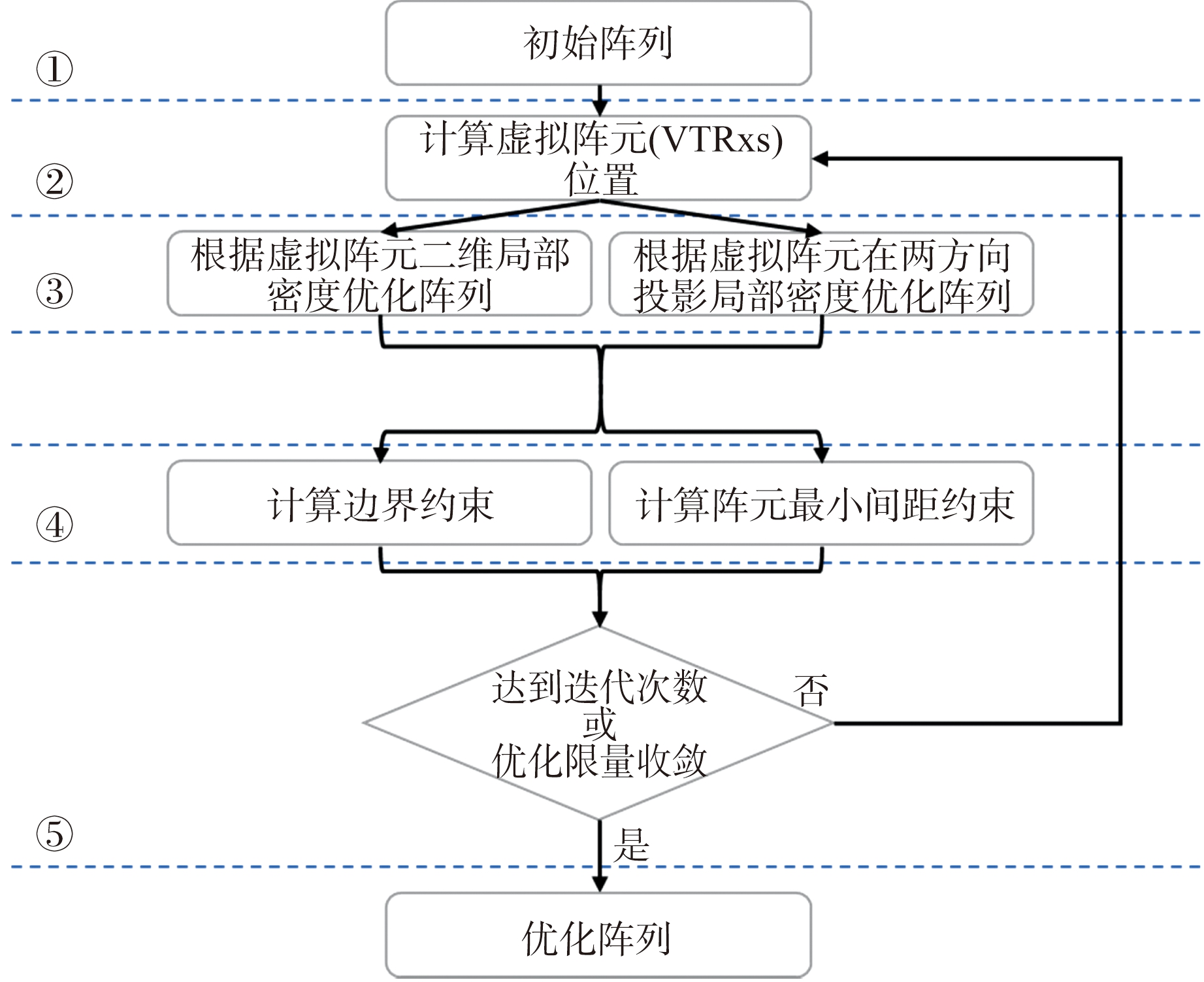
图2 MIMO阵列优化流程图
第一步，获得初始阵列：
构建一个形如图3(b)所示的方形阵列作为初始阵列。图中，红色圆圈表示发射阵元，蓝色六角星表示接收阵元，而黑色方块表示它们形成的虚拟阵元。图3(b)中的灰度图表示虚拟阵元的局部密度。而图3(a)和(c)则分别表示虚拟阵元在竖直方向及水平方向上的局部投影密度。实际上，对于初始阵列而言，除了天线阵元数量应与所需阵列相同，并没有其他特殊要求。随着迭代优化的进行，各阵元会逐渐移向优化位置，使阵列获得较小重叠。
第二步，计算虚拟阵元位置：
在每次循环迭代开始前，需要根据前次循环迭代结果或初始阵列中各收发阵元位置，按照((xT,yT,zT)+(xR,yR,zR))/2计算各虚拟阵元位置。
第三步，计算两优化向量：
获得各虚拟阵元位置后，分别计算虚拟阵元在水平、竖直方向局部投影密度及在整个阵面上的二维局部投影密度作为优化目标。计算优化目标所对应的梯度下降方向作为优化向量，推动各阵元向优化位置移动。
第四步，计算两约束向量：
计算优化向量，并按照优化向量方向移动各阵元后。阵元向优化位置移动。为保证所设计阵列满足实际需求，计算并执行边界约束及最小阵元间距约束，以保证各阵元既不会越过阵列边间，也不会间隔过近。
第五步，重复上述第二到第四步直至循环结束：
在整个循环迭代过程中，各阵元会逐渐移动至优化位置，使阵列位置近似均匀分布并获得较低的重叠。当达到最大迭代次数或两优化目标不再明显下降时，停止迭代并得到设计好的低重叠MIMO平面阵。
图3 初始MIMO阵列示意图((a)虚拟阵元在竖直方向投影的局部密度，(b)虚拟阵二维局部分布密度，(c)虚拟阵元在水平方向投影的局部密度)
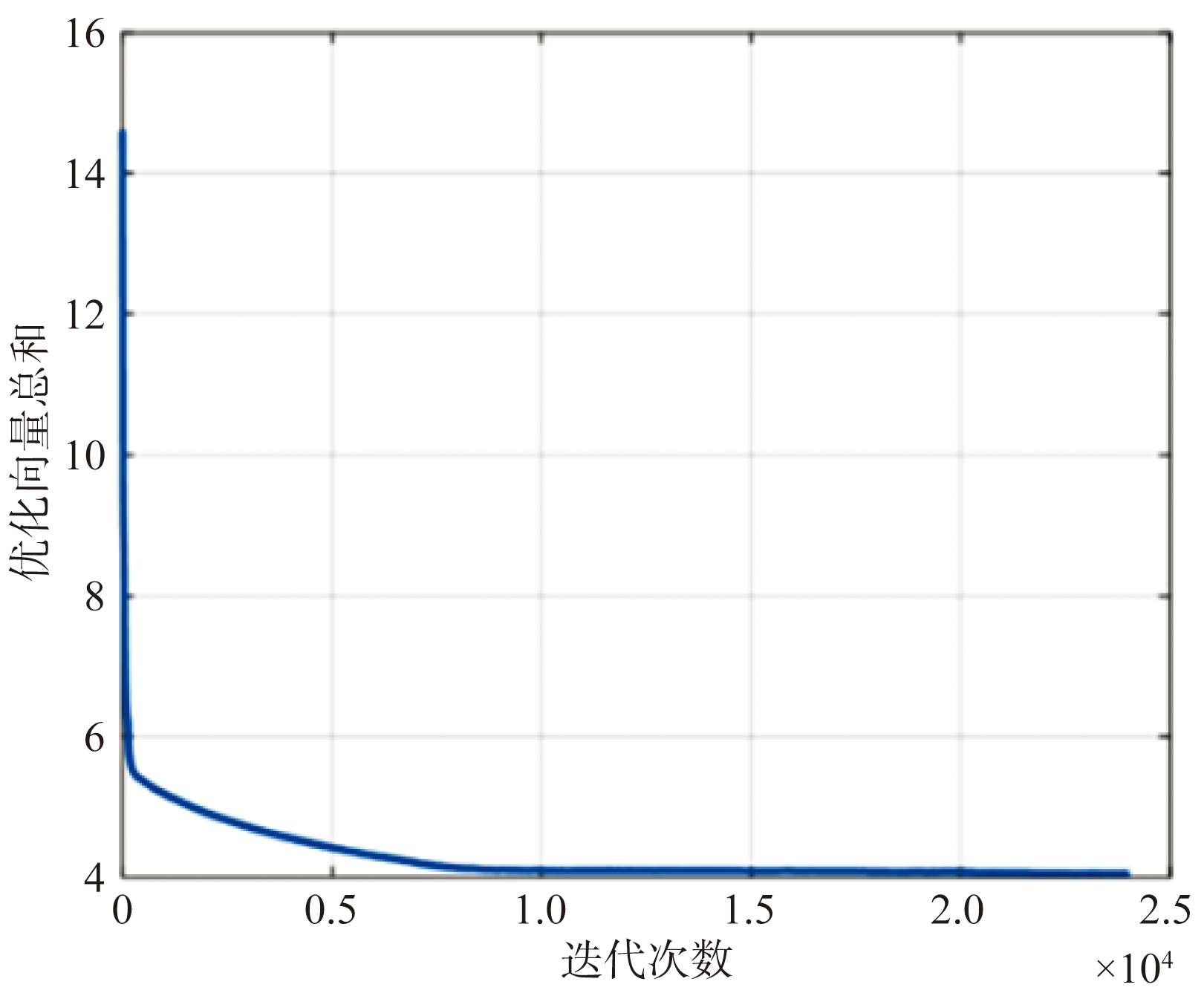
图4 优化目标求和
图5 优化得到的MIMO阵列示意图((a)虚拟阵元在竖直方向投影的局部密度，(b)虚拟阵二维局部分布密度，(c)虚拟阵元在水平方向投影的局部密度)
执行上述优化过程中，上述两优化目标的求和如图4所示。随着迭代优化的进行，各天线单元逐渐移向局部投影密度及二维局部密度更低的区域，以减小重叠。MIMO阵列也从图3所示初始阵列变换为图5中的优化MIMO阵列。在图3中，初始阵列遵循严格的均匀排布，各阵元间距相同。因此它的虚拟阵列在水平方向和竖直方向都具有较高的重叠，从图3(a)和(c)中也可以看出，水平方向和竖直方向的部分区域具有较高的投影密度。较高的重叠会导致阵列具有较高的栅旁瓣及余瓣。而看图5中，优化后的阵列中，虚拟阵元的二维局部密度较低，并且虚拟阵元近似均匀分布在设定的阵列边界内。从图5(a)和(c)中可以看出，相较于图3(a)和(c)初始阵列的局部投影密度，优化后的阵列在水平方向和竖直方向都具有较低且相对平坦的局部投影密度。因此，优化后的MIMO阵列，虚拟阵元具有较低的重叠，这也将使它具有较低的栅旁瓣及余瓣，有助于提升MIMO阵列成像质量。
2 仿真实验
本节将使用该方法设计的随机非均匀阵列(SNUA)与使用文献[4]中的方法设计的均匀阵列(UA)进行了比较，其中，两个阵列的相对孔径长度和元件数量相同。首先比较了两种阵列的仿真成像结果，以及两个阵列在不同相对频带宽度下的最大旁瓣幅度(MSLL，在宽带条件下，栅瓣和旁瓣不能清楚地分开，所以在本节中都简称为旁瓣)，并给出了不同的相对孔径长度条件，以显示所设计阵列的优越性。然后，在2.3节，分析了目标矩阵的相关性，以说明为什么略微不均匀的阵列会给出最佳成像结果。最后，将所提出方法设计的阵列与其他方法设计的4个阵列进行比较。
2.1 成像结果分析
本小节将本文所设计的随机优化MIMO阵列(以下简称优化阵列)与均匀方形MIMO阵列(以下简称均匀阵列)进行对比。两阵列结构分别如图6(a)和(b)所示。各阵元上、下、左、右边界均为0.45 m。阵列发射L/S波段信号，带宽为300 MHz。
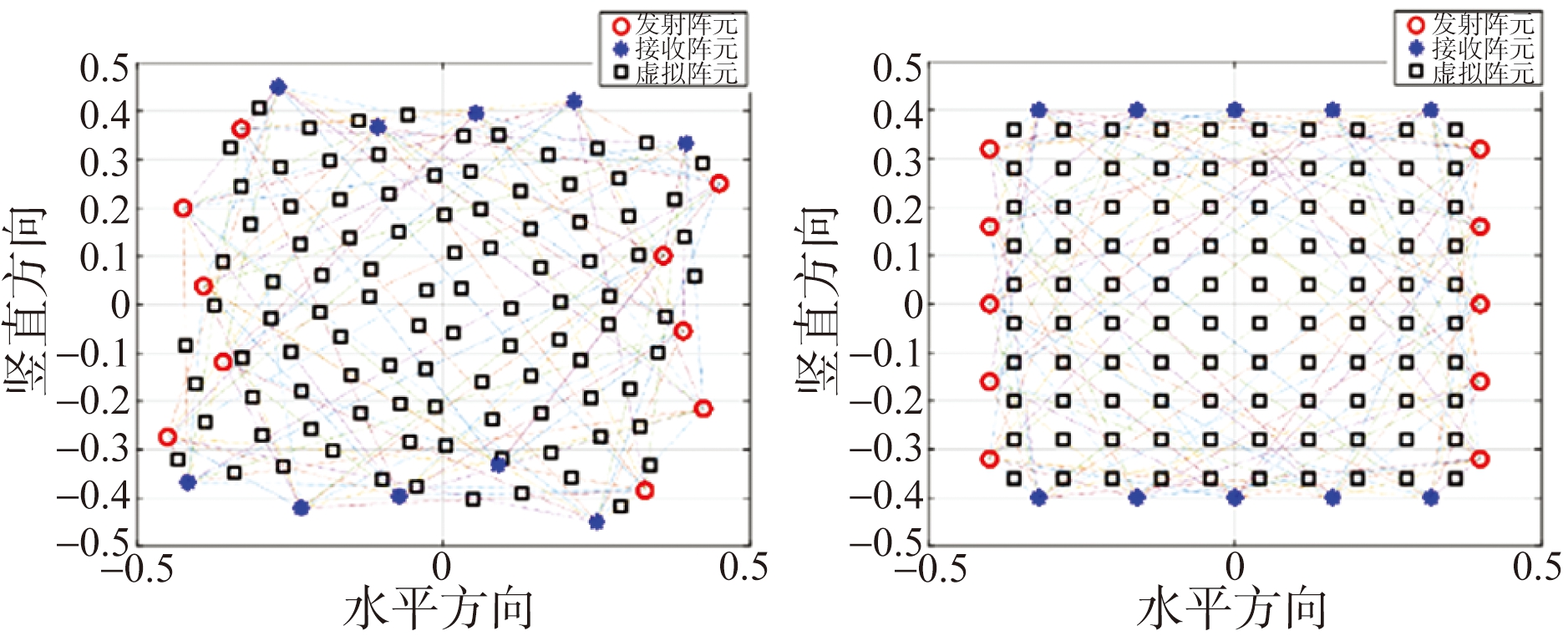
(a) 优化阵列 (b) 均匀阵列
图6 两个MIMO阵列结构图
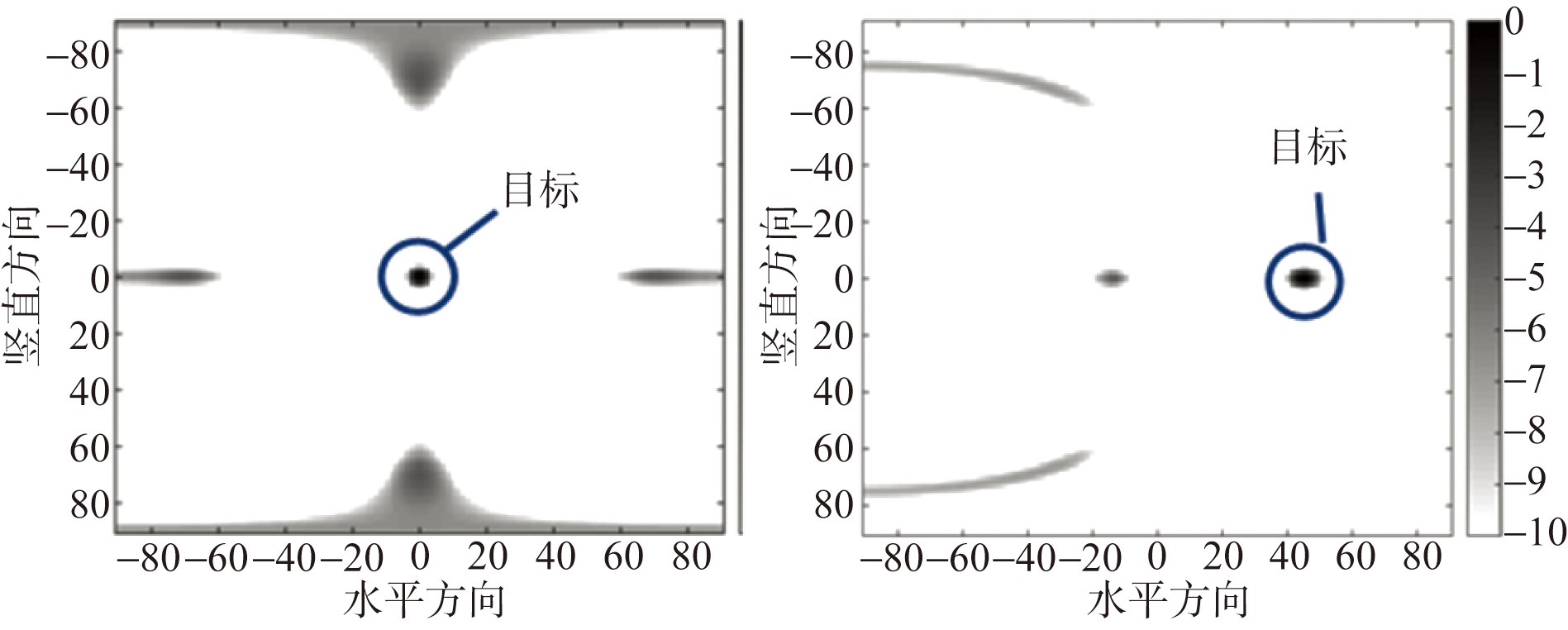
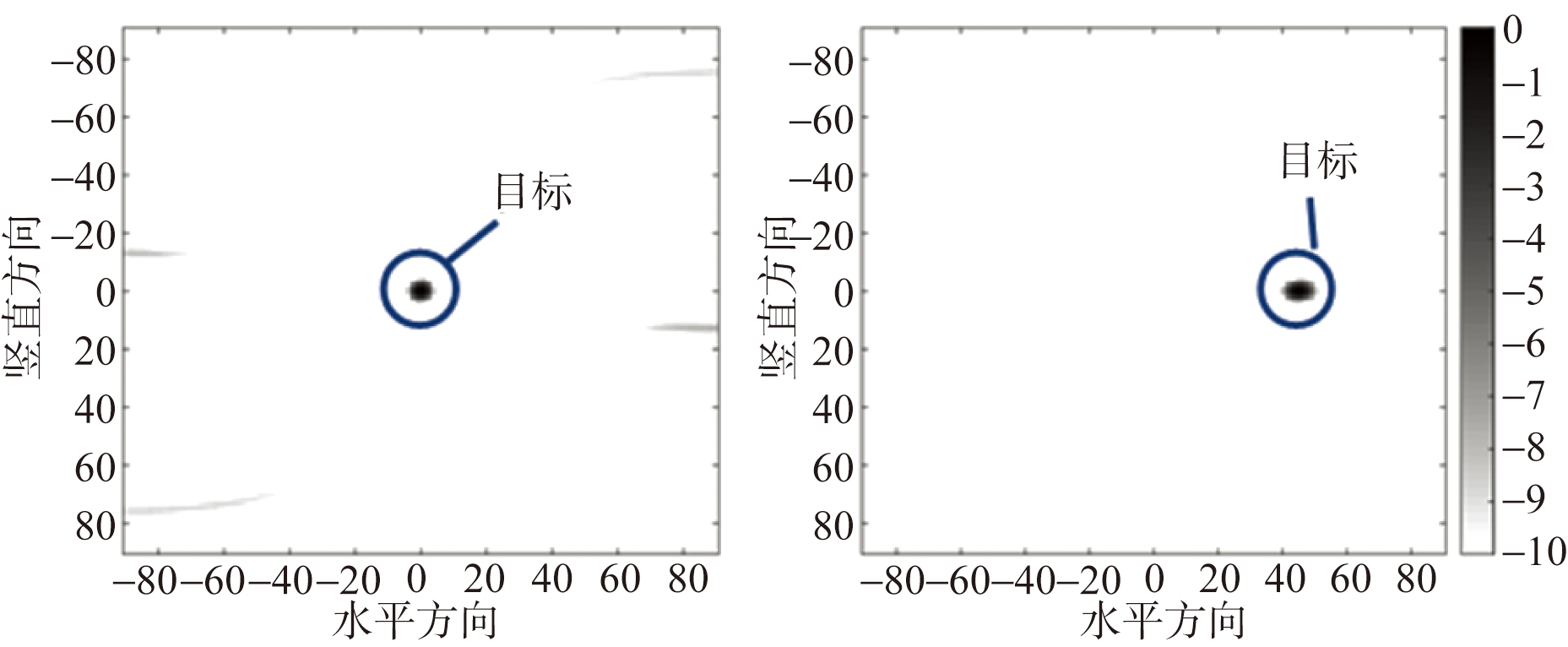
利用上述两阵列分别对距离阵列5 m远处位于成像区域中心及右侧的两仿真目标进行成像的结果展示在图7中。图7(a)为均匀阵列成像结果，图7(b)为优化阵列的成像结果。
(a) 均匀阵列成像结果
(b) 优化阵列成像结果
图7 两阵列成像结果
从成像结果中可以看出，优化阵列比均匀阵列具有更低的栅旁瓣水平。当仿真目标在成像区域中心时，优化阵列的最大栅旁瓣水平比均匀阵列低3.623 dB。而当目标在成像区域右侧时，优化阵列的栅旁瓣比均匀阵列的低了3.45 dB。并且，相比于均匀阵列，优化阵列的成像结果更纯净，图像中的虚假目标也更少。
2.2 不同频率和带宽条件下的性能
本节分析了所设计的阵列在不同频率和不同带宽下的性能。发射信号的中心频率设为fc=2.2 GHz，因此对应的波长为λ=0.136 m。当带宽为300 MHz，孔径长度从0.4 m到1.2 m(3λ到8.8λ)变化时，成像结果的MSLL如图8(a)所示。当孔径长度为0.8 m，频率带宽从8 MHz到1 GHz(0.003 6fc至0.45fc)变化时，成像结果的MSLL如图8(b)所示。从结果可以看出，在大多数情况下，所设计的SNUA可以抑制旁瓣/栅瓣，除了第一个是在相对孔径较低时(如图8(a)左侧所示)，两个阵列都是密度的，所以没有栅瓣，MSLL很低。然而，在这种情况下，低孔径长度会导致低分辨率。
(a) 不同相对孔径宽度情况下最大栅旁瓣
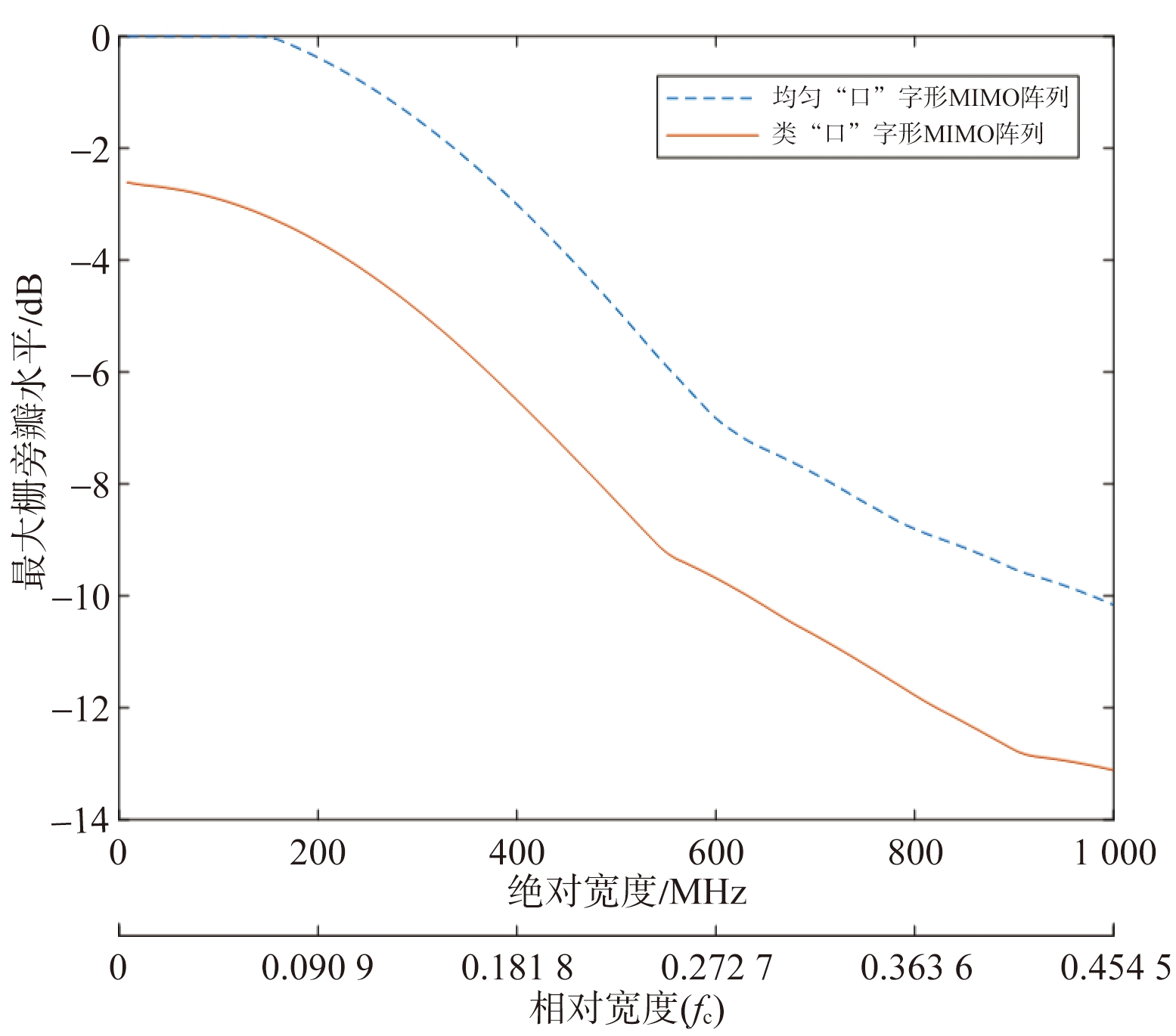
(b) 不同相对带宽下最大栅旁瓣
图8 不同带宽、不同载频情况分析
2.3 观测矩阵分析
从阵列稀疏成像角度进行分析，雷达探测可以利用观测矩阵Ym×1=Hm×nXn×1+nm×1解释。其中向量Xn×1表示待成像区域中的RCS分布，Hm×n是观测矩阵，nm×1为系统噪声，Ym×1为接收信号组成的观测向量。当系统选定一个频点，以及一个收发通道组合，即可执行一次探测，获得一个观测值。因此上式中m等于观测值及虚拟阵元的个数的乘积。n等于待成像区域所划分的网格点总数。观测矩阵Hm×n可以根据电磁传播特性及空间几何关系预先计算。雷达成像实际上是在准确记录雷达回波Ym×1情况下，根据预先计算的Hm×n求解Xn×1得到对场景的成像结果。当Hm×n的行向量具有更低的互相关性时，矩阵求解可以获得更稳健的结果。
将300 MHz宽带雷达波分为5个频点，收发阵元数为10×10个，成像场景为雷达前方距离阵列中心5 m的切平面，成像场景被划分为31×31个网格点。分别计算此场景下优化阵列以及均匀阵列所对应观测矩阵Hm×n的各行向量相关性。其中均匀阵列的各行向量互相关稀疏平均数为0.012 4，而优化阵列则为0.011 9。因此，在此情景下，优化阵列相比于同尺寸均匀阵列能够获得更好的成像效果。
按照
对均匀阵列的各收发单元进行随机移动。改变多组σ，分析观测矩阵各行向量相关系数的平均值，并记录在表1中。
表1 各阵列观测矩阵相关性
阵列平均互相关系数均匀阵列σ=0 0.0124σ=0.010.0123σ=0.020.0122σ=0.030.0123σ=0.040.0129本文设计阵列0.0119
从表中可以看出，尽管对均匀阵列各阵元增加了随机位移，但优化阵列的观测矩阵仍然具有最低的互相关性。其次，随着随机位移方差的增大，均匀阵列观测矩阵的相关性先降低，再升高。弱随机性打破了原有均匀阵列的完全均匀性，降低了阵列重叠，因此，观测矩阵相关性降低，能够获得更好的成像结果。但随着位移方差的继续升高，阵列不再满足基本均匀性，因此观测矩阵相关性显著升高，相对应地成像质量也会受到恶化。
2.4 不同阵列对比
将本节所提方法设计的MIMO阵列与现有方法所设计阵列(如图9所示)进行对比。为便于对比，设置与文献[7]相同的实验环境，即阵列发射载频为6 GHz，相对带宽分别为100%和150%的雷达波。利用本节所提方法设计12发12收MIMO阵列并与基本优化阵列、扩展优化阵列、改进交叉阵列、曲线阵列 [7,16-17]进行对比。本节所设计阵列及上述对比阵列的最大收发天线总数为24，最大孔径均为10λc与文献[7]中一致。对阵列正前方10λc远处点处仿真点目标进行成像。分析并对比各阵列参数及成像结果中最大栅旁瓣水平，记录于表2中。由于所提方法仅依赖各阵元局部特性，对所设计阵列的阵元数量没有强制要求。因此，在收发天线总数(收12+发12=24个)一定的情况下，所设计阵列能够形成最多的虚拟阵元个数，并且所设计阵列为低冗余阵列，具有较好的成像性能。从表2也可以看出，相比于现有优化MIMO阵列，所提阵列能够提供最低的栅旁瓣水平。
图9 4种对比阵列结构[7]
表2 多种阵列参数及栅旁瓣水平
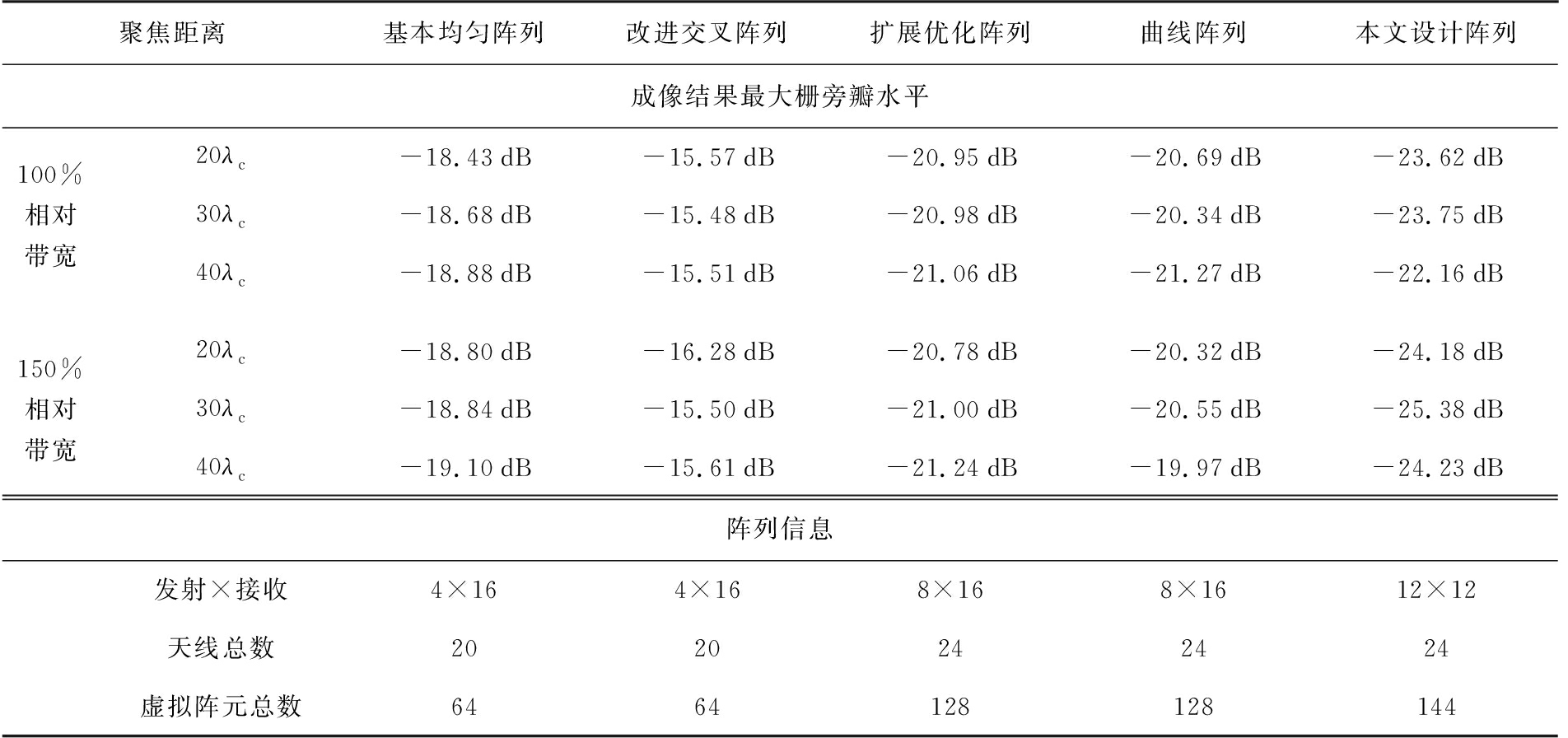
聚焦距离基本均匀阵列改进交叉阵列扩展优化阵列曲线阵列本文设计阵列成像结果最大栅旁瓣水平100%相对带宽20λc-18.43dB-15.57dB-20.95dB-20.69dB-23.62dB30λc-18.68dB-15.48dB-20.98dB-20.34dB-23.75dB40λc-18.88dB-15.51dB-21.06dB-21.27dB-22.16dB150%相对带宽20λc-18.80dB-16.28dB-20.78dB-20.32dB-24.18dB30λc-18.84dB-15.50dB-21.00dB-20.55dB-25.38dB40λc-19.10dB-15.61dB-21.24dB-19.97dB-24.23dB阵列信息发射×接收4×164×168×168×1612×12天线总数2020242424虚拟阵元总数6464128128144
3 实测实验与应用结果
3.1 成像实验
本实验部分制作了一个阵元可以按计划任意移动的MIMO雷达系统。雷达系统发射带宽为1 GHz的S/L波段步进频率连续波(SFCW)信号。这样的UWB雷达系统可用于检测目标并提供目标的3D成像信息。将与仿真部分相同的两个阵列组装起来，分别用于检测同一场景。天线阵列的照片如图10所示，均匀阵列的成像结果如图11所示，所提出的优化阵列的成像结果如图12所示。从图中可以看出，相比于均匀阵列，利用优化阵列对场景进行成像时，图像中栅旁瓣水平受到大约3 dB的抑制，图像纯净度更高，并且分辨率没有受到影响。
(a) 均匀阵列照片 (b) 基本均匀阵列照片
图10 MIMO系统阵列照片
(a) 方位-距离平面成像结果 (b) 方位-高度平面成像结果
图11 均匀阵列成像结果
(a) 方位-距离平面成像结果 (b) 方位-高度平面成像结果
图12 优化阵列成像结果
3.2 成像实验MIMO阵列应用实验
为了对本文所设计的阵列的实际使用性能进行验证，系统参数与3.1节一致，本文设计了人体生命体征监测和人体姿态重构两个功能验证实验。其中生命体征监测算法首先对MIMO雷达三维成像结果进行相干积累，对人体目标进行定位，提取胸腔所在位置的相位信息，进一步分离出呼吸和心跳信号；人体姿态重构算法使用训练好的深度神经网络对MIMO雷达三维成像结果进行姿态重构。两个功能都是基于雷达成像结果进行设计实现的，所以良好的成像结果是雷达系统多域信息感知应用的前提。
本文所设计的验证实验场景如图13所示，探测对象为站立和坐立的人体目标，坐立的人体目标使用接触式呼吸、心跳采集装置为系统性能验证提供对比参考。
图13 系统实测场景
本实验采用多进程的方式同步进行呼吸、心跳信号的提取和人体姿态重构两个任务。对于人体姿态重构信号处理，首先对探测场景进行二维成像，如图14(a)所示，检测得到人体目标位置，然后分别对人体目标进行三维成像，其中坐立人体目标和站立目标的三维成像结果的方位-高度投影图如图14(b)和(c)所示。图14(d)是通过人体姿态重构网络预测得到的姿态重构结果，将此结果与光学参考图像图13相比可知，本文将MIMO雷达三维成像结果转化为人体三维姿态，且姿态重构结果与目标实际姿态基本一致，证明了本文所设计的MIMO阵列提供了丰富且良好的成像结果，为人体姿态重构任务的实现奠定了基础。
图14 MIMO雷达探测成像及人体姿态重构结果
对于人体呼吸、心跳信号提取流程，首先通过对雷达成像结果进行高阶积累实现对多个人体目标的增强成像和定位，增强成像的结果对比如图15所示。然后分别从人体目标的成像结果中提取生命体征信号，截取实验中提取的两个站立和坐立的目标的生命体征信号如图16所示。该生命体征信号是呼吸信号和心跳信号的叠加，其中呼吸信号的幅度较大、频率较低，而心跳信号的幅度较小、频率较高。为了多方位检测系统的生命体征信号提取能力，在实验的过程中，目标2先正常呼吸，然后闭气一段时间，从信号提取结果中可以明显看出10 s后目标2的信号幅度变小，仅包含心跳信号。进一步使用信号分离算法，分别得到两个人体目标的呼吸和心跳信号，我们将目标1提取的呼吸和心跳信号与接触式生命体征监测器得到的呼吸和心跳信号进行对比，对比结果如图17所示，其中图17(a)是本系统提取的呼吸信号与参考信号的对比，图17(b)是心跳信号与参考信号的对比。由对比结果可知，本系统可同时获取多人的生命体征信号，且信号提取和分离结果与参考信号基本一致，证明了MIMO阵列有良好的目标探测性能。
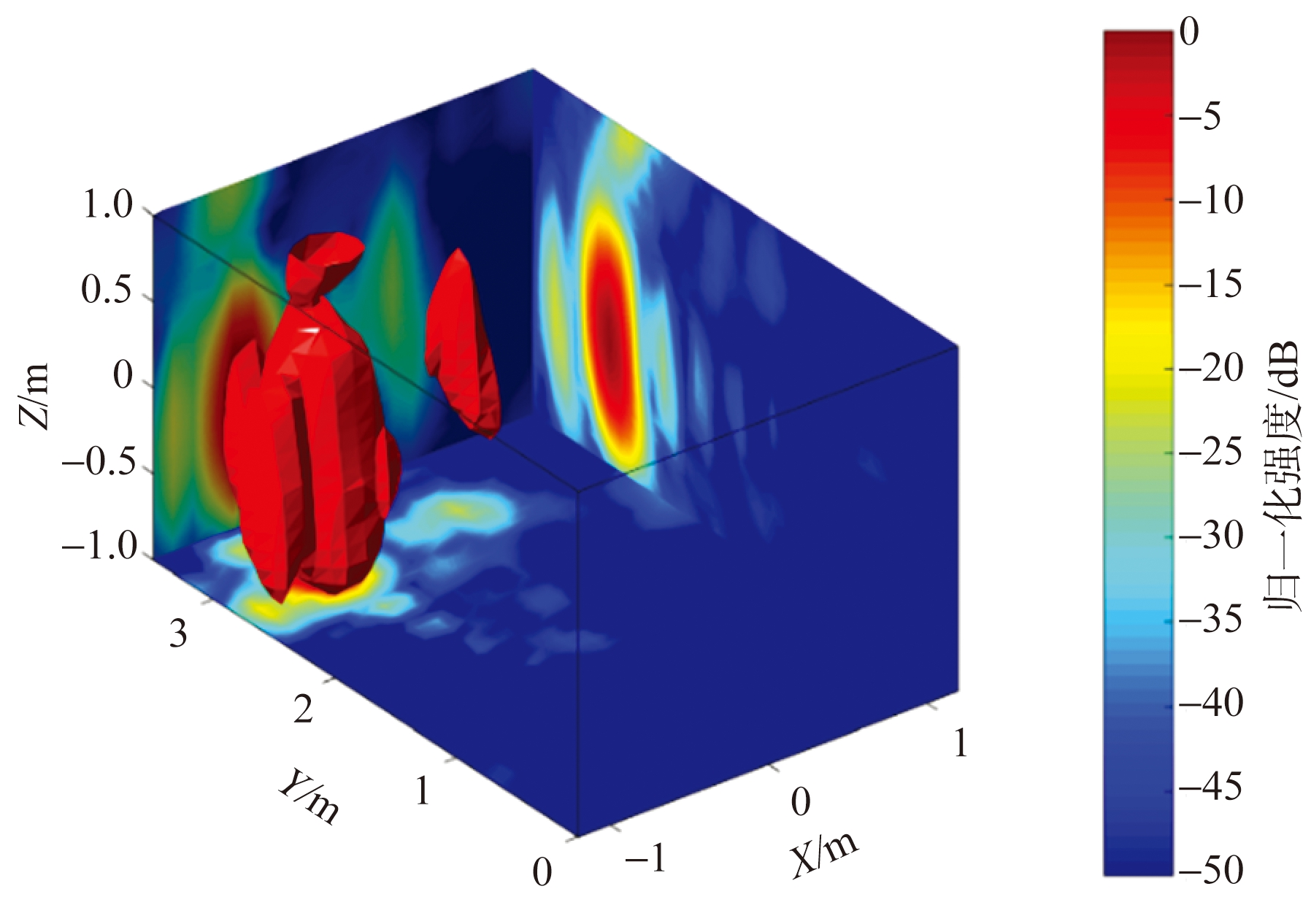
图15 MIMO雷达相干成像结果
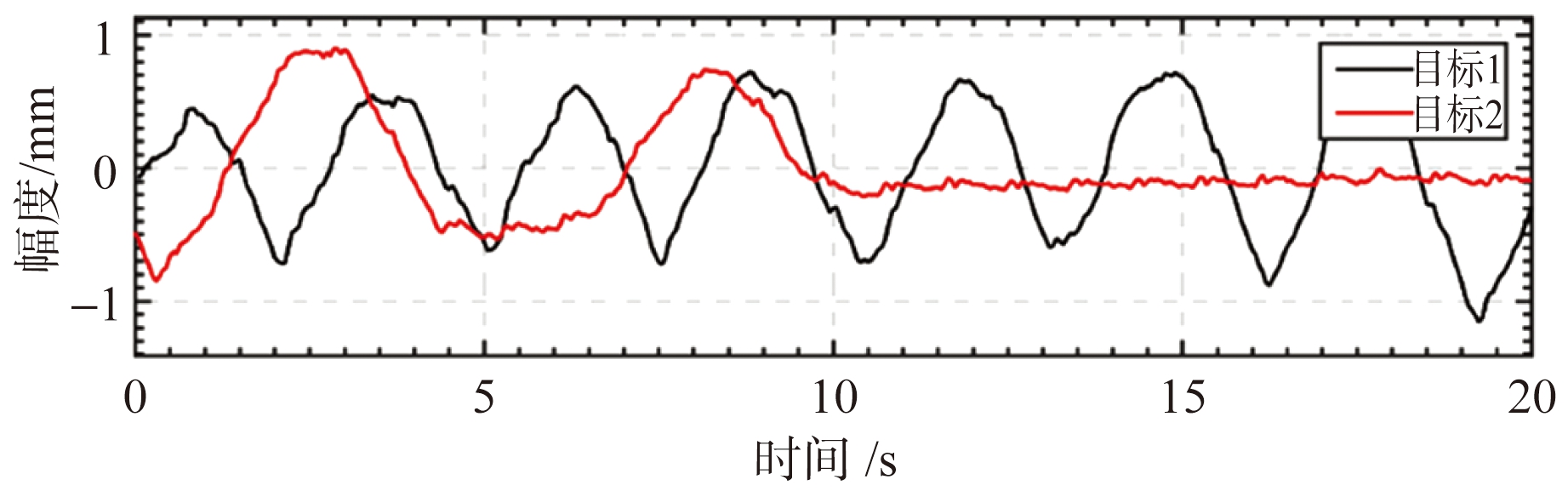
图16 人体目标生命体征信号提取结果
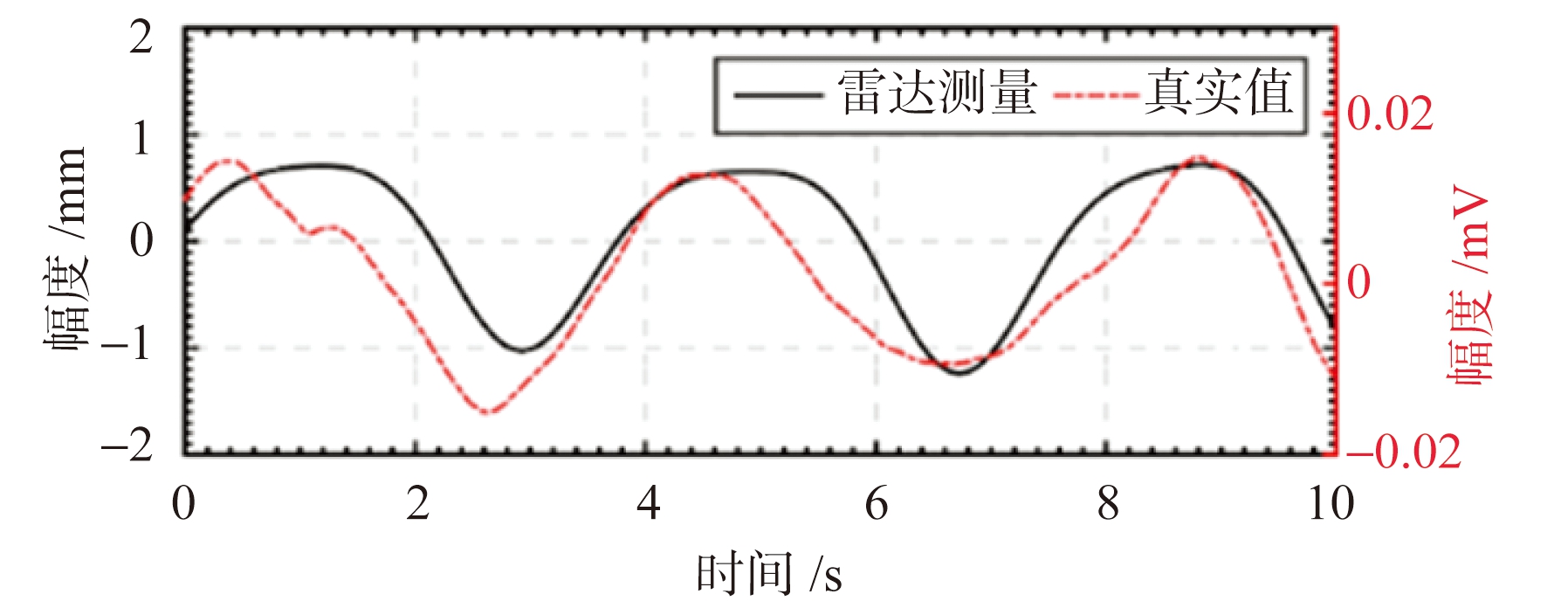
(a) 呼吸信号提取结果与参考对比
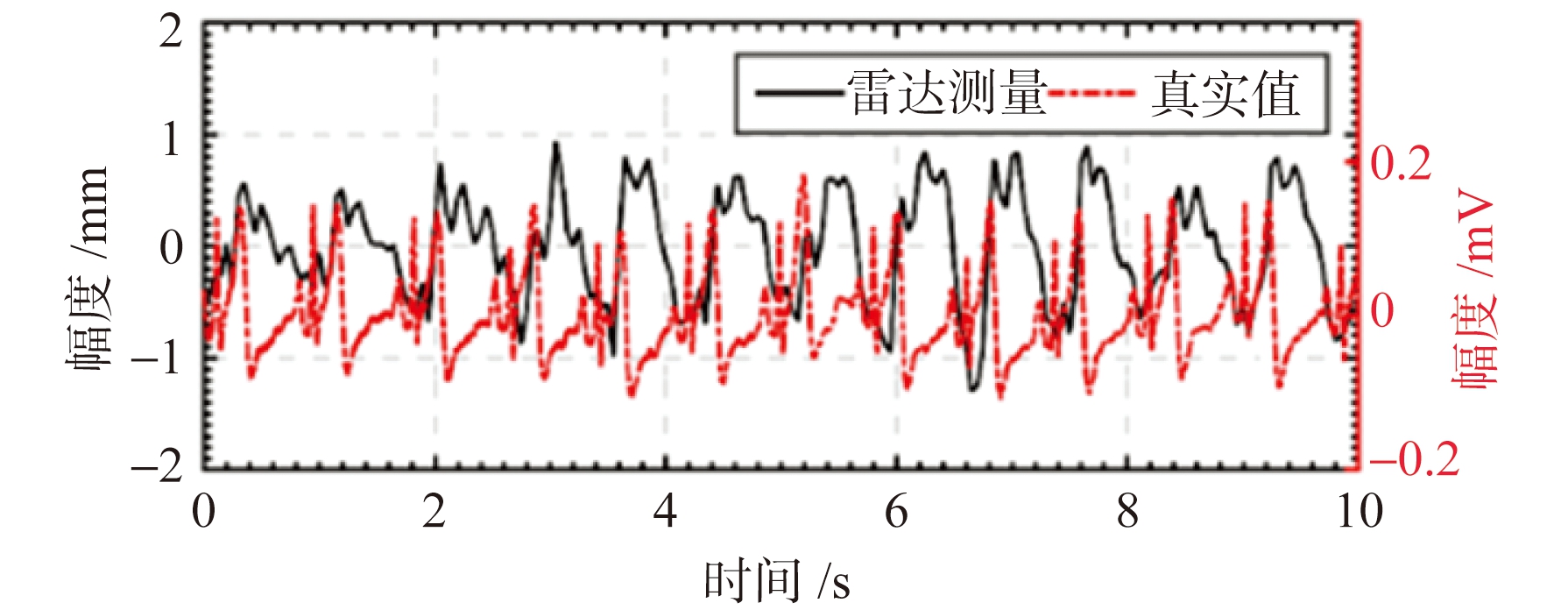
(b) 心跳信号提取结果与参考对比
图17 系统呼吸、心跳信号提取结果与参考信号对比
4 结束语
本文提出了一种基于阵元局部特性的二维MIMO阵列设计方法，根据每个阵元的等效阵元投影局部密度和二维局部密度，结合边界约束和最小间距约束，通过迭代的方式将阵元优化到最优位置。与现有方法相比，本文所提方法有两大优势:第一，该方法对天线单元数没有要求，它可以包含一个重要的阵列设计情况，即发射天线的数目等于接收天线的数目；第二，采用该方法设计的非均匀阵列受旁瓣/栅瓣的影响较小。通过仿真和实测数据实验验证了该方法的优越性，应用实验证明本文所设计的阵列可应用于人体生命体征探测和人体姿态重构等人体目标多域信息感知领域，可广泛应用于灾后救援、医疗监控、隐蔽测谎和偷渡检测等多种军民领域，有效保护人民生命安全、维护社会稳定和谐。
[1] ZHOU J, ZHU R, JIANG G, et al. A Precise Wavenumber Domain Algorithm for Near Range Microwave Imaging by Cross MIMO Array[J]. IEEE Trans on Microwave Theory and Techniques,2019,67(4):1316-1326.
[2] 刘杰,安健飞,周人,等.应用在人体安检中的太赫兹近场MIMO-SAR技术[J]. 光电工程,2020,47(5):90-100.
[3] ZHUGE X D, YAROVOY A G. Study on Two-Dimensional Sparse MIMO UWB Arrays for High Resolution Near-Field Imaging[J]. IEEE Trans on Antennas and Propagation, 2012,60(9):4173-4182.
[4] 刘鹏飞, 陆必应, 孙鑫, 等. 基于子阵划分的二维穿墙MIMO阵列设计[J]. 雷达科学与技术, 2014,12(5):539-545.
[5] ZHUGE X D, YAROVOY A G. A Sparse Aperture MIMO-SAR-Based UWB Imaging System for Concealed Weapon Detection[J]. IEEE Trans on Geoscience and Remote Sensing, 2011,49(1):509-518.
[6] TAN K, WU S Y, WANG Y C, et al. A Novel Two-Dimensional Sparse MIMO Array Topology for UWB Short-Range Imaging[J]. IEEE Antennas and Wireless Propagation Letters, 2016,15:702-705.
[7] TAN K, WU S Y, WANG Y C, et al. On Sparse MIMO Planar Array Topology Optimization for UWB Near-Field High-Resolution Imaging[J]. IEEE Trans on Antennas and Propagation, 2017,65(2):989-994.
[8] BHATTACHARJEE S, KUMAR A, NAJA M. Array Factor Optimization of an Active Planar Phased Array Using Evolutionary Algorithm[J]. International Journal of Antennas, 2016,2(3):1-11.
[9] DONG J, LIU F, GUO Y, et al. MIMO Radar Array Thinning Optimization Exploiting Almost Difference Sets[J]. Optik (Stuttgart), 2016,127(10):4454-4460.
[10] AHMED S S, SCHIESS A, SCHMIDT L P. Near Field mm-Wave Imaging with Multistatic Sparse 2D-Arrays [C]∥2009 European Radar Conference (EuRAD), Rome, Italy:IEEE, 2009:180-183.
[11] CIVI O A, SEKER I, ANADOL E, et al. UWB 3D Near-Field Imaging with a Sparse MIMO Antenna Array for Concealed Weapon Detection [C]∥ Proceeding of SPIE, Radar Sensor Technology XXII, Orlando, Florida:SPIE,2018:1-15.
[12] DAHL C, VOGT M, ROLFES I. Fractal Antenna Arrays for MIMO Radar Applications[J]. International Journal of Microwave and Wireless Technologies, 2017,9(10):2019-2028.
[13] WERNER D H, KUHIRUN W, WERNER P L. Fractile Arrays: a New Class of Tiled Arrays with Fractal Boundaries[J]. IEEE Trans on Antennas and Propagation, 2004,52(8):2008-2018.
[14] NAPIER P J, THOMPSON A R, EKERS R D. The Very Large Array: Design and Performance of a Modern Synthesis Radio Telescope[J]. Proceedings of the IEEE, 1983,71(11):1295-1320.
[15] SCHWARTZ J L, STEINBERG B D. Ultrasparse, Ultrawideband Arrays[J]. IEEE Trans on Ultrasonics, Ferroelectrics, and Frequency Control, 1998,45(2):376-393.
[16] HU X, TONG N, HE X, et al. High Resolution 3D Imaging in MIMO Radar with Sparse Array[J]. Multidimensional Systems and Signal Processing, 2018,29(2):745-759.
[17] YANG B, YAROVOY A, AUBRY P, et al. Experimental Verification of 2D UWB MIMO Antenna Array for Near-Field Imaging Radar[C]∥2009 European Microwave Conference , Rome, Italy:IEEE, 2009:97-100.
