0 引 言
单脉冲雷达仅通过一个脉冲回波即可获取测量的距离和角度，具有较强的抗干扰能力，被广泛应用于目标跟踪、导弹末端制导等军事领域。为了提高重要军事目标的战场生存能力，对单脉冲雷达的干扰是电子战领域的研究热点。
对单脉冲雷达的干扰受到了国内外学者的广泛关注，交叉眼干扰是对抗单脉冲雷达最有效的干扰技术手段之一。交叉眼干扰技术由闪烁干扰[1]发展而来，通过两路干扰信号产生角闪烁效应，使单脉冲雷达指向偏离目标，来对单脉冲雷达实施角度欺骗干扰。文献[2]通过对单脉冲雷达和差通道的结果进行推导，来对两点源反向交叉眼干扰进行了全面的数学分析，指出反向天线结构能够克服交叉眼干扰苛刻的参数容限，使得交叉眼干扰在实际工程中得以实现。文献[3]对于反向交叉眼干扰和非反向交叉眼干扰进行仿真分析，对两种结构的干扰效果进行比较。文献[4]在考虑目标回波的情况下对两点源反向交叉眼干扰进行建模，分析了目标回波对角度欺骗干扰效果的影响。文献[5]在文献[4]的基础上建立了单脉冲雷达接收机仿真模型，研究干扰参数的变化对角度欺骗效果的影响。文献[6]通过杨氏双缝干涉实验类比分析了交叉眼干扰中两个相干干扰信号的干涉条纹对雷达测角处理的和差信号的影响，从新的角度分析了交叉眼干扰的原理和影响因素。为了进一步解决参数容限苛刻和干信比要求高等限制因素，许多学者进行了采用天线阵列提高交叉眼干扰效果的研究。文献[7]首次提出了多源反向交叉眼干扰的概念，通过增加系统自由度灵活控制相位波前。文献[8]对基于线性天线阵和圆形天线阵的多点源反向交叉眼干扰进行数学建模分析，得出多点源反向交叉眼能造成更大的测角误差，同时具有更优的参数容限和干信比。文献[9]提出了正交多点源反向交叉眼干扰，在干扰平台旋转、抖动或者被不同方向上的单脉冲雷达扫描时仍能保持干扰效果的稳定性。文献[10]提出了矩形阵反向交叉眼干扰，对矩形阵不同布局方式进行研究。文献[11]对多环路反向交叉眼干扰进行分析，研究了干扰环路之间的路径差对干扰性能的影响。文献[12]运用波前分析法对多环路交叉眼干扰最优参数进行研究。文献[13]通过多元矢量辐射源建模来分析交叉眼干扰，推导了相干干扰源的空间等效散射点。多点源反向交叉眼干扰和多环路反向交叉眼干扰的本质都是通过增加系统自由度提高干扰性能，区别在于多个干扰环路的相位中心的位置是否相同[14]。但是以上研究均未考虑平台运动带来的不同干扰环路之间的多普勒频率差对交叉眼干扰性能的影响。
本文将比相单脉冲雷达作为干扰对象，基于单脉冲测角原理对多环路反向交叉眼和差通道回波进行分析，对不同干扰环路之间的多普勒频率差进行了严格的数学推导，仿真分析了多普勒频率差对多环路反向交叉眼干扰效果的影响，研究了对多普勒频率差进行补偿的敏感度。研究结果可以为设计多环路反向交叉眼干扰系统设计提供理论参考。
1 多环路反向交叉眼干扰
多环路反向交叉眼干扰如图1所示，左侧的两个雷达天线单元构成雷达系统，雷达孔径长度为dp，多环路反向交叉眼干扰系统由偶数个天线阵元组成，天线阵元2n-1和天线阵元2n组成干扰环路n，干扰单元之间的距离为dcn。雷达中心点与干扰系统几何中心点的连线为水平基线，雷达中心点到干扰系统几何中心点的距离为r。雷达中心点到干扰环路n中心点的连线与雷达中心点到该环路两个干扰单元之一的连线的夹角为半张角θen，雷达的视轴方向与雷达中心点到干扰环路n中心点连线的夹角为雷达转角θrn，干扰系统的视轴方向与雷达中心点到干扰环路n中心点连线的夹角为干扰机转角θcn。
图1 多环路反向交叉眼干扰示意图
由几何关系可知，雷达视轴与干扰环路n的干扰单元的夹角为θrn±θen，则比相单脉冲雷达的和通道与差通道的归一化增益分别为
(1)
(2)
式中，Pr(θrn±θen)为雷达天线波束在θrn±θen方向上的增益，
为相位常数。
通过和差化积公式进行变换可得
S2n-1,2n=cos(krn±kcn)Pr(θrn±θen)
(3)
D2n-1,2n=jsin(krn±kcn)Pr(θrn±θen)
(4)
其中krn和kcn为
(5)
(6)
假设每个干扰环路中的两个天线阵元间的幅度比为a，相位差为φ，则干扰环路n在单脉冲雷达和通道与差通道回波分别为
SJn=S2n-1Pc(θcn+θen)S2nPc(θcn-θen)+
aejφS2n-1Pc(θcn+θen)S2nPc(θcn-θen)
(7)
DJn=S2n-1Pc(θcn+θen)D2nPc(θcn-θen)+
aejφS2n-1Pc(θcn+θen)D2nPc(θcn-θen)
(8)
式中，Pc(θcn±θen) 为干扰机天线波束在θcn±θen方向上的增益。
在没有其他误差干扰的情况下，则单脉冲雷达总的和通道与差通道回波分别为
SJ=
[cos(2krn)+cos(2kcn)]
(9)
DJ=
(1-aejφ)sin(2kcn)]
(10)
式中，
Pn=Pr(θrn-θen)Pc(θcn-θen)·
Pr(θrn+θen)Pc(θcn+θen)
(11)
根据单脉冲雷达测角原理，用和通道回波对差通道回波进行归一化处理，结果的虚部即为单脉冲比：
(12)
由于多环路交叉眼干扰机位于单脉冲雷达天线的辐射远场，因此dcn≪r，干扰天线的半张角θen的值很小，θcn≈θc，θrn≈θr，
(13)
(14)
(15)
MJ≈
+
(16)
则交叉眼增益为
(17)
而单脉冲比又可表示为
(18)
则单脉冲雷达指示角为
θi=
(19)
2 多环路反向交叉眼干扰下多普勒频率差分析
2.1 多普勒频率差的数学推导
在干扰平台运动时，任意两个天线单元的径向速度的不同会引入多普勒频率差，对于两点源反向交叉眼干扰，通过采用反向天线结构，使得引入两路干扰信号中的多普勒频率差相同，因此不会对两点源反向交叉眼干扰产生影响。但对于多环路反向交叉眼干扰，干扰环路分布在对称中心的两侧，不同干扰环路间的多普勒频率差没有被补偿，因此平台运动会在不同环路间引入多普勒频率差。不同干扰环路间的多普勒频率差可能会导致交叉眼干扰被雷达识别，也会在干扰环路间引入相位差，使得交叉眼干扰效果被削弱，甚至使干扰机成为信标机。
以最基本的四阵元两环路反向交叉眼干扰为例进行分析，图2为任一干扰天线单元n运动示意图，dn为干扰天线n到两干扰环路对称中心的距离，干扰系统的视轴方向与水平基线的夹角为干扰机转角θc，雷达中心点到干扰天线单元n的连线到水平基线的夹角为张角θn，干扰天线单元随干扰机以速度v运动，则干扰天线单元n相对于雷达的径向速度为
(20)
则多普勒频率为
(21)
式中，正负号分别指代远离和靠近单脉冲雷达的干扰天线单元，λ为波长，由雷达频率决定。
图2 干扰天线单元运动示意图
将多普勒频率fjn在θn=0处进行泰勒级数展开：
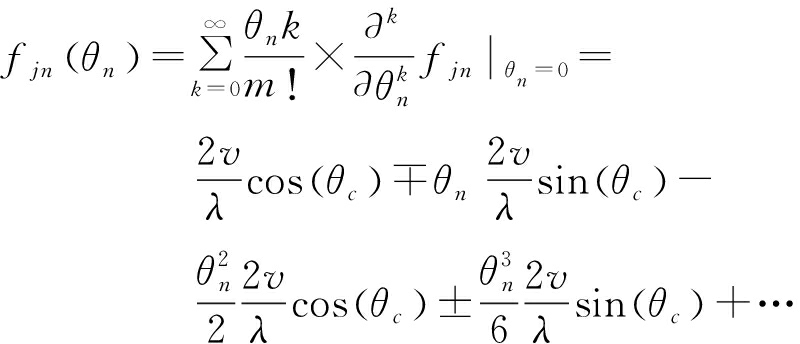
(22)
泰勒级数展开的最大误差取决于忽略的高阶项，而忽略高阶项所产生的最大误差为
当v=300 m/s，dn=10 m，r=1 km，θc=30°，且单脉冲雷达工作在9 GHz时，产生的最大误差小于0.000 4 Hz，在实际应用场景下误差可以忽略不计。因此干扰天线n的多普勒频率为
(23)
因此,4个天线的干扰信号的多普勒频率分别为
(24)
(25)
(26)
(27)
由几何关系可以得出，天线阵元n相对于雷达视线的半张角θn为
(28)
由于多环路交叉眼干扰机位于单脉冲雷达天线的辐射远场，因此rn≫dn，θn的值非常小，tan(θn)可以近似为θn，且
(29)
两个干扰环路相对几何中心对称分布，因此θ1=θ4，θ2=θ3，干扰环路1与干扰环路2之间的多普勒频率差为
fΔ=f1+f2-f3-f4≈
(30)
则由多普勒频率差引入的干扰环路相位差为
(31)
通过对干扰环路相位差进行补偿，可以避免干扰效果的降低。
2.2 多普勒频率差补偿敏感度分析
多普勒频率差是由于干扰天线单元相对于雷达的径向速度不同所产生的，受到速度、干扰机转角和干扰距离等多个因素的影响，对多普勒频率差的补偿，需要对载机平台速度v、干扰机转角θc和干扰距离r进行测量，因此载机平台速度v、干扰机转角θc和干扰距离r的测量精度会影响到多普勒频率差的计算精度，进而影响其补偿精度。
将多普勒频率差公式对载机平台速度v求偏导数:
(32)
偏导数绝对值的大小代表多普勒频率差对于载机平台速度v测量误差的敏感程度，在一定的测速误差下，偏导数绝对值越大，则多普勒频率差的计算值与实际值的误差越大。
当其他参数一定时，
为常数，因此补偿误差随着测速误差线性变化，由导数的定义可得，补偿误差Δδ与测速误差Δv的关系为
(33)
将多普勒频率差公式对干扰机转角θc求偏导数:
(34)
偏导数绝对值的大小代表多普勒频率差对于干扰机转角θc测量误差的敏感程度，在一定的测角误差下，偏导数绝对值越大，则多普勒频率差的计算值与实际值的误差越大。
在
时，
因此在测角误差一定的情况下，干扰机转角θc越靠近
由测角误差引起的多普勒频率差的补偿误差也越小，反之则越大。由导数的定义可得，补偿误差Δδ与测角误差Δθc的关系为
(35)
将多普勒频率差公式对干扰距离r求偏导数:
(36)
偏导数的绝对值大小代表多普勒频率差对于干扰机距离r测量误差的敏感程度，在一定的测距误差下，偏导数绝对值越大，则多普勒频率差的计算值与实际值的误差越大。
当θc不为0，则
是关于干扰距离r的单调递减函数，且始终大于0，因此在测距误差一定的情况下，干扰距离r越近，由测距误差引起的多普勒频率差的补偿误差就越大，反之则越小。由导数的定义可得，补偿误差Δδ与测距误差Δr的关系为
(37)
3 仿真分析
3.1 多普勒频率差仿真分析
考虑最基本的分布式两环路四点源交叉眼干扰的情况，两个干扰环路中心距离为10 m，天线阵列长度为15 m,干扰机天线干扰环路基线比为1，载机速度为300 m/s，雷达频段为X波段，频点为9 GHz，雷达孔径为2.54λ，λ为波长，天线波束宽度为10°，两个干扰环路的干扰单元间幅度增益都为-0.5 dB，干扰单元间相位差都为179°。以此仿真基本参数来分析不同参数对干扰环路间的多普勒频率差和其补偿精度的影响。
图3所示的是多普勒频率差随着干扰距离的变化曲线，曲线是在设定不同的干扰机转角后，根据公式(30)计算得到。从图3可以得出，当干扰机转角不同时，不同干扰环路间的多普勒频率差不同。当干扰机转角为45°，干扰环路间的多普勒频率差最大，而当干扰机转角为0°或90°，即干扰机天线完全对准单脉冲雷达或者单脉冲雷达位于天线阵列的端射方向时，干扰环路间不存在多普勒频率差。
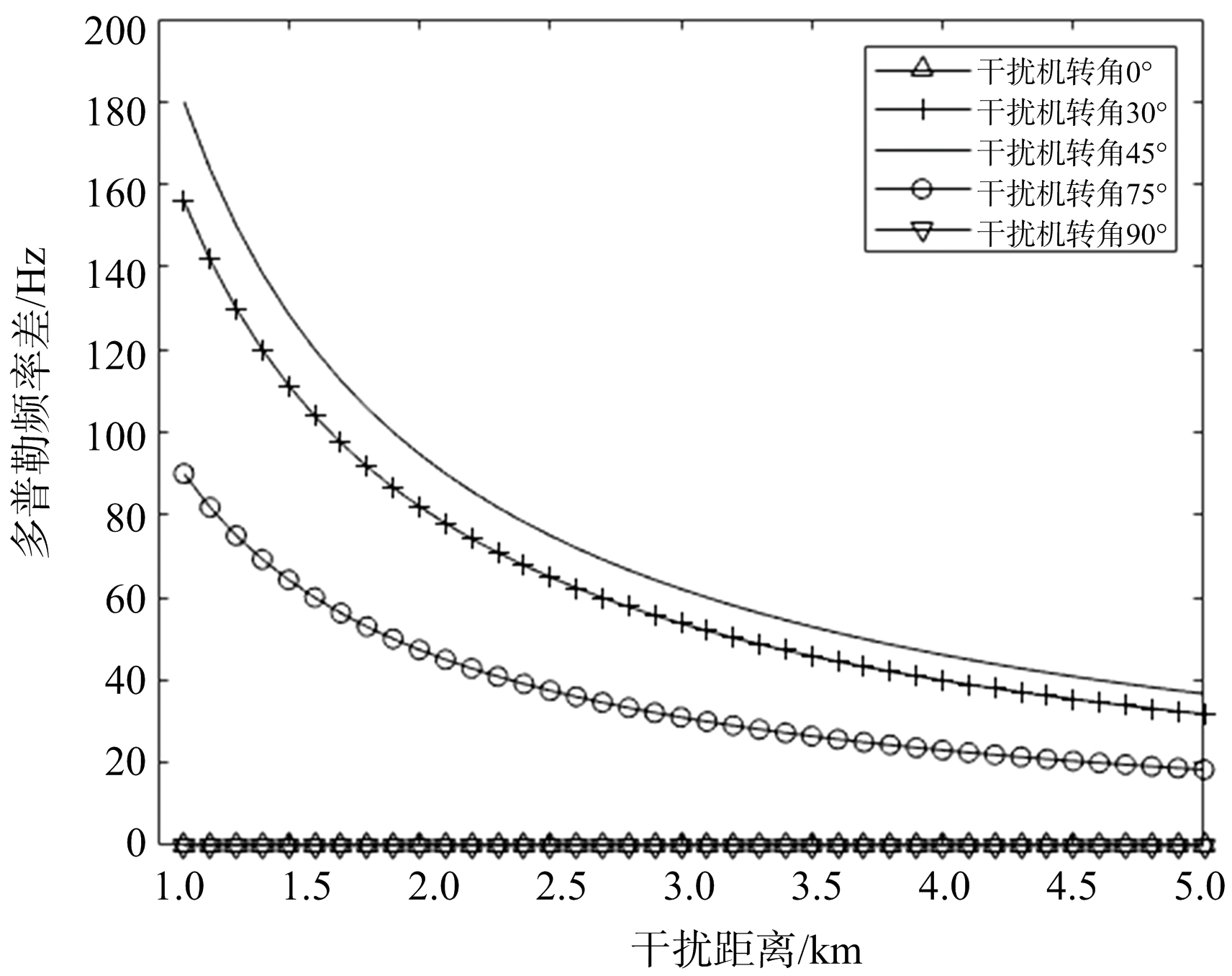
图3 干扰机转角对环路间多普勒频率差的影响
从第2节的分析中可以得出，干扰机转角θc会影响天线阵列半张角θe的值，进而影响干扰环路n的半张角θn和kcn的值，最终对角度偏差θi的结果产生影响，因此角度偏差θi是关于干扰机转角θc的函数。对角度偏差θi关于干扰机转角θc求偏导数:
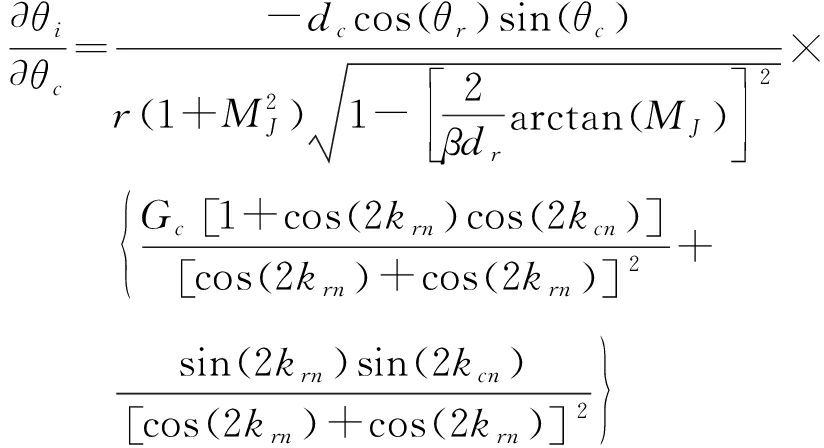
(38)
令偏导数等于零，得出极值点为θc=0，当
角度偏差θi是关于干扰机转角θc的单调增函数，而当
角度偏差θi是关于干扰机转角θc的单调减函数。当干扰机转角θc为0，即干扰机天线对准单脉冲雷达，角度偏差θi取得最大值，干扰机转角θc越大，所能产生的角度偏差θi就越小，干扰机转角的存在会降低交叉眼干扰的效果。极限情况下，当单脉冲雷达位于天线阵列端部时，交叉眼干扰所能造成的测角误差为0，此时交叉眼干扰失效。
图4是干扰机转角
时，角度偏差θi关于雷达指向角θr的全部曲线，根据公式(19)计算得到。通道回波在第一波束零处θr= ±11.35°会发生符号改变，在雷达3 dB波束宽度内，即θr∈[-5°,5°]，当角度偏差θi等于雷达指向角θr时，单脉冲雷达跟踪并锁定目标，当存在交叉眼干扰时，θi>θr，当角度偏差θi=0时，雷达指向角θr即为交叉眼干扰所产生的角度误差。
图4 固定干扰机转角下角度偏差关于雷达指向角的变化情况
图5为设定不同干扰机转角下，角度偏差随着雷达指向角的变化曲线，三条曲线分别为干扰机转角0°,45°和90°时的情况。从图5可以得出，当干扰机转角
此时单脉冲雷达位于干扰阵列的端射方向，雷达指向角θr始终等于角度偏差θi，交叉眼干扰失效，雷达始终跟踪并锁定目标，当干扰机转角θc=0，此时干扰机天线完全对准单脉冲雷达，角度偏差θi始终大于雷达指向角θr，不存在零点，使得单脉冲雷达失锁，交叉眼干扰取得较好的干扰效果。
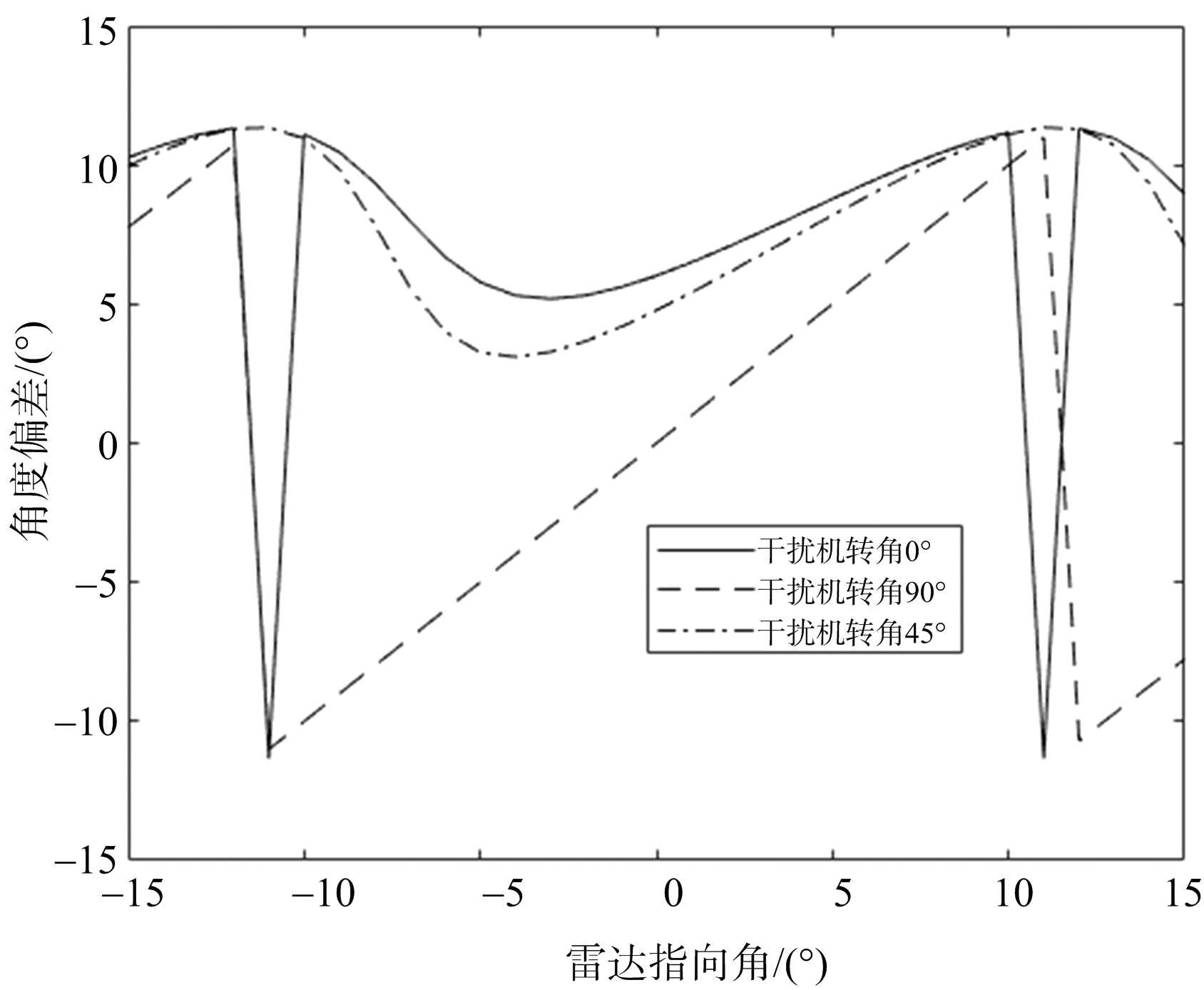
图5 特定干扰机转角下角度偏差关于雷达指向角的取值
为获得良好的干扰性能，干扰机天线应尽可能对准单脉冲雷达，在取得良好干扰效果的同时也能减小多普勒频率差。但在实际情况下，干扰机无法实时灵活地调整干扰机转角，以将干扰机天线始终对准单脉冲雷达，因此多普勒频率差是不可避免的，需要进行补偿。
3.2 多普勒频率差补偿敏感度仿真分析
在仿真基本参数设定下，假设载机平台速度测量误差为0.1 m/s，由于载机平台的径向速度由载机平台速度和干扰机转角共同决定，因此根据公式(32)和公式(33)计算得出，在固定速度300 m/s下，多普勒频率补偿误差与干扰机转角的关系如图6所示。从图6可以得出，当测速误差在0.1 m/s以内，多普勒频率差最大为20 Hz，在干扰机转角为45°时取得，根据上一节的分析可知，此时两环路的干扰单元相对于雷达的径向速度差最大。
图6 存在测速误差时的补偿误差变化曲线
在仿真基本参数设定下，假设干扰机转角测量误差为0.1°，根据公式(34)和公式(35)计算得出多普勒频率补偿误差与干扰机转角的关系，如图7所示。从图7可以得出，当测角误差在0.1°以内，多普勒频率补偿误差最大约为7 Hz，在干扰机转角为0°或90°取得，而当干扰机转角为45°时，多普勒频率补偿误差不存在。对比图7与图6，补偿误差的变化曲线是完全相反的，但相比较于测速误差带来的补偿误差，测角误差带来的补偿误差较小，因此干扰机天线仍应遵循尽量对准单脉冲雷达这一原则。
图7 存在测角误差时的补偿误差变化曲线
在仿真基本参数设定下，假设干扰距离测量误差为20 m，根据公式(36)和公式(37)计算得出多普勒频率补偿误差与干扰距离的关系，如图8所示。从图8可以得出，当测量误差在20 m之内，干扰距离为1 000 m时，多环路反向交叉眼干扰的多普勒频率补偿误差约为7 Hz。而在干扰距离增大到一定数值后，补偿误差对于干扰距离的增大变得较为不敏感，干扰环路差的补偿误差的下降速度越来越缓慢。
图8 存在测距误差时的补偿误差变化曲线
当交叉眼干扰机针对工作在高频段的单脉冲雷达进行干扰时，反向交叉眼干扰的参数容限更加苛刻，对于幅度和相位精确控制的要求更加高，因此需要对多普勒频率差进行补偿。从本小节的仿真分析中可以得出，当载机平台速度、干扰机转角和干扰距离的测量误差分别为0.1 m/s，0.1°和20 m以内时，多普勒频率差的补偿误差足够小，能够满足对多普勒频率差的补偿要求，因此对多环路反向交叉眼干扰的多普勒频率差补偿是可行的。
3.3 多普勒频率差对参数容限的影响分析
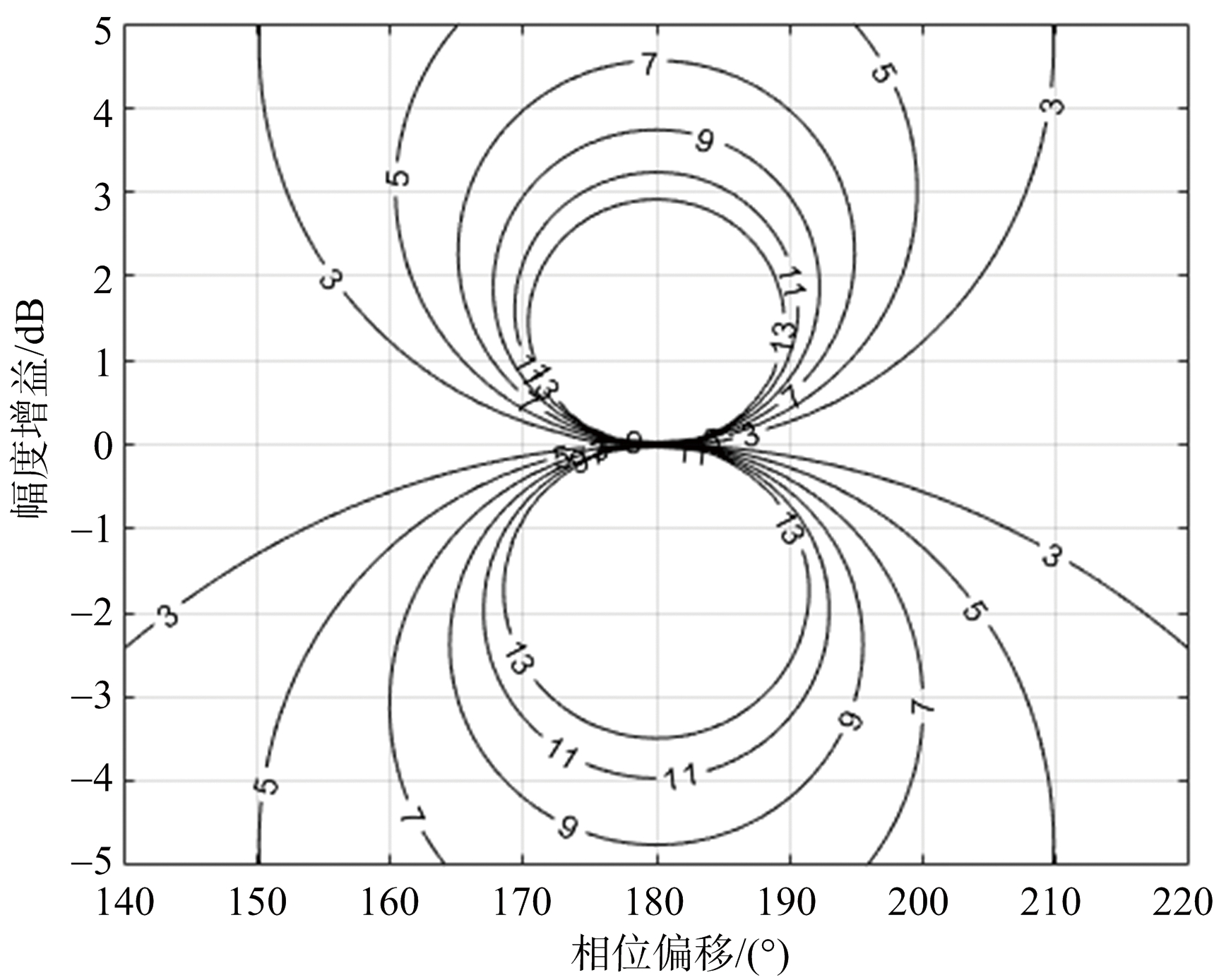
为了分析由多普勒频率差导致的干扰环路相位差对多环路反向交叉眼干扰的系统参数容限的影响，对不同干扰环路相位差下的参数容限进行计算，绘制等高线图进行分析。根据公式(17)计算得到交叉眼增益等高线图，如图9所示，分别仿真了干扰环路相位差为0°，75°和150°三种情况，相位差为0°即为不存在多普勒频率差或者多普勒频率差被精确补偿的情况。
(a) 干扰环路相位差为0°
(b) 干扰环路相位差为75°
(c) 干扰环路相位差为150°
图9 不同干扰环路相位差对参数容限影响
随着干扰环路相位差的增大，等高线范围逐渐减小，参数容限要求变得苛刻。干扰环路相位差的存在还使得等高线发生倾斜，说明它会导致在干扰回路幅度增益接近0 dB时多环路反向交叉眼的不同干扰环路无法稳定在同一侧产生假目标，这会使不同的干扰环路相互抵消，严重影响干扰效果。
4 结束语
本文在分析多环路反向交叉眼干扰的基础上，研究了由于干扰平台运动导致不同干扰环路之间存在多普勒频率差的问题。运用泰勒级数展开推导出多环路反向交叉眼干扰下多普勒频率差的表达式，得出了多普勒频率差与干扰机转角的关系，给出干扰环路相位差的补偿公式。通过典型参数的仿真实验对不同干扰机转角下的多普勒频率差进行分析，研究了补偿多普勒频率差对不同干扰参数的敏感度和多普勒频率差对参数容限的影响。分析仿真实验结果可以得出，多普勒频率差在干扰机转角为45°时达到最大，干扰机天线应尽可能对准单脉冲雷达以减少引入多普勒频率差，并且在实际情况下多普勒频率差不可避免，需要进行补偿。 对不同环路之间的多普勒频率差补偿得越精确，干扰环路相位差越小，参数容限就越宽松，多环路反向交叉眼的干扰效果就越稳定。
[1] SHIZUME P K. Angular Deception Countermeasure System: US,4117484[P]. 1978-09-26.
[2] DU PLESSIS W P. A Comprehensive Investigation of Retrodirective Cross-Eye Jamming[D]. Pretoria: University of Pretoria,2010.
[3] 王建路,戴幻尧,张扬,等.反向交叉眼干扰特性建模与仿真[J]. 雷达科学与技术,2016,14(5):471-477.
WANG Jianlu,DAI Huanyao,ZHANG Yang,et al. Analysis of Cross-Eye Jamming Characteristic with Reverse Structure[J].Radar Science and Technology,2016,14(5):471-477.(in Chinese)
[4] 周亮,孟进,吴灏,等.考虑目标回波的两点源反向交叉眼干扰建模[J].电子与信息学报,2019,41(4):816-821.
[5] 周亮,孟进,吴灏,等.反向交叉眼对单脉冲雷达干扰效果分析及仿真验证[J].航空学报,2019,40(8):156-165.
[6] 石荣,杜宇.从杨氏双缝干涉实验解释交叉眼干扰原理[J].雷达科学与技术,2019,17(4):455-460.
SHI Rong，DU Yu. Explanation of the Principle of Cross-Eye Jamming from Young’s Two-Slit Interference Experiment[J]. Radar Science and Technology,2019,17(4):455-460.(in Chinese)
[7] HARWOOD N M, DAWBER W N, KING D J, et al. Multiple-Element Crosseye[J].IET Radar, Sonar & Navigation,2007,1(1):67-73.
[8] 刘天鹏.多源反向交叉眼干扰技术研究[D].长沙:国防科学技术大学,2016.
[9] 刘松杨,董春曦,董阳阳,等.旋转的正交多点源反向交叉眼干扰分析[J].电子与信息学报,2016,38(6):1424-1430.
[10] 刘伟,孟进,周亮,等.矩形阵反向交叉眼干扰建模[J].系统工程与电子技术,2019,41(11):2453-2459.
[11] DU PLESSIS W P. Path-Length Effects in Multiloop Retrodirective Cross-Eye Jamming[J]. IEEE Antennas and Wireless Propagation Letters,2015,15:626-629.
[12] 王国伟，王红卫，张曦．多环路交叉眼干扰的波前相位畸变研究[J].信号处理，2018,34(10):1188-1196.
[13] 余忠卿.无人机平台多源矢量辐射源建模及空间电磁场分析[D].成都:电子科技大学,2019.
[14] 刘天鹏,魏玺章,刘振,等.交叉眼干扰研究综述[J].雷达学报,2019,8(1):140-150.
