0 引 言
超宽带穿墙雷达三维成像不仅能提供距离向和方位向上的目标位置信息，还能提供俯仰等更多维度的信息，满足了建筑内部的结构特征、人体目标的姿势等信息的需求。其现有的三维成像有后向投影算法[1]和衍射层析(Diffraction Tomographic，DT)算法[2-3]等。但是这些成像算法不仅需要进行大量的数据采样、存储和处理，而且所成像还存在主瓣较宽、旁瓣较高的问题。
为此，国内外学者已将压缩感知(Compressive Sensing，CS)理论应用于穿墙雷达成像(Through- the-Wall Radar Imaging，TWRI)中，不仅减少了数据的采集时间、采集量和存储代价，还可以获得高分辨成像。文献[4]首次将CS应用于穿墙场景中，利用稀疏随机矩阵的采样方法可在随机的采样天线中随机选择频点以减少数据采集量。在此基础上，文献[5]通过正交匹配追踪(OMP)算法对墙后目标成像，提高了成像质量和减少了旁瓣干扰。由于OMP重构算法易受到信号信噪比影响导致成像质量较差，文献[6]在贝叶斯算法的基础上通过噪声先验信息，同时考虑扩展目标像素间的结构信息，对目标进行高分辨成像。考虑到贝叶斯算法复杂度高，计算量大，文献[7]在低秩稀疏约束下提出了一种基于奇异值和l1范数的快速软阈值迭代(FISTA)的凸优化算法重构，该算法具有计算量小、收敛速度快的特点。但是，这种稀疏重构方法的字典矩阵是通过目标到成像网格的时延构建的，对于三维成像，字典矩阵所需内存太大，难以提供硬件需求；而且它往往需要预先确定阀值参数，而恰当地选择该参数对重建图像质量具有非常重要的影响。
目前，深度神经网络(Deep Neural Networks， DNNs)已经在图像去噪、图像复原等领域展现出优势。而模型驱动[8-9]作为DNNs中特殊的一类，将凸优化算法中的单次迭代过程映射为网络结构的每一层，进而利用少量的样本即可学习出最优参数。此外，因网络结构的显示表达，所以也保证了高质量的图像重建。鉴于此，本文基于这种模型驱动的思路，通过衍射层析成像算法构造快速傅里叶变换算子，避免了字典矩阵的构建，减少了所需内存；通过修正近似消息传递(Approximate Message Passing，AMP)算法进行重构，并将其迭代过程映射成多层神经网络，最后通过数据驱动学习近似消息传递算法中可调参数，实现高分辨、高效率的三维图像的重建。
1 信号模型
如图1所示，使用收发天线共置的雷达系统平行于前墙的方向对墙后目标进行探测。系统发射步进频率信号，扫频范围从f0开始，步进频率为Δf，频率点数为K；采用M行N列二维收发共置天线阵列，天线空间坐标向量记为(xR,yR,zR)。空间区域被分成3个区域，区域0和区域2为自由空间，区域1为墙体，自由空间的介电常数和磁导率记为ε0和μ0，墙体介电常数和磁导率记为εb和μb，所述隐蔽目标位于区域2中；设x方向为方位向，y方向为高度向，z方向为距离向，墙体的厚度为d。
图1 穿墙雷达探测场景
根据文献[2]和[3]，图1所示场景的衍射层析三维成像表达式为
式中，O(x,y,z)代表目标像函数,k=2πf/c代表自由空间波数(这里的c为光速)，kx代表方位向波数，ky代表高度向波数，kz代表距离向波数， ξ0=120π代表自由空间中的波阻抗,F(kx,ky,k)代表并矢函数，即
F(kx,ky,k)=
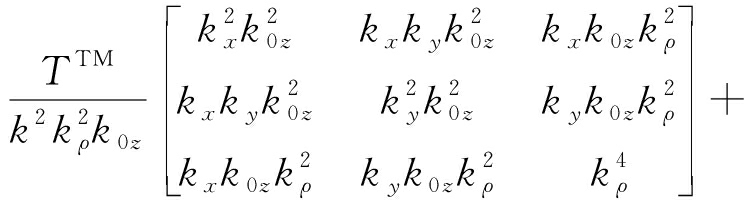
式中，
这里TTE,TM中的RTE=
和RTE中的
其中的
表示墙体介质的波数。此外，式(1)中的
为
exp(-jkxxR-jkyyR)dxRdyR
(2)
式中的E(xR,yR,k)代表全采样回波散射数据。可以看出，式(2)的右边部分实际上是一个二维空域傅里叶变换，可用算子F2D(·)表示，即
ky,k)=F2D[E(xR,yR,k)]。接下来，令
J(kx,ky,k,z)=
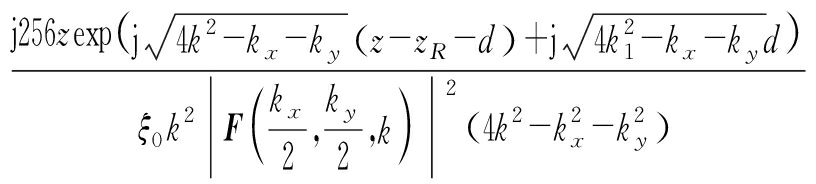
则式(1)可以简化为
O(x,y,z)=
J(kx,ky,k,z)exp(jkxx+jkyy)
这里，等式右边的第2和第3个积分项也是一个二维空域傅里叶逆变换，则式(2)就继续简化为
O(x,y,z)=
J(kx,ky,k,z)}
(3)
由于使用步进频率雷达信号，自由空间波数k积分可以转化为求和形式，则式(3)可进一步变为
O(x,y,z)=
J(kx,ky,k,z)}
(4)
可以看出，式(4)是将回波散射数据变换为目标图像。因此，我们可以借鉴文献[10]的方法，将其利用傅里叶变换反演，得到衍射层析成像正向变换，即
E(xR,yR,k)=
J-1(kx,ky,k,z)}
(5)
令快速傅里叶变换算子
将式(5)可以表示为矩阵的形式，即
E=Ψ(O)
(6)
式中，假设O与E的维度相同，均为M×N×K；当O和E的维度在不等的情况可以通过补零来实现。
在压缩感知理论框架下，对频点和阵元位置进行随机降采样，但对阵元位置进行随机选取后要对未被选取的阵元作补零处理，则式(6)改写为
Y=ΦE=ΦΨ(O)+N
(7)
式中，Y∈CM×N×K′(K′≪K)为随机降采样得到的测量数据，Φ∈CK′×K为随机测量矩阵，N∈CM×N×K′为高斯白噪声。对于整个成像空间，目标在空间中满足稀疏性，即O满足稀疏性。通过求解l1范数的最优化问题，可得到目标像O的稀疏估值
其目标函数是
(8)
式中，λ为正则化参数。
2 算法描述
2.1 LAMP网络构建
对于式(8)，可以采用AMP算法[11]求解。但是，其迭代过程还必须考虑衍射层析模型中的快速傅里叶变换算子Ψ，所以得到修正的AMP算法为
(9)
(10)
(11)
(12)
式中，ΨH为Ψ的共轭转置算子，由式(4)可得
为第t次迭代目标像估值；Dt为第t次迭代残差值；bt为残差系数；λt为阈值参数，αt为阈值可调参数；ηst为复数软阈值函数[12]。以上迭代过程，需要首先通过上一次目标像
计算残差系数bt，接着结合上一次的残差Dt-1对残差更新得到Dt，然后用Dt求解阈值参数λt，最后根据软阈值函数更新目标像得到
根据文献[11]的模型驱动学习方法，我们将式(9)～(12)的AMP迭代过程映射成多层神经网络，然后通过数据驱动进行学习，即所谓的学习近似消息传递算法(Learning Approximate Message Passing，LAMP)。LAMP的网络结构如图2所示，设定有T层。根据式(9)～(12)的迭代过程，它的每一层应设计成如图3所示的3个隐层，分别是残差层、算子更新层和非线性变换层，具体如下：
1) 残差层：对上一层残差Dt-1进行更新，输出本层的残差Dt。为简化网络结构，将式(9)代入式(10)，可得
(13)
2) 算子更新层：利用
和Dt作为输入，输出本层的非线性输入参数Rt和阈值参数λt，具体计算为
(14)
(15)
3) 非线性变换层：利用Rt和λt作为输入，采用非线性变换输出本层的图像估值
这里选取的非线性收缩函数[11]是
η(Rt;λt)=sign(Rt)ReLU{|Rt|-λt}
(16)
式中， ReLU为整流线性单元。
2.2 LAMP网络训练
纵观图2和图3，我们可以看出整个网络结构中需要学习的参数有α1，α2到αT。令
为学习参数的估值
到
集合，我们采用批量梯度下降法进行训练[8]，并以归一化均方误差函数作为损失函数，通过反向传播和Adam方法更新网络参数。其中，损失函数的具体形式为
(17)
图2 LAMP网络结构
图3 第t层LAMP的内部结构
式中，N表示训练样本数，n为第n个样本，f(Θ)为网络输出的重构结果，
表示第n个样本的目标图像，L(Θ)表示归一化的均方误差。基于式(17)的损失函数，采用Adam方法进行求解[13]，其更新参数过程为
(18)
式中，i为第i次训练，gi为损失函数的梯度，β1，β2为矩估计的指数衰减率，β1,β2∈[0,1)，mi为偏差的一阶矩估计，νi为偏差的二阶矩估计，
为β1的i次方，
为β2的i次方，
为偏差修正的一阶矩估计，
为偏差修正的二阶矩估计，γ为学习率，κ为趋近0的值(避免分母为0)。这里，因Adam方法利用梯度的一阶矩估计和二阶矩估计动态调整每个参数的学习率，适用于求解式(8)涉及的带噪声数据和稀疏问题。
3 算法复杂度分析
从前文可知，衍射层析算法构建的压缩感知模型与文献[4]构建的压缩感知模型区别在于字典矩阵的构建。对于模型空间复杂度，一般字典矩阵的大小为天线数×频点数×成像网格数[4]，即矩阵维度为MNK×MNK(假设目标像O与回波数据具有相同大小)；对于本文的衍射层析模型而言，快速傅里叶变换算子的J决定了它的大小，J的维度降为MNK×K，明显小于字典矩阵所占内存。对于模型时间复杂度，字典矩阵构建时间采用大O记法可以表示为O(M2N2K)，衍射层析模型构建时间为O(MNK2)；对于凸优化算法运行时间主要体现在计算Ψ(O)上，文献[4]计算所需M2N2K2+MNK次，本文如表1所示，总体小于文献[4]所需时间。
表1 衍射层析模型运行次数
计算方法运行次数方位向FFT5MNKlog10M高度向FFT5MNKlog10N方位向IFFT5MNKlog10M高度向IFFT5MNKlog10N匹配滤波器MNK与系数J相乘MNKK沿频率求和MNKK
4 仿真与实验数据结果分析
4.1 仿真数据测试结果分析
根据图1所示的场景，成像空间是墙体右边的1 m(长)
1 m(宽)1 m(高)的区域。假设由 71×71个天线单元的二维面阵组成，阵元距离墙体2 m，发射信号是载波频率为4 GHz、带宽为2 GHz的步进频率连续波信号。墙体厚度为0.2 m，介电常数为4.5。所有点目标均设置在空间内的任意位置，目标数目被随机设定为1～4，另外信噪比又设为-5，-1，0，1和5 dB等多种情况，一共生成400组样本，每个样本包含50%降采样回波数据和生成的一幅目标图像。实验平台在配置为Intel i7，24 GB RAM，GTX1050Ti的电脑上完成，所提LAMP网络利用Python torch编写实现。
假设LAMP网络层数T=4，其初值
每次训练数据为20组，共计训练50次，经过训练后得到的Θ=[11.369 7, 11.185 9, 11.169 8, 11.168 1]。图4显示了训练50次时均方误差曲线图，从图中可以看出，随着训练次数增加，均方误差变化趋于平缓，说明网络成像结果与目标像趋近，训练结果趋于稳定，网络收敛。
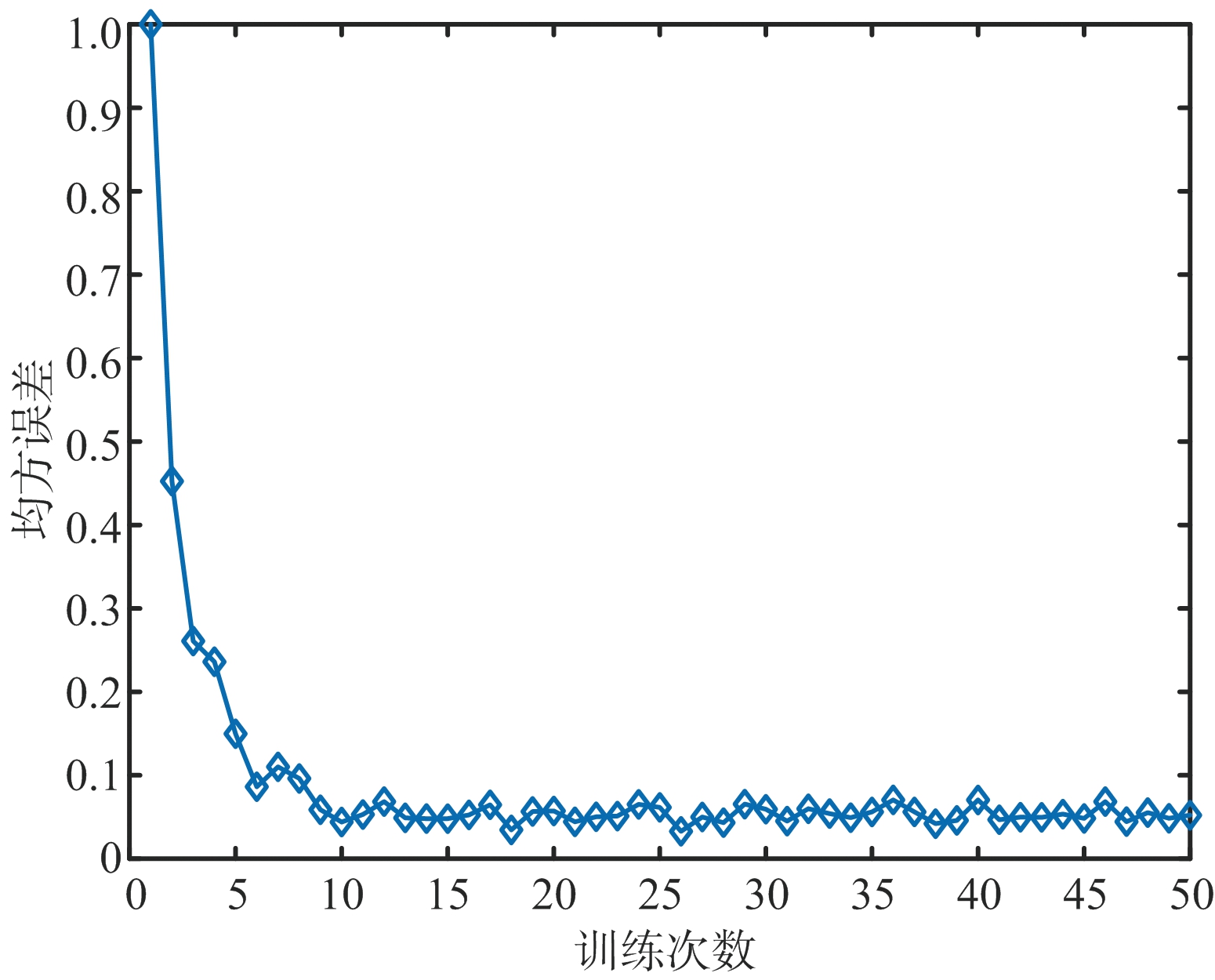
图4 均方误差
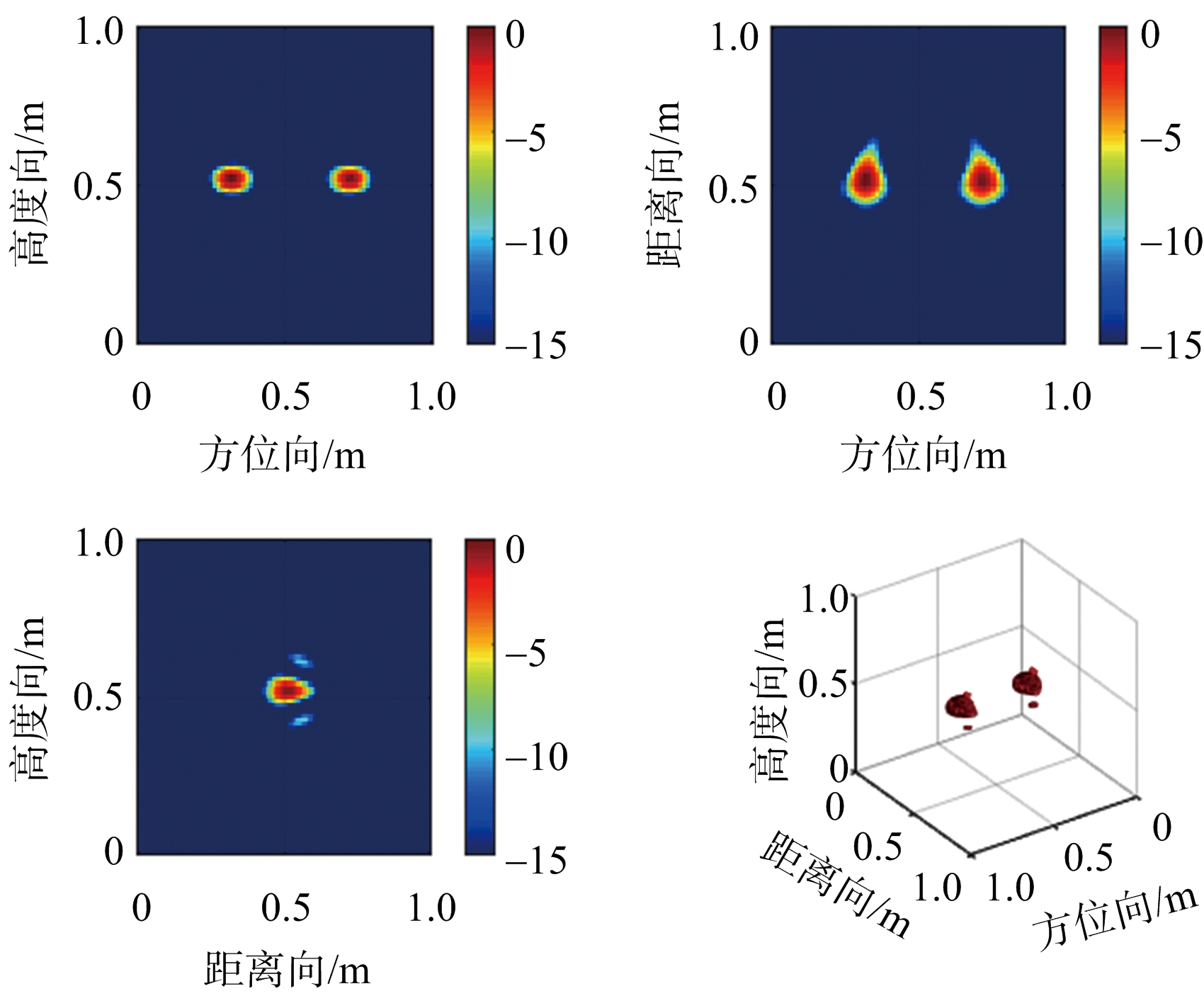
下面，设验证场景为放置在空间坐标为(0.3,0.5,0.5)，(0.7, 0.5,0.5)的点目标，其对应反射系数均为0.5，信噪比为0 dB，对数据50%降采样。LAMP网络成像结果如图5所示，左上图为沿距离向z=0.5 m处方位-高度切片图，右上图为沿高度向y=0.5 m 处方位-距离切片图，左下图为沿方位向x=0.3 m处距离-高度切片图，右下图为三维立体图，可以看出在没有手工调整阈值参数的情况下，成像网络得到的重建图像去除了旁瓣和杂波，准确对点目标成像。
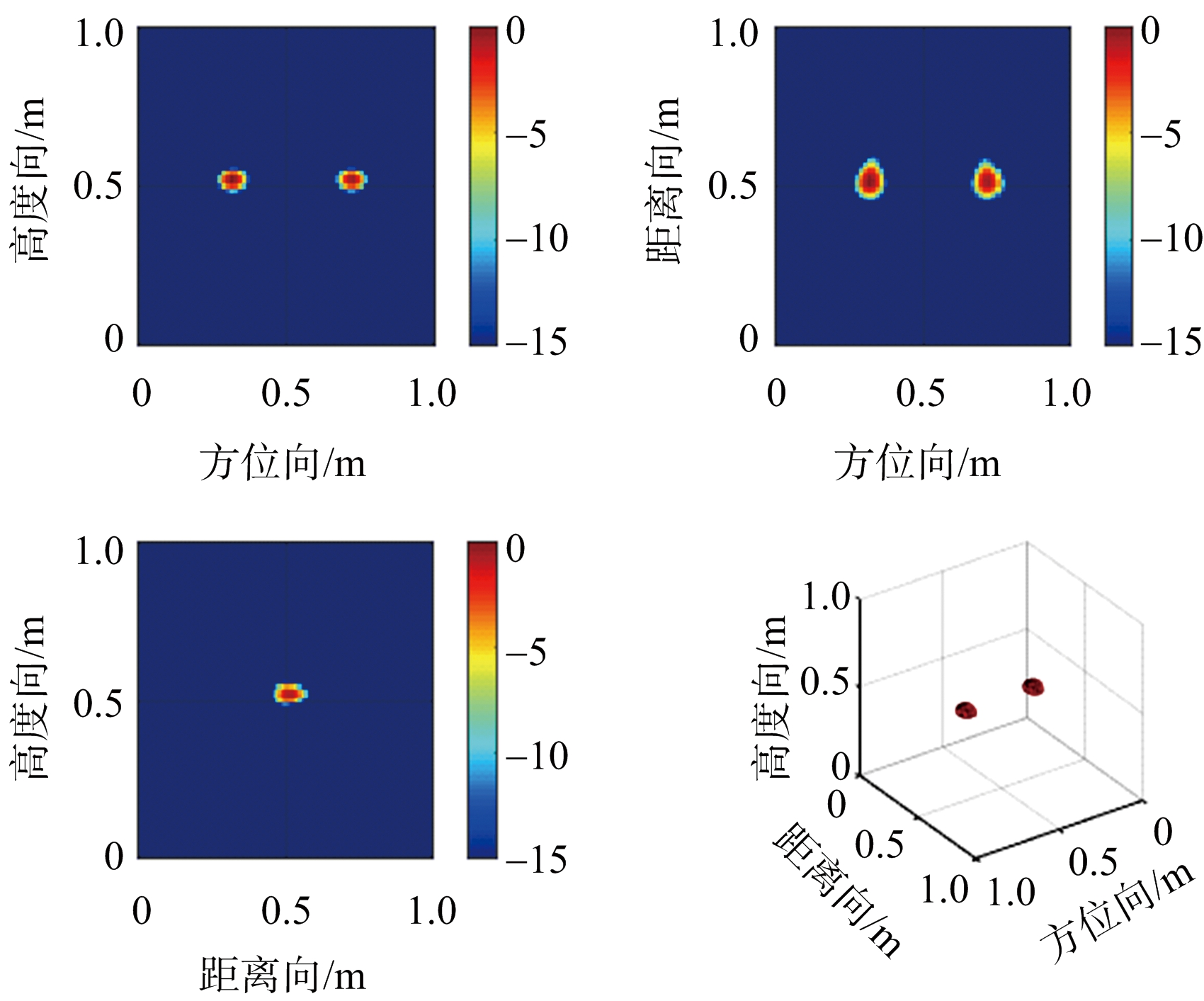
图5 LAMP网络成像结果
图6给出了不同算法的成像结果对比。其中图6(a)为DT算法成像结果，图6(b)为迭代软阈值算法(ISTA)算法成像结果，图6(c)～图6(e)给出了α=1,5,10时AMP算法的成像结果。与图5的成像结果对比，衍射层析算法成像中旁瓣的存在导致成像结果杂波较多；ISTA算法图像与图5像基本相同，但是ISTA算法阈值参数需要手动调整；AMP算法在不同的α下对旁瓣滤除效果明显不同，表明人工设定阈值参数将很大程度上决定最终的成像结果。
(a) DT算法成像结果
(b) ISTA算法成像结果
(c) α=1时AMP算法成像结果
(d) α=5时AMP算法成像结果
(e) α=10时AMP算法成像结果
图6 LAMP网络与其他成像算法的比较
为了更直观地对算法性能进行对比，表2给出其在TCR、ENT、MFOD、PRT方面的对比，分别反映了目标杂波比、图像熵、目标的边缘轮廓特性和算法运行时间。从表中可以看出，DT算法成像的PRT值最小，程序运行时间较短，但其TCR、ENT和MFOD较大，图像聚焦度不够高，杂波较多，轮廓特性不明显；ISTA算法TCR、ENT和MFOD较小，成像质量较高，但其PRT值为691 s，反映出程序迭代次数过多，运行时间较长；AMP算法在不同α值下TCR、ENT和MFOD不同，表明了阈值参数对重建图像质量的影响；LAMP网络TCR值比手动调参下小3 dB，ENT与MFOD也小于其他算法，所成图像最清晰，此外，AMP单次迭代时间约为40 s，而LAMP单层网络使用GPU运行时间约为4 s，PRT值小于ISTA和AMP算法，表明了本文方法运行时间小于其他方法。
表2 TCR、ENT、MFOD、PRT的比较
算法TCR/dBENTMFODPRT/sDT32.38660.47620.0046195.5576ISTA61.45090.37542.8822e-04691.6029AMP,α=142.49360.44670.0021631.3017AMP,α=553.33530.39867.0096e-04—AMP,α=1061.47690.37253.3146e-04—LAMP64.45030.36602.5936e-04211.3920
4.2 实测数据结果分析
采用维拉诺瓦(Villanova)大学高级通信中心(CAC)与空军研究实验室(AFRL)合作收集得到的穿墙雷达成像实验数据，探测场景如图7所示[14]。选取6557平面阵列所得到的数据进行三维穿墙成像，发射信号是载波频率为2 GHz，带宽为1 GHz的步进频率波形，步进间隔为5 MHz。对数据进行预处理，使用背景相消法消除墙体杂波和噪声。使用Populated Scene场景回波数据生成训练样本，加入信噪比为-5～5 dB范围内噪声，一共生成50组样本。使用Calibrated Scene场景进行实验验证，DT算法成像结果如图8所示，LAMP网络下回波数据50%降采样成像结果如图9所示。在图8、图9中，图(a)为高度为1.2 m处切片图，图(b)为三维成像立体图。通过对比可知，DT算法存在目标周围旁瓣较多、受噪声干扰严重、数据量大等缺点；LAMP网络的成像目标周围基本不存在旁瓣干扰，随机噪声也得到了很好的抑制，同时没有损坏目标的边缘特性。表3给出了DT算法和LAMP网络所成像的TCR、ENT、MFOD和PRT值。
(a) 探测场景图
(b) 雷达穿墙场景图
图7 实验场景
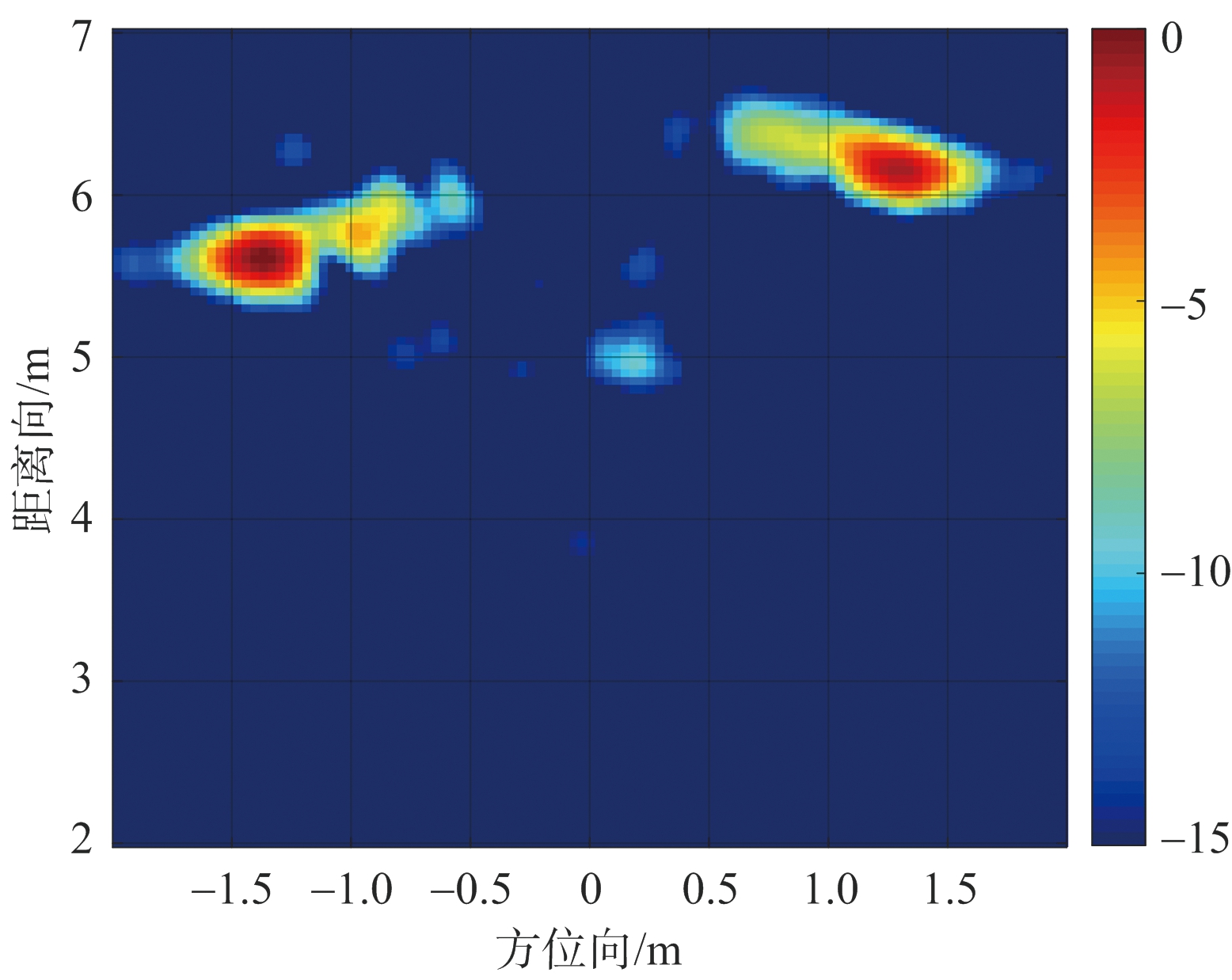
(a) 方位-距离向切片图
(b) 三维成像立体图
图8 DT算法成像结果
(a) 方位-距离向切片图
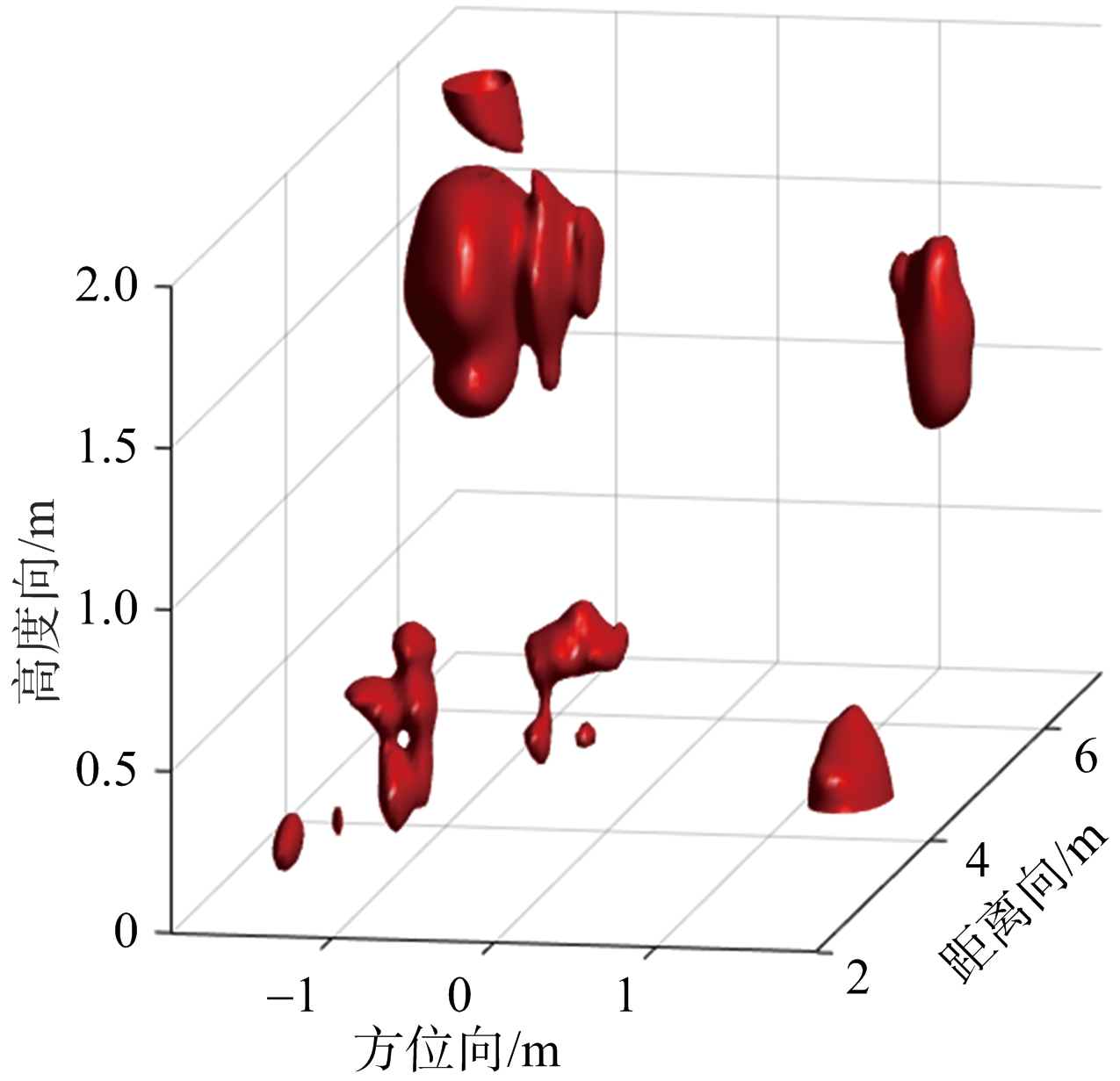
(b) 三维成像立体图
图9 LAMP网络成像结果
表3 TCR、ENT、MFOD、PRT的比较
算法TCR/dBENTMFODPRT/sDT33.02300.96760.0034398.5300LAMP50.16960.72830.0013416.3270
5 结束语
本文提出了一种衍射层析稀疏模型下的学习成像方法，通过构建衍射层析稀疏模型降低了存储空间，并通过设计LAMP网络自动学习可调参数，提高了成像质量，适用于三维穿墙雷达成像。还需注意的是：在衍射层析稀疏模型中没有使用深度学习卷积层替换其他参数，也没有考虑墙体杂波与目标回波的分离，下一步拟对网络结构和训练样本作一定的更改，实现它们的分离。
[1] AHMAD F,ZHANG Y,AMIN M G. Three-Dimensional Wideband Beamforming for Imaging Through a Single Wall[J]. IEEE Geoscience and Remote Sensing Letters,2008,5(2):176-179.
[2] ZHANG W, HOORFAR A. Three-Dimensional Real-Time Through-the-Wall Radar Imaging with Diffraction Tomographic Algorithm [J]. IEEE Trans on Geo-science and Remote Sensing, 2013,51(7):4155-4163.
[3] REN K, CHEN J, BURKHOLDER R J. A 3-D Uniform Diffraction Tomographic Algorithm for Near-Field Microwave Imaging through Stratified Media[J]. IEEE Trans on Antennas and Propagation,2018,66(6):3034-3045.
[4] YOON Y S, AMIN M G. Through-the-Wall Radar Imaging Using Compressive Sensing Along Temporal Frequency Domain[C]∥IEEE International Conference on Acoustics Speech & Signal Processing, Dallas, TX, USA :IEEE,2010:2806-2809.
[5] GAO Y, PENG W, QU Y, et al. Through-the-Wall Imaging Based on Modified Compressive Sampling Matching Pursuit[C]∥ 2017 Sixth Asia-Pacific Conference on Antennas and Propagation, Xi’an, China: IEEE,2017:1-3.
[6] 张燕,晋良念.结合TV约束的穿墙雷达扩展目标成像方法[J].雷达科学与技术,2017,15(3):229-235.
ZHANG Yan, JIN Liangnian. Through-the-Wall Radar Extended Target Imaging with TV Constraints [J]. Radar Science and Technology, 2017, 15(3):229-235.(in Chinese)
[7] TANG V H, BOUZERDOUM A, PHUNG S L. Compressive Radar Imaging of Stationary Indoor Targets with Low-Rank Plus Jointly Sparse and Total Variation Regularizations [J]. IEEE Trans on Image Processing,2020,29:4598-4613.
[8] ITO D, TAKABE S, WADAYAMA T. Trainable ISTA for Sparse Signal Recovery[J]. IEEE Trans on Signal Processing,2019,67(12):3113-3125.
[9] 罗迎, 倪嘉成, 张群. 基于“数据驱动+智能学习”的合成孔径雷达学习成像[J].雷达学报,2020,9(1):107-122.
[10] LI Shiyong, ZHAO Guoqiang, SUN Houjun, et al. Compressive Sensing Imaging of 3-D Object by a Holographic Algorithm[J]. IEEE Trans on Antennas and Propagation,2018,66(12):7295-7304.
[11] BORGERDING M, SCHNITER P, RANGAN S. AMP-Inspired Deep Networks for Sparse Linear Inverse Problems [J]. IEEE Trans on Signal Processing,2017,65(16):4293-4308.
[12] 侯彦, 上官伟, 孙进平. 基于复近似消息传递的前视雷达成像分辨率增强算法[J]. 航空工程进展,2020,43(1):60-65.
[13] KINGMA D, BA J. Adam: A Method for Stochastic Optimization[C]∥the 3rd International Conference for Learning Representations, San Diego:[s.n.],2014:1-15.
[14] DILSAVOR R, AILES W, RUSH P, et al. Experiments on Wideband Through-the-Wall Radar Imaging [C]∥Algorithms for Synthetic Aperture Radar Ima-gery XII, Orlando, FL, US:IEEE,2005:196-209.
