0 引 言
目标距离、速度和方位估计值作为目标跟踪的输入信息,其估值精度直接影响后续跟踪质量优劣、战场态势判断的准确性。目标参数估计通常是在目标检测之后进行[1-5]。为了获得目标距离的精确估计值,文献[6]提供了一种基于邻近单元比幅法(Adjacent Cell Amplitude Comparison, ACAC)进行目标距离估计的工程应用方案,但没有对其数学原理进行理论建模与分析;文献[7]在ACAC方法的基础上,结合雷达系统中不同窗函数的选取分析了距离维目标谱线主瓣、峰值谱线与相邻谱线之间的幅度关系,对目标的距离、径向速度采用插值法进行估计,提高了估值精度;文献[8-11]针对不同的临近单元比幅模型进行了进一步深入研究;文献[1,5]理论分析了机械扫描雷达中天线转动对目标参数估计带来的影响,提出了广义相参积累模型和相应的高精度参数估计方法,通过仿真和实测数据处理结果进行验证。然而,现有的距离、速度估计方法的研究成果通常仅局限于理论研究,并未关注其在实际应用中存在的不足,例如由通道幅相不一致性引入的潜在的估值偏差以及触发电路等内部因素引入的系统误差等。这类问题制约雷达系统的工作性能,在实际应用中亟待解决,但相关的补偿方法、手段尚未见公开资料进行全面的分析研究。
角度估计主要是对目标的方位角、俯仰角进行测量。对于海面舰船来说人们主要关心其方位角,对空中目标则还需要进行俯仰角的估计。在现代雷达中通常采用单脉冲测角技术来进行角度估计。单脉冲测角技术利用瞬时双波束接收到的目标回波之间的幅度、相位差异判断目标偏离波束轴线的角度,具有较高的测角精度并可用于雷达自动测角。常见的单脉冲测角技术包括直接比幅法、直接比相法、和差比幅(Sum-Difference Amplitude-Comparison, SDAC)法与和差比相法[12]。其中和差比幅单脉冲方法是一种成熟的单脉冲测角技术,在实际雷达系统中得到了广泛应用[13]。该方法首先计算和差通道中目标回波信号的幅度之比,再通过查询先验的单脉冲比曲线来获得目标偏离波束中心的瞬时角误差。虽然单脉冲测角精度高,但它对和差通道的幅相一致性要求较高,否则会影响测量精度。考虑到天线、射频中频模拟电路受温度、工作时间等外部因素的影响,在实际工作中需要对雷达系统和差通道的不一致性进行校正。文献[14]定量分析了接收通道幅相不一致对和差比幅单脉冲测角精度的影响;文献[15-16]给出了在射频、中频以及数字基带信号进行通道补偿的方法并给出了定量的仿真结果。上述方法均是基于补偿系数能够准确获取的假设前提下进行设计与仿真的。在某些系统中,实际回波通路与补偿信号通路并不完全一致,如功分器引入的附加幅相不一致性,并且存在一些器件幅相特性测试困难。因此,在已有理论方法上研究设计雷达系统补偿的工程方案对现代雷达发展具有重要意义。
文献[17]基于某实际雷达系统提出了一种基于后验数据的单脉冲雷达系统方位角估计的补偿方法,并提出了“系统补偿”的概念。该方法通过对基于实测数据的目标方位估值参数进行统计分析获得待定相位项,结合已有和差通道补偿系数进行系统补偿,从而获得全局最优的补偿效果与测角精度。本文在前文的基础上,建立了一种广义化的基于后验数据辅助(Posterior Data-Aided, PDAid)的系统补偿框架,将系统补偿的适用范围扩展到距离估计上,结合实际两坐标雷达系统进行方位角、距离估计值补偿,提高目标参数估计精度,通过实测数据处理结果对本文方法的有效性进行验证。
1 经典参数估计方法
1.1 角度测量
和差比幅单脉冲技术采用瞬时和差双波束接收目标回波,利用目标在和、差通道的幅相信息估计目标偏离和波束中心轴线的角误差,结合此刻波束中心瞬时指向,获得目标的真实方位的估计值,其基本原理如图1所示。和差比幅单脉冲测角技术采用两个相同的且彼此部分交叠(通常为3 dB波束交叉)的波束,其偏离等信号轴的角度值为θk,如图1(a)中的波束A、B。两个基本波束经过和、差处理后获得等效的和差天线波束方向图,如图1(b)所示。
在实际工程中,目标在和差波束中强度的比值可以近似为角误差的线性函数[13],即
FΔ(Δθ)/FΣ(Δθ)=κΔθ
(1)
式中,FΔ(Δ θ)、FΣ(Δ θ)分别为目标的和、差波束信号,Δ θ为目标角误差,κ为单脉冲斜率常数。当Δ θ很小时,κ≈F′(θk)/F(θk)。若单次估计时天线波束中心指向为θ0,则目标真实方位θt可以表示为
θt=θ0+Δθ
(2)
在理想情况下,目标和、差通道基带信号可表示为
Σt=AΣexp(jφ0)
(3)
Δt=AΔexp(jφ0)
(4)
式中,AΣ、AΔ分别为对应和、差天线方向图的幅度,f0为雷达工作频率,φ0为初始相位。则和差比幅单脉冲测角结果可以表示为
(5)
实际工程中,由于噪声的影响,目标和、差基带信号的相位难以保持绝对同相或反相,因此在实际处理时,通常采用如式(6)的形式来进行角误差估计值的计算,即
(6)
式中,sgn(·)为取符号运算,θΔ/Σ为Δt/Σt的相角。
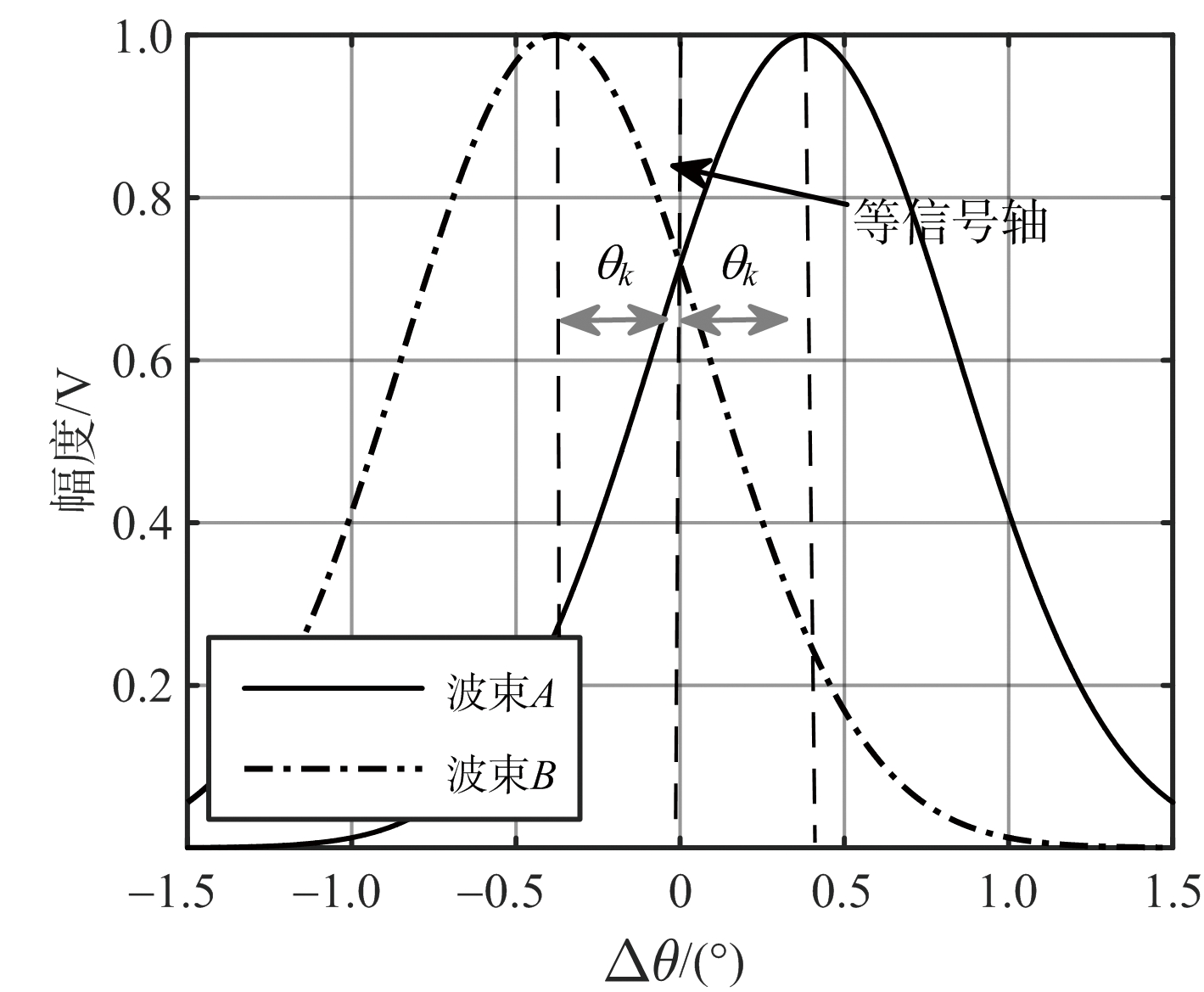
(a) 基本波束方向图

(b) 和、差波束方向图
图1 天线波束方向图
1.2 距离测量
由于脉冲压缩与相参积累都是在对雷达回波信号进行数字采样之后通过信号处理软件进行,因此目标在实际距离-多普勒二维谱图中通常位于离散的谱线上。由于目标检测只能获得其在距离-多普勒二维谱图上的离散位置,为了保证后续目标跟踪的精确性,需要对目标的距离、速度的精确值进行估计。
文献[1]基于目标点扩散函数(Point Spread Function, PSF)对在实际雷达系统中广泛应用的ACAC方法[6]进行数学建模,提出并完善了该方法的理论体系。由于在二维谱图上距离、速度估计方法完全一致,本节仅以目标距离估计为例对该方法进行简要回顾与介绍。
为不失一般性,本节考虑理想点目标模型,假设其PSF为辛格(sinc)函数,对应的表达式为
sinc(x)=sin(πx)/πx
(7)
图2给出了ACAC法的距离估计示意图。假设Tt为目标在距离-多普勒二维谱图上的理论真实位置,由于距离-多普勒谱图为离散化后的信号矩阵,因此只有在特定采样位置的样本信息是直接可用的(例如采样点JR或者JR+1),采样点之间的间距对应一个距离单元。同样地,目标检测器只能检测获得目标真实位置附近的具有局部幅度最大值的采样点并将其确定为目标位置,即图2中的JR,其样本幅度值大小为EJR。
为方便起见,称JR为目标的“检测位置”,Tt为目标的“真实位置”。令采样点JR左右相邻的两个采样点JR-1和JR+1所对应样本的幅度值分别为EJR-1和EJR+1(图2中并未给出JR-1和EJR-1)。可以预计的是,当EJR-1>EJR+1时,Tt会位于检测位置JR的左侧,但间距不会超过半个距离单元;当EJR-1<EJR+1,Tt会位于检测位置JR的右侧,其间距同样也不会超过半个距离单元。为了方便起见,在后续分析中若未加特殊说明皆假设EJR-1<EJR+1,即图2中对应的情况。
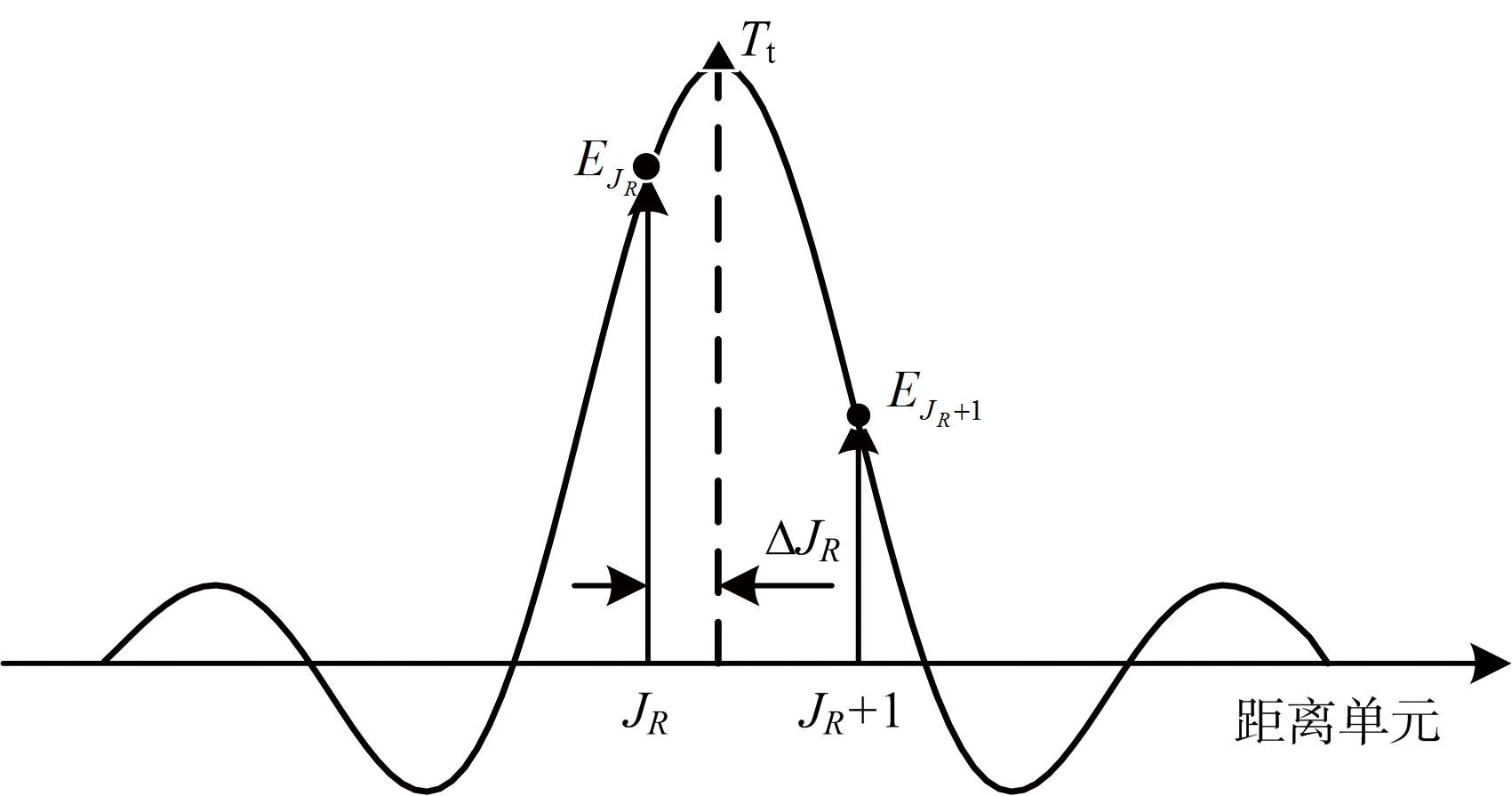
图2 距离估计方法示意图
此时,对目标真实位置Tt的估计可以转化为对目标真实位置与检测位置JR之间的间距ΔJR的估计。若令Tt=(JR+ΔJR)ΔRbin,其中ΔRbin为距离单元大小。则有
(8)
因此,可以获得
αR=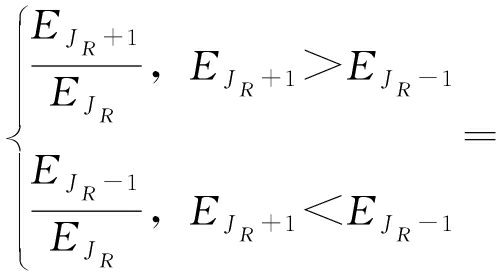
FR(ΔJR),|ΔJR|≤1/2
(9)
当EJR+1>EJR-1时,式(9)中的ΔJR>0;反之,ΔJR<0。
为方便起见,在本文中我们将式(9)中相对于自变量ΔJR变化的函数FR(·)称为距离比幅插值曲线。在实际雷达系统中,FR(·)可以利用雷达参数仿真获得,在实时处理中通常以查找表(Look-Up Table,LUT)的形式预先存储在雷达信号处理机中。基于上述分析,目标的距离估计值可以表示为
![]()
(10)
1.3 传统系统补偿方案
为了获得较高的目标参数估计精度,在实际应用中通常需要对和差通道的幅相一致性进行校正。典型的校正方法是在射频端对和差波束接收支路分别灌入相同的基准信号,经过后续相同的混频、下变频和正交解调处理获得和差两路的I、Q正交基带信号,利用基带信号分析幅相差异并选取某一支路作为参考,计算另一通路的幅相补偿因子。在雷达正常工作时,先利用该补偿因子对和差基带复数据进行补偿,再进行目标参数估计[18]。
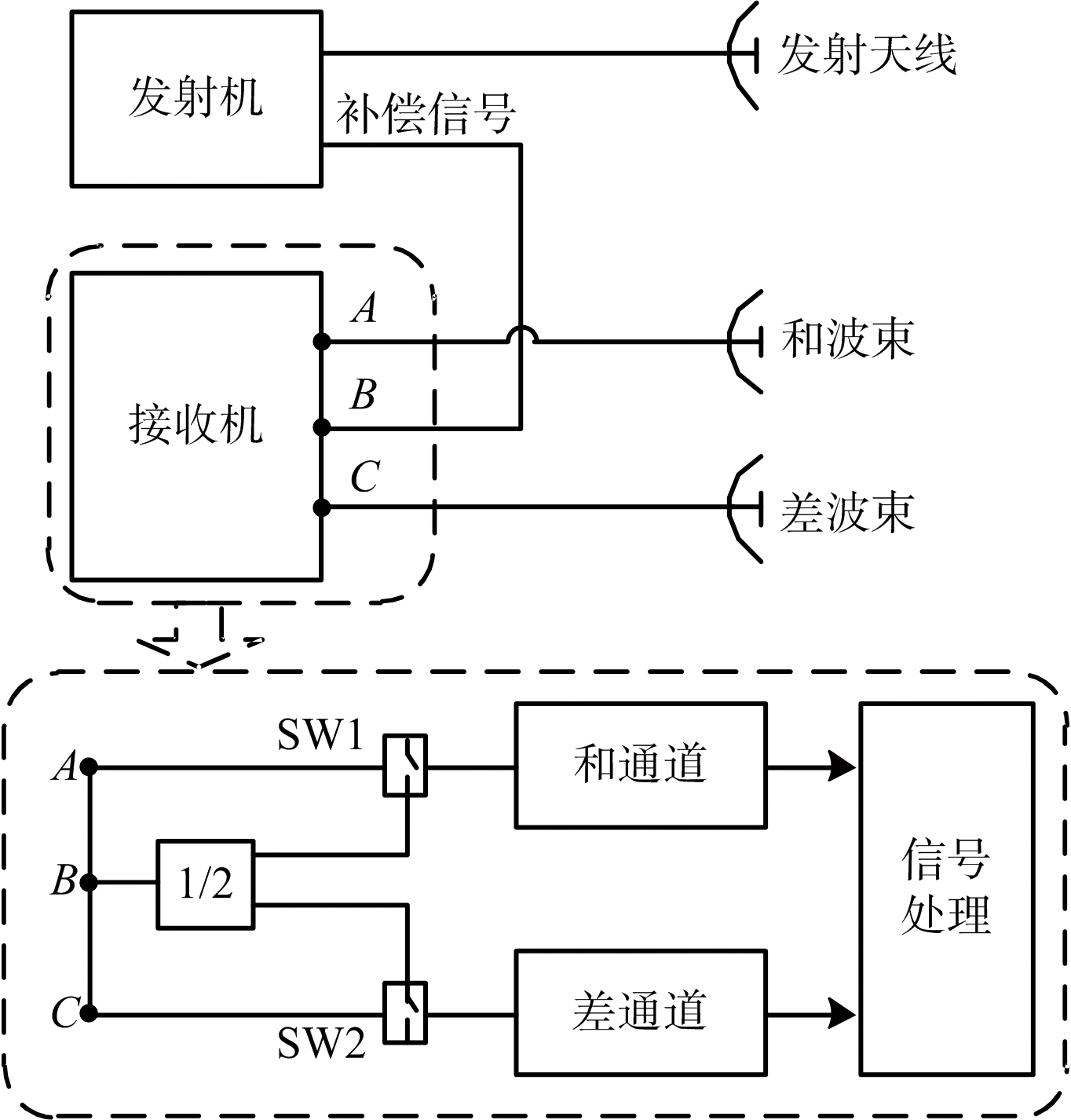
图3 实际雷达补偿原理框图
这类校正方法原理简单,但是在射频端的控制繁琐。因此,本文中的试验雷达采用如图3所示的系统原理框图进行系统校正。和、差波束接收信号分别从A、C两个接口输入到接收机,校正信号作为独立的一路信号输入到接收机的B接口。图3中下方的虚线框示意性地给出了接收机的内部结构:在正常工作时,数据开关SW1和SW2将A、C接口分别连通至和、差通道并进行后续的信号处理;当工作于补偿模式时,校正信号通过B进入接收机,并通过功分器与数据开关SW1、SW2将信号输入至和、差通道,雷达系统通过后续的信号处理来获得相应的补偿因子并记录,以备系统转入正常工作时使用。
2 目标参数估计影响因素分析
2.1 角度测量
为方便起见,本文以和通道基带输出信号作为参考,雷达工作于线性调频连续波体制。比幅单脉冲天线的一个重要指标是零深,它决定了单脉冲测角系统的灵敏度。零深是由和差两路信号的相位不一致性决定的,这种相位差称为高频相移[14]。由于高频相移的存在,和差器的输出不再是两路信号简单的幅度相加减,而是矢量信号的加减。这意味着,即使和差器的两路输入信号幅度相等,但其差通道信号的幅度也不为零,从而导致跟踪雷达伺服系统会不停地调整天线波束中心指向而无法达到一个相对稳定的状态。这对于跟踪雷达来说是无法容忍。因此,当和差信号存在高频相移且和差通道存在幅相不一致时,需要对雷达系统进行补偿才能获得较高的角度估值精度。
为不失一般性,令差通道基带输出信号为
Δ′t=ηAΔexp[j(φ0+φψ+φch)]
(11)
式中,η为幅度不一致性引入的幅度因子,φψ为高频相移ψ引入的高频相差,φch为通道相位误差。结合式(6),当系统幅相不一致未进行补偿时的角误差估值结果为
(12)
考虑到存在高频相移时,当天线等信号轴对准目标,即使通过两个基本波束接收并进入和差器的信号幅度相等,此时差通道信号的幅度AΔ不为零,使得采用如式(6)计算获得的角误差估值结果始终不为零。针对该影响,文献[19]提出了一种改进的角误差估值方法,如式(13)所示:
(13)
由式(12)和式(13)可以看出,和差通道幅度不一致性会引起角误差估值大小的偏差,不会影响测角符号(即相对于天线轴线的角度偏差方向);和差通道相位不一致性与高频相移会影响测角符号。考虑到高频相移是在和差器之前产生,无法在后续信号处理模块中进行补偿,而由前文已经获知高频相移与和差通道相位不一致对测角符号的影响是紧密耦合的,因此在设计补偿方法时需要对这些因素同时进行分析考虑。由于图3给出的校准信号经过了功分器后才进入和差通道,在进行系统补偿时,功分器引入的附加相差也需要考虑在内。经典的和差通道幅相不一致性补偿方法是建立在某些特定假设前提下的(如高频相移为5°),在实际工程中有一定的局限性。
2.2 距离测量
连续波雷达距离单元大小为
![]()
(14)
式中,c为光速,fs为采样频率,M为采样点数,μ=B/T为发射信号调频斜率,B为发射带宽,T为调频周期。
典型的产生调频连续波的激励信号的方法通常包括锁相环(PPL)和直接频率合成(DDS)两种,本节对这两种方法进行简要介绍。
2.2.1 锁相环(PLL)
PLL的工作原理是通过鉴相器(Phase Detector,PD)和电荷泵(Charge Pump,CP)将鉴相器输入 端信号的相位差转换误差成电压信号输出,经过低通滤波器去除噪声、干扰成分后形成压控振荡器(Voltage-Controlled Oscillator,VCO)的控制电压,对VCO输出信号的频率实施控制,在通过反馈通路将VCO输出信号的频率、相位反馈至鉴相器。
利用锁相环直接产生调频连续波信号具有构造电路简单、调试难度小的特点,是目前较为流行的一种低成本的设计方案。目前已有技术成熟的基于PLL的频率综合器芯片可供使用。然而,由于PLL芯片采用编程方式进行输出频率配置且频率量化间隔通常与芯片本身设计有关,不可避免的量化误差导致难以获得完全符合预设发射带宽的配置参数。虽然某些先进芯片具有实现零误差的“精确频率模式”,但在实际应用中配置相对复杂,且对输出频率具有诸多约束与限制,当需要实现扫频、变频时难以灵活运用。尤其当雷达工作于频扫体制时,雷达系统需要通过改变工作频点实现天线波束的电扫描并不断通过扫频获得所需的发射带宽,通常难以产生一组在各波束中心指向上恰好满足起始扫频频率、截止扫频频率、扫频时宽的参数。
2.2.2 直接频率合成
直接数字频率合成技术(Direct Digital Frequency Synthesis,DDS)是继直接频率合成和间接频率合成之后,随着数字集成电路和微电子技术的发展而迅速发展起来的第三代频率合成技术。它以数字信号处理理论为基础,从信号的幅度相位关系出发进行频率合成,具有极高的频率分辨率、极短的频率转换时间、较大的相对带宽、连续的信号相位和可变的输出波形等诸多优点。
DDS通过控制频率调谐字、相位控制字和幅度控制字来生成所需的调频信号。由于DDS通过频率量化来实现调频的,这同样带来了量化误差。当频率累加器的寄存器位数足够宽时,DDS的频率分辨率理论上可以达到无限小,但是由于后续相/幅变换器的容量有限,工程上频率累加器的位宽通常也是有限的。
需要注意的是,式(14)中c为自然常量,fs、M和T由雷达系统设定,在实际应用中可以准确界定;由于B通常与激励信号产生的机理和实现的电路相关,在实际应用中很难精确达到理论设计值,导致距离单元大小偏离预设值。
基于上述分析,由于工作方式、产生机理的不同,通过PLL和DDS方式产生的线性调频信号的调频斜率与理论设计值无可避免地存在差异,且难以事先获得精确的测量值,这对于后续的目标距离精确估计存在影响。在典型的线性调频连续波搜索雷达工作参数(例如发射带宽B=20 MHz,调频周期T=500 μs)下,其距离单元大小偏差δRbin是厘米级的。当雷达对远区目标进行距离估计时,由于此时JR数值约为数百,由式(10)可知会引入数十米的估值偏差,即
(15)
式中,![]() 为距离估值相对于真值的偏差。这在实际应用中会严重影响雷达探测精度,必须进行相应的校正与补偿。
为距离估值相对于真值的偏差。这在实际应用中会严重影响雷达探测精度,必须进行相应的校正与补偿。
3 基于后验数据辅助的系统补偿方法
本节主要针对在目标方位、距离估计中难以进行直接补偿的因素,提出一种基于后验数据辅助(PDAid)的系统补偿方法,其核心问题主要包括目标真值的获取与量测值的处理。该方法结合实时测量的目标真值,通过对目标方位、距离实际测量结果进行统计分析,获得影响参数估计精度的各项因素并进行系统补偿,从而获得全局最优的补偿效果和参数估计精度,其原理框图如图4所示。本节分别介绍了角度测量和距离测量中基于PDAid的系统补偿基本流程,并结合实际雷达系统,通过实测数据处理结果评估验证所提方法的性能。
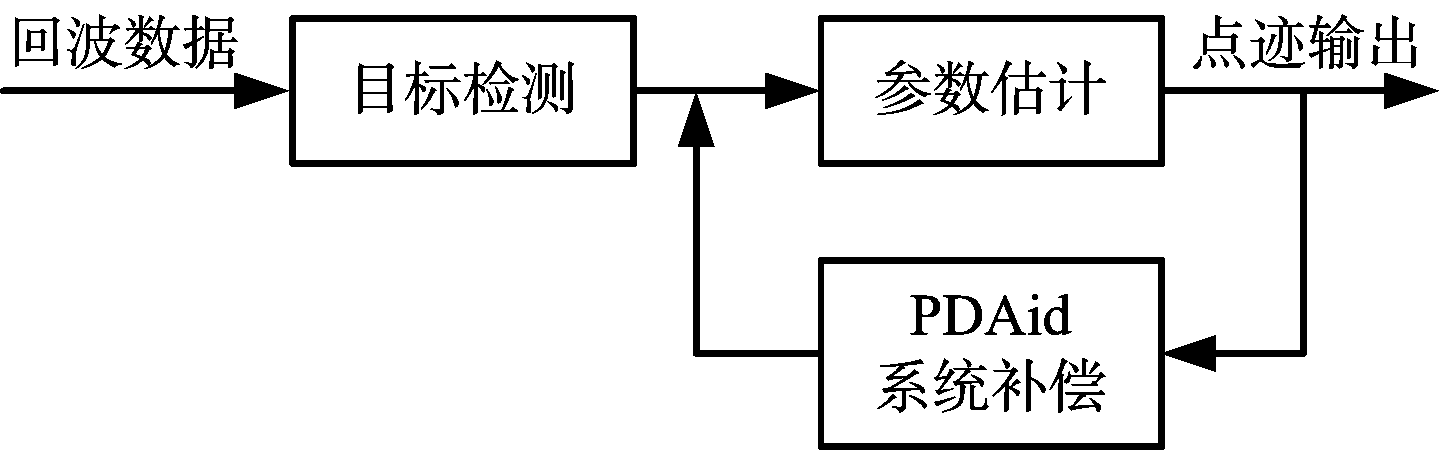
图4 基于后验数据辅助的系统补偿方法原理框图
3.1 角度补偿
在实际系统中,和差通道的幅度不一致性经过初步校正后通常可以忽略,而且在绝大多数情况下调整比较方便[14]。此外,幅度的不一致性仅影响角误差估计值的大小,不影响方向,因此本文中仅重点探讨存在相位不一致性时的系统补偿。
3.1.1 数据获取
数据获取主要包括基准数据获取和量测数据获取两方面。
1) 基准数据获取
以对海雷达为例,为了尽可能减少外部非理想环境对系统补偿效果的影响,在选择参考目标时需尽量选择海面静止点目标,通常可选择锚定浮标作为参考海面静止点目标,其具体位置可通过事先测量精确获得。考虑到浮标位置可能随洋流的影响随机微动,试验中可在浮标上安装高精度差分GPS实时测量其位置用以后续数据处理。本试验中海面浮标实物图如图5所示。

图5 海面浮标实物图
2) 量测数据获取
为了充分地验证单脉冲测角及补偿方法的有效性,同时尽可能地在单位时间内获取更多的目标有效回波样本以达到较高的处理精度,试验中雷达天线工作于扫描模式,以固定的转速对锚定浮标进行周期性照射。雷达接收系统与浮标上放置的差分GPS精确对时,实时记录回波和天线伺服的瞬时波束中心指向。
3.1.2 补偿方法
1) 探测模式
为不失一般性,本文的角误差估计采用式(13)的计算方法。角度补偿的核心在于补偿式(13)中的高频相移φψ和通道相位误差φch。令人工补偿相位为φc,则如式(13)计算获得的目标角误差估计值为
![]()
(16)
理想情况下有φψ+φch+φc=0,但考虑到不同系统、接收通道、补偿通道物理上的非一致性,通常需要通过分析大量的实测数据来获得一组全局最优的人工补偿相位φc。其基本流程框图如图6所示。
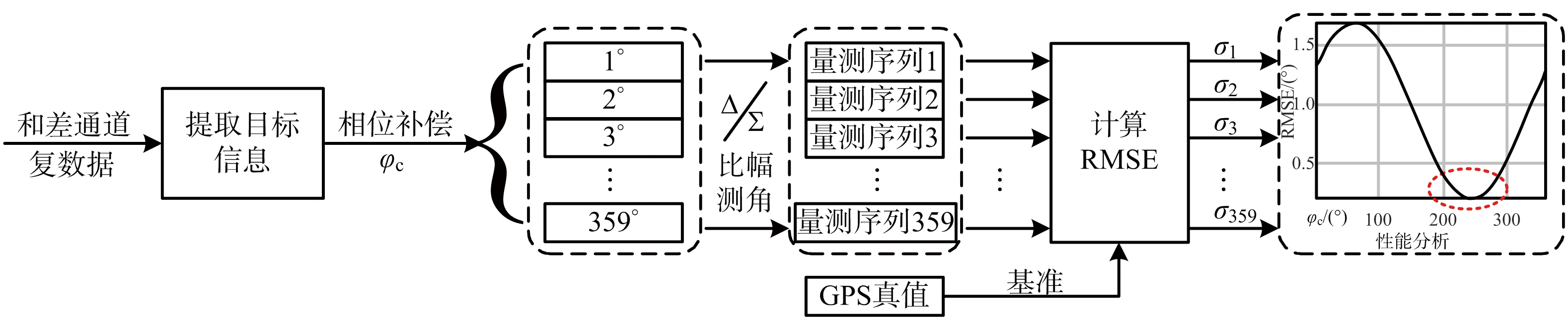
图6 角度补偿原理框图
为直观地展示系统补偿对角度估计带来的性能提升,图7给出了一个基于实测数据的人工相位补偿实例;其中φc=85°,横坐标为相参积累周期数,每个周期共积累256个脉冲;纵坐标为方位角。由于天线工作于扫描模式,因此天线波束中心指向会随时间变化而变化,如黑色实线所示。理想情况下,由于目标位置几乎固定不变,因此其方位在各个相参积累周期中的估计值应不受天线转动的影响,如图7中黑色虚线所示。然而,由于高频相差φψ、和差通道相位误差φch等因素的影响,若不经过系统补偿,由于式(16)中cos(·)项的存在,目标角误差估计值大小会偏离真实值,甚至会出现符号反号的情况,如图7中黑色点划线所示。经过人工补偿后,φψ和φch的影响得到有效抑制,目标方位估计值趋近于真实值,如图7中的“-o-”线所示。
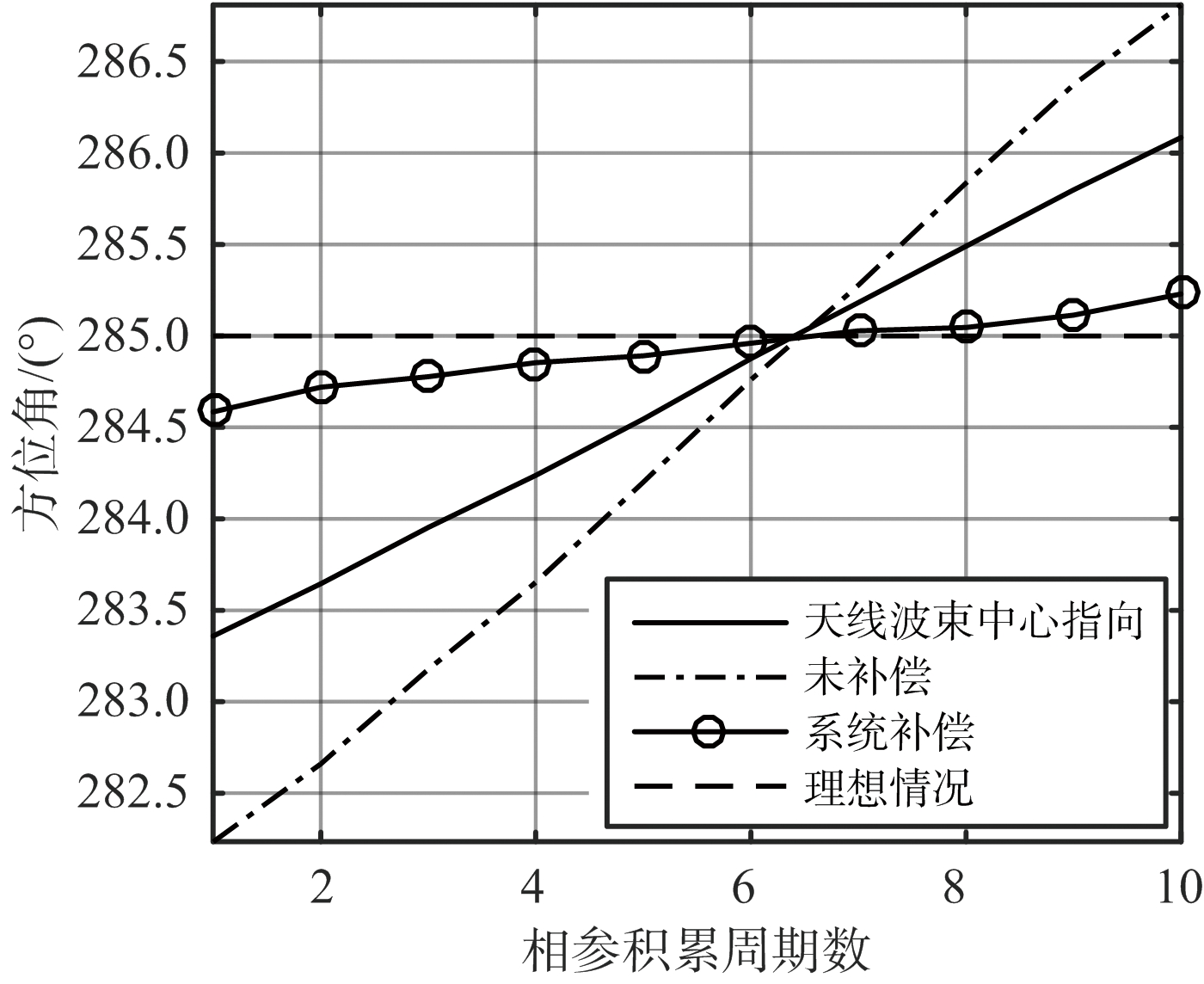
图7 和差比幅单脉冲测角实测结果
由处理结果可以看出,虽然经过系统补偿后的目标方位估计值未完全达到真实值,而且在一定程度上与天线转动有一定耦合,但这种情况是受制于实际系统中天线和波束主瓣宽度以及单脉冲比的线性度,且系统补偿对方位角估计带来的性能改善是明显的。
考虑到上述结果仅为φc=85°时的一个特例,为获得实际雷达系统全局最优的相位补偿角度φc,可选用同一批含有目标的雷达回波数据进行不同φc的相位补偿,计算各个相参积累周期中获得的目标角度估值结果相对于目标角度真值(通过差分GPS精确获得)的均方根误差(Root Mean Squared Error,RMSE)绘制成曲线。显然,RMSE统计最小值对应的φc即为本系统的全局最优相位补偿值。
通过对大量实测数据的统计分析,获得了该雷达在探测与成像模式下不同工作频率时的系统补偿结果,如图8所示。图8(a)给出了探测模式下不同工作频率的补偿角度-方位角估值RMSE曲线。横坐标对应了系统补偿的人工附加角度φc,纵坐标为在天线扫描期间10个相参积累周期角度估计值的RMSE。需要注意的是,当雷达工作于不同频点时其对应的全局最优相位补偿值(对应RMSE最小的区域)通常也会发生变化,但变化趋势有规律,而且可选择的最佳范围约为180°。为降低系统工作复杂度,我们选取各个工作频率最佳补偿范围的公共区间,即70°~100°的中间值作为系统补偿附加相移。

(a) 探测模式
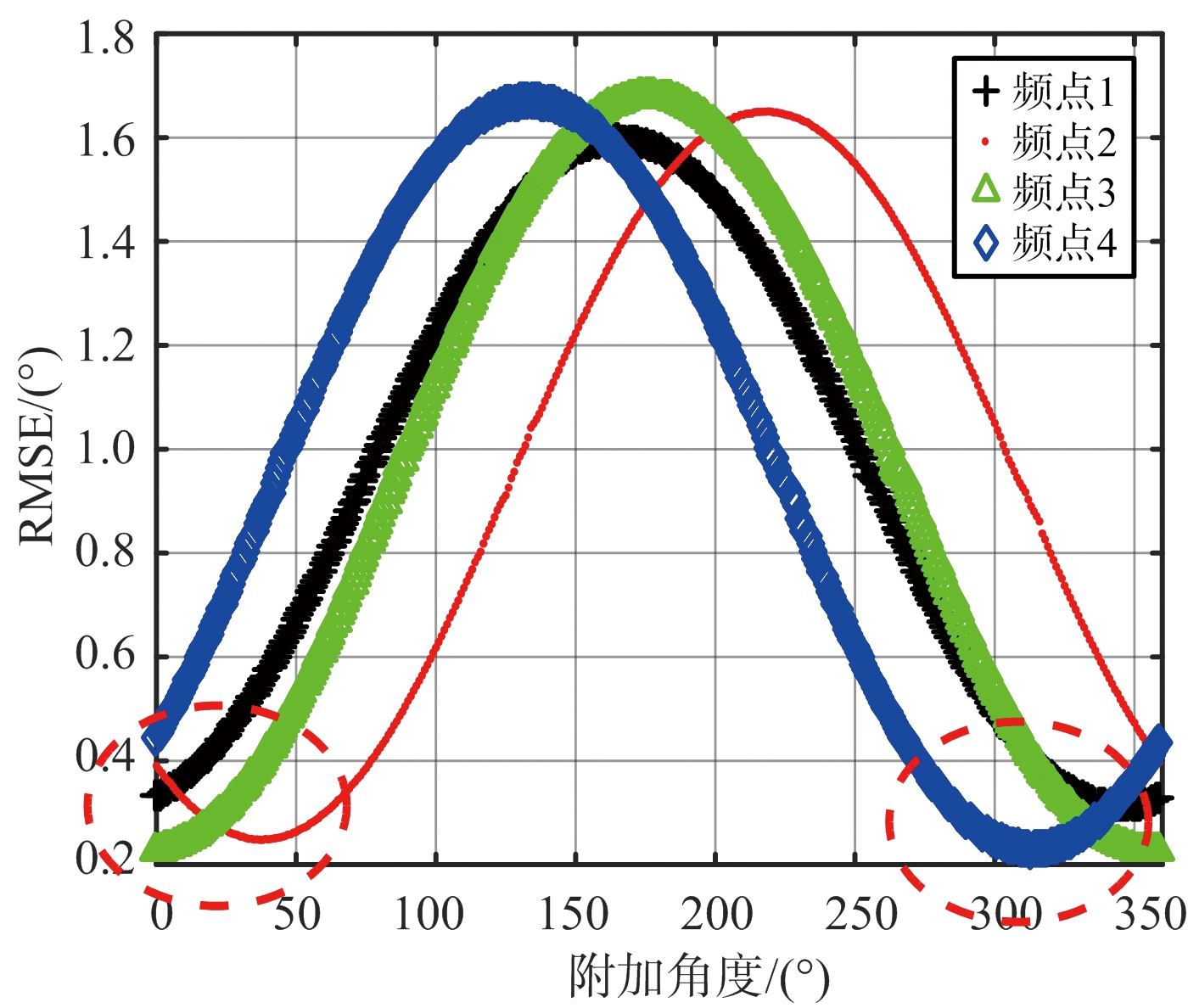
(b) 成像模式
图8 不同工作频率下的系统补偿角度-方位角估值RMSE结果
图9给出了探测模式下对图5所示浮标的角度估计实测结果,其中浮标相对于雷达方位角真值由高精度GPS测量得出(本例中为285°),共采集了256个相参积累周期的处理结果。蓝色点迹为进行系统补偿前的角度估计结果,可以看出此时方位角测量值出现最大2.8°的差异,且方位角测量结果的样本方差为0.9°;考虑到合作目标为短时间内几乎静止不动的浮标,该结果在实际应用中是难以接受的。红色点迹为经过系统补偿之后的角度估计结果,可以明显观察到方位角测量值的最大偏差仅为0.6°,点迹在方位维的聚集程度明显优于补偿之前的点迹,且统计结果表明此时样本方差为0.1°。上述实测数据处理结果充分证明系统补偿有助于显著改善方位角估计精度。
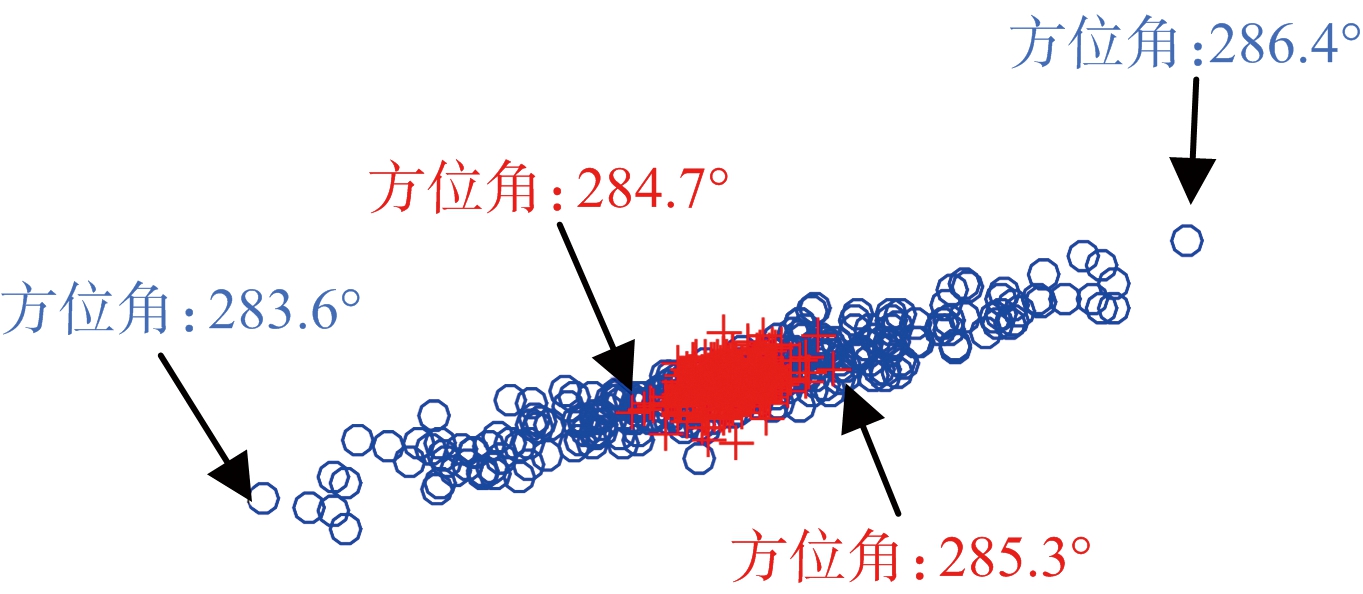
图9 探测模式下角度估计实测结果(蓝:补偿前;红:补偿后)
2) 成像模式
当雷达工作在成像模式时,对于威胁较大的机动目标如近海的舰艇,人们希望能够对其进行长时间观察与监视,通过连续成像来获得其不同运动姿态的ISAR像;对摆动较小的大型运动目标,人们希望能够延长相参积累时间从而提高多普勒分辨率。由于检测、成像分时工作的特点,如果在一次成像期间目标运动出天线照射范围或者目标有效回波移出采样窗口,则会导致目标信息丢失;此时需要对警戒区域再次进行扫描检测来实现对目标的重新捕获与跟踪,但考虑到目标运动的随机性,该过程通常需要耗费若干个天线扫描周期的时间,对于威胁目标来说这种长时间的等待是非常危险而且无法容忍的。因此,直接利用宽带信号对目标进行距离、方位连续跟踪从而实时调整距离采样窗口位置与天线指向,保证目标在成像期间始终处于“捕获”状态,可以避免常规ISAR的重检测过程,使得对机动威胁目标的连续成像得以实现,也有利于对一些低信噪比的目标进行长时间积累。
为保证对运动目标的连续成像,需要对目标进行距离、方位的实时跟踪[20],即通过估计目标的距离差、方位差来分别调整采样窗口的时延与天线波束中心指向,从而保证目标有效回波信号被采样且始终被天线捕获。其中,方位跟踪在本文提到的试验雷达系统中也采用与探测模式一致的和差比幅单脉冲测角技术。由于实际雷达系统波束宽度较窄,如果目标方位估计值出现较大偏差而导致调整后的天线波束中心偏离目标,则会导致目标丢失,无法实现目标连续ISAR成像。因此,在实际应用中必须对雷达进行系统补偿。
图8(b)给出了成像模式下的补偿角度-方位角估值RMSE曲线。从图中可以看出,系统补偿的最佳附加相移φc虽然在数值大小上与探测模式的情况不一致,但这是与系统工作频率、工作带宽等因素密切相关的,而且最佳附加相移在数值变化、最佳范围等因素上同样有规律可循,在实际雷达工作中同样可以选取其最佳补偿范围的公共区间来减小系统工作复杂度。考虑实际情况以及图8(b)的结论,本文的雷达系统在成像模式下的系统补偿附加相移为0°。
此次试验中,ISAR系统具备成像期间目标跟踪功能。此时,雷达可对合作目标进行实时连续的距离、方位跟踪,即使合作目标产生距离和方位上的位移,雷达系统依旧能够始终捕获目标瞬时位置并进行不间断的ISAR成像,而不需转回探测模式对目标进行二次检测。在本次外场试验中,雷达系统经过系统补偿后,实现了在成像模式下对运动船目标进行了连续而稳定的跟踪,同时对船目标进行不间断ISAR成像,如图10所示。图10中ISAR像A成像时间为当地时间11点55分,此时目标航向与天线波束指向的夹角为10°,近似为径向运动,成像结果应为船体的侧视像;随着目标船的继续运动,其航向与天线夹角逐渐增大至约45°,运动方式为切向运动与径向运动的混合情况,则成像结果应为船体的斜视投影像,如ISAR像B所示;在12点06分时,目标船航向与天线波束指向几乎垂直,近似为切向运动,此时的成像结果为目标的迎头像,如ISAR像C所示;随后,合作目标逐渐拐弯并远离雷达航行,其航向与天线波束指向不再垂直,此运动状态对应的成像结果应为船体的斜视投影像,这与12点23分的ISAR像D的情况吻合。

图10 合作目标的运动轨迹与ISAR像
试验结果表明,经过系统补偿后雷达系统成功对合作目标船连续捕获、ISAR成像约40 min,且实时处理的ISAR像结果与目标航向状态完全一致。
3.2 距离补偿
3.2.1 数据获取
1) 基准数据获取
选定合适的合作目标按照指定的线路运动,合作目标上放置高精度定位设备实时记录目标瞬时的经纬度、海拔高度作为目标真值。
2) 量测数据获取
在距离测量中,仅需要利用和通道的目标回波,因此为了充分地验证距离补偿方法的有效性,同时尽可能地在单位时间内获取更多的目标有效回波样本以达到较高的处理精度,试验中雷达天线工作于定向模式,在试验数据录取阶段始终照射目标,同时要求目标沿雷达视线径向匀速直线运动。本例中,合作目标为一艘冲锋舟,船身放置一套高精度差分GPS,其运动信息如图11所示,且在两个距离段中分别保持近似匀速直线运动。雷达接收系统与合作目标上放置的差分GPS精确对时,实时记录回波。
3.2.2 补偿方法
基于后验数据辅助的距离估计补偿方案原理框图如图12所示,具体可以分为以下3个步骤:
1) 选定合适的合作目标按照指定的线路运动,合作目标上放置高精度定位设备实时记录目标瞬时的经纬度、海拔高度作为目标真值,雷达工作于搜索探测模式,正常进行目标检测与距离估计。为了尽可能保证补偿系数的准确获得,通常要求目标沿雷达视线径向匀速直线运动。本例中,合作目标为一艘冲锋舟,船身放置一套高精度差分GPS,其运动信息如图11所示。其中,合作目标在试验期间基本上在同一个雷达波束中运动,且在两个距离段中分别保持近似匀速直线运动。

图11 合作目标运动状态
2) 读取雷达测得的目标距离估计值![]() 并与差分GPS记录的目标真值R作一次差。考虑到目标距离估计值由式(10)计算获得,因此由式(15) 给出的在不同距离上对应距离估计偏差可以近似表示为
并与差分GPS记录的目标真值R作一次差。考虑到目标距离估计值由式(10)计算获得,因此由式(15) 给出的在不同距离上对应距离估计偏差可以近似表示为
![]()
(17)
式中:k为距离估计偏差斜率,表征为单位距离上产生的距离估计偏差; δRsys为距离系统误差,与雷达系统自身硬件特性有关,在应用中通常可直接进行校准。图13给出了某次试验中计算获得的![]() 和相应的线性拟合结果。由图13可知,随着目标相对于雷达距离的增大,距离估计值相对于真值的偏差也逐渐增大,且增长速率可利用式(17)进行线性建模。
和相应的线性拟合结果。由图13可知,随着目标相对于雷达距离的增大,距离估计值相对于真值的偏差也逐渐增大,且增长速率可利用式(17)进行线性建模。
3) 通过线性拟合获得k和δRsys后,将这组系数记录在信号处理机中用于后续的目标距离估计。当需要进行目标距离估计时,可利用式(17)给出的数学关系对目标距离估计值进行补偿,即有
(18)
式中,![]() 为补偿后的目标距离估计值。
为补偿后的目标距离估计值。

图12 距离补偿原理框图

图13 目标距离一次差统计结果
为了进一步验证上述结论,笔者进行了多次外场试验进行深入分析与研究。图14分别给出了同一合作目标在相同外部条件下进行的两次独立试验,区别在于图14(a)对应尚未进行系统补偿的距离估计结果,图14(b)对应经过如式(18)给出的系统补偿的距离估计结果。由于两次独立试验中雷达记录的目标点迹数据难以严格按照距离一一对应,因此在图中仅用距离样本序号指代距离,且序号越大对应的目标距离越远。
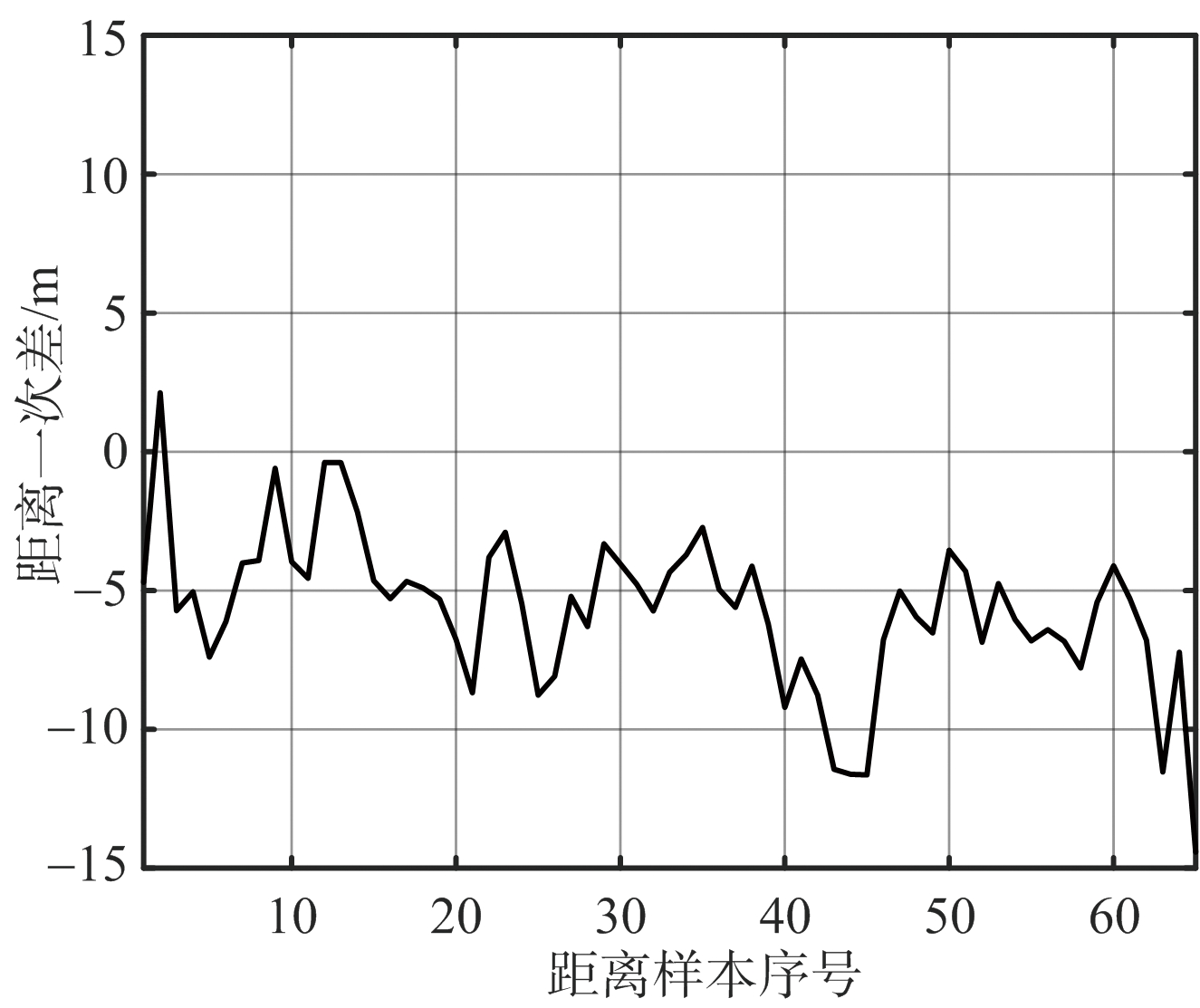
(a) 未进行系统补偿的试验结果
(系统误差5.69 m,标准差2.80 m)
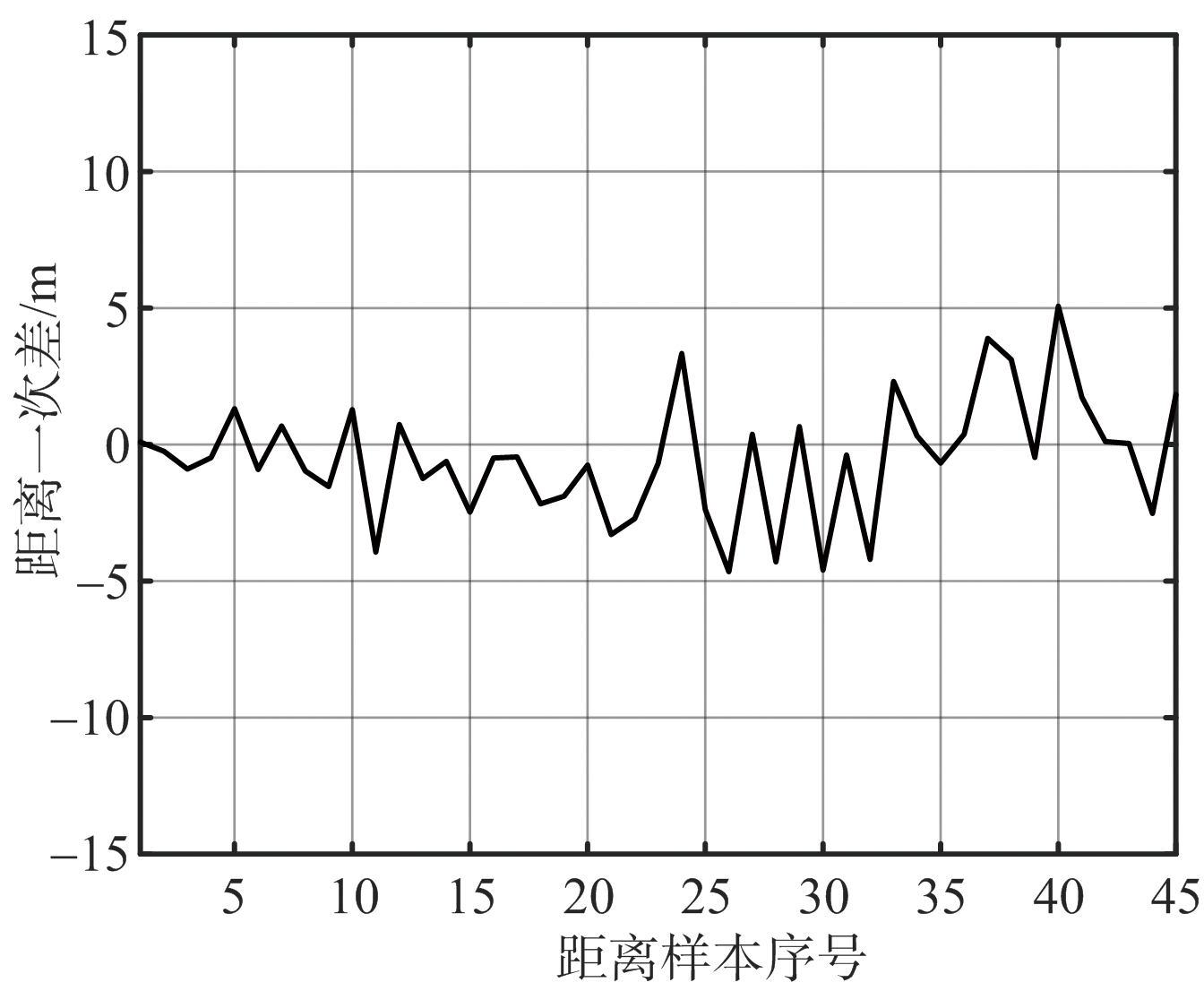
(b) 进行系统补偿的试验结果
(系统误差-0.50 m,标准差2.21 m)
图14 两次独立试验实测数据处理结果
由实测数据可知,未经过补偿的目标距离估计值相对于真值存在明显的系统误差,且估计偏差大小随着距离的增大而增大,具有明显的线性关系;这与前文的理论分析一致。补偿后的目标距离估计值的系统误差得到极大改善,由补偿前的5.69 m降低为0.50 m,且由标准差结果可知相比于未补偿的情况具有更优的估值精度。
4 结束语
本文基于ACAC比幅法测距与和差比幅单脉冲测角技术,建立了相应的参数估计数学模型,理论分析了影响测距、测角精度的各类因素,结合某实际雷达系统设计并提出了一套基于后验数据辅助的系统补偿方法,实测数据处理结果以及外场试验验证了本文方法的有效性。
本文提出的PDAid系统补偿框架仅通过雷达采集的测量数据和目标真值进行分析与处理,方案简便易行,可用于岸基、舰载的海面预警雷达和成像雷达,具有较强的普适性。相关的处理思路、流程与方案对实际雷达系统的设计与研制具有一定指导意义。
[1] ZHOU W, XIE J H, LI G P, et al. High-Precision Estimation of Target Range, Radial Velocity, and Azimuth in Mechanical Scanning LFMCW Radar [J]. IET Radar Sonar & Navigation,2017,11(11):1664-1672.
[2] ZHOU W, XIE J H, ZHANG B Q, et al. Maximum Likelihood Detector in Gamma-Distributed Sea Clutter [J]. IEEE Geoscience and Remote Sensing Letters,2018,15(11):1705-1709.
[3] ZHOU W, XIE J H, LI G P, et al. Robust CFAR Detector with Weighted Amplitude Iteration in Nonhomogeneous Sea Clutter [J]. IEEE Trans on Aerospace and Electronic Systems,2017,53(3):1520-1535.
[4] ZHOU W, XIE J H, XI K, et al. Modified Cell Averaging CFAR Detector Based on Grubbs Criterion in Non-Homogeneous Background [J]. IET Radar Sonar & Navigation,2019,13(1):104-112.
[5] ZHOU W, XIE J H, YUAN Y S, et al. Angle Mea-surement Accuracy Analysis of Sum-Difference Amplitude-Comparison Monopulse in Onshore or Shipborne ISAR [C]∥International Conference on Digital Signal Processing, Hong Kong, China: IEEE,2014:531-535.
[6] WANG W, PENG Y N. An Interpolation Algorithm to Improve Range Estimation for the Linear Frequency Modulated Radar [J]. IEEE Aerospace and Electronic Systems Magazine,1999,14(7):45-47.
[7] 谢俊好. 舰载高频地波雷达目标检测与估值研究 [D]. 哈尔滨:哈尔滨工业大学,2001.
[8] 鞠荣华, 纪永刚, 黎明,等. 高频地波雷达船只目标距离参数估计与评价[J]. 中国海洋大学学报,2019,49(1):128-133.
[9] 石阳升, 文必洋, 杨静,等. 基于旁瓣信息的高频地波雷达高精度测距方法[J]. 中北大学学报(自然科学版),2015,36(2):219-224.
[10] 陈祝明, 丁义元, 向敬成. 提高线性调频连续波雷达测距精度的最大值估值算法[J]. 系统工程与电子技术, 1999, 21(6):39-42.
[11] 耿籍. 扩展比值插值算法的雷达测距、测速精度分析[J]. 现代防御技术,2010,38(5):107-109.
[12] BARTON D K. Radar Technology Encyclopedia [M]. USA:Artech House,1998.
[13] 谢俊好, 熊卫明. 传统单脉冲方法的数学原理及工程实现 [J].系统工程与电子技术,2004,26(4):467-473.
[14] 刘养林, 董胜波, 梅光宗,等. 毫米波单脉冲测角中幅相不一致的影响及补偿[J]. 宇航计测技术,2011,31(1):1-6.
[15] 张梅仓, 姬长华. 相位补偿技术在和差单脉冲雷达中的应用[J]. 现代雷达,2016,38(5):29-32.
[16] 郑建荣. 单脉冲雷达测角幅相不一致影响及校正[J]. 现代电子技术,2012,35(9):1-3.
[17] 周围, 席堃, 杜玉晗,等. 基于后验数据的单脉冲雷达系统补偿方法[C]∥第十四届全国雷达学术年会论文集, 成都:中国电子学会,2017:1-5.
[18] 吴顺君, 梅晓春. 雷达信号处理和数据处理技术[M]. 北京:电子工业出版社,2008.
[19] 梁士龙, 郝祖全. 单脉冲雷达的一种角误差提取方法[J]. 系统工程与电子技术,2003,25(1):18-20.
[20] XIE J H, ZHOU W, ZHOU G J, et al. Tracking of Range and Azimuth for Continuous Imaging of Marine Target in Monopulse ISAR with Wideband Echoes [J]. International Journal of Antennas and Propagation,2016(1):1-17.





