0 引 言
低副瓣是阵列天线的一项重要指标。在复杂电磁干扰环境下,降低阵列天线的副瓣可以提高雷达系统的抗杂波干扰和生存能力[1-3]。阵列天线的方向图副瓣电平受天线单元幅度、相位和位置影响。降低天线副瓣的方法有:幅度加权、相位加权[4]和密度加权[5]。唯相位加权法工程实现简单,但实现极低副瓣较为困难,密度加权相比幅度加权可以减少能量损失,但同时也增加了工程实现的复杂度,且部分单元失效对方向图性能影响较大。在高集成度相控阵雷达系统中,综合考虑方向图性能和系统复杂度,一般采用幅度加权法。
经典的幅度加权法有切比雪夫综合法[6]、泰勒综合法[7]等。其中,泰勒分布有更好的口径效率得到广泛的应用。然而,阵面经过切角处理后,泰勒综合法得到的方向图难以达到预期效果。为了在不降低天线增益的前提下,得到更低副瓣的远场方向图,本文对切角阵天线单元进行计分排序,选取部分单元作为优化变量,使用遗传算法通过约束天线增益对幅度加权分布进行优化。在实际工程中,幅度加权分布还受到T/R组件的幅相精度及量化误差等影响[8],因此,对切角阵面进行暗室实测,验证遗传算法优化幅度加权分布的实用性。通过仿真与实测对比,遗传算法优化得到的幅度加权分布,与泰勒综合法相比,方向图副瓣电平优化3 dB。
1 阵列天线原理
假定直角坐标系XOY平面上,M×N个方向图相同的辐射单元组成矩形阵列,如图1所示。阵列方向图可以表示为
F(u,v)=EP(u,v)·AF(u,v)
(1)
式中,EP(u,v)为单元方向图函数,AF(u,v)为阵列因子,为M×N个阵元的空间响应,表达式为
AF(u,v)=![]()
(2)
式中,u=sinθcosφ,v=sinθsinφ,λ为阵列天线工作波长,dx和dy表示x、y方向上阵元间距,A(m,n)为天线单元的电压激励,且有
A(m,n)=a(m,n)exp[-jφ(m,n)]
(3)
式中,a(m,n)为单元激励幅度值,φ(m,n)为阵面扫描时的补偿相位。

图1 平面阵列天线示意图

图2 切角阵面示意图
由式(2)可知,阵列天线方向图受单元激励幅度的影响,因此单元幅度加权是阵列天线实现低副瓣的重要手段之一,泰勒加权兼顾方向图副瓣电平和波束宽度,且天线有较好的口径效率,得到广泛应用。在高集成度的相控阵雷达系统中,天线阵面尺寸受限,通常对矩形阵列进行切角处理,阵面示意图如图 2所示。由于切角的存在,泰勒幅度加权得到的远场方向图难以达到预期效果。因此,本文采用遗传算法优化得到新的幅度加权分布,在特定增益约束下,优化阵列天线的峰值副瓣。
天线法向方向性系数表达式为
(4)
式中,Ap为天线阵面的电讯有效物理面积,εA为孔径效率,阵列天线中常用锥削效率εT等效[8]。
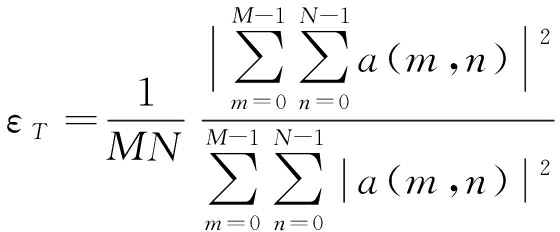
(5)
由式(5)可知,约束锥削效率优化幅度加权分布,可以在满足天线增益指标的前提下优化阵列天线副瓣电平。
2 遗传算法副瓣优化
切角阵副瓣电平优化目标函数由式(6)给出。
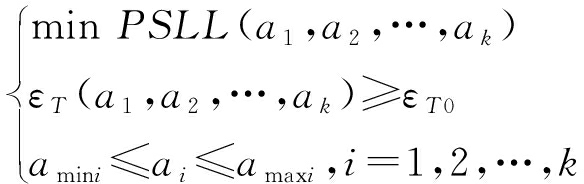
(6)
式中,PSLL(a1,a2,…,ak)为阵列天线方向图的峰值副瓣电平函数,k=(MN-Q)/4,Q为全阵面切角单元个数,εT0表示锥削效率指标,amini的值为T/R组件的最大衰减值,amaxi取1。
对于大规模天线阵面来说,过多的幅度变量导致计算缓慢且优化效果不明显,因此减少优化变量数目显得尤为重要。一般而言,幅度加权由阵面中心单元向边缘单元按照从大到小对称分布,因此,本文对四分之一阵面每个单元进行计分并按照从大到小排列为一维向量,其中计分公式如式(7)。
(7)
(8)
(9)
式中,Lmn表示第(m,n)个单元到中心单元的距离,xmn、ymn为第(m,n)个单元的横纵坐标,Dmn表示第(m,n)个单元到边缘单元的最小距离,xei、yei为边缘单元的横纵坐标,图3为天线单元计分方法示意图。

图3 天线单元计分示意图
阵面单元经过计分排序后,得到排序矩阵P和排序后的单元分布向量b,阵面分布amp可以表示为
amp=bP-1
(10)
为了减少优化变量,选取b中部分元素作为优化变量进行优化,挑选的天线单元幅度组成新的向量记为as,在优化过程中,b可由as插值得到。
遗传算法[10]是一种模拟自然界物种基因遗传变异的全局优化算法,适用于复杂模型最优化求解问题,被广泛应用在社会经济、工程设计等领域。遗传算法由遗传编码、适应度函数、选择算子、交叉算子、变异算子等部分构成。本文的适应度函数即为阵列天线峰值副瓣电平PSLL(a1,a2,…,ak),遗传算法优化步骤如下:
1) 初始化种群,确定优化变量as元素个数和初始种群个体数目Num;
2) 设置T/R组件最大衰减值amin,设定最小锥削效率值εT0,峰值副瓣电平优化目标值PSLL0;
3) 由优化变量as插值得到b向量,根据式(10)得到阵面的幅度分布,并对幅度进行约束,计算种群中Num个个体的适应度值,即远场方向图峰值副瓣电平PSLL(a1,a2,…,ak),计算锥削效率εT并进行约束;
4) 对种群中的个体执行交叉、变异操作,得到新个体,选择一定数量个体组成新种群;
5) 判断种群中最优个体是否满足峰值副瓣优化目标PSLL0以及锥削效率约束条件,若满足,则输出种群最优个体,若不满足返回第3)步继续执行。
3 仿真与实测
本文选用四角切角的均匀矩形栅格阵列,为了满足小于-30 dB的峰值副瓣电平指标,对阵列幅度进行-35 dB的泰勒加权,并将泰勒加权幅度分布作为初始个体加入到遗传算法初始种群中。方向图仿真结果如图4、图5所示。
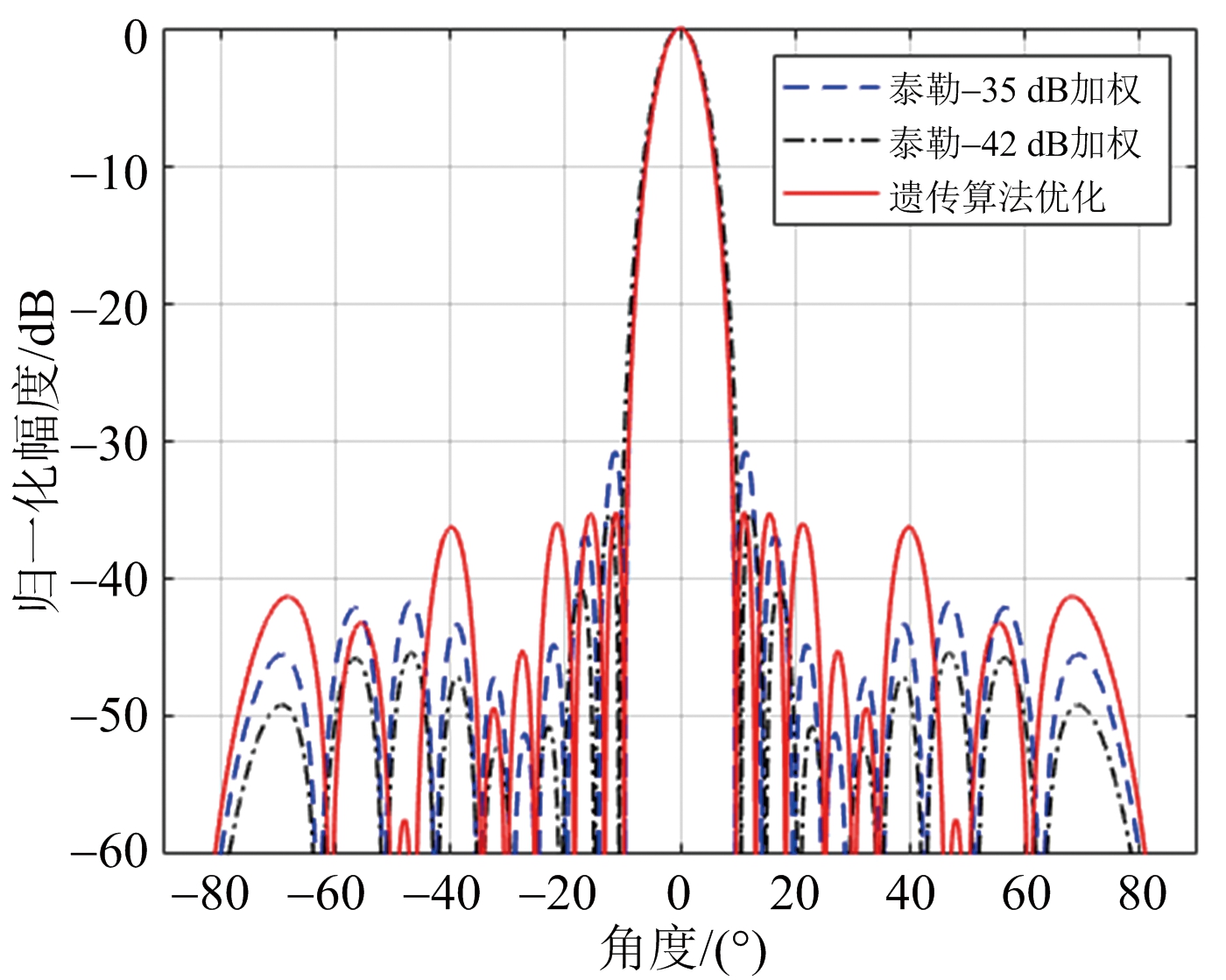
图4 理论仿真水平切面方向图

图5 理论仿真垂直切面方向图
从理论仿真来看,-35 dB的泰勒加权与遗传算法优化加权得到的方向图具有相同的方向系数,但遗传算法获得的峰值副瓣电平降低了4.4 dB。-42 dB的泰勒加权可实现与遗传算法优化加权同样的峰值副瓣电平抑制效果,但其方向图主瓣与遗传算法相比有略微展宽,方向性系数下降约0.5 dB。
为了验证遗传算法对天线阵列峰值副瓣电平优化的实际效果,对切角阵列进行-35 dB泰勒幅度加权和遗传算法优化幅度加权,在微波暗室采用近场测量方法,得到实测远场方向图,结果如图6、图7所示。

图6 暗室实测水平切面方向图

图7 暗室实测垂直切面方向图
由于阵列单元存在幅相误差,实际测出的方向图的指标与仿真相比发生恶化。两种幅度加权方式得到的方向图主瓣宽度大致相同,泰勒幅度加权得到的远场方向图水平切面峰值副瓣为-29.7 dB,已不满足指标要求,而遗传算法优化的幅度分布方向图仍然具有很好的低副瓣性能。两种幅度加权方式得到的方向图指标如表 1所示。
表1 两种幅度加权方向图指标对比

加权方式水平切面PSLL/dB垂直切面PSLL/dB方向性系数/dBi泰勒-35dB(仿真)-30.7-33.728.05泰勒-42dB(仿真)-35.2-39.227.52遗传算法(仿真)-35.1-35.428.06泰勒-35dB(实测)-29.7-31.127.95遗传算法(实测)-33.8-32.727.97
遗传算法优化得到的幅度加权分布与泰勒幅度加权分布相比,在阵列天线增益相同的情况下,方向图的峰值副瓣更低,实际测量优化了3 dB。
4 结束语
幅度加权是降低阵列天线副瓣的重要手段之一,本文针对切角阵面的幅度分布特点,对天线单元计分并挑选合适的单元幅度作为优化变量,达到减少优化变量数目的效果,采用遗传算法对切角阵面幅度分布进行优化。实测的结果表明,与传统泰勒幅度加权相比,在增益相同的情况下,峰值副瓣电平得到了3 dB优化。
[1] MANIKANDAN R, JAWAHAR P K,RAO P H. Low Sidelobe Level CSRR Loaded Weighted Array Antenna[J]. IEEE Trans on Antennas and Propagations,2018,66(12):6893-6905.
[2] 赵嘉伟. 波导缝隙阵列天线快速建模和低副瓣设计[D]. 西安:西安电子科技大学,2019.
[3] SACCO G,ATANASIO P D,PISA S. A Wideband and Low-Sidelobe Series-Fed Patch Array at 5.8 GHz for Radar Applications[J]. IEEE Antennas and Wireless Propagation Letters,2020,19(1):9-13.
[4] 丛友记,卞美琴,简玲. 一种唯相位加权降低天线副瓣技术研究[J].雷达与对抗,2015,35(2):45-48.
[5] 刘畅,郭陈江,杜建春,等.多阶密度加权实现低副瓣相控阵[J].科学技术与工程,2011,11(8):1713-1716.
[6] 卢晓鹏,赵怀成,赖清华. 一种X波段宽带低副瓣微带阵列天线设计[J].雷达科学与技术,2013,11(2):219-222.
LU Xiaopeng, ZHAO Huaicheng, LAI Qinghua.Design of an X-Band Microstrip Array with Wideband and Low Sidelobe[J].Radar Science and Technology,2013,11(2):219-222.(in Chinese)
[7] ZHAO Jiafei,ZOU Le,JIANG Rongkun,et al. Hybrid Antenna Arrays with High Angular Resolution for 77 GHz Automotive Radars[J]. IEICE Electronics Express,2019,17(2):1-6.
[8] 陆小凯,张磊,吴俭.一种改善相控阵雷达收发通道幅相误差的校准方法[J].舰船电子对抗,2020,43(3):22-25.
[9] KEIZER W P M N. Synthesis of Scan and Frequency Invariant Low Sidelobe Tapers for Planar Array Antennas[J].IEEE Trans on Antennas and Propagation, 2016,64(8):3703-3707.
[10] GUO Qiang, WANG Yani, YUAN Ding, et al. Optimization of Sparse Concentric Ring Arrays Based on Multiple Constraints[J]. IEEE Antennas and Wireless Propagation Letters,2020,19(5):781-785.
